I. 서 론
수면무호흡(OSA, obstructive sleep apnea)은 최근 전세계에서 약 4 % 남성들 및 2 % 여성들에게 나타나는 대표적인 질환이다[1]. 여기서, OSA는 수면 중 상부 기도가 막혀 10초 이상 호흡이 멈추는 현상[2]을 의미하며, OSA 진단은 수면다윈검사(polysomography)를 통해 가능하지만 불편한 접촉식 검사 과정에서 많은 환자들이 불편함을 호소하고 있다[3]. 따라서, 수면 과정에서 비접촉식 산소포화도(SO2, oxygen saturation) 모니터링을 통한 OSA 진단 방법이 필요하다.
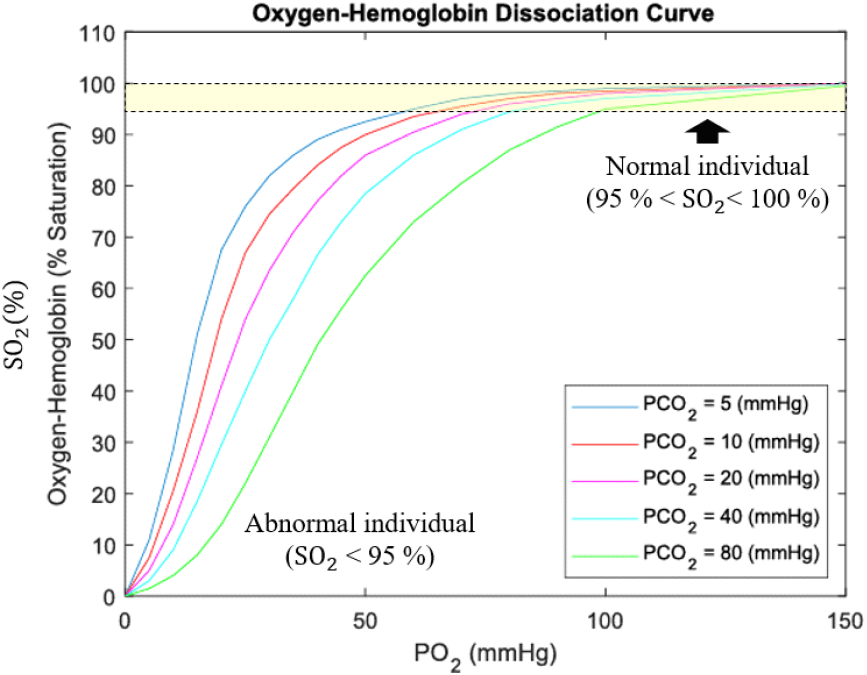
최근 비접촉식 산소포화도 센싱을 위하여 광학센서와 레이다센서가 적극 활용되고 있다[4]~[10]. 먼저, 광학센서의 경우 사람의 코와 입 주변 관심 영역(region of interest)에 대한 카메라 영상 픽셀 변화 패턴을 분석하는 광혈류측정법(PPG, photoplethysmography)을 사용하나 치명적인 초상권 침해 문제가 존재한다[4],[5]. 반면에 최근 구강을 통한 공기 호흡과 생체 신호에 의한 상체 움직임에 따라 SO2가 연관성이 있음을 실험을 통해 검증하였으며, 이는 레이다 센서를 통해 사람의 생체 신호(e.g., 호흡수, 심박수) 및 이 신호에 따른 1차원 상체 움직임 변화 궤적을 추출 할 경우 SO2의 추정이 가능함을 보여준다[6]. 의학적 측면에서 그림 1과 같이 세로축 값인 SO2는 산소-헤모글로빈 분열 커브(ODC, oxygen-hemoglobin dissociation curve)에서 이산화탄소 분압(PCO2) 및 산소 분압(PO2)에 따라 변화함을 알 수 있다[7],[8]. 그리고 최근 연구에서는 사람의 생체 정보(i.e., 호흡수, 심박수, 생체 신호에 의한 1차원 상체 움직임 변화 궤적, 키, 몸무게)에 따라 비선형적 알고리즘 모델로 PCO2와 PO2의 추정이 가능함을 증명하였다[9],[10]. 최종적으로 레이다센서로 호흡수, 심박수, 생체 신호에 의한 1차원 상체 움직임 변화 궤적만 추정 가능할 경우, 이 정보들을 통해 PCO2와 PO2를 단계별로 추정하고, 이어서 그림 1과 같은 2차 전달 함수 모델을 활용하여 SO2의 추정이 가능하다[6]~[10]. 하지만, 기존 방식[9],[10]의 경우 선형주파수변조신호를 활용하여 거리 축에서 나타나는 생체 신호에 의한 1차원 상체 움직임 변화 궤적을 추정하고, 불필요한 사람의 움직임에 대한 영향을 신경망 구조로 억제하였다. 이러한 구조는 레이다 하드웨어 비용 및 알고리즘의 복잡성을 증대시키기 때문에, OSA 진단을 위한 상용 의료기기로 활용되기 위해서는 보다 간단한 구조의 비접촉식 레이다 시스템에 계산량이 상대적으로 적은 알고리즘이 탑재되어야 한다.
본 논문에서는 비접촉식 레이다를 활용한 효율적인 사람의 SO2 추정 알고리즘을 제안한다. 먼저, 레이다를 활용하여 사람 표적의 복소 수신 신호를 획득한 후, 탄젠트 역함수[11],[12]를 활용하여 1차원 위상 변화 궤적을 추출한다. 그리고 1차원 위상 변화 궤적에는 주변 클러터 및 원하지 않는 사람의 움직임이 포함되어 있기 때문에, 1차 이동 평균 필터[11] 및 2차 버터워스 대역 통과 필터를 통해 생체 신호만 나타는 1차원 위상 변화 궤적으로 전처리한다. 이후, 이 궤적에 스케일링을 적용하여 1차원 상체 움직임 변화 궤적으로 바꾸고, 동시에 1차원 상체 움직임 변화 궤적의 주파수 스펙트럼 분석[11]을 통해 호흡수와 심박수를 추정한다. 다음으로 추정된 호흡수, 심박수, 1차원 상체 움직임 변화 궤적 및 사람의 키, 몸무게를 입력으로 사용하여 기존 기법[9],[10]의 알고리즘에 따라 단계별로 폐내압력(PI(t), pulmonary ventilation), 호흡량(Vt(t), tidal volume)을 계산하고, 버터워스 필터링 및 극대점(local maximum value)을 활용하여 분당 환기량을 추정한다. 마지막으로 앞서 추정된 값들 및 사람 생체 정보를 활용하여 PCO2와 PO2를 예측하고, 이를 그림 1과 같은 2차 전달 함수 모델의 입력 변수로 사용하여 SO2를 출력 변수로 계산한다.
본 논문에서는 제안된 기법의 성능을 검증하기 위하여 시뮬레이션 분석 및 레이다 측정 실험을 수행하였으며, 그 결과 제안된 기법으로 사람의 SO2 추정이 가능함을 검증하였다.
II. 사람 생체 정보와 SO2 간의 관계
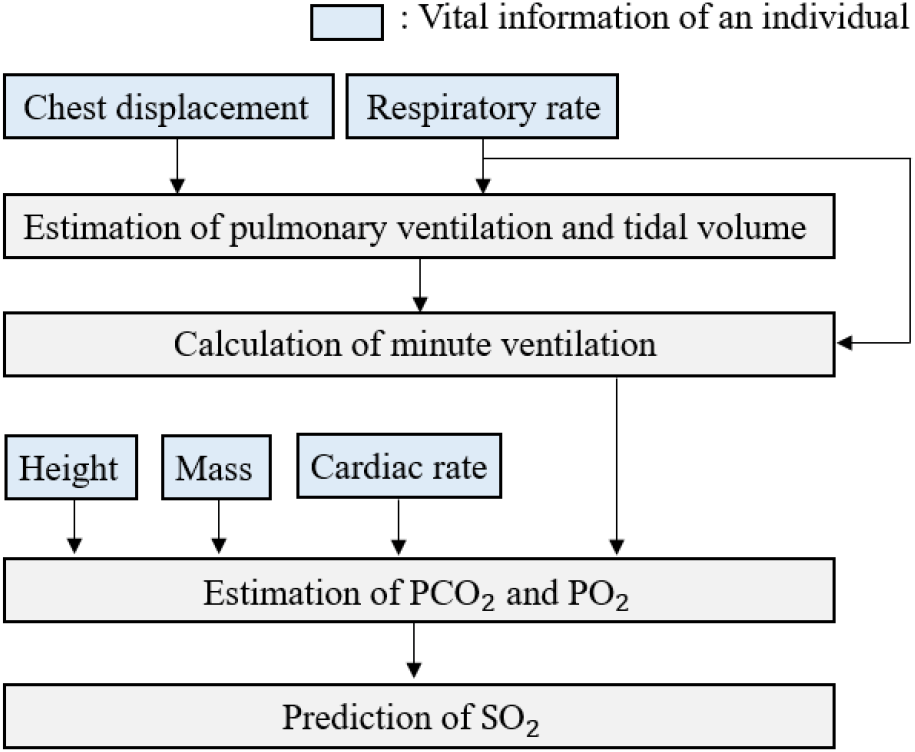
SO2를 추정하기 위해 활용되는 사람 생체 정보(vital information)는 키(H, height), 몸무게(M, mass), 호흡수(fRR, respiratory rate), 심박수(fCR, cardiac rate) 및 1차원 상체 움직임 변화 궤적(dc(t), chest displacement)과 같다. 여기서, 호흡수, 심박수 및 1차원 상체 움직임 변화 궤적은 레이다 센서로 추정 가능하다[11],[12]. 그리고 추정된 사람 생체 정보를 활용한 PCO2 및 PO2와 SO2의 전반적인 추정 과정은 그림 2와 같다[9]. 본 절의 2-1에서는 사람 생체 정보와 PCO2 및 PO2 간의 비선형적 관계[10]를 간략히 설명한다. 다음으로 2-2에서는 PCO2 및 PO2와 SO2 간의 관계를 보여주는 2차 전달 함수 모델[9]과 기존 기법 문제점[9],[10]을 간략히 서술한다.
키 H m 및 몸무게 M kg인 사람의 1차원 상체 움직임 변화 궤적 dc(t) m와 호흡수 fRR Hz를 성공적으로 추정했다고 가정할 경우, 폐내압력 PI(t) Pas−1과 dc(t) 간의 관계는 식 (1)과 같은 미분방정식[10]으로 정의된다.
여기서 g는 중력가속도 m/s2, BMI는 체질량지수(BMI, body mass index= M/H2)이며, 정상적인 성인의 경우 BMI는 평균적으로 약 28이다. 이때, PI(t)는 dc(t)와 반비례 관계를 가진다(그림 3). 다음으로 추정된 PI(t)를 활용하여 사람의 호흡량 Vt(t)을 식 (2)와 같이 추정한다.
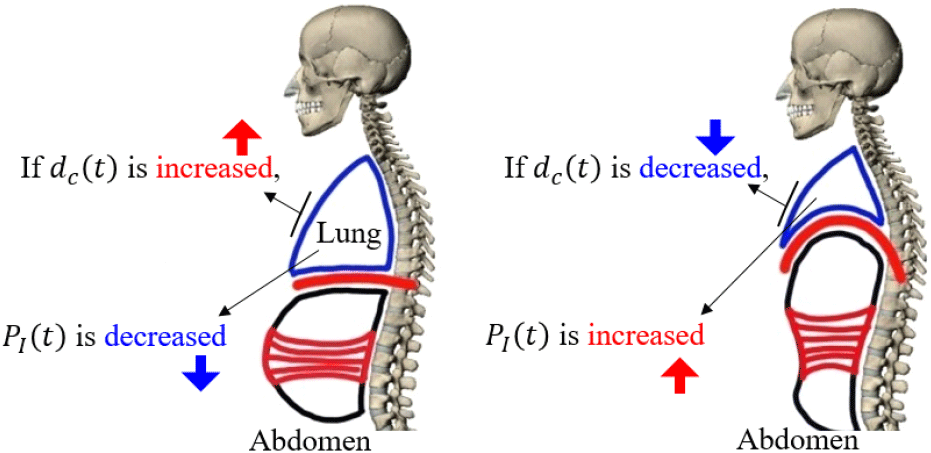
여기서 VTLC는 총호흡량이며 정상적인 성인의 경우 평균 4,200 mL를 가진다. 그리고 Wt는 실제 사람 키 H m에 대한 이상적인 몸무게(Wt = (H/33.34)1/0.3922 kg)이다.
다음으로 Vt(t)의 평균 호흡량 E{Vt(t)}을 추정해야하며, 정상적인 성인의 경우 평균 호흡량은 대략 400 mL< E{Vt(t)}<500 mL와 같다. 이를 위하여 기존 기법[10]은 경계값을 정의하여 식 (3)의 호흡량을로 재구성한다.
여기서 기존 기법[10]은의 극값(local extrema)을 추정하여 한 주기 내 극대값 및 극소값의 차이들의 평균값을 평균호흡량으로 추정한다(그림 4).
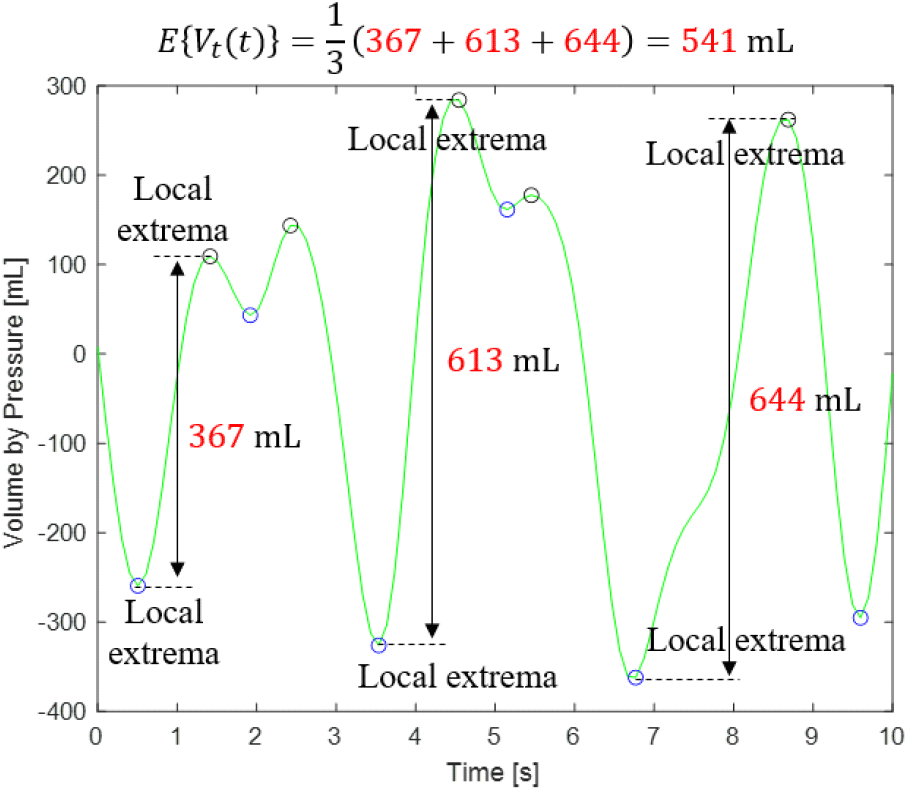
다음으로 추정된 평균호흡량에 호흡수 fRR를 곱할 경우 분당 환기량 VE(t) L을 식 (4)와 같이 추정할 수 있다.
이때, PCO2는 식 (4)와 심박수 fCR, 키 H, 몸무게 M를 활용하여 식 (5)와 같이 정의된다.
여기서 RQ는 호흡지수(respiratory quotient)[10]이며, 탄수화물, 지방, 및 단백질의 경우 RQ=1, 0.7, 및 0.8과 같다.
PO2는 식 (5)와 공기 내 산소량 FiO2(보통 지구상에서는 0.21), 대기압 Patm(해수면 기준 760 mmHg), 폐포내 증기압(보통 47 mmHg)을 활용하여 식 (6)과 같이 정의된다.
SO2는 앞서 2-1절에서 추정된 PCO2 및 PO2를 입력변수로 하는 그림 1의 2차 전달 함수 모델[9]에 대한 라플라스 역변환을 통해 식 (7)와 같이 추정될 수 있다.
여기서
이다(식 (8), 식 (9), 및 (10)에 사용되는 서브 함수는 기존 논문[9],[10]을 참조).
식 (7)로 추정되는 SO2는 수신된 복소 수신 신호에서 추출되는 1차원 상체 움직임 변화 궤적 dc(t) 내 열잡음 및 원하지 않는 사람의 움직임에 따라 매우 민감하게 변화한다. 이러한 문제점을 분석하기 위하여 연속파로 수신된 레이다 신호를 사람의 1차원 상체 움직임 변화 궤적 dc(t)을 사용하여 식 (11)과 같이 정의할 수 있다.
여기서 Pr는 수신전력, λ는 파장, u(t)는 원하지 않는 사람의 움직임, n(t)는 열잡음 신호이며, E{|n(t)|2}를 열잡음의 앙상블평균전력이라 정의할 경우 신호 대 잡음비(SNR, signal-to-noise ratio)은 식 (12)와 같이 정의된다.
이때, 불필요한 움직임이 없는(i.e., u(t)=0) 사람에 대한 60 초의 측정 시간 동안, 표 1의 변수들을 사용하고, SNR =10 dB 및 −20 dB에서 100번의 몬테 카를로 시뮬레이션으로 SO2를 추정하였을 때, 참값(ground truth)을 기준으로 SNR=10 dB에서는 평균 제곱근 오차(RMSE, root mean squared error)가 4.22로 나타났으나, SNR=20 dB에서는 RMSE=38.71로 나타났다. 이러한 이유는 열잡음에 의해 dc(t)가 민감하게 왜곡되기 때문이다. 따라서, 사람의 불필요한 움직임 및 열잡음 영향 속에서 선형주파수변조신호를 활용하는 기존 기법[9],[10]과 달리 보다 간단한 레이다 구조의 연속파 신호를 활용하면서 보다 안정적으로 dc(t)를 추정하기 위한 방안이 필요하다.
| λ [m] | 0.0517 | fRR [Hz] | 0.25 |
| M [kg] | 70 | fCR [Hz] | 1.33 |
| H [m] | 1.70 | g [m/s2] | 9.80665 |
| Wt [kg] | 63.6626 | BMI | 24.2215 |
| VTLC [mL] | 4,369.9 | Vth [mL] | 578.0505 |
| RQ | 0.95 | FiO2 | 0.2095 |
| Patm [mmHg] | 760 | [mmHg] | 47 |
III. 제안된 기법
본 절에서는 SO2의 보다 안정적이고 효율적인 추정을 위하여 기존 기법[9],[10]과 달리 도플러 레이다 수신 신호의 1차원 위상 변화 궤적를 활용하고, 원하지 않는 사람의 움직임 및 열잡음에 대한 영향을 줄이기 위한 전처리 방법을 제안한다.
먼저, 식 (11)의 복소 수신 신호 대한 탄젠트 역함수[11],[12]를 식 (13)과 같이 적용하여 1차원 위상 변화 궤적을 추출한다.
여기서 real{·}및 imag{·}는 각각 실수부 및 허수부 추출 함수이고, nθ(t)는 열잡음 신호의 위상 성분이다. 이때, 원하지 않는 사람의 움직임 u(t)는 사람이 매우 급격하게 움직이지 않는다면 dc(t) 보다 상대적으로 저주파 위상 변화 궤적을 가진다(그림 5(a))[11],[12]. 따라서 Nwin개의 위상 변화 샘플들에 대한 재귀(recursion) 방식의 이동 평균 필터(i.e., 저역통과필터)[11]가 아래와 같이 이상적으로 적용될 경우, 원하지 않는 사람의 움직임에 대한 위상 변화 궤적 θM(t)을 추정할 수 있다.
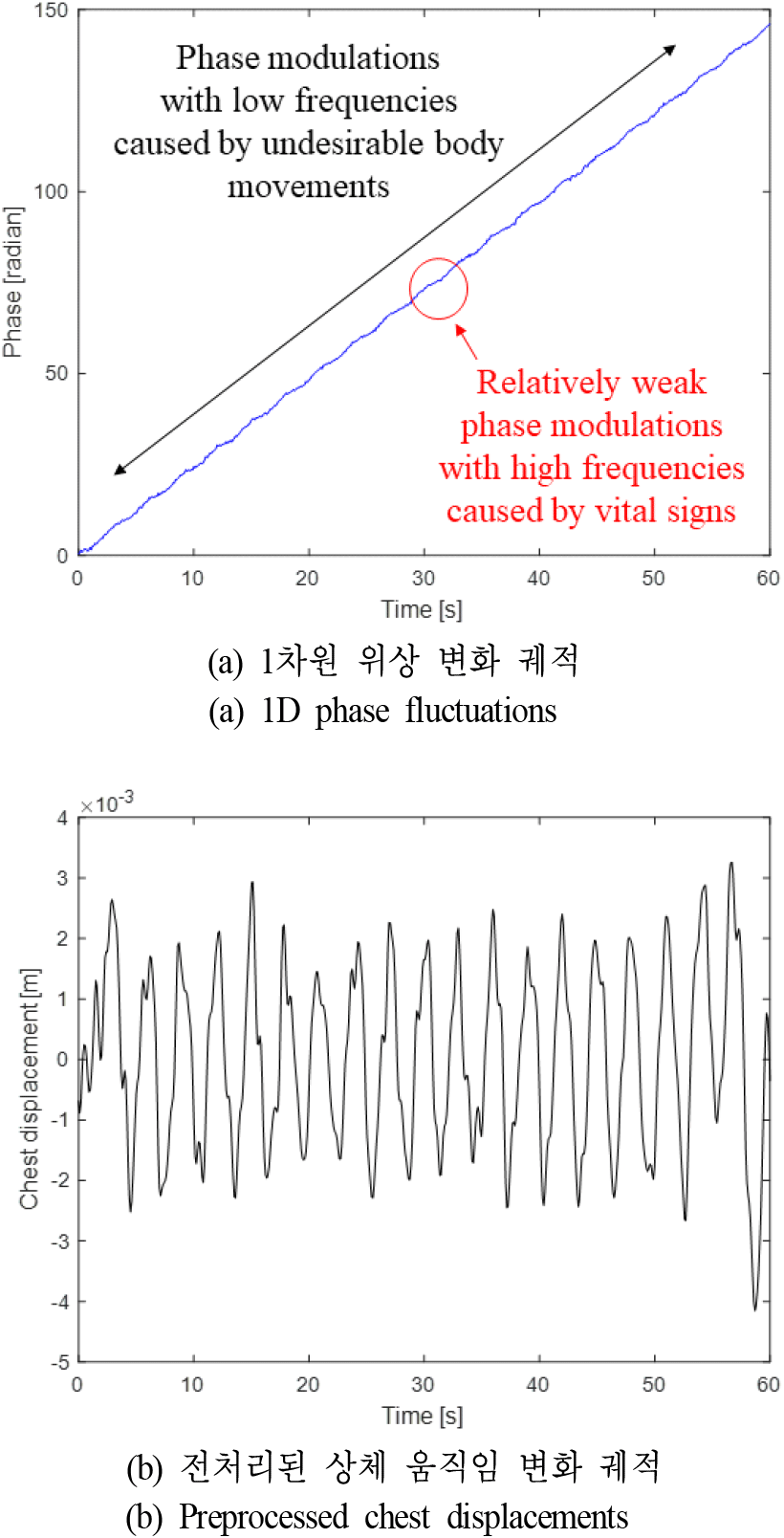
식 (14)를 활용하여 1차원 위상 변화 궤적 θ(t)내에 원하지 않는 사람의 움직임 u(t)에 대한 영향을 아래와 같이 완화시킬 수 있다.
하지만 식 (15)에는 여전히 고주파 열잡음 위상 성분 nθ(t)에 대한 영향이 있으며, 기존 SO2 추정 과정[9],[10]에서 식 (1)의 미분방정식(i.e., 고역통과필터)을 활용함에 따라 추정되는 폐내압력 PI(t)가 nθ(t)에 매우 민감하게 반응하게 된다. 따라서, 제안된 기법은 식 (15)에서 가장 공진이 크게 나타나는 호흡수 fRR와 두 번째 공진주파수인 심박수 fCR를 식 (15)에 대한 주파수 스펙트럼 분석을 통해 추정한 후, 차단 주파수 Ωc를 호흡수 fRR와 심박수 fCR로 사용한 버터워스(Butterworth) 대역통과필터링을 식 (15)에 적용하여 최대한 생체 신호와 관련된 위상 변화 궤적만 아래와 같이 추출한다.
여기서는 버터워스 대역통과필터 함수이고, 라플라스 영역에서 다음과 같은 2차 전달 함수로 구성된다.
식 (16)에 대한 스케일링을 수행할 경우, 1차원 위상 변화 성분 θ(t)에서 열잡음과 원하지 않는 사람의 움직임 영향이 완화된 dc(t)를 추정할 수 있다(그림 5(b)). 그리고, 전처리된 및 추정된 사람 생체 정보값들은 그림 2의 알고리즘에 입력 변수로 활용되어 SO2가 기존 기법[9],[10] 보다 안정적이고 효율적으로 추정된다.
마지막으로 제안된 기법은 기존 기법[9],[10]에서 그림 4와 같이 지역 극값이 나타나는 문제를 해결하기 위하여 극대값은 양수만, 극소값은 음수만 선택하여 이들의 차이값들의 평균을 평균호흡량 E{Vt(t)}으로 추정하여 보다 안정적으로 SO2 추정이 되도록 한다.
IV. 시뮬레이션 및 실험 결과
본 절에서는 제안된 알고리즘으로 원하지 않는 움직임에 의해 야기되는 저주파 위상 변화 궤적을 제거하여, SO2를 보다 안정적으로 추정하는 시뮬레이션 및 실험 결과를 도시한다. 이때, 시뮬레이션은 점산란원 표적의 등속도 몸 움직임을 가정하였으며, 실제 측정 결과에서는 원하지 않는 사람의 비선형 랜덤 몸 움직임을 가지는 3명의 사람 표적들에 대하여 실험을 각각 수행하였다. 결과 분석 과정은 Intel i5기반의 Window 10 운영체제에서 MATLAB R2021b버전을 통해 진행되었다.
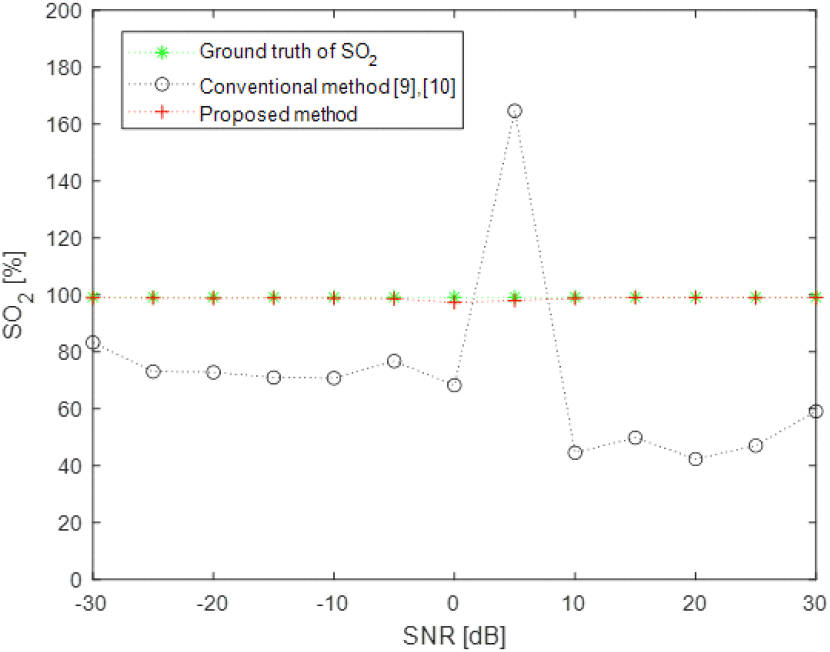
원하지 않는 사람의 등속도 움직임은 Vu = 0.001 m/s의 속도로 u(t) = Vu × t와 같이 나타남을 가정할 경우, 사람에 대한 60초의 측정 시간 동안 표 1의 변수들을 사용할 때 SNR을 5 dB 단위로 −30 dB~30 dB까지 변화시키면서 100번의 몬테 카를로 시뮬레이션으로 SO2를 추정한 결과는 그림 6과 같다. 여기서, 기존 기법은 원하지 않는 사람의 움직임과 열잡음에 대한 영향으로 왜곡이 없을 때 나타나는 참값에 비해 오차가 심하게 나타남을 확인할 수 있었다. 반면에, 제안된 기법의 경우 1차원 위상 변화 궤적에 대한 전처리 및 안정적인 평균 호흡량 추정을 통해, 원하지 않는 사람의 움직임 및 열잡음 영향에서도 참값과 유사하게 나타남을 확인할 수 있었다.
본 절에서는 제안된 기법을 통한 SO2의 추정 성능을 검증하기 위하여 실내 공간에서 3명의 본 논문 저자들에 대해 측정 실험을 수행하였다(그림 7). 이때, 그림 8(a)와 같은 61.2084 GHz의 중심 주파수를 가지는 상용 FMCW (frequency modulated continuous waveform) 레이다의 데이터를 거리축 방향으로 투영하여 도플러 레이다처럼 활용하였으며, SO2의 추정 성능 검증을 위하여 그림 8(b)와 같은 접촉식 상용 의료 장비를 사용하였다. 측정된 2차원 거리-시간 영역 데이터는 시간축에 대한 투영을 통해 25 ms 단위로 샘플링된 1차원 시간축 데이터로 재구성하여 진행하였으며, 약 50초 정도 시간 동안 사람 표적의 생체 신호를 측정하였다.


먼저, 열잡음이 존재하는 실제 측정 환경에서는 사람이 미세하게 원하지 않는 비선형 움직임을 가지기 때문에, 첫 번째 표적에 대해 측정 실험을 하였을 때 그림 9(a)와 같이 위상 변화 궤적에 다양한 왜곡이 발생하나, 이동평균필터 및 대역통과필터로 구성된 전처리 과정을 통해 그림 9(c)와 같이 오직 호흡 활동에 대한 위상 변화 궤적을 기존 기법과 달리 보다 안정적으로 획득할 수 있었다. 그리고, 이 위상 변화 궤적들에 전처리 과정을 단계별로 진행할 때 나타나는 주파수 스펙트럼은 그림 9(d), 그림 9(e) 및 그림 9(f)로 나타났으며, 최종적으로 제안된 전처리 과정으로 기존기법과 달리 호흡수 30.709 bpm이 안정적으로 공진되어 나타남을 확인할 수 있었다.
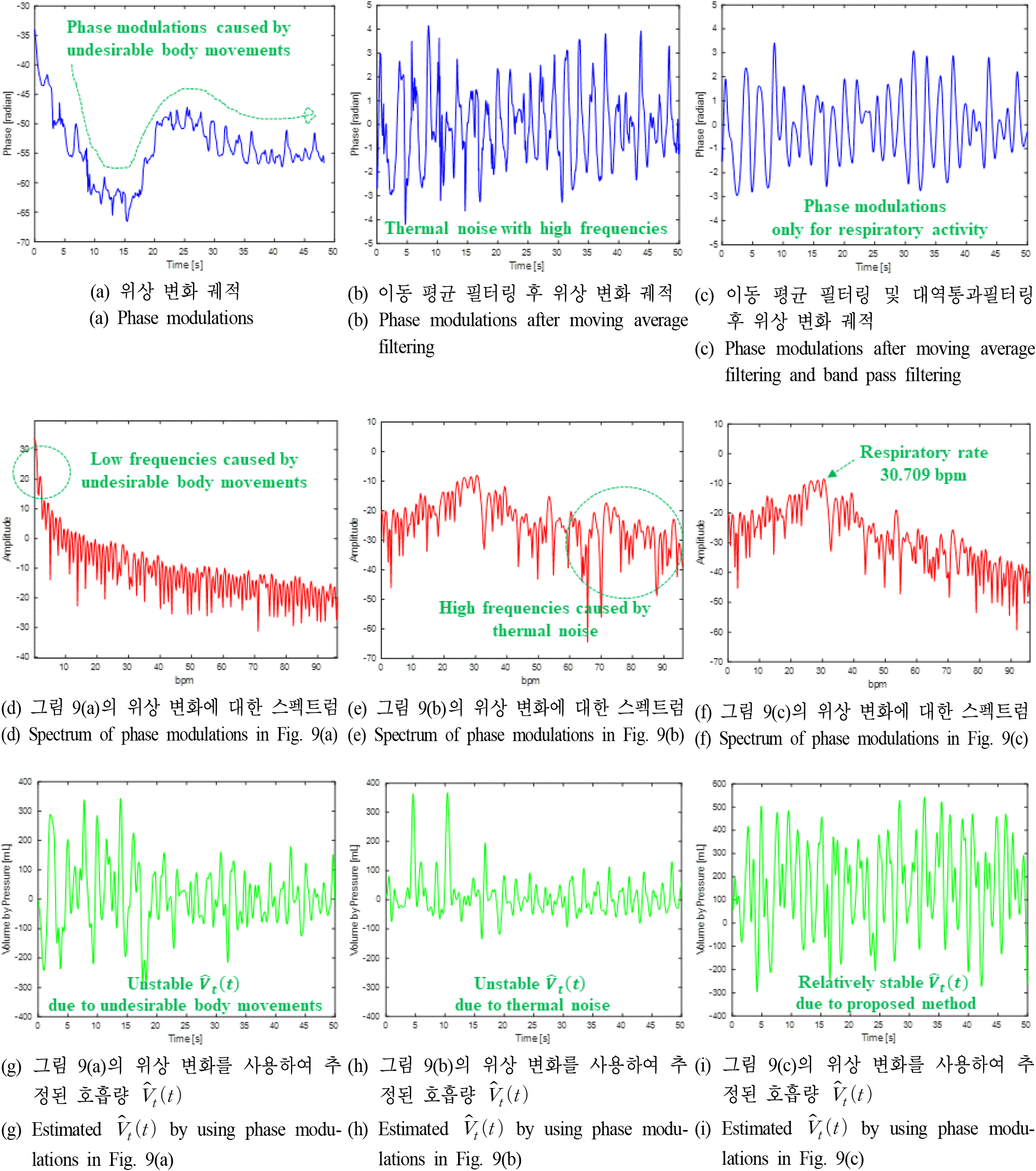
다음으로 앞서 전처리 과정 단계별로 나타나는 위상 변화 궤적을 스케일링하여 상체 움직임 변화 궤적을 추 정한 후, 첫 번째 표적의 호흡량을 추정한 결과는 그림 9(g), (h) 및 (i)와 같다. 특히, SO2 추정 모델에서 SO2의 안정적인 추정을 위해서는의 안정적인 추정이 반드시 필요하다. 그림 9(i)의 결과와 같이, 제안된 전처리 과정을 통해의 안정적인 추정이 가능함을 확인할 수 있었다.
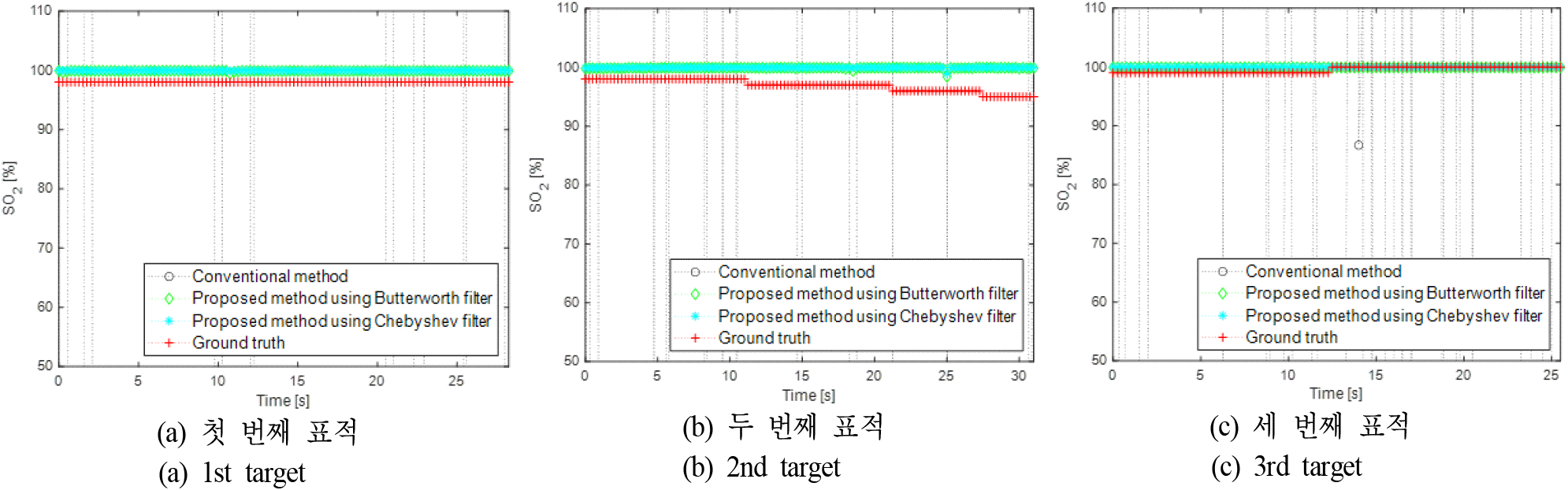
그림 7의 세 명의 표적들에 대한 실시간 SO2 추정 결과 분석을 위하여, 약 50초 동안 측정된 위상 변화 궤적에서 25초의 프레임으로 서브 위상 변화 궤적을 추출한 후, 0.25초 간격으로 프레임을 천이하면서 실시간 SO2를 추정하였다. 이때, SO2의 추정 정확도를 검증하기 위하여 그림 8(b)의 실시간 접촉식 검증 도구에서 나타나는 SO2를 카메라 센서로 인식하였다. 그 결과, 세 명의 표적들에 대한 실시간 SO2의 추정 결과는 그림 10과 같이 나타났다. 일단, 정상적인 사람에 대한 접촉식 검증 도구의 실시간 SO2는 대부분 98 % 근처로 나타났다. 특히, 의학 분야에서는 35 mmHg<PCO2<45 mmHg 및 80 mmHg<PO2<110 mmHg 범위를 정상적인 사람으로 판단하기 때문에, 정상적인 사람의 SO2 또한 상대적으로 높은 95 %<SO2<100 % 범위에서 나타난다. 이와 유사하게, 레이다 센서 및 제안된 기법을 통해 추정된 결과는 정상적인 산소포화도로 나타남을 확인할 수 있었다. 반면에, 기존 기법은 사람의 원하지 않는 움직임에 의해 왜곡이 심하게 발생함을 확인할 수 있었다. 하지만, 그림 10(b)와 같이 두 번째 표적의 실제 SO2가 실시간 98 %에서 95 %로 조금씩 변화하는 경우, 레이다 센서로 추정된 결과가 이 변화 경향을 정확하게 따라 가지 못 함을 확인할 수 있었다. 따라서, 보다 정확한 SO2 추정 성능 분석을 위해서는 생명윤리 및 안전에 관한 법률에 따라 다양한 환자들에 대한 레이다 측정 데이터 베이스가 필요할 것으로 판단된다.
V. 결 론
본 논문에서는 기존기법[9],[10]보다 효율적이고 안정적인 비접촉식 SO2 추정을 수행하기 위하여 1차원 위상 변화 궤적 활용 및 열잡음과 원하지 않는 사람 움직임 영향을 완화하기 위한 전처리 방식을 제안하였다. 제안된 기법을 검증하기 위한 시뮬레이션 및 실험 결과, 카메라 센서가 아닌 레이다 센서를 활용하여 사람의 SO2 추정이 가능함을 확인할 수 있었다. 하지만, 여전히 여러 예측하기 어려운 미지 변수들이 존재하기 때문에, 의료 분야에서 레이다 센싱의 상용성을 보다 높이기 위하여 향후에는 딥러닝 알고리즘 및 다양한 레이다 측정 데이터 베이스를 활용하여 다양한 환경에서 실시간 변화하는 SO2의 추정을 수행할 예정이다.