The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(1):38-50

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.1.38

논문/REGULAR PAPERS

전투기 레이다의 원거리 표적 탐색 및 능동추적을 위한 파형 설계

김태형^†

, 이성원

, 박준현

, 강명일

, 이행수

Waveform Design for Fighter Radar’s Long-Range Target Search and Active Tracking

Tae-Hyung Kim^†

, Sung-Won Lee

, June-Hyune Park

, Myoung-Il Kang

, Hang-Soo Lee

LIG넥스원(주)

LIG Nex1 Co., Ltd.

^†Corresponding Author: Tae-Hyung Kim (e-mail: thkim07@gmail.com)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 11, 2024; Revised: Sep 09, 2024; Accepted: Oct 14, 2024

Published Online: Jan 31, 2025

요 약

전투기 레이다가 공대공 표적을 MPRF(medium pulse repetition frequency) 파형으로 탐지할 때 플랫폼의 고도가 낮으면 부엽클러터에 의해 공대공 표적 탐지거리가 제한된다. 부엽클러터에 의한 공대공 표적 탐지거리 제한을 없애기 위해서 지상 클러터 영향이 없는 조건에서 표적 탐지가 가능한 HPRF(high pulse repetition frequency) 파형을 사용할 수 있다. 전투기 레이다의 원거리 공대공 표적 탐색/추적 모드를 위한 M-of-N 탐지 정책을 사용하는 HPRF 파형 설계를 제시한다. 설계한 파형의 성능과 효용성을 분석과 전투기 레이다 SILS(software-in-loop simulation) 시험을 통해 확인한다.

Abstract

When a fighter radar detects an air-to-air target with a medium pulse repetition frequency (MPRF) waveform, if the altitude of the platform is low, the air-to-air target detection range is limited by the sidelobe clutter. A high-pulse repetition frequency (HPRF) waveform, which can detect air-to-air targets in clutter-free areas, can be used to remove the air-to-air target detection range limit caused by sidelobe clutter. We present an HPRF waveform design that uses an M-of-N binary integration for the long-range air-to-air target search/tracking mode of a fighter radar. The performance and effectiveness of the designed waveform were confirmed through analysis and fighter radar software-in-loop simulation (SILS) testing.

Keywords: Fighter Radars; Long-Range Air-to-Air Targets; Waveform Design; PRF Design; SILS

I. 서 론

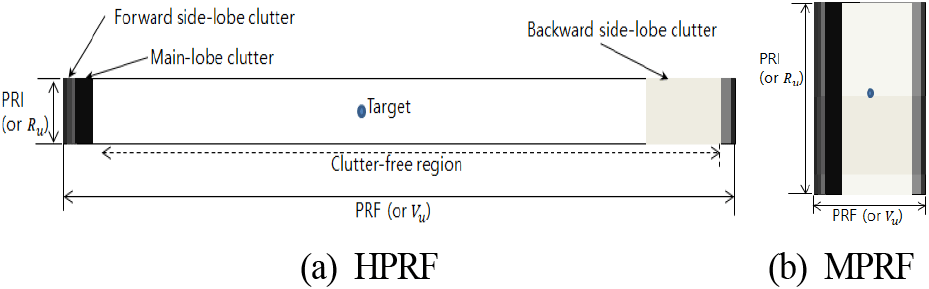
전투기 레이다의 공대공 표적 탐지에서 LPRF(low pulse repetition frequency) 파형은 지상 클러터 간섭에 취약하다. 전투기 레이다에서 지상 클러터 회피 및 전방향 공대공 표적의 거리/속도를 탐지하고 추적하는 데 장점이 많아서 MPRF(medium pulse repetition frequency) 파형이 자주 이용된다. MPRF 파형은 MPRF 파형의 거리/속도 영역에서 여러 거리와 속도의 신호가 겹치는(folded) 현상으로 부엽 클러터가 모든 거리 영역에 영향을 미치기 때문에 플랫폼의 저고도에서 높게 들어오는 부엽 클러터 전력이 MPRF 파형의 모든 거리/속도 영역에 영향을 미친다^[1]. 즉, 플랫폼 저고도에서는 MPRF 파형을 사용해도 부엽 클러터가 원거리 공대공 표적 탐지성능을 제한한다^[2]. 이런 플랫폼의 저고도에서 레이다 탐지성능 저하 현상은 안테나 부엽 이득 크기를 낮추지 않으면 탐지시간을 길게 하거나 파형의 에너지를 높인다고 해서 해결되지 않는다. 어떤 전투기 레이다는 HPRF(high pulse repetition frequency) 파형을 사용해서 공대공 원거리 표적을 탐지한다^[3]. HPRF 파형은 속도 영역에서 모호성이 없으며 속도 영역에서 여러 속도 신호들이 겹쳐서 보이지 않는다. 그리고 상대적으로 표적의 저속 영역(보통 50 m/s 이하)에 지상 클러터가 존재하고 고속 영역은 지상 클러터가 존재하지 않는 영역(clutter-free region)이 된다. 즉 HPRF 파형은 표적의 거리 및 플랫폼 고도와는 상관없이 지상 클러터를 완전히 배제할 수 있는 도플러 영역에서 표적을 탐지할 수 있다. 그림 1(a)는 전투기 레이다에서 HPRF 파형이 표적의 속도가 상대적으로 높은 도플러 영역에서 지상 클러터가 존재하지 않는 영역을 형성하는 것을 거리/도플러 영역의 개념적인 클러터 프로파일로 보여 준다^[3]. 그림 1(a) 및 그림 1(b)에서 V_u는 비모호성(unambiguous) 속도로서 모호성 없이 탐지되는 속도의 최대치이며 R_u는 비모호성 거리로서 모호성 없이 탐지되는 거리의 최대치이다. 그림 1(b)는 비교를 위해 전투기 레이다에서 거리/도플러 영역에서의 MPRF 파형의 클러터 프로파일을 개념적으로 보여 준다. 그림 1(b)에서 볼 수 있듯이 낮은 플랫폼 고도에서 부엽 클러터 전력의 크기가 커지면 모든 거리/도플러 영역에서 겹쳐진 부엽 클러터가 표적 신호를 간섭하여 표적 탐지성능을 저하시킨다^[1],[2]. HPRF 파형은 속도 모호성은 없으나 거리 모호성은 존재하며, FM (frequency modulation) ranging 등의 방법으로 거리 모호성을 해결하는 방법이 있다^[3]. 그러나 FM ranging 기법은 클러터 확산 및 표적 거리에 따른 표적 도플러 주파수 이동 현상으로 근거리의 표적 탐지가 제한을 받는 약점이 있다^[3]. 또한 3-of-3 탐지 정책 때문에 단일 버스트(burst)로 탐지했을 때보다 긴 버스트 길이를 요구하여 원거리 표적 탐지를 위해서 요구되는 버스트 길이는 더 길어지게 된다. 높은 상대 속도를 가지는 공대공 표적은 긴 버스트 시간 내에서 거리 셀 이동 현상^[4]을 발생시키며 이것은 버스트 내의 동기 적분(coherent integration)^[5]을 위한 동기 유지 시간의 제한을 가져온다. 즉 높은 속도의 표적 탐지를 위한 버스트 길이가 상대적으로 많이 제한되며, 단일 버스트로 표적을 탐지하거나 FM ranging 기법을 이용할 때 파형의 버스트 길이 증가를 통한 표적 탐지거리 증대 설계가 상대적으로 제약을 많이 받게 된다.

그림 1. | Fig. 1. HPRF와 MPRF 파형의 거리/도플러 영역에서 개념적 클러터 프로파일 | Conceptual clutter profiles of HPRF and MPRF waveforms in range/Doppler.

Download Original Figure

본 논문에서는 FM ranging의 단점을 극복할 수 있는, 원거리의 고속 공대공 표적을 탐지/추적하는, HPRF 파형을 사용하는 M-of-N 탐지 정책^[1]을 제시하고 제시한 탐지 방법을 M-of-N HPRF 정책이라고 이름 지었다. 제시한 M-of-N HPRF 정책을 사용한 표적 탐지방법은 거리모호성을 해결할 수 있으며 적절한 M과 N의 선택으로 버스트 길이 제한에 상대적으로 자유롭게 파형을 설계할 수 있다. 또한 FM ranging 방법에 비해 상대적으로 짧은 시간의 빔 운용으로도 보다 원거리의 표적 탐지가 가능하다. 그리고 클러터 확산에 의한 근거리 표적 탐지가 제약받는 현상도 없으며 접근과 퇴각 표적을 모두 탐지하고 거리/속도를 추출할 수 있다. 참고로 제시한 M-of-N HPRF 정책은 펄스 도플러 레이다에 적용하며 송신 펄스에 단순 펄스 신호 이외에도 Chirp 신호(FM 신호) 등의 다양한 변조 신호를 사용가능하다. 본 논문에서는 M-of-N HPRF 정책을 위한 HPRF 파형 설계를 제시한다. 원거리 공대공 표적을 탐지하기 위한, 적절한 PRF(pulse repetition frequency) 가용 범위 및 M과 N의 값을 보이고 최적의 PRF 집합을 보인다. 그리고 최적의 PRF 집합을 이용한 원거리 공대공 표적에 대한 탐색/추적 파형 운용 방법을 제시한다. 설계한 파형 및 파형 운용 방법의 성능과 효용성을 분석과 전투기 레이다 SILS(software-in-loop simulation) 시험을 통해 확인한다.

II. M-of-N 탐지 정책에서 최대 탐지거리 분석과 M과 N의 선택

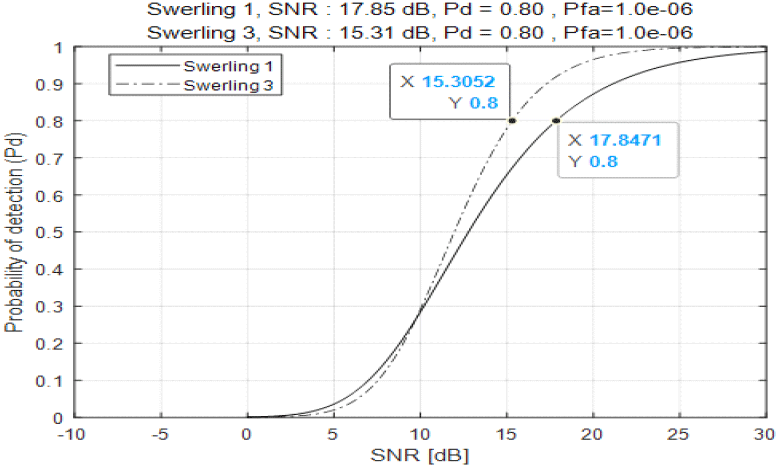
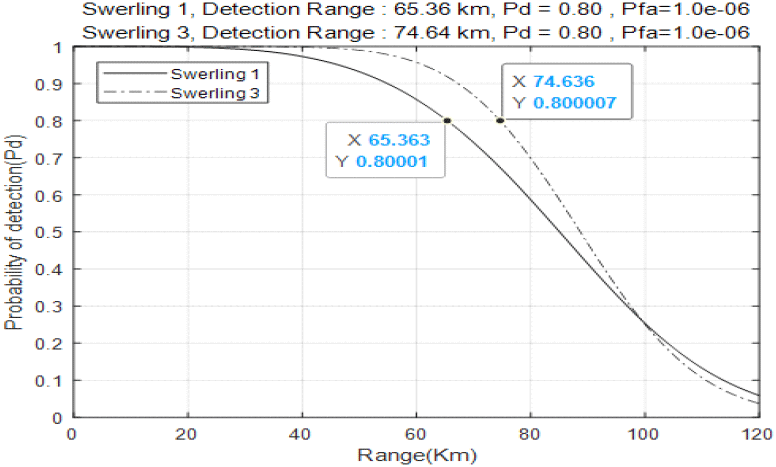
이 장에서는 M-of-N 탐지 정책에서 탐색 빔의 송신 시간을 되도록 짧게 하면서 최대한 긴 탐지거리를 확보할 수 있는 M과 N을 선택한다. 이것은 단일 버스트의 탐색 빔으로 획득되는 최대 탐지거리와 동일한 최대 탐지거리를 가지는 M-of-N 탐지 정책의 탐색 빔의 송신 시간을 M과 N의 값에 따라 비교하는 작업을 통해 하고자 한다. 그림 2는 표적 오탐지확률(P_fa) 10⁻⁶에서 표적 Swerling 모델 1과 3에 대한 표적 SNR(signal-to-noise ratio)에 따른 표적 탐지확률(P_d)을 나타낸다^[6]. 참고로 Swerling 모델 1과 3을 이용한 것은 버스트 내에서 표적 RCS(radar cross section)값이 일관성을 유지한다는 가정을 하였다. 이후로 기술하는 분석 결과 자료들을 표적 Swerling 모델 1을 기준으로 나타냈으며 참고를 위한 비교를 위하여 표적 Swerling 모델 3에 대한 자료도 동시에 나타냈다. 그림 2에서 보듯이 P_fa = 10⁻⁶에서 P_d가 0.8 이상을 만족하려면, Swerling 모델 1인 표적은 SNR이 17.85 dB 이상이여야 한다(참고로 Swerling 모델 3의 표적은 SNR이 15.31 dB 이상). 본 논문에서는 T_b = OOms 길이의 단일 버스트 빔으로 그림 3과 같은 표적 거리별 탐지확률을 나타내는 전투기 레이다를 가정하여 기술하였다. 그림 3은 표적 RCS tgt_RCS = OO로 가정하고 P_fa = 10⁻⁶에서 P_d가 0.8 이상을 만족하는 탐지거리를 그림 2를 이용하여 나타내었다. 그림 3을 기준으로 보면 P_fa = 10⁻⁶와 P_d = 0.8의 조건에서 표적 Swerling 모델 1의 표적 탐지거리는 65.36 km이다(참고로 표적 Swerling 모델 3은 74.64 km).

그림 2. | Fig. 2. 오탐지확률 10⁻⁶에서 표적 SNR 별 탐지확률 | Detection probabilities for target SNRs in the condition of false alarm rate 10⁻⁶.

Download Original Figure

그림 3. | Fig. 3. 오탐지확률 10⁻⁶에서 표적 거리 별 탐지확률 | Detection probabilities for target ranges in the condition of false alarm rate 10⁻⁶.

Download Original Figure

이제 그림 3과 동일 P_d및 탐지거리를 만족하기 위한 몇 가지 M-of-N 탐지 정책의 송신 빔 시간을 구하여 본다. 먼저 2-of-3 탐지 정책부터 해본다. 2-of-3 탐지 정책의 송신 빔은 연속된 동일한 길이와 동일한 듀티(duty)를 가지는 3개의 버스트로 구성된다. 탐지거리를 만족시키기 위해 요구되는 각 버스트의 시간 길이를 분석한다. 이를 위해 먼저 3개의 각 단일 버스트에서 오탐지확률을 식 (1)을 이용하여 정한다. M-of-N 탐지 정책에서 사용하는 N개의 버스트들에서의 탐지 결과를 누적하는 방법(M-of-N binary integration)은^[7]식 (1)과 같이 버스트 단위 오탐지확률 P_fa을 정하면 M-of-N 탐지 정책 빔의 오탐지확률 P_Cfa이 정해진다^[7].

P C f a = N C M P f a M

(1)

식 (1)에서 _NC_M은 N개에서 M개를 선택하는 조합의 수를 나타낸다. 식 (1)에 의하면 2-of-3 탐지 정책의 경우에는 P_Cfa = 10⁻⁶이 되는 P_fa의 값은 5.8 × 10⁻⁴이다. 즉 각 버스트에서 오탐지확률이 5.8 × 10⁻⁴ 정도만 되어도 빔 단위에서 10⁻⁶의 오탐지확률을 획득할 수 있다. N개의 버스트에서 탐지 결과를 누적할 때 탐지 결과들을 버스트들 간에 클러스터링(clustering)하는데 클러스터링 과정에서 오탐지가 증가할 수 있다. 이런 현상 및 버스트들간에 클러스터링하는 윈도우 크기를 고려(9개의 셀을 고려)하여 P_C9fa = 5.8 × 10⁻⁴ = 1 − (1 − P_fa)이 되는 P_fa의 값을 각 단일 버스트에서 요구되는 오탐지확률로 정한다. 즉 P_Cfa = 10⁻⁶ = (₃C₂)(P_C9fa)²이 되는 P_fa의 값을 각 단일 버스트에서의 오탐지확률 P_fa로 정하고자 한다. 그러면 P_fa = 6.4 × 10⁻⁵로 정하게 된다. 이제 2-of-3 탐지 정책을 사용하는 빔의 각 버스트에서 오탐지확률을 6.4×10⁻⁵로 하여 T_b길이의 단일 버스트 빔과 동일한 탐지확률 및 탐지거리를 가지게 하는 각 버스트의 시간 길이를 구한다. 듀티를 동일하게 가져갈 경우에 T_b길이의 버스트에서 표적 SNR을 SNR_Tb라고 하면 T_x 길이의 버스트에서는 SNR_Tb × T_x/T_b의 표적 SNR을 가진다. T_x 길이의 버스트에서 표적 SNR과 오탐지확률 P_fa을 이용하여 각 버스트에서 표적 탐지확률을 구할 수 있으며, T_x길이의 버스트에서 표적 탐지 확률 P_d과 식 (2)를 이용하여 M-of-N 탐지 정책에서의 표적 탐지확률 P_Cd을 구할 수 있다^[7].

P C d = ∑ r = M N N C r P d r 1 − P d N − r

(2)

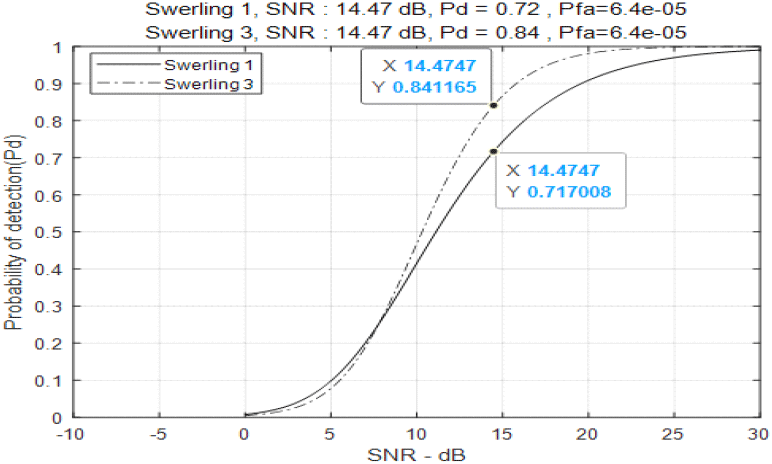
식 (2) 등을 통해 구한, P_Cd가 0.8 이상이 되는 P_d 및 표적 SNR을 2-of-3 탐지 정책에 대해서 그림 4에 나타내었다. P_fa = 6.4 × 10⁻⁵ 및 표적 Swerling 모델 1을 기준으로 표적 SNR이 14.47 dB일 때 P_d = 0.72이며 2-of-3 탐지 정책의 P_Cd = 0.8이 된다. 2-of-3 탐지 정책의 한 버스트 길이를 T_x = T_b × 10^{(14.47 − 17.85)/10} = 0.46 × T_b로 정하면 표적 Swerling 모델 1을 기준으로 2-of-3 정책의 탐지 빔은 오탐지확률 10⁻⁶ 조건에서 T_b 길이의 단일 버스트 탐지 빔과 동일한 탐지확률 0.8 및 탐지거리를 가지게 된다. tgt_RCS = OO의 가정에서 2-of-3 탐지 정책의 각 버스트 길이를 0.46 × T_b로 설정하고 P_Cfa = 10⁻⁶조건에서 P_Cd가 0.8 이상을 만족하는 탐지거리를 그림 5에 나타내었다. 그림 3과 그림 5에서 볼 수 있듯이 표적 Swerling 모델 1과 빔 단위 오탐지확률 10⁻⁶ 조건에서 2-of-3 정책의 탐지 빔이 0.46 × T_b 길이의 버스트들로 구성되면 단일 버스트 탐지 빔과 거의 동일한 표적 탐지거리 성능을 나타냄을 확인할 수 있다. 앞에서 기술한 2-of-3 탐지 정책의 빔에 대한 분석 과정을 여러 가지 M-of-N 탐지 정책에 대하여 동일하게 적용하여 분석한 결과를 표 1에 정리하였다. 표 1에 표적 Swerling 모델 1을 기준으로 분석한 결과를 정리하였다. 표 1의 빔의 탐지거리(detection range of the beam) 항목에서 괄호안의 거리값은 참고를 위하여 표적 Swerling 모델 1과 동일한 한 버스트의 길이 및 P_Cfa, P_Cd 등의 조건에서 표적 Swerling 모델 3에 대해 분석한 탐지거리값을 나타내었다. 표 1의 분석 결과에서 볼 수 있듯이 T_b길이의 단일 버스트 송신 빔과 동일한 탐지거리를 확보하기 위해서 4-of-N에 비해서 2-of-N 또는 3-of-N 탐지 정책의 송신 빔이 대체로 적은 송신 빔 시간을 필요로 함을 알 수 있다. N이 커질수록 필요한 송신 빔 시간이 적지만 M-of-N PRF 정책에서 가해독성(decodability)을 보장하는 운용 PRF 집합^[1]을 N이 커질수록 확보하기 힘들기에 N = 7까지만 정리하였다. III장에서 M과 N을 선택하기 위한 다른 지표인 가해독성을 만족하는 운용 PRF 집합 및 가시성(visibility)^[1]을 확인해 본다.

그림 4. | Fig. 4. 오탐지확률 6.4 × 10⁻⁵에서 표적 SNR과 탐지확률 | Detection probabilities for target SNRs in the condition of false alarm rate 6.4 × 10⁻⁵.

Download Original Figure

그림 5. | Fig. 5. 2-of-3 탐지 정책과 P_Cfa = 10⁻⁶에서 표적 거리 별 탐지확률 | Detection probabilities for target ranges in conditions of 2-of-3 binary integration and P_Cfa = 10⁻⁶.

Download Original Figure

표 1. | Table 1. M-of-N 탐지 정책의 다양한 M과 N에서 요구되는 버스트의 길이 및 탐지거리의 분석 | Analysis of required burst’s length and detection range for various M and N of binary integrations.

Beam type	Burst number in the beam	Length of one burst	SNR of one burst (dB)	P_fa of one burst	P_d of one burst	Length of the beam	P_Cfa of the beam	P_Cd of the beam	Detection range of the beam (km)
1-of-1	1	T_b	17.85	10⁻⁶	0.8	T_b	10⁻⁶	0.8	65.36 (74.64)
2-of-3	3	0.46 × T_b	14.47	6.4 × 10⁻⁵	0.72	1.38 × T_b	10⁻⁶	0.8	65.63 (72.22)
2-of-4	4	0.29 × T_b	12.44	4.5 × 10⁻⁵	0.58	1.15 × T_b	10⁻⁶	0.8	65.40 (69.45)
3-of-4	4	0.48 × T_b	14.70	7.0 × 10⁻⁴	0.79	1.93 × T_b	10⁻⁶	0.8	65.39 (73.84)
2-of-5	5	0.22 × T_b	11.27	3.5 × 10⁻⁵	0.49	1.10 × T_b	10⁻⁶	0.8	65.38 (68.09)
3-of-5	5	0.30 × T_b	12.62	5.2 × 10⁻⁴	0.68	1.50 × T_b	10⁻⁶	0.8	65.47 (71.06)
4-of-5	5	0.52 × T_b	15.02	2.4 × 10⁻³	0.83	2.61 × T_b	10⁻⁶	0.8	65.39 (75.27)
2-of-6	6	0.18 × T_b	10.50	2.8 × 10⁻⁵	0.42	1.10 × T_b	10⁻⁶	0.8	65.46 (67.31)
3-of-6	6	0.22 × T_b	11.35	4.1 × 10⁻⁴	0.59	1.34 × T_b	10⁻⁶	0.8	65.45 (69.48)
4-of-6	6	0.32 × T_b	12.90	1.8 × 10⁻³	0.73	1.92 × T_b	10⁻⁶	0.8	65.58 (72.35)
2-of-7	7	0.16 × T_b	9.89	2.4 × 10⁻⁵	0.37	1.12 × T_b	10⁻⁶	0.8	65.41 (66.66)
3-of-7	7	0.18 × T_b	10.50	3.4 × 10⁻⁴	0.52	1.29 × T_b	10⁻⁶	0.8	65.51 (68.55)
4-of-7	7	0.24 × T_b	11.58	1.5 × 10⁻³	0.65	1.65 × T_b	10⁻⁶	0.8	65.58 (70.64)

Download Excel Table

III. M-of-N HPRF 정책에서 가해독성 보장과 M 과 N의 선택 및 PRF 집합의 가시성 분석

M-of-N HPRF 정책과 HPRF 파형을 사용한 원거리 표적 탐색을 위한 파형 설계에서 먼저 가용한 PRF 범위를 설정한다. PRF 범위는 관심 표적의 최대 속도와 구현 가능한 최저 펄스폭 등을 고려하여 설정한다. 그림 1(a)에서 보듯이 관심 표적의 최대 속도를 이용하여 모호성 없이 지상 클러터가 존재하지 않는 영역에서 최대 속도의 표적을 탐지할 수 있는 PRF값(또는 V_u값)으로 가용한 PRF 범위의 최솟값을 설정할 수 있다. 본 논문에서는 송신주파수 대역으로 x-band를, 최대 표적 관심 속도를 마하 +4로 가정하여, 최대 PRI(pulse repetition interval)를 11.2 μs로 설정했다. 가용한 PRF 범위의 최대값은 최소 송신 펄스폭과 송신 듀티를 고려하여 설정할 수 있다. 본 논문에서는 최소 송신 펄스폭을 0.6 μs로 그리고 송신 듀티를 10 %로 가정하여 최소 PRI를 6 μs로 설정했다. 설정한 가용한 PRI 범위에서 0.2 μs단위로 가용 PRI들을 정하고 가용 PRF 범위에서 가해독성^[1]을 만족하는 M-of-N HPRF 정책을 위한 운용 PRF 집합들을 구한다.

II장에서처럼 여러 M-of-N HPRF 정책들 중에서 먼저 2-of-3 PRF 정책부터 구한다. 2-of-3 HPRF 정책을 위한 운용 PRF 집합은 표적의 최소와 최대 관심거리/관심속도 범위에서 고스트 없이 표적을 탐지하고 거리와 속도의 모호성을 해결할 수 있는 PRF들을 원소로 하는 집합이다. 즉 가해독성을 보장하는(decodable) PRF들을 원소로 하는 집합이다(참고로 가해독성을 보장하는 PRF 집합을 사용하면 거리모호성으로 인한 고스트 표적 발생 등의 탐지성능저하를 발생시키지 않으며 일반적인 오표적 확률 등의 관리로 레이다의 성능을 관리할 수 있다). 가해독성을 알아보는 방법은 참고문헌 [1]에서 설명한 방법을 사용하였다. 가해독성 확인을 위한 관심거리 범위는 최소 탐지 거리(송신 펄스폭 정도 거리)에서 300 km로 하고 관심속도 범위는 마하 −4에서 마하 +4로 하였다. 가해독성 여부 판단의 기준 값으로 사용하는 모호성 문턱값^[1]은 거리 영역에서는 거리 해상도의 2배 값으로 속도 영역에서는 속도 해상도의 4배 값으로 하였다(현 PRF 범위에서 속도 쪽은 모호성이 존재하지 않으므로 속도 영역에서 모호성 문턱값은 의미가 없음). 2-of-3에서 가해독성을 보장하는 PRF 집합을 조사해 보니 가해독성을 보장하는 PRF 집합을 얻을 수 없었다. 앞에서 기술한 과정을 동일한 관심거리/관심속도 범위와 모호성 문턱값을 사용하여 여러 M과 N에 대하여 PRF 집합을 조사한 결과를 표 2에 나타내었다. 표 2에 각 M-of-N HPRF 정책에 대해서 획득한 가해독성을 보장하는 PRF 집합들의 개수를 표현하였으며 표 1에서 나타내었던 M-of-N HPRF 정책의 송신 빔의 시간 길이를 다시 보였다. 또한 M-of-N HPRF 정책에서 구하여진 PRF 집합들 중에서 최고의 가시성을 가지는 PRF 집합과 그 집합의 가시성을 나타내었다.

표 2. | Table 2. M-of-N 탐지 정책의 다양한 M과 N에서 가해독성을 보장하는 PRF 집합 및 가시성 분석 | Analysis of decodable PRF sets and visibility for various M and N of binary integrations.

Beam type	Number of PRF sets	Length of the beam	PRI set representing maximum visibility among decodable PRF sets
1-of-1	-	T_b	-
2-of-3	0	1.38 × T_b	-
2-of-4	0	1.15 × T_b	-
3-of-4	172	1.93 × T_b	{9.2 μs, 10.6 μs, 10.8 μs, 11.2 μs} (Visibility : 91.78 %)
2-of-5	0	1.10 × T_b	-
3-of-5	7	1.50 × T_b	{7.6 μs, 9 μs, 9.2 μs, 9.6 μs, 10.2 μs} (Visibility : 98.42 %)
4-of-5	0	2.61 × T_b	-
2-of-6	0	1.10 × T_b	-
3-of-6	0	1.34 × T_b	-
4-of-6	0	1.92 × T_b	-
2-of-7	0	1.12 × T_b	-
3-of-7	0	1.29 × T_b	-
4-of-7	0	1.65 × T_b	-

Download Excel Table

M-of-N HPRF 정책을 위한 PRF 집합의 가시성은 참고문헌 [1]에서 제시한 방법을 사용하여 구하였다. 가시성 계산에서 고려한 음영(blindness) 요소^[1]는 주엽클러터와 송신펄스이며 HPRF 파형이므로 부엽클러터에 의한 음영 요소는 고려하지 않았다. 주엽클러터 요소에 의한 음영폭^[1]은 도플러 속도 영역에서 ±50 m/s 속도 영역의 폭으로 정하였고 송신펄스에 의한 음영폭은 거리 영역에서 듀티 10 % 등을 고려한 송신 펄스폭으로 정하였다. 표 2에서 볼 수 있듯이 가해독성을 보장하는 PRF 집합들이 존재하는 정책은 3-of-4 HPRF 정책과 3-of-5 HPRF 정책이다.

표 1 및 표 2의 결과에서 시간자원 효율성과 가시성 등을 같이 고려한다면 3-of-5 HPRF 정책을 선택하는 것이 바람직하다. 분석결과를 바탕으로 3-of-5 HPRF 정책을 선택하고 IV장에서 탐색과 추적 파형 운용 등에 대해 기술하였다. 참고로 3-of-5 HPRF 정책에 대해 구하여진 7개의 PRF 집합들에 대한 가시성은 높은 것부터 차례로 98.42 %, 98.41 %, 98.3 %, 98.26 %, 98.08 %, 97,99 %, 97.90 %이다. 그리고 3-of-6 HPRF 정책의 경우에 관심거리를 최소 탐지 거리에서 300 km까지 두었을 때는 가해독성을 보장하는 PRF 집합이 없었지만 관심거리를 최소 탐지 거리에서 150 km까지로 두었을 때는 가해독성을 보장하는 PRF 집합을 17개 획득할 수 있었고 관심거리를 최소 탐지 거리에서 180 km까지로 하면 2개, 관심거리를 최소 탐지 거리에서 190 km까지로 하면 1개의 가해독성을 보장하는 PRF 집합을 획득할 수 있었다(PRF 집합들의 가시성들은 모두 99.6 % 이상이었다). 그러므로 에너지를 줄인 파형으로 관심거리를 150 km 이하로 낮추면 3-of-6 HPRF 정책도 사용 가능하며 송신 빔의 시간 길이도 3-of-5 HPRF 정책보다 짧게 유지할 수 있다.

IV. M-of-N HPRF 정책을 사용하는 탐색과 추적 파형 및 최적 PRF 집합 선택 방법

II장과 III장의 분석 결과를 이용하여 3-of-5 HPRF 정책을 선택하였다면, 탐색 및 추적에 사용할 운용 PRF 집합을 결정한다. 먼저 탐색을 위한 PRF 집합을 결정해 보면 7개의 가해독성이 보장된 PRF 집합 중에서 하나를 선택하여 고정된 PRF 집합을 탐색 파형 운용에 사용할 수 있다. 하드웨어 상황 및 필요한 여러 조건을 기준으로 하여 선택할 수 있을 것이며, 본 논문에서는 최소 탐지 거리에서 150 km까지의 관심거리 범위에서 가시성이 높은 것(가시성 98.4 %)과 고정 듀티를 사용했을 때 펄스폭이 다른 PRF 집합보다 큰 PRF 원소들로 이루어진 PRF 집합을 선택하는 조건으로 {10 μs, 10.2 μs, 10.6 μs, 10.8 μs, 11.2 μs}을 선택하였다. 선택한 PRF 집합을 사용하면 플랫폼이 움직이지 않을 때 특정 거리에서(1.6 %의 음영 영역) 표적을 탐지하지 못할 수 있지만 전투기 레이다의 플랫폼은 지속적으로 이동하기 때문에 탐지하기 못하는 거리 영역을 표적이 금방 벗어나서 표적을 탐지할 수 있다.

능동추적^[8](한 표적에 대해 주기적인 별도의 빔을 능동적으로 조사하여 추적 유지)을 위한 추적 빔을 사용하는 경우에는 탐색 빔과는 달리 추적 빔은 추적중인 표적을 반드시 탐지할 수 있는 빔을 사용해야 한다. 즉 추적중인 표적이 존재하는 예상 거리 및 속도 위치는 송신 빔의 음영 영역에 있지 않아야 하며 반드시 가시 영역에서 탐지할 수 있는 파형을 사용해야 한다. 본 논문에서는 능동추적 빔을 위한 추적 파형으로 탐색과 동일하게 3-of-5 HPRF 정책을 사용하는 파형을 사용하기를 제안한다. 참고로 단일 버스트를 사용하는 파형을 추적 빔^[1]으로 사용하기도 하지만 추적주기가 길면 M-of-N HPRF 정책을 사용하는 파형을 추적 빔으로 사용하는 것이 추적 유지에 유리할 수 있다^[9]. 추적 파형은 현재 추적중인 표적을 최적으로 반드시 탐지할 수 있는 파형을 사용해야 함으로 실시간으로 현재 추적중인 표적을 최적으로 탐지할 수 있는 파형을 선택해야 한다.

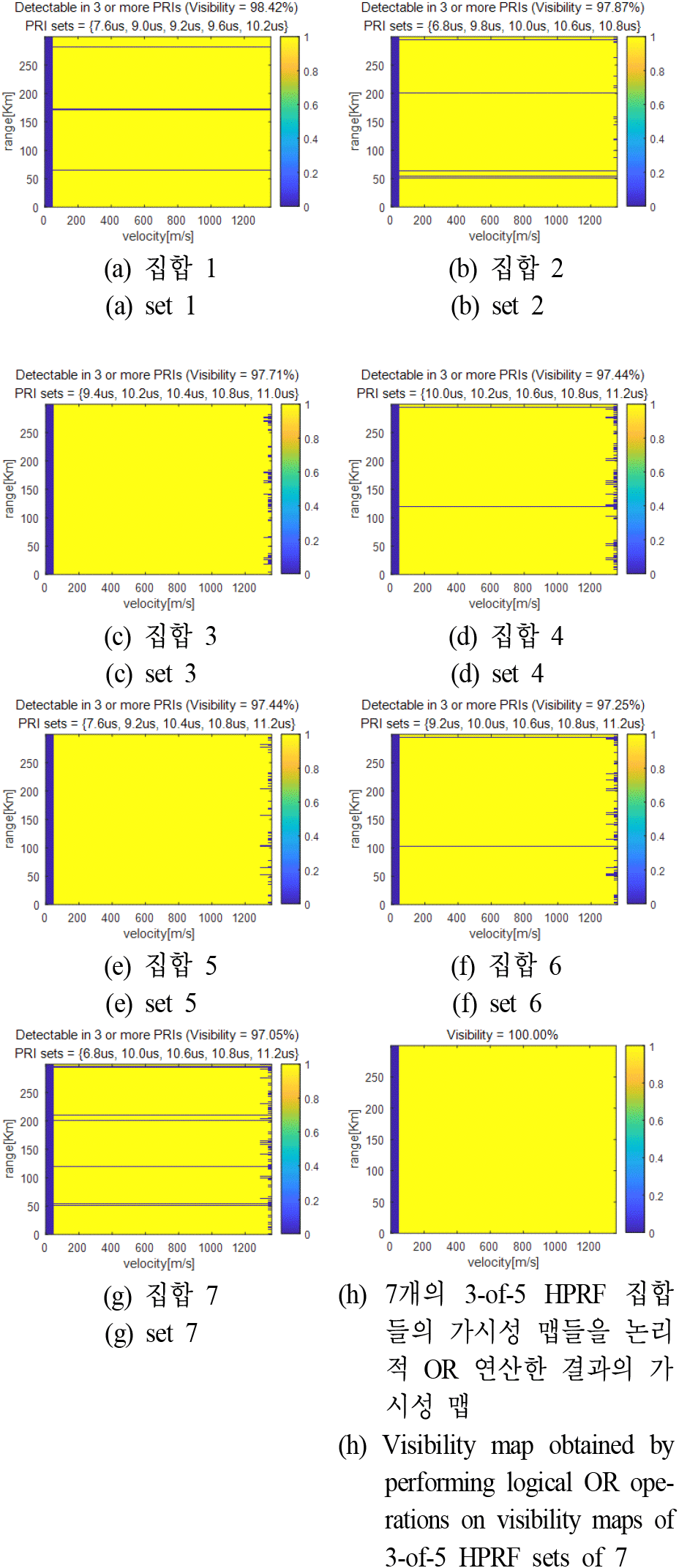
본 논문에서는 II장과 III장의 분석을 통해 획득한 가해독성이 보장된 7개의 3-of-5 HPRF 집합(3-of-5 HPRF 정책을 위한 5개의 PRF 원소로 이루어진 PRF 집합)들 중에서 실시간으로 현재 추적중인 표적을 최적으로 탐지할 수 있는 PRF 집합 하나를 선택하여 추적 파형으로 사용하기를 제안한다. 그림 6(a)에서 그림 6(g)까지는 가해독성을 만족하는 7개의 3-of-5 HPRF 집합들의 가시성 맵^[1]들을 나타내었다(각 그림의 상단에 PRI 집합과 가시성을 표시함). 그림 6(h)는 가해독성을 만족하는 7개의 3-of-5 HPRF 집합들 각각의 가시성 맵들을 논리적 OR 연산하여 구한 가시성 맵을 나타내었다. 가시성 맵들의 논리적 OR 연산은 가시성 맵들의 모든 거리/속도 셀들에 대해 각 가시성 맵의 동일 거리/속도 셀 위치의 가시성 논리값(해당 셀이 3-of-5 탐지 정책으로 보이면 1의 값, 보이지 않으면 0의 값)^[1]들을 논리적 OR 연산하는 것을 말한다. 논리적 OR 연산 결과의 가시성 맵은 100 %의 가시성을 보여준다. 참고로 가시성 계산에서 50 m/s 이하의 속도 영역과 펄스폭에 해당하는 거리 영역은 제외하였으며 음의 속도 영역 가시성은 양의 속도 영역과 대칭이므로 생략하였다. 그림 6(h)의 결과에서 알 수 있듯이 7개의 3-of-5 HPRF 집합들 중에서 하나를 실시간으로 선택하여 추적 빔에 사용하면 최소 탐지 거리에서 300 km의 거리 범위 및 마하 −4에서 마하 +4의 속도 범위에 있는 표적을 100 % 탐지할 수 있다. 해당 표적의 거리/속도 위치를 탐지할 수 있는 PRF 집합이 7개의 3-of-5 HPRF 집합들 중에서 하나 이상 존재한다. 능동추적은 추적 중인 표적의 예상 거리 및 속도값을 이용하여 파형을 결정하고 추적 빔을 송신할 수 있다. 그래서 현재 추적중인 표적의 예상 거리 및 속도값을 이용하여 현재 추적중인 표적을 최적으로 탐지할 수 있는 PRF 집합을 실시간으로 7개의 3-of-5 HPRF 집합들 중에서 하나 선택하여 추적 파형을 결정하는 방법을 제시하고자 한다. 본 논문에서 제시하는 실시간 PRF 집합 선택 방법은 참고문헌 [9]에서 제시한 방법과 유사하다. 참고문헌 [9]에서 언급한 비실시간 과정인 실시간 선택을 위한 PRF 집합 후보들을 선정하는 과정은 본 논문의 7개의 3-of-5 HPRF 집합들을 확보하는 과정과 유사하다고 볼 수 있다. 그리고 참고문헌 [9]의 실시간 과정은 선정한 PRF 집합 후보들 중에서 실시간으로 추적 중인 표적의 예상 거리/속도를 이용하여 최적으로 탐지할 수 있는 PRF 집합 하나를 선정한다는 점에서 본 논문에서 제시한 실시간 추적을 위한 PRF 집합 선정과 유사하다.

그림 6. | Fig. 6. 7개의 PRI 집합들에 대한 가시성 맵들 | Visibility maps for 7 PRI sets.

Download Original Figure

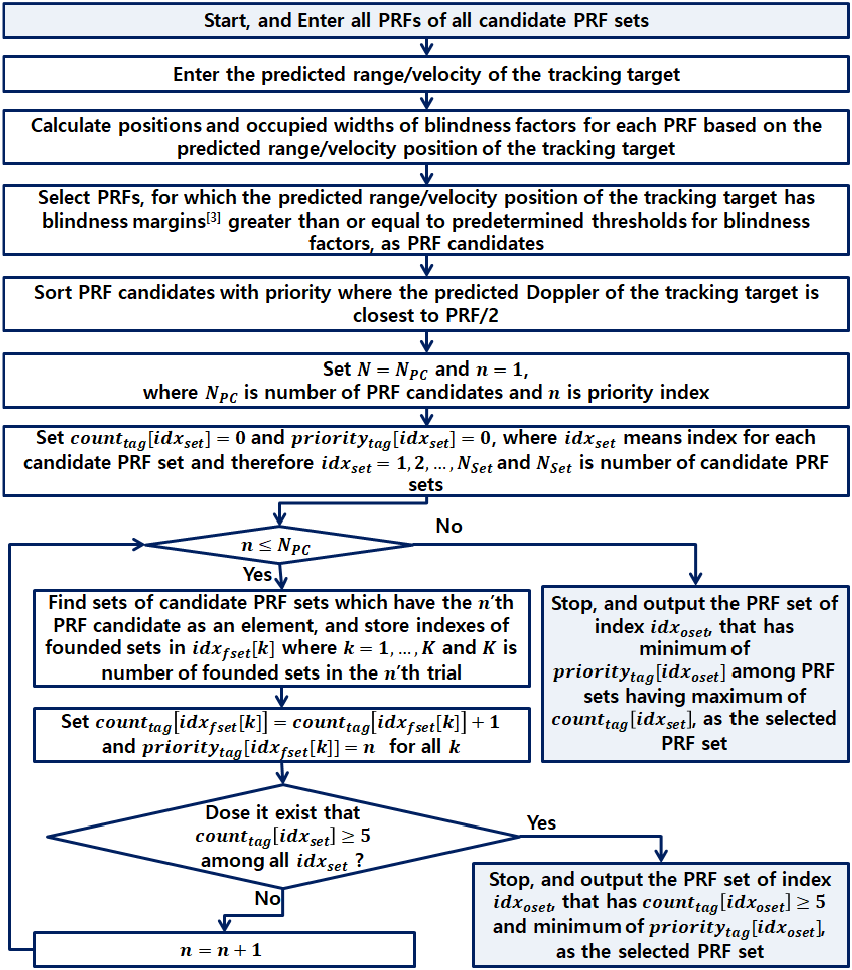
그림 7은 본 논문에서 제시하는, 실시간 추적 파형 결정을 위한 PRF 집합 하나를 선정하는 방법을 나타낸다. 추적중인 표적의 예상 거리/속도와 추적 오차 등을 고려하여 추적 표적의 예상 거리/속도 위치를 중심으로 하는 현재 추적 표적의 관심 거리/속도 범위를 설정하고 7개의 후보 PRF 집합들 중에서 그 범위에 대해서 최적인(최대한의 가시성을 가지는) PRF 집합을 선정하는 개념이다. 추적 파형의 PRF 집합 선택에서 가시성 판단을 위해 사용한 요소는 III장에서처럼 속도 영역에서 주엽클러터에 의한 음영 요소와 거리 영역에서 송신펄스 등에 의한 음영 요소이며, 해당 추적 표적의 관심 거리/속도 영역이 PRF 집합의 각 PRF에 따라 형성되는 음영 요소가 점유하는 거리/속도 영역을 최대한 벗어나게 PRF 집합을 선정한다. 그림 7의 방법에서 우선 3장의 분석을 통해 비실시간 과정으로 선정된 7개의 후보 PRF 집합들을 구성하고 있는 모든 PRF 원소들을 입력 받는다. 본 논문의 경우 참고로 7개의 후보 PRF 집합에서 총 14개 (6.8 μs, 7.6 μs, 9.0 μs, 9.2 μs, 9.4 μs, 9.6 μs, 9.8 μs, 10 μs, 10.2 μs, 10.4 μs, 10.6 μs, 10.8 μs, 11 μs, 11.2 μs)의 PRI 값들을 입력 받는다. 이 총 14개의 PRF들 중에서 PRF 후보들을 선정하는 데 PRF 후보들을 선정하는 방법은 참고문헌 [1]의 실시간 추적 PRF 선택 알고리즘에서 부엽클러터 음영 요소를 생략하여 준용한 방법이다. 그리고 그림 7의 음영 여유(blindness margin)^[1]는 표적의 예상 거리/속도 위치에서 음영 요소들이 떨어져 있는 정도를 나타내는 지표이며 음영 여유가 미리 정한 문턱값 이상인 PRF들을 후보로 선정한다. 후보들로 PRF들이 선정되면 선정된 PRF 후보들을 표적의 도플러가 PRF/2에 가장 가까운 순서로 정렬한다. 우선순위에 따라 정렬된 PRF 후보들의 순서를 기준으로 7개 후보 PRF 집합들 중에서 높은 우선순위의 PRF 후보들을 원소로 최대한 많이 가진 PRF 집합을 찾아서 PRF 집합 하나를 선택한다. 이렇게 현재 추적중인 표적을 반드시 탐지할 수 있는 PRF 집합을 선택하여 3-of-5 HPRF 정책을 사용하는 추적 빔에 사용한다. 참고로 추적하는 표적의 거리가 150 km 미만이라면 3-of-6 PRF 정책을 위한 PRF 집합을 선택하여 추적 파형을 형성할 수 도 있다. 3장의 분석 결과에서 관심거리를 150 km까지로 두었을 때 3-of-6 HPRF 정책을 위한 가해독성을 보장하는 PRF 집합이 17개였다. 이 17개의 PRF 집합들에 대해 그림 6과 같은 방법으로 가시성 맵을 통해 가시성을 분석하니(거리 영역에서 가시성 분석은 150 km까지) 100 %의 가시성을 보여 주었다.

그림 7. | Fig. 7. 3-of-5 HPRF 정책의 추적 빔을 위한 PRF 집합의 실시간 선정 방법 | The method of real-time selection of a PRF set for the tracking beam using the 3-of-5 HPRF schedule.

Download Original Figure

V. SILS를 통한 시험과 결과 분석

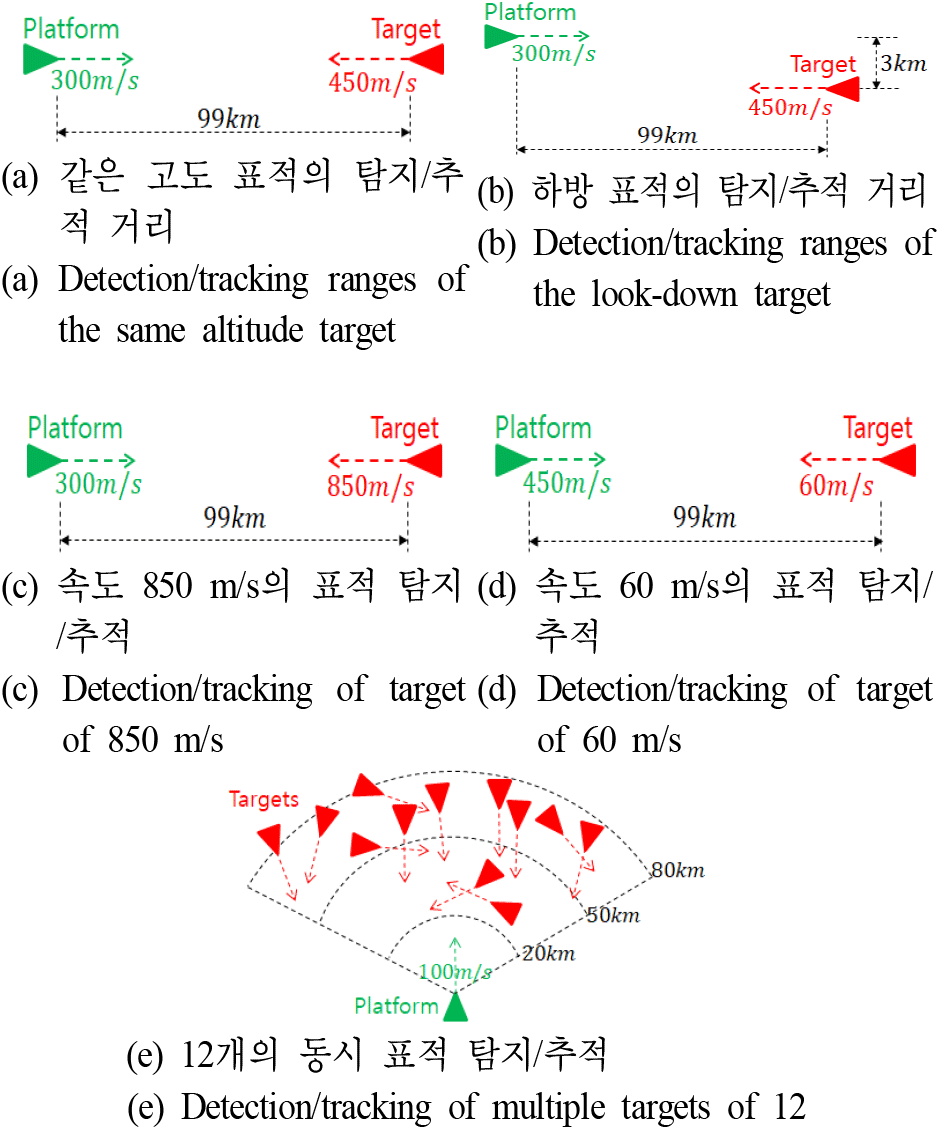
본 장에서는 본 논문에서 제시한 방법으로 획득한 원거리 표적 탐색 및 추적을 위한 3-of-5 HPRF 정책의 탐색 PRF 집합과 실시간 선정한 추적 PRF 집합의 성능과 효용성을 SILS 시험을 통해 확인한다. 전투기 레이다 SILS 시스템은 참고문헌 [8]에서 제시한 전투기 AESA(active electronically scanned array) 레이다 시험 시스템을 사용하였다. 시험에 사용한 플랫폼과 표적의 기동 시나리오는 그림 8과 같다. 그림 8(e)에서 12개 표적 속도들은 300 m/s에서 600 m/s까지 다양하게 구성하였다. 표적 RCS 및 전투기 레이다 시스템 파라메타 등은 II장과 III장에서 가정한 값들을 사용하고 Swerling 모델 1의 표적을 가정하였다. 그림 8의 모든 시나리오에서 플랫폼은 등속 운동으로 수평 비행을 하였다. 그림 8(a)~그림 8(d)의 시험 시나리오에서 전투기 레이다의 탐색 빔은 방위 방향으로 ±10° 스캔 및 고각 방향 0°로 1 bar 스캔을 하였다(탐색 빔들 중에서 방위각 방향 0°로 조향일 때 안테나 빔패턴 주엽의 중심 방향에 표적이 존재하는 시나리오). 중간/최대/최저의 표적 속도에서 시험결과를 비교하기 위하여 그림 8(a), 그림 8(c) 및 그림 8 (d)의 시험 시나리오의 표적 속도들을 설정하였다. 그림 8(b)의 시험 시나리오에서는 방위 방향으로 ±10° 스캔 및 고각 방향 −2.3°와 +2.3°로 2bar 탐색 빔 스캔을 하였다(안테나 빔 패턴 주엽의 중심 방향에 정확히 표적이 존재하는 탐색 빔이 없는 시나리오). 그림 8(e)의 시험 시나리오에서는 방위 방향으로 ±60° 스캔 및 고각 방향 0°로 1 bar 탐색 빔 스캔을 하였다. 본 장의 시험에서 탐색 및 추적에 사용한 PRF 집합은 IV장에서 언급한 PRF 집합들을 사용했다. 표적의 탐지 거리와 속도의 확인으로 제안한 표적 탐색 파형의 성능 및 효용성을 확인할 수 있으며, 능동추적 빔을 이용하여 단일 및 다중 표적의 추적을 유지하도록 레이다를 운영하여 제안한 추적 파형 선정 방법의 효용성을 확인할 수 있도록 하였다. 능동추적에서 추적 주기는 1초가 되도록 능동추적 빔을 운용하였다.

그림 8. | Fig. 8. 시험 시나리오 | Test scenarios.

Download Original Figure

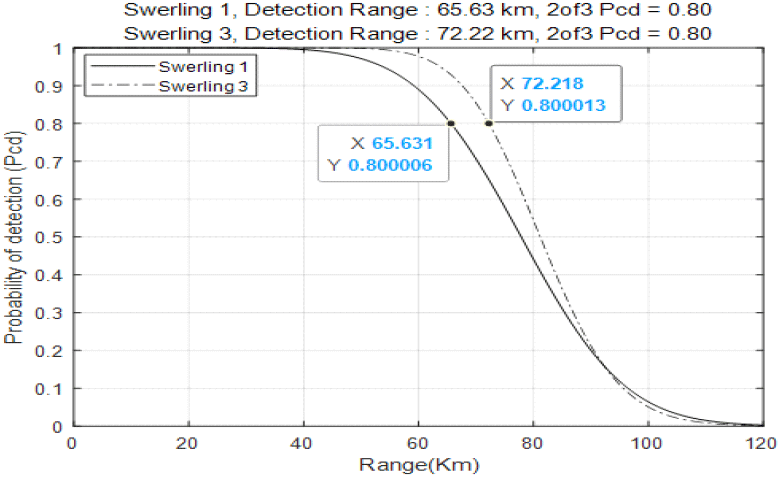
그림 8(a)의 시나리오로 10번 반복 시험한 결과를 표 3에 나타내었다. 표 3에서 보듯이 각 시나리오에서 표적 탐색 과정 중에 표적의 최초 탐지 거리들의 평균은 90.9 km임을 볼 수 있다. 이 시험 결과를 확인하기 위하여 표적의 누적탐지확률 및 탐지거리 분석을 하고자 한다^[10]. 누적탐지확률을 분석하기 위하여 먼저 3-of-5 탐지 정책 빔의 표적 거리 별 탐지확률을 그림 9와 같이 구하여 보았다. 그림 9는 표 1에 나타내고 있는 3-of-5 탐지 정책 빔에 대한 단일 버스트 길이 및 SNR, 오탐지확률 등의 파라메타를 고려하여 구하였다. 그림 8(a)의 시험 시나리오가 표적 거리 99 km부터 시작하므로 99 km부터 시작하여, 3-of-5 탐지 정책 빔의 표적 거리별 탐지확률(그림 9)과 방위각 ±10° 및 고각 1 bar 스캔의 스캔주기를 고려하면서 표적 거리별 누적탐지확률 분석 그래프를 그림 10(a)와 같이 구하였다. 그림 10(a)에서 보듯이 누적탐지확률 P_{d Cum} = 0.8로 90.06 km 거리의 표적을 탐지할 수 있는 것을 확인할 수 있다. 표 3의 시험 결과에서도 누적탐지확률 분석과 비슷하게 10번의 시험에서 90.06 km 이상의 거리에서 표적을 탐지한 횟수가 8번인 것을 확인할 수 있다. 그리고 시험 결과의 평균 표적 탐지거리의 값도 90.9 km로서 누적탐지확률 0.8의 표적 탐지거리가 90.0 6km라는 분석값과 유사하다.

표 3. | Table 3. 플랫폼과 동일 고도의 단일 표적의 시험 시나리오에서 표적 탐지/추적 거리 시험 결과 | Target detection/tracking range test results in the test scenario of a same-altitude target as platform.

Tests	1	2	3	4	5	6	7	8	9	10	Avg.
Range (km) of first detection	93.4	84.5	91.5	91.5	91.5	90.1	92.6	92.5	87.1	94.8	90.9
Tracking range (km)	78.0	67.0	78.2	71.0	60.9	66.6	77.6	65.3	61.6	74.3	70.0

Download Excel Table

그림 9. | Fig. 9. 3-of-5 탐지 정책과 에서 표적 거리 별 탐지확률 | Detection probabilities for target ranges in conditions of 3-of-5 binary integration and .

Download Original Figure

그림 10. | Fig. 10. 제안한 3-of-5 탐지 정책의 PRF 집합을 이용한 표적 거리별 누적탐지확률 분석 | Cumulative detection probability analysis according to target ranges using proposed PRF sets of 3-of-5 binary integration.

Download Original Figure

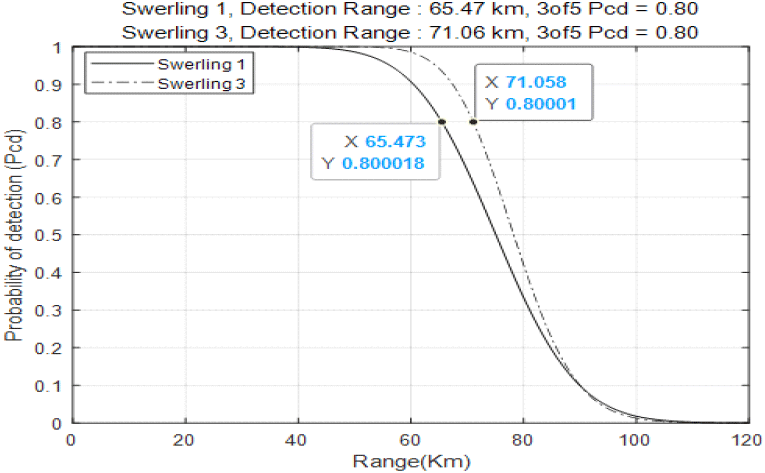
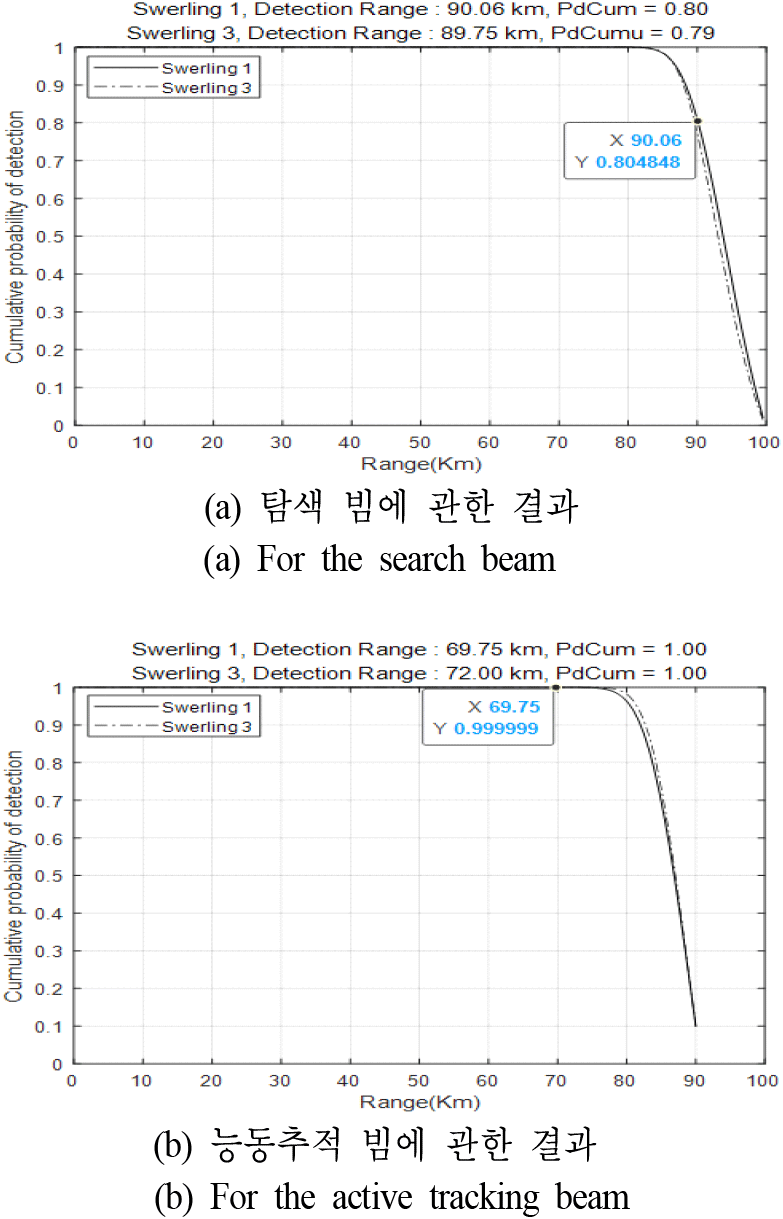
그림 10(b)는 표적 추적형성거리를 분석한 그래프이다. 본 논문의 시험에서는 최초 표적 탐지 이후에 추적을 유지 및 형성하기 위하여 1초 단위로 추적 빔을 운용하였다. 즉 추적형성거리를 확인하려면 최초 표적탐지거리에서부터 1초 단위 추적 빔 주기를 고려하여 표적 거리별 누적탐지확률을 분석한다. 그래서 추적형성거리를 분석하기 위하여, 표 3의 평균 최초 표적탐지거리(0.8 탐지확률의 최초 표적탐지거리의 평균값) 90.9 km부터 시작하여 3-of-5 탐지 정책 빔의 표적 거리별 탐지확률과 1초 단위 추적 빔 주기를 고려하면서 표적 거리별 누적탐지확률 분석 그래프를 그림 10(b)와 같이 구하였다. 누적탐지확률로 추적형성거리를 분석하였다. 그림 10(b)의 분석결과에서 보듯이 거의 100 % 확률로 표적 추적이 끊어지지 않고 연속적으로 유지되기 시작하는 거리는 69.75 km임을 알 수 있다. 이것은 표 3의 능동추적 빔에 의한 10번의 추적거리 시험결과의 평균 추적거리인 70.0 km와 유사하다. 표 3의 10번의 추적거리 시험에서 10개의 추적거리 시험결과들이 각기 상당한 차이를 보이는 이유는, 능동추적은 현재 탐지한 표적의 거리/속도/방향 측정값으로 추적필터를 갱신 및 다음 추적빔의 빔조향 방향을 결정하므로 추적 중인 표적에 대한 거리/속도/방향 측정 오차, 추적 거리/속도/방향 추정 오차 및 빔조향 오차 등의 원인으로 표적 SNR 변화(Swerling 모델 1) 및 능동추적 상황에 따라 추적 거리 형성에 상당한 차이를 보일 수 있기 때문이다. 만약 빔조향 및 추적필터 최적화 등을 행하여 능동추적 성능을 높인다면 그림 10(b)의 분석 수치에 보다 근접하게 10번의 시험결과 값들이 분포할 것으로 예상된다.

그림 8(b)의 시나리오로도 10번 반복 시험을 하였으며, 최초 표적탐지거리의 평균은 88.2 km, 추적형성거리는 67.4 km를 나타내는 결과를 보였다. 그림 8(b)의 시험은 고각 2 bar 스캔 등의 시나리오 조건 때문에 표적이 탐색 안테나 빔의 중앙(빔패턴 주엽의 중심)에 위치하지 않아서 그림 8(a)의 시험보다는 최초 표적탐지거리와 추적형성거리가 적다(양방향 6 dB 주엽 빔폭을 조건하여 보았을 때 표적이 빔패턴 주엽의 중심에서 벗어나면 표적 SNR을 최대 6 dB까지 손해 볼 수도 있음).

그림 8(c) 및 그림 8(d)는 높은 850 m/s 속도 및 낮은 60 m/s 속도의 표적을 탐지하는 지를 확인하는 시험 시나리오이며, 시험결과로 90.23 km 거리에서 850 m/s 속도의 표적을 거리/속도값 추출 오류 없이 탐지하였고 91.5584 km 거리에서 60 m/s 속도의 표적을 거리/속도값 추출 오류 없이 탐지하였다. 즉 제안한 3-of-5 HPRF 정책을 위한 탐색/추적 PRF 집합 선택 방법으로 선정한 탐색/추적 PRF 집합들의 탐지 성능 및 거리/속도 탐지 능력의 효용성을 시험결과로 확인할 수 있다.

그림 8(e)는 12개의 표적에 대해 능동추적으로 다중표적 추적을 유지하는 지를 확인하는 시험 시나리오이며, 본 논문에서는 참고문헌 [8]의 SILS 시험 시스템에서 제공하는 시험결과분석 소프트웨어를 이용하여 그림 8(e)에 대한 다중표적의 능동추적 시험결과를 확인하였다. 그림 11은 능동추적 시험결과를 분석 소프트웨어로 나타내었다. 그림 11에서 적색 사각 점의 심볼은 표적 추적 필터의 표적의 위치 출력값을 지도위에 나타내었다. 그리고 흑색 사각 점의 심볼은 표적 추적 필터의 메모리 추적에^[11] 의한 표적의 위치 출력값을 지도위에 나타내었다. 보라색 둥근 점의 심볼은 탐색 빔에서 탐지된 표적의 위치 측정값을, 보라색 사각 점의 심볼은 추적 빔에서 탐지된 표적의 위치 측정값을 지도 위에 나타내었다. 참고로 하늘색 둥근 심볼은 플랫폼의 위치들을 지도위에 나타내었다. 그림 11의 결과를 보면 4개 표적들에 중간에 표적 추적을 놓치고 다시 표적을 탐지하고 추적을 유지하는 것을 볼 수 있고 나머지는 8개의 표적들은 추적 유지를 잘하는 것을 볼 수 있다. 이것은 12개의 표적 중에서 4개의 표적들이 기동상황 중에 잠시 동안 레이다가 탐지하기 힘든 영속도 영역에 들어가거나(표적의 aspect 각도가 ±90°에 가까워지면 표적의 시선방향 절대속도는 0에 가까워지게 되어 표적이 주엽클러터 영역에 위치하게 됨) 먼 거리(70 km 이상)에 위치해 있어서 중간에 추적 유지를 실패한 것으로 보인다. 영속도 영역에서의 표적 미탐지 현상은 대부분의 레이다에서 발견되는 현상이며 제안한 파형에서도 나타나고 있다. 이런 현상은 신호처리와 표적 추적 필터 최적화를 통해 개선될 수 있으나 본 논문의 실험에서는 최적화를 수행하지는 않았다. 그림 11의 다중표적의 능동추적 시험결과로 제안한 실시간 추적 파형 및 3-of-5 HPRF 정책의 PRF 집합 선정 방법이 잘 동작하며 제안한 방법이 효용성 있음을 확인할 수 있다. 참고로 그림 8의 시나리오들에 대하여 본 논문에서 언급한 3-of-6 HPRF 정책에 의한 시험결과도 3-of-5 HPRF 정책과 유사한 시험 결과들을 얻었다. 즉 본 논문에서 언급한 3-of-6 HPRF 정책을 위한 PRF 집합들도 100 km 이하의 표적을 대상으로 할 때는 충분히 사용가능한 것으로 보인다.

그림 11. | Fig. 11. 제안한 3-of-5 탐지 정책의 PRF 집합 선정 방법을 이용한 12개 표적의 능동추적 시험결과 | The active tracking test result for the scenario of 12 targets using the proposed method of selection of PRF set for 3-of-5 binary integration.

Download Original Figure

VI. 결 론

전투기 레이다에서 원거리 공대공 표적을 탐지/추적하기 위한 HPRF 파형 설계 방법을 제시하였다. 원거리 공대공 표적 탐지에 HPRF 파형 사용의 장점 및 HPRF 파형 기반의 기존 표적 탐지 및 표적 거리 측정 방법의 단점과 약점을 설명하였다. 즉, HPRF 파형 사용에서 기존의 단일 버스트로 탐지할 때 탐지거리 증대를 위한 버스트 길이 늘이기가 제한되는 것과 기존의 표적 거리 측정방법(FM ranging 기법)의 단점을 언급하였다. 기존 방법의 단점을 극복할 수 있는 HPRF 파형 기반의 M-of-N 탐지 정책의 사용의 이유를 설명하였다. 즉, N개의 버스트에서의 탐지 결과를 조합하여 표적을 탐지하는 M-of-N 탐지 정책이 단일 버스트로만 표적을 탐지하는 방법보다 버스트 길이 늘이기를 통한 탐지거리 확장 설계에 유리하고 기존 거리 측정방법의 단점을 극복할 수 있음을 설명하였다. 그래서 M-of-N HPRF 정책을 사용하는 HPRF 파형 설계 방법과 탐색 및 능동추적 빔에 사용할 PRF 집합 선택 방법을 제시하였다. M-of-N HPRF 정책의 사용에서 문제점은 4이 큰 PRF 범위를 사용한다는 특성으로 거리모호성 해결이 가능한 M과 N의 설정 및 가용한 PRF 집합 설계가 쉽지 않다는 것이며, 본 논문은 설계하기 쉽지 않은 M-of-N HPRF 정책의 파형 설계에서 표적탐지거리 및 탐지빔의 시간 길이와 함께 가해독성과 가시성을 고려해서 M과 N을 선정하는 기준과 방법을 제시하였다. 그리고 그 기준과 방법에 따라 자연스럽게 가용한 PRF 집합을 선정할 수 있음을 보여 주었다.

AESA 레이다에서 많은 수의 다중표적을 능동추적으로 모두 관리하고자 할 때는 1초 이상의 긴 추적 주기를 가져갈 수밖에 없으며, 긴 능동추적 주기로 하여 많은 다중표적을 관리하려면 제안한 3-of-5 탐지 정책의 추적 파형을 사용하여 모호성이 해결된 거리와 속도를 추출하여 거리와 속도값을 추적 유지에 모두 사용하는 것이 유리하다. 본 논문에서 제시한 추적 파형은 단일 PRF의 탐지 빔을 사용^[1]하는 것이 아니며, 추적하고 있는 표적을 최적으로 탐지하는 3-of-5 탐지 정책의 추적 파형(5개의 PRF 사용)을 실시간으로 계산하여 운용하는 방법을 제시한 것이다.

설계한 파형과 제시한 PRF 집합 선택 방법 및 파형 운용 방법의 성능과 효용성을 전투기 레이다 SILS 시험을 통해 보였다. 제안한 원거리 표적 탐색 및 능동추적을 위한 파형은 FA-50과 같은 전투기를 위한 AESA 레이다에 적용하여 사용할 수 있다.

References

[1].

T. H. Kim, E. H. Kim, and S. W. Lee, “Real-time PRF selection for search/track in MPRF waveform airborne radar,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 25, no. 10, pp. 1050-1061, Oct. 2014.

[2].

T. H. Kim, H. W. Jeon, J. H. Shin, and Y. D. Kang, “Improvement of detection ranges for targets in sidelobe clutter surroundings by sigma-delta STAP for airborne radars,” Journal of Electromagnetic Engineering and Science, vol. 19, no. 4, pp. 234-238, Oct. 2019.

[3].

T. H. Kim, S. H. Ryu, J. H. Shin, H. W. Jeon, S. H. Jang, and S. J. Kim, “Design of signal processing for target detection and tracking based on high pulse repetition frequency waveforms in airborne active electronically scanned array radars,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 30, no. 12, pp. 951-963, Dec. 2019.

[4].

T. H. Kim, J. G. Seo, J. S. Yoon, and J. H. Bae, “Range cell migration compensation for coherent integration in air-to-air mode of aircraft radar,” in Proceedings of the Korea Institute of Military Science and Technology 2017, Jeju, Jun. 2017, pp. 151-153.

[5].

M. I. Skolnik, Radar Handbook, 3rd ed. New York, NY, McGraw-Hill, 2008.

[6].

B. R. Mahafza, Radar Systems Analysis and Design Using MATLAB, 2nd ed. New York, NY, Chapman and Hall/CRC, 2005.

[7].

M. A. Richards, Fundamentals of Radar Signal Processing, New York, NY, McGraw-Hill, 2005.

[8].

T. H. Kim, H. W. Jeon, S. W. Lee, J. T. Park, M. I. Kang, and J. H. Park, “Software-in-loop simulation system implementation for fighter radar developments,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 33, no. 9, pp. 730-738, Sep. 2022.

[9].

T. H. Kim, J. H. Park, M. I. Kang, and H. S. Lee, “Real-time waveform selection for air-to-air target tracking on aircraft radar,” in The KIEES Summer Conference 2023, Goseong, Aug. 2023, p. 459.

[10].

E. H. Kim, J. E. Roh, “Calculation of the detection range for a given cumulative probability in airborne surveillance radars,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 1, pp. 24-27, Jan. 2018.

[11].

E. Brookner, Tracking and Kalman Filtering Made Easy, Hoboken, NJ, John Wiley & Sons, 1998.