FMCW 전파고도계의 딥러닝 기반 고도 추정

I. 서 론

전파고도계(radar altimeter)는 전파를 이용하여 비행체(aerial vehicle)와 지표면 사이의 거리를 측정하는 장치이다. 전파고도계는 지표면을 향해 방사하는 송신파와 지표면에서 반사되어 되돌아오는 수신파의 시간 지연을 분석하여 고도를 추정한다.

전파고도계는 주파수 변조 연속파(FMCW, frequency-modulated continuous-wave) 방식의 레이다이다. 주파수 변조 연속파 방식은 송⋅수신 간 시간 지연이 주파수의 차로 변환된다. 주파수 변조된 송신파와 시간 지연된 수신파를 주파수 혼합하여 얻는 차 주파수인 비트(beat)주파수가 고도에 비례하여 증감하므로 측정된 비트주파수를 분석하면 고도를 추정할 수 있다^[1],[2].

전파고도계는 단순히 고도를 측정하는 것만이 아니라 지형참조항법(TRN, terrain referenced navigation)의 지형 측정 센서로 활용된다. 지형참조항법은 지표고(地表高)와 수치표고모델(DEM, digital elevation model)을 비교하여 비행체의 위치(위도, 경도)를 추정하는 항법 기술이다^[3],[4]. 지형참조항법에 이용되는 지표고를 측정하기 위해 기압고도계와 전파고도계가 필요하다. 기압고도계가 측정한 진고도(true altitude)⎯평균 해수면부터 비행체까지의 높이⎯에서 전파고도계가 측정한 상대고도⎯지표면에서 비행체까지의 높이⎯를 빼면 지표고를 산출할 수 있다^[5],[6]. 현재 추정 위치를 기준으로 비행체가 일정 시간 동안 이동한 비행 궤적 내에서 축적된 지표고를 수치표고모델과 비교하여 위치 오차가 최소화되는 해가 비행체의 위치가 된다^[7],[8].

지형참조항법은 지형 험준도 지수를 계산하여 임계치 이상일 때만 위치 해가 가용하도록 판단 논리를 운용한다^[7],[9]. 지형의 험준도(roughness)와 유일성(uniqueness)이 높은 지역에서 정확한 지표고를 측정하여 수치표고모델과 비교하면 비행체 위치 해의 강건성이 높다^[8]. 즉, 지표면의 윤곽이 뚜렷한 산지에서 운용될 때 지형참조항법의 성능이 우수하다. 반면, 전파고도계는 평지나 해수면 대비 산지에서 정확도가 낮다. 산지에서는 비슷한 수신전력을 갖고 넓게 퍼지는(spread) 형태의 비트주파수 스펙트럼이 수신되는데, 이 중에서 직하방 고도(nadir altitude)에 해당하는 정확한 비트주파수를 선택하는 것이 어렵기 때문이다. 지형의 험준도와 유일성이 높은 산지에서 전파고도계가 정확한 고도를 측정할 수 있어야 지형참조항법에 활용되는 지표고의 정확도를 높여 정확한 비행체의 위치를 추정할 수 있다.

종래의 전파고도계는 수신전력이 문턱값(threshold) 이상인 유효 비트주파수(고도)의 무게중심을 선택하는 방식으로 고도를 추정하였다. 안테나가 비추는 영역 내 지표면의 매질이 같다는 가정하에 수신전력이 큰 비트주파수가 직하방 고도에 가깝다는 직관에 따른 것이다. 각 비트주파수 스펙트럼 내에서 정확한 직하방 고도를 알 수 없으므로 통계적인 직관을 도입한 것이다.

직관의 임의성을 배제하고, 다양한 지형, 특히 험준한 산지의 비트주파수 스펙트럼에 대해 적응적으로 직하방 고도를 추정하기 위해 전파고도계에 기계학습(machine learning)을 도입하였다. 다수의 비트주파수 스펙트럼과 레이저 거리 측정기(LRF, laser range finder)로 동시에 측정한 직하방 고도를 입력하여 전파고도계를 지도 학습(supervised learning)한 후, 학습된 결과를 기반으로 고도를 추정한다. 기계학습 방법 중 뇌의 신경 세포를 모사해서 만든 다수 노드(node)의 네트워크인 인공신경망(ANN, artificial neural network)을 학습 모델로 이용하는 딥러닝(deep learning)을 전파고도계에 적용하였다.

딥러닝 방법은 학습 과정(learning process)과 추론 과정(inferencing process)으로 구성된다^[10]. 학습 과정에서는 비행시험을 통해 다양한 지형에서 비트주파수 스펙트럼과 직하방 고도를 수집한 후 인공신경망에 입력하여 각 층 노드 간의 가중치(weights)를 학습한다. 추론 과정에서는 학습된 인공신경망에 임의의 지표면에서 수집된 비트주파수 스펙트럼을 입력하여 각 비트주파수가 직하방 고도일 확률분포(probability distribution)를 출력한다.

서론에 이어 II장에서는 종래의 고도 추정 방법에 대해 언급한 후, 딥러닝 방법을 이용한 고도 추정 방법에 대해 상세히 기술한다. III장에서는 비행시험을 통해 수집한 데이터를 이용해 종래의 방법과 딥러닝 방법으로 고도를 추정하고, 고도 오차를 비교⋅분석한다. IV장에서는 전체 내용을 종합하여 결론을 맺는다.

II. 딥러닝 기반 고도 추정 방법

2-1 종래의 고도 추정 방법

전파고도계의 안테나가 비추는 지표면 영역에는 여러 형태의 지형(능선, 계곡 등)과 레이다 단면적이 다른 매질(수면, 지면 등)이 포함된다. 지표면의 지형과 매질에 따라 여러 거리에서 반사되는 신호가 각기 다른 수신전력을 가지고 한꺼번에 수신된다. 따라서 비트주파수 스펙트럼은 여러 주파수(고도)를 가지며, 주파수별 수신전력도 다르게 퍼진 형태로 나타난다. 고도를 정확히 추정하기 위해서는 퍼진 형태의 비트주파수 스펙트럼 내에서 비행체 직하방에서 반사된 전파에 의한 비트주파수(고도)를 정확히 선택해야 한다.

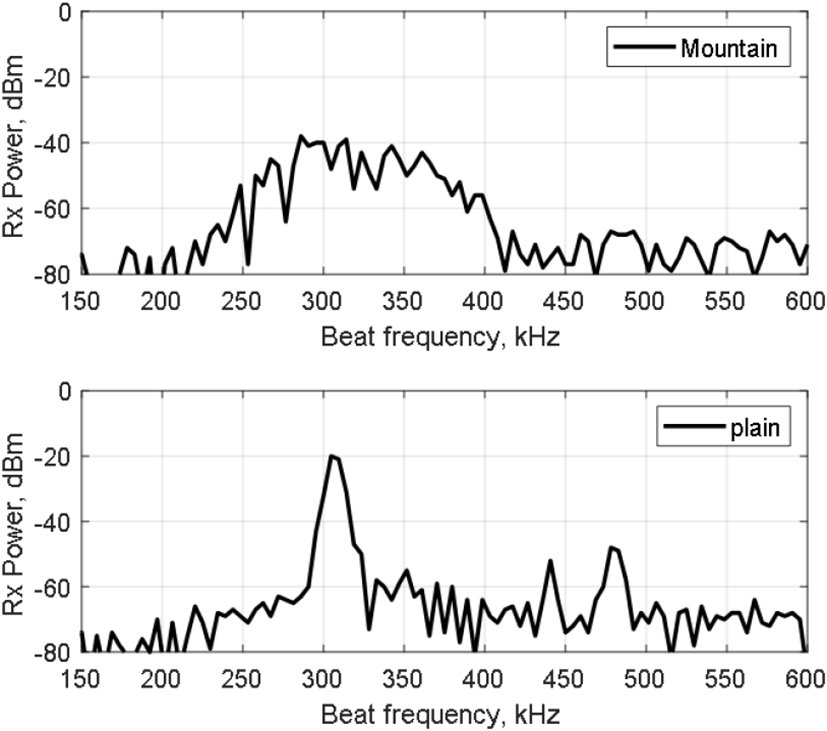
그림 1은 산지와 평지에서 측정된 비트주파수 스펙트럼의 예이다. 평지와 비교해 산지의 경우 스펙트럼의 주파수 분포가 넓고, 수신전력의 첨둣값이 낮으므로 상대적으로 정확한 고도 선택이 어려움을 직감할 수 있다.

그림 1. | Fig. 1. 산지와 평지에서 측정된 비트주파수 스펙트럼 | Beat-frequency spectrum measured above mountain and plain.

Download Original Figure

비행체의 항행에 따라 실시간 측정되는 비트주파수 스펙트럼의 형태가 계속 변화하고 있고, 각 비트주파수 스펙트럼 내에서 정확한 직하방 고도는 알 수 없는 상황이다. 종래의 고도 추정 방법은 다양한 지표면에 대한 다수의 비트주파수 스펙트럼을 수집⋅분석하여, 큰 오차가 발생할 가능성을 줄이도록 설계되었다.

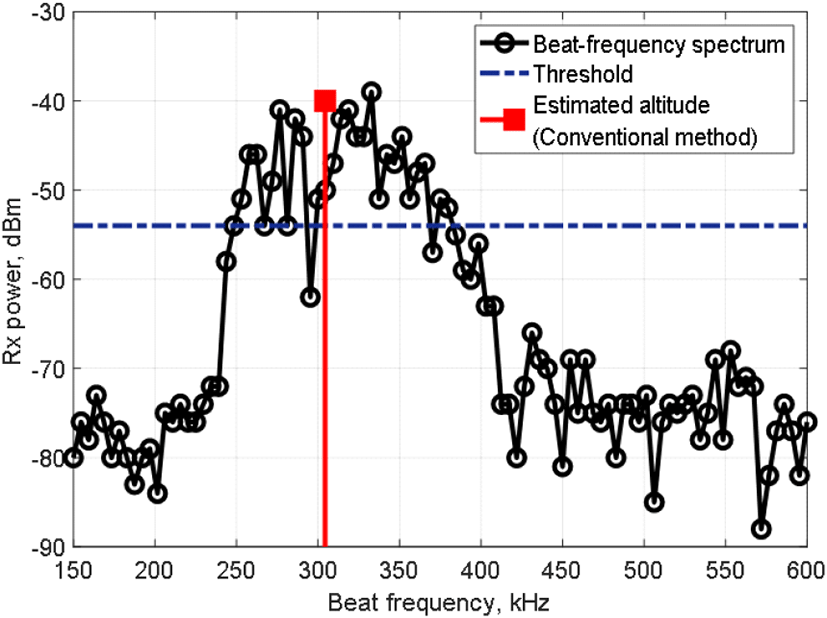
종래의 고도 추정 방법은 다수의 비트주파수 스펙트럼과 GPS(global positioning system) 고도에서 수치표고모델의 표고를 뺀 상대고도를 비교 관찰한 후 직관에 의존해 선택한 것이다. 직관에 따르면 산지에서는 문턱값 이상의 수신전력을 가지는 유효 비트주파수의 무게중심을, 평지 또는 해수면에서는 첨두 수신전력의 비트주파수를 고도로 추정하면 위의 상대고도에서 크게 벗어나지 않는다. 그림 2에는 종래의 고도 추정 방법을 나타내었다. 실시간 측정되는 비트주파수 스펙트럼 분포에서 첨둣값을 찾고, 문턱값(첨둣값 −15 dB) 이상의 수신전력을 가지는 비트주파수를 유효고도로 분류한 후(수신전력−문턱값)을 가중치로 계산한 가중 평균(weighted average)값을 고도로 추정한다.

그림 2. | Fig. 2. 종래의 고도 추정 방법 | Conventional method of estimating altitude.

Download Original Figure

직관에 따른 종래의 고도 추정 방법⎯유효고도 분류, 무게중심⎯은 문턱값의 설정에 따라 분류되는 유효고도의 범위가 달라지므로 임의적이고, 첨둣값이 낮아 잡음 수준 대비 문턱값이 높지 않으면 유효고도가 없을 수도 있다. 비교 관찰의 기준이 되는 상대고도도 GPS의 고도 오차와 수치표고모델의 격자 간격⎯수십 m⎯에 따른 오차를 포함하고 있어 정확도가 낮다.

직관의 임의성을 탈피하기 위해 데이터에서 모델을 스스로 찾아내는 기법인 기계학습을 전파고도계의 고도 추정 방법에 도입하였다. 지도학습을 위해 비행시험을 통해 다양한 지형에서 비트주파수 스펙트럼 데이터를 다수 확보하고, 기준 상대고도의 정확성을 높이기 위해 레이저 거리 측정기를 동시에 탑재하여 항공기의 직하방 고도를 측정하였다.

2-2 딥러닝을 이용한 고도 추정 방법

전파고도계의 고도 추정 방법으로 기계학습 방법 중 딥러닝을 적용하였다. 기계학습은 학습 과정과 고도 추정(추론) 과정으로 구성되며, 딥러닝은 인공신경망을 학습 모델로 활용한다^[10]. 그림 3에는 딥러닝을 이용한 고도 추정 개념을 나타내었다.

그림 3. | Fig. 3. 딥러닝을 이용한 고도 추정 개념 | Concept of altitude estimation with DL.

Download Original Figure

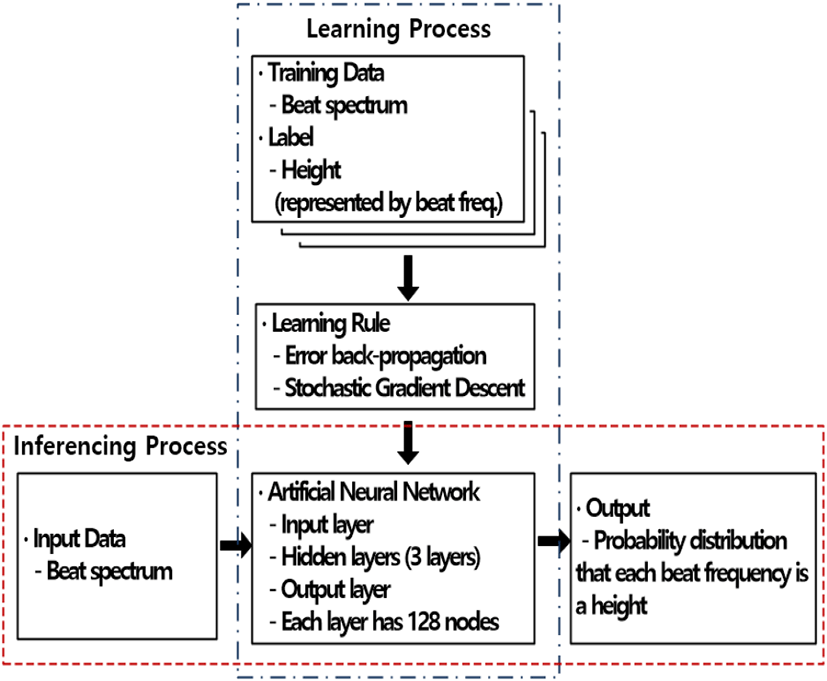
학습 과정에서는 인공신경망의 지도학습을 수행한다. 지도학습의 데이터 세트는 학습 데이터와 레이블로 구성되는데, 학습 데이터는 전파고도계가 수집한 비트주파수 스펙트럼이고, 레이블은 레이저 거리 측정기가 측정한 직하방 고도이다. 인공신경망은 입력층(input layer), 3개의 은닉층(hidden layer), 출력층(output layer)으로 구성되며, 각 층에는 128개 노드가 있다. 학습 규칙으로는 딥러닝에서 일반적인 오차 역전파 알고리즘(error backpropagation algorithm)과 경사하강법(gradient descent method)을 활용한다^[10]. 고도 추정 과정은 비트주파수 스펙트럼 내 각 주파수의 수신전력을 학습된 인공신경망의 입력으로 받아들여, 각 비트주파수가 직하방 고도일 확률분포를 출력하는 과정이다.

인공신경망은 완전 연결 층(fully connected layer) 구조로 가중치가 많아 복잡도가 높지만, 학습이 상대적으로 단순하다. 전파고도계의 비트주파수 스펙트럼은 1차원 데이터로 크기가 128개로 작고 고정되어 있다. 비트주파수 스펙트럼을 입력하여 모든 노드 간에 가중치를 계산하여도 학습 시간이 적게 걸리므로 인공신경망을 학습 모델로 활용할 만하다. 또한, 전파고도계의 고도 추정에 딥러닝을 처음 적용하는 본 연구에서는 구현이 간단한 인공신경망을 활용하여 그 가능성을 확인하고자 하였다. 간섭계(interferometry) 전파고도계와 같이 지표면으로부터 고도와 각도를 동시에 측정할 때나 비트주파수의 개수를 늘려 고해상도로 고도를 측정하고자 할 때는 입력 데이터의 크기가 커지므로 부분 연결 구조로 복잡도를 획기적으로 낮춘 컨벌루션 신경망(CNN, convolutional neural network)을 학습 모델로 적용해야 할 것이다. 전파고도계의 고도 측정 주기가 짧은 경우 고도가 급변하지 않으므로, 이전 주기에서 측정한 고도를 일부 반영하여 고도를 추정할 수도 있다. 이 경우에는 과거의 데이터를 고려하여 순차적으로 학습해야 하므로 순환 신경망(recurrent neural network)을 학습 모델로 활용하는 것이 더 적합할 것이다. 전파고도계의 고도 추정을 위한 학습 모델로 컨벌루션 신경망과 순환 신경망을 활용하는 것은 추후 수행해야 할 연구과제로서 가치가 있다.

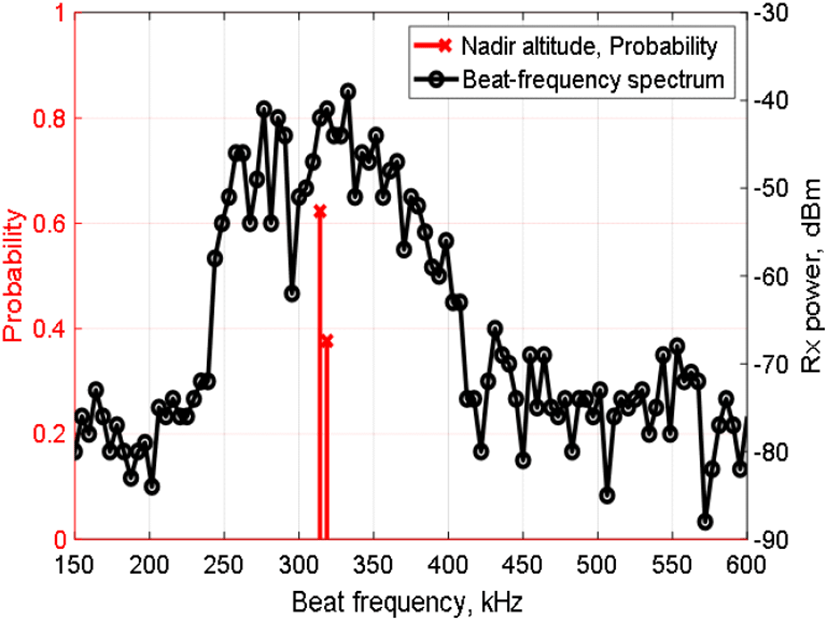
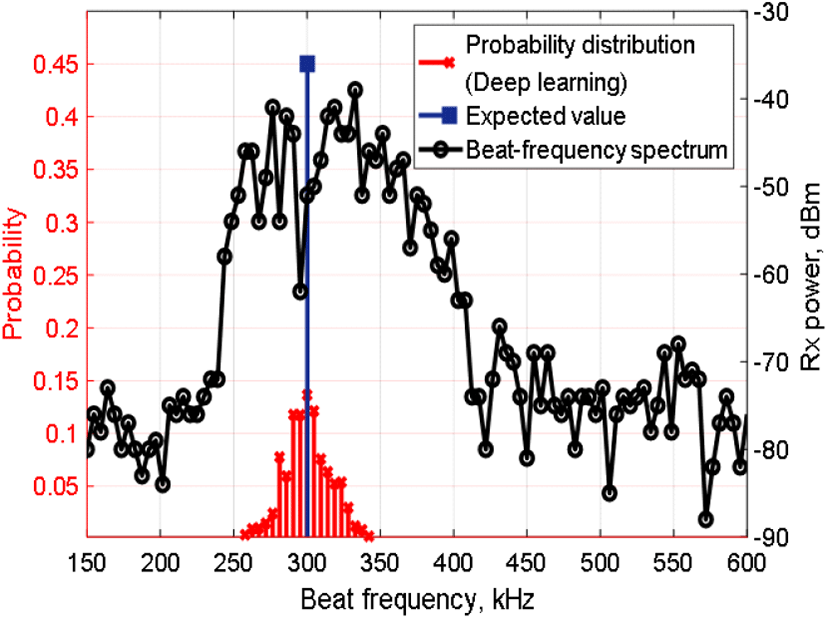
학습 데이터인 비트주파수 스펙트럼과 레이블인 레이저 거리 측정기가 측정한 직하방 고도를 그림 4에 나타내었다. 레이블인 직하방 고도는 확률분포로 변환한다. 직하방 고도에 해당하는 비트주파수에 1의 확률을 할당하는데, 변환된 값이 비트주파수 해상도 사이에 있을 경우 인접한 양 주파수 간의 거리에 따라 확률을 할당하였다. 전파고도계의 비트주파수 해상도는 약 4.7 KHz이고, 레이저 거리 측정기가 측정한 고도를 비트주파수로 변환한 값이 311.2 KHz이므로 직하방 고도가 309.4 KHz에 해당할 확률이 62 %, 314.1 KHz에 해당할 확률이 38 %가 된다.

그림 4. | Fig. 4. 학습 데이터 세트 | Training data set.

Download Original Figure

전파고도계의 학습 과정과 고도 추정 과정에 적용되는 인공신경망을 그림 5에 나타내었다. 고도 추적을 위한 중간주파수(intermediate frequency) 필터(filter)의 대역폭(bandwidth)이 600 KHz이고, 비트주파수의 해상도가 약 4.7 KHz이다. 고도 추적 필터 내 운용되는 비트주파수 개수가 128개이므로 입력층과 출력층의 노드 수는 128개로 결정된다. 입력층은 고도 추적 대역 내 128개 전체 비트주파수의 수신전력을 입력받는다. 은닉층과 출력층의 각 노드는 퍼셉트론(perceptron)으로 다수 신호의 가중합을 입력으로 받아 활성화 함수를 통해 하나의 출력신호로 변환한다. 출력층은 128개 각 비트주파수가 직하방 고도일 확률분포를 출력한다. 은닉층의 수 결정에는 정해진 법칙은 없지만, 이미지 분류와 같은 중간 정도로 복잡한 문제에는 일반적으로 은닉층의 수 3~5개를 활용한다는 정보를 바탕으로 은닉층의 수를 1개부터 점진적으로 늘려가며 모의실험(simulation)을 반복적으로 수행하였다. 은닉층의 수에 따른 고도 오차의 평균과 표준편차를 비교해 본 결과 은닉층이 3개 이상이면 유사한 수준의 값을 얻을 수 있어 은닉층은 3개로 결정하였다. 은닉층의 노드 수를 128개, 256개, 512개로 늘려가며 모의실험한 결과 고도 오차의 평균과 표준편차가 모두 유사한 수준이었다. 은닉층의 노드 수는 입출력 층의 노드 수와 같은 128개로 구성하였다. 은닉층의 활성화 함수는 식 (1)의 로 표현하였으며, 시그모이드(Sigmoid) 함수이다. 출력층의 활성화 함수는 식 (2)의 로 표현하였으며, 다 범주 출력에 대한 확률분포를 나타내기에 적합한 소프트맥스(softmax) 함수이다.

그림 5. | Fig. 5. 전파고도계의 인공신경망 모델 | ANN model applied to the radar altimeter.

Download Original Figure

$$\begin{array}{l}{z}^{(n)}=h\left(a^{(n)}\right)=\frac{1}{1+e^{-a^{(n)}}},\hfill \\ a^{(n)}=W^{(n)}\cdot z^{(n-1)}\hfill \end{array}$$

(1)

$$y_k=\sigma \left(a_k^{(n)}\right)=\frac{e^{a_k^{(n)}}}{\sum _{i=1}^{128}{e}^{a_i^{(n)}}}$$

(2)

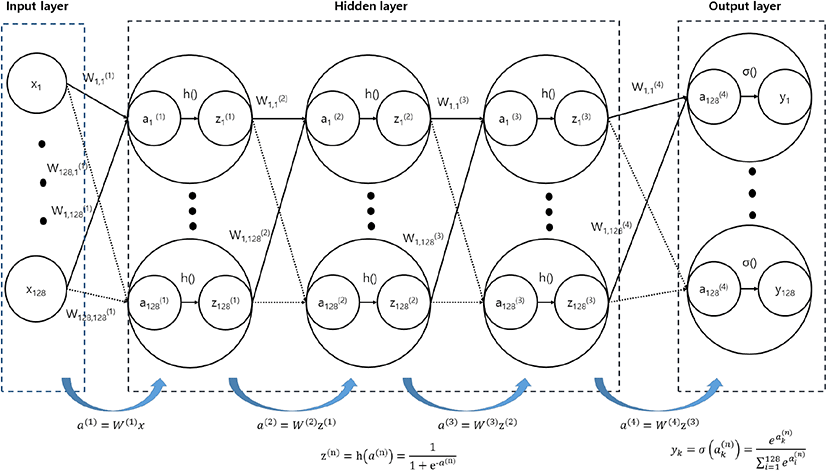
여기서, a⁽ⁿ⁾은 (n)층의 입력으로 (n-1)층의 노드의 가중합 벡터이고, z⁽ⁿ⁾은 활성화 함수 입력 a⁽ⁿ⁾에 대한 출력 벡터이다. W⁽ⁿ⁾은 (n-1)층의 출력과 (n)층의 입력 간 가중치 값을 요소로 갖는 행렬이다.

비트주파수 스펙트럼 입력에 따른 출력과 직하방 고도 간의 오차를 표현하는 함수는 식 (3)의 크로스 엔트로피 손실함수(cross entropy loss function)를 적용하였다.

$$CE=-\sum _{i=1}^{128}\left[t_i\ln \left(y_i\right)+\left(1-t_i\right)\ln \left(1-y_i\right)\right]$$

(3)

여기서, y_i는 출력층 각 노드의 값으로 각각의 비트주파수가 직하방 고도일 확률분포이고, t_i는 직하방 고도에 해당하는 비트주파수에 확률을 할당한 값이다.

비트주파수 스펙트럼 입력에 따른 확률분포 출력과 직하방 고도에 해당하는 비트주파수에 할당된 확률 간의 오차를 오차 역전파법을 통해 출력층에서 은닉층으로 역전파시켜 인공신경망의 각 노드 간 가중치를 갱신한다. 경사하강법은 반복 수행을 통해 손실함수의 최적 해를 찾는 방법으로 학습률에 따라 가중치 값을 조정하면서 오차의 최솟값을 찾는다. 크로스 엔트로피 손실함수는 볼록(convex) 함수이므로 최적화 연산을 수행하여 찾은 값이 전역 최솟값(global minimum)임을 보장한다.

학습 과정의 연산은 전파고도계가 아닌 지상 실험실의 고성능 워크스테이션(workstation) 컴퓨터에서 이루어진다. 고도 추정 과정은 전파고도계에서 4단계의 연쇄적인 행렬 연산으로 수행된다. 인공신경망의 구조가 완전 연결 층이므로 부동 소수점 연산의 수(FLOPs, floating point operations)는 입력과 출력이 각각 128개인 내적(inner product) 연산이 32,640 FLOPs, 512개의 활성화 함수의 연산이 2,048 FLOPs로 총 34,688 FLOPs가 된다. 인공신경망의 입력값, 출력값, 각 가중치는 모두 4-byte 부동소수점(32-bit, float32)으로 저장되므로 필요한 메모리의 용량을 600 kByte이다. 전파고도계에는 Texas instrument 社의 코어당 20 GFLOPS(giga floating point operation per second) 성능을 갖는 듀얼 코어 DSP(digital signal processor)와 512 Mbyte DDR3(double data rate 3) 메모리가 적용되어 있으며, 고도 측정 주기인 10 ms 이내에 시스템 제어 및 고도 추정 연산이 완료된다.

학습 데이터 세트를 입력으로 받아 학습 규칙에 따라 학습하면, 인공신경망의 각 층 노드 간의 가중치를 포함하는 총 4개(W⁽¹⁾~W⁽⁴⁾)의 128✕128 행렬이 계산된다. 고도 추정 과정에서는 임의의 비트주파수 스펙트럼 데이터를 입력하면 학습된 인공신경망의 연쇄적인 행렬 연산을 거쳐 각 비트주파수가 직하방 고도일 확률분포를 출력한다. 학습 데이터와 고도 추정 결과 비교를 위해 그림 4와 같은 데이터를 입력하여 고도 추정한 결과를 그림6에 나타내었다. 표 1에는 그림 6의 측정 지점에서 레이블인 레이저 거리 측정기가 측정한 직하방 고도와 종래의 방법을 이용하여 추정한 고도, 딥러닝을 이용한 고도 확률분포의 기댓값과 최고확률이 나타나는 고도를 비교 정리하였다. 측정 지점은 비트주파수 스펙트럼 넓게 퍼진 형태로 나타나는 산지로 정확한 고도 추정이 어려운 지형이다. 유효고도의 무게중심을 고도로 추정하는 종래의 방법 대비 레이저 거리 측정기가 측정한 직하방 고도가 낮다. 레이블로 레이저 거리 측정기가 측정한 직하방 고도를 활용했으므로 딥러닝을 이용한 고도 추정 결과 역시 종래의 방법 대비 낮게 추정됨을 확인할 수 있다.

표 1. | Table 1. 종래의 방법과 딥러닝 방법에서 추정된 고도비교 | Comparison of altitude estimated by conventional method and DL method.

	Nadir altitude (LRF)	Conventional method	Deep learning method
			Expected value	Max. probability
Beat frequency [KHz]	311.2	317.4	303.7	304.7
Altitude [m]	296.1	299.3	292.5	293.0

Download Excel Table

그림 6. | Fig. 6. 그림 4의 비트주파수 스펙트럼에 대한 고도 추정 결과 | Estimated altitude for the beat-frequency spectrum in Fig. 4.

Download Original Figure

III. 비행시험

기계학습에서 학습 데이터로부터 찾아낸 모델이 실제 데이터에 대해서도 잘 작동하기 위해서는 일반화(generalization)가 중요하다^[10]. 즉, 실제 데이터 특성이 반영되어 있고, 편향되지 않은 학습 데이터를 확보할 필요가 있다. 딥러닝을 이용한 고도 추정 방법에서는 다양한 지형에서 다수의 학습 데이터 세트를 수집하여 인공신경망 모델을 학습시켜야 신뢰도 높은 고도를 추정할 수 있다.

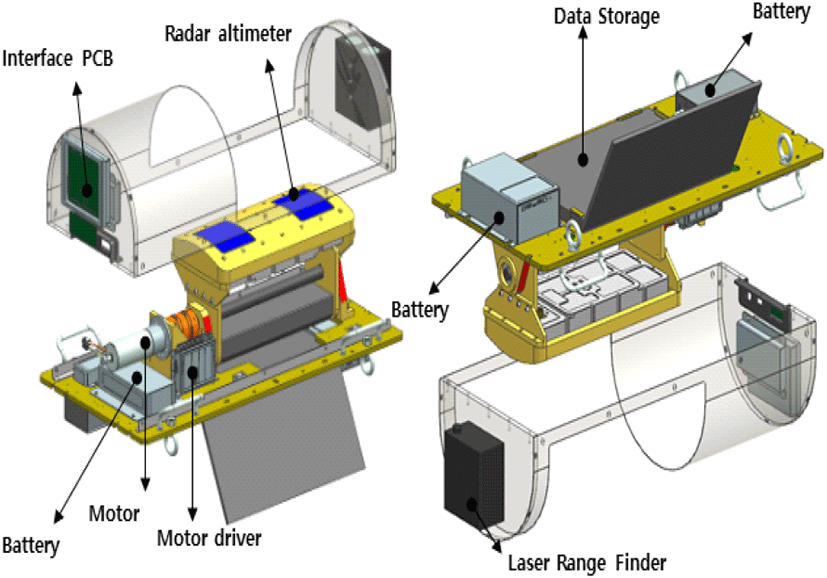
비트주파수 스펙트럼 수집을 위한 전파고도계와 직하방 고도 측정을 위한 레이저 거리 측정기를 포함한 데이터수집장치를 항공기에 탑재하고 비행시험을 수행하였다. 그림 7은 비행시험을 위한 데이터수집장치의 구성도 이다. 전파고도계와 레이저 거리 측정기에 더하여 두 장치가 측정한 고도를 시각 동기에 맞추어 저장하기 위한 노트북 등의 데이터 저장장치가 탑재되고, 각 장비에 전원을 공급하기 위한 배터리 3개가 탑재된다. 전동기와 제어장치가 포함되어 있는데, 전파고도계가 탑재될 비행체의 기동을 모사하기 위한 장치이며, 비행 자세에 따른 신호 특성을 확인하기 위한 것으로 학습 데이터 세트 수집 목적과는 무관하다. 그림 8은 항공기에 탑재한 데이터수집장치의 사진이다. 항공기의 배면에 데이터수집장치를 탑재하고, 대전-무주-금산-논산-부여-대전을 거치는 경로를 따라 비행하며 산지, 수면, 평지, 도시 등 다양한 지형의 상공에서 다수의 학습 데이터 세트를 수집하였다.

그림 7. | Fig. 7. 데이터수집장치의 구성 | Configuration of the data-acquisition-system.

Download Original Figure

그림 8. | Fig. 8. 데이터수집장치의 항공기 탑재 사진 | Photo of the data-acquisition-system mounted on an airplane.

Download Original Figure

비행시험을 통해 수집한 비트주파수 스펙트럼의 총량은 약 30,000개였으며, 각 비트주파수 스펙트럼 데이터에 레이저 거리 측정기 측정 고도를 레이블로 붙여 데이터 세트를 구성하였다. 데이터 세트를 1,000개씩 30개 블록으로 나눈 후, 이 중 무작위로 20개 블록을 추출하여 학습 과정에 투입하였다. 나머지 10개 블록은 고도 추정 과정에 입력하여 각 비트주파수 스펙트럼에 대한 직하방 고도 확률분포를 출력으로 얻고, 기댓값을 계산하였다.

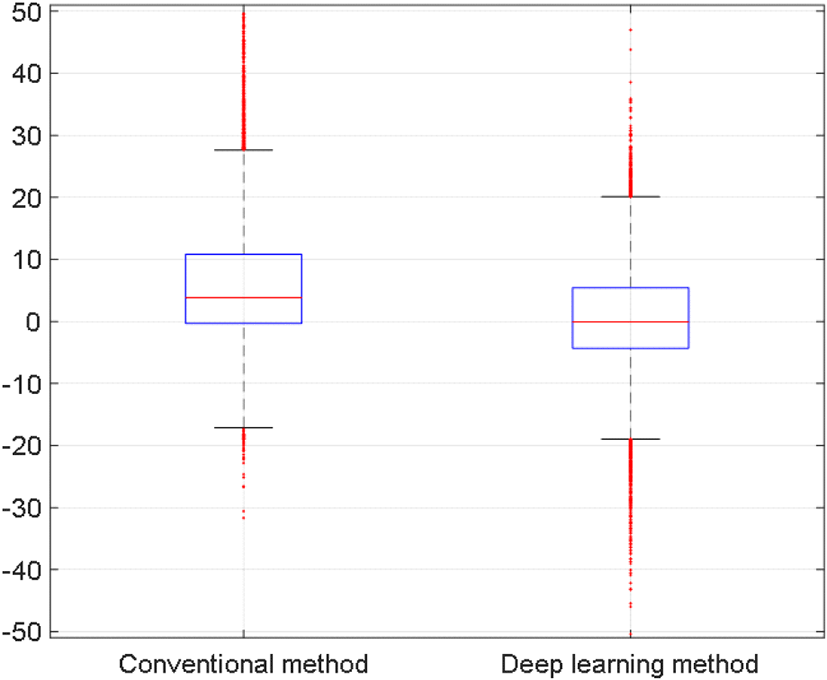
레이저 거리 측정기가 측정한 고도를 정확한 직하방 고도로 간주하고, 종래의 방법과 딥러닝 방법을 이용해 추정한 고도와 직하방 고도를 비교하여 통계적인 오차 분석을 수행하였다. 고도 추정 과정에 투입된 10개 블록의 데이터 세트에 대해 직하방 고도 대비 종래의 고도 추정 방법과 딥러닝을 이용한 고도 추정 방법의 고도 오차를 그림 9의 상자 그림(box plot)에 표현하였고, 표 2에는 고도 오차의 평균과 표준편차를 정리하였다. 상자 그림에서 상자 내부의 선은 2사분위수(중앙값)를 나타낸다. 2사분위수를 기준으로 전체 데이터의 50 %는 상위에 나머지 50 %는 하위에 분포한다. 상자 그림의 상자는 1사분위수(25 %)부터 3사분위수(75 %) 데이터의 분포를 나타낸다. 상자 그림을 통해 종래의 고도 추정 방법이 딥러닝을 이용한 고도 추정 방법 대비 고도 오차가 양(+)의 값으로 치우쳐 있음을 알 수 있다. 종래의 고도 추정 방법은 고도 오차의 평균이 약 6 m였으며, 딥러닝을 이용한 고도 추정 방법은 고도 오차의 평균이 0 m에 가까웠다. 종래의 고도 추정 방법의 고도 오차의 평균은 양의 값을 가지는데, 이는 직하방 고도와 비교해 종래의 방법으로 추정한 고도가 평균적으로 큰 값을 가짐을 의미한다. 반면, 딥러닝을 이용한 고도 추정 방법의 경우 직하방 고도를 기준으로 학습하였으므로 고도 오차의 평균이 0 m에 수렴하고, 오차의 분포도 0 m 기준으로 양(+)/음(−)방향으로 대칭적으로 나타난다.

그림 9. | Fig. 9. 종래의 방법과 딥러닝 방법 간의 고도 오차 비교 | Altitude error comparison between conventional method and DL method.

Download Original Figure

종래의 고도 추정 방법과 딥러닝을 이용한 고도 추정 방법의 고도 오차 평균 차이는 전파고도계 안테나와 레이저 거리 측정기 광학렌즈의 빔 폭 차이가 주된 원인이다. 전파고도계는 전파를 활용하므로 상대적으로 넓은 안테나 빔 폭을 가지며, 산지에서는 안테나 빔이 조사하는 지형 내 여러 거리에서 반사되는 신호가 수신된다. 산지는 대부분이 상승․하강 경사면이고, 안테나 빔이 경사면을 비출 때는 평지에서 빔을 기울이는 경우와 유사하게 빔이 비추는 영역이 경사면을 따라 넓어지므로 비트주파수 스펙트럼의 형태가 수신전력이 첨둣값을 갖는 비트주파수를 기준으로 큰 주파수 쪽으로 퍼지는 형태가 된다. 따라서 종래의 고도 추정 방법에 따라 비트주파수 스펙트럼 내 유효고도의 무게중심을 구하면 상대적으로 큰 비트주파수(높은 고도)가 선택된다. 반면, 레이저 거리 측정기의 경우 광학렌즈의 빔 폭이 좁아 상대적으로 낮은 고도가 측정된다. 딥러닝을 이용한 고도 추정 방법의 경우 레이저 거리 측정기가 측정한 직하방 고도를 레이블로 학습하였으므로, 레이저 거리 측정기와 평균적으로 유사한 고도를 추정한다.

비트주파수 스펙트럼 30,000개 모집단에 대해 10,000개의 표본을 무작위로 추출하여 표본평균과 표본표준편차를 계산한 결과가 표 2이다. 모집단의 고도 오차가 정규분포를 따른다고 가정하면, t-분포(student’s t-distribution)를 이용해 100(1−α) % 신뢰 구간에 대해 식 (4)에 따라 모평균을 추정할 수 있다^[11].

여기서, m은 모평균, $\overline{X}$는 표본평균, t_a/2,n−1은 기각한계값(critical value), $\overline{S}$는 표본표준편차, n은 표본의 수, N은 모집단의 수이다. $\sqrt{\frac{N-n}{N-1}}$은 유한모집단 수정계수(FPC, finite population correction)이다.

고도 오차의 모평균을 추정한 결과 신뢰도 99 %에서 종래의 고도 추정 방법의 경우 5.71~6.11 m 구간에, 딥러닝을 이용한 고도 추정 방법의 경우 0.01~0.41 m 구간에 있다. 통계적 추정 결과 두 방법 간 고도 오차 모평균의 차이가 5 m 이상이었다.

종래의 고도 추정 방법과 딥러닝을 이용한 고도 추정 방법의 고도 오차 평균의 차이가 유의미한지 검증하기 위해 통계적 가설검정을 수행하였다. 두 방법의 고도 오차 표본은 같은 고도 측정 결과로부터 추출된 것이므로 서로 종속이다. 이러한 자료를 쌍체 표본(paired samples)이라고 한다. 모집단의 쌍체 차(d)의 표준편차 σ_d가 알려지지 않았고, 표본의 크기가 크다면(n ≧ 30), 평균 μ_d에 대한 가설검정을 위해서 t-분포를 사용할 수 있다^[11]. ‘1 % 유의수준에서 딥러닝 방법을 이용하는 것이 종래의 방법과 비교하였을 때 평균적으로 고도 오차를 줄일 수 있는가?’가 본 가설검정의 질문이다. 두 모평균(고도 오차의 평균)의 차에 대하여 귀무가설은 ‘두 방법이 고도 오차에서 유의미한 차이가 없다.’이고, 대립가설은 ‘고도 오차에서 두 방법이 유의미한 차이가 있다.’가 된다. 가설검정 결과 p-값(p-value, probability value)을 구해보면, 유의수준인 0.01보다 작아서 귀무가설이 기각되고, 대립가설이 채택된다. 따라서 두 방법에 따라 구해진 고도 오차의 평균에는 유의미한 차이가 있고, 딥러닝 방법을 이용하는 것이 종래의 방법 대비 평균적으로 고도 오차를 줄일 수 있다고 할 수 있다.

전파고도계 고도 오차의 표준편차는 항공기가 비행한 다양한 지형의 형태와 매질, 고도에 따라 가변하는 해상도에 의해 비행할 때마다 조금씩 다른 값으로 나타난다. 본 비행시험과 같이 수백 m 고도로 주로 산지 상공(전체의 2/3 구간)을 비행하였을 경우 고도 오차의 표준편차가 표 2에 나타낸 수준이었다. 종래의 방법과 딥러닝 방법은 같은 지형과 고도에서 수집된 비트주파수 스펙트럼에 대해 고도를 추정하는 방법만 달리하므로 고도 오차의 표준편차는 유사한 수준이어야 한다.

인공신경망을 학습하는 과정에서 과적합(overfitting) 여부를 판단하기 위해 고도 오차의 표준편차를 활용하였다. 학습된 인공신경망을 이용하여 고도를 추정한 결과, 고도 오차의 표준편차가 종래의 고도 추정 방법의 그것과 유사한 수준이 되도록 학습률(learning rate)과 학습 횟수(epoch)의 수를 조정하였다. 학습률을 0.02, 학습 횟수를 100회 수행하였을 때 표 2의 고도 오차의 표준편차를 얻을 수 있었다. 학습률을 더 낮추거나, 학습 횟수를 1,000회로 늘리면 고도 오차의 표준편차가 11 m 수준으로 커졌으며, 이는 과적합에 의한 것으로 판단된다. 기계학습에서 일반화 성능이 저하되는 주요인이 과적합이므로 이를 방지하는 것이 모델의 성능 확보를 위해 중요하다.

IV. 결 론

전파고도계는 지형참조항법의 지형 측정 센서로 활용된다. 지형참조항법이 주로 운용되는 산지에서 전파고도계가 정확한 고도를 추정할 수 있어야 비행체의 위치를 정확히 계산할 수 있다.

종래의 전파고도계는 직관에 따라 수신전력이 임계값 이상인 유효고도의 무게중심을 고도로 추정하였다. 직관의 임의성을 배제하고 정확도 높은 직하방 고도의 추정을 위해 전파고도계에 딥러닝 방법을 도입하였다. 임의의 지형에서 측정된 각 주파수에서 수신전력을 입력하여 각 비트주파수가 직하방 고도일 확률분포를 출력하도록 인공신경망을 구성하였다. 전파고도계의 비트주파수 스펙트럼과 레이저 거리 측정기로 동시에 측정한 직하방 고도를 입력하여 인공신경망을 지도 학습하였다.

비행시험을 통해 다양한 지형에서 비트주파수 스펙트럼과 레이저 거리 측정기가 측정한 직하방 고도를 수집하여 학습과 고도 추정(추론)을 수행하고, 종래의 방법과 딥러닝 방법의 고도 오차를 통계적으로 비교⋅분석하였다. 직하방 고도 비교하였을 때 종래의 방법 대비 딥러닝 방법으로 고도를 추정한 결과 평균적으로 고도 오차가 적어지는 결과를 얻을 수 있었다. 종래의 방법과 딥러닝 방법의 고도 오차의 표준편차가 유사하게 학습률과 학습 횟수를 조정하여 인공신경망을 학습함으로써 과적합을 방지하였다.