클러터 도플러 확산 회피를 위한 PRF 선택 알고리즘

Ⅰ. 서 론

레이다가 저고각 표적을 향해 빔을 방사하였을 시, 지상 클러터에 의한 영향을 줄이는 것은 레이다 설계의 주요 과제 중 하나이다. 지상 클러터의 영향이 강해지면 표적의 탐지확률을 떨어뜨리므로, 이러한 클러터에 대응하는 다양한 방안들이 알려져 있다. 일반적으로 사용하는 방법은 좁은 송신빔 사용, 레이다 고고도 배치, 저속 표적 삭제, 단파장 파형 사용 등이 있다^[1].

그러나 이러한 방식으로 대응이 어려운 형태의 클러터가 클러터 도플러 확산이다. 클러터의 신호 크기가 충분히 큰 특정 거리에서는 모든 도플러 영역에 걸쳐 배경잡음보다 높은 파워의 잡음이 나타난다. 본 논문에서는 여러 가지 원인에 의한 도플러축 부엽과 이로 인해 RV(range-velocity) map 상에 발생하는 띠 형태의 잡음을 '클러터 도플러 확산'으로 명명하여 서술한다.

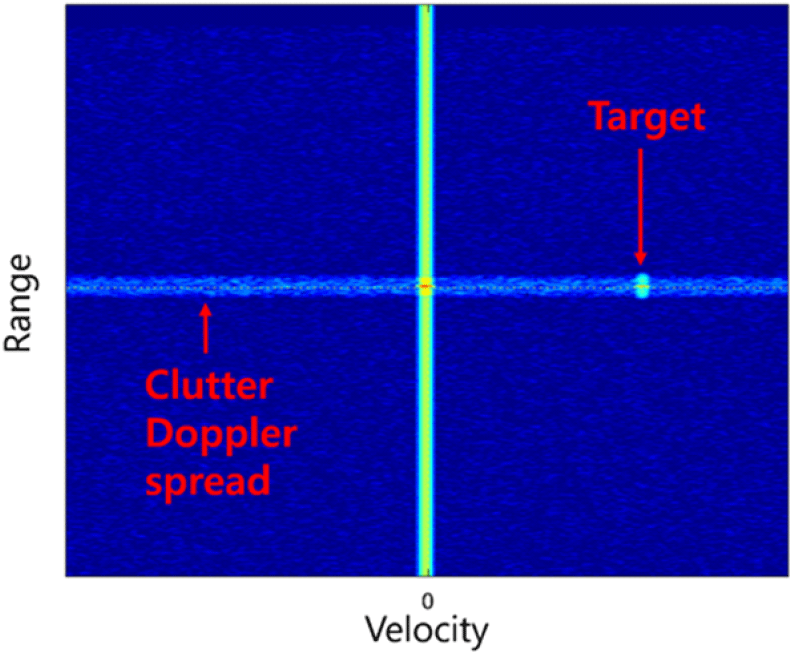
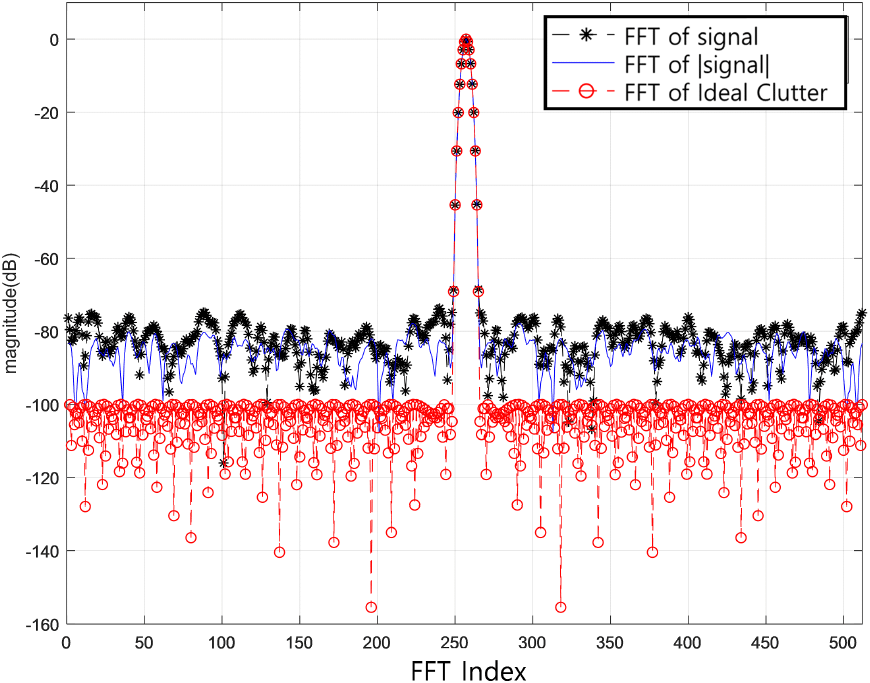
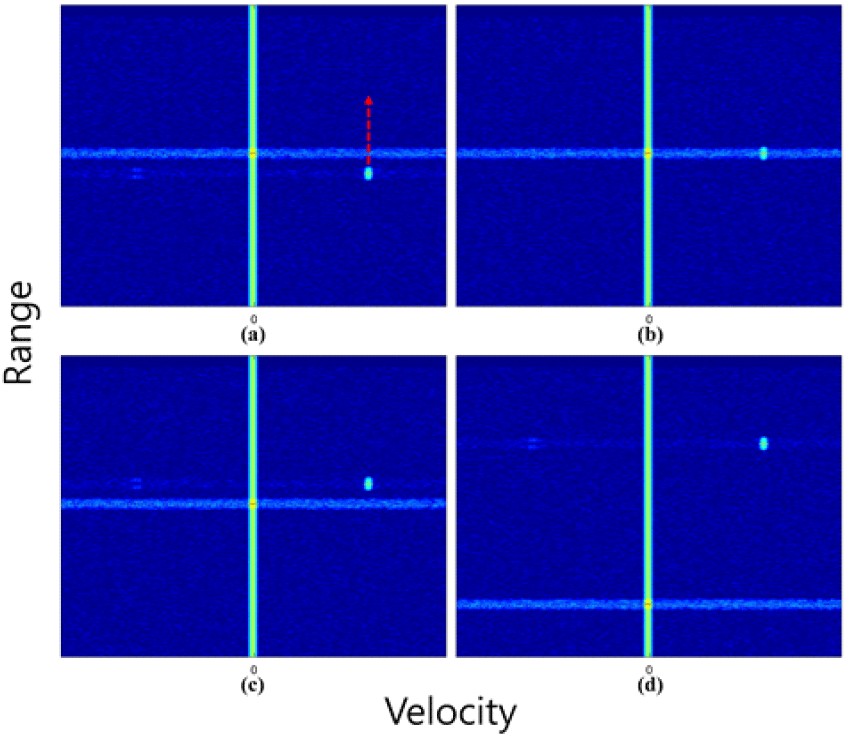
그림 1은 클러터 도플러 확산의 한 예이다. 크기가 큰 지상 클러터가 존재할 시 클러터 도플러 확산이 발생할 수 있고, 표적이 이곳에 위치하는 경우 탐지 성능이 감소한다. 이러한 클러터 도플러 확산의 발생 원인으로 클러터의 신호 크기와 위상에 의한 두 가지 원인이 고려된다. 첫 번째 원인은 지상 클러터의 수신 신호에서 펄스 간 신호의 크기 변화가 큰 경우이다. 이상적인 지상 클러터의 수신 신호는 각 펄스마다 동일한 크기를 가진다. 하지만 클러터 신호 크기가 일정하지 않은 경우 펄스-도플러 처리(pulse-Doppler processing) 시 도플러축에서 부엽을 유발한다. 신호 크기의 변화가 도플러축 부엽을 만드는 것을 확인하기 위해 지상 클러터 신호, 신호의 크기, 이상적인 클러터 신호에 각각 Chebyshev window를 적용한 신호처리결과를 그림 2에 나타내었다. 그림 2는 지상 클러터의 수신 신호(흑색), 신호의 크기(청색), 이상적인 클러터 신호(적색)의 신호 크기를 정규화하여 주파수축에서 나타낸 것이다. 신호와 신호 크기는 이상적인 클러터 신호의 처리결과에 비해 20 dB 정도의 속도축 부엽 억제 성능 열화를 보였다. 한편 지상 클러터의 수신 신호와 신호 크기의 처리결과에 유사한 성능 열화가 관찰되는 것은 위상 잡음의 영향이 없더라도 현상이 발생함을 보여준다. 두 번째 원인은 위상 잡음에 의한 도플러 부엽이다^[2]. 시간에 따라 변하는 신호의 위상은 도플러축 부엽으로 나타난다. 이러한 위상 잡음의 원인은 레이다의 열잡음이다^[3]. 클러터 도플러 확산과 표적을 분리하기 위해 레이다는 추적 중 표적의 거리 및 속도에 따라 적절한 PRF의 파형을 선택해야한다^[4]. 그림 3은 레이다에서 멀어지는 표적과 클러터 도플러 확산의 수신 신호를 RV map에 나타낸 것이다. 그림 3(a)는 클러터 도플러 확산 진입 직전의 표적이다. 동일한 파형으로 추적할 경우 다음 송신빔에서 그림 3(b)와 같이 표적이 클러터 도플러 확산에 진입하고, 마지막 송신빔에서 그림 3(c)와 같이 표적이 클러터 도플러 확산에서 탈출한다. 그러나 표적과 클러터가 동일한 거리에 있는 것이 아니라면 그림 3(b)에서 적절한 파형을 선택하여 그림 3(d)와 같이 표적 신호를 클러터 도플러 확산으로부터 분리할 수 있다. 본 논문에서는 PRF 선택 알고리즘을 사용하여 레이다가 클러터 영향을 회피하는 방안을 제안한다.

그림 1. | Fig. 1. RV map 상 클러터 도플러 확산과 내부에 존재하는 표적 신호 | RV map of clutter Doppler spread and target on CDS.

Download Original Figure

그림 2. | Fig. 2. 주파수축에서 지상 클러터 신호(흑색), 신호의 크기(청색), 이상적인 클러터 신호(적색)의 정규화된 크기 | Normalized magnitude of signal (black), absolute value of signal (blue), ideal clutter signal (red) in frequency domain.

Download Original Figure

그림 3. | Fig. 3. RV map 상 클러터 도플러 확산과 원거리 방향으로 이동중인 표적. (a) 통과 직전 (b) 통과 중 (c) 통과 후, (d) 파형, PRF 변경 시 (b). | RV map of clutter Doppler spread and outgoing target. (a) before CDS, (b)on CDS, (c)after CDS, (d), (b) when changing PRF of waveform.

Download Original Figure

II. Representative Value and Threshold Value

RV map 상에서 클러터 도플러 확산이 존재하는 거리 게이트는 인접한 거리 게이트에 비해 전체 에너지가 높지 않다. 따라서 거리 게이트별 전체 에너지 총합 또는 신호 크기 평균값을 기준으로 해당 거리의 클러터 도플러 확산 유무를 판별하는 것은 적절하지 않으며, 중간값(median)이 대푯값으로서 적절하다. 각 대푯값의 중간값에 잡음 특성을 반영한 상수를 곱하여 문턱값을 결정할 수 있다. 이를 수식으로 쓰면 식 (1)과 같다.

식 (1)에서 T는 문턱값, T_offset은 상수 offset, MED( · )는 중간값을 구하는 함수, A_i는 i 번째 거리 게이트 대푯값이다. A_i는 식 (2)와 같이 구할 수 있다.

식 (2)에서 A_i,j는 i 번째 거리 게이트, j 번째 도플러 게이트를 의미한다. 중간값 계산은 정렬 알고리즘을 사용하는 경우 시간 복잡도가 O(nlogn)이다. 반면, median of medians 및 quickselect 알고리즘을 혼합하여 적용하는 경우 시간 복잡도는 O(n)이 된다. 그러나 거리 게이트와 도플러 게이트가 충분히 크지 않다면 이러한 알고리즘은 오히려 정렬 알고리즘보다 느린 속도를 보여준다. 따라서 속도 문제를 해결하기 위해 median 대신 mean of mins 방법을 적용할 수 있다. 이에 따른 대푯값 결정 방법은 식 (3)과 같다.

식 (3)에서 M은 FFT size, j는 도플러 게이트, L은 도플러 방향 샘플 간 간격이다. 같은 방법으로 전체 문턱값도 mean of mins로 구할 수 있으며, 수식은 식 (4)와 같다.

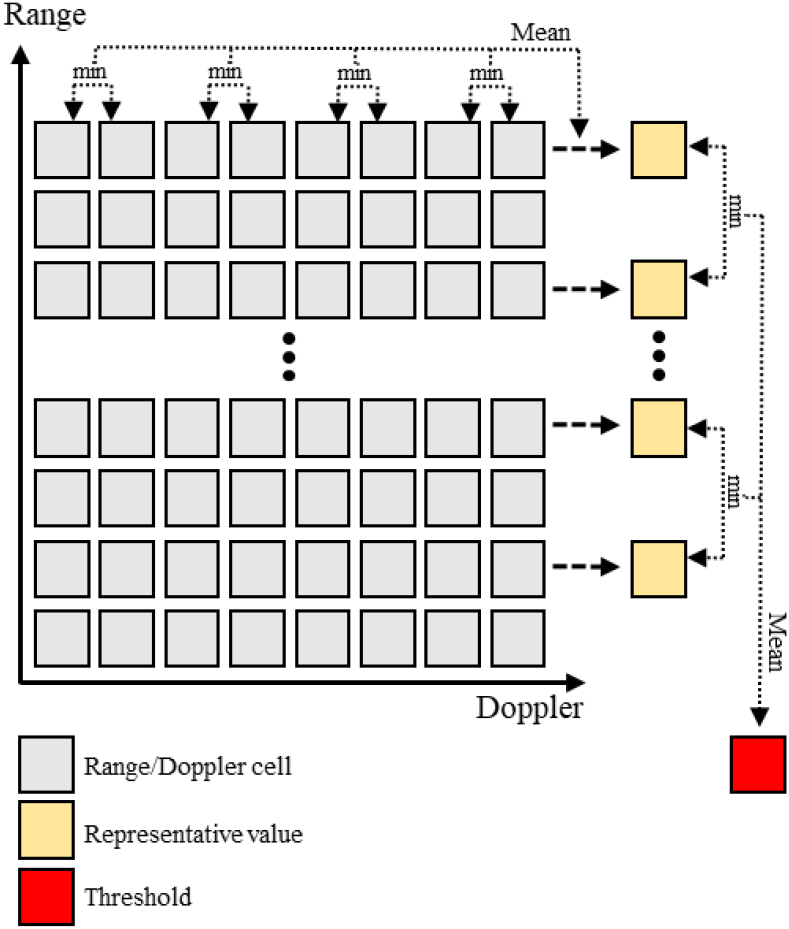
식 (4)에서 A는 median이 아닌 mean of mins를 사용함으로서 잃은 손실 보상, N은 거리 게이트 개수, K는 거리 방향 샘플 간 간격이다. 이러한 과정의 예시를 L은 2, K는 3로 두고 그림 4에 표현하였다.

그림 4. | Fig. 4. 문턱값 계산 예시 | Example of threshold calculation.

Download Original Figure

III. Prediction of Folded Range on Every Waveform

추적 중인 표적의 다음 거리가 클러터 도플러 확산이 존재하는 거리 게이트에 들어가는 경우 해당 파형을 사용하지 않는 설계가 필요하다. MPRF의 경우, PRI가 길어 서로 다른 클러터에서 발생한 잡음 간 결합하는 경우가 HPRF에 비해 적으므로 거리축으로 넓은 노이즈가 발생한다. 근거리 지상 클러터의 영향이 클러터 도플러 확산 생성에 가장 큰 영향을 주므로, MPRF 내에서 추적 파형을 바꿔 새로 folding되더라도 클러터 도플러 확산의 위치는 거의 변화하지 않는다. 따라서, MPRF 추적 시에는 표적의 예측 위치가 현재 발생한 클러터 도플러 확산에 빠지지 않도록 해야 한다. K개의 파형 중 다음 추적 파형을

결정한다고 할 때, RV map 상 표적의 다음 예측 거리는 식 (5)와 같다.

식 (5)에서 R_k,1는 k 번째 파형을 사용했을 때 1 번째 PRI 내부에 클러터가 존재하는 경우 RV map 상 표적의 예측 거리, R_pred는 추적 필터의 거리 예측값, PRI_k는 k 번째 파형의 PRI(pulse repetition interval), c는 빛의 속도이다. 식 (5)는 클러터 도플러 확산이 파형의 첫 번째 PRI 내부에 있는 클러터에 의해 만들어졌다는 가정에 근거한다. 클러터 도플러 확산을 생성한 클러터가 2 번째 PRI, 혹은 그 이상의 거리에 존재하는 경우 식 (5)로 표적 위치를 찾더라도 클러터 위치 또한 folding되어 바뀌므로 의미가 없다. MPRF는 PRI가 HPRF에 비해 크기 때문에 2 번째 PRI까지만 고려하여 클러터 위치를 예측한다. 다만, 클러터 위치를 새로 folding하여 계산하는 것은 많은 연산량을 필요로 하므로 표적 위치를 옮겨 노이즈 대비 표적 위치를 추정한다. 이에 따른 표적의 다음 예측 거리는 식 (6)과 같다.

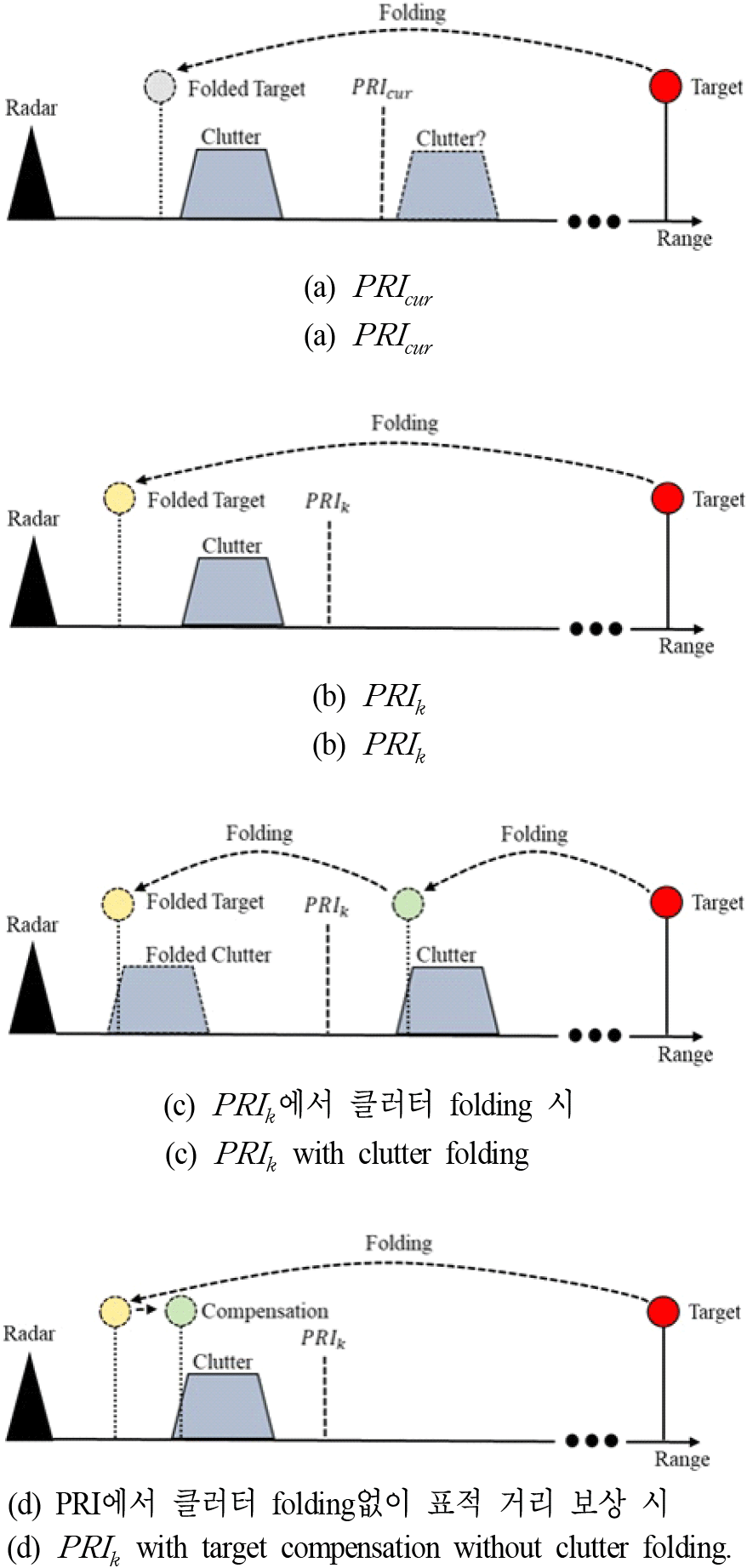
식 (6)에서 R_k,2는 k 번째 파형을 사용했을 때, 2 번째 PRI 내부에 클러터가 존재하는 경우 RV map 상 표적의 예측 거리, PRI_cur는 사용된 빔의 PRI, PRI_k는 k 번째 파형의 PRI이며, 이를 그림 5에 나타내었다. 그림 5(a)에서 PRI_cur 파형 사용 시 클러터와 레이다와의 거리는 정확히 알 수 없다. 클러터가 PRI_k 내부에 있는 경우, 그림 5(b)와 같이 단순한 folding으로 표적이 클러터 도플러 확산 내부에 존재할지 예측가능하다. 그러나, 클러터가 PRI_k 외부에 있는 경우 클러터 또한 folding되어 나타나므로 이에 대한 연산이 추가로 필요하다. 이 때, 연산량이 과도하게 커지게 된다. 따라서, 그림 5(d)와 같이 표적의 위치를 보상하여 현재 클러터 위치 정보만으로 PRI_k 바깥에 위치한 클러터에 표적이 위치할 것인지 예측한다.

그림 5. | Fig. 5. 파형별 클러터 위치에 따른 표적 거리 예측 | Target range prediction considering clutter position on each waveform.

Download Original Figure

표적의 예측 거리 중 하나가 클러터 도플러 확산 내부에 존재하는 경우, k 번째 파형은 다음 추적 파형 스케줄링에서 우선 순위를 낮춘다. HPRF는 PRI가 짧아 근거리 클러터를 모두 고려한다면 folding 횟수가 많기 때문에 연산량이 매우 크다. 따라서, 모든 파형에 대해 예측하는 MPRF와는 달리, HPRF는 현재 사용하는 파형만 고려한다. 표적이 현재 속도로 계속 기동할 시 클러터 도플러 확산을 벗어나는 시간을 계산하고, 그 시간 동안 현재 파형의 스케줄링 우선 순위를 낮춘다. 계산에 필요한 수식은 MPRF와 동일하다. 전체 알고리즘은 그림 6의 순서도에서 확인할 수 있다.

그림 6. | Fig. 6. 알고리즘 순서도 | Algorithm flow chart.

Download Original Figure

Ⅳ. 결 과

표 1은 민항기 표적을 대상으로 레이다 송신 시험한 결과를 나타낸 것이다. 총 9개의 표적에 대해 시험을 수행하였으며, 각 표적의 출발 지점과 종료 지점에 대한 방위각(Az), 고각(El), 시선 거리(range), 고도(height), 평균 시선 속도(avg vel.) 정보를 기재하였다. 표의 가장 오른쪽 열 'CDS/all beam count'는 추적 중 사용된 모든 빔 개수 대비 클러터 도플러 확산(CDS) 대응 알고리즘 사용 횟수를 나타낸 것이다. 저고각 표적의 경우 클러터에 진입하는 경우가 많아 알고리즘의 효용이 높았다. 고고각에 존재하는 표적은 클러터에 의한 영향이 적기 때문에 알고리즘 사용 빈도가 적거나 사용되지 않았다. 원거리, 저고각 표적의 경우 빔 내부에 지상 클러터가 광범위하게 존재하였으나 알고리즘이 높은 빈도로 적용되어 표적이 클러터 도플러 확산을 회피하였다. 알고리즘 작동 시 folding된 표적의 신호가 효과적으로 클러터 도플러 확산을 회피하는 것을 확인하였다.

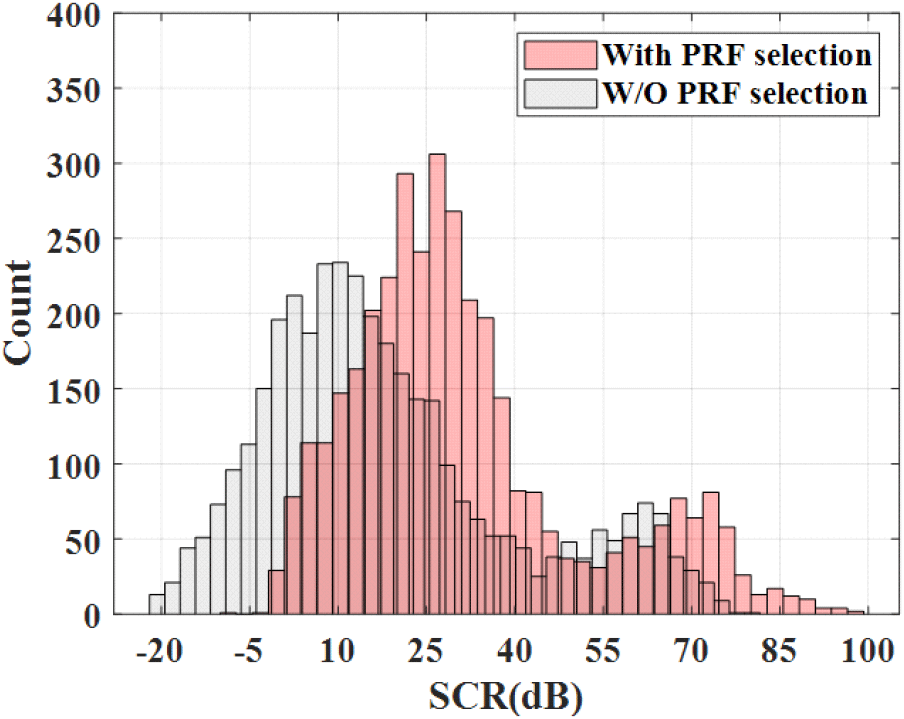
그림 7은 민항기를 대상으로 송신시험을 수행한 결과이며, PRF 선택 알고리즘이 사용된 경우의 표적 SCR (signal to clutter ratio)과 사용되지 않은 경우의 표적 SCR을 비교한 히스토그램이다. 시험은 PRF 선택 알고리즘을 적용하여 시행하였으며, PRF 선택 알고리즘이 미적용된 SCR의 경우 클러터 도플러 확산의 신호 크기를 바탕으로 역산하였다. 클러터 도플러 확산이 존재하는 경우 PRF 선택 알고리즘이 적용될 시 약 15 dB의 SCR 이득이 있음을 확인하였다.

그림 7. | Fig. 7. PRF 선택 알고리즘 적용 전후 SCR 비교 | Comparison of SCR with and without PRF selection algorithm.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 지상 클러터에 의해 발생하는 클러터 도플러 확산을 회피하는 운용 기법을 제안하였다. 중간값에 비해 비교적 빠르게 대푯값을 계산하는 방법을 사용하여 특정 거리에 클러터 도플러 확산이 존재하는지 확인하였고, 파형별로 표적의 위치를 계산하여 해당 클러터를 회피하는 기법을 제안하였다. MPRF와 HPRF의 클러터 특성을 고려하여 각각 다른 기법을 적용하였고 민항기를 대상으로 시험하여 알고리즘의 효용을 확인하였다.