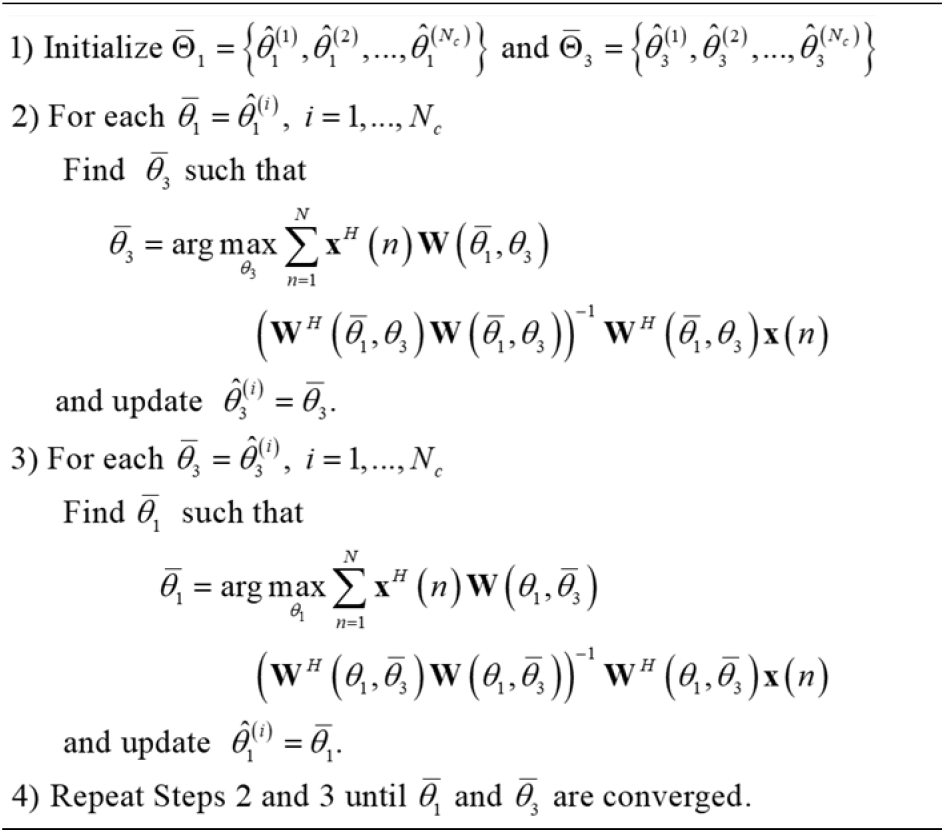Study of Two-Target Elevation Estimation Techniques Using Refined ML in a Multipath Environment

Kim, Ji-Won; Kang, Jong-Sung; Park, Jaehyun; Park, Minkyu; Yang, Wooyong

doi:10.5515/KJKIEES.2024.35.7.595

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(7):595-603

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.7.595

논문/REGULAR PAPER

다중 경로 환경에서 Refined ML을 이용한 두 표적 고각 추정 기법 연구

김지원

, 강종성

, 박재현^†

, 박민규^*

, 양우용^*

Study of Two-Target Elevation Estimation Techniques Using Refined ML in a Multipath Environment

Ji-Won Kim

, Jong-Sung Kang

, Jaehyun Park^†

, Minkyu Park^*

, Wooyong Yang^*

Author Information & Copyright ▼

^{부경대학교 전자정보통신공학부 전자공학전공}

^*한화시스템

^{Maj. of EE, Div. of Electronics and Communications Engineering, Pukyong National University}

^*Hanwha Systems

^†Corresponding Author: Jaehyun Park (e-mail: jaehyun@pknu.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 03, 2024; Revised: Apr 29, 2024; Accepted: Jun 03, 2024

Published Online: Jul 31, 2024

요 약

저고도로 비행하는 물체의 각도를 정확히 추적하기 위해서는, 지표면으로부터의 여러 간섭에 능동적으로 대응할 수 있어야 한다. 다중 경로의 기하학적 관계를 활용하는 Refined ML(maximum likelihood) 기법은 다중 경로 등의 방해 요소로부터 상대적으로 우수한 고각 성능 추정 성능을 보인다고 알려져 있다. 하지만, 기존 고각 추정 기법들은 하나 이상의 표적이나 간섭 신호가 존재할 경우, 고각 추정 성능 저하가 발생된다. 또한, 두 표적이 존재할 때 Refined ML 기법을 통해 추정하는 파라미터의 개수가 늘어날수록, 계산량은 기하급수적으로 증가한다는 단점이 존재한다. 본 논문에서는 두 개의 표적이 존재할 때, ML 추정 식을 유도하고, 직접 경로와 반사 경로의 기하학적 관계와 최소평균제곱오차 기법을 이용한 복소 포락선 추정치 결과를 접목하여 두 표적 고각 추정을 위한 Refined ML 기법을 제안한다. 또한, 2차원 탐색 과정을 회피하기 위한 저복잡도 반복(iterative) Refined ML 기법을 제안한다. 기존 Refined ML, BDML(beam domain ML), 제안하는 반복 Refined ML 기법의 평균 제곱근 오차 비교를 통해 제안하는 알고리즘의 성능을 검증하였다.

Abstract

Active adaptation to various types of interference from the ground surface is critical for accurately tracking the angles of objects flying at low altitudes. Among the angle-estimation algorithms used in multipath environments, the refined maximum likelihood (ML) technique has been actively investigated. However, it suffers from performance degradation when multiple targets or interference signals exist. In addition, computational complexity increases exponentially as the number of parameters estimated using the refined ML technique increases when multiple targets exist. In this study, we derive an ML estimation formula when two targets are present and propose a refined ML technique for estimating the angles of the two targets by combining the geometric relationship between direct and specular paths with the results of complex envelope estimates using the minimum mean-square-error method. Furthermore, we propose a low-complexity iterative refined ML technique to avoid a two-dimensional grid search. The performance of the proposed algorithm is verified by evaluating its root mean square error and comparing it with those of the conventional refined ML and beam domain ML (BDML).

Keywords: Low-Angle Tracking; Refined Maximum Likelihood; Beam Domain Maximum Likelihood; Beamforming

Ⅰ. 서 론

일반적으로 비행하는 물체의 각도를 추정할 때, 고도가 낮을수록 지상의 간섭을 많이 받는다. 레이다가 전자기파 형태의 신호를 발사하면, 물체에 맞고 되돌아오는 과정에서 직접적인 경로뿐만 아니라, 지표면이나 건물과 같은 여러 장애물에 반사된 신호 또한 수신 신호에 더해지게 되는데, 이러한 요소는 각도의 정확한 추정을 방해한다^[1]~[5].

특히, 저고도 표적의 경우, 해수면 또는 지표면에 반사되어 들어오는 다중 경로의 신호가 직접 경로의 신호와 유사한 거리 빈(range bin)에 위치하여 두 신호의 분리가 어려워, 기존 모노펄스 빔포밍 기법을 통한 고각 추정 결과에 왜곡이 발생할 수 있다^[5],[6]. 이를 해결하기 위해 참고문헌 [5]에서는 다중 경로 방향으로 널(null)이 생성되도록 적응형 모노펄스 빔포밍 기법을 제안하였으며, 참고문헌 [6]에서는 수신빔 그리드에 따른 고각 추정 성능을 분석하였다.

다중 경로의 기하학적 관계를 활용하는 Refined ML (maximum likelihood) 기법^[1],[7]은 다중 경로 등의 방해 요소로부터 상대적으로 우수한 고각(elevation angle) 또는 도래각(AoA, angle of arrival) 성능 추정 성능을 보인다고 알려져 있다. 이 기법은 수신 신호로부터 우도 함수(likelihood function)을 유도하여, 우도 함수가 최대가 되는 고각 파라미터를 찾아내는 기존 ML 기법에 직접 경로(direct path) 고각과 지표면에 반사되는 다중 경로(specular path)의 입사각의 기하학적 관계를 활용하여, 2차원에서 1차원으로 줄인 파라미터 탐색 영역에서 우도 함수를 최대화하는 고각 파라미터 값을 찾는 방식이다. 즉, RML 기법은 시스템 혹은 모델에 맞게 데이터를 정제한 뒤 ML 기법을 적용하므로, 상대적으로 2차원 파라미터 탐색이 필요한 기존 ML에 비해 낮은 복잡도를 가지는 동시에, 고각 추정 정확도가 높다는 장점이 있다. 이는 추적(tracking)과 같은 동적인 상황을 다룰 때 더욱 유용하다. 하지만, 재밍(jamming) 신호가 존재하거나 단일 표적이 아닌 추가적인 표적이 늘었을 때는 우도 함수의 추정 파라미터가 늘어남에 따라 우도 함수의 복잡도 또한 증가하기 때문에, 계산량이 급증한다는 단점이 있다.

본 논문에서는 재밍 신호가 존재하는(또는 두 개의 표적이 존재하는) 다중 경로 환경에서, Refined ML 기법을 이용한 고각 추정 알고리즘을 제안한다. 구체적으로, 기존의 Refined ML 기법을 제안한 논문^[1],[7]과는 달리, 두 개의 표적에 대한 수신 신호 모델을 정립하고, 이로부터 우도 함수를 유도한다. 유도된 우도 함수는 4차원의 도래각 (Angle-of-arrival, 1차 표적의 입사각/반사각, 2차 표적[재밍 신호]의 입사각/반사각) 및 복소 포락선에 대한 함수로 주어진다. 즉, 추정 파라미터의 개수가 많기 때문에 ML의 최적해를 구하기 어렵게 된다. 따라서 도래각들의 기하학적 관계와 최소평균제곱오차 기법(minimum mean-square-error)을 이용해 복소 포락선을 추정한 결과를 접목하여 두 표적 고각 추정을 위한 Refined ML 기법을 제안한다. 이를 통해 우도 함수를 최소화하는 파라미터 탐색 차원을 2차원으로 감소시켜 Refined ML을 위한 우도 함수를 유도하였다. 추가적으로 우도 함수를 최대화하기 위한 2차원 탐색을 피하기 위해, 파라미터 두 개 중 하나를 고정시켜 1차원 탐색을 반복하는 반복 1D Refined ML (iterative one-dimensional refined ML)기법을 통해 계산 복잡도를 줄이는 알고리즘을 제안하였다. 제안된 기법의 성능을 확인하기 위해, 대표적인 각도 추정 기법인 기존 단일 표적의 저고도 고각을 추정하는 Refined ML 기법^[1],[7]및 BDML(beam domain maximum likelihood) 기법^[8]과 성능 비교를 수행하였다.

본 논문의 구성은 다음과 같다. Ⅱ장에서는 저고도로 비행하는 두 표적의 수신 신호 모델에 대해 설명하고, Ⅲ장에서는 두 표적의 고각 추정을 위한 Refined ML 기법에 대해 설명한다. 여기서 Refined ML을 위한 우도 함수를 유도한다. Ⅳ장에서는 제안하는 Refined ML 기법의 계산 복잡도를 줄이기 위한 반복 1D Refined ML 기법에 대해 설명한다. Ⅴ장에서는 컴퓨터 모의 실험을 통해 제안하는 알고리즘의 성능을 검증하고, Ⅵ장에서 결론을 맺는다.

Ⅱ. 수신 신호 모델

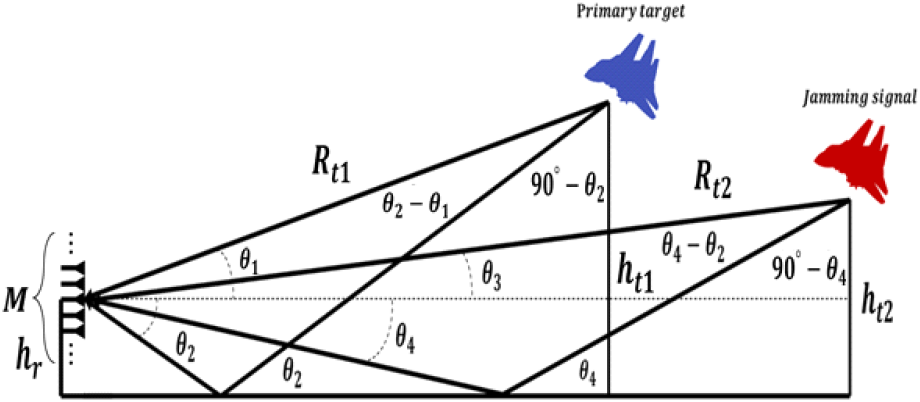
그림 1은 M개의 안테나 요소를 가지는 균일한 선형 배열 안테나(uniform linear array antenna)를 사용한 저고도 표적 탐지 레이다 시스템을 나타내고 있다. 이때 1차 표적과 2차 표적이 각각 h_t1과 h_t2의 높이를 가지고, 레이다 시스템으로부터 각각 R_t1과 R_t2의 거리만큼 떨어진 지점에서 비행한다고 가정한다. 낮은 고도로 비행하는 물체로부터 반사된 레이다 신호는 직접 경로뿐만 아니라, 지표면의 여러 간섭을 받게 된다. 따라서, 1차 표적과 2차 표적의 고각 파라미터(또는 AoA)가 각각 θ₁, θ₃로 주어진다고 하면, 다중 경로에 기반한 수신 신호는 식 (1)과 같이 주어진다.

x (n) = a M θ 1 c 1 (n) + a M θ 2 c 2 (n) + a M θ 3 c 3 (n) + a M θ 4 c 4 (n) + n (n)

(1)

그림 1. | Fig. 1. 수신 신호 모델 | Recieved signal model.

Download Original Figure

여기서 θ₂, θ₄는 반사 경로의 AoA를 나타낸 것이다. 또한, c_i(n)은 각각 집적 경로 및 반사 경로에 해당하는 복소 포락선을 나타내며, 평균이 0이고 분산이 1인 복소 가우시안 분포를 가지는 Swerling I 모델을 따른다고 가정한다. a_M(θ_i)는 배열 응답 벡터(antenna array vector)를, n(n)은 평균이 0이고 공분산이 $σ n 2 I$ 인 가우시안 잡음 벡터 신호를 각각 나타낸다. 구체적으로, a_M(θ_i)는 식 (2)와 같이 표현될 수 있다.

a M θ i = 1 e − j 2 π d sin θ i λ … e − j (M − 1) 2 π d sin θ i λ

(2)

여기서 d는 안테나 요소 간의 간격을, λ는 수신 신호의 파장을 의미한다. 본 논문에서는 d = λ/2을 가정한다.

Ⅲ. 두 표적 고각 추정을 위한 Refined ML 기법

앞 절의 수신 신호로부터 미지의 파라미터를 추정하는 방법으로, 우도 함수를 사용하는 ML 기법이 널리 사용된다. 우도 함수란, 관측된 데이터가 독립적이고 동일한 분포를 가진다고 가정할 때, 구하고자 하는 파라미터에 대한 각 데이터의 확률 밀도 함수(PDF, probability density function) 또는 확률 질량 함수(PMF, probability mass function)들의 곱으로 나타낸 것을 말한다. 이러한 ML 기법은 이 우도 함수를 최대화하는 파라미터를 추정함으로써 확률적으로 높은 가능성을 가지는 파라미터 추정을 가능하게 한다.

3-1 ML 기법을 위한 우도 함수

ML 기법을 이용하여 두 표적의 AoA들을 추정할 때 사용되는 우도 함수는 식 (1)로부터 얻을 수 있다. 식 (1)의 잡음 n(n)은 가우시안 잡음(Gaussian noise)으로, 수신 신호 x(n)은 가우시안 분포(Gaussian distribution)를 따른다. 가우시안 분포의 PDF는 다음과 같다.

f (x) = 1 2 π σ n 2 M / 2 e − | | x − μ θ i, c i (n), i = 1, 2, 3, 4 | | 2 2 σ n 2

(3)

식 (3)의 μ(θ_i,c_i(n),i=1,2,3,4)는 다음과 같이 주어진다.

μ θ i, c i (n), i = 1, 2, 3, 4 = a M θ 1 c 1 (n) + a M θ 2 c 2 (n) + a M θ 3 c 3 (n) + a M θ 4 c 4 (n)

이를 바탕으로 우도 함수를 유도하면 다음의 수식으로 표현할 수 있다.

L θ i, c i (n), i = 1, 2, 3, 4 ∣ x (n)) = − | | x − μ θ i, c i (n), i = 1, 2, 3, 4 | | 2 + c i (n)

(4)

따라서 ML 기법은 이 우도 함수를 최대화하도록 파라미터들을 추정하는 다음과 같은 최적화 문제로 표현할 수 있다.

θ^i, c^i (n), i = 1, 2, 3, 4 = arg m a x θ i, c i (n), i = 1, 2, 3, 4 L θ i, c i (n), i = 1, 2, 3, 4 ∣ x (n)

(5)

하지만 위의 최적화 문제는 추정 파라미터의 개수가 많기 때문에 ML의 최적해를 구하기 어렵게 된다. 따라서 다음 절에서는 AoA들의 기하학적 관계와 최소평균제곱오차 기법을 이용해 복소 포락선을 추정한 결과를 접목하여 두 표적 고각 추정을 위한 Refined ML 기법을 제안한다.

3-2 Refined ML 기법을 위한 직접/반사 경로 기하 관계를 이용한 우도 함수

참고문헌 [1] 및 참고문헌 [7]에 따르면, 표적이 저고도 고각을 가질 경우, 그림 1에서 복소 포락선은 다음과 같은 관계가 있다.

c 2 (n) ≈ ϵ 1 c 1 (n) c 4 (n) ≈ ϵ 3 c 3 (n)

(6)

즉, 반사 경로의 복소 포락선 c₂(n), c₄(n)은 식 (6)과 같이 반사 감쇠 계수 ϵ_i와 직접 경로의 복소 포락선 간 곱으로 근사화할 수 있다. 이때, ϵ_i는 다음과 같이 주어진다.

ϵ i = ρ e − j Δ ψ i, i = 1, 3

(7)

식 (7)의 ρ는 표면 반사 계수를, Δψ_i는 직접 경로와 반사 경로 간의 차이로 인해 나타나는 위상차를 나타낸다. 또한, Δψ는 그림 1에서의 직접 경로와 반사 경로의 기하학적 관계로부터 Δψ₁ = 4πh_r(sinθ₁ + h_r/R_t1)/λ와 같이 표현이 가능하다. 따라서, 이를 식 (7)에 대입하면, 다음과 같은 수식을 얻을 수 있다.

ϵ 1 = ρ e − j 4 π h r sin θ 1 + h r / R t 1 λ ϵ 3 = ρ e − j 4 π h r sin θ 3 + h r / R t 2 λ

(8)

또한, 그림 1에서 직접 경로와 반사 경로의 기하학적 관계로부터 θ_i+1를 θ_i으로 표현한 식을 다음과 같이 유도할 수 있다.

θ 2 = − arctan 2 h r + R t 1 sin θ 1 R t 1 cos θ 1 ≡ g 1 θ 1 θ 4 = − arctan 2 h r + R t 2 sin θ 3 R t 2 cos θ 3 ≡ g 3 θ 3

(9)

따라서 식 (8) 및 식 (9)를 이용하면 식 (1)은 다음과 같이 나타낼 수 있다.

x (n) = a M θ 1 c 1 (n) + a M g 1 θ 1 ϵ 1 c 1 (n) + a M θ 3 c 3 (n) + a M g 3 θ 3 ϵ 3 c 3 (n) + n (n)

(10)

이때 w(θ_i), i=1,3를 다음과 같이 정의하면,

w(θ_i) ≡ a_M(θ_i) + ϵ_ia_M(g_i(θ_i)),

식 (10)은 다음과 같이 표현할 수 있다.

x (n) = c 1 (n) w θ 1 + c 3 (n) w θ 3 + n (n) = w θ 1 w θ 3 c 1 (n) c 3 (n) + n (n) = W θ 1, θ 3 c (n) + n (n)

(11)

즉, 경로 간 기하학적 관계를 이용한다면, 추정해야 할 파라미터의 개수를 줄일 수 있음을 의미한다.

참고로 두 개의 표적들이 동일한 입사각을 가질 경우, 일반적으로 거리 빈이 다르기 때문에, 거리 측면에서 분리하여 신호처리가 가능하다. 따라서, 본 논문에서는 두 개의 표적들이 동일한 입사각을 가지는 경우의 문제는 고려하지 않도록 한다.

식 (11)에서 복소 포락선 벡터 c(n)은 수신 신호 벡터와 행렬 W(θ₁, θ₃)을 이용해 최소평균제곱오차 해를 구한다면, 다음과 같다.

c (n) = W H W + σ n 2 I − 1 W H x (n)

(12)

식 (12)를 식 (5)에 대입해서 유도하면, 다음과 같은 정제된 최우도 기법에 기반한 Refined ML의 최적화 문제로 표현할 수 있다.

min θ 1, θ 3 ∑ n = 1 N ∥ x (n) − W W H W + σ n 2 − 1 W H x (n) ∥ 2

(13)

식 (13)의 파라미터 N은 수신 신호 샘플 개수이며, W는 (θ₁, θ₃)의 함수로 주어지므로, 식 (13)의 최적화 해는 다음과 같이 정리할 수 있다.

θ 1, θ 3 = argmax θ 1 θ 3 ∑ n = 1 N x H (n) W θ 1, θ 3 W H θ 1, θ 3 W θ 1, θ 3 + σ n 2 I − 1 W H θ 1, θ 3 x (n)

(14)

따라서 표적이 두 개인 경우, 제안하는 Refined ML 기법을 통해 최적해 θ₁, θ₃을 추정하기 위한 2차원 파라미터 탐색이 필요하다.

Ⅳ. Iterative One-Dimensional Refined ML 기법

앞 장에서는 2개의 표적에 대해 고각을 Refined ML에 기반하여 추정하는 알고리즘을 제안하였다. 하지만, 이 경우 여전히 2차원 파라미터 탐색 과정이 필요하다. 본 장에서는 2차원 탐색 과정을 줄이기 위해 반복 1D Refined ML 기법을 제안한다.

구체적으로 식 (14)의 비용함수에 θ₁을 해당 범위 안의 임의의 값으로 고정한다면, 식 (14)는 단일 목표물의 고각 (θ₃)에 대한 최적화 문제로 변환되어, 기존 1차원 탐색을 통해 최적해를 구할 수 있다. 이를 통해 찾은 최적해 θ₃를 식 (14)에 대입하여 고정한다면, θ₁에 대한 최적화 문제로 변환되어 역시, 1차원 탐색을 통해 해를 구할 수 있게 된다. 이를 해가 수렴할 때까지 반복하게 된다면, 2차원 탐색에 비해서 적은 계산 시간을 소요하면서 최적해를 찾을 수 있게 된다.

반복 Refined ML 기법을 통해 찾은 해는 지역적 최적해(local optimal solution)에 수렴하여 전역적 최적해를 찾지 못할 수 있기 때문에 제안하는 반복 Refined ML 기법에서는 초기 후보값을 N_c개의 임의의 값을 설정하여 각각의 초기값에 대해 위의 과정을 반복하여, 수렴된 값 중 비용함수가 작은 최적해를 구한다면, 지역적 최적해에 빠지는 경우를 피할 수 있게 된다. 위에서 논의한 반복 Refined ML 기법을 정리한다면 알고리즘 1과 같이 나타낼 수 있다.

본 논문에서는 2개의 표적(재머, 1차 표적)을 고려하지만, 3개 또는 그 이상의 표적이 존재할 경우 제안한 모델과 유사하게 Refined ML기법을 확장할 수 있다. 다만, 표적의 개수를 K개라 두면, K 차원의 격자 탐색 과정을 거쳐야 하기 때문에 복잡도가 증가할 것으로 예상된다. 또한, 비용함수의 지역적 극소값(local minima)에 수렴할 수 있는 가능성이 있을 수 있어, 초기 후보값 개수(N_c)를 높게 설정할 필요가 있다. 따라서 3개 이상의 목표물에 대해서는 추가적인 연구 및 분석이 필요할 것으로 예상되며, 이는 추후 연구 내용으로 남겨둔다.

Algorithm 1. Iterative refined ML algorithm.

Download Original Figure

Ⅴ. 모의 실험 결과

본 논문에서는 MATLAB 기반 모의실험을 통해 제안한 알고리즘을 구현 및 검증하였다. 실험에 사용된 파라미터의 값들은 표 1에 정리하였다. 이중 수신 안테나와 첫 번째 표적 사이의 거리를 나타내는 R_t1은 2 km에서부터 10 km까지 800 m 간격으로 설정하여 성능을 평가하였다.

표 1. | Table 1. 모의 실험 파라미터 | Simulation parameters.

Parameter	Value
Number of antennas (M)	60
Operation frequency	500 MHz
Target range 1 (R_t1)	2~20 km
Target range 2 (R_t2)	30 km
Target height 1 (h_t1)	50 m
Target height 2 (h_t2)	25 m
Antenna height (h_r)	15 m
SNR [dB]	0~50

Download Excel Table

5-1 제안된 Refined ML 기법 구현 및 성능 평가

그림 2는 제안한 Refined ML 기법 기반의 각도 추정 알고리즘을 SNR과 R_t1을 변화시켰을 때, θ₁의 추정 및 성능 평가를 나타낸 것이다. 구체적으로 그림 2(a)는 SNR에 따라 θ₁의 추정치 $θ^1$ 의 RMSE 지표를 나타낸 것으로, SNR이 높을수록, 즉, 수신 환경이 좋을수록 RMSE가 감소하는 것을 확인할 수 있다.

그림 2. | Fig. 2. SNR과 R_t1에 따른 θ₁ 추정 및 성능 평가 | Estimation and performance evaluation based on SNR and R_t1.

Download Original Figure

그림 2(b)는 R_t1에 따른 θ₁과 $θ^1$ 의 추정 결과를 도식하였다. θ₁과 $θ^1$ 모두, 물체와의 거리가 상대적으로 가까워질수록 저각에서 고각으로 변하는 현상을 확인할 수 있다. 또한, 거리가 멀수록 추정 성능의 열화가 발생하는데, 이는 거리가 멀수록 저각이므로 반사 경로의 간섭에 영향을 더 많이 받아, 상대적으로 거리가 짧을 때보다 추정 성능이 저하된 것으로 판단된다.

5-2 N_c에 따른 RMSE의 변화

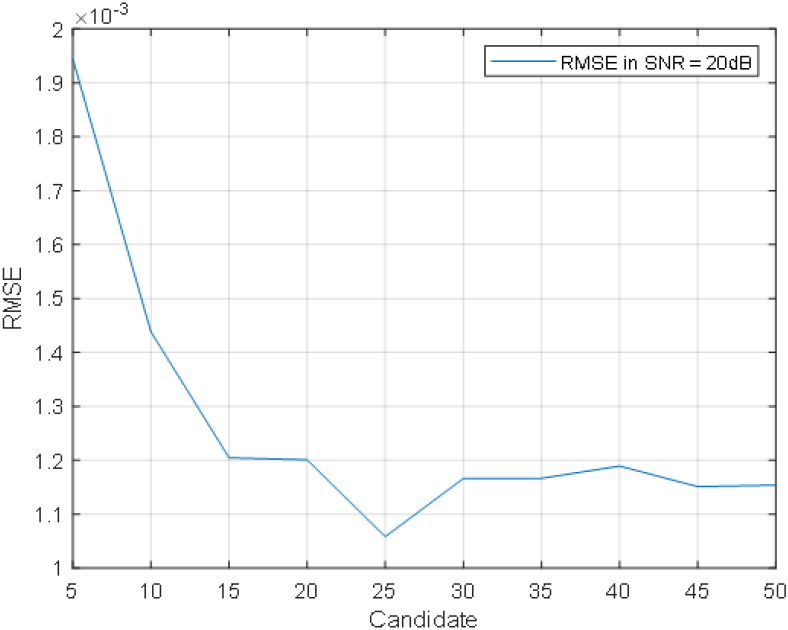
제안된 반복 1D Refined ML 기법의 경우, IV장에서 언급하였듯이, 반복 과정에서 지역적 최적해에 빠질 수 있다. 따라서 이를 방지하기 위해 초기 후보값을 N_c개의 다중 값을 설정하여 반복하도록 하였다. 초기 후보값은 관심 탐색 범위(본 모의 실험에서는 [0,5]°)를 N_c 만큼 등간격으로 나눠서 설정하였다. SNR을 20 dB로 고정하였고, 모의 실험 환경은 표 1의 설정과 동일하게 하였다. 그림 3에서 확인할 수 있듯이, N_c가 커짐에 따라 RMSE가 감소하는 것을 확인할 수 있으며, 특히 N_c가 15개일 때 추정 성능이 급격하게 개선되는 것을 확인할 수 있다.

그림 3. | Fig. 3. N_c(

θ ¯ 1

개수)에 따른 RMSE 성능 변화 | Change in RMSE performance depending on N_c.

Download Original Figure

5-3 Iteration에 따른

θ^1, θ^3

수렴 그래프

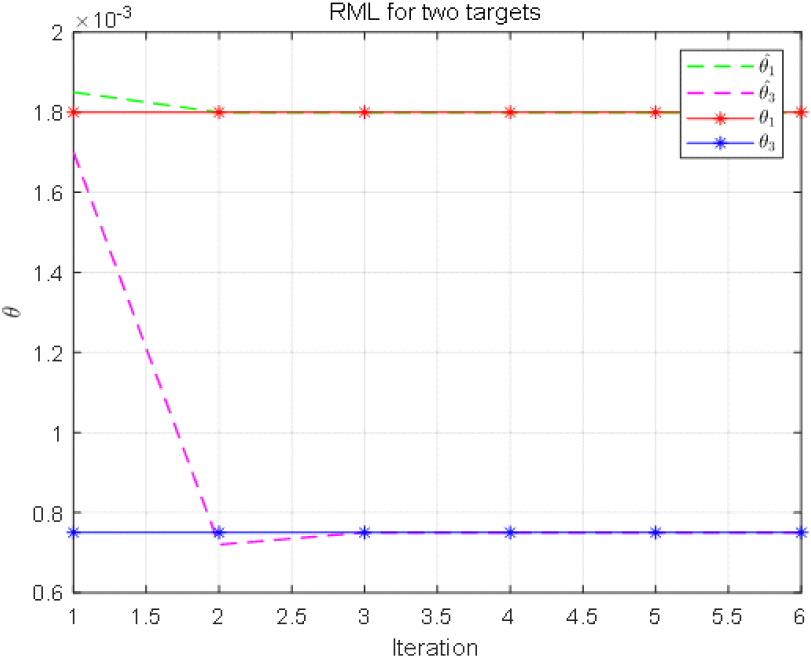
제안된 반복 1D Refined ML 기법의 수렴성을 확인하기 위해 반복 횟수에 따른 추정 결과를 그림 4에 나타내었다. 그래프에서 확인할 수 있듯이, 최적해에 수렴하기까지 2~3회의 반복 과정이 필요한 것을 확인할 수 있었다.

그림 4. | Fig. 4. Iteration 횟수에 따른

θ^1, θ^3

결과 |

θ^1, θ^3

as the number of iterations.

Download Original Figure

또한, N_c에 따른 계산 복잡도를 평가하기 위해 연산 시간을 비교하였다. 연산 환경은 Intel(R) Core(TM) i5-3570 CPU@3.4GHz의 CPU와 메모리 8GB RAM을 활용하였으며, MATLAB의 버전은 R2014a를 활용하였다. 그래프에서 확인할 수 있듯이, iteration 횟수에 비례해서 연산 시간이 증가하는 것을 확인할 수 있으며, 또한 N_c에 비례해서 선형적으로 연산 시간이 증가하는 것을 확인할 수 있다(표 2).

표 2. | Table 2.

θ ¯ 1, θ ¯ 3

개수 및 Iteration 횟수에 따른 계산 시간 | Running time as the number of

θ ¯ 1, θ ¯ 3

and iteration.

Candidate	1	15	30	45	50
Interaction	1	15	30	45	50
1	231 s	3,344 s	6,674 s	10,010 s	11,145 s
5	1,110 s	16,555 s	33,107 s	49,973 s	55,613 s

Download Excel Table

5-4 고각 추정을 위한 세 가지 기법의 RMSE 비교

제안한 반복 1D Refined ML 기법의 성능을 객관적으로 평가하기 위해, 그림 5에서는 기존의 Refined ML 기법 및 BDML 기법에 대해 RMSE 성능을 각각 비교하였다. 제안한 반복 1D Refined ML 기법에서 N_c는 15로 설정하였다.

그림 5. | Fig. 5. SNR에 따른 세 기법의 RMSE 비교 | RMSEs of conventional RML, BDML, and proposed refined ML for various SNR.

Download Original Figure

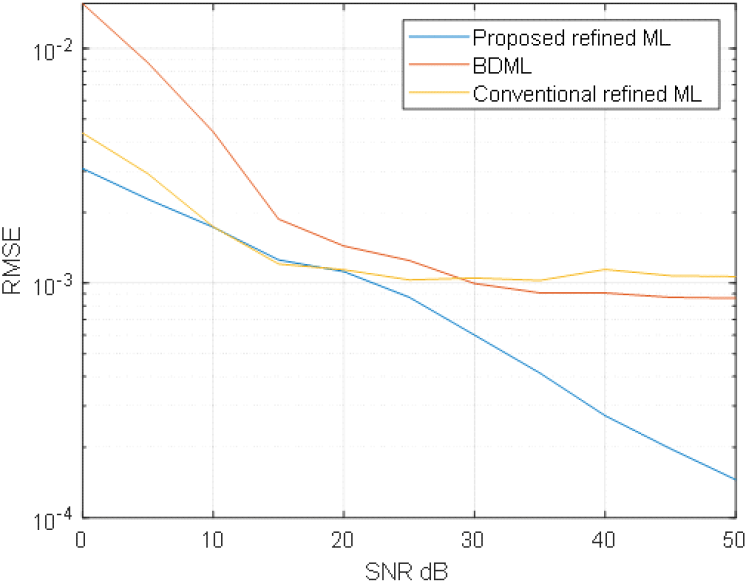
그림 5에서 확인할 수 있듯이, 제안한 기법이 다른 두 기법에 비해 우수한 성능을 나타내는 것을 확인할 수 있으며, 특히 높은 SNR에서 그 성능 차이가 커지는 것을 확인할 수 있는데, 이는 낮은 SNR 환경에서는 비용함수 크기에 잡음의 영향이 크기 때문에 목표물이 1개라고 가정하고 Refined ML을 적용한 기존 기법과 제안한 기법과의 성능 차이가 적은 반면에 높은 SNR에서는 잡음보다는 목표물 2개로부터 발생되는 간섭 신호가 비용함수에 높은 비중을 차지하게 되므로 제안하는 기법을 통해 비용함수가 최소가 되는 해를 구하는 기법의 성능이 기존 기법들에 비해 우수한 성능을 나타낸다고 분석할 수 있다. 즉 높은 SNR에서는 다중 목표물로 인한 간섭 영향이 고각 추정 성능에 큰 영향을 주기 때문에, 다중 목표물로 인한 간섭을 고려하지 않은 기존의 Refined ML 기법이나 BDML의 경우 높은 SNR에서 RMSE가 10⁻³에서 수렴하는 반면 제안하는 기법은 SNR이 증가함에 따라 RMSE 성능이 감소하는 것을 확인할 수 있다.

Ⅵ. 결 론

본 논문에서는 재밍 신호가 존재하는 (또는 두 개의 표적이 존재하는) 다중 경로 환경에서, Refined ML을 이용한 고각 추정 알고리즘을 제안하였다. 기존의 Refined ML 기법과는 달리, 두 개의 표적에 대한 수신 신호 모델을 정립하고, 이로부터 우도 함수를 유도하였다. 유도된 우도 함수는 4차원의 도래각 및 복소 포락선에 대한 함수로 주어지기 때문에 추정 파라미터의 개수가 많다. 이로 인해 ML 기반 최적해를 구하기 어렵게 된다. 따라서 도래각들의 기하학적 관계와 최소평균제곱오차 기법을 이용해 복소 포락선을 추정한 결과를 접목하여 두 표적 고각 추정을 위한 Refined ML 기법을 제안하였다. 이를 통해 우도 함수를 최소화하는 파라미터 탐색 차원을 2차원으로 감소시켜 Refined ML을 위한 우도 함수를 유도하였다. 추가적으로 우도 함수를 최대화하기 위한 2차원 탐색을 피하기 위해, 파라미터 두 개 중 하나를 고정시켜 1차원 탐색을 반복하는 반복 1D Refined ML 기법을 제안하였다. 컴퓨터 모의 실험을 통해 제안된 추정 기법의 RMSE 성능 및 연산 시간 등을 평가하였으며, 기존 단일 표적의 저고도 고각을 추정하는 Refined ML 기법 및 BDML 기법과 성능 비교를 통해 높은 SNR에서 우수한 추정 성능을 내는 것을 확인하였다.

Acknowledgements

본 연구는 2024년도 한화시스템의 연구비 지원 및 일부 정부(과학기술정보통신부)의 재원으로 연구재단의 지원(RS-2023-00241706)을 받아 수행되었음.

References

[1].

T. Lo, J. Litva, "Use of a highly deterministic multipath signal model in low-angle tracking," IEE Proceedings F(Radar and Signal Processing), vol. 138, no. 2, pp. 163-171, Apr. 1991.

[2].

J. Liu, Z. Liu, and R. Xie, "Low angle estimation in MIMO radar," Electronics Letters, vol. 46, no. 23, pp. 1565-1566, Nov. 2010.

[3].

T. H. Kim, C. H. Jung, H. S. Lee, J. H. An, S. H. Kim, and J. H. Park, "Elevation angle measurement of sea-skimming targets for fine tracking in multipath environments of sea surfaces," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 32, no. 4, pp. 396-406, Apr. 2021.

[4].

K. S. Kim, M. S. Chung, and C. S. Jung, "Hybrid compensation technique on low elevation angle errors for multibeam surveillance radar in multipath environment," Journal of the Korea Institute of Military Science and Technology, vol. 16, no. 3, pp. 365-372, Jun. 2013.

[5].

D. Park, E. Yang, S. Ahn, and J. Chun, "Adaptive beamforming for low-angle target tracking under multipath interference," IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 4, pp. 2564-2577, Oct. 2014.

[6].

D. Kwon, B. Cho, K. S. Kim, and B. S. Lee, "Performance analysis of elevation estimation with respect to received beam grid in multipath environment," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 3, pp. 190-196, Mar. 2023.

[7].

Y. Zhu, Y. Zhao, and P. Shui, "Low-angle target tracking using frequency-agile refined maximum likelihood algorithm," IET Radar, Sonar & Navigation, vol. 11, no. 3, pp. 491-497, Mar. 2017.

[8].

M. Zoltowski, T. S. Lee, "Beamspace ML bearing estimation incorporating low-angle geometry," IEEE Transactions on Aerospace and Electronic Systems, vol. 27, no. 3, pp. 441-458, May 1991.