표적 조우 환경에서의 근거리장 RCS 모델링을 이용한 수신전력 계산

I. 서 론

현대 국방체계에서 군사 작전의 효율성을 향상하기 위하여 유도무기는 필수적인 요소로 인식된다. 하지만 최근 스텔스 기술과 재밍 기술의 발전으로 인해 유도무기가 표적을 탐지하는 데에 어려움이 증가하고 있다. 따라서 표적의 RCS나 클러터와 같은 다양한 변수를 고려하여 유도무기가 표적을 잘 탐지할 수 있도록 설계해야 한다. 유도무기는 레이다를 탑재하여 표적을 탐지한다. 잘 알려져 있는 레이다 방정식은 수신전력을 송신전력, 안테나 이득, 파장, 레이다 반사 단면적 RCS와 레이다와 표적 사이의 거리 로 표현된다. 하지만, 레이다 방정식은 레이다와 표적 사이의 거리가 충분히 먼 원거리장일 때 유효하고, 유도무기와 표적이 조우하는 환경에서 산란 전자기장은 일반적으로 근거리장에서 위치하게 된다^[1],[2]. 레이다 방정식에서 안테나 이득은 지향성과 안테나 효율의 곱으로 표현되는 물리량으로써, 지향성은 원거리장이라는 가정 하에, 거리에 대해 정규화한 물리량이다. 그리고 근거리에서는 레이다 안테나의 주빔이 반드시 표적을 지향하지는 않으므로 레이다 안테나와 표적 사이의 위치에 따라 안테나 이득값을 다르게 적용해 주어야 한다. 따라서 근거리장에서는 안테나 이득을 다시 정의할 필요가 있다^[3]. 마찬가지로 RCS는 원거리장이라는 가정하에, 표적에 평면파가 입사할 때 입사 전력밀도 대비 표적 방향 산란 전력밀도의 비로 표현되는 값이므로 근거리장에서 RCS도 다시 정의할 필요가 있다^[4].

근거리에서 레이다와 표적 사이의 거리와 안테나 이득을 수정하여 근거리장 RCS를 계산한 연구^[5]가 수행되었다. 이 연구에서는 안테나 이득과 레이다와 표적 사이의 거리를 재정의하여 RCS1과 RCS2를 제시하고, 시뮬레이션 결과와 비교하였다. 하지만 제시한 RCS를 반영한 시뮬레이션 결과에 따르면, 표적을 지향하지 않는 높은 지향성을 갖는 안테나에 대해서는 시뮬레이션 값과 계산값이 일치하지 않는 문제점이 있다. 그리고 근거리 전자기장 세기값으로 근거리장 RCS를 계산한 연구^[4]와 PO/PTD, 그리고 SBR 기법을 이용하여 근거리장 RCS를 계산한 연구^[6]가 수행되었지만 표적과 레이다 안테나가 고정되어 있는 정적인 환경만 고려하였다는 문제점이 있다.

따라서 본 논문에서는 실제 유도무기가 표적을 조우하는 동적인 환경을 모델링하고, 유도무기의 레이다 안테나를 고려하여 근거리장 이득과 근거리장 RCS를 분석한다. 분석한 이득과 RCS를 이용하여 레이다 방정식과 결합하여 수신전력을 계산한다. 근거리장 분석을 통해 계산된 수신전력을 원거리장 레이다 방정식을 통해 계산된 수신전력과 HFSS SBR⁺ 시뮬레이션 결과값과 비교하여 그 타당성을 검증한다.

II. 표적 조우 환경 모델링

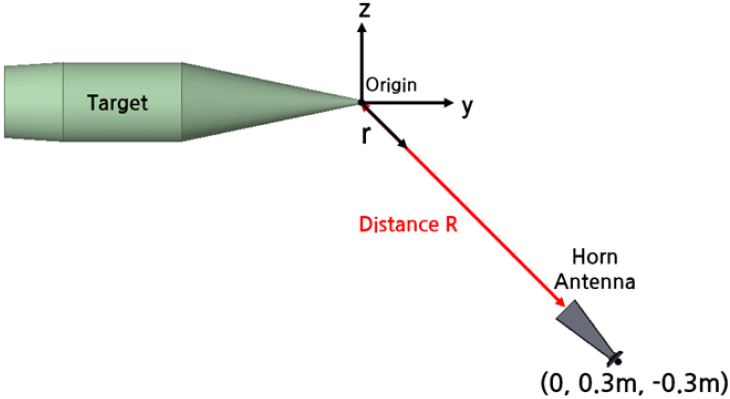
표적과 조우하는 환경을 단순하게 모델링하기 위하여 유도무기를 8.2~12.4 GHz에서 동작하는 혼 안테나(Pasternack 社 PE9856B-15)로 대체하였고, 동작 주파수는 10 GHz, 표적은 알루미늄 물성의 일반적인 미사일 형상을 갖도록 설계하였다. 분석의 편의성을 위하여 안테나가 표적을 45°로 지향하도록 설정하였다. 유도무기와 표적이 서로 움직이는 동적인 환경을 표현하기 위해서 그림 1과 같이 표적의 한 끝점을 원점으로 고정하고, 안테나를 (0, 0.3 m, −0.3 m) 기준으로 매개변수를 이용하여 r축 방향, y축 방향, z축 방향으로 움직이도록 설정하였다. 표 1은 동적 모델링을 위한 매개변수의 범위와 간격을 나타낸 표이다. 안테나의 좌표를 x=0 m, y=0.3 m+t+y_var, z=−0.3 m−t+z_var 로 설정하여 r축 방향(x=0 m)으로 움직일 때는 t, y축 방향으로 움직일 때는 y_var, z축 방향으로 움직일 때는 z_var를 달리하여 움직이는 안테나를 모델링하였다. 이 때 표적과 안테나 사이의 거리 은 혼 안테나 개구면과 원점 사이의 거리로 정의한다.

그림 1. | Fig. 1. 모델링한 표적 조우 환경 | Modeled target encounter environment.

Download Original Figure

안테나 시뮬레이션 데이터를 기반으로 하여, 안테나를 위치를 변화시킬 수 있는 근거리장 source로 변환하였고 동작 주파수는 10 GHz로 설정하였으며, 표적과 안테나를 충분히 포함하는 구 형태의 해석 boundary를 설정하여 시뮬레이션 환경을 모델링하였다. 해석 방식은 높은 정확도를 갖는 SBR(shooting and bouncing rays) 기법을 선택하였다.

III. 근거리장 이득 분석

주어진 혼 안테나는 10 GHz에서 동작하고 원거리장을 계산하는 식 (1)에 의하여 원거리장 거리 R_ff을 계산할 수 있다^[7].

L은 혼 안테나 길이, 는 파장이다. L=130 mm, λ=30 mm이므로 R_ff ≃1.12 m로 계산된다. 모델링한 동적 환경에서 표적과 혼 안테나 사이의 거리는 R_ff 이내이므로 근거리 이득을 다시 정의해야 한다. 식 (2)는 혼 안테나의 근거리장 이득 G^[3]이다.

G₀는 원거리장 이득이고, $R_H^{\prime }$와 $R_E^{\prime }$는 각각 H-plane과 E-plane gain factor이고 식 (3)과 같이 표현된다.

δ_H(x)와 δ_E(y)는 path length error이고 식 (4)과 같이 표현된다.

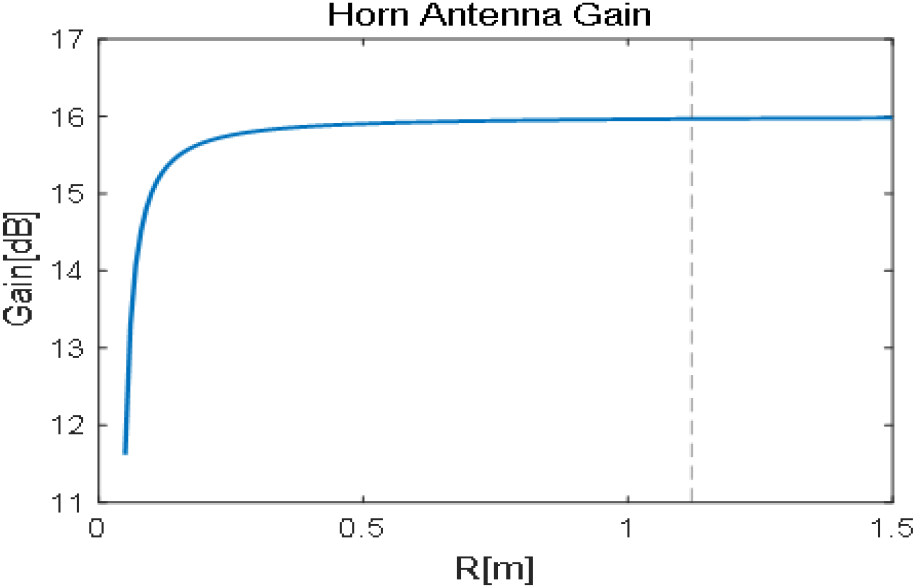
a는 혼 안테나 개구면의 가로 길이, b는 개구면의 세로 길이이다. R은 안테나로부터의 거리이고, $k=\frac{2\pi }{\lambda }$이다. 혼 안테나의 원거리장 최대 이득은 16.12 dBi이고, 혼 안테나의 물리적 크기를 통해 $R_H^{\prime }$와 $R_E^{\prime }$를 계산할 수 있다. 다음 그림 2는 거리에 따른 혼 안테나 이득을 나타낸 그래프이다. 거리 R이 멀어질수록 원거리장 이득에 수렴하는 것을 확인할 수 있다.

그림 2. | Fig. 2. 거리에 따른 혼 안테나 이득 | Horn antenna gain over distance.

Download Original Figure

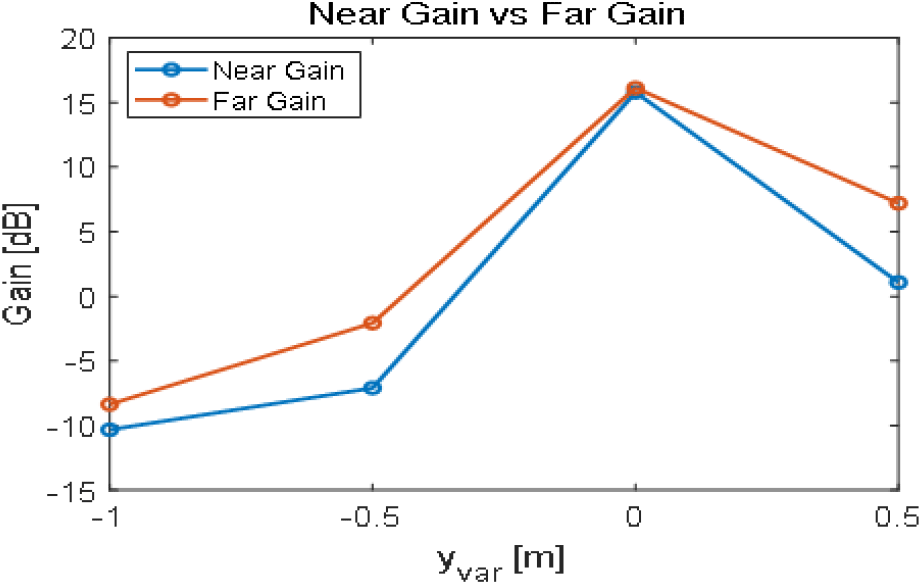
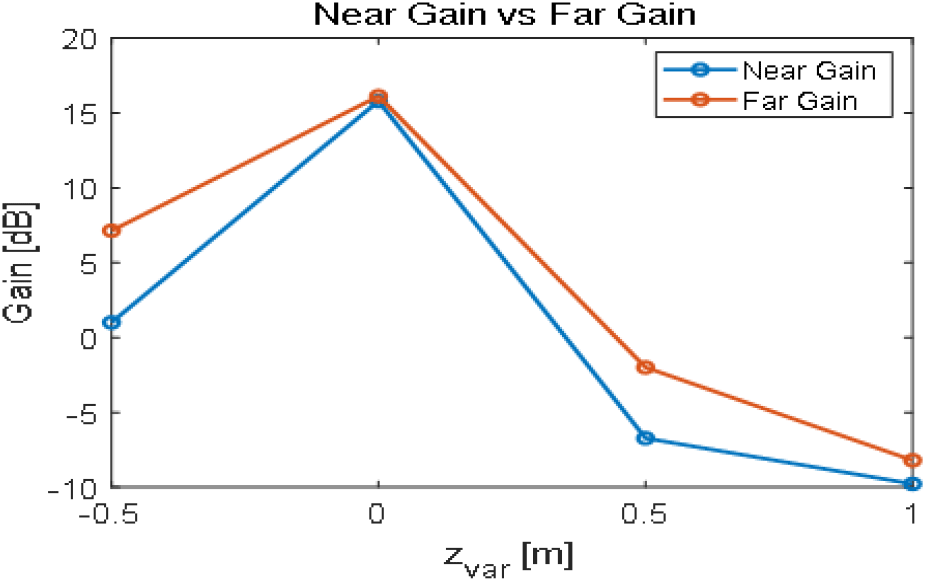
안테나가 r축 방향으로 움직일 때는 안테나의 main lobe가 표적을 지향하기 때문에 G₀에 최대 이득값을 사용하면 되지만, 안테나가 y축 또는 z축 방향으로 움직일 때는 안테나의 side lobe가 표적을 지향하게 되므로 에 표적을 지향하는 방향으로의 이득값을 사용해야 한다. $R_H^{\prime }$와 $R_E^{\prime }$는 혼 안테나의 물리적 크기에 의해 결정되는 값이므로 side lobe가 표적을 지향할 때에도 동일하게 계산해 주었다. 그림 3 및 그림 4는 안테나가 각각 y축, z축 방향으로 움직였을 때의 근거리장 이득과 원거리장 이득을 y_var, z_var에 따라 나타낸 그래프이다. y_var, z_var에 따라 수신전력을 계산할 때의 편의성을 위해서 이득을 각도가 아닌 거리에 따라 그래프를 표현하였다.

그림 3. | Fig. 3. y_var에 따른 근거리장 이득 | Near field horn antenna gain over y_var.

Download Original Figure

그림 4. | Fig. 4. z_var에 따른 근거리장 이득 | Near field horn antenna gain over z_var.

Download Original Figure

원거리장이라는 조건 하에는 표적과 혼 안테나 사이의 거리를 표적은 원점인 (0, 0, 0)을 기준으로 삼고, 혼 안테나는 (0, 0.3 m, −0.3 m)를 기준으로 삼아서 거리와 각도를 적용하였다. 하지만, 근거리장에서 표적과 혼 안테나 사이의 거리를 적용할 때는 원점과 혼 안테나 개구면을 기준으로 삼고 거리와 각도를 적용하였기 때문에 y_var, z_var이 변화함에 따라 이득값에도 차이가 발생하였다. 예를 들면, 그림 3에서 y_var=0.5 m에서는 y_var=0 m에 비해 표적과 안테나 사이의 거리가 멀어졌지만, 각도 변화에 의한 이득의 side lobe의 감소량이 더 크기 때문에 이득이 원거리장 이득에 비해 감소하였다.

IV. 근거리장 RCS 분석

근거리장 RCS 는 식 (5)와 같이 표현된다^[2].

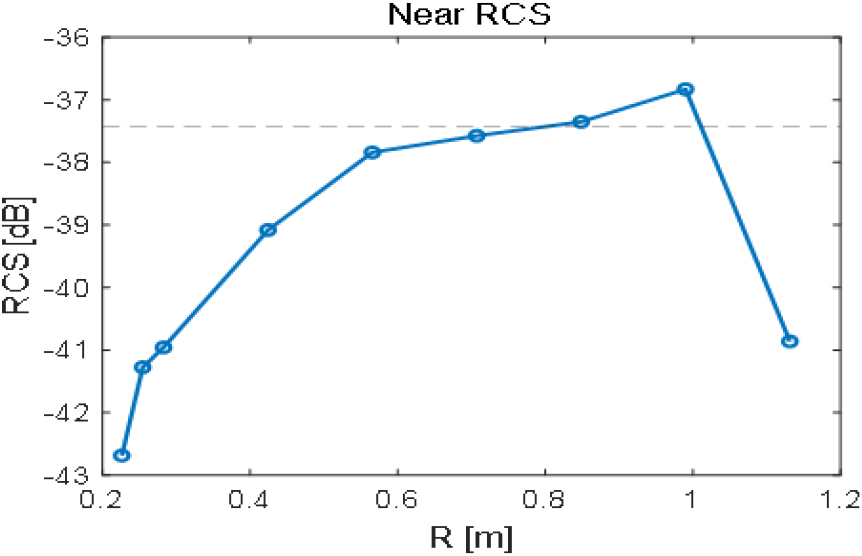
$\overrightarrow{E_s}$와 $\overrightarrow{H_s}$는 산란 전기장과 산란 자기장이고, $\overrightarrow{E_i}$와 $\overrightarrow{H_i}$는 입사 전기장과 입사 자기장이다. $\left|\overrightarrow{E_s}\times \overrightarrow{H_s^{*}}\right|$와 $\left|\overrightarrow{E_i}\times \overrightarrow{H_i^{*}}\right|$를 각각 산란 Poynting Vector의 크기와 입사 Poynting Vector의 크기로 계산한다. Poynting Vector의 크기는 HFSS SBR⁺ 시뮬레이션으로 구하였다. 그림 5는 안테나가 r축 방향으로 움직였을 때 근거리장 RCS를 거리 R에 따라 나타낸 그래프이며, 점선은 원거리장 RCS값이다. 근거리장에서의 입사파는 표적과 근접해 있는 혼 안테나로부터 방사된 전자기장으로 가정하였고, 원거리장에서의 입사파는 균일 평면파로 가정하였다. 또한, 근거리장에서의 RCS를 계산할 때에도 이득을 구할 때와 마찬가지로 안테나와 표적 사이의 거리와 각도를 반영한 입사파를 통하여 계산하였다.

그림 5 | Fig. 5. 거리 R에 따른 근거리장 RCS | Near field RCS over distance R.

Download Original Figure

거리 R이 증가함에 따라 근거리장 RCS 그래프가 원거리장 RCS값에 가까워지다가 1 m를 넘어가게 되면 차이가 커지게 된다. 이는 표적에 입사하는 전자파가 균일 평면파가 아니기 때문이라고 분석된다.

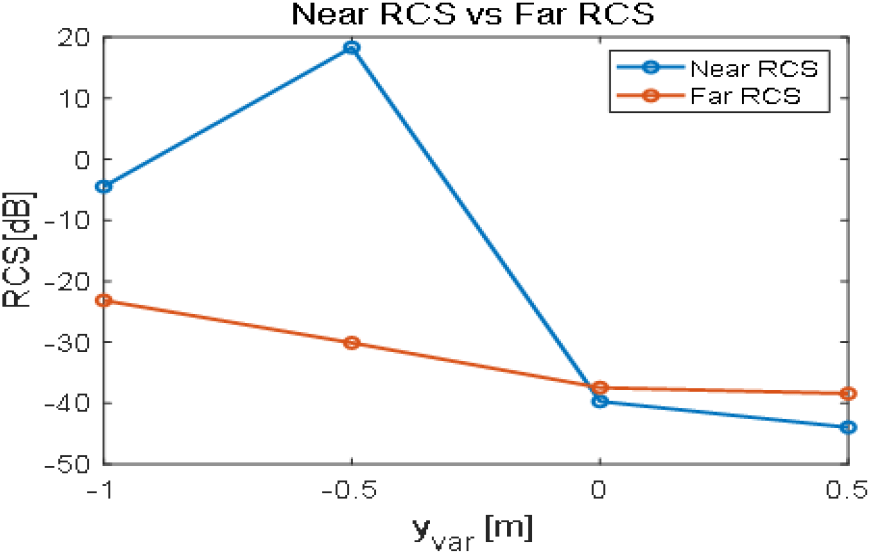
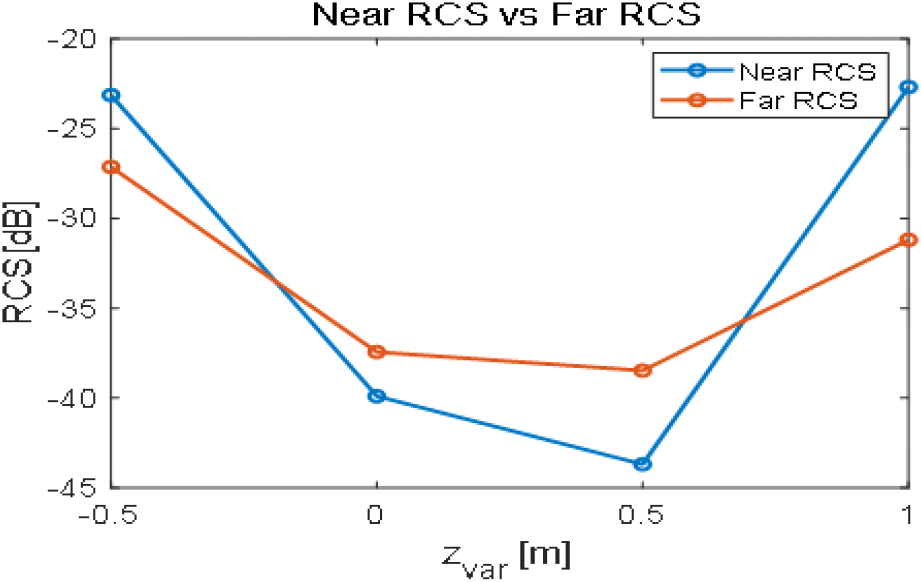
그림 6 및 그림 7은 안테나가 각각 y축, z축 방향으로 움직였을 때의 근거리장 RCS와 원거리장 RCS를 y_var, z_var에 따라 나타낸 그래프이다. 마찬가지로, 수신전력을 계산할 때의 편의성을 위해서 이득을 각도가 아닌 거리에 따라 그래프를 표현하였다.

그림 6. | Fig. 6. y_var에 따른 근거리장 RCS | Near field RCS over y_var.

Download Original Figure

그림 7. | Fig. 7. z_var에 따른 근거리장 RCS | Near field RCS over z_var.

Download Original Figure

근거리장 RCS를 분석할 때에도 마찬가지로, 근거리에서는 새로 거리를 정의했으므로 거리와 각도 차이에 의해 원거리장 RCS와 차이가 발생하였다. 특히, 그림 6에서 y_var=−0.5 m에서 표적과 안테나가 제일 가까워지기 때문에 근거리장 RCS가 원거리장 RCS에 비해 매우 크게 계산되었다. 그리고 두 경우 모두, 표적과의 거리가 멀어질수록 근거리장 RCS와 원거리장 RCS의 차이가 커졌는데, 이 또한 주어진 거리에서의 입사 전자파가 균일 평면파가 아니기 때문이라고 분석된다.

V. 근거리장에서의 수신전력 계산

새로 정의한 거리 R과 분석한 근거리장 안테나 이득 G와 RCS 값을 사용하여 레이다 방정식에 대입하여 수신전력을 계산한다. 레이다 방정식은 식 (6)과 같이 표현된다^[8].

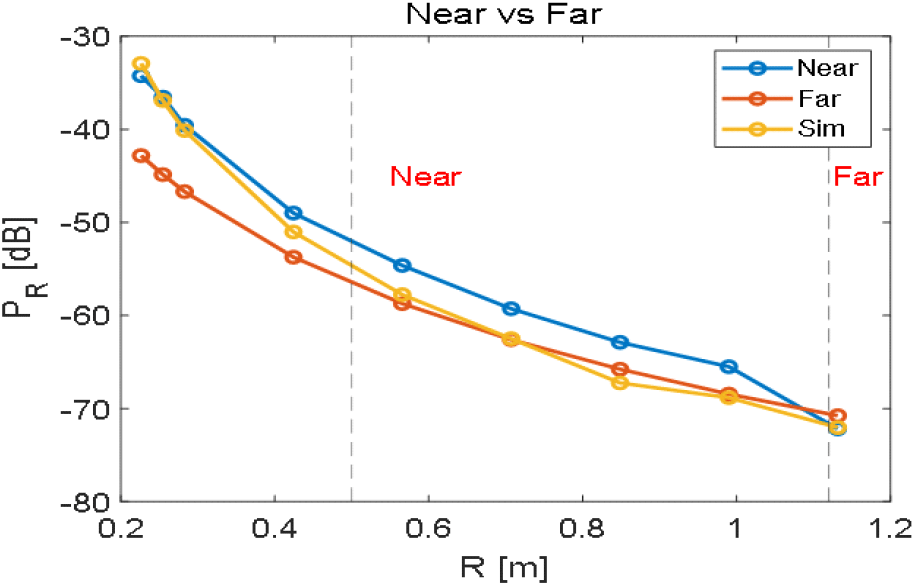
P_R은 수신전력, P_T는 송신전력, G는 안테나 이득, λ는 파장, σ는 표적의 RCS, R은 표적과 레이다 사이의 거리이다. 레이다의 송신 안테나와 수신 안테나가 동일한 경우를 가정한다. 레이다의 송신 안테나로부터 방사된 전자파는 표적에 도달하게 되는데, 표적에 도달한 전자파는 표적에 의해 반사되어 2차적으로 방사된다. 2차적으로 방사된 전자파가 레이다의 수신 안테나에 도달하게 되어 레이다는 표적을 탐지한다. 레이다 방정식은 이러한 과정을 수식으로 표현한 것이다. 그림 8은 안테나가 r축 방향으로 움직였을 때 근거리장 이득과 근거리장 RCS를 레이다 방정식에 대입하여 계산한 수신전력(Near로 표기), 원거리장 이득과 원거리장 RCS를 레이다 방정식에 대입하여 계산한 수신전력(Far로 표기), HFSS SBR⁺ 시뮬레이션을 통해 구한 수신전력(Sim으로 표기)을 거리 R에 따라 나타낸 그래프이다. 송신전력 P_T는 1 W로 가정하였다.

그림 8. | Fig. 8. 거리 R에 따른 수신전력 P_R | Received power P_R over distance R.

Download Original Figure

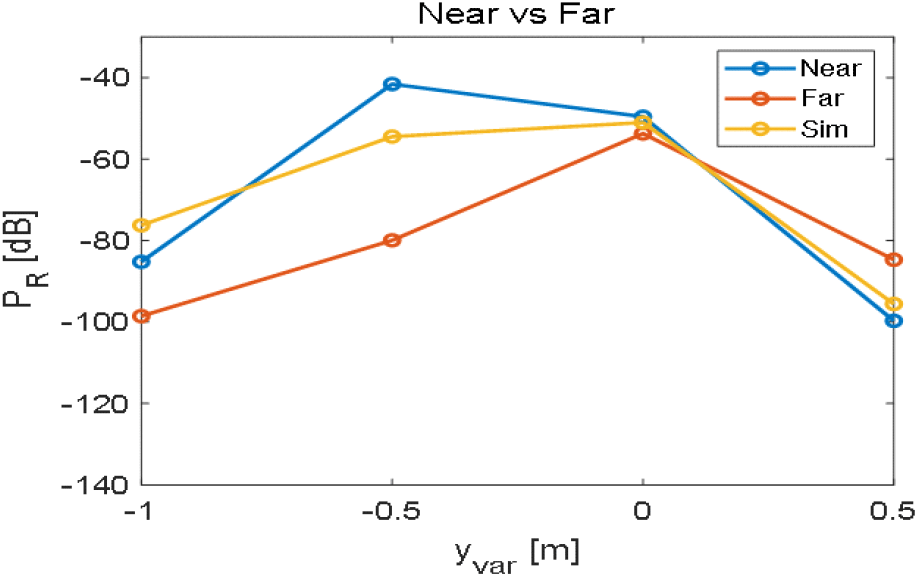
혼 안테나의 원거리장 영역 근처인 약 1 m 부근에서는 원거리장 이득과 원거리장 RCS를 사용한 레이다 방정식 그래프와 시뮬레이션 그래프가 수렴하는 경향을 보이지만, 약 0.7 m 이내에서는 시뮬레이션 그래프와의 차이가 발생하며 표적에 더 근접할수록 근거리장 이득과 근거리장 RCS를 사용한 레이다 방정식 그래프와 시뮬레이션 그래프가 수렴하는 경향을 보인다. 그림 9 및 그림 10은 각각 안테나가 y축, z축 방향으로 움직였을 때 근거리장 이득과 근거리장 RCS를 레이다 방정식에 대입하여 계산한 수신전력, 원거리장 이득과 원거리장 RCS를 레이다 방정식에 대입하여 계산한 수신전력, HFSS SBR⁺ 시뮬레이션을 통해 구한 수신전력을 각각 y_var, z_var에 따라 나타낸 그래프이다.

그림 9. | Fig. 9. y_var에 따른 수신전력 P_R | Received power P_R over y_var.

Download Original Figure

그림 10. | Fig. 10. z_var에 따른 수신전력 P_R | Received power P_R over z_var.

Download Original Figure

그림 9 및 표 2와 같이, 원거리장 이득과 원거리장 RCS를 사용하였을 때보다 근거리장 이득과 근거리장 RCS를 사용하였을 때의 수신전력이 시뮬레이션과의 차이가 감소하였음을 확인할 수 있다. 특히, y_var=−0.5 m에서 근거리장 RCS가 원거리장 RCS보다 크게 계산되었기 때문에 차이의 크기가 25.46 dB에서 12.9 dB로 크게 감소하였다.

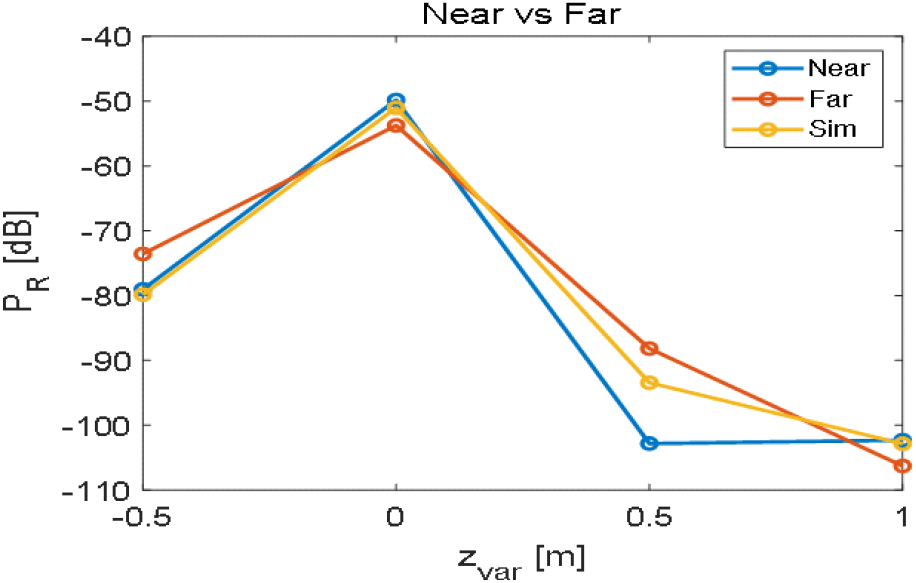
그림 10 및 표 3과 같이, z_var=0.5 m를 제외하고 원거리장 이득과 원거리장 RCS를 사용하였을 때보다 근거리장 이득과 근거리장 RCS를 사용하였을 때의 수신전력이 시뮬레이션과의 차이가 감소하였음을 확인할 수 있다.

VI. 결 론

본 논문에서는 유도무기와 표적이 근접하였을 때의 표적 조우 환경을 모델링하고, 재정의된 거리와 근거리장 이득과 근거리장 RCS를 분석하여 유도무기의 안테나를 통하여 수신되는 수신전력을 계산하는 방법을 제안하였다. 제안한 방법을 통해 근거리장 이득과 근거리장 RCS값을 사용하여 계산한 수신전력은 원거리장 이득과 원거리장 RCS값을 사용하는 기존의 방법에 비해, 표적과 조우하는 매우 가까운 거리에서 시뮬레이션과의 차이가 최대 12.56 dB 감소하였다. 따라서 적절한 표적 조우 환경과 이득 및 RCS를 모델링함으로써 근거리에서도 레이다 방정식을 통한 수신전력 계산값과 시뮬레이션의 차이를 크게 줄여 레이다 방정식을 보완할 수 있다. 제안한 유용한 모델링을 통해 표적 조우 환경에서의 유도무기 및 레이다 시스템 분석 정확도를 높일 수 있을 것이다.