결합계수 및 코일 자기 인덕턴스 변화에 따른 무선전력전송 시스템의 입력 임피던스 변화에 관한 연구

I. 서 론

현대의 다양한 전자 시스템들은 전기 에너지를 이용하여 동작하며, 해당 전기 에너지는 배터리에 저장되고 시스템에 전력을 공급한다. 따라서, 배터리를 충전하는 다양한 방법들이 필요한데, 최근 무선전력전송(WPT, wireless power transfer) 시스템이 기존의 유선충전 시스템을 대체할 차세대 시스템으로 주목받고 있다^[1],[2]. WPT 시스템은 이미 다양한 연구들에서 그 편리성과 안전성이 증명되었다^[3]~[5]. 따라서, 인간과 가장 밀접하게 가까운 곳에서 동작하는 전자제품(consumer electronics)에 WPT 시스템이 가장 먼저 적용되고 있으며, 특히 스마트폰의 경우에는 무선충전 시스템의 관련 국제 표준도 존재한다^[6].

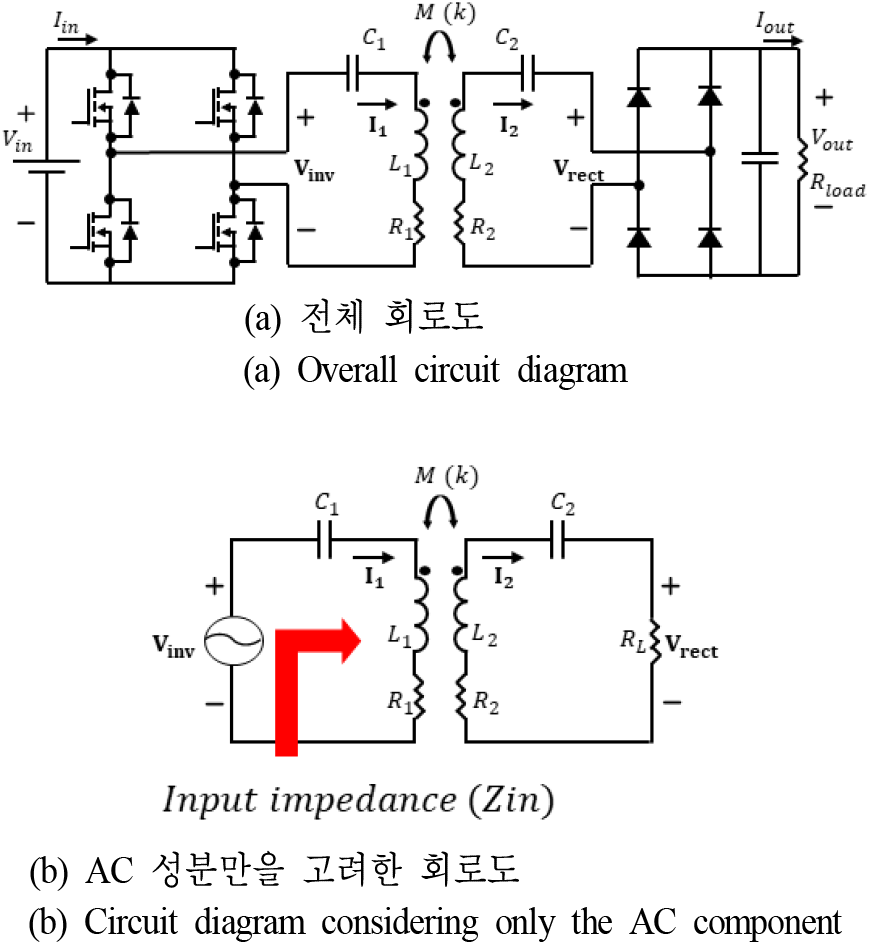
전자제품에 적용된 WPT 시스템은 주로 직렬-직렬 (SS, series-series) 토폴로지가 사용된다. SS 토폴로지는 그림 1(a)와 같이 송신측(TX, transmitting side)과 수신측(RX, receiving side)에 공진을 위한 보상회로가 커패시터가 직렬로 각각 하나씩 존재하는 토폴로지를 의미한다. SS 토폴로지는 용량이 작으면서 동시에 작은 공간을 차지해야 하는 소형 애플리케이션에 주로 채택된다^[5].

그림 1. | Fig. 1. SS 토폴로지가 채택된 WPT 시스템의 회로도 | Circuits diagram of wireless power transfer with series-series topology.

Download Original Figure

SS 토폴로지에 대한 다양한 연구들이 진행되었다. 특히, SS 토폴로지에서 코일 간의 결합계수가 매우 중요한데, 결합계수의 크기에 따라 입력 임피던스의 위상이 0이 되는 주파수(ZPA, zero phase angle)^[6]와 최대 전력 전송 주파수(maximum power transfer frequency)가 한 점에서 세 점으로 분할되는 주파수 분할 현상(frequency split phenomenon) 등에 관한 연구가 진행되었다^[7]. 이러한 문제점들을 고려하여 SS 토폴로지는 적절하게 설계되어야 한다. 하지만, 기존 연구들은 모두 결합계수가 증가했을 때 전력전송 관점에서의 단점에 관한 연구만을 진행하였지만^[7],[8], 결합계수와 입력 임피던스의 크기 관계에 관한 연구는 진행되지 않았다. 특히, 기본파(fundamental) 이외에서의 입력 임피던스의 크기는 고조파 전류의 크기와 직결되므로, 이는 반드시 연구되어야 한다.

본 논문에서는, SS 토폴로지를 채택한 WPT 시스템에서 코일의 자기 인덕턴스와 결합계수에 따른 입력 임피던스의 관계에 대해 분석하였다. 구체적으로, 코일 간의 결합계수가 증가할수록 시스템의 입력 임피던스 크기의 기울기가 작아지고, 코일의 자기 인덕턴스의 크기가 클수록 입력 임피던스 크기의 기울기가 커지는 현상에 대해 분석하였다. 입력 임피던스 크기의 기울기가 작아지면 기본파 이외의 고조파에서의 전류가 커지며, 기울기가 작아지면 고조파에서의 전류가 작아지게 된다. 해당 내용들은 시뮬레이션과 실험을 통해 분석되었다.

본 논문의 전개는 다음과 같다. 서론에 이어서 section Ⅱ에서는 결합계수와 자기 인덕턴스에 따른 WPT 시스템의 입력 임피던스 크기의 기울기에 대해 분석하며, 분석된 내용들을 section Ⅲ에서 시뮬레이션과 실험을 통해서 각각 검증하도록 한다. 최종적으로 section Ⅳ에서 결론으로 본 논문을 마무리한다.

Ⅱ. 결합계수와 자기 인덕턴스 변화에 따른 WPT 시스템의 입력 임피던스 변화

그림 1(a)는 인버터와 정류기가 포함된 DC to DC WPT 등가회로를 나타내며, 그림 1(b)는 SS 토폴로지를 채택한 WPT 시스템을 분석하기 위해 AC 성분만을 고려한 등가회로를 나타낸다. 그림 1(b)에서 입력 전원은 인버터 후단의 구형파 전압원 V_inv으로 모델링되었으며, 정류기를 포함한 부하 저항은 R_L로 모델링되었다. 본 논문에서 분석하고자 하는 SS 토폴로지의 입력 임피던스의 정의는 그림 1(b)과 같이 전원에서 바라본 WPT 시스템의 임피던스이다. 입력 임피던스는 식 (1)과 같다.

식 (1)에서 R_in과 X_in은 입력 임피던스의 저항 성분과 리액턴스 성분을 나타낸다. ω는 동작 각주파수를, M은 TX측과 RX측의 상호 인덕턴스를 나타낸다. 식 (1)에서 부하 등가 저항 R_L은 RX측의 코일과 커패시터의 기생 저항 R₂보다 충분히 크다고 가정하였다. 또한, X₁과 X₂는 각각 TX측과 RX측의 리액턴스 성분을 나타내며, 식 (2) 및 식 (3)과 같다.

SS 토폴로지를 가지는 WPT 시스템에서는 코일의 인덕턴스를 보상해 주기 위해서, 시스템의 동작주파수 (인버터의 동작주파수 ω_o)에서 TX측과 RX측의 리액턴스가 0이 되도록 공진 커패시턴스 설계한다^[9]. 즉, 식 (2) 및 식 (3)이 0이 되는 조건이 되므로, 공진 조건에서의 입력 임피던스 식 (1)은 식 (4)와 같이 된다.

식 (4)에서 알 수 있듯이, 상호 인덕턴스 M이 일정하면, 공진 조건에서는 입력 임피던스가 일정하며, 순수한 저항 성분만을 갖는다.

한편, 시스템의 동작 주파수보다 높은 고조파에서는 입력 임피던스의 식 (2) 및 식 (3)이 0이 되지 않는다. 즉, 식 (1)에서 리액턴스 성분이 남아있게 된다. 고조파에서의 입력 임피던스의 크기는 식 (5)와 같다.

식 (5)에서 k는 TX와 RX 코일 간의 결합계수 $\left(k=M\sqrt{L_1{L}_2}\right)$이다. 식 (5)에서 알 수 있듯이, 공진 조건이 벗어난 입력 임피던스의 크기는 입력 리액턴스 X_in로 근사 될 수 있다. 식 (2) 및 식 (3)에서 알 수 있듯이, 동작주파수보다 충분히 큰 주파수에서는 리액턴스가 충분히 큰 값을 가지게 되어 리액턴스 X₁, X₂가 TX 코일의 저항 R₁과 등가 부하 저항 R_L이 비해 충분히 크기 때문이다. 따라서, 입력 저항 R_in보다 X_in이 충분히 크게 된다. 입력 임피던스의 크기의 최저점은 시스템이 공진 조건을 만족할 때 식 (4)와 같으므로, 고조파에서의 주파수에 대한 입력 임피던스 크기의 기울기를 구하면 입력 임피던스 크기의 전체를 알 수 있다. 주파수에 대한 입력 임피던스 크기의 기울기의 정확한 계산은 식 (5)에 식 (2) 및 식 (3)을 각각 대입하면 된다. 각주파수 ω가 충분히 크고, 식 (5)에서 계산된 입력 임피던스 크기의 분자의 ω의 최고차항은 6차, 분모의 최고차항이 5차이므로, 기울기의 정의를 이용하여 최고차항의 계수를 통한 입력 임피던스 크기의 근사는 식 (6)과 같다.

식 (6)에서는 자기적으로 결합된 결합계수의 정의 $M=k\sqrt{L_1{L}_2}$를 이용하여 상호인덕턴스를 결합계수와 자기 인덕턴스들로 나타내었다. 식 (6)에서 알 수 있듯이 SS 토폴로지를 채택한 WPT 시스템의 입력 임피던스 크기의 기울기는 TX측 코일의 인덕턴스와 결합계수에 의존한다는 것을 알 수 있다. 앞서 분석한 내용을 정리한 것을 그림 2에서 나타내었다.

그림 2. | Fig. 2. TX 코일 인덕턴스(L₁)와 결합계수 k에 따른 입력 임피던스 크기 변화 | Change in input impedance size according to TX coil inductance (L₁) and coupling coefficient k.

Download Original Figure

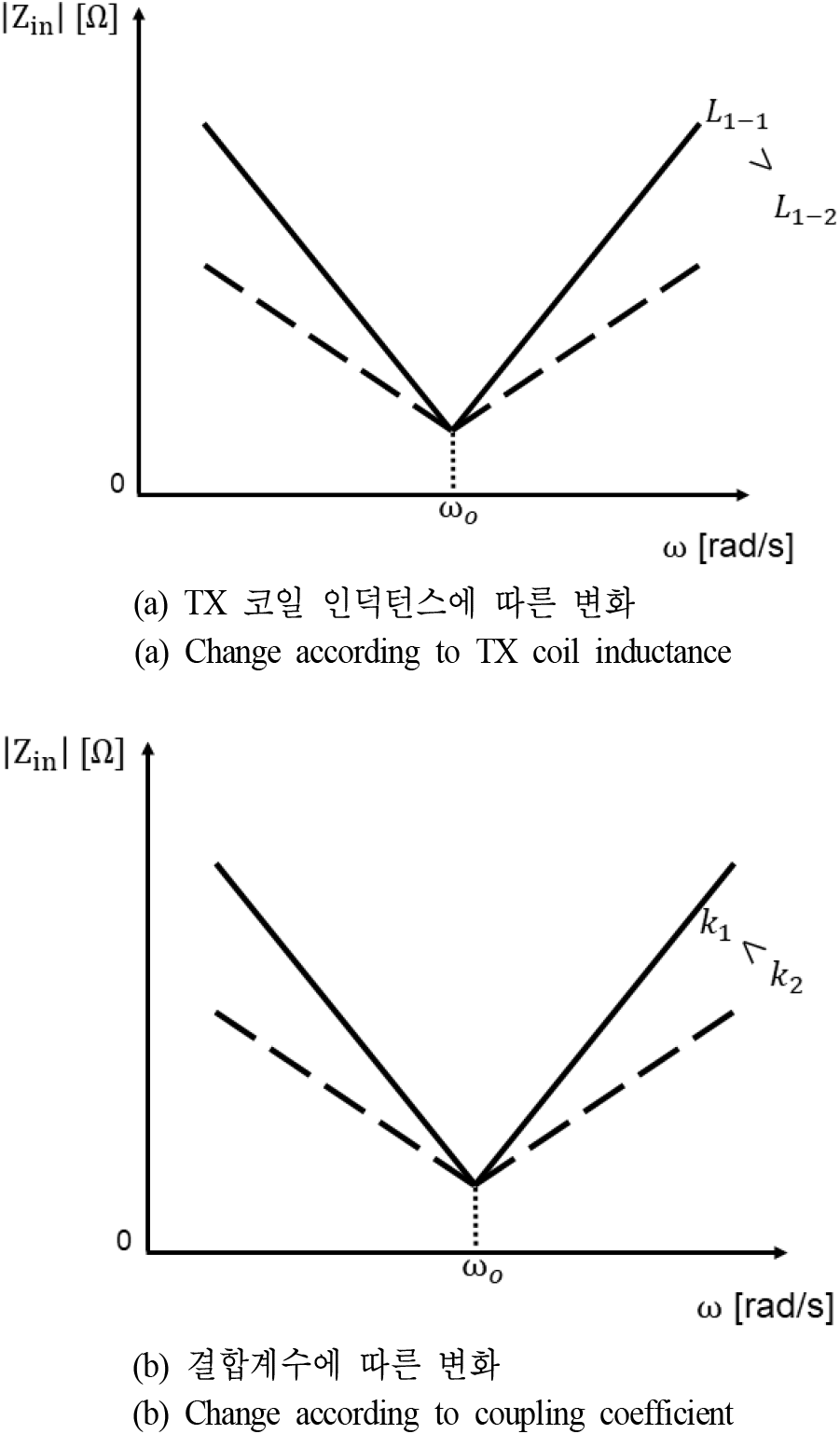
기존 연구들에서 WPT 시스템의 누설 자기장은 전류에 비례한다는 것이 연구되었다^[10]. 따라서, 식 (6)과 그림 2에서 알 수 있듯이, TX 인덕턴스가 클수록, 그리고 결합계수가 작을수록 고조파에서의 WPT 입력 임피던스의 크기는 커지게 된다. 입력 임피던스는 그림 1에서와 같이 인버터의 구형파를 정현파로 필터링 해주는 역할을 하는데, 만약 고조파에서의 입력 임피던스가 크다면 필터의 성능이 향상되어 인버터의 출력이 보다 정현파에 가까워지게 된다. 즉, 코일 전류의 고조파 성분이 감소할 것이다. 즉, 식 (7)과 같이 WPT 시스템의 고조파 전류는 입력 임피던스에 반비례할 것이다.

Ⅲ. 실험과 시뮬레이션을 통한 TX 인덕턴스와 결합계수에 따른 WPT 시스템의 입력 임피던스와 고조파 전류의 측정

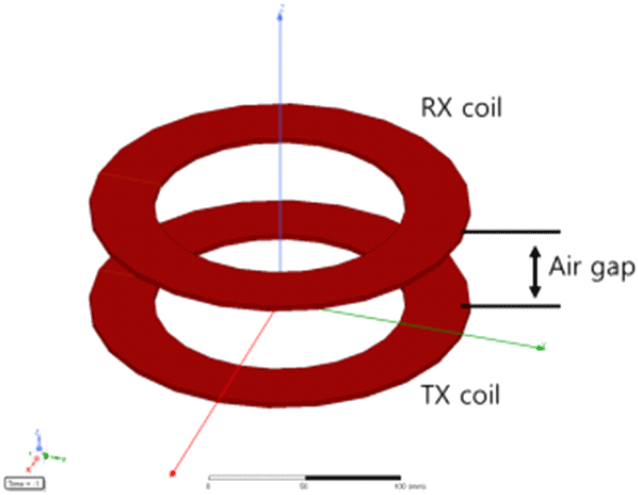
WPT 시스템의 송신 코일과 결합계수가 입력 임피던스에 미치는 영향을 시뮬레이션으로 증명하기 위하여, 유한요소법 기반 자기장 시뮬레이션(ANSYS MAXWELL)을 이용하여 코일을 설계하였다. 시뮬레이션을 통해 설계된 형상과 설계 사양은 그림 3과 표 1에서 보여준다. TX 코일의 인덕턴스(L₁)의 변화에 따른 입력 임피던스 변화를 확인하기 위하여 인덕턴스를 0~60 μH 추가하여 시뮬레이션하였으며, 또한 결합계수를 조정하기 위하여 송신 코일과 수신 코일 사이의 공극(air gap)을 30 mm에서 150 mm까지 5단계로 조절하여 시뮬레이션하였다. 각 공극에 따른 결합계수와 상호 인덕턴스 값을 표 2에서 정리하였다. 표 2의 결합계수들은 결합계수의 정의$\left(k=M/\sqrt{L_1{L}_2}\right)$를 이용해서 계산되었다.

그림 3. | Fig. 3. 분석된 내용을 증명하기 위해 시뮬레이션을 통해 설계된 WPT 코일 | WPT coil designed through simulation to prove analysis results.

Download Original Figure

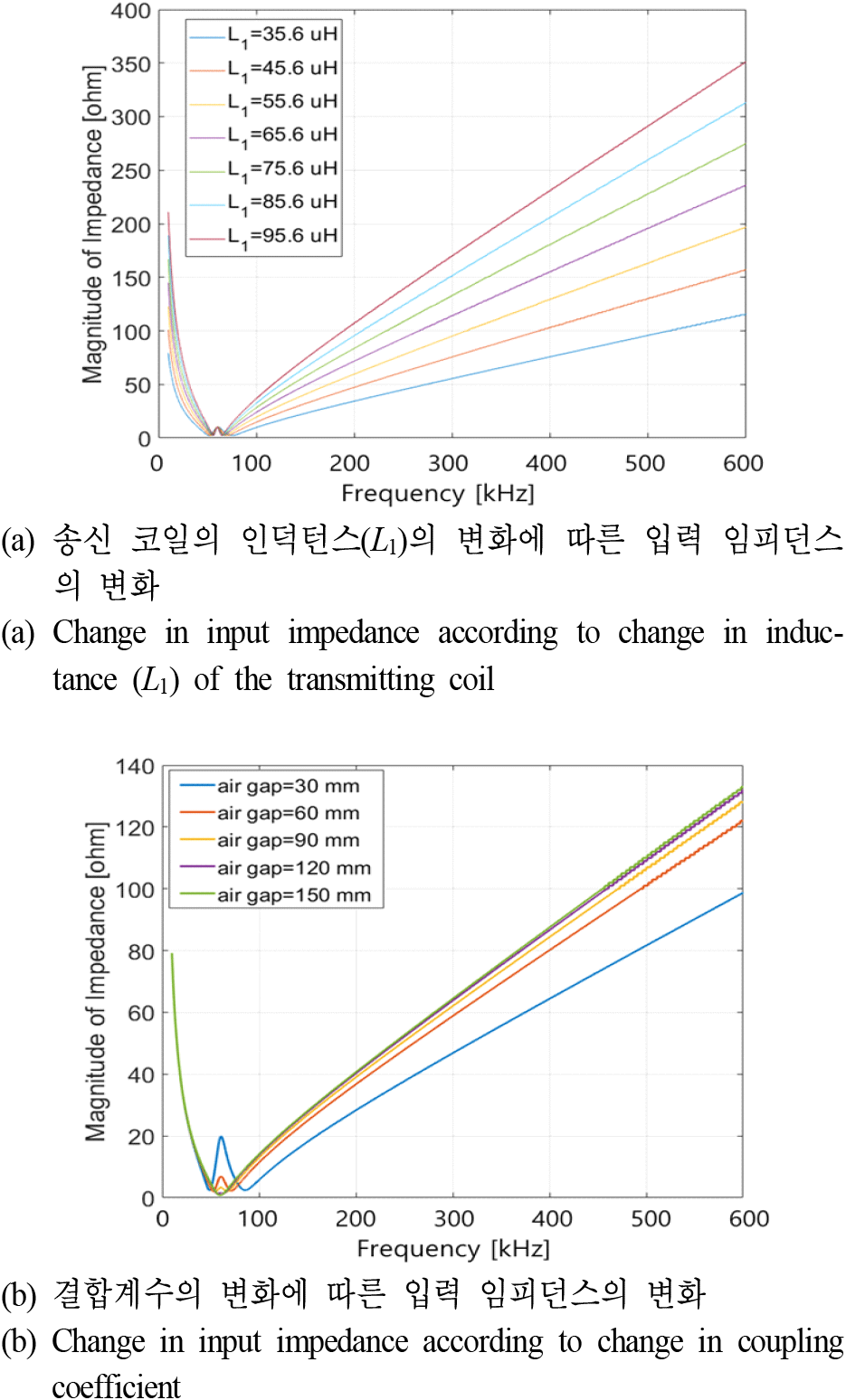
그림 4(a)는 TX 코일의 인덕턴스 (L₁)의 변화에 따른 입력 임피던스 변화를 보여준다. 앞서 식 (6)에서 예상되었듯이, TX 인덕턴스(L₁)가 증가할수록 인버터에서 바라본 WPT 시스템의 입력 임피던스가 증가하는 것을 알 수 있다. 또한, 그림 4(b)는 공극에 따른 입력 임피던스의 변화를 나타낸다. 마찬가지로 식 (6)에서 예상되었듯이, 송신 코일과 수신 코일 사이의 공극이 증가할수록 결합계수는 감소하기 때문에 WPT 시스템의 입력 임피던스는 감소함을 알 수 있다.

그림 4. | Fig. 4. 입력 임피던스의 변화 시뮬레이션 결과 | Simulation results of change in input impedance.

Download Original Figure

다음으로 TX 인덕턴스와 결합계수에 따른 임피던스의 변화가 WPT 시스템의 고조파 전류에 어떤 영향을 끼치는지 확인하기 위하여, 회로 시뮬레이션을 수행하여 TX 인덕턴스와 결합계수(공극)에 따른 고조파 전류들의 변화를 확인하였다. 회로 시뮬레이션은 그림 1(a)와 같이 회로를 구성하여 수행하였으며, 회로 시뮬레이션이 수행된 환경은 표 2와 같다. 전류의 고조파 성분은 회로 시뮬레이션 프로그램의 자체 FFT 기능을 통해서 확인되었으며, 30 W의 전력이 부하로 전달될 때의 고조파 전류를 확인하였다.

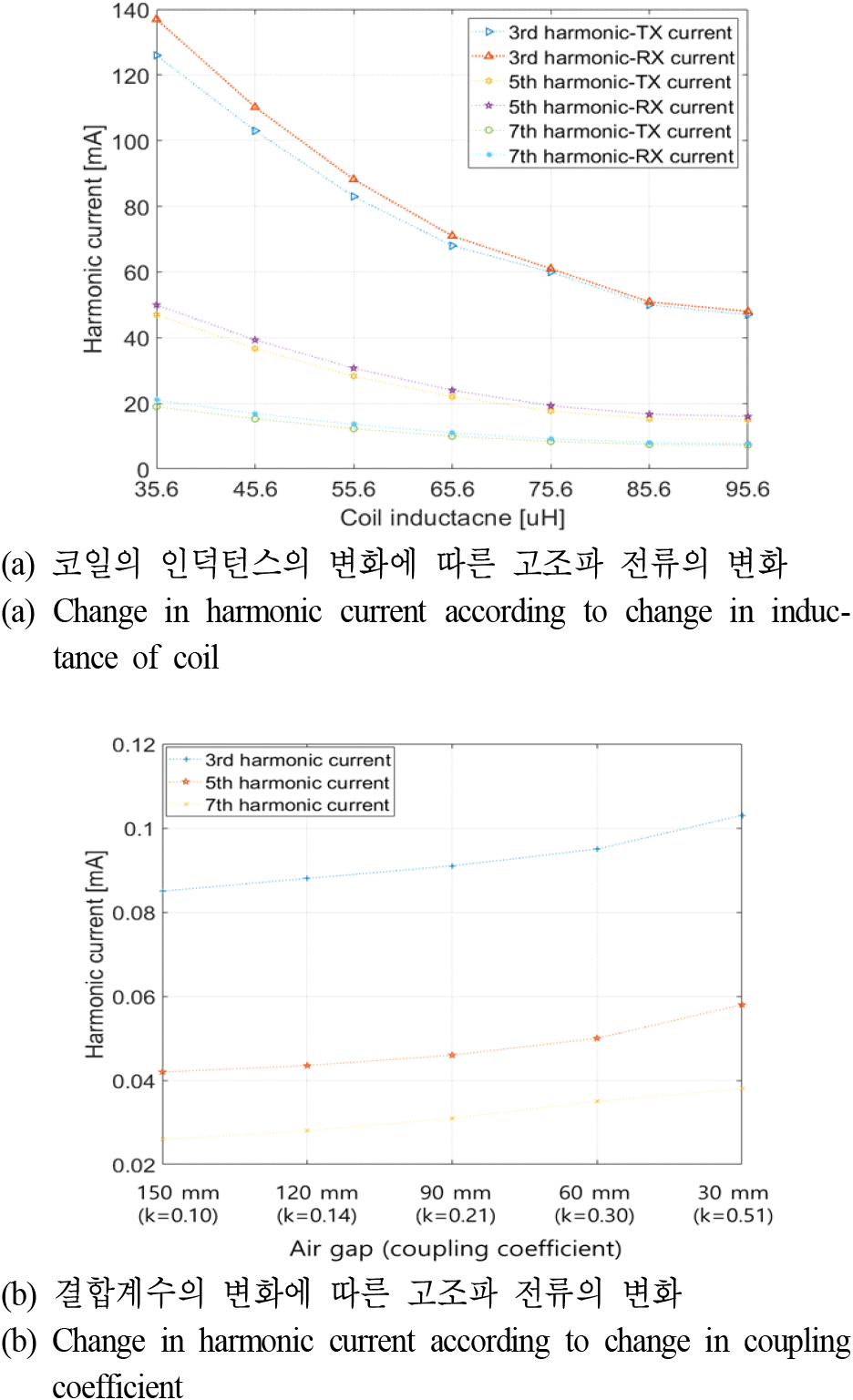
그림 5(a)는 시뮬레이션으로 분석된 코일의 인덕턴스에 따른 송․수신 코일 전류의 고조파 성분을 나타낸다. 앞서 그림 4(a)에서 분석한 바와 같이, 코일의 인덕턴스가 커질수록 고조파에서의 입력 임피던스는 커지므로, 코일의 인덕턴스가 커질수록 WPT 코일 전류의 고조파 성분이 작아지게 된다. 한편, 그림 5(b)는 코일 간의 공극(결합계수)에 따른 TX 코일 전류의 고조파 성분을 보여준다. 그림 4(b)에서 분석된 바와 같이, 공극이 작아질수록 결합계수가 커지고, 결합계수가 커지면 입력 임피던스 크기의 기울기가 작아지기 때문에 입력 임피던스가 작아지게 된다. 입력 임피던스가 작아졌으므로, WPT 코일에 흐르는 전류의 고조파 성분이 증가하는 것을 확인하였다.

그림 5. | Fig. 5. WPT 동작 시 코일의 고조파 전류 성분 시뮬레이션 결과 | Simulation results of harmonic current components of the coil during wireless power transfer system operation.

Download Original Figure

시뮬레이션 결과를 정리하면, 앞서 수식적으로 증명된 바와 같이 시스템의 동작 주파수가 아닌 고조파 주파수에서의 입력 임피던스는 송신 코일의 인덕턴스(L₁)가 클수록, 코일 간의 결합계수가 작을수록 증가함을 알 수 있다. 앞서 설명한 대로, WPT 시스템의 공진 시스템은 인버터의 구형파를 정현파로 변환하는 필터 역할을 하는데, 고조파에서의 입력 임피던스가 클수록 구형파의 고조파 성분이 작아지게 된다. 따라서, 입력 임피던스가 클수록 전류의 고조파 성분이 감소할 것이라 예상할 수 있었고, 이는 그림 5의 시뮬레이션을 통해 확인되었다.

그림 6(a)는 실험을 위해서 그림 3과 표 1의 설계 사양을 실제로 코일로 제작한 그림을 보여준다. TX 및 RX 코일 간의 결합계수는 변화시키지 않으면서 TX와 RX측의 자기 인덕턴스만을 변화시키기 위하여, 그림 6(a)의 코일 외에 그림 6(b)와 같이 토로이달 코어 인덕턴스를 송신측과 수신측에 각각 추가하였다. 해당 인덕턴스들은 WPT 코일과는 별도로 추가되었고, TX와 RX 간의 자기적 결합이 없기 때문에, 자기 인덕턴스의 값은 변화시키지만, 상호 인덕턴스에는 영향을 주지 않는다. 코일의 선재, 크기 등은 표 1과 같으며, 실제 WPT 코일의 인덕턴스 측정값과 실험을 위한 설계 사양은 표 3과 같다.

그림 6. | Fig. 6. 실험을 위한 제작된 WPT 코일 및 인덕턴스 | Fabricated WPT coil and inductance for experiment.

Download Original Figure

TX 인덕턴스(L₁)의 변화에 따른 입력 임피던스의 변화를 확인하기 위하여 기본 코일의 인덕턴스(34.8 μH)에 그림 6(b)의 토로이달 코어를 이용한 인덕턴스 30, 60, 90 μH를 각각 추가하여 입력 임피던스를 측정하였다. 또한, 결합계수에 따른 입력 임피던스의 변화를 확인하기 위해서, 공극을 30 mm(k=0.40), 60 mm(k=0.26), 90 mm(k=0.13), 총 3 단계로 구분하여 입력 임피던스를 측정하였다. 입력 임피던스는 그림 2와 같이 인버터에서 바라본 WPT 시스템의 전체 임피던스를 확인하였으며, 임피던스 분석기(KEYSIGHT E4990A)를 이용하여 측정하였다.

그림 7(a)는 TX 인덕턴스의 변화에 따른 WPT 시스템의 입력 임피던스 변화를 보여준다. 앞서 수식적 분석과 시뮬레이션에서 예상되었던 것처럼, TX 인덕턴스가 증가할수록 WPT 시스템의 입력 임피던스가 증가하는 것을 확인할 수 있었다. 또한, 그림 7(b)는 코일 간의 공(결합계수)에 따른 입력 임피던스의 변화 측정 결과를 보여준다. 이 역시 앞서 수식에서 분석된 것처럼, 결합계수가 클수록(공극이 작을수록) 고조파에서의 입력 임피던스가 작아진다는 것을 알 수 있다.

그림 7. | Fig. 7. 입력 임피던스의 변화 측정 결과와 시뮬레이션 결과 비교 | Comparison of input impedance change measurement results and simulation results.

Download Original Figure

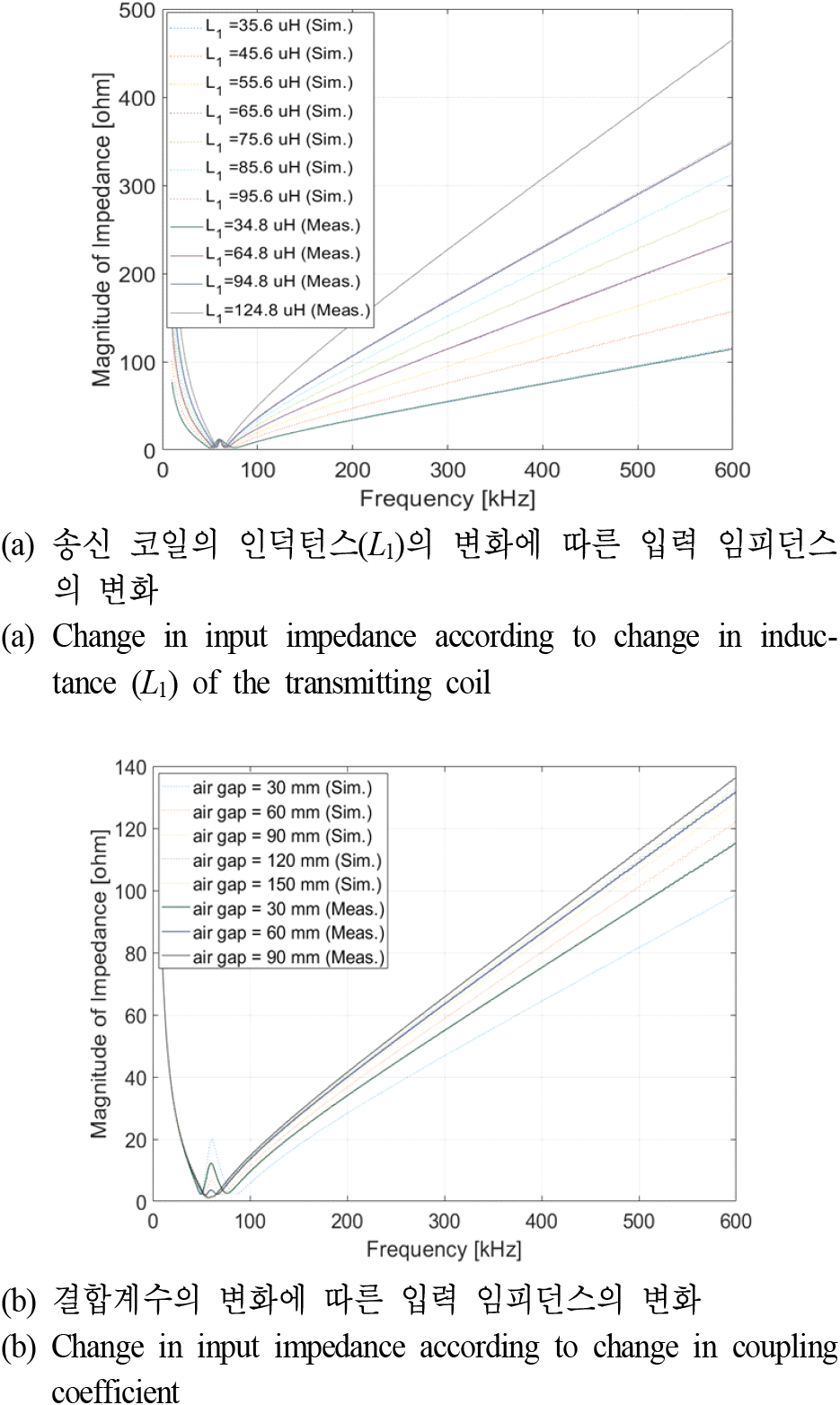
그림 7에서 알 수 있듯이, 수식으로 분석된 내용, 시뮬레이션 결과, 그리고 실험 결과의 경향성이 매우 일치하는 것을 알 수 있다. 구체적으로 논의하면, 자기 인덕턴스에 따른 입력 임피던스의 변화는 시뮬레이션과 실험의 결과가 1 % 미만의 오차로 일치하는 것을 알 수 있었다. 또한, 공극(결합계수)에 따른 입력 임피던스의 변화도, 결합계수가 커질수록 입력 임피던스가 달라지는 경향성이 일치하는 것을 알 수 있었다. 구체적으로, 시뮬레이션에서 결합계수가 0.14인 공극이 140 mm인 케이스와, 실험에서 결합계수가 0.13인 공극이 90 mm인 케이스에서 3 % 미만의 오차를 보이는 것을 확인할 수 있었다.

본 논문에서 분석한 TX 인덕턴스와 결합계수에 따른 임피던스의 변화가 WPT 시스템의 고조파 전류에 어떤 영향을 끼치는지 알아보기 위해 그림 8과 같이 실험을 진행하였다. 코일은 그림 6에 있는 코일을 사용하였으며, 그림 1(a)와 같이 인버터와 정류기를 포함한 전체 실험을 구성하였다. 시스템의 동작 주파수는 60 kHz로 선정하였으며, 전자 부하에 30 W가 도달하는 것을 기준으로 하였다. 즉, 동일한 전력이 전달될 때(30 W) TX측 인덕턴스와 결합계수에 따라 WPT 코일의 전류의 고조파 성분에 어떤 영향을 끼치는지 측정하였다. 전류의 고조파 성분 분석은 오실로스코프로 측정하였으며, FFT를 통하여 고조파 성분의 크기를 분석하였다.

그림 8. | Fig. 8. WPT 동작 실험을 위한 셋업 | Setup for WPT operation experiment.

Download Original Figure

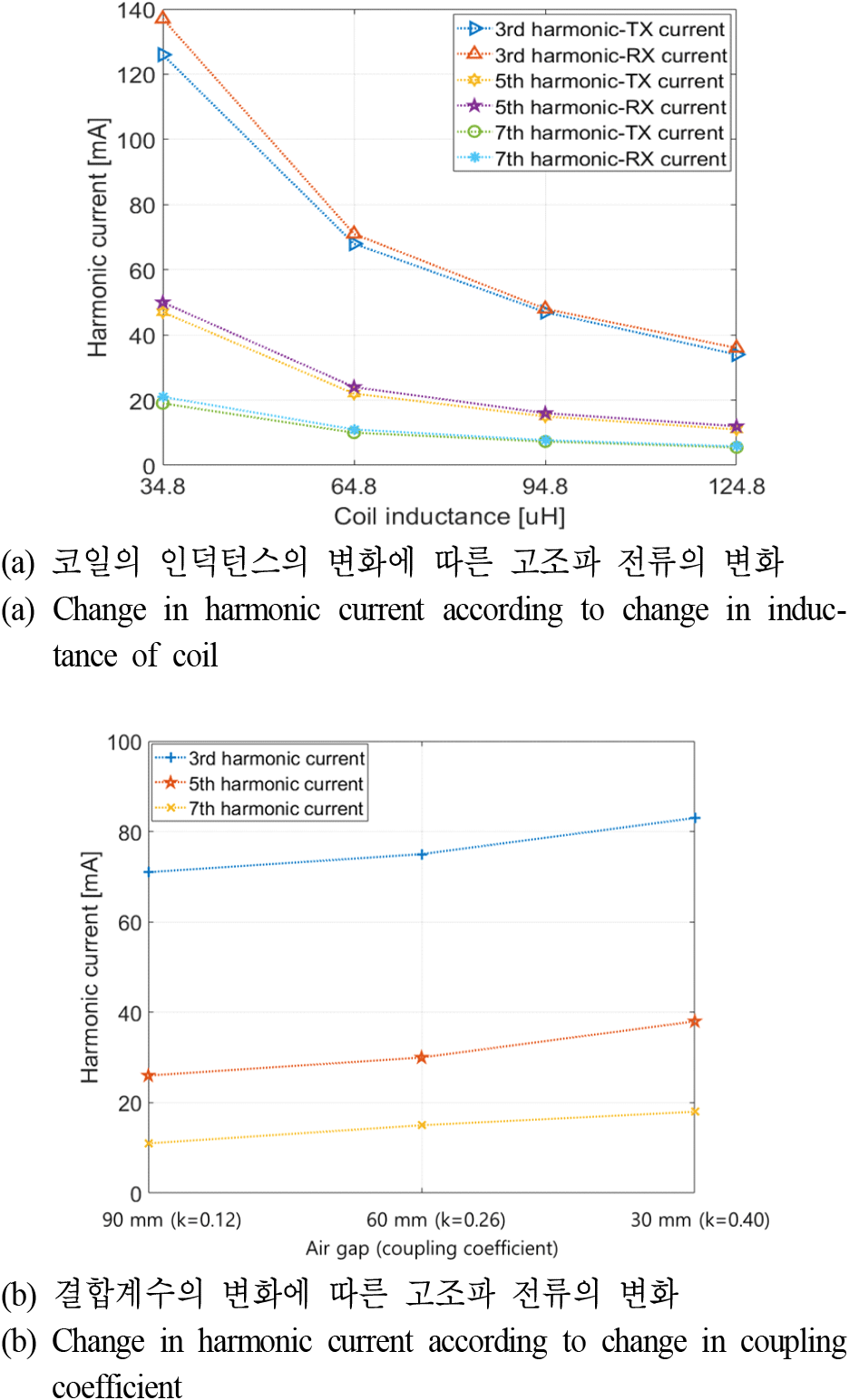
그림 9(a)는 코일의 인덕턴스에 따른 송신 및 수신 코일의 고조파 전류 크기의 측정값을 나타낸다. 그림 7(a)와 같이 코일의 인덕턴스가 커질수록 고조파에서의 입력 임피던스는 커지므로, 코일의 인덕턴스가 커질수록 WPT 코일 전류의 고조파 성분이 작아지게 된다. 한편, 그림 9(b)는 공극(결합계수)에 따른 TX 코일 전류의 고조파 성분을 나타낸다. 공극이 작아질수록 결합계수는 커지게 되고, 결합계수가 커지면 식 (6)에서 알 수 있듯이 입력 임피던스 크기의 기울기가 작아져서 그림 7(b)처럼 고조파에서의 입력 임피던스가 작아지게 된다. 고조파에서의 입력 임피던스가 작아졌으므로, WPT 코일에 흐르는 전류의 고조파 성분이 증가하는 효과가 있다는 것이 분석되었다.

그림 9. | Fig. 9. WPT 동작 시 코일의 고조파 전류 성분 측정 결과 | Measurement results of harmonic current components of the coil during wireless power transfer system operation.

Download Original Figure

Ⅳ. 결 론

본 논문에서는 WPT 시스템에서 코일의 인덕턴스와 결합계수에 따른 고조파 성분에서의 입력 임피던스의 영향을 분석하였다. 먼저, 수식 분석을 통해서 TX 코일의 임피던스가 클수록, 코일간의 결합계수가 작을수록 전원에서 바라본 입력 임피던스 크기의 기울기가 작아지게 된다는 것이 증명되었다. 따라서, 고조파 성분에서의 입력 임피던스가 작아지게 되는 것이 예상되었다. 분석된 내용들은 시뮬레이션과 실험을 통해서 실제로 코일 인덕턴스가 클수록, 결합계수가 작을수록 임피던스의 기울기가 커진다는 것을 확인하였다. 마지막으로, WPT 실험을 통해서, 고조파에서의 입력 임피던스의 크기는 고조파 전류와 반비례 한다는 것이 증명되었다.