평판형 소재에 대한 반사기반과 투과기반 흡수율의 해석적인 비교

Ⅰ. 서 론

전자파의 흡수는 소재에 유입된 전기적인 에너지가 열적인 에너지로 전환되어 감쇠되는 것으로 손실의 의미를 가진다. 전도성 소재는 도전율에 의해, 유전 소재나 자성 소재는 각각 복소 유전율과 투자율의 허수 성분에 의해서 흡수가 발생한다. 동일한 크기의 전자파가 소재 내로 유입되었다고 가정하면 소재의 흡수 성능은 이러한 물성에 의해 결정되지만, 실제 흡수 성능을 측정할 때는 입사되는 전자파가 일정하므로 소재 표면에서 반사되는 양에 따라 소재 내로 유입되는 양이 변화하여 소재의 흡수율은 달라진다. 전송선로나 안테나 등을 사용하는 이러한 흡수율 측정은 전자파 무반향실에서 사용하는 전파흡수체나 노이즈 저감용 시트 등에서 많이 활용되고 있다^[1],[2].

본 논문에서는 평판형 소재에 대한 수직 입사파의 반사기반 흡수율과 투과기반 흡수율을 이론적으로 유도하고, 해석적인 해를 이용하여 유전 및 자성 소재에 대한 반사율, 투과율 그리고 흡수율을 서로 비교하고 두 정의의 차이를 분석하였다. 또한 3차원 수치해석을 통해 그 결과의 정확성을 검증하였다.

Ⅱ. 흡수율 측정 방법과 그 정의

그림 1에서는 흡수율 측정에 사용되는 두 가지 방법을 도시하였다. 반사기반 흡수율은 1-포트 측정으로 평판형 소재의 뒷면이 도체로 막혀 있어서 투과하는 전자파가 없다(투과율은 0). 따라서 입사면 쪽에서 반사되는 전자파(반사율)를 측정하여 흡수율을 얻는다. 이 방법은 주로 전파흡수체의 흡수율을 측정할 때 많이 사용한다. 투과기반 흡수율은 2-포트 측정으로 평판형 소재의 뒷면에 도체가 없어 투과파가 존재하게 되고 입사면과 투과면에서 각각 반사파(반사율)와 투과파(투과율)를 측정하여 소재의 흡수율을 얻어낸다. 이 방법은 주로 차폐 소재의 흡수율을 측정할 때 많이 사용한다. 따라서 동일한 소재의 흡수율이 측정 방법에 따라 상이할 수 있다. 이들의 관계와 차이를 정확히 알기 위해서 본 논문에서는 수직 입사 조건에서 두 매질에서의 경계조건을 적용하여 반사율, 투과율, 그리고 흡수율에 대한 해석적인 해를 도출하였다.

그림 1. | Fig. 1. 평판형 소재의 두 흡수율 정의 | Two definitions for absorptance of planar materials.

Download Original Figure

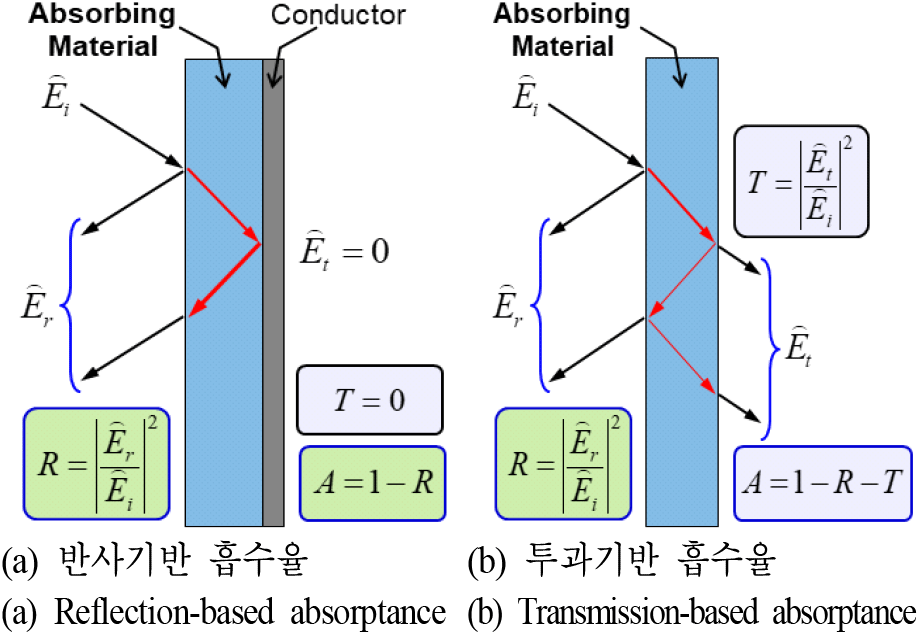
그림 2에서는 두 가지 측정방법의 흡수율에 모두 적용할 수 있도록 평판 형태의 서로 다른 세 매질의 고유 임피던스를 η₀, η, η₂라 할 때, 두 경계면에서의 반사계수인 ρ₁과 ρ₂를 나타내었다. 여기서 η₀는 공기의 임피던스, η은 측정하고자 하는 소재의 임피던스, η₂는 반사기반 흡수율의 경우에는 완전도체의 임피던스인 0이고, 흡수기반 흡수율의 경우에는 공기의 임피던스 η₀이다. 경계조건을 적용하여 식을 유도하면, 그림 1에서 보듯이 입사파$\left({\widehat{E}}_i\right)$와 반사파$\left({\widehat{E}}_r\right)$의 비(S-파라미터 중 S₁₁)와 입사파와 투과파$\left({\widehat{E}}_t\right)$의 비(S₂₁)를 다음과 같이 나타낼 수 있다.

그림 2. | Fig. 2. 서로 다른 매질의 경계면에서의 반사계수 | Reflection coefficients at boundaries between materials.

Download Original Figure

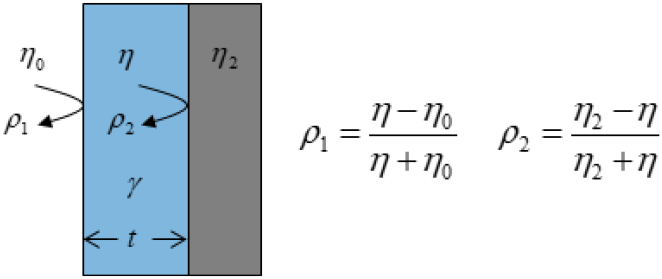
여기서 γ와 t는 흡수율을 측정하고자 하는 매질(소재)의 전파상수와 두께를 나타낸다.

만약 η₂ = 0이고 ρ₂=−1이면

따라서 반사기반 흡수율 측정에서 반사율(R_S)과 흡수율(A_S)은 다음과 같이 정의된다.

여기서 첨자 ‘s’는 η₂ = 0이므로 단락(short)을 의미한다.

만약 η₂ = η₀이고 ρ₂ = −ρ₁이면

따라서 투과기반 흡수율 측정에서 반사율(R₀), 투과율(T₀), 그리고 흡수율(A₀)은 다음과 같이 정의할 수 있다.

여기서 첨자 ‘o’는 η₂ = η₀이므로 개방(open)을 의미한다.

식 (5) 및 식 (6), 그리고 식 (9)~식 (11)을 이용하여 반사기반과 투과기반 측정에서 수직 입사인 경우 반사율, 투과율, 그리고 흡수율을 해석적으로 계산할 수 있다.

Ⅲ. 해석 결과 및 검증

그림 3에서는 각각 2종의 유전 및 자성 흡수체들의 복소 유전율과 투자율을 보여준다. 유전 흡수체의 경우에는 Laird사의 Eccosorb LS26과 LS22 모델을 사용하였는데^[3], 이들의 복소 유전율은 3차원 수치해석 툴인 CST Microwave Studio(MWS)에서 제공한다^[4]. 자성 흡수체의 경우에는 GSS사의 FSA300과 DMEGC사의 FS170 모델을 사용하였으며^[5],[6], 측정을 통해 복소 투자율을 추출하였다. 해석에 사용된 소재의 두께는 모두 30 mm로 설정하였다.

그림 3. | Fig. 3. 유전 및 자성 흡수 소재들의 물성 | Material properties of dielectric and magnetic absorbers.

Download Original Figure

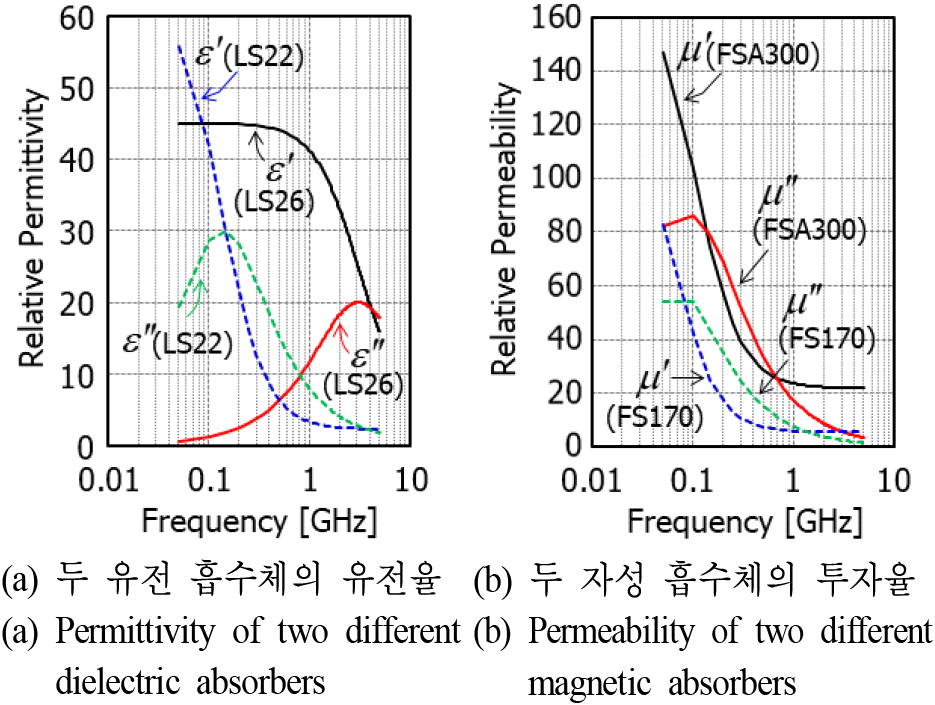
그림 4에서는 5 GHz까지 계산된 두 유전 흡수체의 반사율, 투과율, 그리고 흡수율을 비교하였다. 입사전력을 1이라고 가정할 때 반사와 투과, 그리고 흡수되는 비율을 알기 쉽게 비교하기 위해서 dB 값이 아닌 선형 값으로 표시하였다. LS26의 경우에는 반사기반의 경우 100 MHz 이하의 주파수에서 반사율이 거의 1이다. 따라서 흡수율은 거의 0이 된다. 반면 투과기반의 경우에는 투과파가 존재하여 반사율은 0이 되지 않는다. 주파수가 증가함에 따라 반사율은 증가와 감소를 반복하다가 2 GHz 이상의 주파수 대역에서는 0.5로 수렴한다. 흡수율의 경우 500 MHz까지 0.1 보다 낮으며, 그 이상의 주파수 대역에서 증가와 감소를 반복하다가 0.5로 수렴한다. 반사기반과 투과기반의 흡수율은 많이 다르나, 주파수가 2 GHz 이상이 되면 0.5로 거의 비슷해진다. 이는 주파수가 증가함에 따라 γ가 증가하여 T₀는 0으로 수렴하고, R₀ = R_s ≈ |ρ₁|² 이 되기 때문이다. LS22의 경우에는 그림 3에서 보듯이 100 MHz 이상에서는 LS26에 비해 실수 유전율이 작다. 그로 인해 전 주파수 대역에서 LS26보다 반사율이 낮다. 반사기반의 경우에도 500 MHz 이상의 주파수에서 반사율은 0.5 이하로 줄어든다. 낮은 반사율은 높은 흡수율을 의미한다. 그래서 LS26보다 LS22가 흡수율이 더 높게 나타난다. 3 GHz 이상에서 0.8 이상의 흡수율을 가진다. 그리고 주파수가 증가할수록 투과율이 작아지면서 반사기반과 투과기반의 흡수율 결과는 유사해진다.

그림 4. | Fig. 4. 두 유전 흡수체의 반사율, 투과율, 흡수율 비교 | Comparison of reflectance, transmittance, and absorptance of two dielectric absorbers.

Download Original Figure

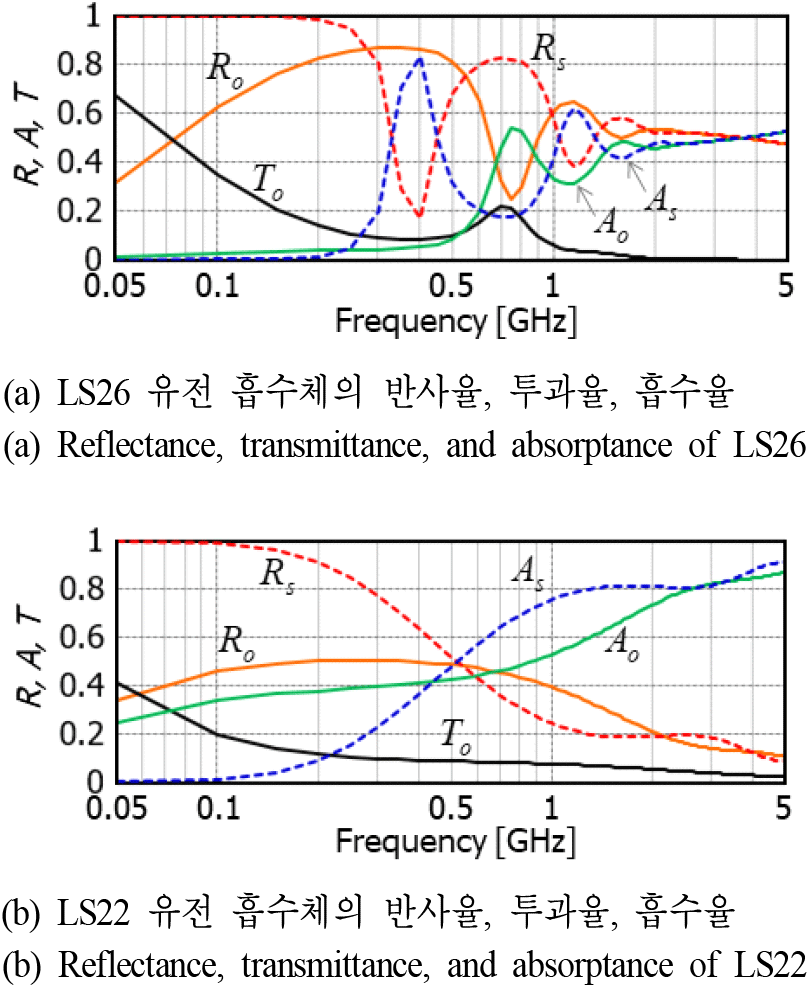
그림 5에서는 두 자성 흡수체의 반사율, 투과율, 그리고 흡수율을 비교하였다. 유전 흡수체와 달리 저주파수 대역에서 투과율이 낮아서 반사기반과 투과기반의 측정 방법에서 반사율과 흡수율의 차이는 적었다. 이 경우에도 FSA300 보다 실수 투자율이 낮은 FS170 모델의 흡수율이 더 높게 나타났다. 결과적으로 실수 유전율과 투자율이 낮은 소재일수록 반사가 적어서 소재 안으로 들어오는 전자파가 많아지고 흡수율이 증가함을 알 수 있다.

그림 5. | Fig. 5. 두 자성 흡수체의 반사율, 투과율, 흡수율 비교 | Comparison of reflectance, transmittance, and absorptance of two magnetic absorbers.

Download Original Figure

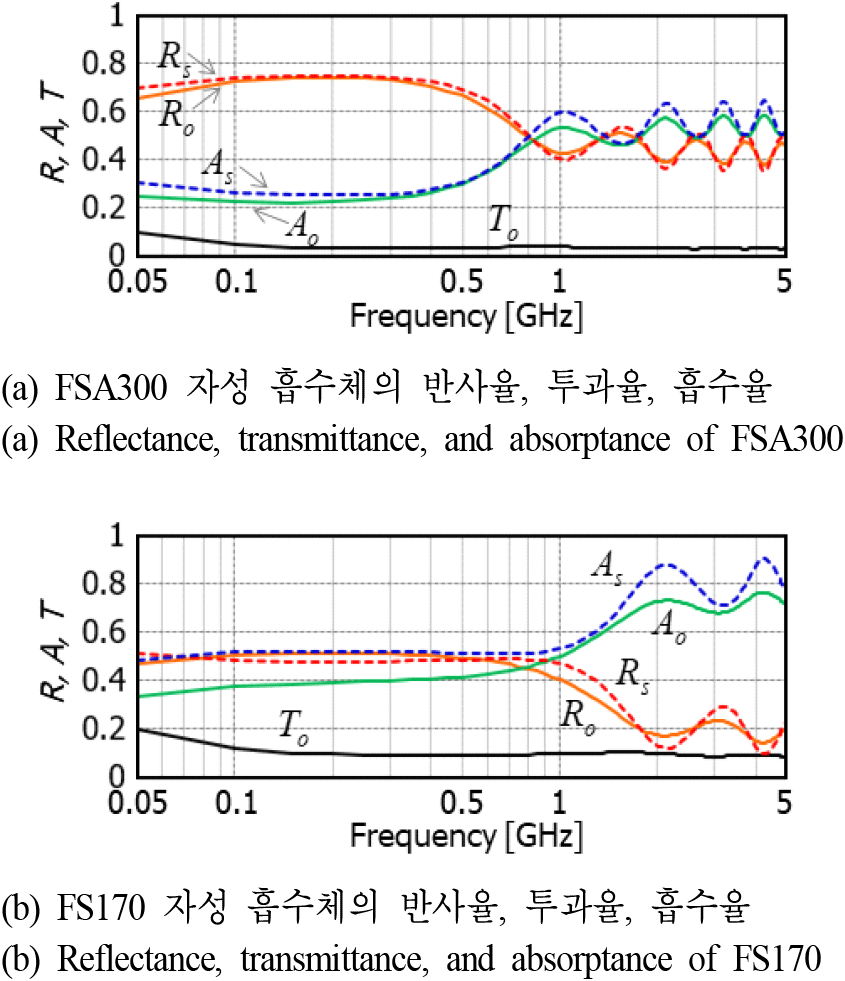
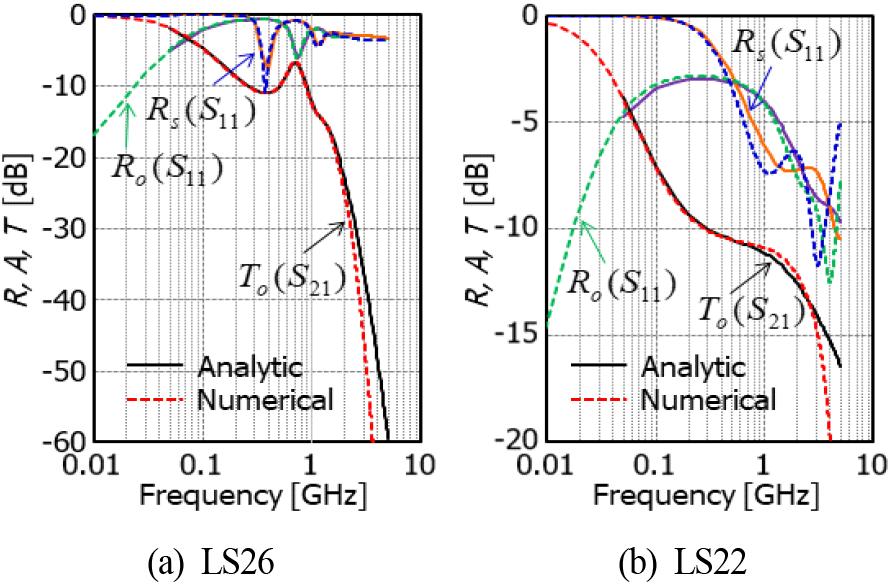
그림 6은 두 유전 흡수체에 대해서 해석적으로 계산한 결과를 CST MWS를 이용한 수치해석 결과와 비교하였다. 수치해석에 사용된 평판형 소재의 크기는 1 m × 1 m 로 설정하였다. 평면파가 수직 입사하도록 포트를 설정하여 S-파라미터를 계산하였다. 반사기반과 투과기반의 측정 방법 모두에서 이론적인 해석 결과는 수치해석 결과와 잘 일치함을 알 수 있다.

그림 6. | Fig. 6. 유전 흡수체의 수치해석 결과와 비교 | Comparison of numerical results of dielectric absorbers.

Download Original Figure

Ⅳ. 결 론

본 논문에서는 평판형 소재에 대한 반사기반과 투과기반의 흡수율을 이론적으로 해석하고, 유도된 수식을 이용하여 유전 흡수 소재와 자성 흡수 소재의 주파수에 따른 반사율, 투과율, 그리고 흡수율을 비교하였다. 또한 3차원 수치해석을 통해 그 결과의 정확성을 확인하였다.