PDF Download
PubReader
Export Citation
Email the Author
Share Facebook
Share Twitter
Cited by 0 Article
Metrics (View:492)
Ⅰ. 서 론
레이다(radar)는 전자파를 이용하여 원하는 표적의 거리 또는 속도 등을 구하는 시스템이다. 전자파를 보내 반사되어 되돌아온 신호를 처리하여 표적을 탐지 및 추적하게 되는데, 이때 돌아오는 신호는 표적에 의한 신호뿐 아니라 다양한 물체를 맞고 들어오는 신호들도 존재한다. 이렇게 레이다에 잡히지만 표적이 아닌 신호를 클러터(clutter) 신호라 한다[1].
클러터 신호는 표적의 탐지를 어렵게 하고 레이다의 성능을 저하하는 요인으로 작용할 수 있으며, 실제 레이다 환경에는 클러터가 존재하기 때문에 레이다의 성능을 시험 또는 개선하기 위해서는 클러터 신호 모의가 필요하다. 그러나 기존의 레이다 시스템에서는 실제 지형 클러터를 모사하지 못하고 가상의 고정된 클러터만 모의하거나 실제 수신된 클러터 데이터를 획득하여 후처리를 통하여 생성하는 것에 그치고 있다. 본 논문에서는 다양한 종류의 클러터 중 지형에 의한 클러터인 지형 클러터에 대해 다루었고, 실제 환경의 지형 클러터를 모델링하기 위한 데이터로는 지형의 위치에 대한 표고를 일정한 간격으로 배열한 수치 정보인 수치표고모델(DEM, digital elevation model)을 활용하였다.
수치표고모델을 이용하여 지형 클러터를 모의하기 위해서는 데이터를 불러오는 과정부터, 좌표 변환, 원하는 영역 선택, 빔 조사면 계산, 클러터 RCS 계산 등의 과정이 필요하다. 상기 과정은 긴 연산 시간을 필요로 하기 때문에 실시간으로 신호를 모의하는데 어려움이 있으며, 이에 지형 클러터 모의 환경에서의 레이다 성능 시험 및 개선이 어려워진다. 따라서 본 논문에서는 레이다의 위치와 시야각(FoV, field of view)에 따른 지형 클러터의 거리 및 RCS(radar cross section)를 미리 계산하는 방안을 제안하였다. 미리 계산된 지형 클러터의 거리 및 RCS 정보를 활용하여 실시간으로 수신 클러터 신호를 생성한다.
Ⅱ장에서는 수치표고모델을 레이다 상황에 적용하는 과정을 나타내었고, Ⅲ장에서는 이를 활용하여 지형 클러터를 모델링하는 과정, Ⅳ장에서는 모델링한 지형 클러터를 이용하여 수신 클러터 신호를 생성하는 방안에 대해 기술하였다.
Ⅱ. 수치표고모델의 적용
수치표고모델은 미국의 NASA(National Aeronautics and Space Administration)에서 제공한 NASADEM 데이터를 사용하였고, 30 m의 해상도를 가지며 한 파일 당 1°×1°의 위·경도 범위를 갖는다. NASADEM 데이터는 EGM96 (Earth Gravitational Model, 1996) 기준의 고도 데이터이기 때문에 레이다 시스템에 적용되기 위해서는 그림 1과 같은 좌표변환이 필요하다. EGM96 모델은 1996년에 개발된 지오이드 모델이고, 어디에서나 중력방향과 수직을 이루며 바다에서는 평균해수면과 거의 일치하는 특징을 갖는다. WGS84(World Geodetic System, 1984)는 1984년도에 개발된 지구타원체 모델이고, 현실 지구를 근사하기 위한 수학적 모델이다.
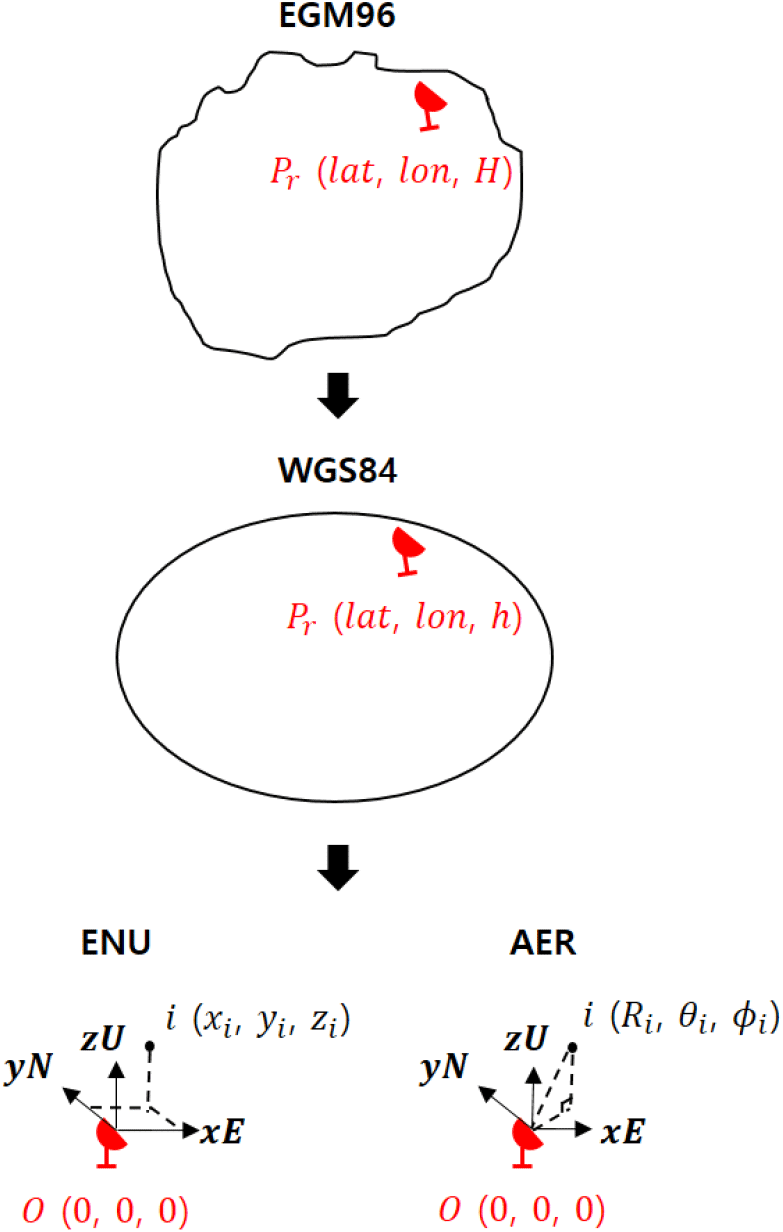
그림 2와 같이 EGM96 모델과 WGS84 모델의 차이를 보정해주기 위해 표고(H)에 지오이드고(N)를 보정하여 타원체고(h)를 구하였다[2]. 이후, 레이다의 최대탐지거리 및 빔 조사면을 계산하기 위해 레이다를 원점 O로 갖고 각 수치표고모델 데이터는 점 i로 갖는 ENU(east north up) 좌표계와 AER(azimuth elevation range) 좌표계로 변환하는 과정을 진행하였다.
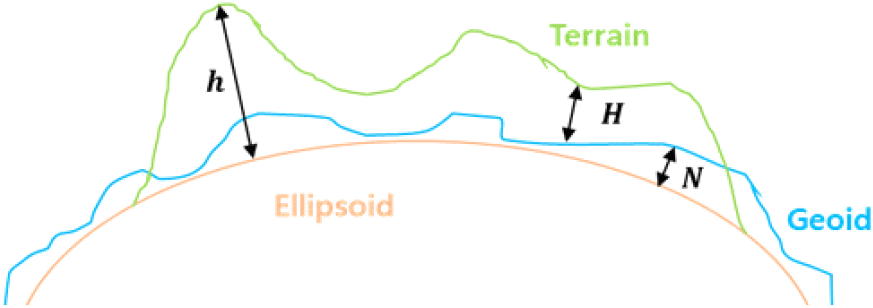
그림 3에서 볼 수 있듯이 수치표고모델 데이터는 임의의 레이다 위치에 따라 최대탐지거리 내의 범위를 포함시킬 수 있도록 DEM 4개의 파일을 이용하였으며, 레이다의 위치로부터 가로축과 세로축 방향으로 최대탐지거리 이내에 들어오는 범위를 계산하여 해당 범위의 데이터를 추려내었다. 또한, 레이다 상황 모의를 위한 시야각을 설정하여 방위각 방향으로의 시야각을 해당 그림에 나타내었고, 본 논문에서는 레이다의 최대탐지거리 이내로 추려진 데이터를 이용하여 지형 클러터 모델링을 진행하였다.
본 논문에 사용된 파라미터는 다음과 같다. 레이다의 동작 주파수는 10 GHz, 안테나 편파는 수직 편파로 설정하였고, 최대탐지거리는 10 km, 방위각 방향으로의 시야각은 −50°~50°, 고각 방향으로의 시야각은 −5°~35°로 설정하였다.
Ⅲ. 지형 클러터 모델링
본 절에서는 수치표고모델 데이터를 활용하여 지형 클러터를 모델링하는 과정에 대해 기술하였다. 우선, 레이다와 지면의 높이에 따라 레이다 빔이 조사되는 면과 그렇지 않은 영역이 생기기 때문에 빔 조사면을 계산하였다. 이후, 빔이 조사된 영역에 대해서 클러터의 RCS를 계산하는 방식으로 지형 클러터 모델링을 진행하였다.
그림 4(a)의 점 A, B, C, D는 수치표고모델 패치의 중심점이며 앞서 설명한 ENU 좌표계 상의 데이터이다. 이때 패치는 그림 2에서 가로와 세로 방향으로 각각 1 샘플로 이루어진 격자 셀의 단위를 의미한다. 빔 조사면을 계산하기 위해 우선 레이다와 지면 사이의 거리(R) 및 각도(φ)를 계산하였고, 이는 식 (1) 및 식 (2)에 나타내었다.
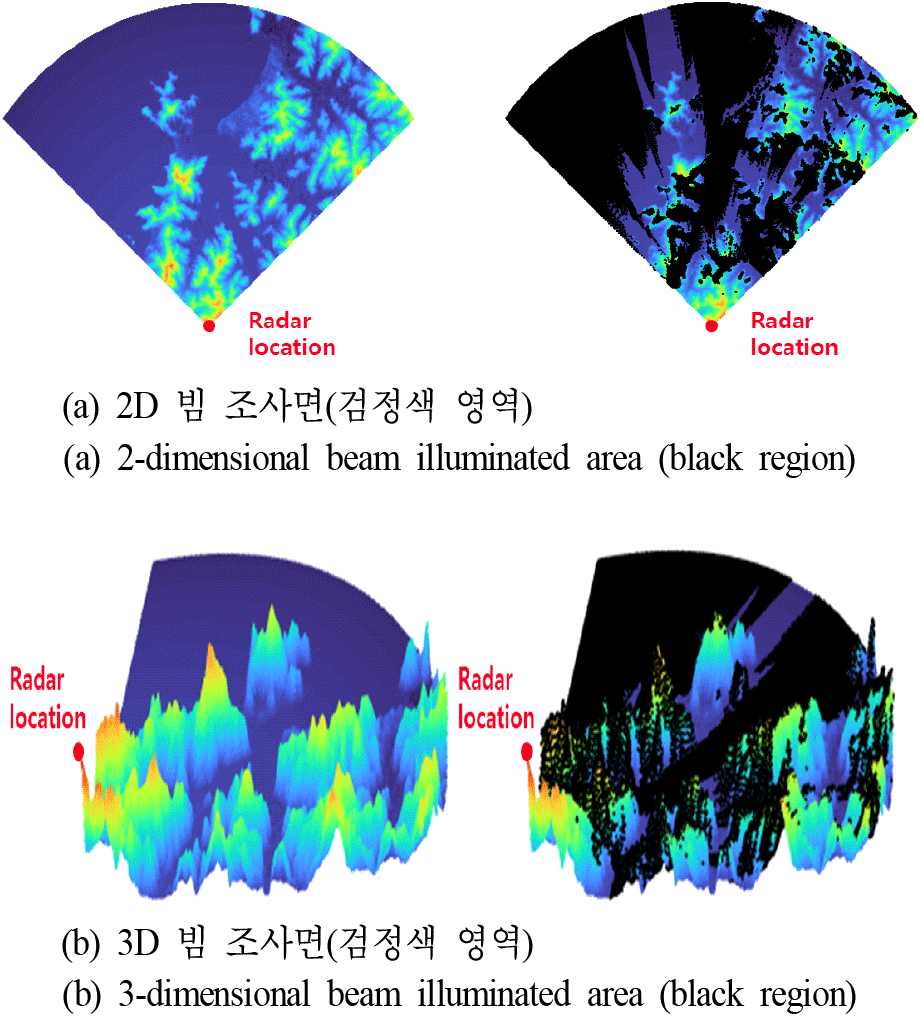
이때, i는 각 수치표고모델 패치의 인덱스이며, n은 방위각 스캔별 거리 방향으로의 수치표고모델 패치의 총 개수이다. x, y, z는 3차원 좌표계상의 좌표를 의미하고, 레이다의 위치를 원점으로 갖는다. 거리(R)와 각도(φ)를 이용하여 레이다의 위치에서 빔이 조사되지 않는 영역, 즉, 가려진 영역을 계산하였다. 임의의 점 i와 임의의 점 j에 대해, 만일 Ri < Rj이면서 φi ≤ φj이면 점 j는 보이지 않는다[3]. 예를 들어 그림 4(b)에서, 점 C는 점 A의 거리보다 멀기에 RA < RC이면서, φC는 φA보다 크기에 φA ≤ φC를 만족한다. 반면에, 점 B는 RA < RB이면서 φA ≤ φB를 만족하지 않는다. 따라서 점 C는 보이지 않고, 점 B는 보이는 것을 확인할 수 있으며, 빨간색 영역은 가려져 보이지 않고 파란색 영역은 보이는 것을 알 수 있다. 각 방위각 스캔마다 모든 패치에 대해 거리와 각도를 비교하여 레이다의 빔 조사면을 계산하였으며, 이를 그림 5에 나타내었다. 검정색 영역이 빔이 조사된 영역이며, 지형 클러터에 의한 반사 신호가 생성되는 영역이다.
레이다가 수신하는 반사 신호의 세기는 레이다 방정식에 의해 송신 전력, 동작 주파수, 탐지 거리, 안테나 이득, 대상의 RCS에 의해 결정된다. 반사 대상의 위치는 대상의 거리에 의한 수신 신호의 딜레이로써 나타난다. 클러터에 의한 반사 신호 또한 동일한 방식으로 나타나므로, 지형 클러터 모델링을 위해서는 레이다와 지면 사이의 거리 및 클러터의 RCS가 필요하다. 지형 클러터의 거리는 앞선 식 (1)로부터 구하였기에 남은 과정인 RCS를 구하는 과정에 대한 내용이 이어지겠다.
클러터의 RCS는 σ0ΔS로 나타내어지고, 이때 σ0은 후방 산란 계수, ΔS는 클러터의 면적이다. σ0은 normalized RCS로도 불리며, 지표각(φ, grazing angle), 지형 특성, 동작 주파수, 안테나 편파 등에 의해 결정된다. 본 논문에서는 지형 특성에 대하여 지상의 경우 ‘UlabyDobson’ 모델을 이용하였고[4], 해상의 경우 ‘GIT(georgia institute of technology)’ 모델을 이용하였다[5]. 동작 주파수 및 안테나 편파는 앞서 기술하였듯이 10 GHz, 수직 편파로 설정하였다. ΔS는 레이다의 시야각 기준으로 바라본 면적으로, 방위각과 고각 방향으로의 스캔 각도에 따라 지형이 보이는 면적으로 구하였으며, 다음 절에서 자세히 설명하였다. 이로써 수치표고모델을 활용한 지형 클러터 모델링을 수행하였으며, 다음 절에서는 이를 이용해 레이다 수신 신호를 생성하는 방안에 대한 내용이 이어지겠다.
Ⅳ. 레이다 수신 신호 생성 방안
본 절에서는 Ⅲ절에서 모델링된 지형 클러터를 이용하여 레이다 수신 신호를 생성하는 방안에 대해 기술하였다. 우선, 앞서 모델링한 지형 클러터를 레이다에서 활용하기 위해, 레이다 시야각을 통해 바라볼 수 있도록 하였다. 이후, 실제 수신 신호로 생성하는 방안에 대한 내용을 기술하였다.
앞서 구한 후방 산란 계수(σ0)와 거리 결과는 해당 지형의 위치에 계산되어있는 결과이며, 이를 레이다 수신 신호 생성에 활용하기 위해서는 레이다의 시야각을 통해 바라봐야 한다. 앞서 언급했듯이 클러터의 면적(ΔS) 또한 시야각 기준으로 바라보았으며 충분히 작은 면적으로 고려하였다. 빔 조사면 계산을 통해 지형 클러터가 존재하는 영역이 구해진 후, 레이다의 시야각을 스캔 각도(Δθ) 간격으로 나누어 바라보았을 때 지형 클러터가 존재하는 경우, 해당 스캔 영역을 클러터 면적으로 고려하였으며 이는 그림 6에 나타내었고, 그 수식은 식 (3)에 나타내었다.
이때, R은 식 (1)을 따르는 레이다와 클러터 패치 사이의 거리이고, Δθ는 레이다 시야각에서 방위각과 고각 방향으로의 스캔 각도이며, 각 방향에 대해 0.1°로 설정하여 ΔS를 충분히 작은 면적으로 고려하였다. 레이다의 위치에서 바라보는 각도에 지형 클러터가 존재하는 경우, 해당 영역에 계산된 후방 산란 계수와 거리 결괏값을 이용하여 레이다 시야각에 따른 RCS와 거리값을 구하였다. 그 결과는 그림 6에 나타내었으며 레이다 시야각을 통해 바라본 지형의 RCS와 거리 결과이다. 앞서 언급한대로 방위각 시야각은 −50°~50°, 고각 시야각은 −5°~35°으로 계산하였으며, 지형 클러터는 레이다의 시야각 기준으로 낮은 고각에 존재하므로 그림 7에는 지형 클러터가 존재하는 고각 −5° ~ 5°의 영역을 도시하였다. 그림 7(a)와 그림 7(b)를 보면, 동일한 스캔 각도임에도 클러터와의 거리가 멀어질수록 레이다에서 바라본 클러터 면적이 증가하여 RCS가 큰 경향이 있다. 또한, 동일한 거리임에도 지상과 해상 클러터의 후방 산란 계수(σ0) 차이에 의해 RCS 차이가 뚜렷한 경우도 확인할 수 있다.
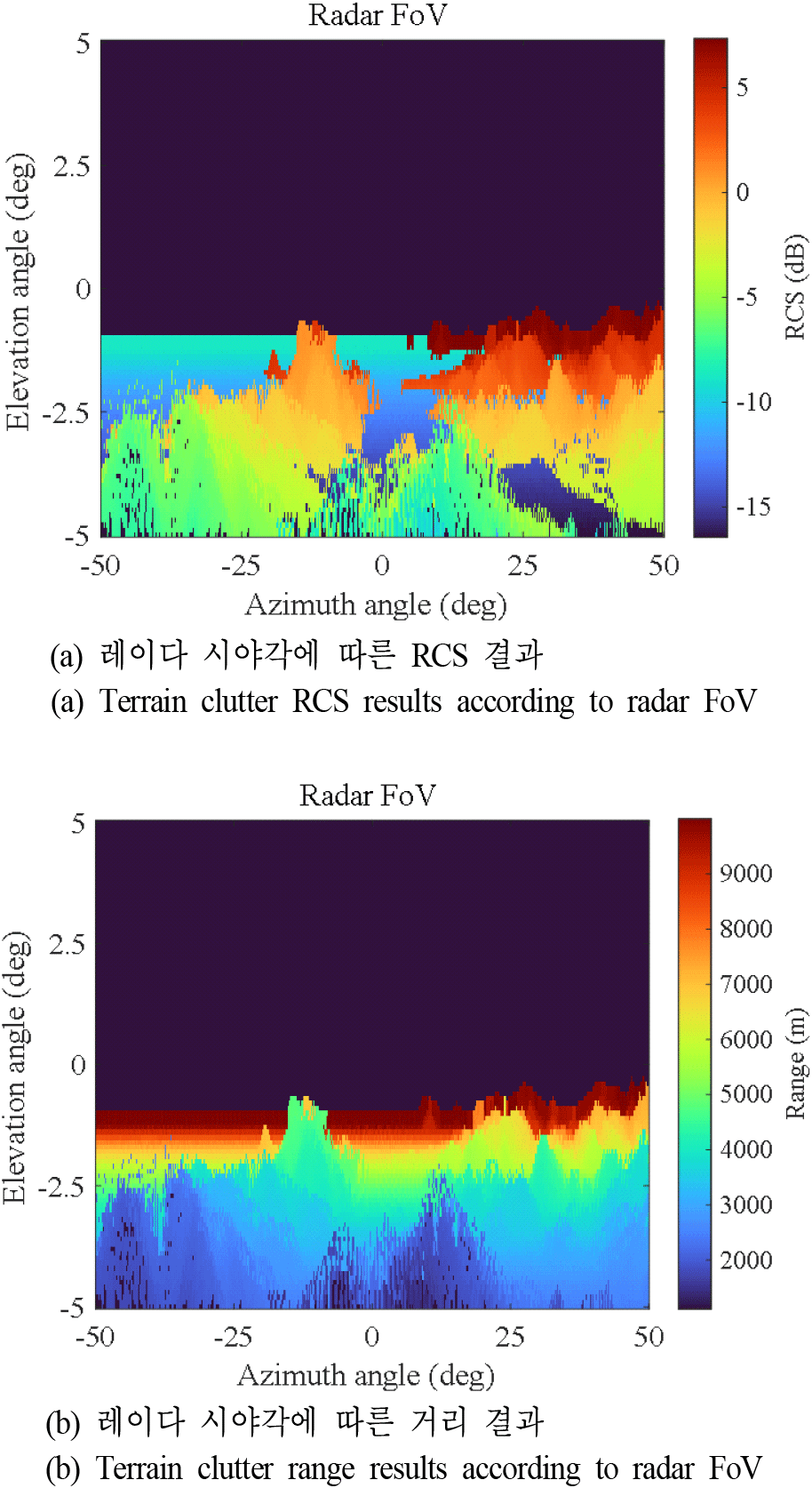
그림 7의 결과를 이용하면 레이다 수신 신호 모의 시 필요한 반사 신호의 세기 및 대상의 거리에 의한 지연 시간을 모의할 수 있다. 즉, 레이다의 위치와 시야각이 고정된 경우 추가적인 연산 과정 없이 원하는 방향의 지형 클러터 신호를 생성할 수 있다. 따라서 본 논문에서는 지형 클러터의 RCS 및 레이다와 지형 클러터와의 거리를 미리 계산해놓음으로써, 추가적인 연산 과정 없이 지형 클러터 모의 환경에서 레이다의 성능 시험 및 개선이 가능하도록 클러터 신호를 생성하는 방안을 제안한다.
Ⅴ. 결 론
현재 레이다시스템에서는 가상의 클러터를 생성하거나 실제 수신된 데이터로만 성능 분석이 가능하였다. 실제 클러터 신호를 생성하기 위해서는 대용량의 데이터 및 긴 생성시간이 필요하다. 본 논문에서는 실시간으로 실제 클러터 신호를 생성하는 대신에 수치표고모델을 활용하여 지형 클러터 신호를 미리 생성하는 방안에 대해 기술하였다. 레이다의 최대탐지거리 및 빔 조사면을 계산하기 위해 수치표고모델 데이터의 좌표 변환을 수행한 후, 레이다 파라미터에 따른 빔 조사면을 계산하였다. 이후, 클러터 신호 생성을 위해 빔이 조사된 클러터 패치에 대하여, 레이다 시야각에 따른 RCS 및 레이다와의 거리를 계산하였다. 이를 통해, 레이다의 위치와 시야각이 고정된 경우, 추가적인 연산 과정 없이 실시간으로 지형 클러터 신호 생성 및 지형 클러터 모의 환경에서의 레이다 성능 시험 및 개선이 가능해짐을 기대할 수 있다.
그러나 본 논문에서 제안한 방안은 레이다의 위치와 시야각이 정해져 있는 고정 레이다 시스템에서만 적용가능하다는 단점이 있다. 그리고 DEM 데이터가 지형 변화를 반영하지 못하여 현재 지형 정보와 차이가 있을 수 있다. 추후 최신 DEM 데이터를 반영하여 실제 레이다 수신 데이터를 획득하여 실제 클러터와 비교하여 분석토록 하겠다.
