Analysis of Ionospheric Propagation Paths over the Korean Peninsula Based on Three-Dimensional Electron Density Data

Lee, Do Hyeon; Yang, Junmo; Lim, Sangho; Choi, Ik-Hwan; Park, Yong Bae

doi:10.5515/KJKIEES.2024.35.11.920

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(11):920-928

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.11.920

논문/REGULAR PAPER

3차원 전자밀도 데이터 기반 한반도 상공 전리층 전파 경로 분석

이도현^*

, 양준모^*

, 임상호^**

, 최익환^**

, 박용배^*^,^***^,^†

Analysis of Ionospheric Propagation Paths over the Korean Peninsula Based on Three-Dimensional Electron Density Data

Do Hyeon Lee^*

, Junmo Yang^*

, Sangho Lim^**

, Ik-Hwan Choi^**

, Yong Bae Park^*^,^***^,^†

Author Information & Copyright ▼

^*아주대학교 AI 융합네트워크학과

^**국방과학연구소

^***아주대학교 전자공학과

^*Department of AI Convergence Network, Ajou University

^**Agency for Defense Development

^***Department of Electrical and Computer Engineering, Ajou University

^†Corresponding Author: Yong Bae Park (e-mail: yong@ajou.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 30, 2024; Revised: Oct 24, 2024; Accepted: Nov 02, 2024

Published Online: Nov 30, 2024

요 약

전자파가 전리층을 통과하는 경우 굴절로 인해 자유공간을 가정한 전파 경로와 다른 경로로 진행한다. 본 논문은 비균질 3차원 전자밀도 데이터를 기반으로 한반도 상공의 전리층을 통과하는 전자파의 전파 경로를 계산한다. 이러한 계산 결과를 바탕으로 운용 주파수, 고도각 및 일, 주, 월, 연간, 태양 주기에 따라 변화하는 정량적인 굴절 오차를 분석한다. 그 결과, 높은 고도각 및 높은 주파수 대역에 비해 낮은 고도각 및 낮은 주파수 대역에서 전리층에 의한 굴절 오차가 크게 증가함을 확인하였다. 또한 태양 활동 주기에 따른 굴절 오차의 변화를 분석하였으며, 태양 극대기 시점에 가까워질수록 굴절 오차가 증가함을 확인하였다. 본 연구에서 제시한 결과는 위성통신, 우주감시레이다, 합성개구레이다(SAR)의 굴절 오차 보정에 적용할 수 있다.

Abstract

When electromagnetic waves propagate through the ionosphere, they deviate from the free-space propagation path because of refraction. This paper presents an analysis of the propagation paths of electromagnetic waves passing through the ionosphere over the Korean Peninsula, based on inhomogeneous 3D electron density data. On the basis of this analysis, the quantitative refraction errors are calculated considering the operating frequency, elevation angle, and variations across daily, weekly, monthly, yearly, and solar cycles. The results reveal that the refraction error caused by the ionosphere increases significantly at lower elevation angles and frequency bands than at higher elevation angles and frequency bands. Further, the refractive error is calculated according to the solar activity cycle, confirming that the refractive error increases as the solar maximum approaches. The analysis findings can help rectify refraction errors in satellite communication, space surveillance radar, and synthetic aperture radar (SAR) systems.

Keywords: EM Wave Propagation; Ionosphere; Electron Density Data; Satellite Communication; Space Surveillance Radar

Ⅰ. 서 론

지상-위성 간 통신이나 우주 감시 레이다 운용과 같은 상황에서 전자파는 대기권을 통과하여 전파된다. 대기권은 온도에 따라 대류권, 성층권, 중간권, 그리고 열권으로 구분되지만, 전자파에 대한 영향으로는 대류권, 성층권 상부 및 중간권, 전리층으로 분류할 수 있다.

대기권의 약 90 % 이상을 차지하는 전리층은 고도 약 90~1,000 km에 이르는 영역으로 대기 중의 원자나 분자가 태양의 극자외선 및 X선에 의해 이온화되어 플라즈마 상태로 존재한다. 플라즈마 상태의 전리층에 지구 자기장의 영향이 더해져, 전리층은 비균질성(non-homogeneous), 비등방성(anisotropic), 분산성(dispersive), 시공간적 변화 (time and space-varying)와 같은 특성을 갖는다. 이러한 특성은 전리층을 통과하는 전자파에 굴절, 시간 지연, 도플러 주파수 이동, 편광 회전(페러데이 회전), 주파수 확산 등의 영향을 미친다. 또한, 전리층의 불균일성이 빠르게 변화하는 경우 신호의 진폭 및 위상에 변화를 일으키는 신틸레이션 현상이 발생할 수 있다^[1]. 이는 결과적으로 자유공간을 가정한 전파 경로와는 다른 경로로 진행하도록 만들며, 따라서 굴절로 인한 오차를 정량적으로 분석하는 것이 필수적이다.

기존 연구에서는 전리층의 총 전자 함유량(TEC)을 계산하고, 시간 지연에 따른 거리 오차를 분석하였다^[2]. 그러나 전리층에 의한 오차는 시간 지연으로 인한 거리 오차뿐만 아니라 굴절로 인한 오차도 포함한다. 현재까지 3차원 비균질 전자밀도 데이터를 활용하여 전리층의 굴절 오차를 정량적으로 분석한 연구는 아직 이루어지지 않았다.

따라서 본 연구에서는 3차원 전자밀도 데이터를 활용하여 전리층을 통과하는 전파 경로를 계산하고, 굴절 오차를 분석하였다. 이러한 3차원 데이터 기반의 계산방법은 전리층 전자밀도의 공간적 및 시간적 변화를 반영하여 전파 경로의 굴절 현상을 보다 정밀하게 모델링할 수 있는 장점이 있다. 비균질한 전리층의 특성을 고려하기 위해 3차원 전자밀도 데이터를 활용하고, 고주파 근사기법인 광선 추적법(ray tracing)을 적용하여 전리층의 전파 경로를 모델링하였다. 이를 적용하여 주파수, 고도각, 일간, 주간, 월간, 연간 및 태양 주기(약 11년)에 따른 수신 지점의 정량적 거리 및 각도 오차를 분석하였다. 본 연구에서는 전리층의 영향만을 정량적으로 분석하기 위하여 대류권의 영향을 배제한다.

Ⅱ. 전리층 전파 환경 분석 및 경로 모델링

전리층을 통과하는 전파의 특성은 전리층 각 층의 굴절률(n)에 의해 결정된다. 전리층의 굴절률은 Appleton - Hartree 방정식으로 계산되며, 300 MHz 이상에서는 지구자기장 및 전자충돌이 무시된 Simplified Appleton - Hartree 방정식을 적용할 수 있다^[3]. 따라서 전리층의 굴절률(n)은 전자밀도(N_e)와 주파수(f)의 함수로 식 (1)과 같이 정리된다.

n 2 = 1 − X = 1 − N e e 2 ϵ 0 m e ω 2 = 1 − 80.64 N e f 2

(1)

본 연구에서는 국제 전리층 참조 모델(IRI_2016)을 이용하여 전자밀도 데이터를 기반으로, 각 지점에서의 굴절을 계산하였다^[4].

그림 1은 한반도 상공 위도 33도, 경도 126도, 고도 90~1,000 km, 24. 02. 28. 05:30 UTC 시각의 전리층 전자밀도(그림 1(a))와 Simplified Appleton-Hartree 방정식을 적용하여 계산한 주파수에 따른 굴절률(그림 1(b))을 나타낸 것이다. 그림 1(a)는 고도별 전자밀도 분포를 나타낸 그래프이다. 전리층의 저고도 영역(약 90~200 km)은 대기 밀도가 매우 높아, 태양으로부터 유입되는 극자외선 및 X선과 같은 고에너지 복사가 충분히 흡수되어 이온화가 발생한다. 그러나 저고도에서는 높은 대기 밀도로 인해 재결합률이 매우 높아, 이온화된 전자와 양이온이 빠르게 재결합하여 중성 상태로 돌아가게 된다. 이러한 특성으로 인해 저고도 영역의 전자밀도는 낮은 값을 갖는다. 중간고도 영역(약 200~400 km)은 대기 밀도가 저고도보다는 낮지만 충분한 원자 및 분자가 존재하며, 태양 복사 강도가 증가함에 따라 이온화가 활발하게 일어난다. 이 영역에서는 이온화된 전자가 재결합되기 전까지 유지되므로, 가장 높은 전자 밀도 값을 나타낸다. 고고도 영역(약 400~1,000 km)에서는 태양 복사 강도가 더욱 증가하지만, 고도 상승에 따라 대기 밀도가 지수 함수적으로 감소하므로 이온화에 기여할 수 있는 대기 분자의 수가 급격히 줄어들게 되어, 결과적으로 전자밀도가 다시 감소하는 경향을 보인다.

그림 1. | Fig. 1. 전리층 고도별 전자밀도(24. 02. 28. 05:30 UT) (a) 및 주파수에 따른 굴절률(b) | Electron density by ionospheric altitude (24. 02. 28. 05:30 UT) (a) and refractive index by frequency (b).

Download Original Figure

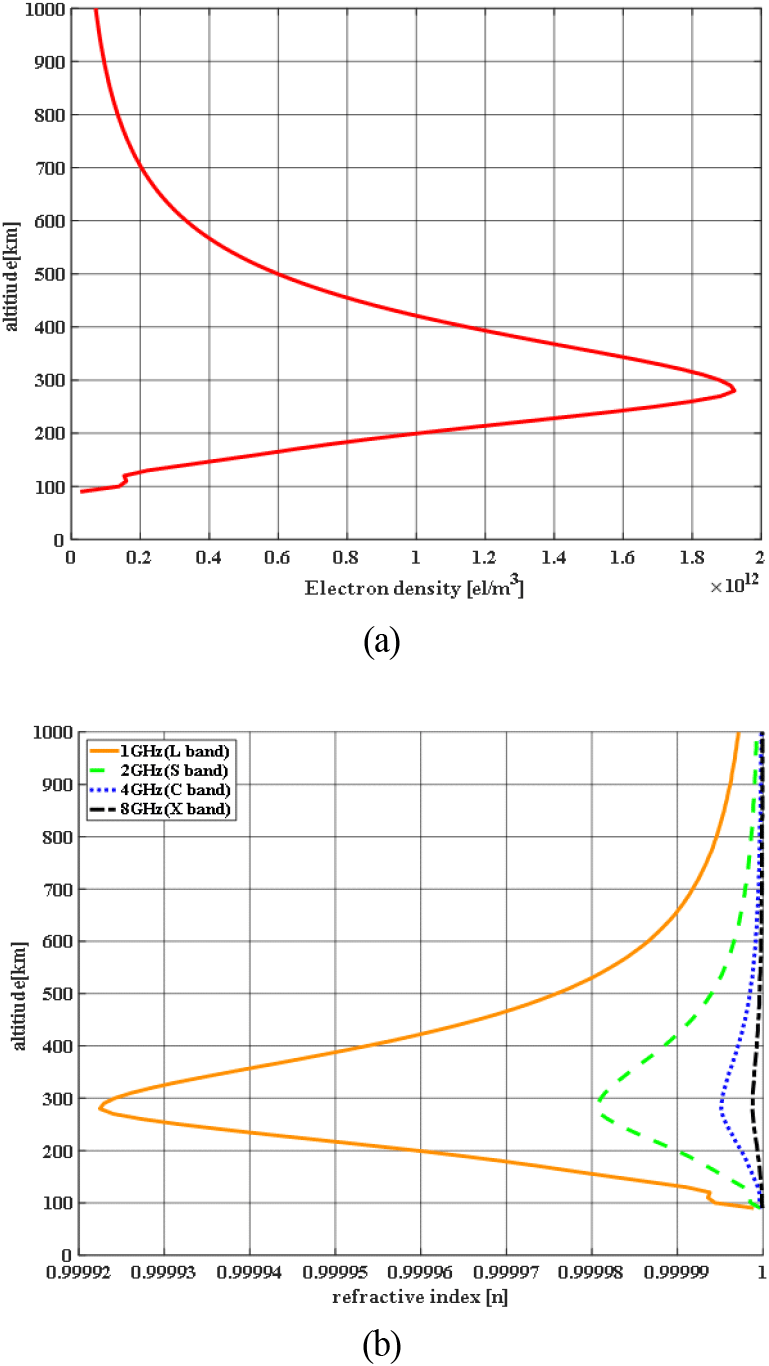
그림 1(b)는 전리층의 고도별 전자밀도 분포(그림 1(a))를 기반으로, 식 (1)을 적용하여 고도에 따른 굴절률을 계산한 결과이다. 주파수가 감소함에 따라 고도에 따른 굴절률 변화가 커짐을 확인할 수 있으며, 반대로 주파수가 증가할수록 굴절률은 자유공간의 굴절률 값인 1에 수렴하는 특성을 보인다. 이는 주파수가 증가할수록 전리층을 통과하는 전자파의 굴절 특성을 분석할 때 전리층의 영향을 무시할 수 있음을 의미한다.

그림 2은 자유공간을 가정했을 때의 전자파의 전파 경로와 전리층 굴절률을 고려한 전자파의 전자 경로를 나타낸다. 자유공간을 가정했을 때는 전체 공간에 대해 굴절률이 1인 균일한 매질로 가정하기 때문에 매질에 의한 전파 속도의 변화가 없으므로 직선으로 진행하지만, 실제 전리층에서는 고도에 따라 굴절률이 변화하기 때문에 전파 경로가 그림 2의 곡선과 같이 굴절된 경로로 진행한다. 이러한 전파 경로의 변화는 전리층 전자밀도 및 주파수로 결정되는 전리층 굴절률과 광선추적법을 이용하여 계산할 수 있다. 광선추적법은 전자기파를 직선으로 진행하는 광선으로 가정하여, 굴절률이 다른 매질을 통과하거나 반사할 때 경로를 계산하는 기법으로, 전리층을 굴절률이 다른 다수의 층으로 분할하고 스넬의 법칙(Snell’s law)을 적용하여 입사각 및 투과각을 계산할 수 있다.

그림 2. | Fig. 2. 전리층 전파 경로 모델링 및 거리오차, 각도 오차 정의 | Ionospheric propagation path modeling and definition of distance and angle errors.

Download Original Figure

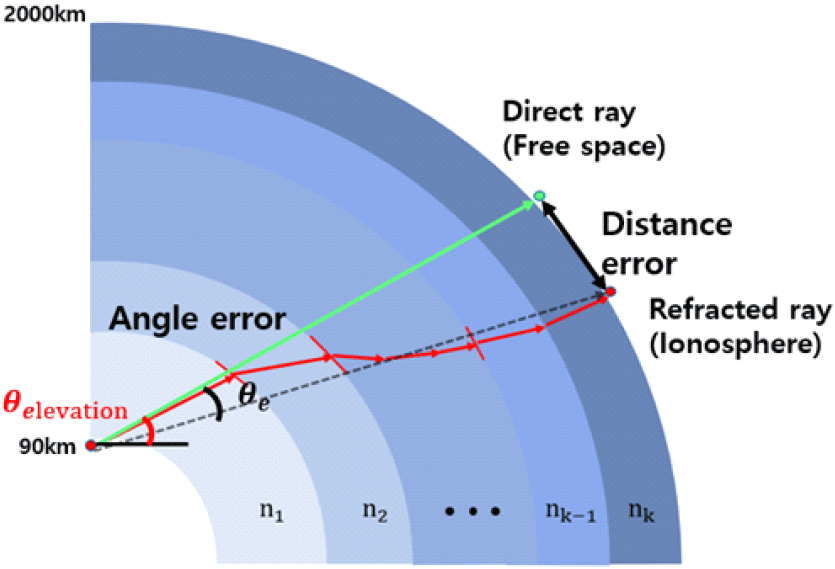
거리 오차(distance error)는 자유공간을 가정하여, 전자파가 전리층의 특정 고도에 도달하였을때의 수신 지점과 전리층에 의한 영향을 고려하여 계산된 전자파의 수신 지점 사이의 거리 차이로 정의하며 각도 오차(angle error)는 전파 송신 지점에서 바라본 두 수신 지점의 각도차이로 정의한다.

Ⅲ. 전리층 굴절 특성 및 오차 분석

전리층의 굴절 특성 및 오차 분석을 위해서 표 1에서와 같이 전파 출발 지점과 전자파의 도달 고도를 설정하였다. 이 때, 전리층 전자밀도는 24 .02. 28 05:30 UTC의 데이터를 활용하였다. 표 1의 5가지 파라미터가 결정되면 광선 추적법을 이용하여 굴절된 전파 경로를 모델링하고 수신 지점의 좌표 정보를 계산하여, 자유공간을 가정한 전파수신 지점과의 거리 오차 및 각도 오차를 분석한다. 이를 바탕으로 주파수, 고도각 및 일, 주, 월, 연간, 태양 주기에 따른 정량적 굴절 오차를 분석한다.

표 1. | Table 1. 전리층 전파 송수신 파라미터 | Ionospheric propagation transmission and reception parameters.

Parameters	Example
Operation date and time	24. 02. 28. 05:30 UTC
Location	Latititude: 33° Longitude: 126°
Steering direction	Azimuth angle: 0° Elevation angle: 30°~90°
Frequency	300 MHz 1, 2, 4, 8, 12, 18, 27, 40 GHz
Propagation altitude	2,000 km

Download Excel Table

3-1 운용 주파수 변화에 따른 오차 분석

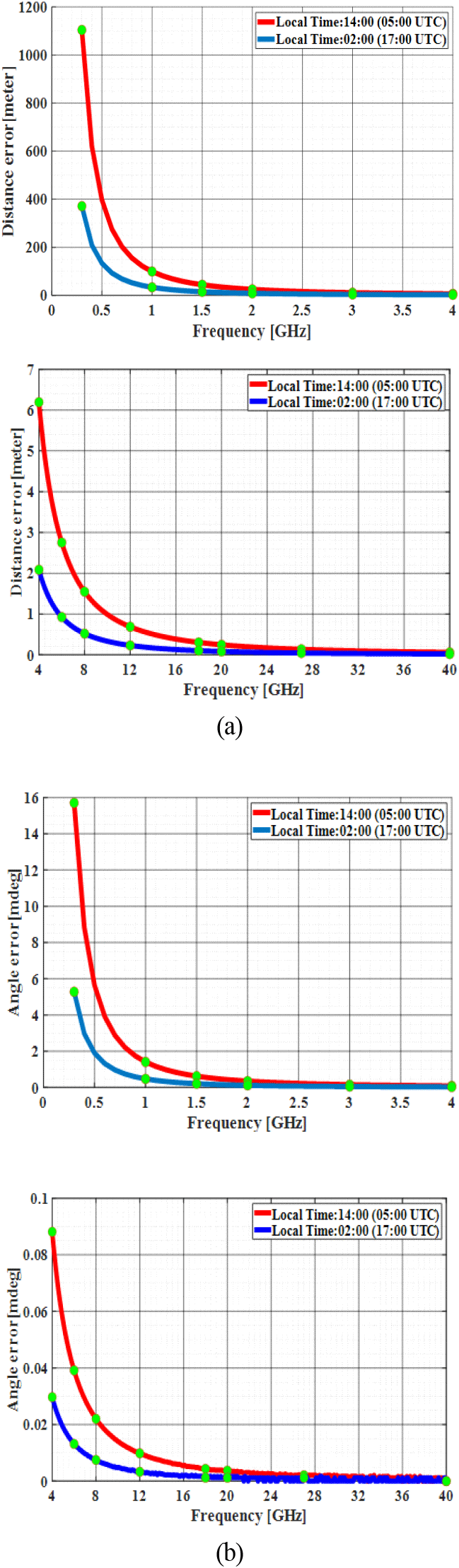
운용 주파수 변화에 따른 전리층의 굴절 오차를 분석하기 위해 주파수를 변화시키며 거리오차 및 각도 오차를 분석하였다. 안테나 지향 방향은 방위각 0°, 고도각 30°로 설정하였으며, UHF 대역의 가장 낮은 주파수인 300 MHz부터 Ka 대역의 가장 높은 주파수인 40 GHz까지의 주파수 영역에 대해 분석하였다. 이를 전리층의 전자밀도가 높은 주간 14:00 시각 및 전자밀도가 낮은 야간 02:00 시각에 대해 거리오차 및 각도 오차를 계산한다. 그림 3에서 주파수가 증가함에 따라 거리오차 및 각도 오차가 감소하는 것을 확인할 수 있으며, 주간 14:00 시각의 경우 야간 02:00 시각보다 더 많은 거리오차 및 굴절 오차가 발생하는 것을 알 수 있다. 이는 전리층의 전자밀도가 높은 낮의 경우 밤보다 더 많이 전파가 굴절되어 자유공간을 가정한 전파 경로와 차이가 크게 발생함을 의미한다. 주간인 시각 14:00 및 주파수 300 MHz일때 1,104.24 m의 거리오차 및 15.71 mdeg의 각도오차가 발생하였으며, 야간인 시각 02:00 및 주파수 300 MHz일 때는 371.20 meter의 거리오차 및 5.28 mdeg의 각도오차가 발생하였다.

그림 3. | Fig. 3. 운용 주파수 변화에 따른 거리오차(a) 및 각도 오차(b) | Distance error (a) and angle error (b) with variation in operating frequency.

Download Original Figure

3-2 고도각 변화에 따른 오차 분석

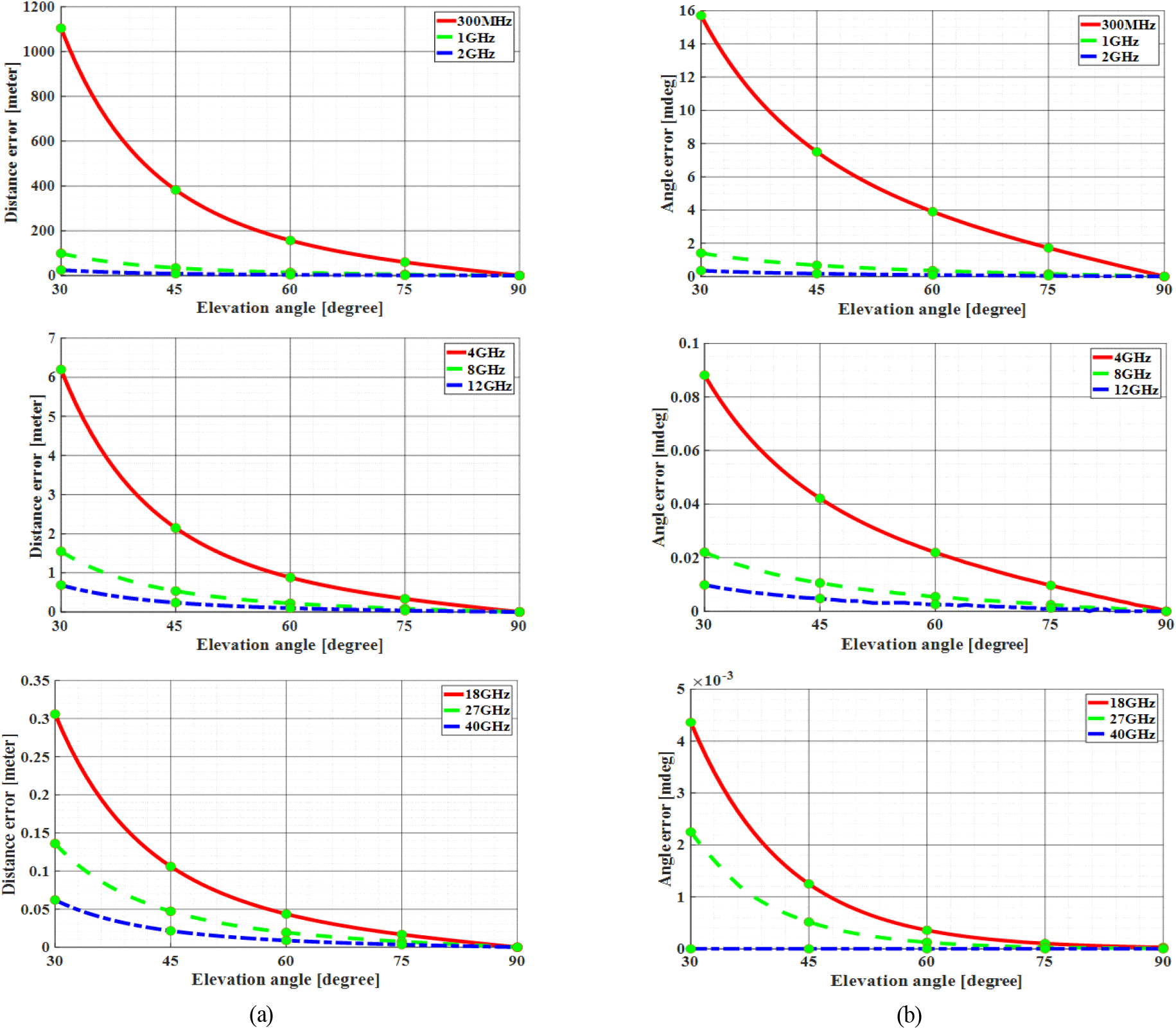
고도각(elevation angle) 변화에 따른 전리층의 굴절 오차를 분석하기 위해 주파수를 변화시키며 거리오차 및 각도 오차를 분석하였다. 300 MHz 부터 40 GHz까지를 분석하였으며, 고도각이 낮아질수록 수신 고도인 2,000 km 까지 전파가 진행하는 거리가 길어지므로 더 많은 거리오차 및 각도 오차가 계산되는 것을 확인할 수 있다. 마찬가지로 주파수가 높아질수록 거리오차 및 각도오차가 감소하는 것을 확인할 수 있다(그림 4).

그림 4. | Fig. 4. 24. 02. 28. 05:00 UTC 시점의 고도각 변화에 따른 거리오차(a) 및 각도 오차(b) | Distance error (a) and angle error (b) with variation in elevation angle at 05:00 UTC 24. 02. 28.

Download Original Figure

3-3 일간, 주간, 월간, 연간, 태양주기에 따른 오차 분석

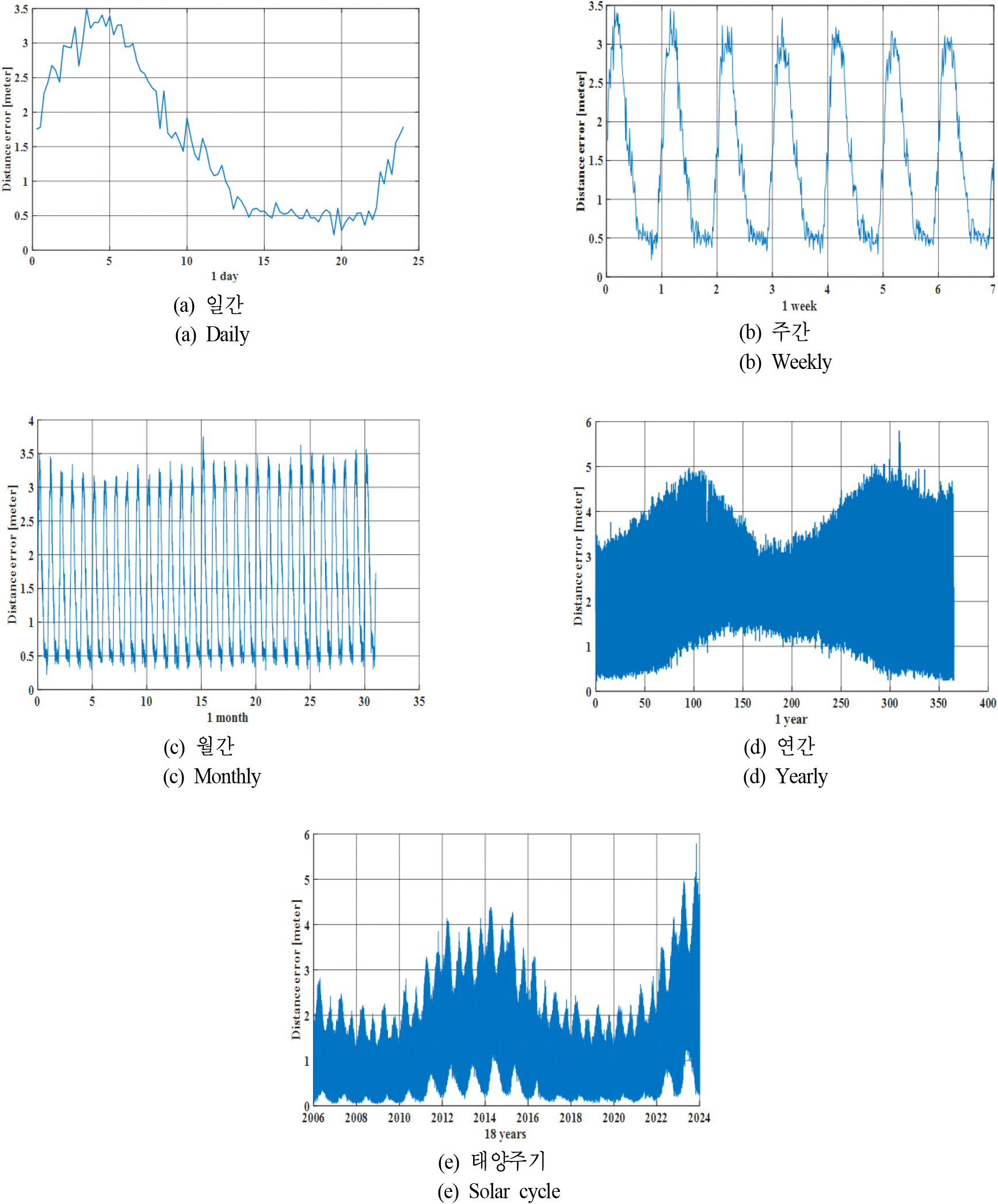
일간, 주간, 월간, 연간, 태양주기인 11년을 반영한 총18년간 거리오차를 분석하였다. 시뮬레이션 파라미터는 표 1과 동일하며, 운용 주파수는 2 GHz, 고각은 60°이다. 이를 분석기간을 달리하여 분석하였다. 기간에 따른 최대 및 최소 거리 오차는 표 2와 같이 정리된다.

표 2. | Table 2. 기간별 전리층 거리오차 분석 | Analysis of ionospheric distance error by period.

	Period	Distance error [meter]
Day	23. 01. 01. 00:00~23:45 UTC (15-minute intervals)	Max: 3.49761 Min: 0.222974
Week	23. 01. 01.~23. 01. 07.	Max: 3.49761 Min: 0.222974
Month	23. 01. 01.~23. 01. 31.	Max: 3.75392 Min: 0.222974
Year	23. 01. 01.~23. 12. 31.	Max: 5.792762 Min: 0.222974
Solar cycle	06. 01. 01.~23. 12. 31.	Max: 5.792762 Min: 0.045078

Download Excel Table

일간 변화(그림 5(a))에서는 4 UTC에서 가장 큰 거리오차가 발생하였으며, 20 UTC에서 가장 작은 거리오차가 발생하였다. 한국은 UTC+9 시간대에 속하므로 UTC 시간에 +9를 해주면 한국 환산 시간을 계산할 수 있다. 주간 변화(그림 5(b))의 경우 일간 변화가 반복되는 형태를 나타낸다. 월간 변화(그림 5(c))도 마찬가지로 주간 변화가 크게 변하지 않고 반복되는 그래프 형태를 나타낸다. 연간 변화(그림 5(d))의 경우 전자밀도가 높은 봄과 가을에 거리오차가 높게 나타나는 것을 알수 있다. 일반적으로 날씨가 더운 여름에 전자밀도가 높을 것이라고 생각할 수 있지만, 중위도 지역에 해당하는 한반도의 전리층 전자밀도는 태양의 복사량 뿐만 아니라 자기장 구조와 계절에 따른 태양 위치 변화에 따라 영향을 받는다. 따라서 여름철에 가장 전자밀도가 최소화 되는 계절적 특이 현상(seasonal anomaly)이 나타나므로 7,8월의 거리오차가 작게 나타난 것을 확인할 수 있다^[5]. 마지막으로 태양 주기인 11년을 반영하여 2006년부터 2023년까지 총 18년간의(그림 5(e)) 거리오차를 분석하였다. 태양의 극소기 시점인 2008년 12월, 2019년 12월에 가장 작은 거리오차가 발생하였으며, 태양의 극대기 시점인 2014년 4월 경에 높은 거리오차가 발생한 것을 알 수 있다. 현재는 태양 주기 25의 예상 극대기인 2025년 7월에 근접해가고 있는 시점이므로 거리오차가 증가하는 추세이다.

그림 5. | Fig. 5. 분석 기간에 따른 거리 오차 | Distance error according to analysis period.

Download Original Figure

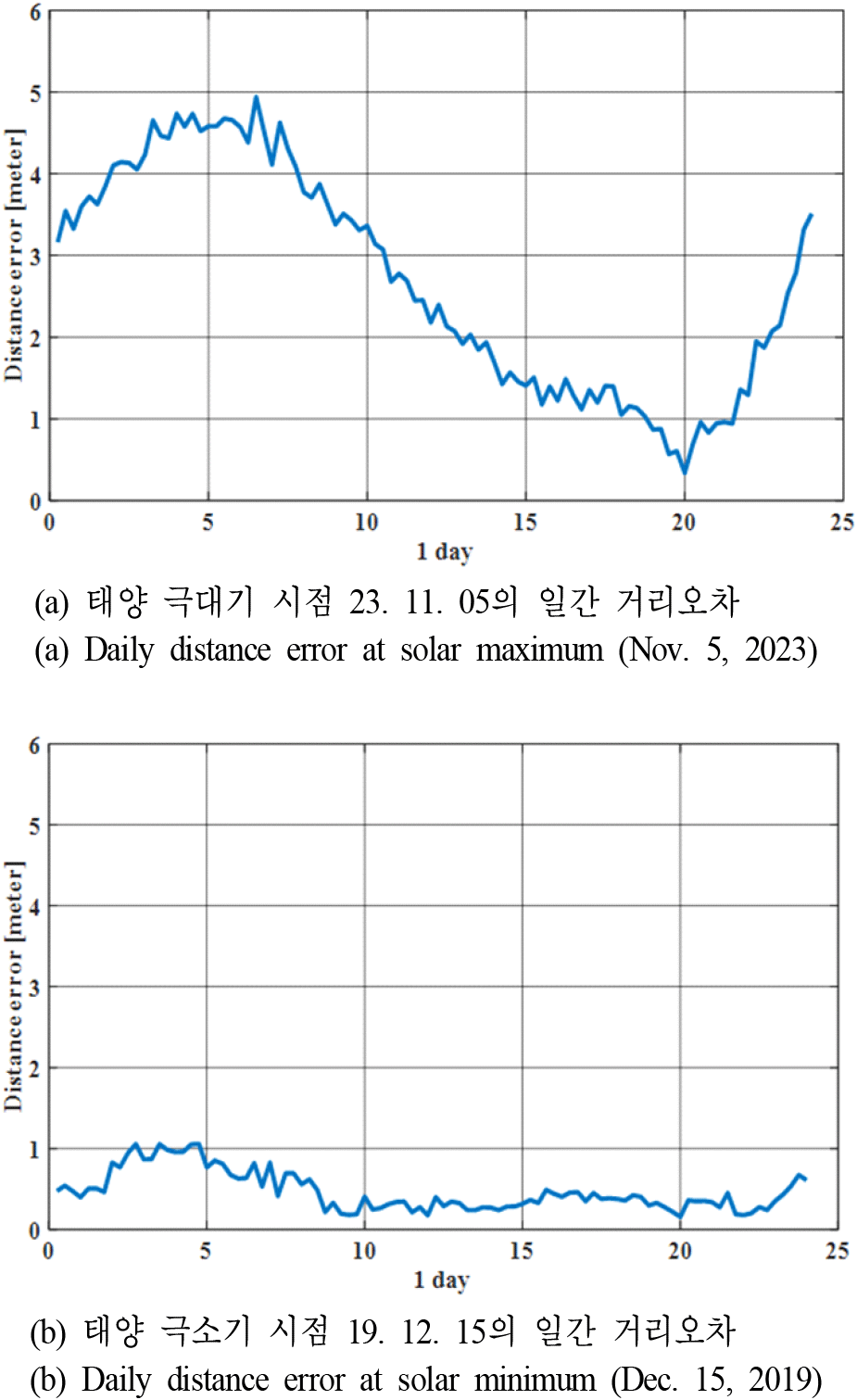
마지막으로 태양의 극대기 및 극소기 시점에서 24시간동안 거리오차를 분석하였다. 태양의 극대기 시점인 2023년 11월 5일(그림 6(a))의 경우 낮과 밤의 거리 오차가 최대 5.532 meter, 최소 0.3667 meter이며, 태양 극소기 시점인 2019년 12월 15일(그림 6(b))의 경우 최대 1.106 meter, 최소 0.1544 meter 로 분석되었다. 이는 태양의 극대기 시점에는 더 태양으로부터 더 많은 자외선 및 X선이 방출되어 대기중의 분자 또는 원자의 이온화률이 높아 전자밀도가 낮동안에는 높게 유지되다가 밤에는 재결합으로 전자밀도가 빠르게 낮아지기 때문이다. 극소기 시점에는 태양의 활동이 활발하지 않으므로 낮과 밤의 전자밀도의 변화가 크지 않으므로 거리오차 역시 큰 차이를 보이지 않는 것을 알 수 있다.

그림 6. | Fig. 6. 태양 극대 및 극소기 시점 일간 거리오차 | Daily distance error at solar maximum and minimum.

Download Original Figure

Ⅳ. 결 론

본 논문에서는 전리층의 영향을 고려한 전파 경로 모델링을 통해 자유공간을 가정한 전파 경로와 비교하여 수신지점의 거리오차 및 각도오차를 분석하였다. 고도별 굴절률을 계산하기 위해 Simplified Appleton-Hartree 방정식의 입력으로 국제 전리층 참조 모델(IRI-2016)을 통해 계산된 비균질한 3차원 전리층의 전자밀도 데이터를 활용하였다. 이후 광선 추적법을 적용하여 전리층을 투과하는 전자파의 전파 경로를 예측하였다. 주파수가 낮고, 고도각이 낮으며, 전자밀도가 높은 조건(낮 시간, 봄/가을, 태양 극대기)에서 자유공간 가정과의 굴절 오차가 크게 증가함을 확인하였다. 본 연구에서 제시하는 전리층 전파 경로 모델링 및 시뮬레이션 기법은 위성 통신과 우주 감시 레이다 등 전리층을 통과하는 전자파의 정확한 경로 예측에 적용될 수 있다. 본 연구는 전리층의 영향을 고려한 정밀한 우주 전파 모델링에 기여할 것으로 기대된다.

Acknowledgements

본 연구는 대한민국 정부(산업통상자원부, 과학기술정보통신부 및 방위사업청) 재원으로 민군협력진흥원에서 수행하는 민군기술협력사업의 연구비 지원으로 수행되었습니다(과제번호 23-CM-RS-12).

References

[1].

K. G. Budden, Radio Waves in the Ionosphere: The Mathematical Theory of the Reflection of Radio Waves from Stratified Ionised Layers, London, Cambridge University Press, 1961.

[2].

H. W. Moon, E. J. Choi, J. Lee, J. Yeum, S. Kwon, and S. Hong, et al., "A study on the effect of atmosphere on the space surveillance radar," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 8, pp. 648-659, Aug. 2018.

[3].

S. H. Bickel, R. H. T. Bates, "Effects of magneto-ionic propagation on the polarization scattering matrix," Proceedings of the IEEE, vol. 53, no. 8, pp. 1089-1091, Aug. 1965

[4].

Community Coordinate Modeling Center[Online]. Available: https://ccmc.gsfc.nasa.gov/

[5].

E. Kim, J. K. Chung, Y. H. Kim, G. Jee, S. Hong, and J. Cho, "A climatology study on ionospheric F₂ peak over Anyang, Korea," Earth, Planets and Space, vol. 63, pp. 335-349, Jun. 2011.