Extracting Resistance, Inductance, and Capacitance Matrices Using Finite Element Method

Jo, Mincheol; Park, Woobin; Kim, Moonseong; Lee, Woochan

doi:10.5515/KJKIEES.2024.35.1.7

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(1):7-14

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.1.7

특집논문/SPECIAL EDITION

유한요소법을 이용한 Resistance, Inductance 및 Capacitance 행렬 추출

조민철

, 박우빈

, 김문성^*

, 이우찬^†

Extracting Resistance, Inductance, and Capacitance Matrices Using Finite Element Method

Mincheol Jo

, Woobin Park

, Moonseong Kim^*

, Woochan Lee^†

Author Information & Copyright ▼

^{인천대학교 전기공학과}

^*서울신학대학교 IT융합소프트웨어학과

^{Department of Electrical Engineering, Incheon National University}

^*Department of IT Convergence Software, Seoul Theological University

^†Corresponding Author: Woochan Lee (e-mail: wlee@inu.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 17, 2023; Revised: Dec 16, 2023; Accepted: Jan 11, 2024

Published Online: Jan 31, 2024

요 약

고주파 및 고속 디지털 시스템에서는 신호의 간섭 및 지연, 손실 등을 최소화해야 한다. 이러한 이유로 다중도체 전송선로(MTLs, multiconductor transmission lines)의 역할이 매우 중요하며, 이를 분석 및 최적화하기 위해서는 전자기 수치해석(CEM, computational electromagnetics)이 필수적이다. 본 논문에서는 다중도체 전송선로의 특성을 파악하기 위해 전자기 수치해석 기법의 하나인 유한요소법(FEM, finite element method)을 이용하여 2-D/3-D 다중도체 전송선로에 대해 직접 in-house code를 작성하여 전자기 시뮬레이션을 수행하였다. 그리고, 후처리 과정을 통하여 resistance, inductance, capacitance 행렬을 추출하였으며, 이를 대표적인 전자파 상용 시뮬레이션 소프트웨어인 Q3D의 결과와 비교하여 해석의 정확성을 검증하였다.

Abstract

In high-frequency and high-speed digital systems, minimizing signal interference, delay, and loss is crucial. Therefore, the role of multiconductor transmission lines (MTLs) is highly significant, and computational electromagnetics (CEM) are essential for analyzing their characteristics. In this study, electromagnetic simulations were performed in two- and three-dimensional multiconductor transmission lines using the finite element method. Subsequently, a postprocessing technique was used to extract resistance, inductance, and capacitance matrices. The accuracy of the results was verified by comparing the results with those of Q3D, a commercial electromagnetic simulation software.

Keywords: Computational Electromagnetics; Finite Element Method; Multiconductor Transmission Lines; RLC Matrices

Ⅰ. 서 론

다중도체 전송선로(multiconductor transmission lines, MTLs)는 n+1개의 평행 도체로 구성된 구조를 의미하며, 전기 및 전자 시스템에서 신호를 전송하거나 전력을 공급하는 데 사용된다. 이러한 다중도체 전송선로는 고주파 및 고속회로 설계에 있어 중요한 역할을 하고 있으며, 이를 분석하기 위해 많은 연구가 이루어졌다^[1]~[5].

다중도체 전송선로의 특성은 전파상수(propagation constants)와 특성 임피던스(characteristic impedances)로 결정되며, 이러한 매개변수는 impedance 행렬로부터 얻을 수 있는 resistance 및 inductance 행렬로 계산된다^[5]. 또한, 신호지연(signal delay)이나 crosstalk와 같은 현상을 예측하고 제어하기 위해서는 capacitance 행렬을 추출하는 것은 필수적이다^[6]~[8].

다중도체 선로와 같은 전자기 구조의 해석을 위해서는 Maxwell 방정식에 대한 해를 구해야 한다. 하지만, 이 방정식의 참 해(exact solution)를 구하는 것은 매우 복잡하다. 따라서, 컴퓨터를 통해 Maxwell 방정식에 대한 수치 해(numerical solution)를 구하는 전자기 수치해석(computational electromagnetics, CEM)의 도입이 필수적으로 필요하다^[9]. 이러한 전자기 수치해석 기법의 하나인 유한요소법(finite element method, FEM)은 곡면과 같은 기하학적으로 복잡한 구조의 해석이 가능하며, 비균질성 매질의 해석에 강점을 가진다. 게다가, 유한요소 과정을 통해 얻게 되는 행렬은 0을 많이 포함하고 있는 sparse matrix가 되기 때문에 계산 부하가 적으며, 반복법 및 분할 알고리듬을 적용한 병렬 연산을 적용하기에 적합하다는 장점이 있다^[10],[11].

유한요소법을 통한 다중도체 전송선로 해석에는 full wave 해석과 준정적 해석(quasistatic analysis 또는 quasi-TEM analysis)이 존재한다. Full wave 해석의 경우 정확한 결과를 얻을 수 있지만, eigenvalue problem을 주파수마다 풀어야 하므로 상당한 계산을 요구한다^[3],[4]. 반면에 준정적 해석의 경우 full wave 해석보다 적은 미지수로 계산이 가능하며, eigenvalue problem이 아닌 matrix equation을 풀기 때문에 계산이 비교적 간단하며, full wave 해석에서 발생하는 저주파 불안정성 문제를 피할 수 있다는 장점이 있다^[3],[4]. 하지만 준정적 해석의 경우 비균질 매질에서 주파수가 증가함에 따라 정확도가 감소한다는 단점이 있어, 두 방법을 결합하여 해를 구하기도 한다^[3],[4].

본 논문에서는 100 % 직접 작성한 유한요소 코드를 사용하여 2-D shielded stripline 및 3-D interconnect 구조의 capacitance 행렬을 추출하는 시뮬레이션을 수행하였다. 이와 함께, 2-D 및 3-D 정전기(electrostatic) 문제 해결을 위한 유한요소법 적용 과정과 후처리 과정을 통해 capacitance 행렬을 추출하는 과정에 대해 자세히 다루었다. 아울러, 유한요소법을 이용한 다중도체 전송선로 구조 해석에 있어 full wave 해석 대신 준정적 해석을 통해 다중도체 및 microstrip line 구조에 대한 per-unit-length resistance와 inductance 행렬을 계산하는 방법에 대해 논의하고, 이를 이용하여 직접 시뮬레이션을 수행하여 자체 유한요소 코드의 정확성을 확인하였다.

본 논문에서 구현된 기법은 국내 전파해석 소프트웨어 개발에 있어 해석 시나리오 및 포트폴리오를 추가하는 데 상당한 기여를 할 것으로 사료된다. 추가로, 본 논문은 학술대회에서 발표된 참고문헌^[12],[13]을 수정 보완한 확장판임을 밝힌다.

Ⅱ. 2-D 유한요소해석

2-1 2-D 정전기 문제 해석

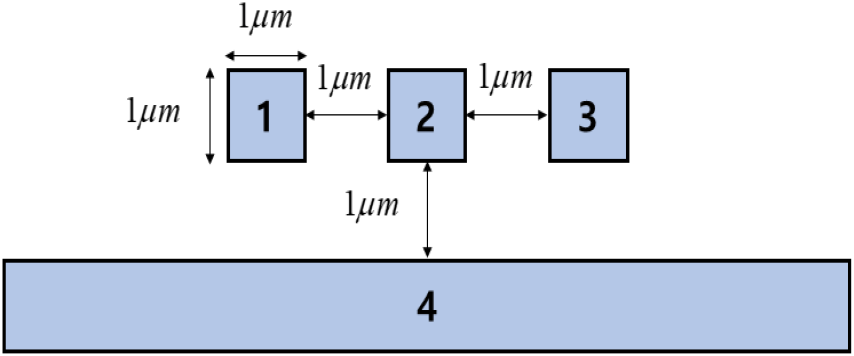
본 절에서는 2-D 유한요소법을 적용하여 그림 1과 같은 shielded stripline 구조에 대한 전압분포 해석과 후처리 과정을 통해 capacitance 행렬을 추출하는 시뮬레이션을 수행하였다.

그림 1. | Fig. 1. Shielded stripline 구조의 단면^[12],[14] | Shielded stripline structure cross-section^[12],[14].

Download Original Figure

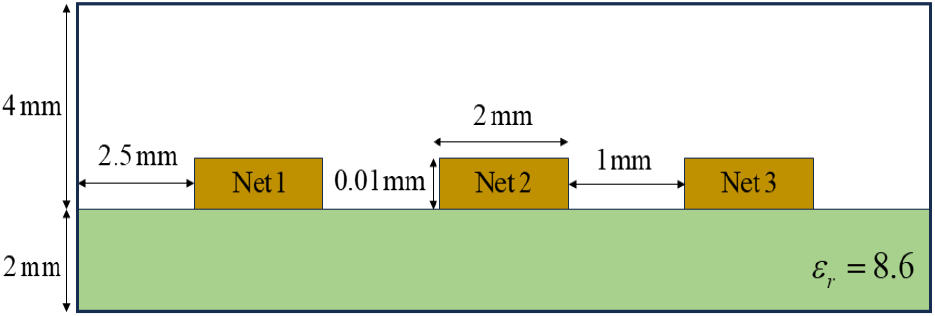
2-D 유한요소해석에서 경곗값 문제(boundary-value problem)는 식 (1)로 정의되며, 그림 1과 같은 정전기 문제에서 전압(V)은 식 (2)와 같은 Poisson 방정식의 지배를 받는다^{[5],[12],[15]}.

− ∂ ∂ x α x ∂ ϕ ∂ x − ∂ ∂ y α y ∂ ϕ ∂ y + β ϕ = f

(1)

− ∂ ∂ x ϵ x ∂ V ∂ x − ∂ ∂ y ϵ y ∂ V ∂ y = ρ v

(2)

유한요소 적용을 위해 식 (2)의 형태를 식 (1) 형태의 일반적인 2계 미분 방정식과 맞춰줘야 하며, 그 결과 식 (3)과 같은 관계를 도출할 수 있다^{[5],[12],[15]}.

ϕ = V, α x = ϵ x, α y = ϵ y, β = 0, f = ρ v

(3)

2-1-1 Capacitance 행렬 추출

유한요소 과정을 통해 전압을 구하면 식 (4)를 통해 저장된 에너지(W)를 구할 수 있으며, 이를 통해 coefficients of capacitance( $C i i'$ ) 및 induction( $C i j'$ ,i≠j)을 계산할 수 있다^{[8],[12],[15]}. 아울러, 식 (4)는 유한요소 적용을 통해 식 (5)와 같이 계산된다^[12],[15].

W = 12 C V 02 = 12 ∫ Ω D → . E → d s = 12 ∫ Ω ϵ d E → . E → d s = 12 ∫ Ω ϵ d ∇ V 2 d s

(4)

W = 12 ∑ e = 1 M ϵ d e E x e 2 + E y e 2 A e = 12 ∑ e = 1 M ϵ d e ∂ V e ∂ x 2 + ∂ V e ∂ y 2 A e

(5)

Capacitance 행렬의 모든 요소를 구하기 위해서는 해석 구조의 도체의 수를 N_c개라고 했을 때, 도체 간의 상호작용을 고려하여 총 N_c+N_c(N_c−1)/2번의 계산이 필요하며, 계산과정에서의 경계조건은 식 (6)과 같다^{[8],[12],[15]}.

V = 0 전압이 인가되지 않은 도체 및 PEC 경계 V = 1 전압이 인가된 도체

(6)

Capacitance 행렬의 원소가 되는 $C i i'$ 및 $C i j'$ 는 식 (7)을 통해 얻을 수 있으며, per-unit-length capacitance는 식 (8)을 통해 계산된다^[1],[8],[15].

C i i' = 2 W i i C i i' = W i j − C i i' + C j j' 2

(7)

C i i = ∑ k = 1 N c C i k' C i j = − C i j'

(8)

2-2 준정적 해석

본 절에서는 2-D 유한요소법과 준정적 해석을 적용하여 그림 2 및 그림 3과 같은 다중도체 전송선로 구조의 per-unit-length resistance 및 inductance 행렬을 추출하는 문제에 대해 다룬다.

그림 2. | Fig. 2. 같은 크기의 직사각형 모양 도체 4개^[3]~[5] | Four equally sized rectangular conductor^[3]~[5].

Download Original Figure

그림 3. | Fig. 3. Coupled microstrip line 구조^[3]~[5] | Coupled microstrip line structure^[3]~[5].

Download Original Figure

손실 도체들로 구성된 전송선로의 경우 변위전류(displacement current)는 무시하고 전도전류(conduction current)만 고려하는 준정적 해석을 적용할 수 있다^[3]~[5],[16]. 준정적 해석을 적용하면 도체 내에서의 transverse electric field는 무시할 수 있다고 가정하며, 이에 따라 도체에 z 방향의 전기장을 인가할 경우 Maxwell 방정식으로부터 식 (9)를 얻을 수 있다^[3]~[5],[16].

∇ × 1 μ r ∇ × A z z^+ j ω μ 0 σ A z z^= μ 0 J i m p z^

(9)

식 (9)에서 σ는 손실 도체의 도전율을, J_imp 는 인가된 전류를 의미한다. 이때, J_imp는 인가된 전기장(E_imp)에 의해 z 방향을 따라 유도된다. 따라서 식 (9)를 식 (10)과 같이 표현할 수 있으며, 유한요소 적용을 위해 식 (1)과 식 (10)의 형태를 맞추면 식 (11)과 같은 관계 식을 얻을 수 있다^[3]~[5].

− ∂ ∂ x 1 μ r ∂ A z ∂ x − ∂ ∂ y 1 μ r ∂ A z ∂ y + j ω μ 0 σ A z = μ 0 σ E i m p

(10)

ϕ = A z, α x = α y = 1 μ r, β = j ω μ 0 σ, f = μ 0 σ E i m p

(11)

그림 2 및 그림 3과 같은 개방 전송선로의 경우 potential A_z가 전송선로에 집중되기 때문에 해당 구조를 매우 큰 상자로 감싼 뒤, homogeneous Dirichlet 또는 Neumann 경계조건을 적용하여 해석할 수 있다^[3]~[5].

2-2-1 Per-unit-length Resistance 및 Inductance 행렬 추출

Per-unit-length resistance 및 inductance 행렬은 per-unit -length impedance 행렬 [Z]=[R]+jω[L]을 통해 얻을 수 있다^[3]~[5]. 이러한 행렬을 계산하기 위해서는 i번째 도체에 E_imp=1을 인가하고 유한요소 과정을 통해 A_z를 계산한 뒤, 식 (12)를 이용하여 I_k를 계산해야 한다^[3]~[5].

I k = ∬ Ω σ k E i m p δ i k − j ω σ k A z d Ω

(12)

도체의 개수만큼 E_imp=1을 인가하여 유한요소 과정을 반복함으로써 식 [Z]=[V][I]⁻¹를 통해 per-unit-length impedance 행렬을 얻을 수 있다^[3]~[5]. 이때, [V]는 E_imp=1로 이루어진 대각행렬이며, [I]는 i번째 열이 식 (12)를 통해 계산된 전류로 이루어진 정방행렬이다.

Ⅲ. 3-D 유한요소 해석

3-1 3-D 정전기 문제 해석

3-D 유한요소 해석에서는 그림 4와 같은 PEC box 안에 있는 3차원 interconnect 구조에서의 전압분포를 해석하고, 이를 이용하여 capacitance 행렬을 추출하였다.

그림 4와 같은 3차원 구조에서 전압은 식 (13)과 같은 일반화된 Poisson 방정식(generalized Poisson’s equation)의 지배를 받는다^{[5],[13],[15]}.

− ∂ ∂ x ϵ x ∂ V ∂ x − ∂ ∂ y ϵ y ∂ V ∂ y − ∂ ∂ z ϵ z ∂ V ∂ z = ρ v

(13)

그림 4. | Fig. 4. PEC 상자 안에 있는 3차원 interconnect 구조^[13],[15] | 3D interconnect structure in the PEC box^[13],[15].

Download Original Figure

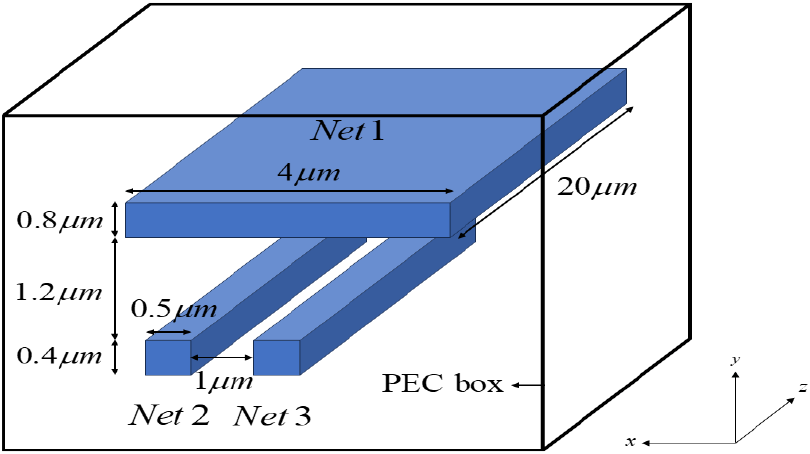
유한요소 해석을 위해서는 식 (13)을 3차원 경곗값 문제의 일반적인 형태인 식 (14)와 형태를 맞춰줘야 하며, 그 결과 식 (15)와 같은 관계 식을 얻을 수 있다^{[5],[13],[15]}.

− ∂ ∂ x α x ∂ ϕ ∂ x − ∂ ∂ y α y ∂ ϕ ∂ y − ∂ ∂ z α z ∂ ϕ ∂ z + β ϕ = f

(14)

ϕ = V, α x = ϵ x, α y = ϵ y, α z = ϵ z, β = 0, f = ρ v

(15)

아울러, capacitance 행렬 계산은 Net에 서로 다른 전압 인가를 고려하여 2차원과 같게 총 N_c+N_c(N_c-1)/2번의 계산이 필요하며, 경계조건 또한 식 (6)과 같다^{[8],[12],[13],[15]}.

이때, 3차원 구조의 경우 저장된 에너지는 식 (16)을 통해 계산할 수 있다^{[8],[13],[15]}. 여기서, v^e는 요소의 부피를 의미한다.

W = 12 ∑ e = 1 M ϵ d e ∂ V e ∂ x 2 + ∂ V e ∂ y 2 + ∂ V e ∂ z 2 v e

(16)

이후에, 저장된 에너지를 통해 계산되는 $C i i'$ 및 $C i j'$ , 그리고 per-unit-length capacitance의 계산과정은 2차원(2-1-1절)과 같다^{[8],[13],[15]}.

Ⅳ. 시뮬레이션 결과

본 장에서는 in-house FEM code와 참고문헌^[5] 및 Q3D^[17]와의 결과 비교를 통해 해석의 정확도와 유효성을 검증하였다. 상용 소프트웨어의 경우 어떤 구체적 알고리듬을 사용하는지 공개되어 있지 않아 in-house FEM code와 엄정한 비교는 현실적으로 쉽지 않다. 따라서 본 논문에서는 상용 소프트웨어와 최대한 같은 상황을 모사하고 이에 대한 정확도와 실행시간 비교 중 정확도에 초점을 맞춰 시뮬레이션을 수행하였다. 또한, 본 장에서 다루는 시뮬레이션의 솔버는 MATLAB에서 built-in으로 제공하는 direct 솔버인 backslash 연산을 선택하여 사용하였다. 채택의 주된 이유는 최종 시스템 행렬의 크기가 아주 크지 않으며, 손실 도체 및 비균일 매질로 인한 condition number의 증가로 iterative 솔버의 수렴속도가 감소하는 현상을 회피하기 위함이다. 추가적으로, 본 장의 2-D 시뮬레이션에서는 node-based triangular basis, 3-D 시뮬레이션에서는 node-based brick basis를 사용하여 해석을 진행하였다.

4-1 2-D Capacitance 행렬 추출

2-D 노드 기반 유한요소법을 사용한 shielded stripline 구조(그림 1) 해석은 직접 작성한 in-house code(MATLAB R2022b 버전)를 이용하여 진행되었으며, 전자기 상용 소프트웨어 Q3D(2D extractor)^[17]와의 결과 비교를 통해 시뮬레이션의 정확성을 검증하였다. 아울러, 삼각형 모양의 요소를 사용하여 해석 영역을 나누었으며, 총 15,600개의 요소와 7,991개의 노드가 사용되었다.

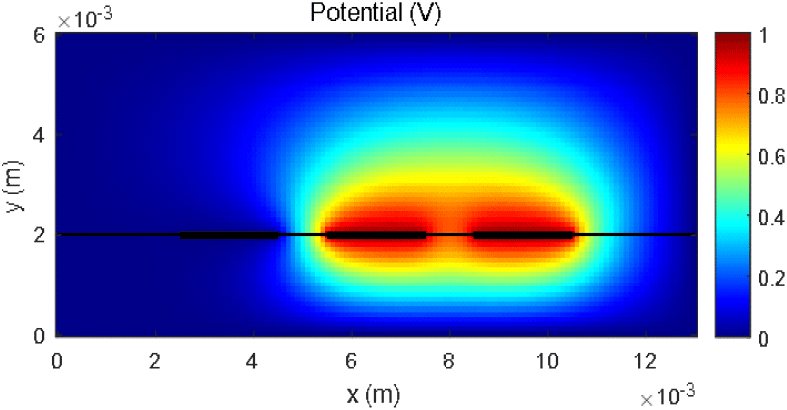
그림 5는 Net 2와 Net 3에 전압을 인가하였을 때의 전압분포 시뮬레이션 결과이며, 후처리 과정을 통해 계산한 capacitance 행렬과 Q3D^[17]와의 결과 비교를 표 1에 정리하였다.

그림 5. | Fig. 5. 전압분포 시뮬레이션 결과 | Voltage distribution simulation result.

Download Original Figure

표 1. | Table 1. Capacitance matrix 결과 비교 (단위: pF/m) | Comparison of capacitance matrix result.

	$C 11'$	$C 22'$	$C 33'$
In-house	167.524	173.637	167.524
Q3D^[17] (2D extractor)	165.514	171.374	165.628
Rel. error (%)	1.214	1.321	1.145
	$C 12' = C 21'$	$C 13' = C 31'$	$C 23' = C 32'$
In-house	−29.19	−0.435	−29.19
Q3D^[17] (2D extractor)	−28.38	−0.431	−28.219
Rel. error (%)	2.854	0.928	3.441

Download Excel Table

4-2 2-D Per-unit-length Resistance 및 Inductance 행렬 추출

다중도체 구조(그림 2) 및 coupled microstrip line(그림 3)의 시뮬레이션은 MATLAB R2022b 버전을 기반으로 실행되었으며, 참고문헌^[3]~[5]과의 결과 비교를 통해 시뮬레이션의 유효성을 검증하였다.

그림 2 구조의 경우 총 107,800개의 삼각형 요소와 54,426개의 노드를 사용하였으며, 도체의 도전율은 aluminum-oxide와 같은 σ=3.6×10⁷ S/m로 설정하였다. 또한, 그림 2 구조를 x 방향으로 33 um, y 방향으로 12 um의 크기를 가진 큰 상자로 감싼 뒤 상자 경계에 PEC 경계조건을 적용하여 계산영역을 한정시켰다.

도체 수가 4개인 그림 2 구조는 식 (17)과 같은 telegrapher equation을 만족한다^[4]. 따라서 본 시뮬레이션에서는 4×4 크기의 per-unit-length impedance 행렬을 구한 뒤, 4번 도체를 reference conductor로 설정하고, 식 I₁+I₂+I₃+I₄=0 을 이용하여 식 (18)과 같은 3×3 크기의 Z_true행렬을 통해 per-unit-length resistance 및 inductance 행렬을 계산하였다^[4].

E 1 E 2 E 3 E 4 = Z 11 Z 12 Z 13 Z 14 Z 21 Z 22 Z 23 Z 24 Z 31 Z 32 Z 33 Z 34 Z 41 Z 42 Z 43 Z 44 I 1 I 2 I 3 I 4

(17)

E 1 − E 4 E 2 − E 4 E 3 − E 4 = Z t r u e I 1 I 2 I 3

(18)

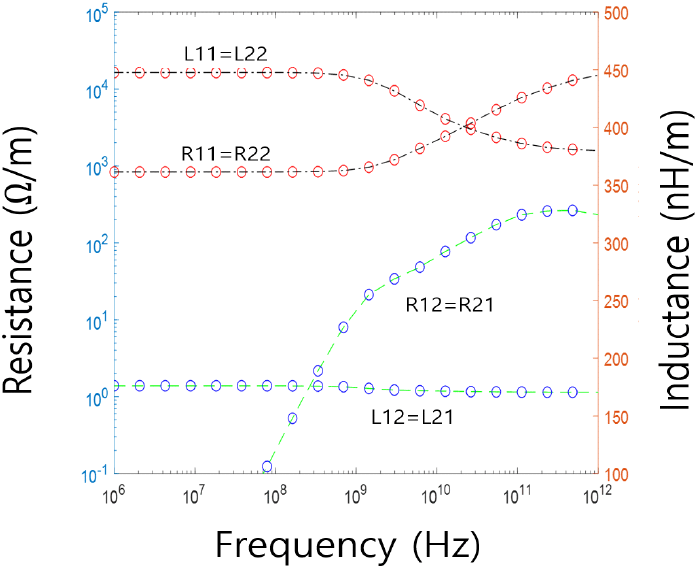
그림 6 및 그림 7은 그림 2 구조에 대한 주파수에 따른 per-unit-length resistance 및 inductance 행렬 시뮬레이션 결과를 나타내며, 참고문헌 [5]의 Figure 4.12 (b) 및 Figure 4.12 (c)의 결과와 잘 일치함이 확인된다.

그림 6. | Fig. 6. 주파수에 따른 per-unit-length resistance 행렬 | Per-unit-length resistance matrix as a function of frequency.

Download Original Figure

그림 7. | Fig. 7. 주파수에 따른 per-unit-length inductance 행렬 | Per-unit-length inductance matrix as a function of frequency.

Download Original Figure

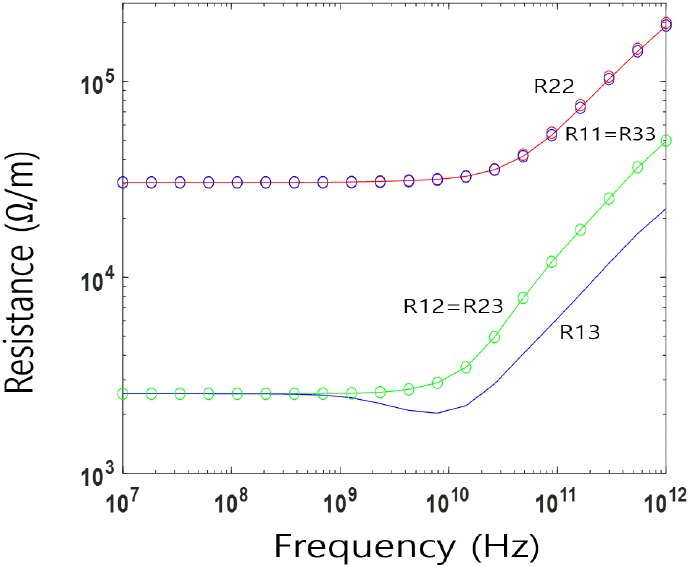
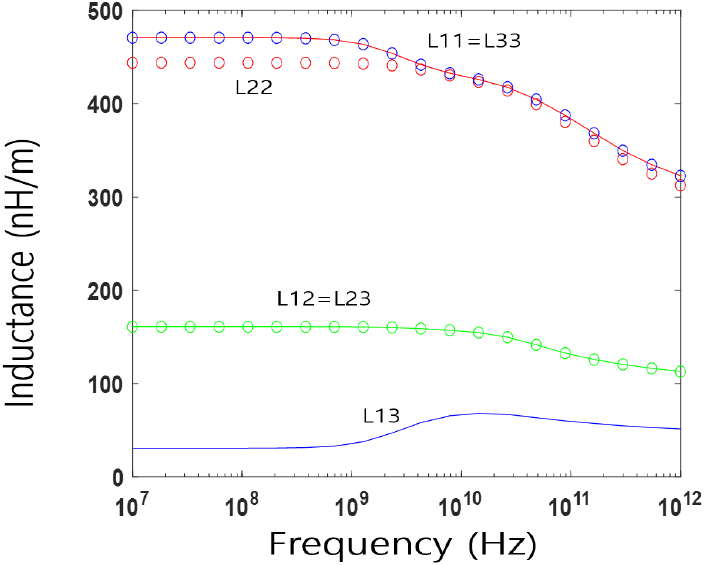
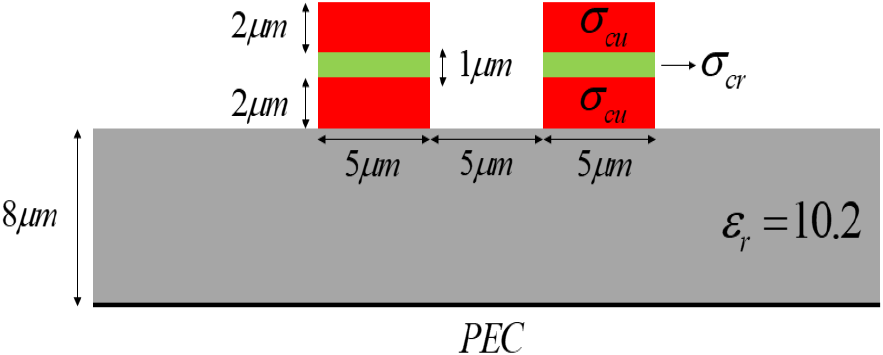
그림 3 구조는 2차원 노드 기반 삼각형 요소를 사용하여 총 126,360개의 요소와 63,685개의 노드를 사용하였으며, 도체의 도전율은 각각 σ_cu=5.8×10⁷ S/m와 σ_cr=7.75× 10⁶ S/m로 설정하였다. 아울러, 그림 3 구조를 감싼 PEC 상자의 크기는 x 방향으로 135 um, y 방향으로 117 um이다. 그림 8은 그림 3에 대한 per-unit-length resistance 및 inductance 행렬 시뮬레이션 결과를 나타낸다. In-house code의 결과와 참고문헌 [5]의 Figure 4.13 (b) 결과가 비교적 잘 일치하지만, 0 근처의 log-scale 그래프의 특성으로 인해 다소간의 오차가 관찰되는 것을 확인할 수 있다.

그림 8. | Fig. 8. 주파수에 따른 per-unit-length resistance 및 inductance 행렬 | Per-unit-length resistance and inductance matrix as a function of frequency.

Download Original Figure

4-3 3-D Capacitance 추출

3-D 노드 기반 유한요소법을 사용한 interconnect 구조(그림4) 해석은 MATLAB R2022b 환경에서 실행되었으며, Q3D^[17]와의 결과 비교를 통해 시뮬레이션의 정확성을 검증하였다. interconnect 구조는 크기가 6×5×30 um인 PEC 상자 내부에 들어가 있으며, 해석을 위해 총 72,000개의 brick 요소와 77,469개의 노드가 사용되었다.

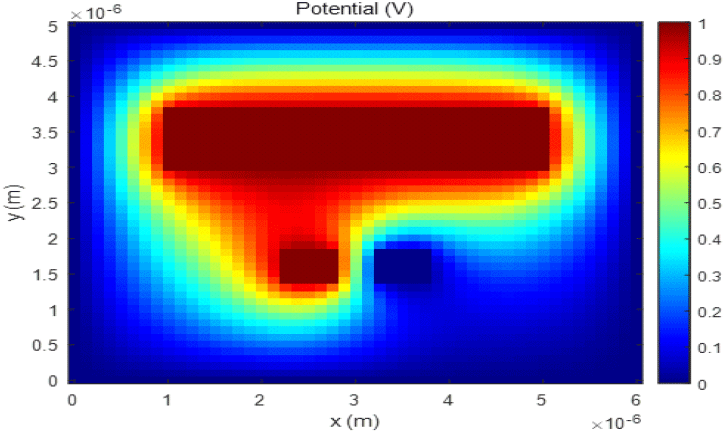
그림 9는 Net 1과 Net 2에 전압을 인가하였을 때, xy 평면(z=15 um)에서의 전압분포를 나타낸다. 또한, 총 6번의 유한요소 과정을 통해 capacitance 행렬을 계산하였으며, Q3D^[17]와의 결과 비교를 표 2에 정리하였다.

그림 9. | Fig. 9. 전압분포 시뮬레이션 결과 | Voltage distribution simulation result.

Download Original Figure

표 2. | Table 2. Capacitance matrix 결과 비교(단위: fF/m) | Comparison of capacitance matrix result.

	$C 11'$	$C 22'$	$C 33'$
In-house	1.92	0.736	0.736
Q3D^[17]	1.863	0.704	0.704
Error (%)	3.06	4.546	4.546
	$C 12' = C 21'$	$C 13' = C 31'$	$C 23' = C 32'$
In-house	−0.199	−0.199	−0.282
Q3D^[17]	−0.193	−0.193	−0.266
Error (%)	3.109	3.109	6.015

Download Excel Table

Ⅴ. 결 론

본 논문에서는 2-D 및 3-D 정전기 문제에 있어, 전압분포 해석과 capacitance 행렬 추출이 가능한 유한요소 자체 코드를 확보하였다. 이 과정에서, 대표적인 전자기해석 시뮬레이션 소프트웨어 중 하나인 Q3D를 사용한 시뮬레이션 결과와 직접 작성한 in-house 코드의 결과를 비교하여 자체 코드의 유효성을 검증하였다. 또한, 손실 도체들로 구성된 전송선로 구조를 간단하게 해석하기 위해서 준정적 해석을 적용하였으며, per-unit-length impedance 행렬을 통해 per-unit-length resistance 및 inductance 행렬을 구하고, 이를 참고문헌과 비교하여 시뮬레이션 결과의 정확성을 확인하였다.

Capacitance 행렬을 구하기 위해선 총 N_c+N_c(N_c-1)/2번, per-unit-length resistance 및 inductance 행렬을 구하기 위해선 총 N_c번의 유한요소 계산이 필요하게 된다. 따라서 N_c의 수가 증가할수록 계산량이 증가하며, 이에 따라 해석시간 또한 증가하게 될 것이다. 그뿐만 아니라, 개방 전송선로 해석을 위해 큰 PEC 상자를 설정하는 과정에서, 계산영역의 증가로 인해 해석시간이 더욱 증가할 수 있다. 이러한 해석시간의 증가는 추후에 domain decomposition, CUDA를 이용한 GPU 병렬처리 등의 병렬화 기법을 통해 더 나은 속도 향상을 기대해 볼 수 있으며, 개방 전송선로의 경우 PML(perfectly matched layer) 등의 적용으로 계산영역을 한정시켜 속도 향상을 도모할 수 있을 것으로 예상한다.

Acknowledgements

본 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. RS-2023-00242558). 또한, 2023년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(No. 2019-0-00098, 차세대 전자파 해석 융합 소프트웨어 개발).

References

[1].

C. R. Paul, Analysis of Multiconductor Transmission Lines, 2nd ed. Piscataway, NJ, Wiley-IEEE Press, 2007.

[2].

S. P. Sim, S. Krishnan, D. M. Petranovic, N. D. Areora, K. Lee, and C. Y. Yang, "A unified rlc model for high-speed on-chip interconnects," IEEE Transactions on Electron Devices, vol. 50, no. 6, pp. 1501-1510, Jun. 2003.

[3].

S. H. Lee, K. Mao, and J. M. Jin, "A complete finite-element analysis of multilayer anisotropic transmission lines from DC to terahertz frequencies," IEEE Transactions on Advanced Packaging, vol. 31, no. 2, pp. 326-338, May 2008.

[4].

S. H. Lee, "Efficient finite element electromagnetic analysis for high-frequency/high-speed circuits and multiconductor transmission lines," Ph.D. disserttation, Illinois University, Champaign, IL, 2009.

[5].

J. M. Jin, The Finite Element Method in Electromagnetics, 3rd ed. Piscataway, NJ, Wiley-IEEE Press, 2014.

[6].

Z. Ren, C. Lage, "3-D capacitance extraction of IC interconnects using field solvers and homogenization technique," IEEE Transactions on Magnetics, vol. 40, no. 2, pp. 703-706, Mar. 2004.

[7].

J. Xu, H. Li, W. Y. Yin, J. Mao, and L. W. Li, "Capacitance extraction of three-dimensional interconnects using element-by-element finite element(EBE-FEM) and preconditioned conjugate gradient(PCG) technique," IEICE Transactions on Electronics, vol. 90-C, no. 1, pp. 179-188, Jan. 2007.

[8].

O. Ozgun, R. Mittra, and M. Kuzuoglu, "CBFEM-MPI: A parallelized version of characteristic basis finite element method for extraction of 3-D interconnect capacitances," IEEE Transactions on Advanced Packaging, vol. 32, no. 1, pp. 164-174, Feb. 2009.

[9].

D. B. Davidson, Computational Electromagnetics for RF and Microwave Engineering, 2nd ed. Cambridge, Cambridge University Press, 2010.

[10].

W. C. Lee, W. B. Park, J. Y. Park, Y. J. Kim, and M. S. Kim, "Parallel iterative FEM solver with initial guess for frequency domain electromagnetic analysis," Intelligent Automation & Soft Computing, vol. 36, no. 2, pp. 1585-1602, Jan. 2023.

[11].

Z. Lou, J. M. Jin, "A novel dual-field time-domain finite-element domain-decomposition method for computational electromagnetics," IEEE Transactions on Antennas and Propagation, vol. 54, no. 6, pp. 1850-1862, Jun. 2006.

[12].

M. C. Jo, W. B. Park, S. H. Lee, and W. C. Lee, "Capacitance extraction of 2-D stripline structures using FEM," in Korean Institute of Electromagnetic Engineering and Science Conference, Hongcheon, Aug. 2023.

[13].

W. B. Park, M. C. Jo, M. S. Kim, and W. C. Lee, "Extraction of multiconductor transmission line parameters using 3-D finite element method," in Korean Society for Industrial and Applied Mathematics Conference, Gwangju, Nov. 2023.

[14].

Ö. Özgün, M. Kuzuoglu, MATLAB-based Finite Element Programming in Electromagnetic Modeling, Boca Raton, FL, CRC Press, 2018.

[15].

S. M. Musa, M. N. O. Sadiku, "Modeling and simulation of shielded microstrip lines," The Technology Interface Journal, vol. 8, no. 1, pp. 1-22, Jan. 2007.

[16].

F. Bertazzi, G. Ghione, and M. Goano, "Efficient quasi-TEM frequency-dependent analysis of lossy multiconductor lines through a fast reduced-order FEM model," IEEE Transactions on Microwave Theory and Techniques, vol. 51, no. 9, pp. 2029-2035, Sep. 2003.

[17].

Ansys, "Ansys Q3D extractor." Available: https://www.ansys.com/ko-kr/products/electronics/ansys-q3d-extractor