대류권 산란파 통신에서의 안테나 방위각 변경을 이용한 산란 손실 최적화 방법

Ⅰ. 서 론

대류권의 상층 대기에는 난류로 인해 유전율이 불규칙한 영역이 존재한다. 이 영역에 전자파가 도달하면 모든 방향으로 산란하게 되는데, 이 산란파는 송신 안테나로부터의 가시거리를 넘어 수백 킬로미터의 거리에서도 수신될 수 있다. 이 현상을 이용하여 지평선을 넘어서는 거리에 대한 통신 링크를 구성할 수 있다. 수백 킬로미터의 장거리 환경에서의 대류권 산란을 이용한 송수신 모델은 지형, 대기 조건 외에도 다양한 변수들의 고려가 필요하다. 다양한 환경 변수들을 고려한 장거리에서의 대류권 산란 손실은 ITU-R P.617 혹은 P.2001의 권고를 참고하여 계산할 수 있다^[1],[2]. 국내에서도 ITU 문서를 참고로 산란 손실에 대한 분석이 진행된 바가 있다^[3],[4].

대류권 산란을 이용한 통신 시스템을 구축하기 위해서는 산란 손실을 가능한 줄이는 것이 중요하다. 산란 손실에 많은 영향을 끼치는 변수 중의 하나는 산란 각도인데, 산란 각도가 1° 증가할 때마다 손실이 10 dB씩 증가한다는 연구결과도 존재한다^[5]. 하지만, 국내 지형 특성상 산지가 많아 항상 낮은 산란 각도를 설정하는 것은 어려움이 있다. 이런 한계를 대류권 산란의 특징을 이용해 해결할 수 있다. 대류권 산란은 전 방향으로 발생하기 때문에 안테나들이 서로 마주 보고 있을 필요가 없다. 안테나의 방위각을 변경함으로써 추가 손실이 발생할 수 있지만, 이는 산란 각도에 의한 손실에 비하면 미미하다. 따라서, 방위각을 변경해 높은 산지를 피하는 것으로 전체 산란 손실을 줄일 수 있다. 하지만 대부분의 연구가 송, 수신 안테나가 서로 마주 보는 상황에서의 대류권 산란 손실에 대한 분석이고, 방위각의 변경에 대한 손실을 분석한 연구사례가 존재하지만^[6], 이를 활용하여 이득을 볼 수 있는 방법에 대한 연구는 진행된 바 없다. 산지가 많은 우리나라에서의 대류권 산란 통신 활용을 위하여, 산지를 피해 방위각을 변경하여 산란 손실의 이득 발생에 대한 분석은 연구가 필요하다.

본 논문에서는 대류권 산란 통신에서 방위각 변경에 의한 손실을 고려하여 전체적인 산란 손실을 최소화하는 방법을 제안한다. 송․수신 안테나를 각각 서울과 부산에 위치시키고, 서로 마주 보고 있을 때와 방위각을 변경했을 때의 산란 각도를 비교 분석하여, 산란 각도가 가장 작은 경우의 산란 손실을 분석하였다.

Ⅱ. 본 론

대류권은 임의의 위치에 대해서 불규칙한 유전율을 가지고 있고, 이는 지나가는 전자파를 산란하게 만든다. 따라서, 송신 안테나를 대기 방향으로 향하게 하여 전자파를 방사하면 대류권 내 임의의 위치에서 산란하여 먼 거리에서 이 전파를 수신할 수 있다. 이러한 대류권 산란파의 개념을 그림 1에 나타내었다. 그림 1과 같이 송․수신 안테나의 빔들은 산란 각도 θ를 만족하는 교점이 생기게 된다. 산란 각도가 클수록 전송 손실이 커지기 때문에 통신 링크 구성에 있어서 낮은 산란 각도의 확보는 필수적이다. 하지만, 장거리에서 운용되는 산란 통신 특성상 국내에서는 링크 경로 안에 산과 같은 높은 지형이 있을 가능성이 크며, 이는 곧 산란 각도와 손실의 증가로 이어진다. 지형의 방해로 인한 손실의 증가를 해결하기 위해서, 두 안테나의 방위각을 변경해 지형을 피할 수 있다. 이 경우 발생하는 방위각 편향에 의한 손실 L_dl은 식 (1)~식 (3)과 같이 계산할 수 있다^[7].

그림 1. | Fig. 1. 대류권 산란파 통신 개요 | Figure of tropo-scatter communication.

Download Original Figure

m은 대기굴절률의 공간 분포도, r은 불규칙한 대기굴절률의 수직, 수평 규모의 비율, θ 는 안테나의 지평선으로부터의 고도 각, ϕ는 두 안테나를 연결한 직선으로부터의 방위각, ψ는 수평 방향의 반 전력 빔 폭(half-power beam width)의 0.6배 한 값, 그리고 D₁, D₂ 는 각각 송, 수신 안테나로부터 산란 지점까지의 대권 경로(great circle route) 길이를 의미한다. 안테나 편향 손실은 안테나들이 마주 보고 있을 때 발생하는 손실과는 독립적으로 합산하여 전체 손실을 예측할 수 있다. 식 (2) 및 식 (3)을 각각 이용하여 송․수신 안테나의 방위각 변경에 의한 편향 손실을 계산할 수 있다. 편향 손실은 방위각이 변경되지 않았을 때 발생하는 산란 손실에 추가로 발생하는데, 해당 손실에 대한 분석은 ITU-R P. 617에서 제공하는 산란 손실 모델을 참고한다^[2]. 해당 산란 손실 모델은 식 (4)와 같이 계산할 수 있다.

f는 주파수, θ 는 산란 각도, h_s는 해수면 기준 지표면의 고도, N₀, dN는 연간 평균 해수면 굴절률과 변화량, h_t 와 h_r 는 각각 송, 수신 안테나의 고도, d는 안테나 사이의 거리, ka는 유효 지구 반지름을 나타낸다. 특히 N₀, dN의 경우 국가에 따른 평균값을 ITU-R P.617에서 제공하고 있다^[1]. 한국의 경우 N₀ = 310, dN=41 정도의 값이 평균으로 되어있어 이 값들을 참고하였다.

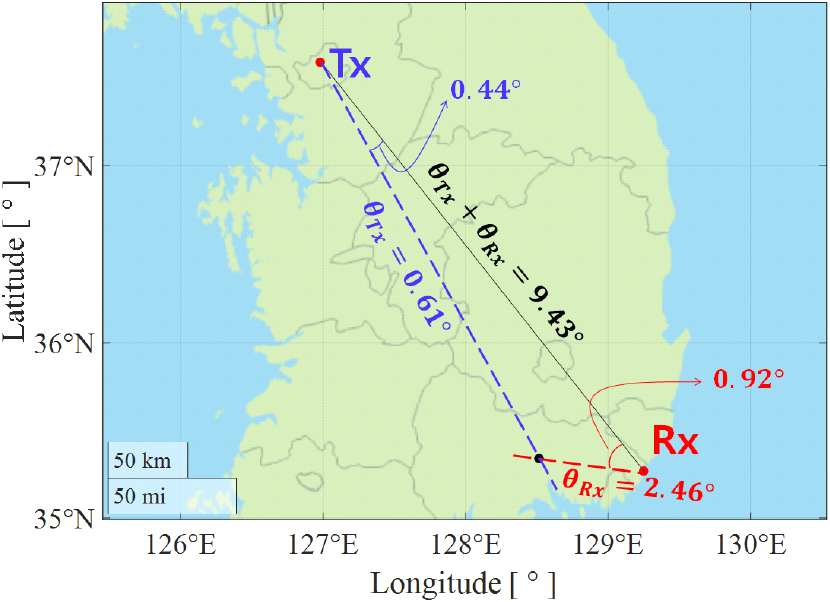
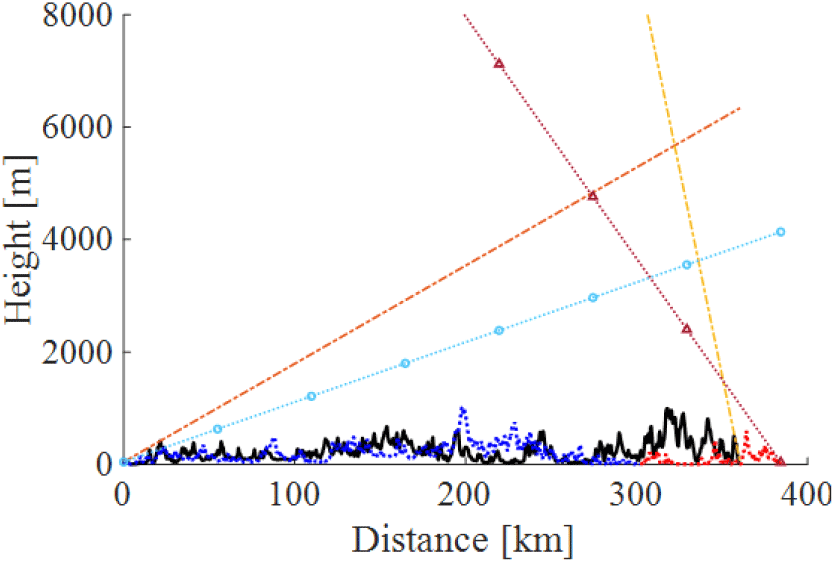
먼저, 장거리의 통신 환경을 모사하기 위해 약 360 km 떨어진 서울과 부산 임의의 위치 각각에 송신 안테나와 수신 안테나가 있다고 가정했다. 그리고, 각각의 안테나는 건물 위를 가정해 약 20 m 정도의 높이에 설치되었다고 가정했다. 송․수신 안테나 사이의 직선 경로에 대해 지형을 분석하여, 지형에 방해받지 않는 최소 고도 각을 계산했을 때, 송신 안테나는 약 1°, 수신 안테나는 약 8.43°로 총 9.43°의 총 고도 각이 필요했다. 직선 경로를 이용해 산란파 통신을 한다고 가정했을 때 식 (4)의 결과로는 평균적으로 약 198.7 dB의 손실이 발생하는 것으로 계산되었다. 손실을 줄일 수 있는 최적의 경로를 찾기 위해 송신 안테나와 수신 안테나의 방위각을 좌, 우로 0°~1°만큼 틀어가며 보상할 수 있는 손실 크기를 분석하였다. 분석 결과는 그림 2와 같고, 송, 수신 안테나의 방위각을 각각 0.44°, 0.92°만큼 왼쪽으로 변경하여 경로를 형성했을 때 고도 각의 합은 총 3.07°로 직선 경로보다 6.36°만큼 낮출 수 있었다. 직선 경로와 비교하여 그림 2와 같이 경로를 형성했을 때의 지형과 송, 수신 안테나의 고도 각에 대한 상세를 그림 3에 나타내었다. 검정 실선은 직선 경로의 지형 분포를, 푸른, 붉은 점선은 각각 송신 안테나에서 그림 2의 검은색 교점까지의 지형과 교점에서 수신 안테나까지의 지형 분포를 나타낸다. 직선에서 벗어난 경로를 가지기 때문에 384.2 km로 직선 경로보다 약 24.2 km 정도 더 긴 지형 분포를 가지게 된다. θ 와 θ′ 는 각각 직선 경로에서와 방위각을 변경했을 때의 고도 각을 나타낸다. 실선으로 표시된 θ 와, 점선으로 표시된 θ′ 를 비교해보면, 송, 수신 안테나의 고도 각 모두가 직선 경로에 비해 낮아진 것을 확인할 수 있다. 방위각을 변경함으로 생기는 지형의 길이 변화, 고도 각의 변화를 모두 고려하여 산란 손실을 식 (1) 및 식 (4)를 이용해 계산하여 그림 4에 나타내었다.

그림 2. | Fig. 2. 직선 경로와 방위각을 틀어서 형성된 경로 | A straight route and route formed as a result of deflecting azimuth angle.

Download Original Figure

그림 3. | Fig. 3. 각 경로에 대한 지형과 고도 각 프로파일 | Terrain and elevation angle profiles for each route.

Download Original Figure

그림 4. | Fig. 4. 각 경로에 대한 산란 손실 분석 결과 | Results of scattering loss analysis for each route.

Download Original Figure

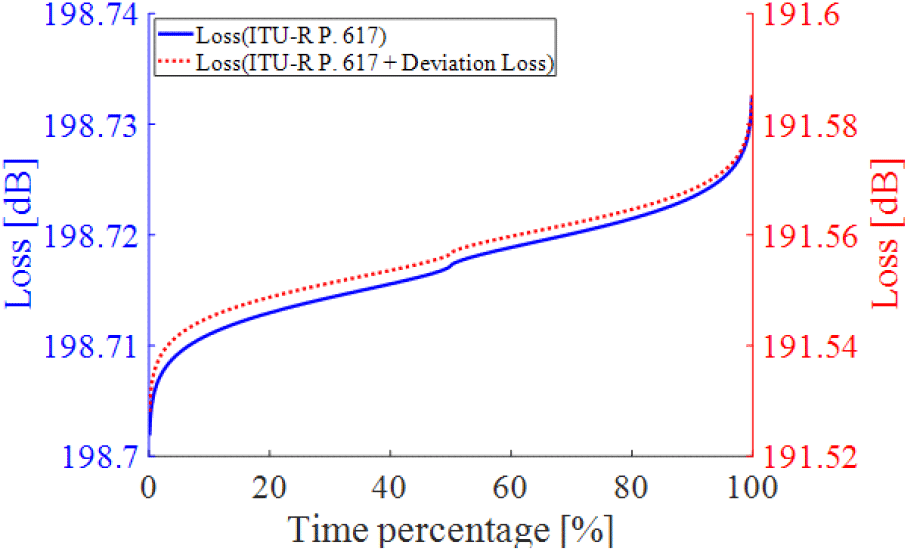
푸른 실선은 안테나가 서로 마주 보고 있는 상태인 직선 경로에 대해 발생하는 산란 손실을 시간 백분율에 대해 계산한 결과이다. 붉은 점선은 송, 수신 안테나의 방위각을 그림 2와 같이 변경했을 때 발생하는 산란 손실과 편향 손실의 합을 나타낸 결과이다. 시간 백분율에 대하여 평균적인 손실을 계산했을 때, 직선 경로보다 약 7.16 dB 정도의 손실을 개선할 수 있었다.

Ⅲ. 결 론

본 논문에서는 국내의 높은 지형을 피해 대류권 산란 통신 링크를 구성할 수 있도록, 안테나의 방위각을 조절해 산란 각도가 가장 낮게 형성되는 각도를 찾아 산란 손실을 계산하였다. 서울, 부산에 대해 통신 링크를 모의한 결과, 방위각을 변경함으로써 고도 각을 약 6.36°만큼 낮추어 산란 손실을 약 7.16 dB 정도 개선할 수 있음을 확인했다. 본 논문에서 제시하는 방법과 결과는 국내 대류권 산란파 통신 링크 구성 시 최적의 안테나 위치나 각도 세팅에 대한 참고자료로 활용 가능할 것으로 생각된다.