PDF Download
PubReader
Export Citation
Email the Author
Share Facebook
Share Twitter
Cited by 0 Article
Metrics (View:1,197)
Ⅰ. 서 론
편파 변환 기술은 채널 용량을 향상시킬 뿐만 아니라 자연환경에 의해 발생하는 다양한 클러터 간섭을 완화할 수 있어 레이다, 모바일 기지국, UAM(urban air mobility) 및 여러 최첨단 무선 통신 기술에서 주목을 받고 있으며, 편파 변환이 가능한 고이득 고효율 안테나에 대한 연구도 활발히 진행되고 있다[1]~[4]. 기존의 편파 변환 안테나들은 PIN 다이오드나 버랙터 다이오드를 급전 안테나 직접 부착하는 것이 일반적이다. 하지만 급전 안테나에 높은 전류가 흐를 경우 PIN 또는 버랙터 다이오드가 손상되는 문제점을 가진다[5],[6]. 본 논문에서는 급전 안테나와 이격된 벽면에 버랙터를 설치하여 사용 가능한 전력을 높일 수 있는 새로운 편파 변환 방법을 제안한다.
제안된 안테나는 AMC(artificial magnetic conductor) 측벽으로 둘러싸인 FPC(Fabry-Perot cavity) 구조이다. 그림 1에 나타낸 것처럼 기존의 FPC 안테나는 이득 감소와 높은 부엽 준위를 야기하는 옆으로 새어나가는 에너지가 존재하는데, 본 논문에서는 AMC 측벽이 옆으로 새는 에너지를 막아주어 그 문제를 해결하였다.
더불어 제안된 안테나는 최초로 공진기의 고유모드(eigenmode)를 조절하여 편파를 변환함으로써, 간단한 구조로도 우수한 편파 변환 성능과 141 %의 매우 높은 개구부 효율을 갖는다. 모든 시뮬레이션은 CST Studio Suite를 사용했다[5].
Ⅱ. 본 론
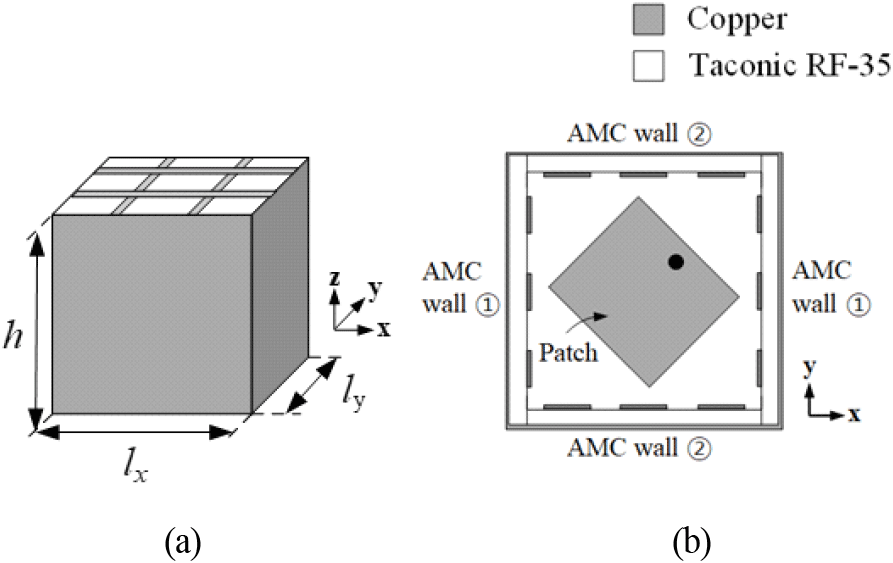
그림 2에는 제안된 안테나의 구조가 나타나있다. 제안된 안테나는 상판인 PRS(partially reflective surface)와 접지면 그리고 4개의 AMC 측벽으로 구성되어 있는 공진기 구조이다. 공진기 내부에서 발생하는 공진을 이용해 고이득과 편파 변환 기능을 동시에 얻을 수 있다.
FPC 안테나는 그림 3과 같이 PRS의 반사 위상과 접지면 사이의 거리를 적절히 조절하여 PRS를 투과한 파들이 목표 파면에서 동위상이 되도록 하여 고이득을 얻을 수 있다. 이때, PRS와 접지면 사이의 거리(h)는 식 (1)의 FP 공진조건을 만족해야 한다[6].
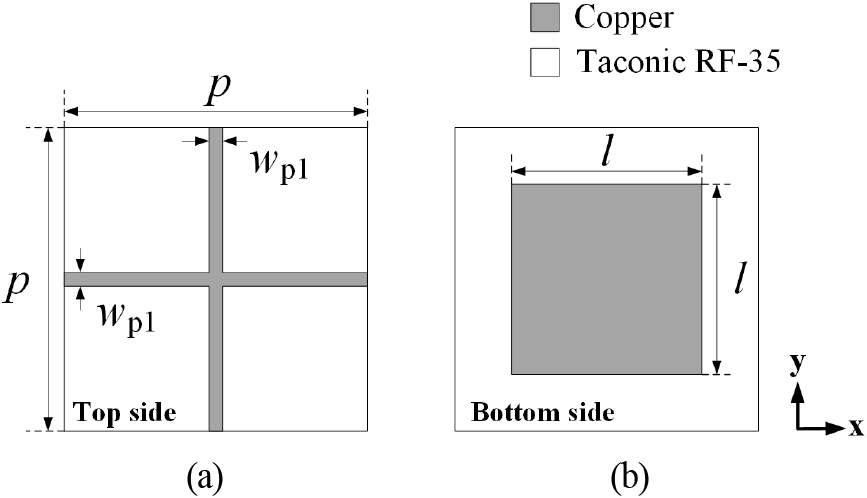
여기서 ϕPRS와 ϕGND는 각각 PRS와 접지면의 반사 위상, f는 동작 주파수이다. 그림 4에 나타나 있는 PRS 단위 셀의 반사 특성과 식 (1)에 의해 h를 구할 수 있다. PRS 단위셀은 윗면 스트립 라인의 폭 wp1과 아랫면 패치의 길이 l을 조절하여 반사 특성을 바꿀 수 있다. PRS 단위셀에 사용된 유전체는 1.52 mm 두께의 Taconic RF-35이다.
본 논문에서는 감쇄파(evanscent waves)를 억제해 고이득 특성을 얻고 편파 변환 기능을 구현하기 위해 AMC로 구성된 측벽을 옆면에 설치하였다[7]. 여섯 면이 모두 도체 벽으로 둘러싸인 일반적인 공진기는 공진기 내부 크기와 벽의 경계 조건에 의하여 내부 공진 모드가 결정된다. 각 모드의 위상 상수 (βr)은 dispersion equation에 의해 식 (2) 및 식 (3)으로 정의된다는 것은 잘 알려져 있다[8].
여기서 βx,βy는 각 방향으로의 위상 상수, m과 n은 정수로 각각 x축과 y 축 방향으로 모드의 개수, lx,ly는 공진기 안쪽의 x축과 y축 방향의 길이를 나타낸다.
이때, 공진기의 측벽이 도체에서 AMC로 대체되면 식 (3)은 식 (4) 및 식 (5)와 같이 변경된다.
여기서 ϕx,ϕy는 각각 x, y 방향에 설치된 AMC 측벽의 반사 위상을 나타낸다.
βz는 βx,βy와 달리 식 (1)의 FP 공진 조건에 의해 식 (6)과 같이 정리된다.
여기서 q는 정수로 z 방향으로의 모드 개수를 나타낸다. 식 (2)를 식 (4)~식 (6)을 이용해 다시 적으면 식 (7)과 같다.
모드 개수를 나타내는 m, n, q에 원하는 각 방향의 모드 수(번호)를 대입하면, 모드 형성에 필요한 AMC 측벽의 반사 위상을 구할 수 있다. 수직편파인 TE 101 모드를 형성하는 AMC의 반사 위상은 m=q=1, n=0으로부터 식 (8)과 같이 구해진다.
식 (8)과 같은 방법으로 수평편파인 TE 011 모드를 형성시키는 AMC의 반사 위상은 식 (9)와 같이 구할 수 있다.
식 (8) 및 식 (9)에서 서로 다른 두 AMC의 반사 위상이 서로에게 영향을 주는 것을 확인할 수 있다. 즉, 식 (8)에서 ϕx를 결정하려면 ϕy 값을 먼저 정해야 하고, 식 (9)도 이와 같이 동작한다. 본 논문에서는 수평편파를 기준으로 ϕx=180°, ϕx=115.7°의 반사 위상을 각각 사용하였다. 두 값을 서로 바꾸면 수직편파를 방사한다.
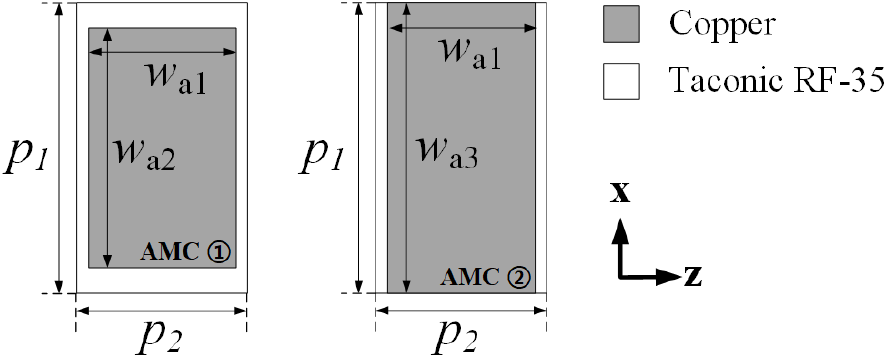
그림 5 및 그림 6에는 식 (8) 및 식 (9)에 따라 설계된 AMC ①과 AMC ②의 단위 셀의 형상을 보여준다. 편파 변환을 위해 수직편파와 수평편파를 형성할 수 있도록 두 가지 AMC 단위 셀을 설계하였다. AMC 단위 셀은 두 종류 모두 1.52 mm 두께의 Taconic RF-35를 사용하였으며, 뒷면은 copper로 완전히 덮여 있다.
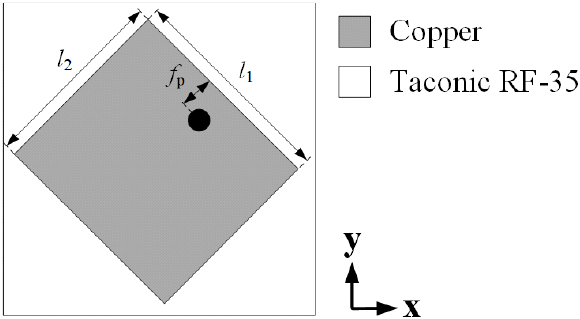
제안된 안테나의 가장 중요한 기술인 편파 변환에 있어 AMC 측벽의 반사 위상 조절과 함께 급전 안테나가 입사 편파 방향이 매우 중요하다. 본 논\문에서는 수직 또는 수평편파를 방사하는 일반적인 패치를 급전 소자로 사용하지 않고 그림 6에 나타나 있는 45° 편파의 패치 안테나를 급전 소자로 사용했다. 제안된 안테나는 내부 전파를 수직 또는 수평 방향으로 선택적 공진시킬 수 있어 편파 변환이 가능하다. 따라서 공진기 내부에는 수직과 수평 성분 모두 존재해야 하는데, 45° 편파는 수직과 수평 성분을 모두 포함하고 있다.
수직편파 모델은 AMC ①이 x 방향, AMC ②가 y 방향에 배치되어야 하고 그때의 공진기 내부 전계 분포는 그림 7(a)와 같다. 수평편파는 AMC ①이 y 방향, AMC ②가 x 방향에 배치되어야 하며, 그때의 공진기 내부 전계 분포는 그림 7(b)와 같다. 그림 8은 실제 제작된 cube 안테나의 모델과 측정 환경을 보여준다. 제작된 안테나는 0.48λ×0.48λ×0.47λ의 매우 작은 크기이다. AMC 뒤편이 모두 copper로 덮여있기 때문에 AMC 측벽은 편파 변환 성능에는 영향을 주지 않는다.
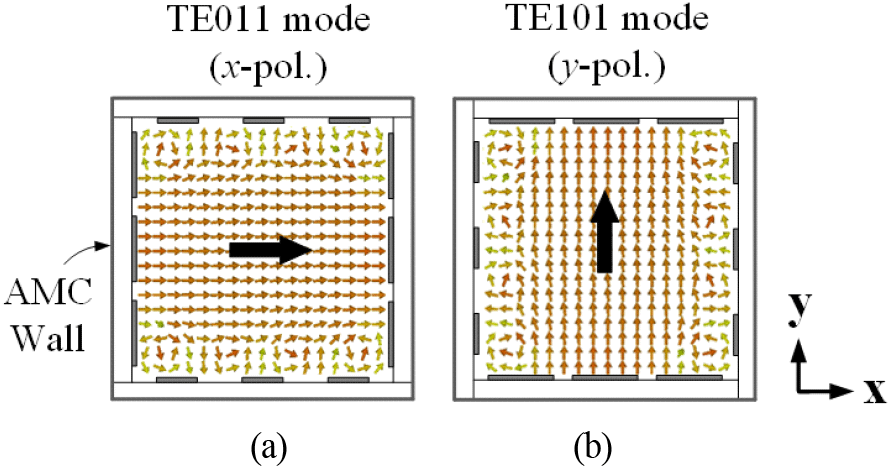
그림 9(a)와 그림 9(b)는 수직 및 수평편파 모델의 S11 특성을 보여준다. 두 모델 모두 패치 안테나를 기준으로 대칭이므로 매우 안정되며 유사한 S11 특성을 갖는다. 측정된 안테나의 −10 dB 대역폭은 각각 446 MHz (8.35 GHz~8.796 GHz)이다. 그림 9(c)와 그림 9(d)는 주파수에 따른 최대 실현 이득(realized gain) 을 나타낸 것이다. 목표 주파수인 8.5 GHz에서 측정된 실현 이득은 각각 6.31 dBi, 6.34 dBi이며, 개구부 효율은 144.65 %와 147.67 %로 매우 높다.
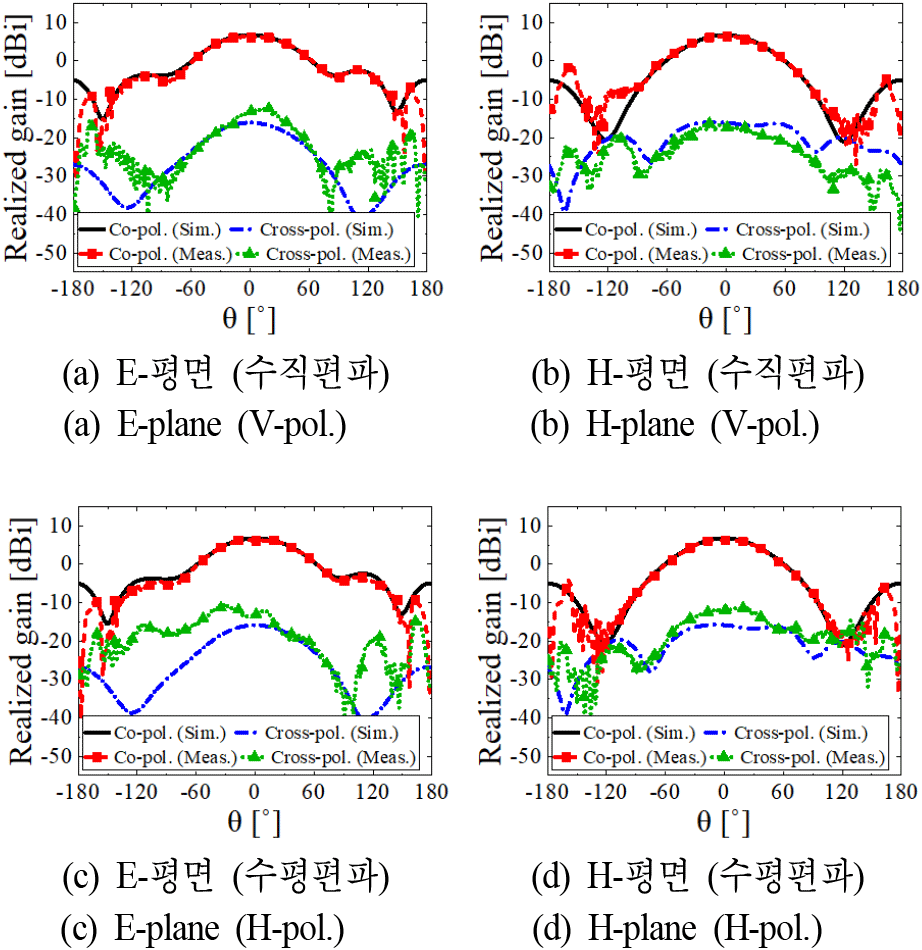
그림 10에는 8.5 GHz에서의 수직편파와 수평편파 모델의 E-평면 및 H-평면 방사 패턴이 주어져 있다. S11 특성과 마찬가지로 수직 및 수평편파에 대한 방사 패턴이 매우 유사함을 알 수 있으며, 이는 제안된 안테나가 두 편파에서 모두 매우 유사한 성능을 보임을 입증하는 중요한 특성이다. 교차 편파 억제율은 목표 복사 각도(0°)에서 약 20 dB로 편파 변환 성능 또한 매우 우수함을 증명한다.
