FMICW 레이다에서 기계 학습을 활용한 다수 표적 탐지 기법 연구

Ⅰ. 서 론

FMICW(frequency modulated interrupted continuous waveform) 레이다는 광대역 신호 생성이 가능하고, 송수신 차폐 구조로 고출력 신호를 송수신할 수 있어 장거리에서 고해상도 파형이 필요할 때 사용된다^[1]~[3]. 일반적으로 FMICW 시스템은 FMCW(frequency modulated continuous waveform)와 유사하게 송신주파수와 수신주파수의 차이인 비트(beat) 주파수를 측정한 후, 표적의 거리와 도플러를 계산한다. 두 시스템의 가장 큰 차이점은 FMICW의 송수신 차폐 구조로 인하여 비트 주파수에 주기적인 스퓨리어스라고 불리우는 하모닉스 신호가 발생된다는 점이다. 그림 1은 FMCW와 FMICW 레이다의 송수신 신호와 각각의 단일 표적 비트 주파수를 나타낸다. FMCW 레이다의 비트 주파수는 그림 1(b)와 같이 하나의 비트 주파수만 생성되지만, FMICW 시스템은 그림 1(d)와 같이 1/(T_a+T_d) 주기의 스퓨리어스가 나타난다. 여기서 T_a는 송신 시간, T_d는 수신 시간, T_t는 수신 신호의 지연 시간이다.

그림 1. | Fig. 1. FMCW과 FMICW 시스템 비교 | Comparison of FMCW and FMICW systems.

Download Original Figure

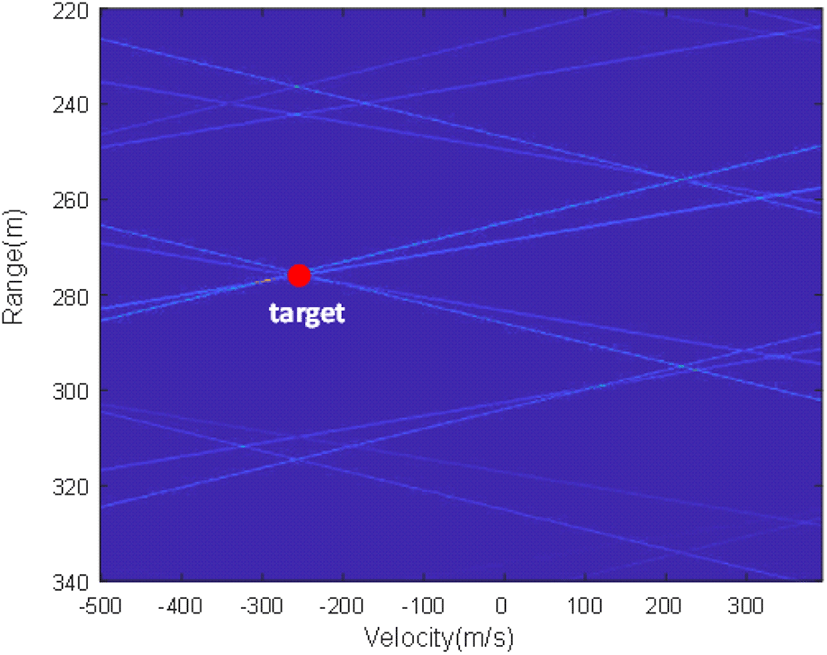
단일 표적에서 그림 1(d)의 중앙에 위치한 피크 신호를 찾는 문제는 비교적 쉽지만, 다중 표적의 경우에는 다수의 스퓨리어스 신호와 수신신호 샘플링 과정에서 발생하는 부정합 현상으로 인해 표적의 중앙에 있는 비트 신호를 찾는 것이 어려워진다. 표적 A와 B가 동일한 크기의 SNR(signal to noise ratio)을 가지더라도, 표적 B의 스퓨리어스 신호가 표적 A의 중앙 스펙트럼 신호 세기보다 큰 경우가 발생할 수 있다. 이러한 상황은 표적 A와 B의 중앙 스펙트럼을 선택하는 것을 어렵게 만든다.

FMICW 레이다에서 스퓨리어스 신호 제거용 대역통과필터(BPF)를 사용하여 스퓨리어스가 없는 영역만 처리하는 방식은 사용할 수 있는 주파수를 크게 제한시키는 단점을 가지고 있다^[3]. 대역통과필터를 적용하여 사용 주파수를 제한하는 FMICW와 일반적인 FMCW 신호 처리는 유사하게 이루어지며, 허상 표적(ghost target)을 제거하기 위해 서로 다른 세 개 이상의 chirp 주파수를 사용하여 거리와 속도를 추정한다^[4]. 그러나 이러한 방식은 표적의 개수가 증가하면 표적의 거리, 속도를 계산하기 위한 알고리즘이 복잡해질 수 있으며 정확히 만족하는 해가 존재하지 않을 수 있다. 이에 본 논문에서는 이러한 단점들을 보완하고 FMICW 레이다에서 다중 표적을 효과적으로 탐지할 수 있는 방법을 제안한다. 우선, MLE(maximum likelihood estimation)를 적용하여 RD-map(range Doppler-map)을 생성하고, 거리와 속도 커플링으로 생성되는 직선의 교점으로 표적을 강화하는 방법을 제시한다. 또한, 강화된 영상에 기계 학습 기반의 객체 탐지 알고리즘인 YOLO(you only look once) 알고리즘을 적용하여 표적을 탐지하는 방법을 제안한다.

본 논문의 구성은 다음과 같다. II장에서는 제안된 방법을 상세히 설명하고, III장에서는 생성된 RD-map 영상에 기계 학습 기반의 YOLO 디텍터를 적용한 탐지 결과를 다양한 조건에서 비교한다. 마지막으로 IV장에서는 결론을 제시한다.

Ⅱ. 제안된 방법

2-1 시스템 구성 및 RD-Map 생성

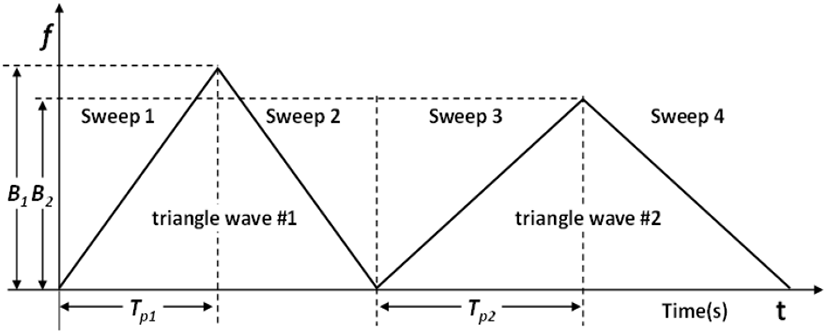
다수의 표적을 탐지하기 위해 다양한 기울기를 사용하는 시스템은 표적의 정보를 더 정확하게 계산할 수 있지만, 필요한 송신 시간이 증가하는 단점이 있다. 특히 고속 표적의 경우에는 신속한 탐지가 필요하므로 다양한 기울기 사용은 적합하지 않다^[5]. 따라서 본 연구에서는 그림 2와 같이 두 개의 기울기(B/T_p)를 가지는 삼각파 신호를 사용하였다.

그림 2. | Fig. 2. 2개의 기울기를 가지는 FMICW 송신 신호 | FMICW transmission signal with two slopes.

Download Original Figure

DFT(discrete Fourier transform)를 사용하여 레이다의 비트 신호를 주파수로 변환함으로써 표적의 거리와 속도를 계산할 수 있다. 주파수 변환을 통해 얻은 결과는 거리와 속도에 대한 정보를 포함하며, 이를 활용하여 거리 해상도를 계산할 수 있다. 식 (1)은 주파수와 DFT 인덱스 간의 관계를 나타내고, 식 (2)는 표적의 거리와 주파수 간의 관계를 보여준다. 식 (1) 및 식 (2)로 거리 해상도를 식 (3)과 같이 정확하게 산출할 수 있다^[6].

$$f=n\Delta f=n{f}_s/N_r=n/(N_r{T}_s)$$

(1)

$$f=K_s{t}_T=K_{s}2r_T/c=K_{s}2n\Delta r/c$$

(2)

$$\Delta r=\frac{c}{2N_r{K}_s{T}_s}$$

(3)

식 (1)~식 (3)에서 사용된 FMICW 레이다의 파라미터는 표 1과 같다.

표 1. | Table 1. FMICW 레이다 파라미터 | The parameter of the FMICW radar.

Parameter	Explanation	Unit
f	Beat frequency at target range	Hz
n	Target index of DFT	-
fs	Sampling frequency	Hz
Nr	Number of DFT	-
Ts	1/fs	sec
Ks	Slope of frequency modulation	Hz/sec
tT	Latency caused by target distance	sec
rT	Target range	m
c	Velocity of light	m/sec
Δr	Range resolution	m

Download Excel Table

본 연구에서 사용되는 2개의 삼각파가 동일한 거리해상도를 가지도록 신호의 주파수 변조폭과 시간을 선정하였으며, 파라미터는 표 2와 같다.

표 2. | Table 2. 두 개 삼각파의 파라미터 | The parameter of the 2 triangle wave.

Parameter	Triangle wave #1	Triangle wave #2
B	622.22 MHz	615.38 MHz
Tp	500 us	714.28 us
Ks	1.244×1012	0.650×1012
Nr	2,700	3,900
Ts	0.1786 us	0.1786 us
Δr	0.25 m	0.25 m

Download Excel Table

Range-Doppler(RD) map을 생성하는 과정을 설명하기 위하여 z_i를 i번째 스윕(sweep)에서 비트 신호의 DFT라고 하고, 4개의 스윕 동안 얻은 이들 측정치를

$$z={\left[z_1^T,z_2^T,z_3^T,z_4^T\right]}^T$$

(4)

로 표시하면 측정치 z의 신호모델은 식 (5)와 같다.

$$\begin{array}{cc}z=a(r,\dot{r})s+n,& n~N(0,{\sigma }^{2}I)\end{array}$$

(5)

여기서 s는 표적의 복소수 신호 값, n은 열잡음이고,  a(r, ṙ)는 거리 r와 속도 ṙ를 가지는 표적이 만드는 DFT 패턴을 의미한다.

이제 각각의 점 (r, ṙ)에 대하여 잡음이 없는 신호 탬플릿 a(r, ṙ)를 계산하여, 측정치 z가 r, ṙ를 가지는 표적에 의한 것일 가능성(likelihood)으로 식 (6)과 같이 나타낼 수 있다^[7].

$$L(r,\dot{r})=\frac{1}{\left|\right|z-a(r,\dot{r})s\left|\right|}$$

(6)

여기서 두 벡터 z가 a(r, ṙ)와 유사하면 likelihood L(r,ṙ)값이 큰 값이 될 것이다. 하지만 r, ṙ는 DFT 패턴만 결정하고, 반사신호의 크기 s값은 주지 않으므로 식 (7)과 같이 추정하여서 사용한다.

$$\widehat{s}=\frac{a^H(r,\dot{r})z}{a^H(r,\dot{r})a(r,\dot{r})}$$

(7)

식 (6) 및 식 (7)에서 a(r, ṙ)를 계산함에 있어서 FMICW 파형은 거리와 속도가 연관되어 있으므로 점 (r, ṙ)으로 겉보기 r을 식 (8)과 같이 계산할 수 있다.

$$\begin{array}{c}upsweapa(r,\dot{r})=a(r_{up})\\ downsweapa(r,\dot{r})=a(r_{down})\end{array}$$

(8)

여기서 r_up, r_down식 (9)와 같이 정의된다.

$$r_{up}=r+\frac{fc}{Ks}\dot{r},r_{down}=r-\frac{fc}{Ks}\dot{r}$$

(9)

그림 3은 단일 표적에 식 (6)을 이용한 RD-map을 보여준다.

그림 3. | Fig. 3. 단일 표적의 RD-map | RD-Map of a target.

Download Original Figure

MLE를 적용한 RD-map의 가장 큰 특징은 속도 거리의 커플링 효과가 다수의 교차하는 직선으로 나타나는 점인데, 직선의 기울기는 송신하는 4개 스윕의 기울기로 결정되며, 표적 위치에는 4개의 직선이 교차한다. 또한 신호의 스퓨리어스 신호로 표적이 아닌 거리, 속도에서도 많은 직선과 교점이 생성되며, 특히 다중 표적에서 FMICW 레이다의 오탐지 확률을 증가시킨다.

일반적인 펄스 도플러 레이다나 FMCW 레이다의 경우, RD-map은 표적의 속도와 거리에서만 표적 신호가 생성되지만 식 (6)으로 얻은 RD-map은 잡음 및 샘플링 부정합 현상으로 인하여 표적의 (r,ṙ)에서 L(r,ṙ)이 최대값이 되지 않을 수도 있으므로, 단순한 CFAR(constant false alarm rate) 등의 과정을 거쳐서 표적을 탐지하는 것이 불가능하다. 그러므로 본 논문에서는 이상에서 설명한 표적 근방에서 보이는 특수한 패턴을 deep learning 기법을 이용하여 탐지하는 방법을 제안하였다.

2-2 표적 후보군 선정

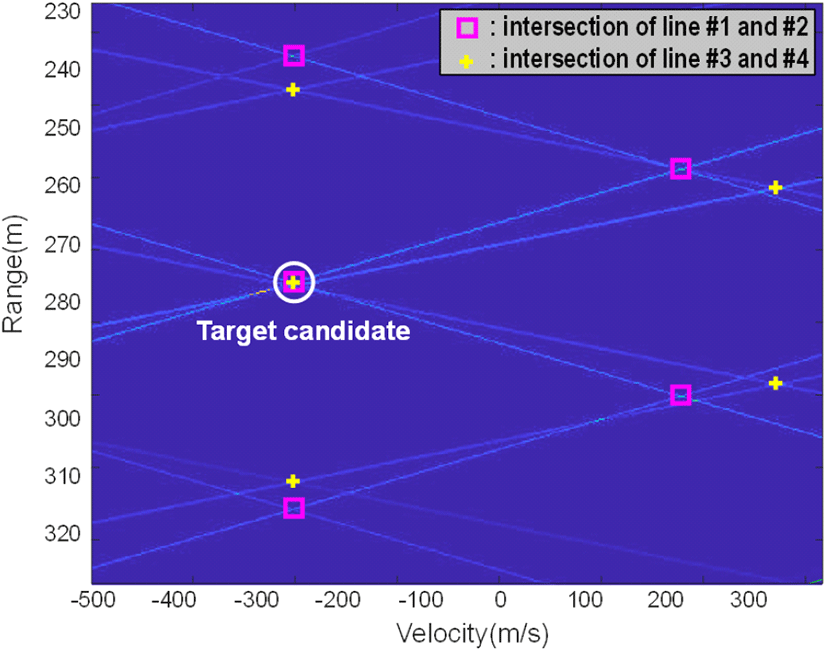
RD-map에서 표적 후보군을 선정하기 위해서는 다음 조건을 충족해야 한다. 먼저, 표적 후보군은 4개의 직선의 교점에 위치해야 하며, 이는 표적의 위치를 정확히 추정하기 위해 필요한 기본 조건이다. 또한, 그림 4와 같이 표적 주변에 주기적으로 나타나는 스퓨리어스에 의한 직선의 교점들이 존재해야 한다. 이는 스퓨리어스 신호의 주기성을 활용하여 표적을 식별하고 추정하는 데 도움을 준다. 스퓨리어스 신호에 의한 주기적인 교점 패턴은 표적 후보군의 신뢰도를 높일 수 있다. 따라서, RD-map에서 표적 후보군을 선택할 때는 4개의 직선 교점에 위치하고, 주기적인 스퓨리어스에 의한 직선 교점들이 표적 주변에 나타나는 특성을 고려해야 한다. 이를 통해 정확한 표적 후보군을 식별하고 추정할 수 있다.

그림 4. | Fig. 4. RD-map에서 표적 후보군의 특성 | Characteristics of target candidates in RD-map.

Download Original Figure

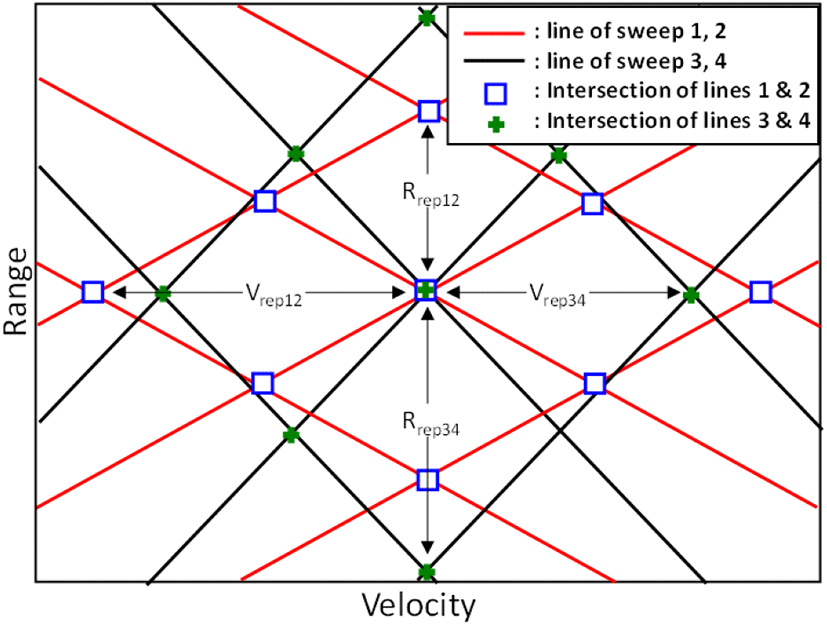
변수 Vrep₁₂는 속도 축에서 직선 1과 2의 교점의 주기를 의미하며, Vrep₃₄는 직선 3과 4의 교점의 주기를 나타낸다. 속도와 유사하게 Rrep₁₂, Rrep₃₄는 각각의 거리 방향의 주기를 의미한다. 거리, 속도 방향의 주기는 스퓨리어스의 주기에 의해 발생하므로 주파수와 속도 및 거리의 관계를 사용하여 식 (10)으로 계산할 수 있다^[8]. 여기서f_rep는 스퓨리어스의 반복 주파수, c는 전파의 속도, K_s는 주파수 변조의 기울기를 나타낸다.

$$\begin{array}{c}{V}_{rep}=\frac{\lambda }{2}{f}_{rep}\\ R_{rep}=\frac{c}{2K_s}{f}_{rep}\end{array}$$

(10)

영상에서 직선은 그림 5와 같이 사전에 알고 있는 기울기로 직선의 윈도우(window)를 생성하여 검출하였다.

그림 5. | Fig. 5. 기울기 윈도우를 활용한 직선 검출 방법 | Line detection method using slope window.

Download Original Figure

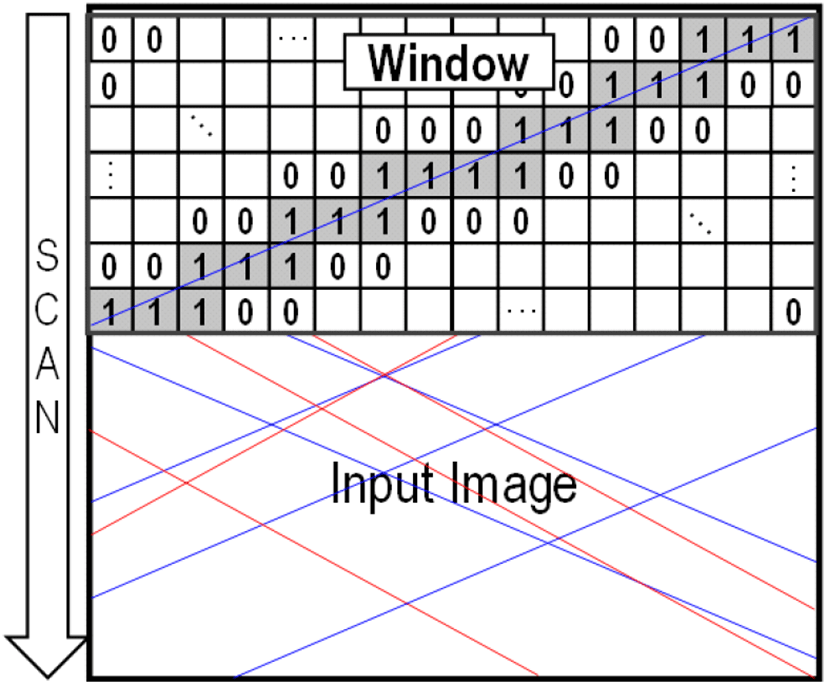
윈도우에 직선이 위치한 영역은 1, 그 외의 영역은 0으로 설정하고, Y축 방향으로 비교하여 임계치가 높은 y축을 찾아서 직선을 찾는 방법이다. 기울기 윈도우를 활용한 직선 검출 결과는 그림 6과 같으며, 직선을 효과적으로 검출하였다.

그림 6. | Fig. 6. 기울기 윈도우를 사용한 직선 검출 결과 | Line detection result of slope window.

Download Original Figure

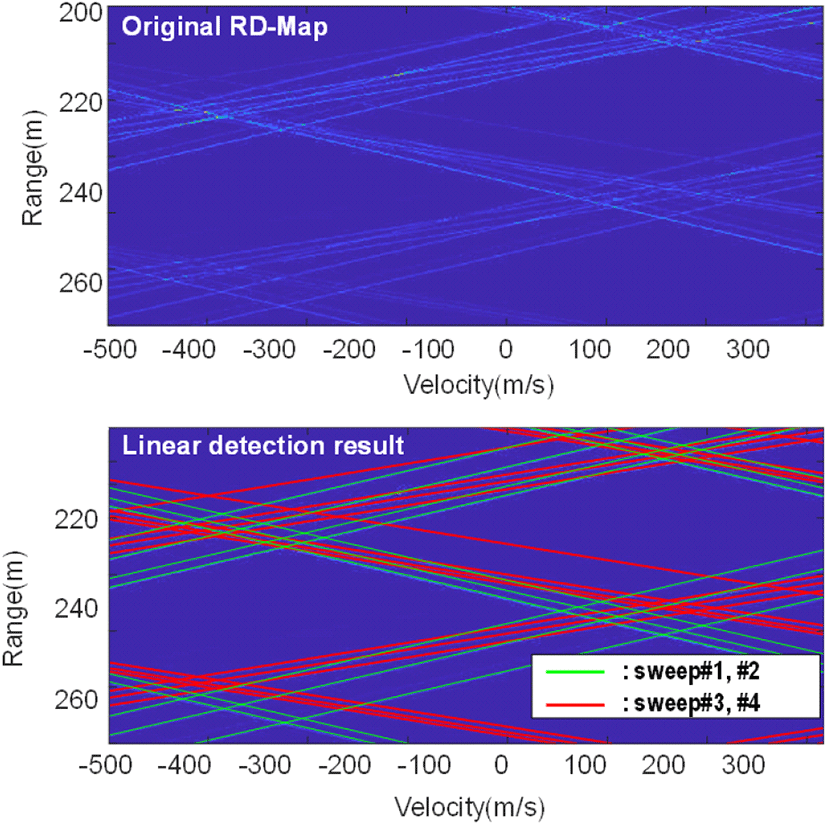
영상에서 4개 직선의 교점을 찾고 주변의 스퓨리어스에 의한 교점이 존재하는 위치를 표적 후보군으로 선정하였으며, 그 결과는 그림 7과 같다.

그림 7. | Fig. 7. 직선의 교점으로 표적 후보군 선정 결과 | Target candidates selected by the intersection of lines.

Download Original Figure

Ⅲ. 영상 학습과 탐지 성능 비교 결과

실험 결과는 표 3과 같이 3가지 경우를 비교하였다.

실험 1에서는 4개 직선의 교점 및 그와 인접한 스퓨리어스에 의한 교점을 기반으로 표적을 탐지하였다. 실험 2에서는 YOLO 디텍터를 활용하여 표적 위치의 패턴을 학습한 후 탐지를 수행했으며, 실험 3에서는 실험 1의 탐지 결과에 영상 강화 과정을 추가하여 YOLO 디텍터로 표적을 탐지했다. YOLO 디텍터는 Faster R-CNN(convolutional neural network)과는 달리 통합된 객체 검출 모델로, 구성이 간단하며 전체 영상을 직접 학습하여 빠른 속도와 우수한 탐지 성능을 가지고 있어 다양한 영상의 디텍터로 활용되고 있다^[9]. 본 연구에서 사용된 버전은 2.0이며, 외부요인으로 인한 변수를 최소화하기 위하여 Matlab에서 제공되는 deep learning toolbox를 활용하여 학습 및 성능평가를 진행하였다. 그림 8은 YOLO v2의 네트워크 구조를 나타내며, 입력과 출력 사이의 레이어를 계층적으로 보여준다^[10].

그림 8. | Fig. 8. YOLOv2 네트워크 구조도 | The network architecture of YOLOv2.

Download Original Figure

학습 및 평가에 사용된 영상은 총 10,000장으로 학습 60 %, 검증 10 % 및 평가 30 %로 구분하여 실험을 진행하였다. 학습용 데이터 셋은 Matlab 시뮬레이션을 통해 비트 신호를 생성 후 MLE를 적용하여 생성하였으며, 상세 조건은 표 4와 같다.

실험의 성능을 표적의 개수에 따라 비교하기 위해 4개의 조건을 비교하였으며, 이때 표적의 속도와 거리는 표 4의 조건 내에서 임의로 생성하였다. 이때 거리는 일식(eclipsing)이 발생하지 않는 거리를 사용하였으며, SNR은 20 dB로 고정하였다. 또한 학습시에는 표적의 위치와 속도를 라벨링하였으며, YOLO 디텍터의 성능 평가 시에는 표적의 개수를 모르는 환경에서 탐지를 수행하고 결과를 확인하였다. 표적 검출 성능은 평균 정확도 AP(average precision)를 사용하였다. 정확도란 시험평가용 영상에서 검출기가 검출한 결과에서 정검출(true positive)의 비율을 의미하며, 사용된 시험평가 영상의 평균 정확도를 계산하여 탐지 성능을 비교하였다.

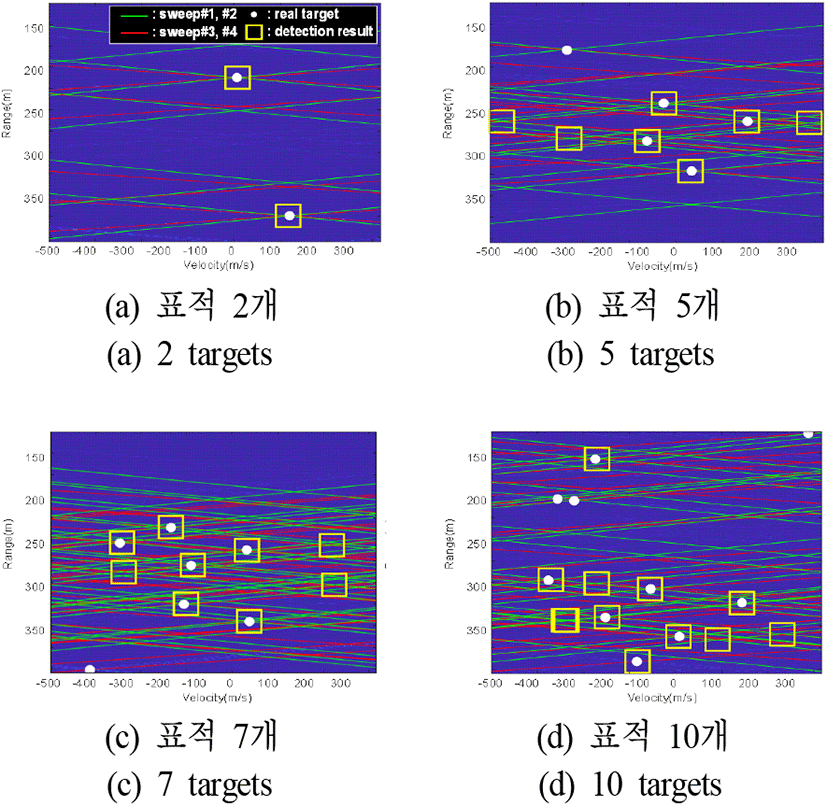
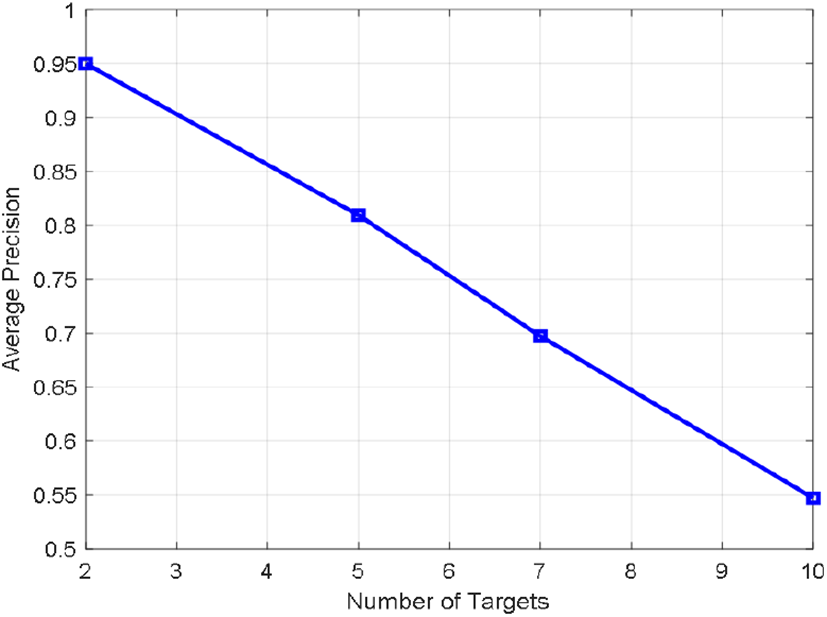
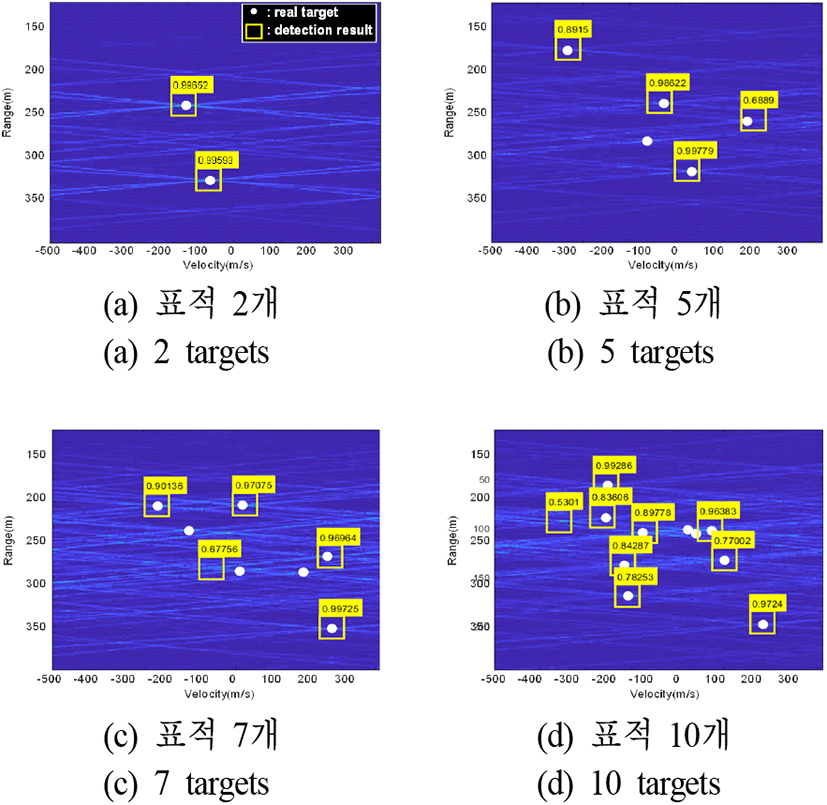
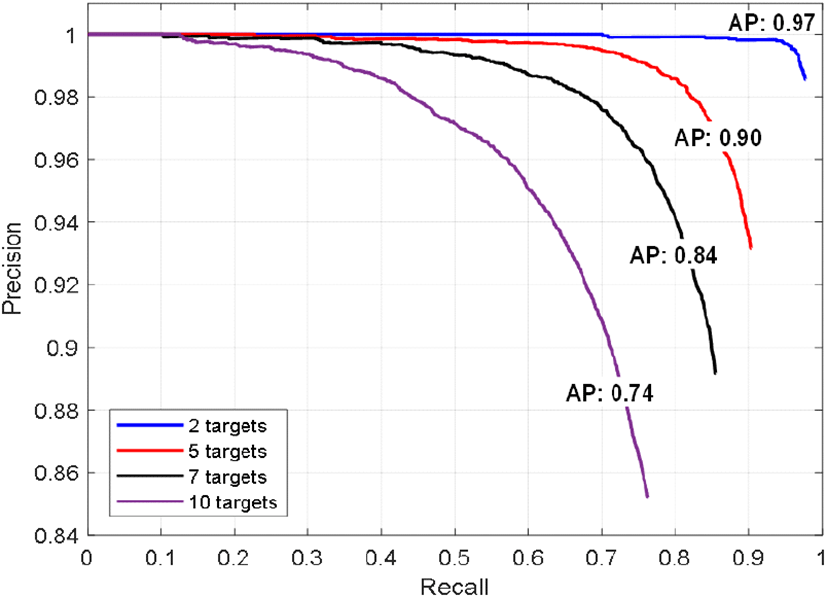
그림 9는 실험 1에서 표적의 개수를 가변하며, 탐지한 결과를 보여준다. 그림에서 흰색 원은 실제 표적의 거리와 속도를 나타내며, 노란색 사각형은 탐지 결과를 나타낸다. 그림 10은 표적의 개수에 따른 평균 정확도를 보여준다. 실험 결과에서는 표적 개수가 증가함에 따라 표적의 검출률이 감소하는 것을 확인하였다. 이는 표적 개수의 증가로 인해 표적 신호뿐만 아니라, 스퓨리어스 신호도 함께 증가하여 허상 표적이 생성되고, 이는 표적의 탐지 성능을 저하시켰다.

그림 9. | Fig. 9. 표적 후보군 선정 결과(실험1) | The result of detecting the target by the intersection of the line (experiment 1).

Download Original Figure

그림 10. | Fig. 10. 실험 1에 대한 표적 개수-평균 정확도 다이어그램 | Number of targets–AP diagram for experiment 1.

Download Original Figure

실험 2에서는 표적 위치가 라벨링된 영상을 학습하여 기계 학습 기반 객체 탐지 알고리즘의 성능을 평가하였다. 탐지 결과는 그림 11과 같으며, 탐지 결과는 표적으로 예측되는 영역인 노란색 박스과 점수(confidence score)로 보여준다. 여기서 confidence score란 해당 박스 내에 표적이 존재할 확률을 의미한다^[11]. 그림 12는 recall과 precision 관계를 나타낸다. 실험 2의 결과는 실험 1과 유사한 경향성을 보여준다. 표적 개수가 2개일 때 평균 정확도가 가장 높았으며, 표적 개수가 증가함에 따라 평균 정확도가 감소한다.

그림 11. | Fig. 11. YOLO 디텍터에 의한 표적 탐지 결과(실험 2) | Target detection by YOLO detector (experiment 2).

Download Original Figure

그림 12. | Fig. 12. 실험 2에 대한 recall-precision 다이어그램 | Recall-precision diagram for experiment 2.

Download Original Figure

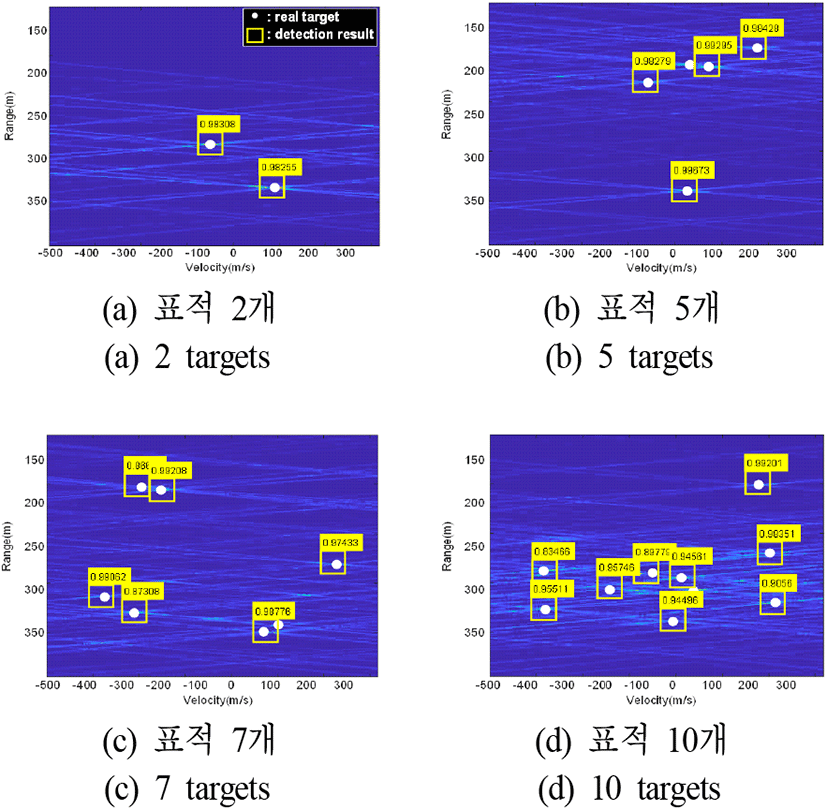
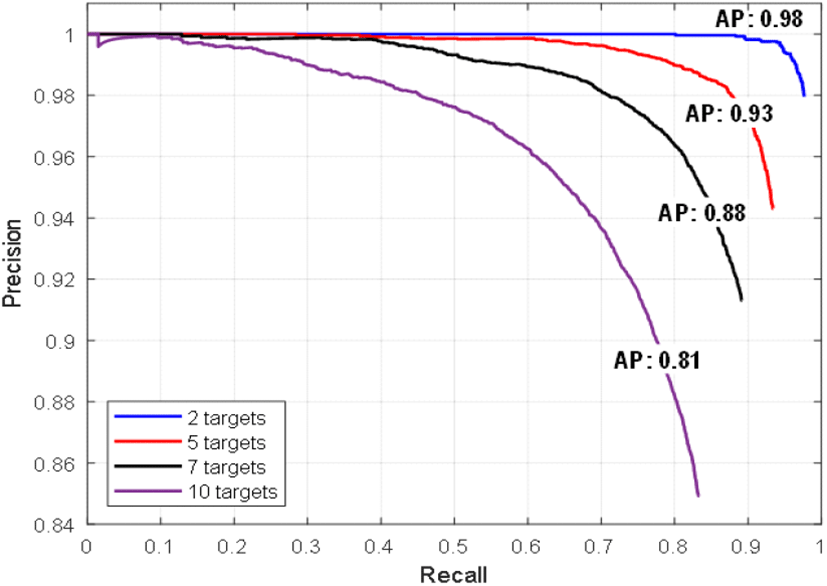
실험 3은 2-2절의 표적 후보군 위치의 영상을 강화한 후 학습하고 결과를 비교하였다. 그림 13은 실험 3의 표적 탐지 결과이며, 그림 14는 recall과 precision 관계이다. 표적의 개수가 증가함에 따라 탐지 확률은 감소하였으며, 표적 10개의 평균 정확도는 81 %로 가장 낮았다.

그림 13. | Fig. 13. 표적 후보군으로 영상을 강화 후 YOLO 디텍터로 표적 탐지 결과(실험3) | Target detection result with YOLO detector after image enhancement with line detector (experiment 3).

Download Original Figure

그림 14. | Fig. 14. 실험 3에 대한 recall-precision 다이어그램 | Recall-precision diagram for experiment 3.

Download Original Figure

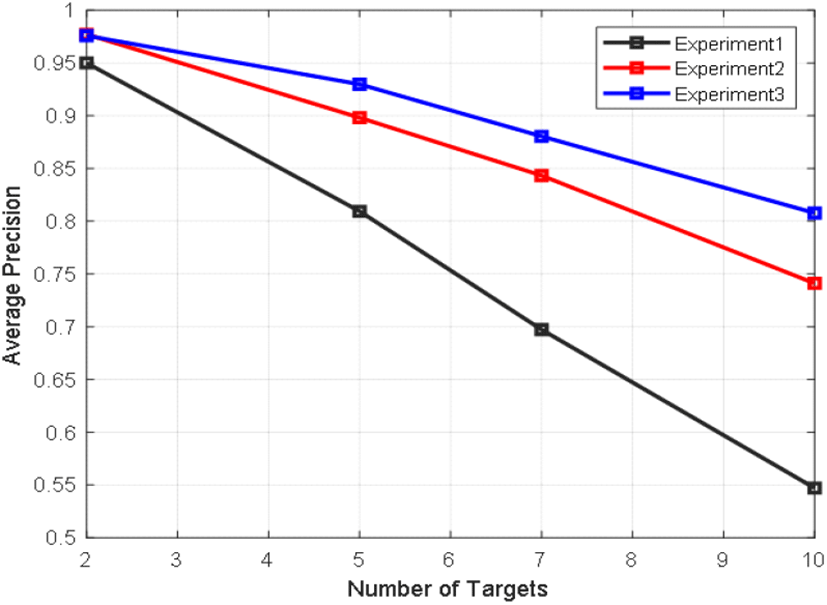
3가지 실험 결과를 비교한 그림 15는 각각의 실험의 평균 정확도를 보여준다. 실험 1은 기계 학습을 적용하지 않은 경우로, 표적의 개수가 증가함에 따라 탐지 확률이 크게 감소하여 5개 표적의 평균 정확도는 81 %이며, 10개 표적에서는 55 %이다. 실험 3은 윈도우 직선 검출기와 기계 학습을 함께 적용한 경우로, 5개 표적에서도 93 %의 평균 정확도를 보여주었으며, 표적 개수와 관계없이 탐지 성능이 가장 우수했다. 또한, 표적 개수가 증가할수록 다른 실험과의 성능 차이가 크게 나타났다. 실험 2는 실험 1과 실험 3의 중간 성능을 보여주었다. 이러한 결과로 볼 때, 표적 개수가 적은 경우에는 상대적으로 연산량이 적은 실험 1의 방법이 효율적이었으며, 표적의 개수가 5개 이상인 경우에는 실험 3의 방법을 사용하는 것이 가장 효과적이었다.

그림 15. | Fig. 15. 실험 1~3의 표적 개수-평균 정확도 다이어그램 비교 | Number of targets-AP diagram for experiment 13.

Download Original Figure

Ⅳ. 결 론

본 연구에서는 고해상도 레이다에서 널리 사용되는 FMICW 레이다의 단점인 제한된 탐지 영역과 다중 표적 탐지 성능을 개선하기 위해 스퓨리어스의 주기적인 특성과 기계 학습 기반의 디텍터인 YOLO를 사용하여 다중 표적의 탐지성능을 확인하였다. 실험 결과, 5개 이하의 표적에서는 93 % 이상의 탐지 성능을 달성하였으며, 10개의 표적에서는 81 %의 탐지 성능을 보였다. 이로써 다양한 속도와 거리에 대해 효과적으로 다중 표적을 탐지할 수 있음을 확인하였다. 또한, 이 연구를 활용함으로써 FMICW를 탐지와 추적에 모두 사용할 수 있는 장점을 얻을 수 있다. 이는 레이다의 하드웨어를 단순화시킬 수 있어 제작 비용을 절감할 수 있다. 더불어 앞으로의 연구 방향으로는 FMICW 레이다의 주파수 변조 기울기를 다양하게 변경하거나 직선 검출기의 성능을 향상시킴으로써 레이다의 다중 표적 탐지 성능을 높일 것으로 기대된다.