이동 표적 탐지 및 추적을 위한 단일 채널 기반 고해상도 위성 SAR 영상 모드 구현

Ⅰ. 서 론

합성 개구 레이다(synthetic aperture radar)는 주․야간, 날씨 등과 관계없이 관심 지역 및 표적에 대한 고해상도 레이다 영상을 획득할 수 있어 민수 및 국방 감시 목적으로 널리 활용된다^[1],[2]. 대부분의 합성 개구 레이다 영상 신호처리 알고리즘은 정지 표적을 가정하고 있으며, 이동 표적에 대해서는 거리 및 방위 방향 속도에 따른 도플러 편이에 의해 방위 방향의 위치 천이 및 에너지 퍼짐 현상을 일으킨다^[3]. 따라서 합성 개구 레이다 영상에 존재하는 이동 표적을 탐지하고, 영상정보를 획득하기 위해서는 지상 이동 표적 탐지 기법(ground moving target indication) 방식의 추가적인 알고리즘이 요구된다. 대표적인 지상 이동 표적 탐지 기법으로는 클러터 억제 기반의 STAP (space-time adaptive processing), DPCA(displaced phase centre antenna), ATI(along-track interferometry) 기법이 있다^[4]~[15]. 그러나 대부분의 지상 이동 표적 탐지 기법들은 높은 연산량을 요구하는 문제점이 있으며, 주로 다중 채널 기반으로 수행된다. 단일 채널 합성 개구 레이다 시스템에서는 긴 합성 개구 시간 및 움직임 보상 오류로 인하여 이동 표적 탐지 성능이 감소한다. 이에 따라, 단일 채널 합성 개구 레이다에서는 2차 키스톤 형성(second-order keystone transfomatting)과 허프 변환(hough transform)을 활용하는 방안^[16]과 압축 센싱을 활용한 방식^[17],[18]이 제안된다. 또한 최근에 낮은 연산량을 통해 이동 표적을 탐지하는 방안으로 이동 표적의 그림자를 추적하는 방안^[19]과 부분 조리개(sub-aperture)를 활용하는 방안이 제시된다^[20],[21].

부분 조리개 기반 이동 표적을 탐지하는 경우, 관측 시간을 짧게 하여 이동 표적의 퍼짐 현상을 감소시켜 포커싱 능력이 향상된다. 또한 원형 운용(circular) 및 스폿(spotlight) 모드로 신호를 수집하여 관심 지역 및 표적의 지속적인 관측을 수행하는 경우, 부분 조리개를 연속적으로 나열한 다중 프레임을 통해 직관적인 이동 표적 식별이 가능하며, 이를 통해 이동 표적의 속도, 경로 등의 정보를 얻을 수 있다.

부분 조리개의 다중 프레임을 활용하여 이동 표적을 탐지한 대표적인 사례로 ICEYE가 있다. ICEYE는 참고문헌 ^[21]에서 긴 관측 시간과 선박의 이동 속도로 인해 영상의 초점이 안 맞는 현상이 발생하였고, 부분 조리개의 다중 프레임을 통해 이동 표적의 초점을 맞춘다.

따라서, 본 논문에서는 단일 채널 SAR 시스템 기반 이동 표적 탐지를 수행하기 위한 시뮬레이터를 구현한다. 또한 제작된 시뮬레이터를 기반으로 이동 표적 영상을 형성하고, 부분 조리개 기반 다중 프레임을 연속적으로 나타내어 이동 표적 탐지 사례를 모사한다.

II. 모의실험 설계

2-1 신호 모델링

본 모의실험에서 합성 개구 레이다는 관심 장면에 대한 지속적인 관측을 수행하고, 높은 해상도의 영상 획득을 위해 그림 1과 같이 스폿 모드를 통한 신호 수집을 수행한다. 스폿 모드는 빔 조향을 통해 비교적 긴 시간 동안 장면을 관측한다. 이에 따라, 스트립맵 모드와 다르게 안테나 빔 폭이 방위 해상도를 제한하지 않으며, 긴 관측 시간을 통한 높은 방위 해상도를 구현할 수 있다.

그림 1. | Fig. 1. 스폿 모드 SAR | Spotlight mode SAR.

Download Original Figure

스폿 모드에서 송신 신호가 식 (1)과 같을 때 정지 표적의 수신 신호는 식 (2)와 같이 나타낼 수 있다.

$$s_t(n,t)=A_0\exp \left(j2\pi f_{c}t+j\pi \gamma {(t-nT)}^2\right)$$

(1)

$$\begin{array}{c}{s}_r(n,t)=a_{t}rect\left(\frac{\widehat{t}-t_d}{T_p}\right)\\ \cdot \exp \left(j2\pi f_c\left(t-t_d\right)+j\pi \gamma {\left(\widehat{t}-t_d\right)}^2\right)\end{array}$$

(2)

식 (2)에서 t_d는 2R_t/c로 지연 시간을 나타내며, R_t는 플랫폼에서 표적까지의 거리를 나타낸다.

표적이 거리 방향으로 v_r의 속도와 a_r의 가속도를 갖고 방위 방향으로 v_a 속도로 이동할 때, 표적의 위치는 식 (3)과 같이 나타낼 수 있다. 이때, 는 방위 시간을 나타낸다.

$$(x,y)=\left(x_0+v_r\eta +\frac{1}{2}{a}_{\text{r}}{\eta }^2,v_0+v_a\eta \right)$$

(3)

이동 표적으로 발생하는 위상 변화는 식 (4) 및 식 (5)와 같이 나타낼 수 있다. ν_ρ는 플랫폼의 속도, R₀는 장면 중심까지의 거리, f′은 순시 주파수와 중심 주파수의 차를 나타낸다.

$$\Phi \left(f^{\prime },\eta \right)=\frac{4\pi }{\lambda }\left(r(\eta )-\sqrt{R_0^2+{\left(v_p\eta \right)}^2}\right)$$

(4)

$$r(\eta )=\sqrt{{\left(R_0+x_0+v_r+\frac{1}{2}{a}_r{\eta }^2\right)}^2+{\left(y_0+v_a\eta +v_p\eta \right)}^2}$$

(5)

식 (4)는 테일러 급수 전개에 의해 식 (6)과 같이 나타낼 수 있으며, f₀는 중심 주파수를 나타낸다.

$$\Phi \left(f^{\prime },\eta \right)=\frac{4\pi }{\lambda }[x_0+x_0\frac{f^{\prime }}{f_0}-y_0\frac{v_p\eta }{R_0}+v_r\eta +\frac{1}{2}{a}_r{\eta }^2-\frac{v_a}{v_p}\frac{{\left(v_p\eta \right)}^2}{R_0}+\cdots ]$$

(6)

식 (6)에서 2, 3번째 항은 표적의 거리 및 방위 위치 정보를 생성하며, 4번째 항은 표적의 거리 방향 속도로 인한 방위 방향 천이를 일으킨다. 그리고 5, 6번째 항은 표적 에너지의 방위 방향 퍼짐 현상을 야기한다^[22].

식 (7)~식 (11)은 ΔR_shift를 산출하는 과정을 나타내며, N_α는 방위 샘플 수, PRF는 펄스 반복 주파수, T_α는 관측 시간, ΔN 은 방위 천이 샘플 수, f_dc는 도플러 중심 주파수, L_a는 방위 개구 크기, d_a는 방위 샘플 간격을 나타낸다.

$$N_a=PRF\cdot T_a=PRF\cdot \frac{\lambda R_0}{L_a{v}_p}$$

(7)

$$\Delta N=\frac{f_{dc}}{PRF}\cdot N_a=\frac{2v_r\cdot N_a}{\lambda \cdot PRF}$$

(8)

$$\Delta N=\frac{2V_t{R}_0}{L_a{V}_p}$$

(9)

$$d_a=\frac{L_a}{2}$$

(10)

$$\Delta R_{\text{shift }}=\Delta N\cdot d_a=\frac{v_r{R}_0}{v_p}$$

(11)

따라서 거리 방향 속도로 인한 방위 방향 천이(ΔR_shift)는 $\frac{v_r{R}_0}{v_p}$만큼 발생하는 것을 식 (11)를 통해 알 수 있다.

방위 위상 오차가 A일 때, 방위 중심에서 끝지점까지 2πA 라디안의 진폭 주기를 갖는 신호에서 위상 오차(ϕ(t)) 및 미분값(ϕ(t))은 식 (12) 및 식 (13)과 같이 나타낼 수 있다.

$$\varphi (t)=\frac{2\pi A{\eta }^2}{{\left(T_a/2\right)}^2}=\frac{8\pi A{\eta }^2}{T_a^2}$$

(12)

$$\dot{\varphi }(t)=\frac{4\pi A\eta }{{\left(T_d/2\right)}^2}$$

(13)

이때 관측 시간(T) 동안 선형 위상은 ±8 π 라디안의 편차를 가지며, 주파수 영역에서 2 π 라디안은 영상에서 방위 해상도(ρ_a)만큼 이동하기 때문에 퍼짐 현상은 -4Aρ_a에서 4Aρ_a까지 8Aρ_a만큼 발생한다.

따라서 방위 속도로 인한 방위 위상 오차(A)와 방위 해상도(ρ_a) 식 (14)를 통해 방위 속도로 인한 블러링(ΔR_smear)은 2v_aη만큼 발생하는 것을 알 수 있다^[22],[23].

$${\rho }_a=\frac{\lambda R_0}{2v_p\eta }$$

(14)

$$A=\frac{v_a{v}_p{\eta }^2}{2\lambda R_0}=\frac{v_a\eta }{4{\rho }_a}$$

(15)

$$\Delta R_{\text{smear }}=8A\cdot {\rho }_a=2v_a\eta$$

(16)

2-2 다중 프레임 구조 기반 이동 표적 속도 추정

본 논문에서는 이동 표적의 블러링을 감소시켜 이동 표적을 탐지 및 추적하기 위해 그림 2의 구조를 제안한다. 이동 표적의 블러링은 관측 시간에 비례하므로, 제안 방식은 부분 조리개를 기반으로 관측 시간 및 블러링을 감소시켜 이동 표적 탐지를 수행한다. 이후 연속되는 다중 프레임 간의 변화를 통해 이동 표적을 시각적으로 추적 가능하며, 이동 표적의 이동 거리 및 프레임 산출 시간을 활용하여 이동 속도를 추정할 수 있다. 제안 방식은 다중 채널에서 수행되는 영상 정합 과정을 포함하지 않아 간단한 과정을 통해 이동 표적 탐지 및 추적이 가능하다.

그림 2. | Fig. 2. 부분 조리개를 활용한 이동 표적 탐지 및 추적 순서도 | Flowchart of moving target indication & tracking based on sub-aperture processing.

Download Original Figure

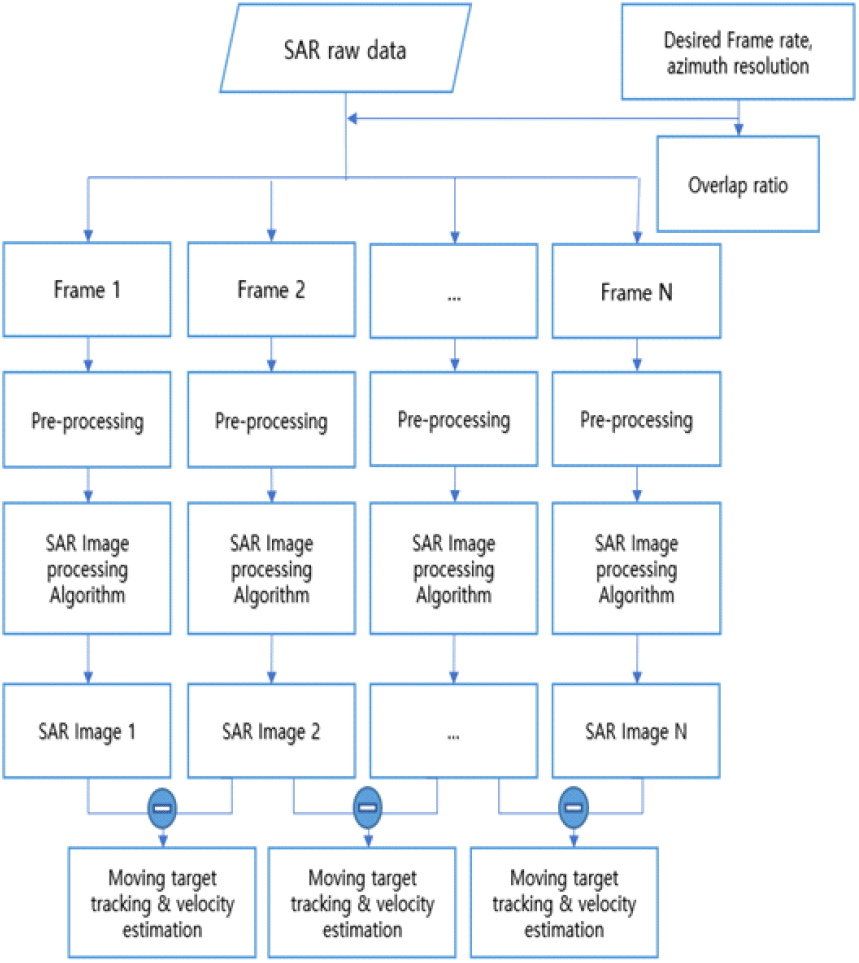
부분 조리개를 활용하여 다중 합성 개구 레이다 영상 프레임을 형성할 경우, 이동 표적은 프레임에 따라 서로 다른 위치에서 생성된다. p_0,rg, p_0,azi가 표적의 초기 위치라고 할 때, 위치 천이가 발생한 이동 표적의 n번째 프레임에서의 거리 방향 및 방위 방향 위치, $p_{\text{false, rg}}^n,p_{\text{false },avi}^n$는 각각 식 (17)~식 (20)과 같이 나타낼 수 있다. Δθ_a는 합성 개구 면적 각도를 나타낸다.

$$p_{\text{fallse,rg }}^n=p_{0,rg}+v_r\cdot T_f\cdot n+\frac{\Delta {\theta }_a}{4}$$

(17)

$$p_{\text{false,avi }}^n=p_{0,avi}+v_a\cdot T_f\cdot n+\frac{v_r\cdot R_0}{v_p}$$

(18)

$$p_{\text{fallse,rg }}^{n-1}=p_{0,rg}+v_r\cdot T_f\cdot (n-1)+\frac{\Delta {\theta }_a}{4}$$

(19)

$$p_{\text{false,asi }}^{n-1}=p_{0,avi}+v_a\cdot T_f\cdot (n-1)+\frac{v_r\cdot R_0}{v_p}$$

(20)

T_f 프레임이 생성되는 시간 간격을 나타내며, 각 프레임 간의 표적 속도는 일정하게 유지된다고 가정한다. n번째 프레임과 (n−1)번째 프레임에서의 생성된 표적의 위치 편차는 식 (21) 및 식 (22)와 같다.

$$p_{\text{false,rg }}^n-p_{false,rg}^{n-1}=v_r\cdot T_f$$

(21)

$$p_{\text{false,avi }}^n-p_{\text{false,avi }}^{n-1}=v_a\cdot T_f$$

(22)

이 정보는 실제 표적의 위치와는 다르며 (n−1), n번째 프레임에서의 표적의 실제 거리 위치 $p_{\text{true,rg }}^n$ 와 방위 위치 $p_{\text{true,avi }}^n$ 는 식 (23)~식 (26)과 같이 표현된다.

$$p_{\text{true,rg }}^n=p_{0,rg}+v_r\cdot T_f\cdot n$$

(23)

$$p_{\text{ture,avi }}^n=p_{0,avi}+v_a\cdot T_f\cdot n$$

(24)

$$p_{\text{true,rg }}^{n-1}=p_{0,rg}+v_r\cdot T_f\cdot (n-1)$$

(25)

$$p_{\text{true,axi }}^{n-1}=p_{0,axi}+v_a\cdot T_f\cdot (n-1)$$

(26)

따라서 n번째 프레임과 (n−1)번쨰 프레임에서의 표적의 실제 이동 거리는 식(27) 및 식 (28)과 같다.

$$p_{\text{true,rg }}^n-p_{\text{true,rg }}^{n-1}=v_r\cdot T_f$$

(27)

$$p_{\text{true,asi }}^n-p_{\text{true,asi }}^{n-1}=v_a\cdot T_f$$

(28)

관측 시간 동안 표적의 속도가 일정하다고 가정하면, 다중 프레임에서 위치 편이가 발생한 표적 이동 거리는 실제 표적의 이동 거리와 같다고 할 수 있다. 따라서 각 프레임에서 단위 시간당 표적의 이동 거리를 측정하여 속도를 추정할 수 있다. u_r,est, u_a,est 는 거리 방향 추정 속도, 방위 방향 추정 속도를 나타낸다.

$$v_{r,est}=\left(p_{f\text{ false,rg }}^n-p_{\text{false,rg }}^{n-1}\right)/T_f$$

(29)

$$v_{\text{a,est }}=\left(p_{\text{false },asi}^n-p_{\text{falles,asi }}^{n-1}\right)/T_f$$

(30)

부분 조리개의 관측 시간을 줄일 경우, 방위 방향 퍼짐 현상을 줄이는 효과가 있으나, 방위 해상도의 저하가 발생한다. 이러한 해상도 저하에 의해 관찰 가능한 이동 표적의 최저 속도는 올라간다. 일반적으로 거리 및 방위 방향 속도로 인한 위치 변위는 블러링을 포함한 합성 개구 레이다 영상의 해상도보다 커야 한다. 각 부분 조리개에서의 표적의 거리 방향 이동 편차는 거리 해상도보다 커야 하며, 식 (31) 및 식 (32)와 같은 조건을 만족해야 한다. c는 빛의 속도, B는 대역폭을 의미한다.

$$v_r\cdot T_f\ge \frac{c}{2B}$$

(31)

$$\frac{c}{2B\cdot T_f}\le v_r$$

(32)

반면 표적의 방위 방향 이동 편차는 방위 방향 블러링보다 커야 하며, 식 (33) 및 식 (34)와 같은 조건을 만족해야 한다.

$$2v_a\cdot T_f\ge \frac{\lambda }{2\Delta {\theta }_a}$$

(33)

$$\frac{\lambda }{4T_f\cdot \Delta {\theta }_a}\le v_a$$

(34)

T_f는 프레임 중첩이 적용되지 않았을 때의 관측 시간으로 N_p와 같으며, 식 (35)와 같이 표현된다. 이때 는 방위 샘플 수, f는 중심 주파수, PRF는 펄스 반복 주파수, R_c는 경사 거리, ρ_a는 방위 해상도를 나타낸다.

$$T_a=\frac{N_p}{PRF}=\frac{R_c\cdot c}{2{\rho }_a\cdot v_p\cdot f_c}$$

(35)

탐지할 수 있는 거리 방향의 최저 속도(v_r,min) 및 방위 방향의 최저 속도(v_a,min)는 식 (36) 및 식 (37)과 같이 나타낼 수 있다.

$$v_{r,\min }=\frac{c}{2B\cdot T_f}$$

(36)

$$v_{a,\min }=\frac{\lambda }{4\cdot T_f\cdot \Delta {\theta }_a}$$

(37)

ATI와 같은 지상 이동 표적 탐지 기법을 활용할 때는 더 미세한 표적의 변화도 탐지가 가능하지만, 주파수 영역에서 분할 후 영상 정합 및 위상 간섭 정보 분석을 수행하는 복잡한 과정을 거쳐야 한다. 따라서 빠른 표적의 변화는 다중 프레임 구조의 간단한 구조를 통해 탐지할 수 있으며 낮은 속도의 이동 표적 탐지를 위해서는 높은 해상도의 다중 프레임을 나열하는 비디오 SAR 모드의 구현이 필요하다.

부분 조리개 영상을 연속적으로 나열하여 이동 표적을 나타낼 때, 각 프레임 사이의 중첩을 활용하여 다중 프레임 사이의 연속성을 증가시킬 수 있다. 또한 부분 조리개 간의 중첩을 통해 활용하는 신호를 늘려 영상의 해상도를 향상시킬 수 있다. 그림 3은 부분 조리개의 다중 프레임 사이의 중첩을 적용했을 때를 나타내는 그림이다.

그림 3. | Fig. 3. 데이터 중첩에 따른 다중 프레임 구조 | Multi-frame structure based on data overlapping.

Download Original Figure

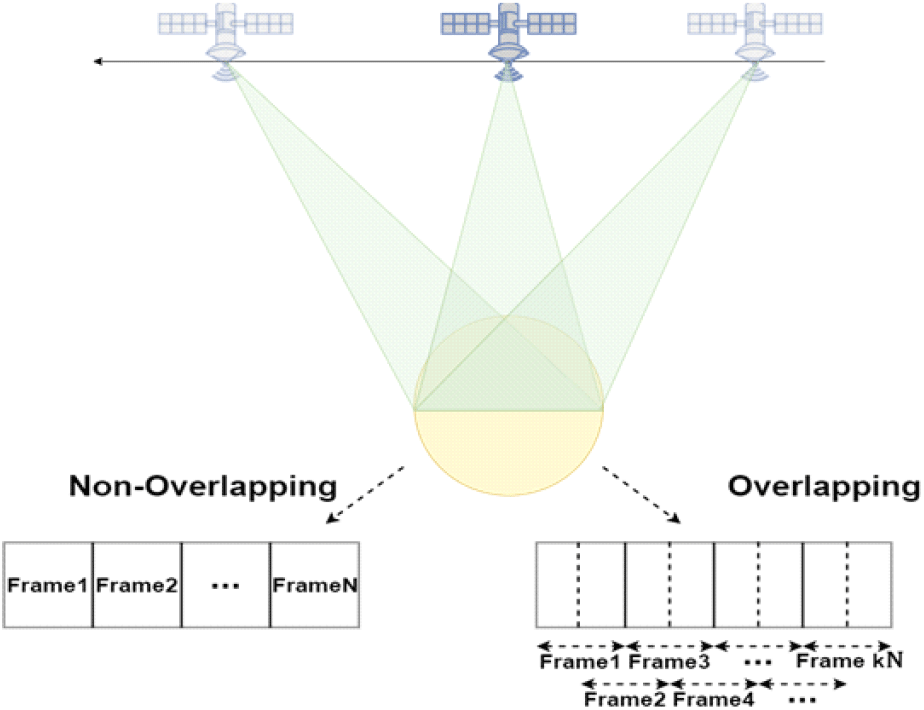
그림 3과 같이 다중 프레임 간의 중첩을 적용했을 때 산출되는 프레임률은 관측 시간 식 (35)의 역수와 중첩률(a)을 통해 표현할 수 있으며 식 (38)과 같이 나타낼 수 있다. 프레임률은 중첩되는 신호의 비율(a), 운용 거리(R₀), 플랫폼의 속도(v_p), 방위 해상도(ρ_a), 중심 주파수(f_c)의 영향을 받는다.

$$F=\frac{1}{T_a(1-\alpha )}=\frac{2{\rho }_a\cdot V_p\cdot f}{R\cdot c\cdot (1-\alpha )}$$

(38)

식 (38)을 통해 프레임 간 중첩 적용을 했을 때, 프레임이 생성되는 시간 간격(T_{f, ov1})은 T_a(1 − a)으로 나타낼 수 있다.

III. 모의실험

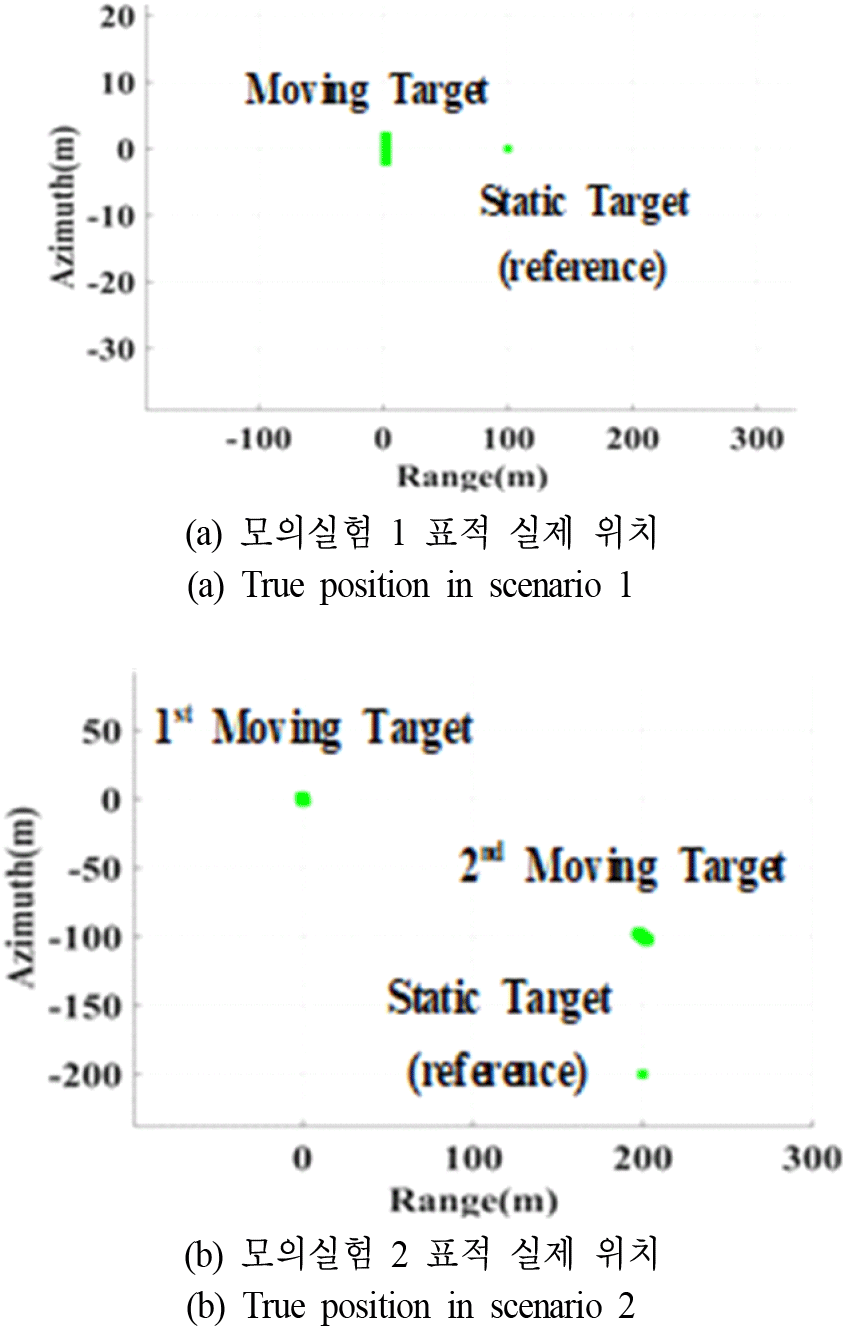
본 연구에서는 제작된 시뮬레이터를 활용하여 부분 조리개의 다중 프레임 구조로 이동 표적의 탐지 및 추적을 할 수 있음을 검증한다. 모의실험에서 플랫폼은 위성을 가정하여 입력 변수를 설정하였으며, 그림 1과 같은 기하 구조를 갖는다. 합성 개구 레이다 영상 처리 알고리즘으로는 PFA(polar format algorithm)을 활용하였다. 모의실험은 참고문헌 [21]에서의 ICEYE 실제 사례를 모사하여 단일 및 다중 표적 시나리오 2가지를 수행한다. 단일 이동 표적 모의실험은 다수의 점 표적으로 생성한 3 m×5 m 차량을 표적으로 가정하였으며, 총 관측 시간이 3.2 s이고, 부분 조리개 관측 시간은 0.4 s이다. 다중 이동 표적 모의실험은 다수의 점 표적으로 생성한 3 m×5 m 차량과 3 m×10 m 차량을 표적으로 가정하였으며, 총 관측 시간은 8 s이고 부분 조리개 관측 시간은 1 s이다. 그림 4를 통해 초기 모의 표적의 위치 및 형태를 볼 수 있다. 합성 개구 레이다 시스템 및 이동 표적의 변수는 표 1과 같다.

그림 4. | Fig. 4. 모의 실험 표적 초기 위치 및 형태 | Initial target configurations for simulation scenarios.

Download Original Figure

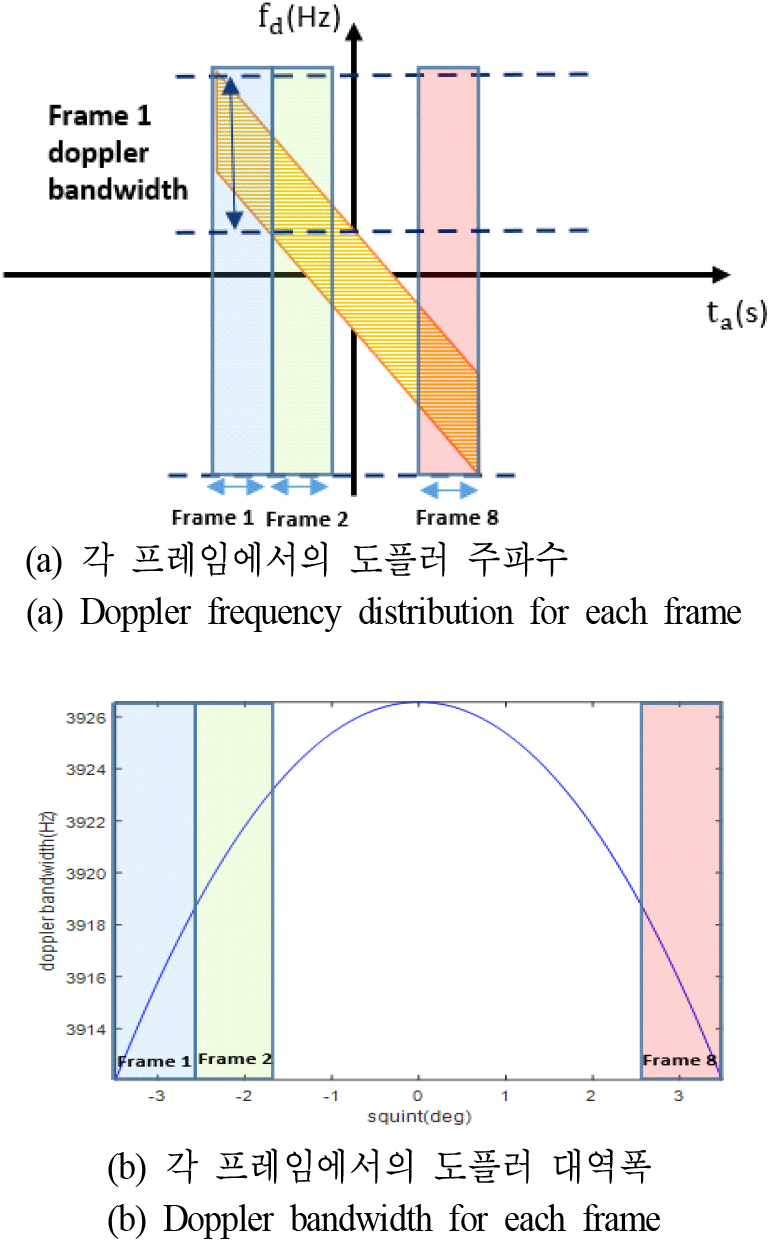
합성 개구 레이다는 스퀸트 각도에 따라 영상의 품질에 차이가 발생할 수 있다. 그러나 모의실험에서는 스퀸트 각도가 크지 않으며, 그림 5를 통해 스퀸트 각도에 따른 부분 조리개 사이의 도플러 밴드 폭의 차이가 작은 것을 확인할 수 있다. 또한 주파수 영역에서 합성 개구 레이다 영상처리를 수행하여 추가적인 스퀸트 각도에 대한 보상을 수행하지 않는다. 그러나 스퀸트 각도가 커졌을 경우, 추가적인 영상처리가 필요하다.

그림 5. | Fig. 5. 스퀸트 각도에 따른 최소 도플러 밴드 폭 | Minimum Doppler bandwidth with squint angle.

Download Original Figure

설계된 시뮬레이터의 성능을 확인하기 위해 거리 및 방위 방향 속도를 각각 입력하여 이동 표적의 방위 방향 천이 및 퍼짐 현상이 2-2절에서 제시한 방식으로 발생하는지 검증한다.

표적은 차량을 가정한 이동 표적과 참고를 위한 점 표적으로 설정하였다. 표 1의 시스템 변수를 통한 탐지 가능한 거리 및 방위 방향 최저 속도는 1.46 m/s, 2.92 m/s이다. 그림 6(a)는 이동 표적과 점 표적이 정지했을 때 영상을 나타낸다. 그림 6(b)는 거리 방향으로 −10 m/s의 속도만 설정했을 때 영상을 나타내며, 거리 방향 속도로 인하여 이동 표적의 방위 방향 이동이 발생한 것을 볼 수 있다. 이때, 방위 이동 거리는 약 1.07 km이다. 그림 6(c)는 방위 방향으로 30 m/s의 속도만 설정했을 때 영상으로 거리 방향 이동 없이 방위 방향의 퍼짐 현상이 발생한 것을 볼 수 있다. 위의 검증을 통해 시뮬레이터 성능을 확인했으며, 이를 바탕으로 단일 및 다중 이동 표적 탐지 모의실험을 수행한다.

그림 6. | Fig. 6. 거리 및 방위 단일 방향 속도에 따른 이동 표적 | Moving target images based on distance or azimuth each velocity.

Download Original Figure

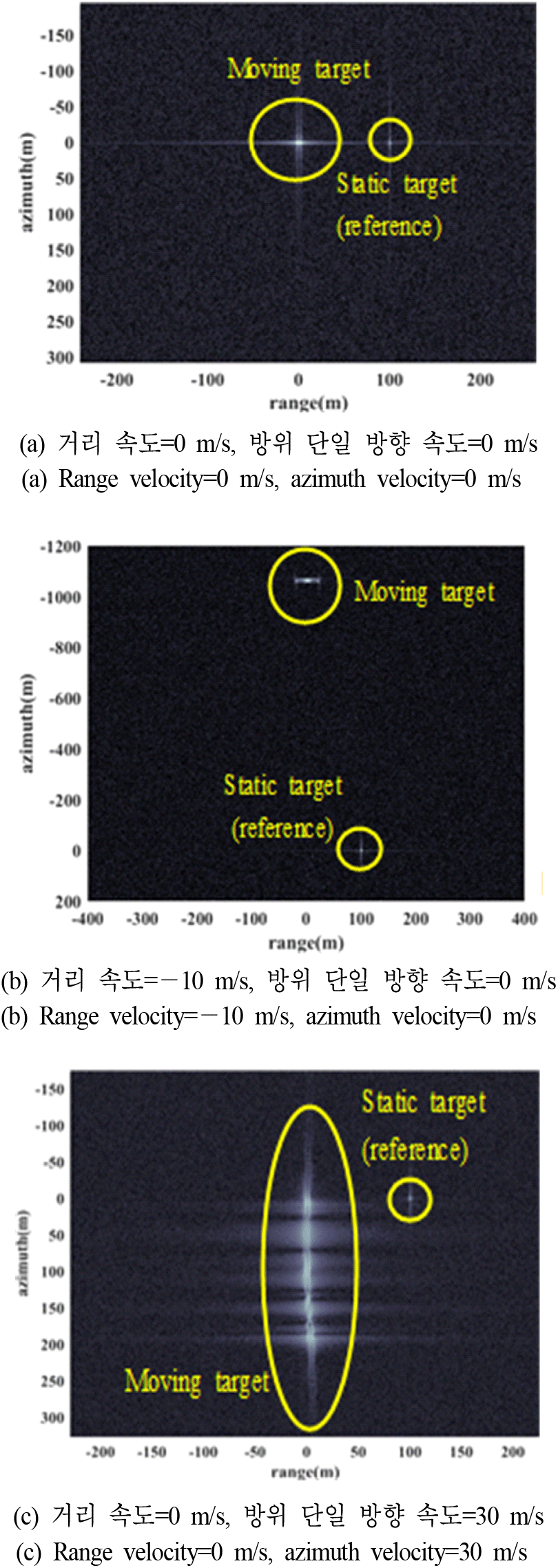
그림 7은 단일 이동 표적의 거리 및 방위 방향 속도를 각각 10 m/s, 30 m/s로 설정했을 때 모의실험 결과를 나타낸 것으로 이동 표적의 방위 방향 위치 천이 및 에너지 퍼짐 현상이 발생한 것을 볼 수 있다. 일반적으로는 이동 표적을 탐지하고 속도 추정을 수행하기 위해 STAP 및 ATI와 같은 지상 이동 표적 탐지 기법을 사용한다. 이와 달리, 본 논문에서는 부분 조리개의 멀티 프레임 구조를 통해 복잡성을 줄이고 이동 표적의 속도를 추정하는 과정을 보인다. 그림 8은 그림 7의 영상을 8개의 서브 프레임으로 나타낸 영상이다.

그림 7. | Fig. 7. 거리, 방위 방향 속도에 따른 단일 이동 표적 | Single moving target images based on both distance and azimuth velocity.

Download Original Figure

그림 8. | Fig. 8. 관측 표적물에 대한 연속 서브 프레임 영상 | Sub-frame image sequences of the target scene.

Download Original Figure

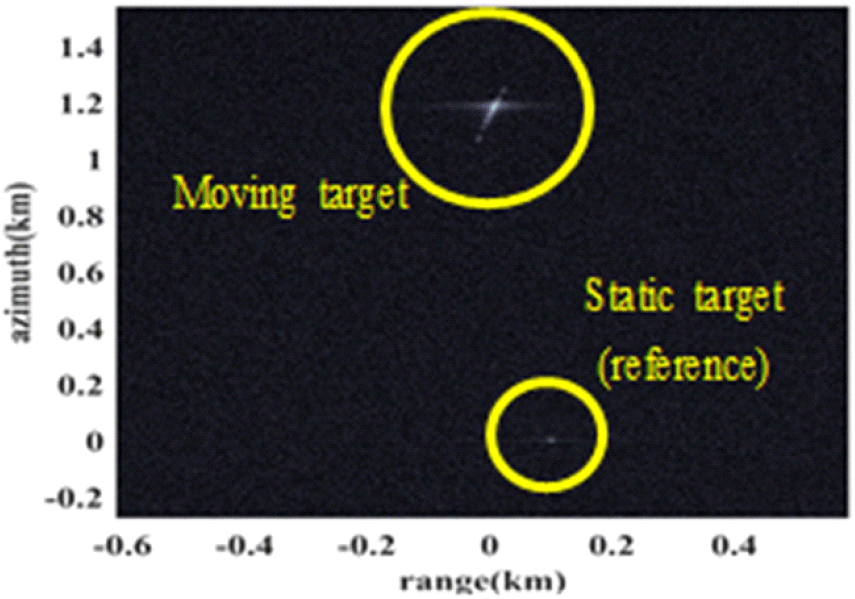
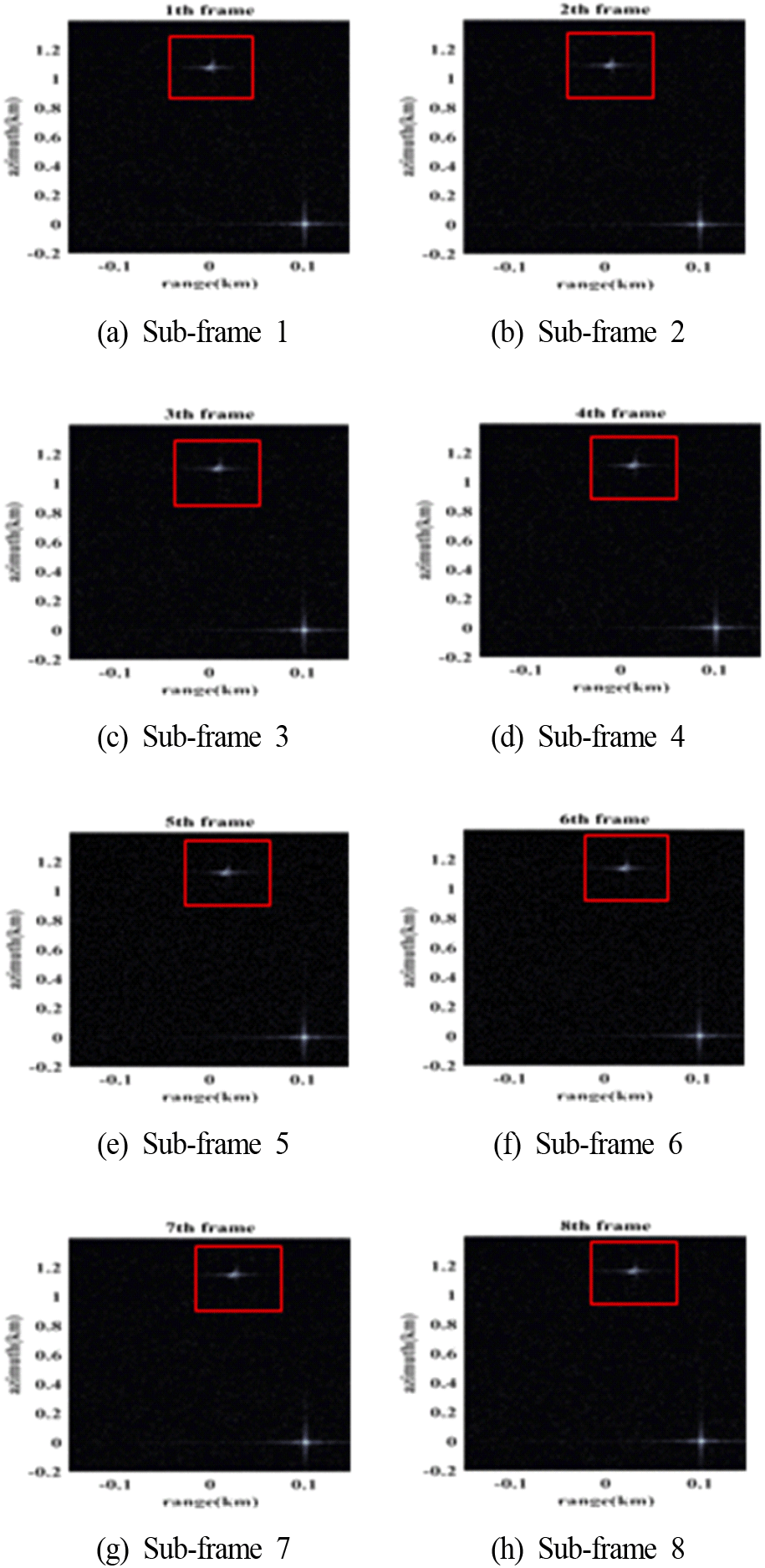
그림 8에서 정지 표적인 점 표적은 서브 프레임에서도 (100,0) m 위치에 정지해 있는 것을 볼 수 있으며 이동 표적이 연속적인 형상에서 벗어난 것을 확인할 수 있다. 또한 이전 프레임과 비교했을 때 상대적으로 표적이 이동한 것을 확인할 수 있으나, 영상의 크기가 이동 거리에 비해 상대적으로 크기 때문에 이동 표적을 확대하여 그림 9로 나타낸다. 본 논문에서는 이동 표적의 속도 추정을 목표로 하여 추가적인 처리를 통하여 표적의 초점을 맞추는 과정은 수행하지 않는다.

그림 9. | Fig. 9. 다중 서브 프레임 영상을 통한 이동 표적의 궤적 | Moving target trajectory analysis with multiple sub-frame images.

Download Original Figure

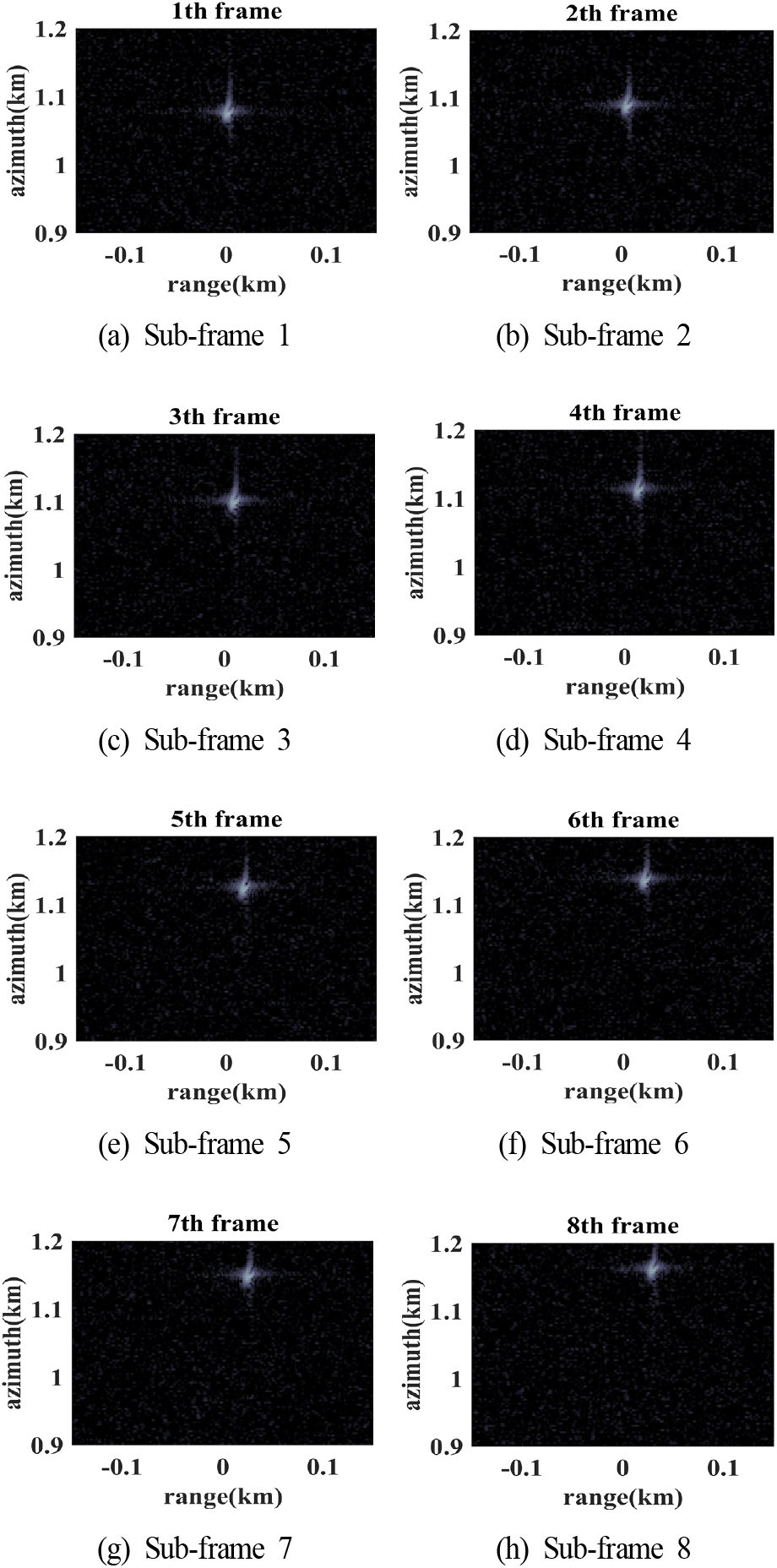
그림 9에서 1번째 서브 프레임에서 이동 표적의 위치는 대략 (0.79, 1,078.97) m이며 8번째 서브 프레임에서는 (29.22, 1159.86) m이다. 전체 관측 시간이 3.2 s이므로 방위 속도는 약 28.89 m/s이며 거리 방향 속도는 약 10.15 m/s로 설정한 속도와 비교하여 약 1 m/s 정도의 오차를 보인다.

각 프레임에 따른 이동 표적의 위치 및 속도는 표 2를 통해 확인할 수 있다. 표 2의 각 프레임에서 이동 표적의 위치는 표적의 중심을 기준으로 산출된 결과이며 속도는 각 프레임 시간 간격(T_f) 동안 표적의 이동 거리를 통해 나타낼 수 있다. 모의 실험에서는 각 프레임의 중첩을 적용하지 않아 프레임이 생성되는 시간 간격은 0.4 s이다. 표 2의 각 프레임 사이의 위치를 비교하여 산출한 속도에서 약간의 큰 오차가 발생한 구간이 있지만 전반적인 프레임에서는 약 1~2 m/s 거리 방향 속도 오차와 약 2~3 m/s 방위 방향 속도 오차를 보인다.

표 2를 실제 입력 속도와 비교하여 그래프로 나타내면 그림 10과 같이 나타낼 수 있으며 그림 11은 그림 9의 홀수번째 서브 프레임 4개를 활용하여 방위 방향으로 천이가 발생한 이동 표적의 경로를 보여준다.

그림 10. | Fig. 10. 단일 이동 표적의 거리, 방위 실제 및 추정 속도 비교 그래프 | Comparison of the estimated and true target velocities.

Download Original Figure

그림 11. | Fig. 11. 이동 표적의 실제 궤적과 추정 궤적 결과 비교 | Comparison of the estimated and true trajectories of the moving target.

Download Original Figure

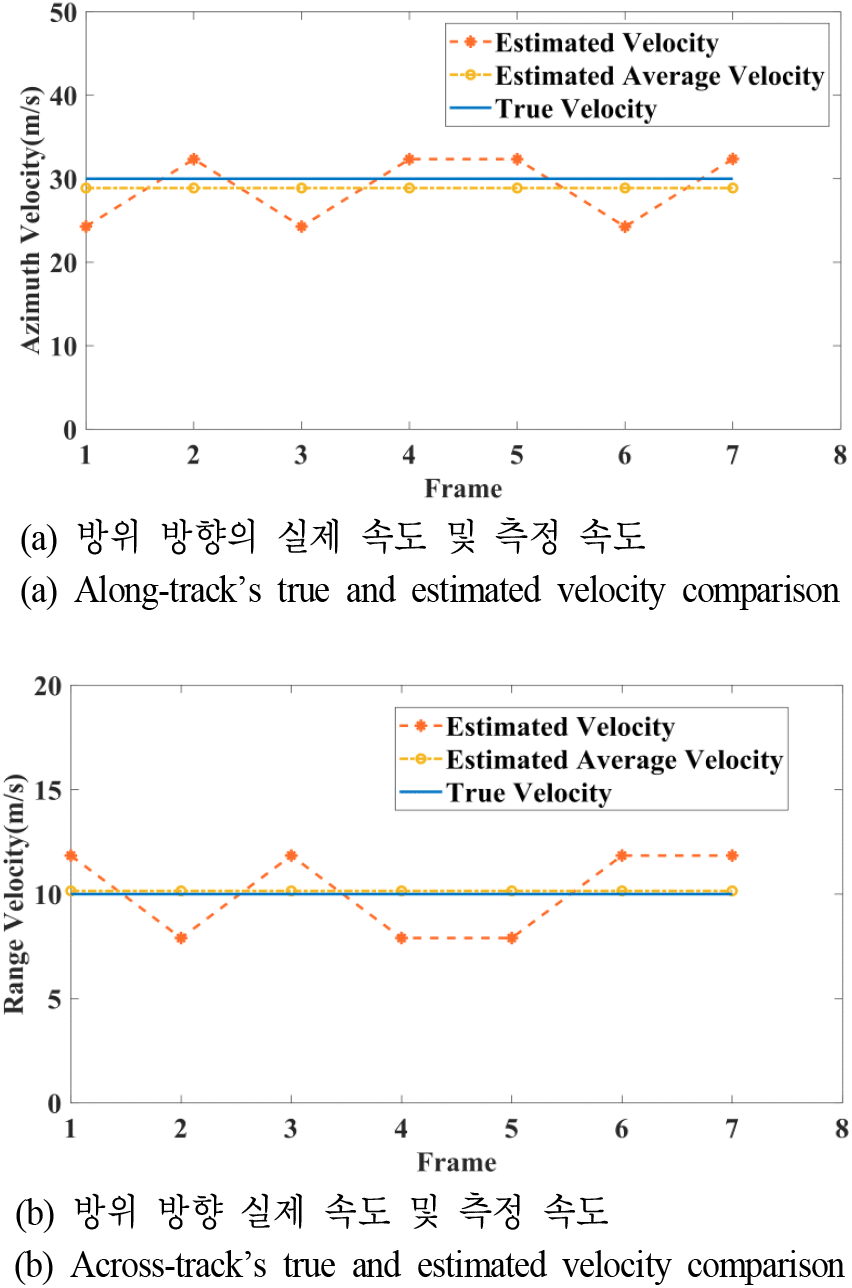
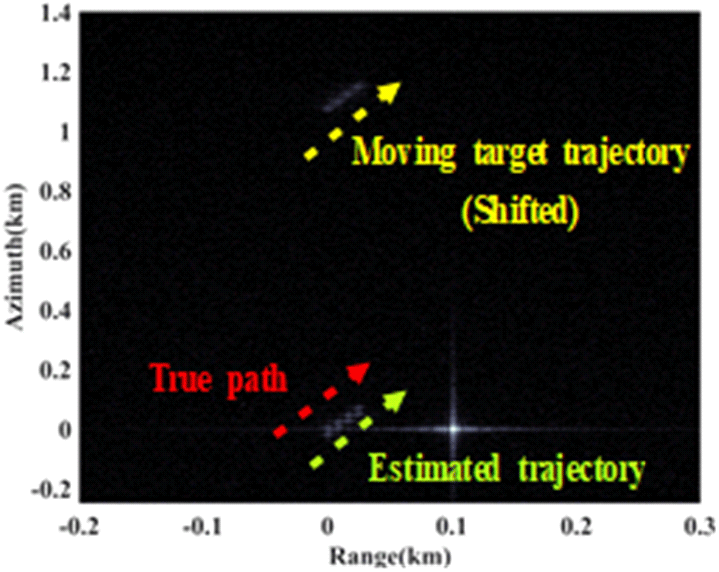
그림 11에서 나타낸 이동 표적의 경로는 각각 천이가 발생한 이동 표적의 경로(shifted), 실제 이동 표적의 경로(Truth), 보상 수행을 가정한 경로(Estimated path)를 나타낸다. 방위 방향 천이 보상은 표 2에서 산출된 거리 방향 평균 추정 속도(v_r,est)인 10.15 m/s를 기반으로 상기한 2절의 수식을 활용한 결과이다. 0.15 m/s의 속도 추정 오차가 발생하였으나, 평균적으로는 실제 표적의 경로와 근접한 결과를 보이는 것을 확인할 수 있다.

2번째 모의실험으로 다중 표적 시나리오를 가정하여 2개의 이동 표적을 추적하고 속도를 추정한다. 제안한 방식은 표적의 이동 위치를 추적하여 속도를 추정하는 방식으로 다수의 이동 표적도 각 표적에 대한 개별적 속도 추정이 가능하다. 그림 12는 2개의 이동 표적을 8초 동안 관측한 영상으로 빨간 원은 거리 방향 10 m/s, 방위 방향 30 m/s로 이동하는 3 m×5 m 차량 표적, 노란 원은 거리, 방위 방향으로 8 m/s로 이동하는 3 m×10 m 차량 표적을 보여주며, 초록 원은 정지한 점 표적을 보여준다.

그림 12. | Fig. 12. 서로 다른 속도를 갖는 다중 표적 관측 모의 실험 영상 | Simulated SAR image on multiple targets having different velocities.

Download Original Figure

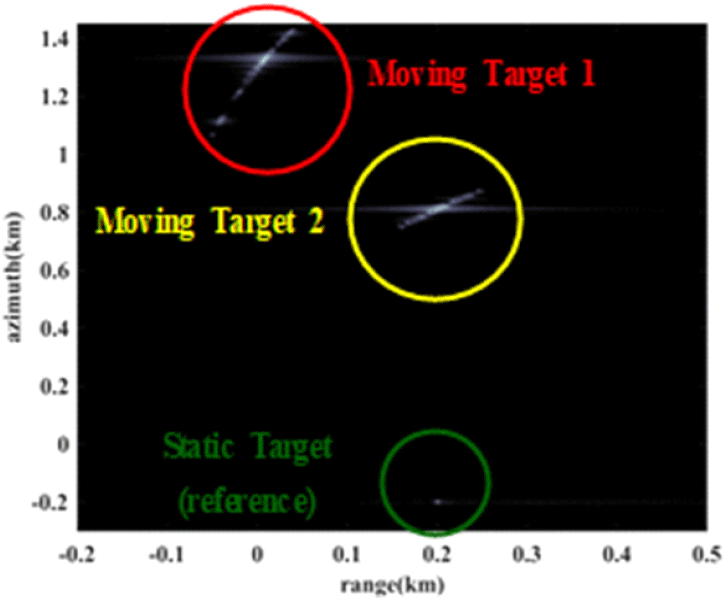
그림 13은 전체 관측 데이터를 1초 동안 관측한 부분 조리개 영상 8개로 나눈 후 그림 11과 같이 4개의 프레임을 활용하여 나타낸 결과이다. 그림 13을 통해 다중 이동 표적의 블러링 감소한 것을 볼 수 있고, 이동 표적을 추적할 수 있음을 확인할 수 있다.

그림 13. | Fig. 13. 다중 이동 표적에 대한 궤적 분석 결과 | Trajectories estimation of multiple moving targets.

Download Original Figure

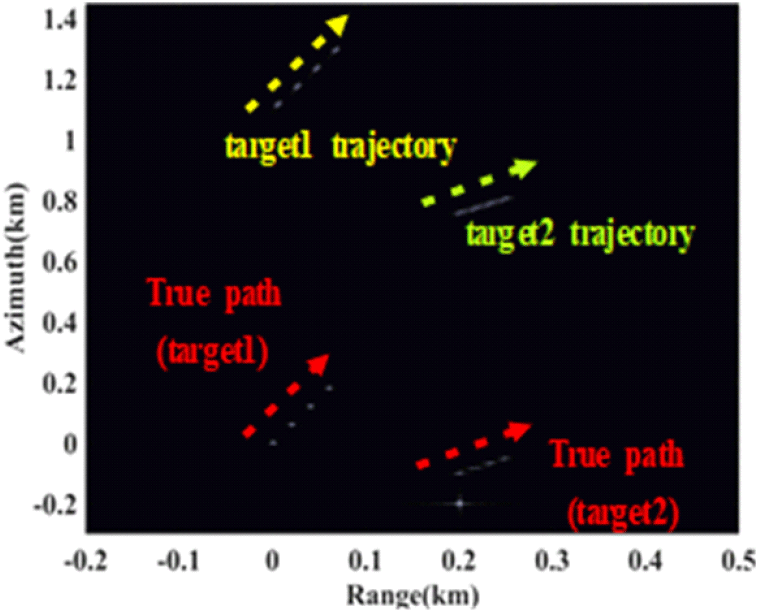
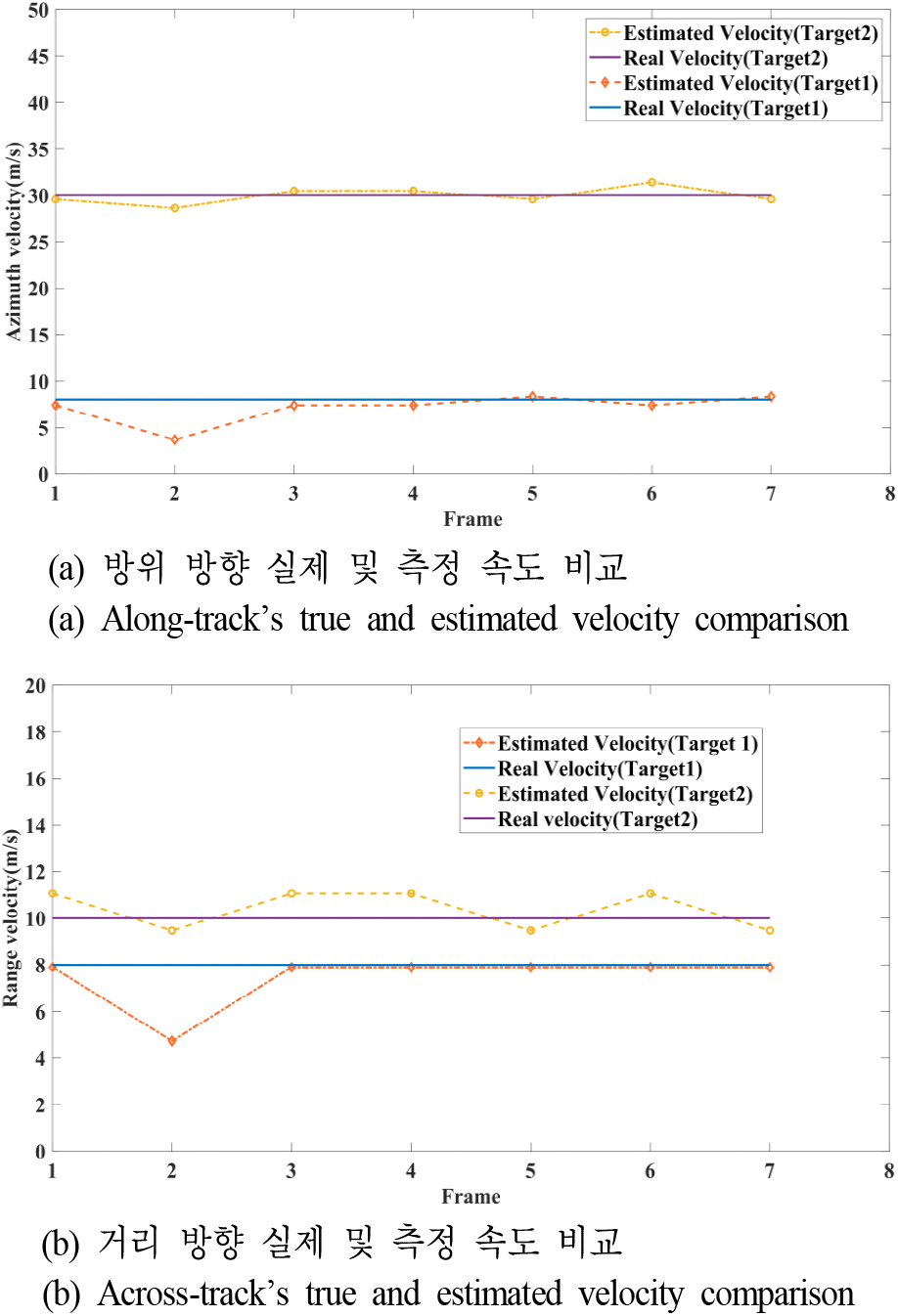
표 3 및 표 4는 각 부분 조리개 영상에서의 이동 표적 위치 및 추정 속도를 나타내며, 그림 14는 실제 속도와 추정 속도를 그래프로 나타낸 결과이다. 1번 표적의 추정 속도의 평균은 각각 거리 방향 10.38 m/s, 방위 방향 29.96 m/s로 설정 속도인 10 m/s와 30 m/s에 근접한 것을 확인할 수 있다. 2번 표적의 추정 속도의 평균은 각각 7.45 m/s, 7.13 m/s로 설정 속도인 8 m/s, 8 m/s와 근접하게 추정된다. 또한 다중 이동 표적 모의실험에서 단일 이동 표적 실험과 같은 속도를 갖는 빨간 원의 1번 표적을 확인했을 때, 부분 조리개의 관측 시간을 증가에 따라 방위 방향의 추정 속도 정확도가 향상된 것을 확인할 수 있다^[24]. 그러나 과도한 관측 시간 증가는 블러링 현상의 증가를 통한 영상 품질 저하를 일으킬 수 있어 교환(trade-off) 관계로 볼 수 있어 적절한 관측 시간 설정이 필요하다.

그림 14. | Fig. 14. 다중 이동 표적의 거리, 방위 실제 및 추정 속도 비교 그래프 | Comparison of the estimated and true velocities of the multiple moving targets.

Download Original Figure

IV. 결 론

일반적으로 합성 개구 레이다에서 이동 표적을 탐지하고 속도를 추정하기 위해서 지상 이동 표적 탐지 기법을 활용한다. 대표적인 지상 이동 표적 탐지 기법으로는 클러터 억제 기반의 DPCA, ATI, STAP과 그림자 추적 방식이 있다. 그러나 ATI, STAP은 높은 연산량과 다중 채널 시스템을 요구하며 그림자 추적 기법은 고사양, 고해상도의 SAR 시스템을 요구한다. 이에 반해, 최근 ICEYE에서는 부분 조리개 기반의 비교적 낮은 연산량으로 이동 표적을 탐지한 사례가 있다. 따라서 본 논문에서는 상기한 사례를 모의실험으로 수행하였으며 부분 조리개를 활용한 다중 프레임을 통해 단일 채널 합성 개구 레이다 시스템에서 비교적 단순한 구조를 통해 단일 이동 표적뿐만 아니라 다중 이동 표적의 추적 및 속도 추정이 가능함을 보였다. 본 연구는 최근 다중 프레임을 활용한 비디오 합성 개구 레이다에서 이동 표적을 탐지하는 목적으로 활용될 수 있으며 기존의 단일 채널 합성 개구 레이다 시스템에서 하드웨어의 구조 변화 없이 이동 표적 탐지가 가능하다. 또한 단일 채널 SAR 시스템에서 낮은 연산량의 이동 표적 속도 추정을 통해 이동 표적 영상화(GMTIm)를 수행하는데 활용될 수 있을 것이다. 단, 본 연구는 이동 표적이 서로 떨어져 있는 상황이 가정되었으며, 다수의 이동 표적이 근접한 경우 표적 분별이 어려워 오차가 발생할 수 있다. 따라서 이에 따른 향후 연구가 필요할 것으로 보여진다.