Mode-Matching Analysis for Capacitances of Strip Transmission Lines

Park, Jae-Youn; Choo, Jaeyul

doi:10.5515/KJKIEES.2023.34.12.890

J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(12):890-898

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.12.890

논문/REGULAR PAPERS

스트립 전송선의 정전용량에 대한 모드정합 분석

박재 윤

, 주재 율^†

Mode-Matching Analysis for Capacitances of Strip Transmission Lines

Jae-Youn Park

, Jaeyul Choo^†

Author Information & Copyright ▼

^{안동대학교 전자공학과}

^{Department of Electronic Engineering, Andong National University}

^†Corresponding Author: Jaeyul Choo (e-mail: jychoo@anu.ac.kr)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 11, 2023; Revised: Nov 25, 2023; Accepted: Dec 13, 2023

Published Online: Dec 31, 2023

요 약

본 연구에서는 다양한 두께와 넓이에 대한 스트립 전송선로의 커패시턴스를 모드정합법을 활용하여 정확하게 계산하였다. 모드정합법을 수행하기 위해서 스트립 전송선로의 구조를 모델링하였으며, 라플라스 방정식과 중첩의 원리를 적용하여 해석공간에 대한 포텐셜을 표현하였다. 도출된 포텐셜 표현식에 포함된 모드계수를 계산하기 위해서 Dirichlet과 Neumann 경계조건을 적용하였다. 또한, 모드정합 해석의 유효성을 검증하기 위해서 특정 위치에 대한 포텐셜의 수렴성을 확인하였으며, 모드정합법과 상용 시뮬레이션의 해석결과를 비교하였다. 검증된 모드정합 해석을 활용하여 스트립 전송선로의 두께와 넓이 변화에 따른 커패시턴스의 변화를 조사하였고, 이를 근사식으로 계산한 커패시턴스와 비교·분석하였다. 분석 결과로부터 근사식으로 계산한 커패시턴스는 스트립 전송선로의 구조에 따라서 오차가 상이하게 발생하였고, 이로부터 엄밀한 전자파 해석으로 커패시턴스를 계산할 필요가 있는 스트립 전송선로의 구조를 확인하였다. 본 연구에서 수행한 모드정합 분석은 스트립 전송선로의 다양한 구조 변화를 반영하여 커패시턴스를 예측할 수 있다는 점에서 수식 기반의 커패시턴스 예측법과는 차별점을 갖는다.

Abstract

In this study, the capacitances of strip transmission lines of various thicknesses and widths were accurately calculated using the mode-matching method. To perform the mode-matching method, a strip transmission line structure was modeled, and the potential for the analysis space was expressed by applying the Laplace equation and the principle of superposition. Dirichlet and Neumann boundary conditions were applied to calculate the mode coefficient included in the derived potential expression. Additionally, to verify the validity of the mode-matching analysis, the convergence of the potential for a specific location was confirmed, and the analysis results of the mode-matching method and commercial simulation were compared. Using the verified mode-matching analysis, the change in capacitance according to the thickness and width changes of the strip transmission line was investigated, the capacitance was calculated using the approximate equation, and bar bridging and analysis were performed. From the analysis results, the capacitances calculated using the approximation formula differed depending on the structure of the strip transmission line. The structure of the strip transmission line that needed to be calculated by rigorous electromagnetic analysis was confirmed. This differs from a previous study in that the mode-matching analysis can precisely predict the capacitance corresponding to the geometrical variation of the strip transmission lines.

Keywords: Strip Transmission Line Width; Strip Transmission Line Thickness; Mode-Matching Method; Fringing Capacitance; Parallel Capacitance; Electromagnetic Analysis

Ⅰ. 서 론

스트립 전송선로(strip transmission line)는 고주파 및 마이크로파 신호를 전송하기 위해 사용되는 전송선로 중 하나이며, 그림 1과 같이 중심 스트립의 너비(w), 두께(t), 무한 접지면과의 간격(b) 등에 의해서 저항(R), 인덕턴스(L), 커패시턴스(C), 컨덕턴스(G) 값이 결정되어 특성 임피던스가 도출된다. 따라서 원하는 특성 임피던스를 갖는 스트립 전송선로를 설계하기 위해서는 스트립 전송선로의 구조에 따른 저항, 인덕턴스, 커패시턴스, 컨덕턴스와의 관계를 분석해야 한다^[1]~[6].

그림 1. | Fig. 1. 스트립 전송선로 구조 | Configuration of a stripline transmission.

Download Original Figure

그림 1에 제시된 것과 같이 스트립 전송선로의 커페시턴스는 평행도체판에 의한 평행 커패시턴스(parallel capacitance, C_p)와 프린징 커패시턴스(fringing capacitance, C_f)로 구성되며, 두 커패시턴스는 각각 식 (1) 및 식 (2)와 같이 표현된다^[7],[8].

C p = ε 2 w b − t = 2 ε r ε 0 χ 1 − γ

(1)

C f = ε π 2 1 − γ ln 1 + 1 1 − γ − 1 1 − γ − 1 ln 1 (1 − γ) 2 − 1 when χ 1 − γ ≥ 0.35

(2)

식 (1) 및 식 (2)에서 γ=t/b, χ=w/b이며, 식 (2)는 χ/(1-γ)≥0.35인 경우에 유효하다. 그러나 C_f를 계산하는 식 (2)는 정확한 값이 아닌 근사화된 값을 도출하는 표현식이기 때문에, 실제 커패시턴스와 오차가 발생할 수 있다. 특히, 중심 스트립의 두께가 커지는 경우, C_f의 값이 증가함에 따라 식 (2)에 의한 예측오차는 증가한다. 또한, 중심 스트립의 위치가 중심으로부터 특정 오차를 가질 경우 역시 구조를 반영한 수치해석에 의한 커패시턴스 계산이 요구된다. 따라서 본 논문에서는 스트립 전송선로의 구조에 따른 커패시턴스를 전자기 해석기법인 모드정합법을 활용하여 분석하였으며, 선행연구의 결과와 비교하여 수행한 모드정합 해석의 유효성을 검증하였다.

Ⅱ. 모드정합 모델링 및 수식표현

그림 1은 모드정합 해석을 위한 스트립 전송선로 구조를 나타내며, 스트립 전송선로는 전압(V)이 인가된 중심 스트립(t=0.4 m, w=0.4 m)과 두 개의 무한 접지면(윗면과 아랫면)으로 구성된다. 또한, 그림 1에 표현된 구조는 z축 방향으로는 무한히 펼쳐져 있다고 가정하였으며, 모드정합법을 적용하기 위해서 그림 1과 같이 전체 해석영역을 4개의 세부 영역(regions Ⅰ-Ⅳ)으로 세분화하였다. 각 영역에 대한 포텐셜(Φ) 표현식은 라플라스 방정식에 변수분리 기법을 적용하여 유도할 수 있으며, 중심 스트립에 전원이 인가된 경우와 인가되지 않은 경우를 고려하여 중첩의 원리(superposition principle)를 적용하였다.

그림 2는 영역 Ⅰ에 변수 분리와 중첩의 원리를 적용하여 포텐셜을 유도하기 위한 스트립 전원 조건을 보여주며, 스트립에 전원이 인가되지 않은 경우(V=0)와 전원이 인가된 경우(V=V₁)를 case a와 case b로 나타내었다. V=0인 case a의 경우, x=x₁과 x=x₂인 경계면에서 포텐셜(Φ₁_a)은 모두 0 V가 되며, y=y₁과 y=y₂인 경계면에서는 각각 영역 Ⅲ과 Ⅳ의 포텐셜(Φ₃_a와 Φ₄_a)과 같아야 한다. 또한, V= V₁인 case b의 경우,x=x₁과 x=x₂인 경계면에서 포텐셜(Φ_1b)은 각각 0 V과 V₁이 되며, y=y₁과 y=y₂인 경계면에서는 각각 영역 Ⅲ과 Ⅳ의 포텐셜(Φ₃_b와 Φ₄_b)과 같아야 한다. 추가적으로 y=y₁과 y=y₂인 경계면은 모두 개방된 것으로 가정하였다. 따라서 영역 I에서 라플라스 방정식으로 유도된 case a와 case b의 포텐셜 표현식에 설명한 경계면에서의 포텐셜 연속조건을 적용하면, case a와 case b에 대한 간략화된 포텐셜 표현식을 식 (3) 및 식 (4)와 같이 유도할 수 있다.

그림 2. | Fig. 2. 영역 Ⅰ에 적용한 중첩의 원리 | Superposition principle applied to region Ⅰ.

Download Original Figure

유도된 case a와 case b의 포텐셜 표현식에 중첩의 원리(Φ_I=Φ_Ia+Φ_Ib)를 적용하면, 식 (5)를 통해서 영역 I의 최종 포텐셜 표현식을 유도할 수 있다.

Φ I a (x, y) = ∑ m 1 = 1 ∞ sin β m 1 x − x 1 A m 1 e − β m 1 y + B m 1 e β m 1 y

(3)

Φ I b (x, y) = V 1 x 2 − x 1 x − x 1

(4)

Φ I (x, y) = ∑ m 1 = 1 ∞ sin β m 1 x − x 1 A m 1 e − β m 1 y + B m 1 e β m 1 y + V 1 x 2 − x 1 x − x 1

(5)

식 (3) 및 식 (5)에서 $β m 1 = m 1 π x 2 − x 1$ 이다.

영역 Ⅱ의 포텐셜 표현식도 영역 Ⅰ의 포텐셜 표현식 유도과정과 유사하게, 라플라스 방정식, 경계조건, 중첩의 원리를 적용하여 유도할 수 있다. 그 외, 영역 Ⅲ과 Ⅳ의 포텐셜 표현식 역시 그림 2의 case a와 동일한 과정을 통해서 유도할 수 있다. 영역 Ⅱ-Ⅳ의 포텐셜 표현식에 대한 보다 상세한 유도과정은 부록(Appendix)에 제시하였다.

식 (5)로 도출된 영역 Ⅰ 포텐셜 표현식과 부록 식 (A1) ~식 (A3)으로 도출된 영역 Ⅱ~Ⅳ의 포텐셜 표현식을 살펴보면, A_m1, B_m1, C_m2, D_m2, E_m3, F_m4로 구성된 총 6개의 모드계수가 존재한다. 해당 모드계수들의 값은 y=y₁과 y=y₂에서의 Dirichlet과 Neumann 경계조건을 적용하여 계산할 수 있다. 식 (6) 및 식 (7)은 각각 y=y₂에서의 Dirichlet과 Neumann 경계조건을 나타낸다.

Φ I I I (x, y) y = y 2 = 0, x < x 1 Φ I (x, y) y = y 2, x 1 ≤ x < x 2 V 1, x 2 ≤ x < x 3 Φ I I (x, y) y = y 2, x 3 ≤ x < x 4 0, x 4 < x

(6)

∂ Φ I I I (x, y) ∂ y y = y 2 = ∂ Φ I (x, y) ∂ y y = y 2, x 1 < x < x 2

(7)

∑ m 3 = 1 ∞ E m 3 e − β m 3 y 2 x 4 − x 1 2 δ m 3 n 3 − ∑ m 1 = 1 ∞ A m 1 e − β m 2 y 2 F x 1, x 2, x 2 − x 1, x 1, x 4 − x 1, x 1 − ∑ m 1 = 1 ∞ B m 1 e β m 1 y 2 F x 1, x 2, x 2 − x 1, x 1, x 4 − x 1, x 1 − ∑ m 2 = 1 ∞ C m 2 e − β m 2 y 2 F x 3, x 4, x 4 − x 3, x 3, x 4 − x 1, x 1 − ∑ m 2 = 1 ∞ D m 2 e β m 2 y 2 F x 3, x 4, x 4 − x 3, x 3, x 4 − x 1, x 1 = ∫ x 1 x 2 ∑ m 1 − 1 ∞ V 1 x 2 − x 1 x − x 1 sin β n 3 x − x 1 d x − V 1 β n 3 cos β n 3 x 3 − x 1 + cos β n 3 x 2 − x 1 + ∫ x 3 x 4 ∑ m 2 = 1, 3, 5, … ∞ V 1 x 4 − x 3 x 4 − x sin β n 3 x − x 1 d x

(8)

∫ x 3 x 4 ∑ m 2 = 1, 3, 5 … ∞ V 1 x 4 − x 3 x 4 − x sin β n 3 x − x 1 d x + ∑ m 1 = 1 ∞ A m 1 e − β m 1 y 2 − B m 1 e β m 1 y 2 m 1 π 2 δ m 1 m 1 − ∑ m 3 = 1 ∞ β m 3 E m 3 e − β m 3 y 2 F x 1, x 2, x 4 − x 1, x 1, x 2 − x 1, x 1 = 0

(9)

식 (6)과 식 (7)의 앙변에 각각 $∫ x 1 x 4 (⋅) sin n 3 π x 4 − x 1 x − x 1 d x$ 와 $∫ x 1 x 2 (⋅) sin n 1 π x 2 − x 1 x − x 1 d x$ 를 적용하면 모드계수가 포함된 식 (8) 및 식 (9)를 얻을 수 있다^[9].

식 (8) 및 식 (9)에서 $β m 1 = m 1 π x 2 − x 1$ , $β m 2 = m 2 π x 4 − x 3$ , $β m 3 = m 3 π x 4 − x 1$ , $β n 3 = n 3 π x 4 − x 1$ , $F (a, b, c, d, e, f) = ∫ a b sin m π c x − d sin n π e (x − f) d x$ , δ는 Kronecker delta이다.

식 (8) 및 식 (9)를 유도한 방법과 유사하게 y=y₁과 y=y₂의 경계면에 대한 나머지 Dirichlet과 Neumann 경계조건을 적용하면 4개의 추가적인 방정식을 유도할 수 있으며, 구체적인 수식은 부록의 식 (A4)~식 (A11)로 제시하였다. 따라서 경계조건으로부터 총 6개의 방정식으로 구성된 연립방정식을 구성할 수 있고, 해당 연립방정식을 풀어 6개의 모드계수 A_m1, B_m1, C_m2, D_m2, E_m3, F_m4에 대한 구체적인 값을 계산할 수 있다. 또한, 계산된 6개 모드계수 값을 포텐셜 표현식에 대입하면, 각 영역에 대한 포텐셜을 정확히 계산할 수 있다. 추가적으로 식 (10)을 이용하면 식 (11)~식 (14)와 같이 각 영역에 대한 전계 역시 계산할 수 있다.

E = − ∇ Φ (x, y) = − a^x ∂ Φ (x, y) ∂ x + a^y ∂ Φ (x, y) ∂ y

(10)

E x I = ∑ m 1 ∞ β m 1 cos β m 1 x − x 1 A m 1 e − β m 1 y + B m 1 e β m 1 y − V 1 x 2 − x 1

(11)

E x I I = − ∑ m 2 ∞ β m 2 cos β m 2 x − x 3 C m 2 e − β m 2 y + D m 2 e β m 2 y − V 1 x 4 − x 3

(12)

E x I I I = − ∑ m 3 ∞ β m 3 E m 3 e − β m 3 y cos β m 3 x − x 1

(13)

E x I V = − ∑ m 4 ∞ β m 4 F m 4 e − β m 4 y cos β m 4 x − x 1

(14)

식 (11)~식 (14)에서 $β m 1 = m 1 π x 2 − x 1$ , $β m 2 = m 2 π x 4 − x 3$ , $β m 3 = m 3 π x 4 − x 1$ , $β n 3 = n 3 π x 4 − x 1$ 이다.

Ⅲ. 모드정합 해석결과

전자파 해석에 있어 모드정합법의 장점은 전자기적 특성을 수렴성에 근거하여 효율적인 유한개의 모드로 계산할 수 있다는 점이다. 따라서 모드정합 해석결과에 대한 수렴성은 모드정합을 이용한 전자기적 분석에서 가장 먼저 확인하여야 한다. 본 연구에서는 영역 Ⅰ~Ⅳ 내부에 임의 위치를 선정하고, 해당 위치에서 모드수 증가에 따른 모드정합 결과의 수렴성을 확인하였다. 그림 3은 영역 Ⅰ~Ⅳ 내부의 특정 위치에서 확인한 포텐셜의 수렴성을 보여주며, 모드수가 증가함에 따라 포텐셜이 특정한 값으로 수렴하는 것을 확인할 수 있다. 이러한 모드정합 해석 결과의 수렴성은 모드정합 해석을 수행할 때 유한개의 모드수만 고려하여도 충분히 정확한 해석결과를 얻을 수 있다는 것을 의미한다.

그림 3. | Fig. 3. 각 영역에서의 포텐셜 수렴성 | Potential convergence in each region (w=0.4 m, b=1 m, t=0.4 m).

Download Original Figure

수행된 모드정합법을 검증하기 위해서, 그림 3에서 확인한 모델에 대한 포텐셜 분포를 상용 시뮬레이터와 모드정합법을 이용하여 계산하였으며, 도출된 포텐셜 분포를 비교하여, 모드정합 해석의 유효성을 재검증하였다^[10].

그림 4는 상용 시뮬레이터와 모드정합법으로 계산한 포텐셜 분포 결과를 보여주며, 그림 4의 포텐셜 분포가 y=0을 기준으로 서로 유사한 크기를 가지며 대칭을 이루는 것을 알 수 있다. 따라서 모드정합법을 이용하여 스트립 전송선로를 전자기적으로 해석할 경우, 상용 시뮬레이터와 유사한 해석 정확도로 전자기적 특성을 예측할 수 있을 것으로 판단한다.

그림 4. | Fig. 4. 모드정합 및 상용시뮬레이션 해석결과 | Stripline analysis of mode matching and commercial simulation (w=0.4 m, b=1 m, t=0.4 m).

Download Original Figure

다음으로 검증된 모드정합 해석을 활용하여 스트립 전송선로의 두께에 따른 커패시턴스 변화를 조사하였다. 커패시턴스는 식 (15)와 같이 중심 스트립을 둘러싼 가우스 표면(Gaussian surface)에 대한 전하량을 계산한 후, 도출된 전하량을 인가 접압으로 나누어 계산하였다. 가우스 표면을 구성하는 중심 스트립에 대한 각 면의 전하량은 식 (16)~식 (19)와 같이 표현되며, Q_I과 Q_II의 합과 Q_III과 Q_IV의 합을 인가전압으로 나누어 평행 커패시턴스 C_p (=Q_I/V₁+Q_II/V₁)와 프린징 커패시턴스 C_f(=Q_III/V₁+Q_IV/V₁)를 계산하였다.

C T = 1 V ∮ c D ¯ ⋅ n^d l = 1 V ∮ c (− ε ∇ Φ) ⋅ n^d l

(15)

Q I = − ε ∑ m 1 = 1 ∞ cos m 1 π A m 1 e − β m 1 − B m 1 e − β m 1 e y 2 − e y 1 − V 1 x 2 − x 1 y 2 − y 1

(16)

Q I I = ε ∑ m 2 = 1 ∞ C m 2 e − β m 2 − D m 2 e − β m 2 e y 2 − e y 1 + V 1 x 4 − x 3 y 2 − y 1

(17)

Q I I I = − ε ∑ m 3 = 1 ∞ E m 3 e − β m 3 y 2 ∫ x 2 x 3 sin β m 3 x − x 1

(18)

Q I V = ε ∑ m 4 = 1 ∞ F m 4 e β m 4 y 1 ∫ x 2 x 3 sin β m 4 x − x 1

(19)

식 (16)~식 (19)에서 $β m 1 = m 1 π x 2 − x 1$ , $β m 2 = m 2 π x 4 − x 3$ , $β m 3 = m 3 π x 4 − x 1$ , $β n 3 = n 3 π x 4 − x 1$ 이다.

그림 5는 중심 스트립 두께 변화에 따른 C_p와 C_f를 근사식과 모드정합법으로 계산한 결과를 보여준다. 그림 5(a)에 제시된 것처럼 모드정합법으로 계산한 C_p가 근사식으로 계산한 C_p보다 다소 작은 값을 가졌으며, t/b가 0.1에서 0.6으로 증가함에 따라 해당 차이는 3.4 pF에서 3.2 pF로 감소하였다. C_f의 경우, 그림 5(b)에 제시된 것처럼 t/b가 0.1에서 0.6인 구간에서 모드정합법으로 계산한 C_f가 근사식으로 계산한 C_f보다 약 4.2 pF 큰 값을 가졌다. 따라서 식 (1) 및 식 (2)로 계산한 C_p와 C_f를 활용할 경우, 중심 스트립의 두께에 따른 커패시턴스 오차가 발생하며, 이러한 결과는 전송선로 특성(예, 특성 임피던스)에 영향을 미칠 수 있을 것으로 판단한다.

그림 5. | Fig. 5. 중심스트립 두께 변화에 따른 모드정합법과 수식의 커패시턴스 C_p와 C_f | Capacitances C_p and C_f derived from the mode matching method and while the thickness of a center stripline changes (w=0.4 m, b=1 m, 0.1 m ≤t≤0.6 m).

Download Original Figure

그림 6은 다양한 너비와 두께의 중심 스트립을 갖는 스트립 전송선로의 C_f 결과를 보여준다. 그림 6(a)의 경우, 식 (20)과 같이 근사식과 모드정합법으로 계산한 C_f의 오차율(%)을 나타낸다.

E r r o r (%) = C f M M M − C f A p p C f A p p × 100

(20)

그림 6. | Fig. 6. 다양한 구조의 중심 스트립의 구조에 대한 C_f의 특성 | Characteristics of C_f while the geometry of the centers stripline varies (0.32 m≤w≤0.6 m, b=1 m, 0.1 m≤t≤0.6 m).

Download Original Figure

여기서 $C f A p p$ 와 $C f M M M$ 은 각각 식 (2)와 모드정합법으로 계산한 프린징 커패시턴스이다. 그림 6(a)에서 확인할 수 있듯이, 중심 스트립의 두께가 두꺼울수록 오차율이 감소하였으며, w/b=0.325고 t/b=0.1일 경우 49.58 %의 가장 높은 오차율을 가졌다. 따라서 그림 6(a)의 결과는 얇은 중심 스트립 조건의 C_f를 계산할 경우, 작은 C_f를 보다 정확히 계산하기 위해서는 엄밀한 전자기해석이 필요하다는 것을 알려준다. 그림 6(b)는 C_T에서 C_f가 차지하는 비율(C_f/C_T)을 조사한 결과를 퍼센트로 보여준다. 그림 6(b)를 검토한 결과, 중심 스트립의 두께가 두껍고 너비가 넓을수록 C_f/C_T가 증가하였으며, w/b=0.6이고 t/b=0.6일 경우에 12.48 %의 가장 높은 C_f/C_T를 가졌다. 따라서 그림 6(b)의 결과는 총 커패시턴스(C_f+C_p)를 계산할 경우, 중심 스트립의 두께와 너비가 증가함에 따라 C_f/C_T이 증가하므로 C_f를 보다 정확하게 계산해야 한다는 것을 알려준다.

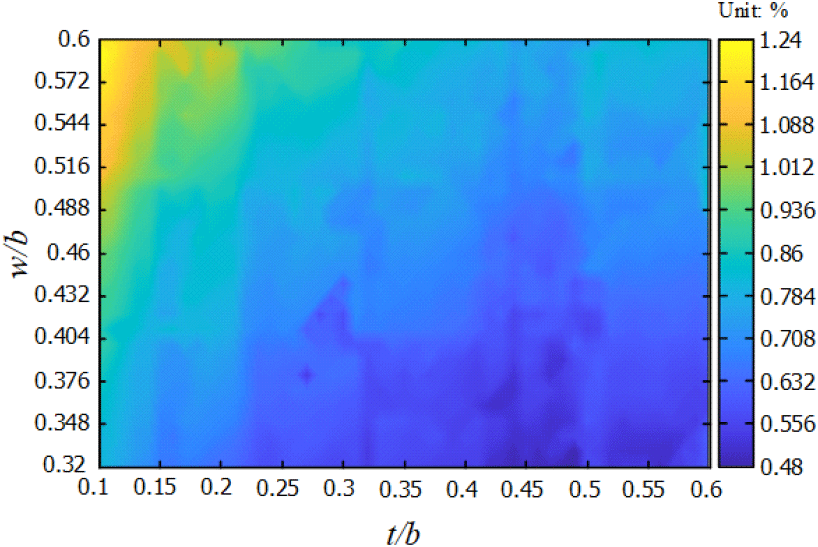
그림 7은 상용 시뮬레이터와 모드정합법으로 계산한 정전용량(total capacitance, C_T)을 비교하여 보여준다. 상용 시뮬레이터와 모드정합법의 결과를 비교하기 위해 식 (21)과 같이 수치해석 결과로 도출된 C_T와 모드정합법의 계산한 C_T의 오차율을 계산하였다. 분석결과, 스트립의 두께가 얇고 너비가 두꺼울수록 정확도가 감소하였으며, w/b=0.6이고 t/b=0.1일 경우 1.24 %의 가장 높은 오차율을 가졌다. 따라서 0.32≤w/b≤0.6, 0.32≤t/b≤0.6 조건에 따른 스트립 전송선로의 정전용량을 모드정합법으로 계산할 경우, 오차율 약 2 % 이내의 정확한 계산이 가능하다.

그림 7. | Fig. 7. 다양한 구조의 중심 스트립의 구조에 대한 정전용량 특성 | Capacitance characteristics while the geometry of the centers stripline varies (0.32 m≤w≤0.6 m, b=1 m, 0.1 m≤t≤0.6 m).

Download Original Figure

추가적으로 모드정합법에 대한 정확도를 분석하기 위해서 다양한 방법으로 도출한 정전용량을 모드정합법으로 계산한 정전용량과 비교하였으며, 비교 결과를 표 1에 제시하였다^[11]. 표 1을 분석한 결과, w/b가 1보다 클 경우에는 수행된 모드정합 분석결과가 다른 방법들로 계산한 결과와 유사하였으나, w/b가 1보다 작을 경우 오차가 다소 발생하였다. w/b가 1보다 작을 경우 발생한 오차의 경우, 다른 방법들(수치해석, 수식, 시뮬레이션)은 스트립 두께를 고려하지 않아서 발생하였다고 판단한다. 따라서 w/b가 1보다 작을 경우는 스트립의 두께를 고려하여 정전용량을 계산해야 한다고 판단한다.

표 1. | Table 1. w/b 비율에 따른 정전용량 분석 | Analysis of capacitance according to w/b ratio.

	Total capacitance (nF)
w/b	Numerical method	Formula	Simulation	Mode-matching method
0.25	0.0586	0.0615	0.0624	0.0438
0.5	0.0802	0.0849	0.0863	0.0688
1	0.1221	0.1298	0.1324	0.1149
2	0.2087	0.22	0.2182	0.2062
5	0.4795	0.4929	0.4473	0.4799

Download Excel Table

E r r o r (%) = C t M M M − C t Sim C t Sim × 100

(21)

여기서 $C t S i m$ 과 $C t M M M$ 은 각각 상용 시뮬레이터와 모드정합법으로 계산한 정전용량이다.

IV. 결 론

본 연구에서는 스트립 전송선로의 구조에 따른 커패시턴스를 정확하게 계산하기 위해서 모드정합 분석을 수행하였다. 스트립 전송선로의 해석구조에 포텐셜 표현식을 유도하기 위해서 해석공간을 4개의 세부영역으로 세분화하였으며, 나누어진 해석공간에 대한 포텐셜 표현식을 라플라스 방정식과 중첩의 원리를 적용하여 도출하였다. 포텐셜 표현식에 포함된 모드계수를 계산하기 위해서 세분화된 영역 사이의 경계조건을 적용하였다. 모드정합 해석결과를 검증하기 위해서 모드수가 증가함에 따른 포텐셜 값의 수렴성을 확인하였고, 상용 시뮬레이터의 결과와 비교하여 모드정합법의 유효성을 검증하였다. 검증된 모드정합 해석을 활용하여 고정된 높이에 대해서 스트립 전송선로의 중심 스트립 두께(t/b) 변화에 따른 커패시턴스 변화를 분석하였다. 또한, 다양한 두께와 너비를 갖는 중심 스트립을 고려한 C_f를 조사하여 C_f와의 오차율과 전체 커패시턴스에 대한 C_f 영향을 분석하였다. 조사결과로부터 중심 스트립의 두께가 증가 할 경우, 근사식과 모드정합 해석 결과의 오차가 증가하고, 중심 스트립의 두께와 너비가 증가함에 따라 전체 커패시턴스에서 차지하는 C_f의 비중이 증가하는 것을 확인하였다. 따라서 스트립 전송선로를 정확하게 설계하기 위해서는 스트립 전송선로의 구조를 고려하여야 하며, 일부 구조에 대해서는 근사식이 아닌 전자기해석을 통한 커패시턴스 예측이 필요하다고 판단한다.

Acknowledgements

이 논문은 안동대학교 기본연구지원사업에 의하여 연구되었음.

References

[1].

T. S. Chen, “Determination of the capacitance, inductance, and characteristic impedance of rectangular lines,” IRE Transactions on Microwave Theory and Techniques, vol. 8, no. 5, pp. 510-519, Sep. 1960.

[2].

J. R. Reid, E. D. Marsh and R. T. Webster, “Micromachined rectangular-coaxial transmission lines,” IEEE Transactions on Microwave Theory and Techniques, vol. 54, no. 8, pp. 3433-3442, Aug. 2006.

[3].

O. R. Cruzan, R. V. Garver, “Characteristic impedance of rectangular coaxial transmission lines,” IEEE Transactions on Microwave Theory and Techniques, vol. 12, no. 5, pp. 488-495, Sep. 1964.

[4].

E. D. Marsh, J. R. Reid and V. S. Vasilyev, “Gold-plated micromachined millimeter-wave resonators based on rectangular coaxial transmission lines,” IEEE Transactions on Microwave Theory and Techniques, vol. 55, no. 1, pp. 78-84, Jan. 2007.

[5].

Y. Liu, B. Tang and Y. Gao, “Sphere-TEM mode in rectangular top horn offset coaxial transmission line,” IEEE Transactions on Electromagnetic Compatibility, vol. 36, no. 4, pp. 390-394, Nov. 1994.

[6].

D. Homentcovschi, A. Manolescu, A. M. Manolescu and L. Kreindler, “An analytical solution for the coupled stripline-like microstrip line problem,” IEEE Transactions on Microwave Theory and Techniques, vol. 36, no. 6, pp. 1002-1007, Jun. 1988.

[7].

C. A. Balanis, Antenna Theory: Analysis and Design, 4th ed. Hoboken, NJ, John Wiley and Sons, 2016.

[8].

S. B. Cohn, “Characteristic impedance of the shielded-strip transmission line,” Transactions of the IRE Professional Group on Microwave Theory and Techniques, vol. 2, no. 2, pp. 52-57, Jul. 1954.

[9].

H. J. Eom, Electromagnetic Wave Theory for Boundary-Value Problems, Berlin, Springer, 2004.

[10].

COMSOL, “Multiphysics 6.0,” 2022. Available: https://www.comsol.com

[11].

D. M. Pozar, Microwave Engineering, 4th ed. Hoboken, NJ, John Wiley & Sons, 2012.

부 록

A. 포텐셜 표현식

그림 1의 구조에서 나타나는 영역별 포텐셜 표현식은 다음과 같다.

Φ I I (x, y) = ∑ m 2 − 1 ∞ sin β m 2 x − x 3 C m 2 e − β m 2 y + D m 2 e β m 2 y + V 1 x 4 − x 3 x 4 − x

(A1)

Φ I I I (x, y) = ∑ m 3 = 1 ∞ sin β m 3 x − x 1 E m 3 e − β m 3 y

(A2)

Φ I V (x, y) = ∑ m 4 = 1 ∞ sin β m 4 x − x 1 F m 4 e β m 4 y

(A3)

여기서 $β m 2 = m 2 π x 4 − x 3$ , $β m 3 = m 3 π x 4 − x 1$ , $β m 4 = m 4 π x 4 − x 1$ 이다.

B. Dirichlet 경계조건

그림 1의 구조에서 y=y₁에서 나타나는 Dirichlet 경계조건은 다음과 같다.

Φ I V x, y 1 = 0, x 1 < x Φ I x, y 1, x 1 ≤ x < x 2 V 1, x 2 ≤ x < x 3 Φ I I x, y 1, x 3 ≤ x < x 4 0, x < x 4

(A4)

∑ m 4 = 1 ∞ F m 4 e β m 4 y 1 x 4 − x 1 2 δ m 4 n 4 − ∑ m 1 = 1 ∞ A m 1 e − β m 1 y 1 F x 1, x 2, x 2 − x 1, x 1, x 4 − x 1, x 1 − ∑ m 1 = 1 ∞ B m 1 e β m 1 y 1 F x 1, x 2, x 2 − x 1, x 1, x 4 − x 1, x 1 − ∑ m 2 = 1 ∞ C m 2 e − β m 2 y 1 F x 3, x 4, x 4 − x 3, x 3, x 4 − x 1, x 1 − ∑ m 2 = 1 ∞ D m 2 e β m 2 y 1 F x 3, x 4, x 4 − x 3, x 3, x 4 − x 1, x 1 = ∫ x 1 x 2 ∑ m 1 = 1, 3, 5... ∞ V 1 x 2 − x 1 x − x 1 sin β n 4 x − x 1 d x − V 1 β n 4 cos β n 4 x 3 − x 1 − cos β n 4 x 2 − x 1 + ∫ x 3 x 4 ∑ m 2 = 1, 3, 5... ∞ V 1 x 4 − x 3 x 4 − x sin β n 4 x − x 1 d x

(A5)

여기서 $β m 1 = m 1 π x 2 − x 1$ , $β m 2 = m 2 π x 4 − x 3$ , $β n 4 = m 4 π x 4 − x 1$ 이다.

C. Neumann 경계조건

그림 1의 구조에서 y=y₁에서 나타나는 Neumann 경계조건은 다음과 같다.

∂ Φ R 3 (x, y) ∂ y y = y 2 = ∂ Φ R 2 (x, y) ∂ y y = y 2, x 3 < x < x 4

(A6)

∑ m 2 = 1 ∞ C m 2 e − β m 2 y 2 − D m 2 e β m 2 y 2 m 2 π 2 δ m 2 n 2 − ∑ m 3 = 1 ∞ E m 3 β m 3 e − β m 3 y 2 F x 3, x 4, x 4 − x 1, x 1, x 4 − x 3, x 3 = 0

(A7)

∂ Φ I V (x, y) ∂ y y − y 1 = ∂ Φ I (x, y) ∂ y y − y 1, x 1 < x < x 2

(A8)

∫ x 1 x 2 ∑ m 1 = 1 ∞ A m 1 e − β m 1 y 1 − B m 1 e β m 1 y 1 m 1 π 2 δ m 1 n 1 + ∑ m 4 = 1 ∞ F m 4 β m 4 e β m 4 y 1 F x 1, x 2, x 4 − x 1, x 1, x 2 − x 1, x 1 = 0

(A9)

∂ Φ I V (x, y) ∂ y y = y 1 = ∂ Φ I I (x, y) ∂ y y = y 1, x 3 < x < x 4

(A10)

∑ m 2 = 1 ∞ C m 2 e − β m 2 y 1 − D m 2 e β m 2 y 1 m 2 π 2 δ m 2 n 2 + ∑ m 4 = 1 ∞ F m 4 β m 4 e β m 4 y 1 F x 3, x 4, x 4 − x 1, x 1, x 4 − x 3, x 3 = 0

(A11)

여기서 $β m 1 = m 1 π x 2 − x 1$ , $β m 2 = m 2 π x 4 − x 3$ , $β m 3 = m 3 π x 4 − x 1$ , $β m 4 = m 4 π x 4 − x 1$ 이다.

Notes

박 재 윤 [국립안동대학교/학부생]

jkiees-34-12-890-i1

https://orcid.org/0000-0002-1155-5939
2017년 3월~현재: 국립안동대학교 전자공학과
[주 관심분야] 안테나 이론 및 기술

주 재 율 [국립안동대학교/교수]

jkiees-34-12-890-i2

https://orcid.org/0000-0002-5804-858X
2004년 2월: 홍익대학교 전기전자공학부 (공학사)
2006년 2월: 홍익대학교 전파통신공학과 (공학석사)
2014년 2월: 한국과학기술원 전기 및 전자공학과 (공학박사)
2020년 9월~현재: 국립안동대학교 전자공학과 교수
[주 관심분야] Antenna 설계 및 EMC 등