I. 서 론
최근 군사 및 이동통신 응용 분야에서 무선 신호의 방향을 탐지하는 기술에 대한 수요가 크게 증가하고 있다[1],[2]. 일반적으로 무선 신호의 방향을 추정하기 위해서는 배열 안테나가 사용되며, 각 배열 안테나에 의해 수신되는 위상 정보를 기반으로 빔스캔을 실시하여 전파 신호의 방향을 추정한다[3]. 광대역 주파수에서 선형 배열로 신호 방향을 탐지하는 경우, 주파수가 증가할수록 생성된 빔의 빔폭이 좁아지게 된다. 이는 신호처리 연산량과 탐지 시간을 증가시킬 수 있다. 또한, 시스템에서 디지털 위상천이기의 bit 수에 따라 생성할 수 있는 빔의 개수가 달라지며, 위상천이기의 bit 수가 n일 때 가질 수 있는 나타낼 수 있는 위상은 360/2n의 정수배일 때만 가능하므로 불연속적인 값을 가진다. 위상천이기의 bit 수가 적을수록 생성 가능한 위상 개수가 감소하며 이로 인해 빔조향 시 부엽의 크기가 증가할 수 있다[4]. 따라서 bit가 적은 위상천이기를 활용할 경우 조향 가능한 빔의 개수가 감소하며 좁은 빔폭을 가진 빔을 운용할 때 스캔 블라인드 영역이 발생할 수 있다. 특히, 전자전 분야에서는 3:1 이상의 넓은 주파수 대역에서 신호 탐지가 요구되므로, 고주파수에서 빔폭이 좁아지는 현상으로 인한 문제가 두드러진다. 이러한 문제를 해결하는 방안으로서, 주파수 균일 빔 (frequency-invariant beampattern, FIB) 기술이 활용될 수 있다. 균일 빔은 목표 주파수 대역에서 일정한 빔폭을 가진 빔패턴을 생성하는 기술이며, 다양한 알고리즘에 기반한 균일 빔 생성 연구가 진행되고 있다[5]~[10]. 그러나 안테나 배열 간격에 따라 균일 빔 특성을 비교하고, 이를 통해 최적의 배열을 설계하는 연구는 부족한 실정이다.
본 연구에서는 목표 균일 빔 특성에 따라 요구되는 최적의 안테나 배열을 도출하는 설계 프로세스를 제안한다. 제안된 프로세스에서는 목표 빔패턴을 생성하고, 해당 빔패턴을 광대역에서 생성하기 위해 균일 빔 가중치를 계산한다. 균일 빔 가중치는 MATLAB을 활용하여 IDFT inverse discrete Fourier transform) 계산을 통해 도출할 수 있으며, 계산된 가중치를 isotropic source 방사패턴을 가정한 배열 안테나에 적용함으로써 균일 빔을 생성할 수 있다. 생성된 균일 빔 특성을 평가하기 위해 균일한 빔폭을 유지하는 주파수 대역(frequency-invariant bandwidth ratio, FIBR), 빔 커버리지, 반전력빔폭(half-power beam width, HPBW), grating lobe free range을 제시한다. 제시된 평가 기준으로 배열 간격에 따른 생성된 균일 빔 특성을 평가하고 이를 기반으로 최종적으로 목표 빔 특성을 만족하는 배열 간격을 도출한다. 또한, 제안한 설계 프로세스의 예제를 제시하였으며 주파수 대역은 6~18 GHz, 위상천이기의 bit 수는 3으로 가정하였다. 설계 프로세스를 활용하여 최적의 배열 간격을 도출하고 균일 빔 특성을 확인하였다.
II. 제안된 배열 설계 프로세스
그림 1은 목표 빔패턴을 광대역에서 균일하게 생성할 수 있는 최적 배열을 도출하는 프로세스이다. 광대역 균일 빔 패턴을 생성하기 위해서, 먼저 운용하기에 적합한 빔폭과 부엽 수준 등을 고려한 목표 패턴을 결정한다. 그 후 해당 목표 패턴을 광대역에서 균일하게 생성하기 위해 활용할 배열 형상과 안테나 소자 수를 선정한다. 선정된 배열에서 안테나 소자 간 간격을 조정하며, 각 배열에서의 균일 빔 가중치를 계산한다. 이때 균일 빔 가중치는 DFT(discrete Fourier transform)을 활용하여 도출할 수 있으며, 균일 빔 가중치를 배열 안테나에 대입하여 균일 빔을 생성한다. 각각의 배열에 따라 생성된 균일 빔은 표 1에서 제시한 평가 기준을 만족하지 못할 경우 해당 배열 간격은 제외된다. 평가 기준에 부합하는 배열 후보군 중 적합한 배열 간격을 선택함으로써 원하는 대역에서의 균일 빔을 생성할 수 있는 최적의 배열을 도출할 수 있다.

| FIBR | ≥ 3 |
|---|---|
| Beam coverage | ±45°(Az), ±25°(El) |
| HPBWtgt (θ) | ≥ 16° (θ=0°) |
| HPBW (frequency) | ≤ HPBWtgt(θ) ±2° (θ=0°) ≤ HPBWtgt(θ) ±5° (θ>40°) |
| Grating lobe free range | θ≤45°(Az), θ≤25°(El) |
그림 2는 광대역 균일 빔 생성을 위한 목표 빔패턴을 나타낸 그래프이다. 이때 목표 빔패턴은 운용 환경에 따라 요구되는 HPBW를 반영하여 다양하게 선정될 수 있다. 3 bit의 위상 천이기를 활용할 경우 8개의 위상 state를 생성할 수 있으며 이에 따라 생성 가능한 빔의 개수가 제한되기 때문에 블라인드 영역 발생할 수 있으므로 블라인드 영역 없이 빔스캔을 하기 위해 전면 방향 기준 16° 이상의 빔폭을 가지는 목표 빔패턴 선정이 요구된다.

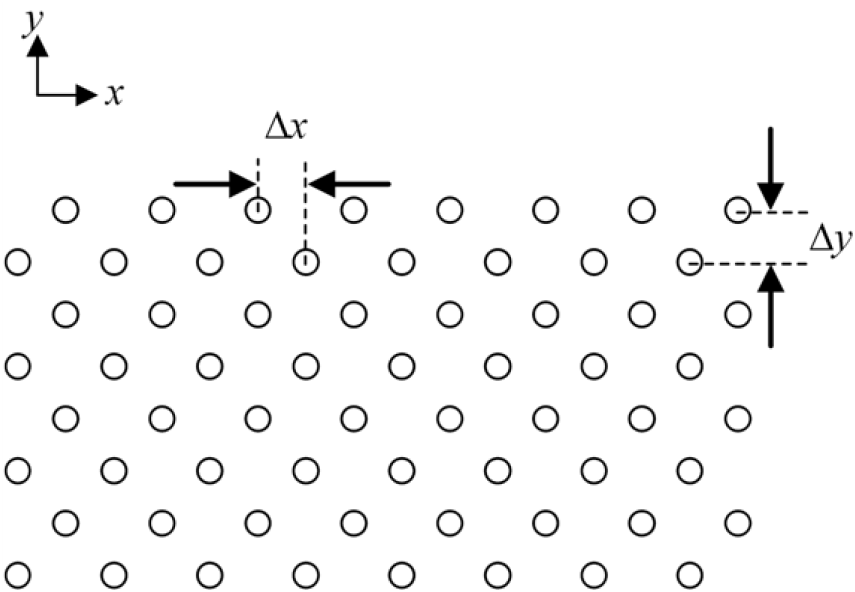
그림 3은 본 예제의 균일 빔 구현하기 위한 배열 형상으로 안테나는 8×8의 삼각 배열을 활용하였다. x축 평면을 방위각 면, y축 평면을 고각 면으로 정의하였고, 안테나 간격은 Δx와 Δy로 나타내었다. 삼각 배열 형상을 활용할 경우, 동일한 소자 수의 정사각형 배열을 활용할 때보다 방위각 면에서 두 배의 배열 크기를 확보할 수 있다. 넓어진 배열 크기는 균일 빔 생성할 시 좁은 빔폭부터 넓은 빔폭까지 생성할 수 있으므로 목표 빔패턴의 자유도가 증가한다는 장점이 있다. Δx와 Δy를 각각 0.4 λmax에서 0.7 λmax로 변화시켜가며 각 배열에서의 균일 빔을 생성하였고, 그 특성을 방위각 면과 고각 면에서 결과를 확인하였다.
본 연구에서 균일 빔을 생성하기 위해 discrete Fourier transform 방식을 활용하여 균일 빔 가중치를 도출하였다[5]. 목표 빔패턴은 임의의 그래프를 활용할 수 있으나, 일반적으로 식 (1)과 같이 band pass filter 형태로 나타낼 수 있다.
이때 ω는 각주파수를 의미하며, bandpass filter를 구성하는 h는 band pass filter의 계수를 나타낸다. h에 따라 패턴의 빔폭, 부엽 크기가 결정되므로 목표 빔패턴을 생성하기 위해서 적절한 h가 요구된다[5]. h의 크기를 도출하기 위해 다양한 window 함수들이 활용될 수 있으며, 본 연구에서는 MATLAB의 Taylor window 함수를 활용하여 h를 도출하였으며, 이를 활용하여 목표 빔폭 별 목표 패턴을 생성하였다. 또한, Ltgt와 Mtgt는 filter 크기, ltgt, mtgt는 filter index를 나타낸다. Bandpass filter 형태의 목표 빔패턴을 생성하기 위해 x축, y축을 따라 무한한 안테나 소자가 있다고 가정하면 빔 응답 B(w, q, f)는 식 (2)에서와 같이 FIB 가중치 D(lΔx, mΔy, w)와 지수함수 형태의 위상 항들과의 합으로 표현할 수 있다.
이때 Δx, Δy는 x축과 y축에서의 안테나 간격을 나타내고, l, m은 안테나 index를 나타낸다. 또한 (ω/c)Δxsinθcosϕ와 (ω/c)Δysinθsinϕ를 각각 ω1, ω2로 치환하면 빔응답은 식 (3)과 같이 DFT 형태로 나타낼 수 있다.
FIB 가중치 D(lΔx, mΔy, ω)는 식 (4)와 같이 M̃개의 주파수 샘플에 대하여 IDFT(inverse discrete Fourier transform)를 적용하여 구할 수 있다.
이때 ω1과 ω2는 l̃과 m̃에 대하여 ω1=−π+2l̃π/M̃, ω2=−π+2m̃π/M̃로 나타낼 수 있다. 또한, 식 (4)에서의 D의 차원은 M̃×M̃×M̃이며 M̃은 안테나 소자 수(L, M)보다 더 크므로, 안테나 소자 수와 차원을 맞추기 위해 D에 적절한 window 함수 적용이 요구되며 본 연구에서는 rectangular window를 적용하였다. 따라서 windowing 이후의 균일 빔 가중치 D의 차원은 L×M×M̃ 해당하며 계산된 균일 빔 가중치를 활용하여 균일 빔을 생성한다.
III. 설계 프로세스 예제
본 논문에서 제시된 설계 프로세스를 바탕으로 안테나 간격을 0.4 λmax에서 0.7 λmax로 변화함에 따라 균일 빔 성능을 분석하였다. 그림 4는 목표 빔폭(HPBWtgt) 변화에 따른 안테나 간격과 FIBR의 관계를 나타낸 그래프이며, 평가 기준에 부적합할 시 ‘×’ 표시를 하였고, 평가 기준을 만족시킨 경우 ‘○’로 표기하였다. 그림 4(a)는 방위각 면에서의 결과로, 일반적인 배열 간격인 0.5 λmax로 균일 빔을 생성할 때 18°보다 큰 빔폭을 가지는 목표 빔패턴으로 선정하면 3 이상의 FIBR을 만족할 수 있다. 보다 좁은 빔폭을 생성하기 위해서는 더 넓은 안테나 간격이 요구되나 안테나 간격이 커짐에 따라 부엽 발생 및 빔패턴의 왜곡으로 인해 평가 기준에 부적합한 배열이 존재한다. 평가 기준에 부합하는 배열 중, 빔 해상도와 블라인드 영역을 고려하여 16°의 빔폭을 가지는 목표 빔패턴을 생성하기 위해 배열 간격 Δx는 0.54 λmax으로 결정될 수 있다. 그림 4(b)는 고각 면에서의 경우이며, 배열 크기는 방위각 면에서의 배열 크기의 절반에 해당하므로 좁은 빔폭을 생성하는데 제한이 있다. 방위각 면과 동일하게 Δy를 0.54 λmax로 결정할 경우 38°의 빔을 생성할 수 있다. 그림 5는 결정된 배열 형상을 활용하여 나타낸 균일 빔 패턴 그래프이며, 그림 5(a) 및 그림 5(b)는 방위각 면에서의 균일 빔 패턴이고 그림 5(c) 및 그림 5(d)는 고각 면에서의 균일 빔 패턴이다. 그림 5(a)는 전면 방향을 지향할 때, 16°의 목표 빔폭을 가지는 패턴을 6~18 GHz 대역에서 균일하게 생성한 것을 나타내었다. 그림 5(b)는 3 bit의 위상천이기를 가정하여 43.98°로 조향하였을 때의 균일 빔 패턴을 나타내었으며, 빔조향에 따라 목표 빔폭은 22.8°로 증가한다. 고주파 대역에서 −90° 방향에서 부엽이 발생하였으나 목표 범위 내에서 발생하지 않았으며, 목표 주파수 대역에서 빔폭이 유지되었다. 그림 5(c)는 전면 방향 지향한 경우의 빔패턴을 나타내었으며, 이때의 목표 빔폭은 38°이고, 6 GHz에서 18 GHz의 목표 대역에서 균일한 빔폭을 유지하였다. 그림 5(d)는 13.38°로 빔조향할 경우, 목표 빔폭은 43°로 넓어지며 부엽 발생 없이 목표 주파수 대역에서 균일한 빔폭을 유지하였다.


그림 6은 빔패턴의 각도 step을 1° 단위로 나타내었을 때의 방위각, 고각 면에서의 HPBW를 나타낸 그래프로, 그림 6(a)는 방위각 면에서 전면 방향을 지향한 경우와 43.98°를 지향한 경우에 주파수에 따른 HPBW를 나타내었다. 전면 방향 지향 시 목표 빔폭에 대한 표준편차는 0.31°이며, 43.98°로 지향한 경우에 표준편차는 0.87°로 균일한 빔폭을 유지하는 것을 확인할 수 있다. 그림 6(b)는 고각 면에서의 주파수별 HPBW를 나타낸 그래프이며, 전면 방향과 13.38° 빔조향한 균일 빔 패턴의 HPBW의 표준편차는 각각 1.64°와 0.77°로 목표 주파수 내에서 균일한 빔폭을 유지하는 것을 확인할 수 있다. 이때 step이 좁아질수록 HPBW 그래프는 보다 연속적으로 나타나며 표준편차 값은 조정될 수 있다. 추가적으로 본 프로세스를 활용하여 도출한 배열 안테나의 성능을 표 2에 나타내었다.

| Parameter | The number of antennas | FIBR | Antenna interval | HPBWtgt | Standard deviation of HPBW (Boresight) |
|---|---|---|---|---|---|
| x-axis | 8 | 3.05 | 0.54λmax | 16° | 0.31° |
| y-axis | 8 | 3.10 | 0.54λmax | 38° | 1.64° |
그림 7은 제시한 최적의 배열에서의 방위각 면과 고각 면의 빔조향 결과를 나타낸 그래프이다. 그림 7(a)는 방위각 면에서 3 bit를 가지는 위상천이기 활용할 경우 ±45°빔 커버리지 내에서 빔조향 가능한 각도 중 0°, 13.38°, 27.58°, 43.98°에서의 빔조향 결과를 나타낸 그래프이며, 그림 7(b)는 고각 면에서 ±25°의 빔 커버리지 내 빔조향 가능한 각도 중 0°, 13.38°로 빔조향 패턴을 나타낸 그래프이다. 고각 면에서의 배열 크기는 방위각 면에서의 배열 크기에 절반이므로 빔 형성 시 상대적으로 넓은 빔폭을 가지기 때문에 두 개의 빔으로도 목표 빔 커버리지 +25° 내에서 빠짐없이 신호를 수신할 수 있다.

IV. 결 론
본 논문에서는 광대역에서 목표 빔폭과 주파수 대역폭을 만족하는 균일 빔 생성에 필요한 배열 간격을 도출하는 설계 프로세스를 제안하였다. 제안된 프로세스는 목표 빔폭을 선정하고 배열 개수와 배열 형상을 결정한 후, 안테나 배열 간격에 따라 균일 빔을 생성한다. 균일 빔을 생성하기 위해서 DFT를 활용하여 균일 빔 가중치를 계산하였으며 생성된 균일 빔은 평가 기준에 따라 적합성이 평가된다. 이를 기반으로 적합한 배열 간격을 도출할 수 있다. 이를 검증하기 위해 제시된 설계 프로세스 예제에서 목표 빔폭은 13°에서 44°로 다양하게 선정하였으며, 목표 빔폭 선정의 자유도를 높이기 위해 더 넓은 배열 크기를 가지는 8×8 삼각 배열을 활용하여 균일 빔을 생성하였다. 안테나 간격은 0.4 λmax에서 0.7λmax로 변화시키며 각 경우에서의 균일 빔을 생성하였다. 균일 빔 평가 기준으로 FIBR은 3 이상을 만족하도록 하였으며, 빔 커버리지, HPBW, grating lobe free range를 제시하였다. 또한, 3 bit의 위상 천이기를 활용한다고 가정하였으며, 방위각 면에서는 빔 스캔과 빔 해상도를 고려하여 목표 빔폭을 16°로 선정하였다. 이를 구현하기 위해 가장 적합한 배열 간격으로 0.54 λmax로 선정하였으며 고각 면에서의 배열 간격은 방위각 면과 동일한 간격은 0.54 λmax로 배열할 때 38°의 목표 빔폭을 3 이상의 FIBR에서 만족하였다. 본 프로세스로 도출한 배열을 활용하여 균일 빔 성능을 확인하였으며 빔조향 시 평가 기준에 위반되지 않는 것을 확인하였다. 또한, 방위각 면에서 전면 방향 조향과 빔조향 시의 HPBW를 나타내었으며 표준편차는 각각 0.31°, 0.87°였다. 고각 면에서의 전면 방향 조향과 빔조향 시 각각의 HPBW 표준편차는 1.64°, 0.77°로 6~18 GHz의 3:1 주파수 대역에서 균일한 빔폭을 유지하는 것을 확인하였다.











