A Study on SAR Jamming Using Single-Frequency Sine Wave

Lee, In-Hyeok; Lee, Kyung-Min; Cho, Min-Gon; Park, Young-Ju; Kim, Sang-Won; Kim, Kyung-Tae

doi:10.5515/KJKIEES.2023.34.11.824

J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(11):824-833

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.11.824

논문/REGULAR PAPERS

단일 주파수 정현파 기반 SAR 재밍 기법에 관한 연구

이인혁

, 이경민

, 조민곤

, 박영주^*

, 김상원^*

, 김경태^†

A Study on SAR Jamming Using Single-Frequency Sine Wave

In-Hyeok Lee

, Kyung-Min Lee

, Min-Gon Cho

, Young-Ju Park^*

, Sang-Won Kim^*

, Kyung-Tae Kim^†

Author Information & Copyright ▼

^{포항공과대학교 전자전기공학과}

^*국방과학연구소

^{Department of Electrical Engineering, Pohang University of Science and Technology}

^*Radar & EW Technology Center, Agency for Defense Development

^†Corresponding Author: Kyung-Tae Kim (e-mail: kkt@postech.ac.kr)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 08, 2023; Revised: Oct 13, 2023; Accepted: Oct 19, 2023

Published Online: Nov 30, 2023

요 약

SAR(synthetic aperture radar)는 이동하는 레이다를 활용해 영상을 형성하는 시스템이다. SAR는 시간과 기후의 제약을 거의 받지 않기 때문에 위성을 플랫폼으로 널리 활용되고 있다. 특히, 탐지 식별 등의 군용 목적으로 활용도가 매우 높다. 따라서 이에 대응하기 위한 SAR 재밍 연구가 이루어져야 한다. 기존의 SAR 재밍 기법은 잡음 재밍과 기만 재밍으로 구분되어 연구되었다. 잡음 재밍은 잡음 신호를 송신하여 SAR 영상의 SNR(signal to noise ratio)을 낮추는 재밍 기법이다. 잡음 재밍은 영상 전체에 퍼져서 드러나며 에너지 효율이 매우 나쁘다. 기만 재밍은 재머가 SAR 신호를 수신한 뒤 재송신해 허위 표적을 생성한다. 기만 재밍은 재머의 존재를 드러내지 않으며 영상의 내용을 조작할 수 있지만 성공적인 기만 재밍을 위한 기술적 요구 사항이 현재 실전에 적용하기 어려운 수준이다. 본 논문에서는 단일 주파수 정현파를 통한 SAR 재밍 기법을 제안한다. 제안된 기법은 영상 내에 직사각형 블록을 생성하여 SAR 영상의 활용도를 낮춘다. 제안된 기법은 송신 신호를 생성하기 쉽고 전력 효율이 우수하다.

Abstract

A synthetic aperture radar (SAR) is a system that uses moving radars to form images. SAR is widely employed, often utilizing satellites as platforms, and has a significantly high utility, especially for military purposes. It exhibits notable advantages in target detection and identification with the added benefit of minimal constraints related to time and weather. Therefore, research on SAR jamming is crucial. Conventional SAR jamming techniques can be categorized into noise and deceptive jamming. Noise jamming involves transmitting noise signals to lower the signal-to-noise ratio (SNR) of SAR images. Noise jamming spreads across the entire image, resulting in poor energy efficiency. In contrast, deception jamming does not reveal the presence of a jammer and allows the manipulation of the SAR image. However, the technological requirements of deception jamming are currently challenging for practical applications. In this study, we propose a SAR jamming technique using a single-frequency sinusoidal waveform. The proposed method reduces the utility of the SAR images by generating rectangular blocks within the images. Moreover, the proposed method can easily generate transmission signals and offers excellent power efficiency.

Keywords: Synthetic Aperture Radar; SAR Jamming; Pulse Compression; Single-Frequency Sine Wave

Ⅰ. 서 론

합성 개구면 레이다(synthetic aperture radar, SAR)는 이동하는 레이다를 활용해 영상을 형성하는 시스템이다^[1],[2]. SAR는 표적 탐지와 식별의 관점에서 우수한 성능을 보이기 때문에 위성을 플랫폼으로 이용해 군사적 목적으로 많이 활용된다^[3],[4]. 따라서, 적 위성 SAR 시스템에 대응하기 위한 SAR 재밍 기법 연구가 필수적이다.

기존의 SAR 재밍 기법은 잡음 재밍과 기만 재밍으로 구분된다^[5]. 잡음 재밍은 잡음을 송신해 SAR 영상의 신호 대 잡음비(signal to noise ratio, SNR)를 낮춰 SAR 영상의 품질을 저하한다^[6]. 잡음 재밍은 신호 형성이 간편하며 이는 잡음 재밍의 장점이다. 하지만, 잡음 재밍은 그 결과가 SAR 전체 영상에 퍼져서 드러나며 대부분의 잡음 신호는 SAR 시스템의 주파수 영역 필터에 의해 제거된다. 따라서 잡음 재밍은 에너지 효율 측면에서 단점이 명확하다. 기만 재밍은 재머가 SAR 신호를 수신한 뒤 정밀하게 조정하여 재송신한다. 즉, SAR 시스템은 표적에 맞고 돌아온 신호와 재머가 송신한 신호를 함께 수신해 영상을 형성한다. 이 과정에서 기만 재밍은 허위 표적을 형성하거나 존재하는 표적을 보이지 않게 하는 것을 목적으로 한다^[7],[8]. 기만 재밍은 재머의 존재가 드러나지 않으며 영상의 내용을 기만하는 높은 수준의 활용도를 갖는다. 그러나, 성공적인 기만 재밍을 위해 요구되는 기술의 수준이 여러 측면에서 매우 높으며 이는 현재 실전에 활용하기 어려운 수준이다^[9].

본 논문에서는 단일 주파수를 활용한 SAR 재밍 기법에 대해 제안한다. 제안된 기법은 영상에 사각형 형태의 블록을 만드는 방식으로 SAR 영상의 활용도를 낮춘다. 제안된 기법은 송신 신호를 형성하기 쉬우며 블록의 위치와 크기 결정에 필요한 신호 변조 기술 수준이 높지 않다. 또한, 영상 전 영역에 에너지가 분산되는 잡음 재밍에 비해 특정 블록에 에너지가 집중되므로 제안된 재밍 기법은 전력 효율이 매우 우수하다.

본 논문에서는 제안된 기법의 검증을 위해 시뮬레이션을 통해 SAR 영상에서의 블록 형성을 형성하고 블록의 위치와 크기를 변조하는 변수들의 역할에 대해 분석한다.

본 논문의 남은 내용은 다음과 같다. Ⅱ장에서는 신호 모델과 SAR의 2차원 압축 원리에 대해 살펴본다. Ⅲ장에서는 제안된 기법에 대해 구체적으로 소개한다. Ⅳ장에서는 시뮬레이션 환경과 분석 결과를 도시했다. 마지막으로 Ⅴ장에서 본 논문의 결론을 기술하였다.

Ⅱ. 위성 SAR 신호 모델 및 SAR 2차원 압축 원리

2-1 위성 SAR 신호 모델

본 논문에서는 그림 1과 같은 기하 구조를 가정한다. 위성 플랫폼은 x축과 같은 방향으로 v의 속력으로 등속 운동하며, 신호는 −CPI/2≤η≤CPI/2에 송신한다고 가정하며 여기서 η는 느린 시간(slow-time) 그리고 CPI는 coherent processing interval이다. 레이다와 영상 중심과의 거리의 최솟값을 R₀, 위성의 고도를 h, 입사각을 θ_i로 나타내며, 지표면의 좌표계는 영상의 중심을 원점으로 한다.

그림 1. | Fig. 1. 위성 SAR 기하 구조 | The geometry of satellite SAR.

Download Original Figure

고해상도 SAR 영상 획득을 위해 SAR 시스템은 다음과 같은 LFM(linear frequency modulated) 신호를 송신한다.

s t = P 0 ω r t e j 2 π f c t + K r 2 t 2

(1)

ω r t = 1, 0 ≤ t ≤ T p 0, o t h e r w i s e

(2)

여기서 P₀는 송신 전력, ω_r(t)는 거리 윈도우, f_c는 캐리어 주파수, K_r은 처프 비율(chirp rate) 그리고 t는 빠른 시간(fast-time), T_p는 송신 신호의 길이이다. 그림 1의 기하 구조와 송신 신호 식 (1)에 따른 수신 신호는 식 (3)과 같이 표현된다.

s r t, η = A ω r t + 2 R η c ω a η − η c × e j 2 π f c t − 2 R η c + K r 2 t − 2 R η c 2

(3)

여기서 A는 산란원의 반사 세기, ω_a (η)는 방위 윈도우, η_c는 beam center offset time, R(η)는 산란원과 레이다의 거리, c는 빛의 속도 그리고 η는 느린 시간(slow-time)이다. 식 (3)에서 수신 신호는 송신 신호가 t축에서 산란원에 따라 특정 값 $2 R η c$ 만큼 지연된 형태로 형성되는 것을 알 수 있다. 위성 플랫폼은 직선 운동을 가정할 수 있으며, R₀가 매우 크기 때문에 R(η)를 식 (4)와 같은 형태로 근사할 수 있다.

R η = v η 2 + R 02 ≈ R 0 + v 2 η 2 2 R 0

(4)

2-2 SAR 2차원 압축 원리

SAR는 다양한 영상 형성 기법이 존재하며 각 기법은 고유의 장단점이 있다. 그중, strip-map 모드 SAR 운용 시 수신 신호는 식 (3)과 같으며 알고리즘에 따른 영상의 차이는 크지 않다. 따라서, 본 절에서는 대표적인 영상 형성 알고리즘으로 알려진 거리-도플러 알고리즘(range-Doppler algorithm, RDA)을 통해 SAR 시스템의 주파수 영역 필터와 영상 형성 원리를 살펴본다.

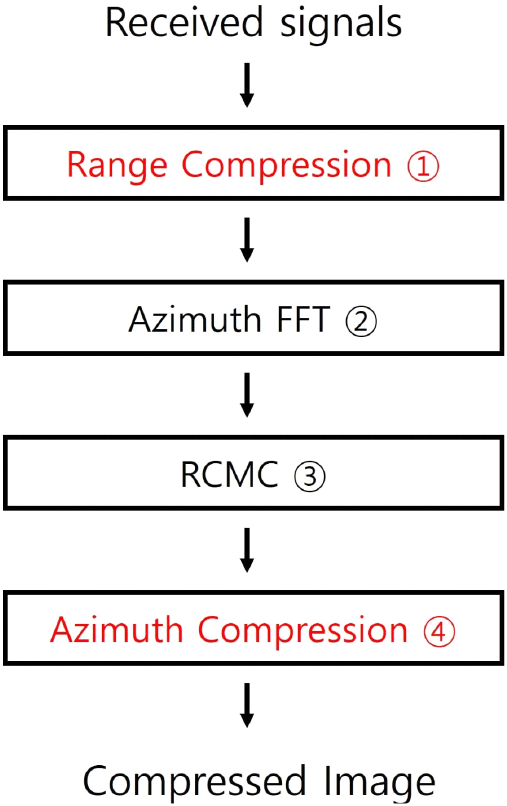
RDA는 다음의 그림 2의 순서도와 같이 수행된다. 수신 신호 식 (3)은 정합 필터^[10]를 통해 거리 압축 (①)된다. 정합 필터는 식 (5)와 같이 표현할 수 있다.

M f t = I F T F f F * f

(5)

그림 2. | Fig. 2. RDA 순서도 | The flowchart of RDA.

Download Original Figure

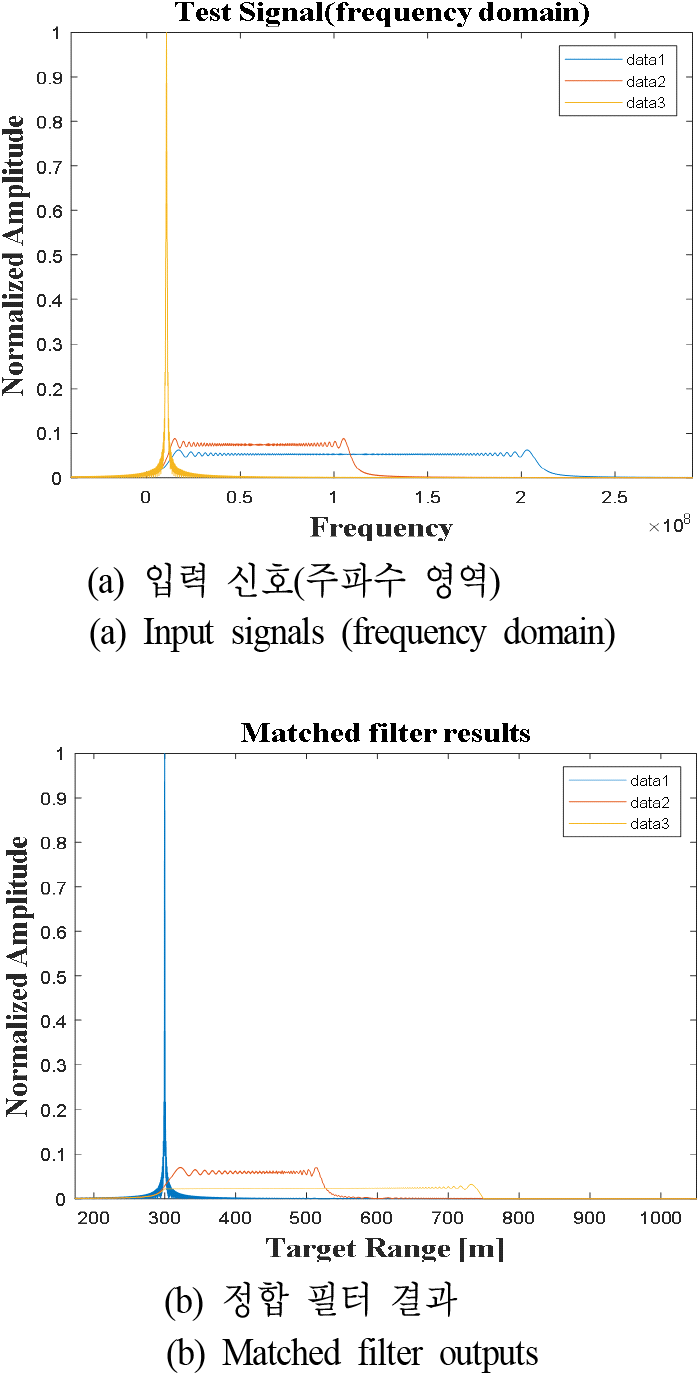
여기서 M[ · ]은 정합 필터, f(t)는 입력 신호, F(f)는 입력 신호의 주파수 영역 표현, [ ]*는 켤레 그리고 IFT[ · ]는 역푸리에 변환(inverse Fourier transform, IFT)을 의미한다. 즉, 정합 필터는 입력 신호를 기반으로 필터가 설계된다. 다음의 그림 3은 정합 필터의 예시를 보여준다. 이때, 파란색 그래프(data 1)는 기준 신호와 대역폭이 일치하는 경우, 빨간색 그래프(data 2)는 기준 신호와 절반의 대역폭이 일치하는 경우 그리고 노란색 그래프(data 3)는 단일 주파수를 사용한 예시이다. 그림 3(a)는 data 1, 2, 3의 신호의 주파수 영역 그래프를 보여준다. 여기서 세 신호는 모두 시간 영역에서 같은 전력과 신호 길이를 갖는다. 순서대로 대역폭이 좁아지는 것을 확인할 수 있다. 그림 3(b)는 정합 필터의 결과를 나타낸다. 그림 3(b)에서 정합 필터가 갖는 주파수 대역과 일치하지 않았을 때 신호 압축에 실패하는 것을 알 수 있다.

그림 3. | Fig. 3. 정합 필터 예시 | Examples of the matched filter.

Download Original Figure

송신 신호 식 (1)을 기준 신호로 활용해 수신 신호 식 (3) 및 식 (5)의 정합 필터를 수행하면 다음과 같이 거리 압축된 신호를 얻을 수 있다. 본 시뮬레이션에서는 300 m 거리에 단일 표적이 존재하는 상황을 가정했다.

s r c t, η ≈ A p r t − 2 R η c ω a η − η c × e − j 4 π f c R 0 c e − j π 2 v 2 λ R 0 η 2

(6)

여기서 p_r(t)는 압축된 거리 윈도우이며 sinc 함수이다. 거리 압축된 신호 식 (6)은 ② 와 ③의 과정을 거쳐 식 (7)과 같이 표현되며 이는 방위 압축(④) 직전 단계이다.

s t m p t, f η = A p r t − 2 R 0 c W a f η − f η c × e − j 4 π f c R 0 c e j π f η 2 K a

(7)

여기서 f_η는 느린 주파수(slow-frequency), W_a(f_η)는 느린 주파수 영역 윈도우, $f η c$ 는 주파수 영역에서의 beam center offset time 그리고 $K a ≈ 2 v 2 λ R 0$ 로 정의한다.

방위 압축은 식 (8)과 같이 수행한다.

s a c t, η = I F T s t m p t, f η H a z f η = A p r t − 2 R 0 c p a η e − j 4 π f c R 0 c e j 2 π f η c η

(8)

여기서 $H a z f η = e − j π f η 2 K a$ , p_a(η)는 압축된 방위 윈도우이며 sinc 함수의 형태이다. 여기서 방위 압축은 H_az(f_η)가 식 (7)의 $e j π f η 2 K a$ 항을 정확히 제거함으로써 수행됨을 알 수 있다.

Ⅲ. 단일 주파수 정현파를 활용한 블록 재밍

이 장에서는 단일 주파수 정현파가 SAR 영상에서 블록을 형성하는 원리에 대해 영상 압축 알고리즘을 기반으로 분석한다. 블록 재밍을 위해 재머는 SAR 신호를 수신하는 즉시 식 (9)를 송신한다. 즉, 재밍 신호 역시 SAR 시스템과 동일한 PRI(pulse repetition interval)를 가지며 신호의 길이는 SAR 신호의 길이 이하로 한다.

s j t, η = P j ω r, j t − R j η c ω a, j η e j 2 π f c + f j t

(9)

여기서 P_j는 재머의 송신 전력, R_j(η)는 레이다와 재머 사이의 거리, ω_r,j(t)는 재밍 신호의 거리 영역 윈도우, ω_a,j(η)는 재밍 신호의 방위 영역 윈도우, f_j는 재밍 주파수이며 t, η와 f_c는 SAR 시스템을 기준으로 한다. 여기서 ω_r,j(t)가 포함하고 있는 시간 지연은 SAR 신호가 재머에 도달하는 데 걸리는 시간을 의미한다. 또한, SAR 시스템의 여러 변수 및 재머와의 위치 관계가 정찰 시스템을 통해 파악된 상황과 재밍 신호가 SAR 수신 빔패턴의 주엽(mainlobew)에 인가됨을 가정한다^[11]~[13].

이 장에서는 재밍 신호 식 (9)가 영상에 나타나는 형상에 대해 거리 방향과 방위 방향 윈도우를 기준으로 알아 본다.

3-1 거리 방향

재밍 신호 식 (9)는 SAR 시스템의 기저대역 변환을 거쳐 식 (10)의 형태로 수신된다.

s j t, η = A j ω r, j t − 2 R j η c ω a, j η × e j 2 π f j t e − j 2 π f c + f j R j η c

(10)

여기서 A_j는 재밍 신호의 수신 세기, R_j(η)는 η에 따른 재머와 레이다의 거리이다. 레이다와 재머 사이의 거리 R_j(η)는 식 (11)과 같이 근사할 수 있다.

R η ≈ R 0, j + v η − a j 2 2 R 0, j

(11)

여기서 R_{(0, j)}는 레이다와 재머 사이의 최소 거리, a_j는 재머의 방위 축 좌표이다.

본 연구에서는 재머가 SAR 신호를 수신하면 재밍 신호를 송신하는 상황을 가정했다. 따라서 식 (10)의 거리 윈도우는 식 (9)의 거리 윈도우가 t축에서 $2 R j η c$ 의 시간 지연을 포함한 형태로 형성된다. 한편, 식 (9)의 위상은 재머와 레이다 사이의 단방향 시간 지연만이 발생해 $R j η c$ 의 단방향 시간 지연이 식 (10)에 나타난다.

SAR 시스템의 정합 필터 통과 이후 식 (10)은 식 (11)과 같이 표현된다.

s r c, j t, η = A j ω r, j t − 2 R j η c + t m ω a, j η × e − j 2 π f c + f j c R 0, j e − j π f c + f j c v η − a j 2 R 0, j

(12)

여기서 $t m = f j T p B W$ 이며 T_p와 BW는 각각 SAR 시스템의 신호 길이와 대역폭이다.

3-2 방위 방향

정합 필터를 통과한 신호 식 (12)는 그림 2의 ②~④과정을 수행한 뒤 식 (13)과 같이 표현된다.

s a c, j t, η ≈ A j ω r, j t − 2 R j η 2 + t m × ω a c, j η ϕ r e s t, η

(13)

여기서 ϕ_res(t, η)는 잔여 위상 성분이며 SAR 영상에 영향을 끼치지 않으며 방위 압축 이후 재밍 신호의 방위 윈도우 ω_ac,j(η)는 식 (14)와 같이 표현된다.

ω a c, j η = 1, 12 η s + a j 2 v ≤ η ≤ 12 η f + a j 2 v 0, o t h e r w i s e

(14)

여기서 η_s와 η_f는 각각 재밍 신호의 송신 시작 시각과 종료 시각이다.

재밍 신호의 방위 윈도우가 표적 신호와 달리 길이와 위치가 변화하는 이유는 재밍 신호의 단방향 위상 지연 때문이다. 다시 말해서, SAR의 수신 신호는 SAR 시스템이 송신한 신호와 재머 신호의 합으로 구성된다. 이때, SAR 시스템이 송신한 신호는 레이다와 표적 사이를 오간 양방향 시간 지연을 갖지만, 재밍 신호는 단방향의 시간 지연만을 가지게 된다. 따라서, SAR 신호의 방위 축 위상 변화는 ④에서 H_az(f_η)와의 곱을 통해 온전히 제거되지만, 재밍 신호가 가진 단방향 시간 지연의 경우 온전히 제거되지 못하고 f_η에 대해 선형적으로 변화한다. 결과적으로 재밍 신호의 방위 축 윈도우 ω_a,j(η)는 영상에서 절반의 길이의 직사각형 윈도우로 변환되며 재머의 위치와 비례하게 평행 이동한다.

종합하면 거리 윈도우는 폭이 유지되며 그 위치는 재밍 주파수 f_j의 영향을 받아 평행 이동한다. 방위 윈도우는 그 폭이 절반으로 감소하며 재머의 위치만큼 평행 이동한다. 다음 장에서는 시뮬레이션을 통해 앞서 언급한 재머 윈도우의 크기와 위치를 분석했다.

Ⅳ. 시뮬레이션 환경 및 재밍 결과 분석

이 장에서는 시뮬레이션을 통해 재밍 신호의 변화에 따른 SAR 영상에서의 블록의 위치와 크기를 분석한다. SAR의 영상 형성 시나리오는 그림 1과 같다.

SAR 시스템은 위의 표 1과 같은 운용 지표를 가정했으며 본 연구에서는 재밍 신호의 1) 길이, 2) 재밍 주파수, 3) 송신 시간 그리고 4) 재머의 위치에 따른 블록의 크기와 위치를 분석했다.

표 1. | Table 1. SAR 시뮬레이션 운용 지표 | SAR simulation parameters.

Parameter	Value
Carrier frequency, f_c	10 GHz
Bandwidth, BW	50 MHz
Pulse width, T_p	5 us
PRF	4 kHz
CPI	0.5 s
Height, h	550 km
Incidence angle, θ_i	50 degrees
Velocity, υ	7,000 m/s

Download Excel Table

4-1 재밍 신호의 길이

본 절에서는 재밍 신호의 길이 변화에 따른 SAR 영상에서 블록의 변화를 분석한다. 본 시뮬레이션에서 재머의 위치는 영상의 원점으로 설정했으며 재밍 주파수 f_j는 대역폭의 절반(BW/2), 재밍 신호의 송신 시간은 SAR의 CPI와 같다.

그림 4에서 재밍 신호의 길이와 블록의 거리 방향 길이는 정비례하며 그 길이는 식 (15)와 같은 관계임을 알 수 있다.

B j, r = T j × c 2

(15)

그림 4. | Fig. 4. 재밍 신호 길이에 따른 블록 영상 | Block images depending on the length of jamming signal.

Download Original Figure

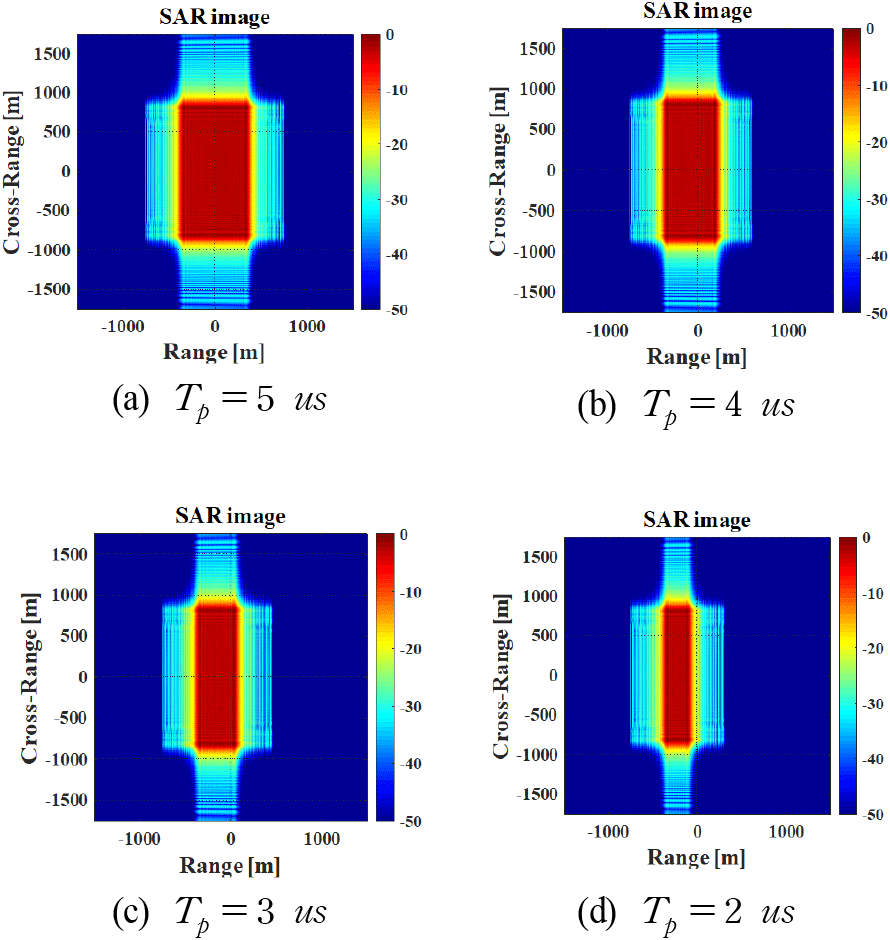
여기서 B_j,r은 블록의 거리 축 길이, T_j는 재밍 신호의 길이 그리고 c는 빛의 속도이다.

4-2 재밍 주파수

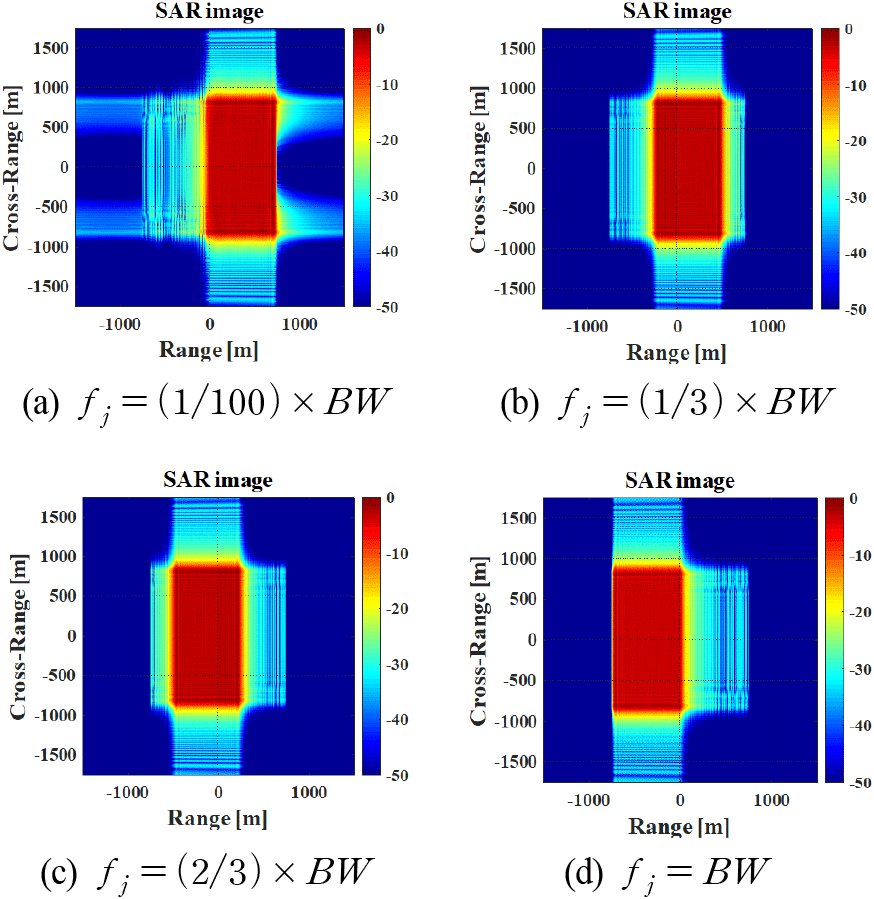
본 절에서는 재밍 주파수 f_j에 따른 SAR 영상에서 블록의 변화를 분석한다. 본 시뮬레이션에서 T_j는 SAR 송신 신호와 같고, 재머의 위치는 영상의 원점으로 설정했으며 재밍 신호의 송신 시간은 SAR의 CPI와 같다.

그림 5에서 f_j에 따른 블록의 이동이 식 (12)의 결과와 일치함을 확인할 수 있다. 결론적으로 SAR 영상에서 형성되는 블록의 폭과 위치는 재밍 신호의 길이와 재밍 주파수 f_j를 통해 특정할 수 있다.

그림 5. | Fig. 5. 재밍 주파수 f_j에 따른 블록 영상 | Block images depending on the jamming frequency f_j.

Download Original Figure

4-3 재밍 신호 송신 시간

본 절에서는 재밍 신호의 송신 시간에 따른 SAR 영상에서의 블록의 변화를 분석한다. 본 시뮬레이션에서 T_j는 SAR 송신 신호와 같고, 재밍 주파수 f_j는 대역폭의 절반(BW/2)이며 재머의 위치는 영상의 원점으로 설정했다.

그림 6에서 수직 거리(cross-range)는 레이다의 속도 (v=7,000 m/s)와 느린 시간(η)의 곱과 같다. 즉, 블록의 방위 거리는 식 (16)과 같다.

B a, r = v 2 η f − η s

(16)

그림 6. | Fig. 6. 재밍 신호 송신 시간에 따른 블록 영상 | Block images depending on the transmission time of the jamming signal.

Download Original Figure

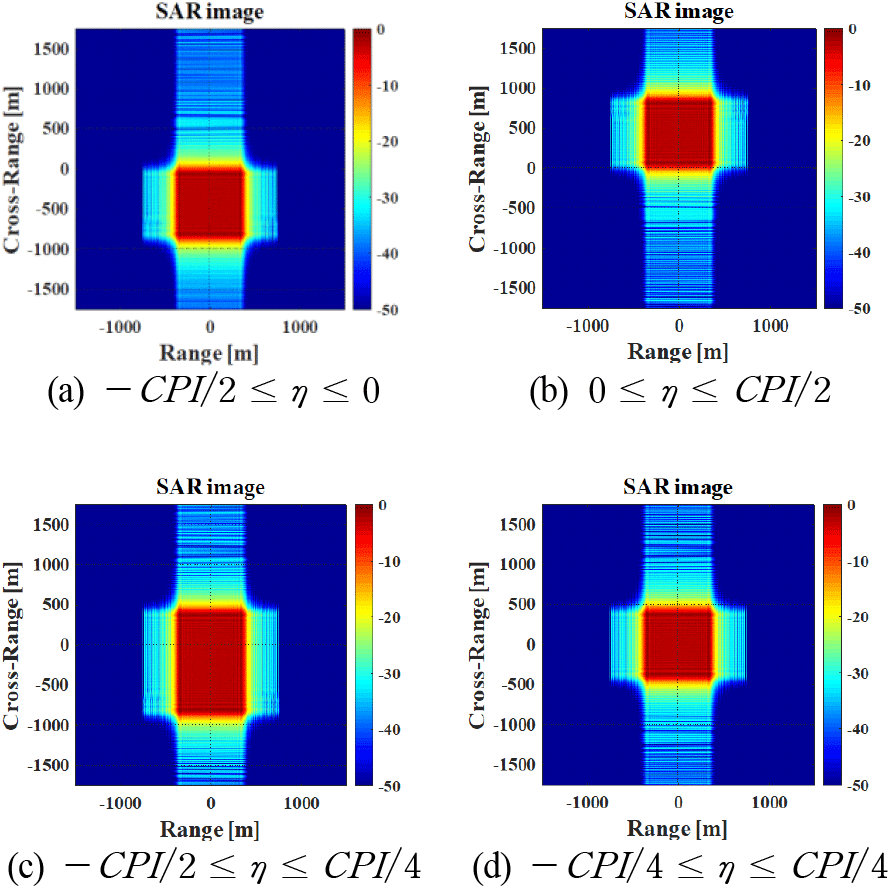
여기서 η_s와 η_f는 각각 재밍 신호의 송신 시작 시각과 종료 시각이다.

4-4 재머 위치

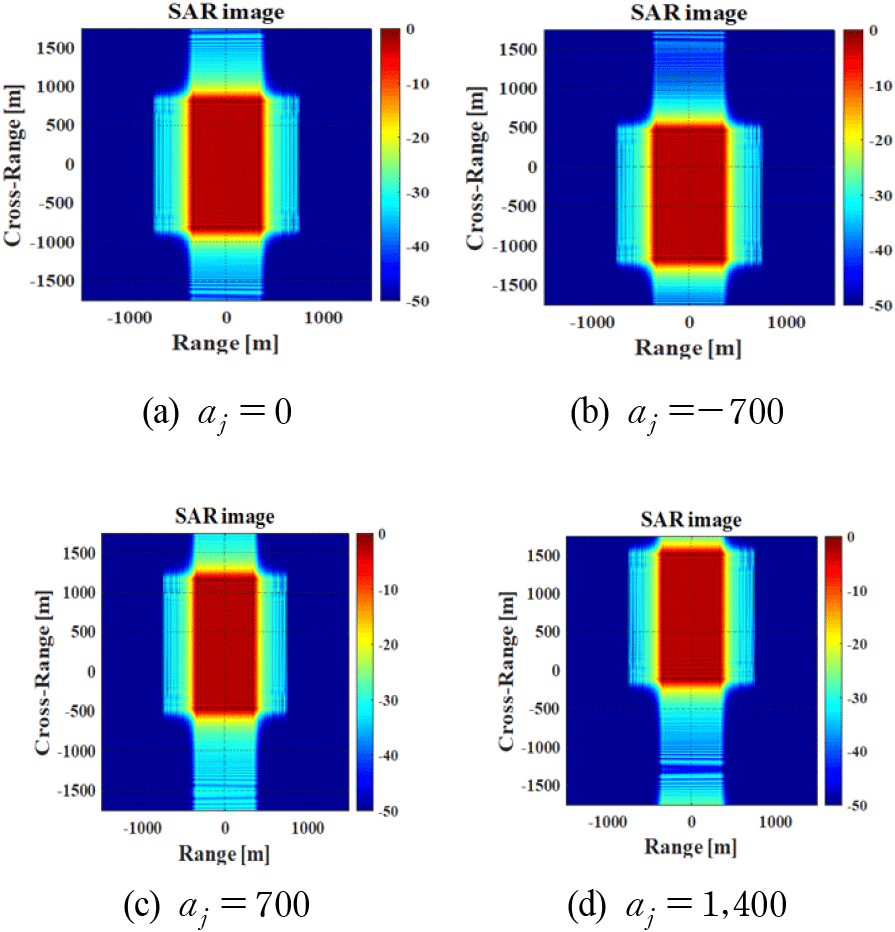
본 절에서는 재머의 위치에 따른 SAR 영상에서 블록의 변화를 분석한다. 재머의 위치는 거리와 방위 축에서 모두 이동할 수 있지만 거리 축의 위치는 영상에 거의 영향을 끼치지 않는다. 따라서 본 절에서는 재머가 영상의 원점에서 방위 축으로 이동하는 경우만을 고려한다. 본 시뮬레이션에서 T_j는 SAR 송신 신호와 같고, 재밍 주파수 f_j는 대역폭의 절반(BW/2), 재밍 신호의 송신 시간은 SAR의 CPI와 같다.

그림 7에서 블록은 영상 중심과 재머의 방위 축 거리의 절반만큼 평행이동 되어 나타남을 알 수 있다.

그림 7. | Fig. 7. 재머의 방위 위치에 따른 블록 영상 | Block images depending on the azimuth position of the jammer.

Download Original Figure

4-5 표적 재밍

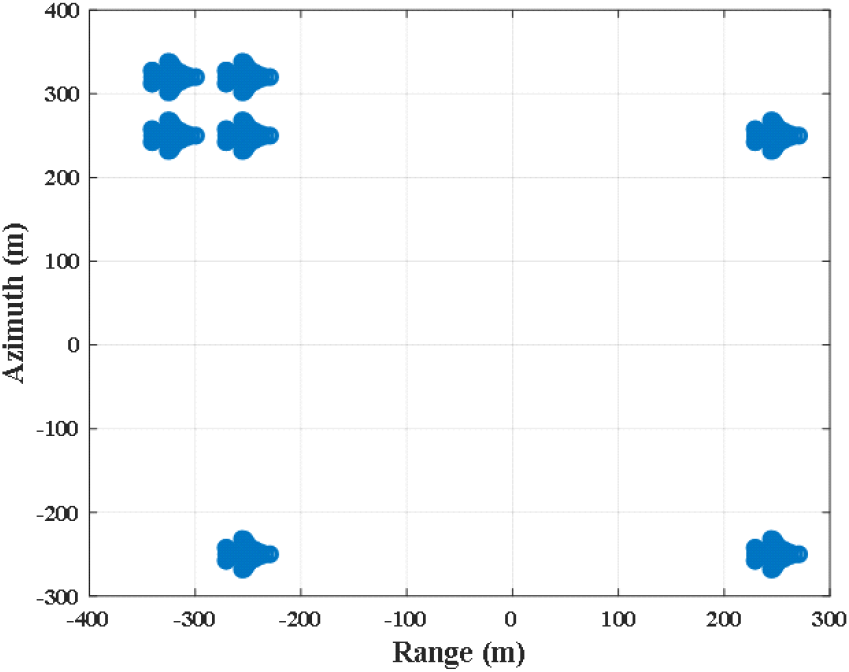
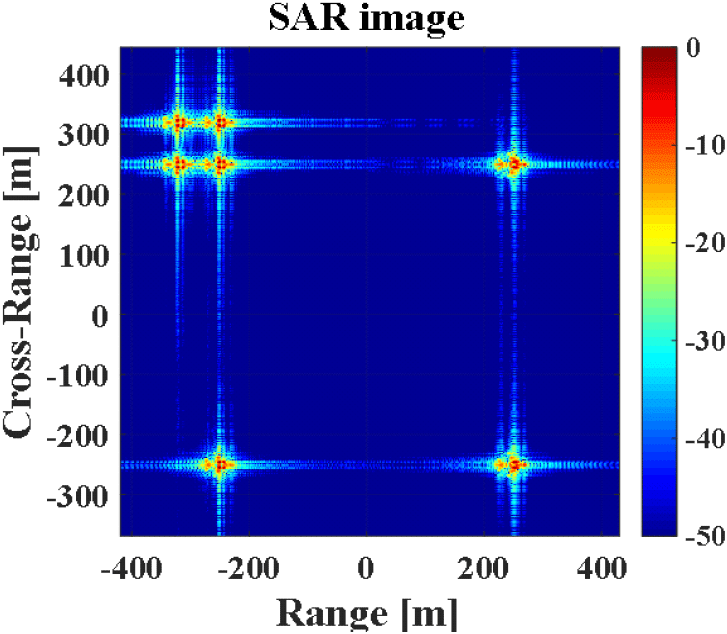
본 절에서는 SAR 영상의 특정 표적을 선택해 재머 사양의 변화를 통해 의도적으로 표적을 가리는 시뮬레이션을 수행했다. 시뮬레이션에 사용된 표적 모델은 다음의 그림 8과 같다.

그림 8. | Fig. 8. 점 표적 모델 | Point scatterer model.

Download Original Figure

본 시뮬레이션은 좌상단의 4개의 표적을 가리기 위한 재밍 신호를 설계하고 결과를 분석했다.

먼저 재밍 신호의 길이는 표적의 거리 폭과 식 (15)를 고려했을 때 신호 길이는 1 μs로 결정할 수 있다. 재밍 주파수는 표적의 위치와 식 (12)를 고려했을 때 f_j는 20 MHz로 결정할 수 있다. 마지막으로, 표적의 위치와 식(13), 식 (14) 및 식 (16)을 고려했을 때 신호를 0.06 s ≤η≤0.11 s에 송신했을 때 블록의 방위 축 폭이 표적을 온전히 가릴 수 있다는 사실을 알 수 있다. 이때 재머는 영상의 중심에 있다고 가정한다.

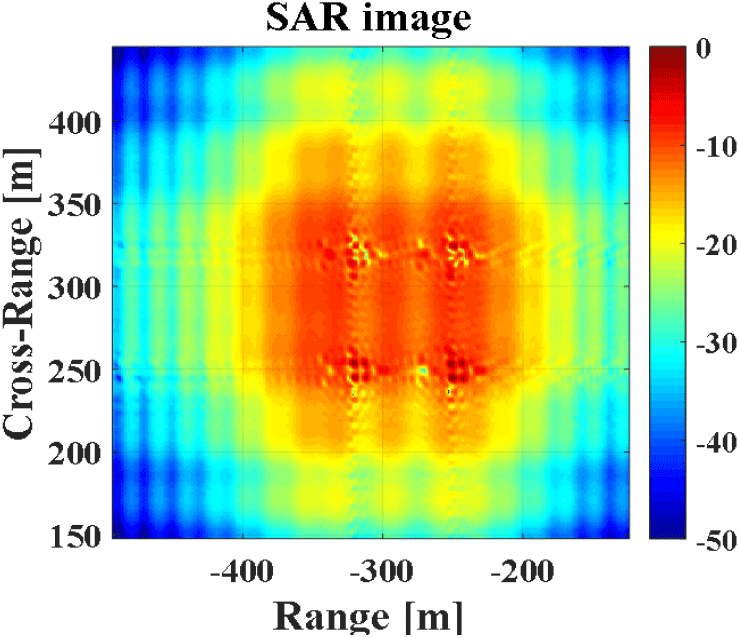
본 절의 시뮬레이션 결과는 그림 9~그림 11을 통해 알 수 있다. 구체적으로 그림 9는 재밍 신호가 없는 상황에서 그림 8의 표적의 SAR 영상이며 그림 10은 표 2의 파라미터를 통해 형성한 재밍이 포함된 SAR 영상이다. 여기서 본 논문에서 제시한 재밍 신호의 파라미터를 통해 SAR 영상의 목표한 위치에 정확하게 블록이 형성됨을 알 수 있다. 마지막으로 그림 11은 블록이 형성된 영역을 확대한 영상이다. 그림 11을 통해 블록의 존재가 표적의 탐지 또는 식별에 어려움을 준다는 것을 확인할 수 있다.

그림 9. | Fig. 9. 재밍이 없는 환경에서의 SAR 영상 예시 | The example of SAR image without the proposed jamming.

Download Original Figure

그림 10. | Fig. 10. 재밍이 있는 환경에서의 SAR 영상 예시 | The example of SAR image with the proposed jamming.

Download Original Figure

표 2. | Table 2. 재밍 신호 설계 지표 | Jamming signal parameters.

Parameter	Value
Carrier frequency, f_c	10 GHz
Pulse width, T_j	1 us
Jamming frequency, f_j	20 MHz
CPI	0.06 s ≤ η ≤ 0.11 s

Download Excel Table

그림 11. | Fig. 11. 재밍이 있는 환경에서의 표적 확대 SAR 영상 | The enlarged SAR image with the proposed jamming.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 단일 주파수 정현파를 송신해 SAR 영상에 블록을 형성함으로써 SAR 영상의 활용도를 낮추는 재밍 기법을 소개했다. 제안된 기법은 재밍 신호 형성이 비교적 간단하며 목적하는 영역만을 가리므로 전력 효율이 아주 우수하다. 특히 본 논문에서는 시뮬레이션을 통해 블록의 크기와 위치를 특정했다. 따라서 그 활용도가 매우 높으며 다수의 재머를 활용한다면 더 높은 활용도를 가질 것으로 기대된다.

Acknowledgements

이 논문은 2023년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UI210012YD).

References

[1].

I. G. Cumming, F. H. Wong, Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation, Norwood, MA, Artech House, 2005.

[2].

M. Soumekh, Synthetic Aperture Radar Signal Processing with MATLAB Algorithms, New York, NY, John Wiley & Sons, 1999.

[3].

A. Moreira, P. Prats-Iraola, M. Younis, G. Krieger, I. Hajnsek, and K. P. Papathanassiou, “A tutorial on synthetic aperture radar,” IEEE Geoscience and Remote Sensing Magazine, vol. 1, no. 1, pp. 6-43, Mar. 2013.

[4].

H. Y. Lee, “Investigation of SAR systems, technologies and application fields by a statistical analysis of SAR-related journal papers,” Korean Journal of Remote Sensing, vol. 22, no. 2, pp. 153-174, Apr. 2006.

[5].

R. S. Harness, M. C. Budge, “A study on SAR noise jamming and false target insertion,” in IEEE Southeastcon 2014, Lexington, KY, Mar. 2014, pp. 1-8.

[6].

W. Ye, H. Ruan, S. Zhang, and L. Yan, “Study of noise jamming based on convolution modulation to SAR,” in 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, Aug. 2010, pp. 169-172.

[7].

F. Zhou, B. Zhao, M. Tao, X. Bai, B. Chen, and G. Sun, “A large scene deceptive jamming method for space-borne SAR,” IEEE Transactions on Geoscience and Remote Sensing, vol. 51, no. 8, pp. 4486-4495, Aug. 2013.

[8].

S. Long, Z. Hong-rong, T. Yue-Sheng, and Z. Chang-Yao, “Research on deceptive jamming technologies against SAR,” in 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, Oct. 2009, pp. 521-525.

[9].

K. M. Lee, I. H. Lee, S. G. Hong, Y. I. Jeon, I. S. Na, and K. T. Kim, “Analysis of the requirements for effective satellite-borne SAR deceptive jamming,” Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 33, no. 2, pp. 146-159, Feb. 2022.

[10].

G. Turin, “An introduction to matched filters,” IRE Transactions on Information Theory, vol. 6, no. 3, pp. 311-329, Jun. 1960.

[11].

[12].

Q. Sun, T. Shu, K. B. Yu, and W. Yu, “Efficient deceptive jamming method of static and moving targets against SAR,” IEEE Sensors Journal, vol. 18, no. 9, pp. 3610-3618, May 2018.

[13].

Q. Sun, T. Shu, K. B. Yu, and W. Yu, “A novel deceptive jamming method against two-channel SAR-GMTI based on two jammers,” IEEE Sensors Journal, vol. 19, no. 14, pp. 5600-5610, Jul. 2019.