J. Korean Inst. Electromagn. Eng. Sci. 2023; 34(11):811-823

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2023.34.11.811

논문/REGULAR PAPERS

FET 패키지의 스위칭 모델 기법에 관한 연구

홍영기https://orcid.org/0000-0002-9922-6207, 최경륜https://orcid.org/0000-0002-3649-0000, 양지현https://orcid.org/0009-0003-1342-8559, 김의혁*https://orcid.org/0009-0002-0621-3288, 김찬규*https://orcid.org/0000-0001-5470-6824, 나완수https://orcid.org/0000-0002-0315-3294
A Study on the Switching Model Technique of FET Packages
Younggi Honghttps://orcid.org/0000-0002-9922-6207, Gyeong-Ryun Choihttps://orcid.org/0000-0002-3649-0000, Jihyun Yanghttps://orcid.org/0009-0003-1342-8559, Euihyuk Kim*https://orcid.org/0009-0002-0621-3288, Chan-Kyu Kim*https://orcid.org/0000-0001-5470-6824, Wansoo Nahhttps://orcid.org/0000-0002-0315-3294
Author Information & Copyright ▼
성균관대학교 전자전기컴퓨터공학과
*LG전자 선행생산기술연구소
Department of Electrical and Computer Engineering, Sungkyunkwan University)
*Production Engineering Research Institue, LG Electronics
†Corresponding Author: Wansoo Nah (e-mail: wsnah@skku.edu)

© Copyright 2023 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 12, 2023; Revised: Sep 24, 2023; Accepted: Aug 19, 2023

Published Online: Nov 30, 2023

요약

본 논문은 FET의 고주파 기생성분을 추출하고 SPICE 모델에 적용한 FET 패키지의 스위칭 모델을 제안한다. 기생성분을 추출하기 위해 Curve tracer 장비(Keysight Tech. B1506A)와 TPA(two probe analysis), 2-포트 측정을 사용한다. FET의 커패시턴스는 VDS에 따라 소자 용량이 변화하여 2-포트 측정 시 바이어스 티를 추가로 연결하는 측정법을 제시하였다. 세 가지 방법으로 추출한 커패시턴스를 비교하여 추출한 기생성분의 타당성을 보였다. 추출한 기생성분을 SPICE 모델에 적용하기 위해 제조사 SPICE 모델을 분석하였으며, 다이오드의 커패시턴스 수식을 사용하였다. 적용한 SPICE 모델은 측정으로 도출한 Z-파라미터와 정합성 비교를 통해 검증하였고, 스위칭 노이즈 재현을 위해 FET의 스위칭 회로를 사용하였다. 시뮬레이션과 측정의 정합성을 높이기 위해 FET가 실장되는 PCB의 기생성분과 파워 서플라이의 입력 임피던스를 추출해 시뮬레이션에 적용하였으며, 시뮬레이션과 측정간 드레인-소스 전압 및 드레인 전류의 정합성을 비교하였다. 이를 통해 제안한 FET의 기생성분 측정법 및 SPICE 모델의 유의미함을 보였다.

Abstract

This study proposes a switching model for field-effect transistor (FET) packages by extracting the high-frequency parasitic components of the FET and applying them to a SPICE model. To extract the parasitic components, a curve-tracer device (Keysight Tech. B1506A), two probe analysis (TPA), and 2-port method are used. The capacitance of the FET varies depending on the drain-source voltage (VDS), thus a measurement method is proposed by connecting an additional bias tee when measuring using the 2-port method. which varies with VDS, a measurement technique involving an additional bias tee is introduced during the 2-port method. The effectiveness of the extracted parasitic components is demonstrated by comparing the capacitance values obtained using the three methods. To apply the extracted parasitic components to the SPICE model, the existing SPICE model was analyzed and the capacitance formula of the diode was used. The applied SPICE model was verified through a consistency comparison with the measured Z-parameters, and an FET switching circuit is used to reproduce the switching noise. To improve the consistency between the simulation and measurement, the parasitic components of the PCB on which the FET is mounted and the input impedance of the power supply are extracted and applied to the simulation, and the consistency of the drain-source voltage and drain current between the simulation and measurement are compared. Thus, the significance of the proposed FET parasitic component measurement method and the SPICE model is demonstrated.

Keywords: MOSFET(Metal-Oxide-Semiconductor Field-Effect Transistor); Switching Noise; Parasitic Components; SPICE Modeling; Z-Parameter

Ⅰ. 서 론

전력 MOSFET(metal-oxide-semiconductor field effect transistor)의 스위칭 손실은 수동 부품의 크기를 줄이기 위해 스위칭 주파수가 증가함에 따라 전력 전자 컨버터의 총 전력 손실에서 지배적인 요인이 되고 있다. 그러나 전력 MOSFET의 스위칭 동작 및 스위칭 손실은 기생 커패시턴스의 비선형 특성 및 전력 전자 컨버터의 유도 부하로 인해 모델링하기 어렵다. 전력 반도체 제조사에서는 제작 이전 MOSFET의 특성을 회로 시뮬레이션에서 분석할 수 있도록 SPICE 모델을 일반적으로 제공한다. 제조사에서 제공하는 SPICE 모델에는 온도 변화에 따른 특성 변화, 다이오드 특성 등이 반영되어 있으나, 특정 상황에 한하여 제공되는 경우가 대부분이다. 그리고 시간영역에서 회로 시뮬레이션을 진행할 경우 전극에서 발생하는 기생 인덕턴스 등의 부재로 인해 측정과 오차가 발생한다. 오차는 시간 영역에서 전류, 전압의 오버슈트, 언더슈트, 상승/하강 시간 등 과도 성분에서 발생한다. 따라서 MOSFET의 기생성분을 정확하게 모사하여 SPICE 모델에 반영하는 연구가 필요하다. MOSFET의 기생성분을 추출하는 연구는 기존 연구에서도 진행된 바 있으며, 두 개의 inductive 프로브를 이용해 FET의 루프 임피던스를 추출하고 FET의 등가모델은 고주파 등가회로를 사용한다[1]. 하나의 프로브로는 신호 발생기를 이용해 소신호를 인가하고, 다른 하나의 프로브는 오실로스코프를 이용해 전류를 측정한다. 루프 임피던스는 옴의 법칙을 이용하여 프로브가 위치한 전압을 측정해 추출할 수 있다. 드레인, 게이트, 소스가 하나의 노드로 연결된 회로에서 각 세 번의 임피던스를 측정하며, 각 노드에서 바라본 임피던스 수식을 연립하여 FET의 드레인, 게이트, 소스의 임피던스를 추출한다. 이러한 프로브를 이용한 추출법은 회로가 동작하고 있는 상태에서도 측정이 가능하며 간접적으로 임피던스를 추출할 수 있어 측정회로에 영향을 주지 않는다는 장점이 있지만 저주파에서 프로브에 유기되는 전압이 작아져 측정된 임피던스의 변화가 심하다는 단점이 있다. VNA(vector network analyzer)를 이용하여 2-포트 측정을 통해 FET의 드레인, 게이트, 소스의 임피던스를 측정하여 저주파에서의 측정 정확도를 높일 수 있다[2]. FET의 등가 모델은 고주파 등가회로를 사용하며, 드레인과 소스에 VNA 포트를 연결하고 게이트는 접지한다. 이를 통해 추출한 S-파라미터를 Z-파라미터로 변환하여 드레인, 게이트, 소스 브랜치의 임피던스를 추출한다. 추출한 임피던스로부터 R, L, C가 우세한 주파수에서 각 소자값을 도출한다. 2-포트 측정법은 프로브를 이용한 측정법보다 저주파에서 임피던스의 변화가 적은 장점이 있다. 그러나 VNA를 사용할 경우 기기의 한계로 인해 Vds의 입력값에 제한이 있게 되며 이에 따라 Vds의 변화에 따른 FET의 특성 변화 측정 범위에 제약이 있게 된다. 본 논문에서는 저주파의 측정 정확도 개선 및 VNA를 사용한 Vds의 인가를 위해 바이어스 티(bias-T)를 사용하였다. 제안한 방법으로 Vds에 따라 변화하는 기생성분을 추출하기 위한 2-포트 측정법의 문제점을 보안하였으며, On-Semiconductor사의 NVTFS5826NL MOSFET을 사용하여 20 kHz~400 MHz에서의 FET의 고주파 특성을 분석하여 FET 패키지의 고주파 SPICE 모델 개발 및 실험을 통해 데이터와 정합성을 맞춰 유효성을 보이고자 한다.

Ⅱ. FET 소자의 I-V 특성 곡선 SPICE 모델링

MOSFET이 동작할 수 있는 구간은 cut-off, triode, saturation 영역으로 나뉜다. Cut-off 영역은 VGS > Vth, VDS ≥ 0인 상태로, 전류가 흐르지 않아 MOSFET이 꺼진 상태이다. Triode 영역은 MOSFET을 주로 증폭기로 사용하는 영역으로서 VGS > Vth, VDS < VGS−Vth인 상태로 선형 저항 소자처럼 동작하며, 전류가 드레인과 소스 사이에 존재해 VDS가 증가함에 따라 드레인 전류(IDS)가 증가한다. Saturation 영역은 VGS > Vth, VDS > VGS−Vth인 상태로 전류가 포화되어 VDS에 무관하고 VGS에만 의존한다. 이 세 구간의 드레인 전류와 드레인-소스 전압(VDS)을 Y축과 X축으로 하는 곡선을 I-V 특성 곡선이라 한다. 이를 이용해 MOSFET의 동작 구간을 정하고 설계를 하게 된다. 본 장에서는 curve tracer(Keysight Tech. B1506A) 장비를 사용해 I-V 특성 곡선을 측정하고 제조사에서 제공된 SPICE 모델을 이용하여 시뮬레이션한 I-V 특성 곡선과 정합성을 비교하고자 한다.

I/V 특성 곡선을 시뮬레이션으로 재현하기 위해서는 실제 측정 환경을 모사하여야 한다. 이를 위해 MOSFET이 실장되는 PCB 라인의 기생 저항 성분을 추출할 필요가 있다. PCB 라인의 기생 저항 성분은 그림 1처럼 Ansys사의 Q3D 시뮬레이션으로 도출하였다.

jkiees-34-11-811-g1
그림 1. | Fig. 1. PCB 라인의 Q3D 시뮬레이션 | Q3D simulation of PCB line.
Download Original Figure

PCB 기판의 기생성분을 추출한 후 I/V 특성 곡선을 위한 전체 시뮬레이션에 적용하여 진행하였으며, 회로는 그림 2와 같다.

jkiees-34-11-811-g2
그림 2. | Fig. 2. I/V 특성 곡선 추출 회로 | Circuit of I/V curve extraction.
Download Original Figure

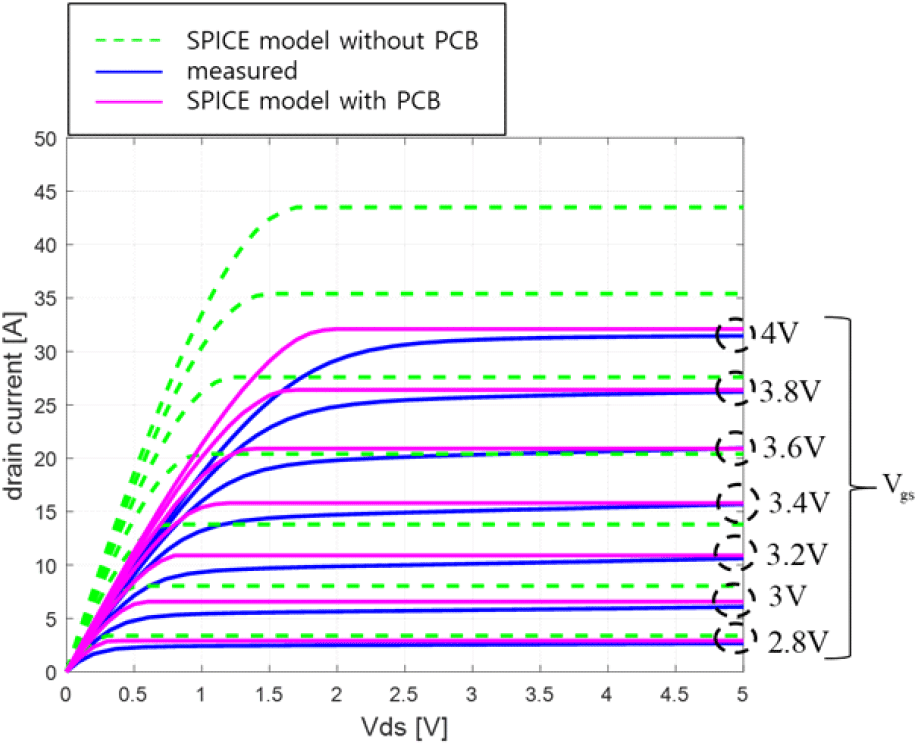
측정과 시뮬레이션 모두 VDS는 0~5 V, VGS는 2.8 V부터 4 V까지 0.2 V 간격으로 인가해주었으며, 결과는 그림 3과 같다. 녹색 점선 그래프는 PCB 기생성분이 없는 SPICE 모델 단일 시뮬레이션 결과이고 파란색은 측정, 빨간색은 PCB의 기생성분을 적용한 시뮬레이션 결과이다. 드레인 전류의 높은 정합성과 측정-시뮬레이션의 결과를 통해 MOSFET이 실장된 PCB의 영향이 크다는 것을 볼 수 있다.

jkiees-34-11-811-g3
그림 3. | Fig. 3. I/V 특성 곡선 | I/V curve.
Download Original Figure

Ⅲ. FET 소자의 기생성분 추출

제조사로부터 제공된 SPICE 모델은 MOSFET의 기생성분이 커패시턴스와 각 선로에 대한 저항 성분으로 구성되어 있다. 하지만 MOSFET의 커패시턴스는 VDS의 크기에 따라 용량이 달라지나 SPICE 모델에는 반영되어 있지 않다. 본 장에서는 TPA(two probe analysis)[3]와 2-포트 측정을 통해 커패시턴스를 추출하고 추가로 2-포트 측정에서는 저항 및 PCB 라인과 MOSFET 전극에 대한 인덕턴스를 추출하고자 한다.

3-1 TPA (Two Probe Analysis)

그림 4에 TPA 측정의 모식도를 나타내었으며 그림 5에 TPA 측정의 등가회로를 나타내었다. V1은 포트 1에서 인가되는 전압에 해당하는 전압원이며 Vp2는 수신 프로브가 있는 포트2에서 측정된 전압이다. 포트1과 포트2의 임피던스는 50 Ω이고, L1과 L2는 각 주입 프로브와 수신 프로브의 1차 인덕턴스, Lw와 rw는 회로 루프를 형성하는 와이어의 인덕턴스와 저항이다. M1은 주입 프로브와 회로 루프 사이의 상호 인덕턴스이고 M2는 수신 프로브와 회로 루프 사이의 상호 인덕턴스이다. Zp1과 Zp2는 주입 프로브와 수신 프로브의 입력 임피던스이다. 최종적으로 TPA 측정법을 통해 측정하고자 하는 임의의 임피던스 ZX는 식 (1)과 같다[3].

Z X = K V p 1 V p 2 − Z setup  = K S 11 + 1 S 21 − Z setup  V p 1 = V 1 + ( 1 + S 11 ) ,   V p 2 = S 21 V 1 +
(1)
jkiees-34-11-811-g4
그림 4. | Fig. 4. TPA의 기본 셋업 | Basic setup of TPA.
Download Original Figure
jkiees-34-11-811-g5
그림 5. | Fig. 5. TPA 측정 셋업의 등가 회로 | Equivalent circuit of TPA measurement setup.
Download Original Figure

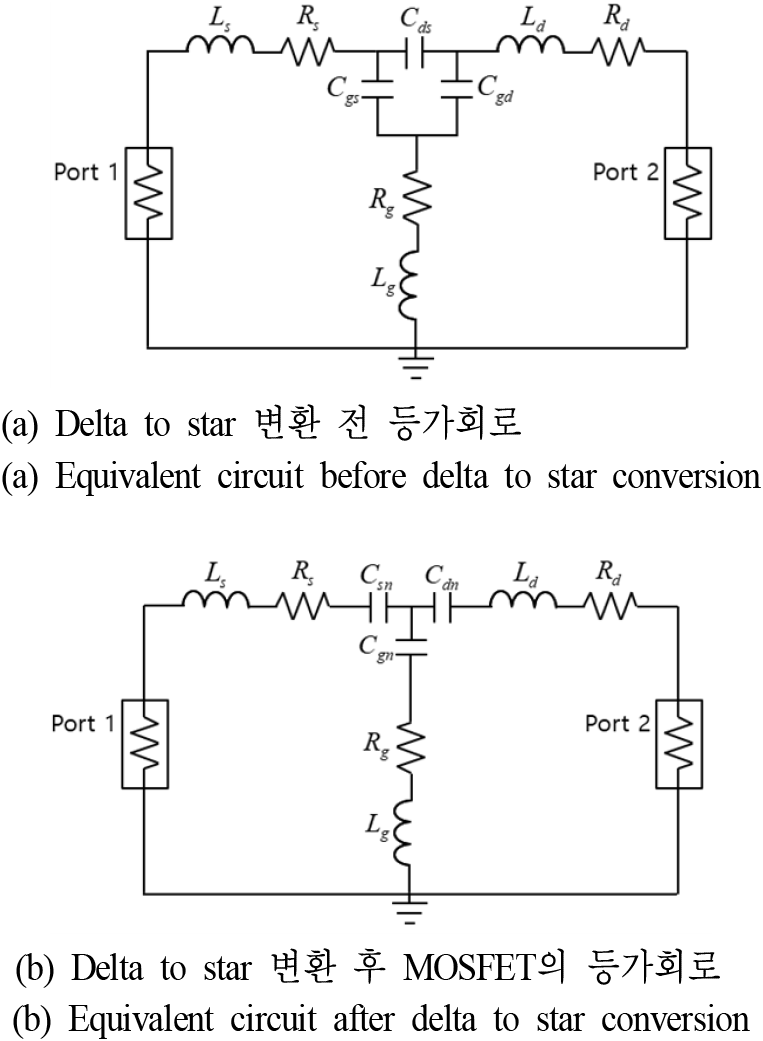
K와 Zsetup은 상수이며, 알고 있는 저항 2.2 Ω, 47 Ω 2개를 측정하여 두 수식의 연립으로 구하였다. TPA를 이용한 MOSFET의 커패시턴스 추출은 MOSFET의 고주파 등가회로 모델을 사용해야 한다. MOSFET의 커패시턴스는 그림 6(a)와 같이 델타 형태로 되어 있으며, 임피던스 추출의 편의성을 위해 식 (2)를 이용하여 delta to star 변환을 한다.

C d n = C g d + C d s + C g d C d s C g s C g n = C g d + C g s + C g d C g s C d s C s n = C g s + C d s + C g s C d s C g d
(2)
jkiees-34-11-811-g6
그림 6. | Fig. 6. MOSFET의 등가회로 모델 | Equivalent circuit model of MOSFET.
Download Original Figure

변환한 등가회로는 그림 6(b)와 같고 Zdn, Zgn, Zsn는 R, L, C가 직렬로 연결된 선로의 합성 임피던스이다.

그림 7의 회로는 TPA를 이용하여 MOSFET의 커패시턴스 추출을 위한 회로이며, 실제 측정 셋업은 그림 8과 같다. 프로브는 Tektronix사의 CT1을 사용하였으며, 주파수 범위는 25 kHz~1 GHz이다. Zext는 각 라인의 기생 임피던스이다. MOSFET에 DC 파워 서플라이로 VDS 전압을 인가하기 위해 1 uF 커패시터를 사용해 DC 개방 및 주파수 신호를 단락하였다. 그 후 a, b, c 노드에서 TPA를 이용하여 회로 루프에 대한 임피던스를 추출하였다.

Z a = Z e x t 1 + Z 1 μ F + Z d n + ( Z e x t 2 + Z g n ) ( Z e x t 3 + Z s n ) ( Z e x t 2 + Z g n ) + ( Z e x t 3 + Z s n ) Z b = Z e x t 2 + Z g n + ( Z e x t 1 + Z 1 μ F + Z d n ) ( Z e x t 3 + Z s n ) ( Z e x t 1 + Z 1 μ F + Z d n ) + ( Z e x t 3 + Z s n ) Z c = Z e x t 3 + Z s n + ( Z e x t 1 + Z 1 μ F + Z d n ) ( Z e x t 2 + Z g n ) ( Z e x t 1 + Z 1 μ F + Z d n ) + ( Z e x t 2 + Z g n )
(3)
jkiees-34-11-811-g7
그림 7. | Fig. 7. TPA의 MOSFET 측정 회로 | MOSFET measurement circuit of TPA.
Download Original Figure
jkiees-34-11-811-g8
그림 8. | Fig. 8. TPA의 MOSFET 측정 회로 셋업 | MOSFET measurement circuit setup of TPA.
Download Original Figure

추출한 임피던스는 각 노드에서 바라본 입력 임피던스이므로 수식으로 나타내면 식 (3)과 같다. 세 개의 수식을 식 (4)와 같다.

Z d n = − 2 Z a Z b Z c ( Z a Z b + Z a Z c − Z b Z c ) Z a 2 Z b 2 − 2 Z a 2 Z b Z c + Z a 2 Z c 2 − 2 Z a Z b 2 Z c − 2 Z a Z b Z c 2 + Z b 2 Z c 2 − ( Z e x t 1 + Z 1 μ F ) Z g n = − 2 Z a Z b Z c ( Z a Z b − Z a Z c + Z b Z c ) Z a 2 Z b 2 − 2 Z a 2 Z b Z c + Z a 2 Z c 2 − 2 Z a Z b 2 Z c − 2 Z a Z b Z c 2 + Z b 2 Z c 2 − Z e x t 2 Z sn  = − 2 Z a Z b Z c ( − Z a Z b + Z a Z c + Z b Z c ) Z a 2 Z b 2 − 2 Z a 2 Z b Z c + Z a 2 Z c 2 − 2 Z a Z b 2 Z c − 2 Z a Z b Z c 2 + Z b 2 Z c 2 − Z e x t 3
(4)

VDS가 0 V일 때 추출한 Zdn, Zgn, Zsn의 임피던스 그래프는 그림 9이며, 커패시턴스가 우세한 주파수 대역에서 임피던스를 추출한다. 추출한 임피던스는 커패시턴스의 임피던스 수식을 통해 Cdn, Cgn, Csn으로 도출할 수 있으며, 식 (5)와 같은 delta to star 역변환 수식으로 Cgs, Cds, Cgd를 추출할 수 있다.

C g d = C g n C d n C d n + C g n + C s n C g s = C g n C s n C d n + C g n + C s n C d s = C d n C s n C d n + C g n + C s n
(5)
jkiees-34-11-811-g9
그림 9. | Fig. 9. Zdn, Zgn, Zsn의 임피던스 그래프 | Impedance graph of Zdn, Zgn, Zsn.
Download Original Figure

추출한 Cgs, Cds, Cgd를 데이터시트와 비교하기 위해 Ciss, Coss, Crss로 변환하며, 변환 수식은 식 (6)과 같다.

C i s s = C g s + C g d C o s s = C d s + C g d C r s s = C g d
(6)

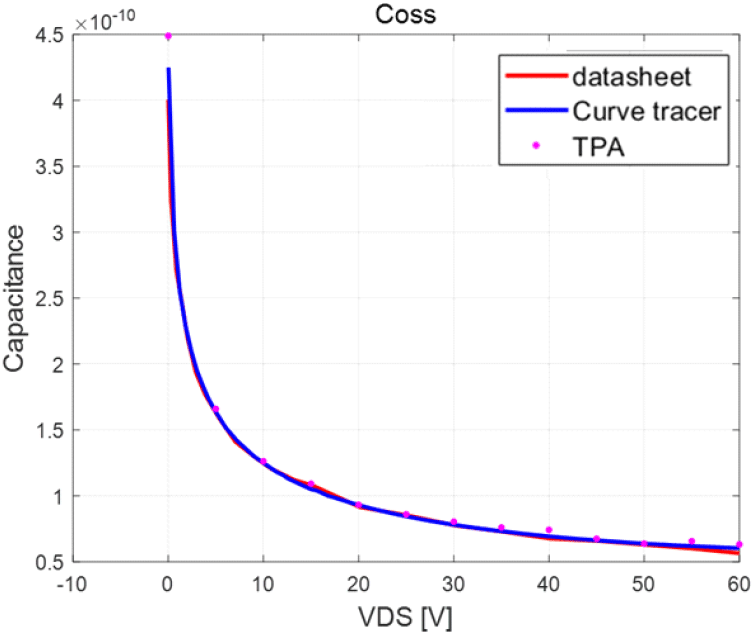
데이터 시트, TPA, curve tracer 장비로 추출한 커패시턴스를 비교한 결과를 그림 10~그림 12에서 나타내었다. Ciss는 데이터 시트와 오차가 발생하지만 curve tracer를 이용한 결과와 정합성이 높은 것을 알 수 있다. 장비 측정 결과와 정합성이 높을 것을 보아 실제 소자와 데이터 시트의 차이가 발생하며, TPA 측정의 유효성을 보였다.

jkiees-34-11-811-g10
그림 10. | Fig. 10. Ciss의 그래프 | Graph of Ciss.
Download Original Figure
jkiees-34-11-811-g11
그림 11. | Fig. 11. Coss의 그래프 | Graph of Coss.
Download Original Figure
jkiees-34-11-811-g12
그림 12. | Fig. 12. Crss의 그래프 | Graph of Crss.
Download Original Figure
3-2 2-포트 측정

2-포트 측정법은 TPA 측정법과 동일한 MOSFET의 고주파 등가회로를 사용하며 등가회로는 그림 13과 같다. 포트1과 포트2는 VNA의 포트 단자이며, 측정된 S-파라미터를 Z-파라미터로 변환하여 각 브랜치에 있는 R, L, C 값을 추출하였다. Z-파라미터의 정의에 의해 각 브랜치를 식 (7)과 같이 나타낼 수 있다.

Z 11 = V 1 I 1 | I 2 = 0 = Z s + Z g Z 12 = V 1 I 2 | I 1 = 0 = Z g Z 21 = V 2 I 1 | I 2 = 0 = Z g Z 22 = V 2 I 2 | I 1 = 0 = Z d + Z
(7)
jkiees-34-11-811-g13
그림 13. | Fig. 13. MOSFET의 등가회로 | Equivalent circuit of MOSFET.
Download Original Figure

VDS를 인가하기 위해 그림 13의 실험 셋업에서 주파수 범위 25 kHz~1 GHz를 가지는 바이어스 티(mini-circuits사의 ZX85-12G-S+)를 추가하였으며, 그림 14에 바이어스 티가 추가된 등가회로를 나타내었다.

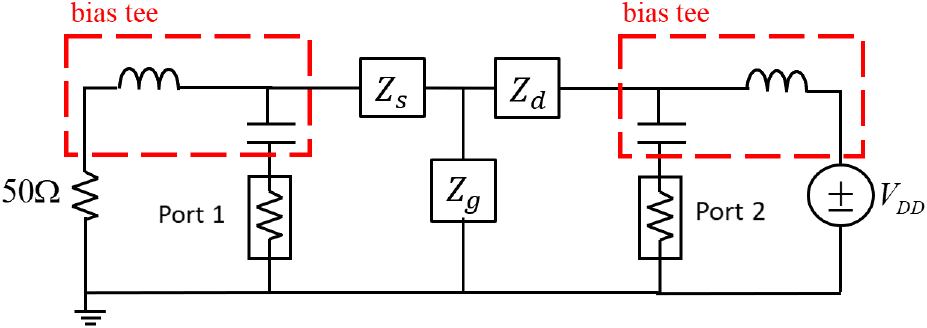
jkiees-34-11-811-g14
그림 14. | Fig. 14. 바이어스 티(ZX85-12G-S+)를 사용한 등가회로 | Equivalent circuit using bias tee (ZX85-12G-S+).
Download Original Figure

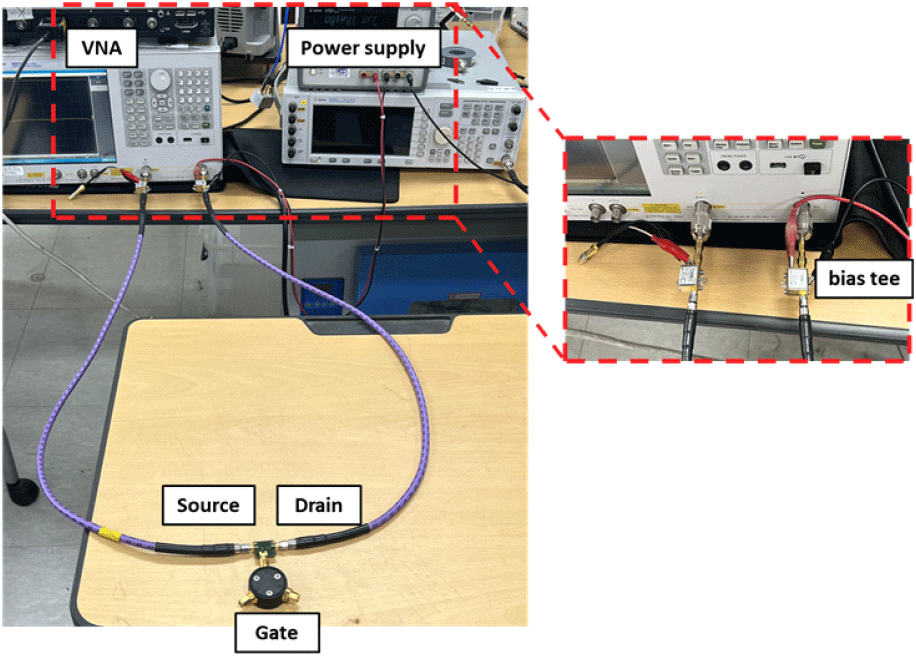
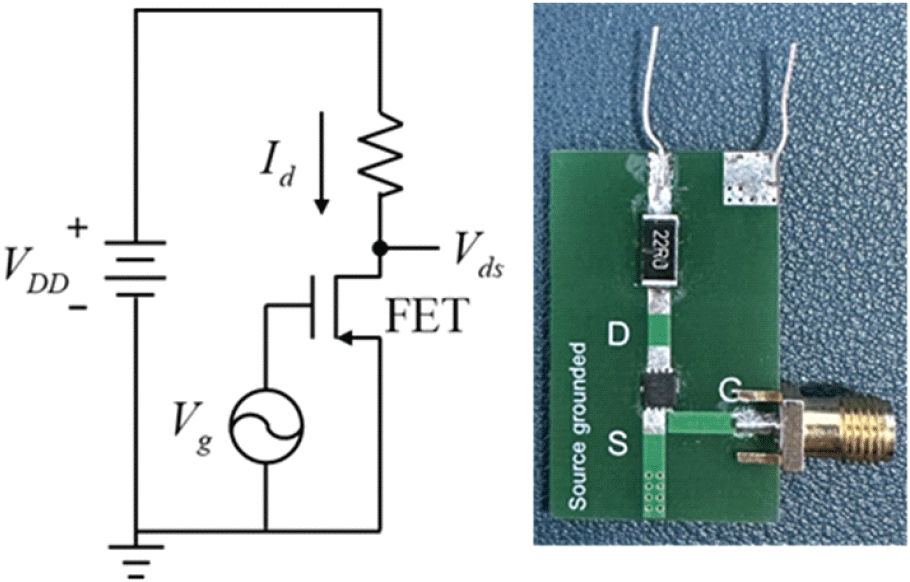
MOSFET의 드레인에 파워 서플라이를 사용해 전압 VDS를 인가하고 소스는 50 Ω 종단하였다. 측정 시 바이어스 티의 영향을 제거하기 위해 바이어스 티를 연결한 상태에서 VNA 교정을 실시하였으며, 실제 실험 셋업은 그림 15와 같다.

jkiees-34-11-811-g15
그림 15. | Fig. 15. 2-포트 측정 실험 셋업 | Two-port method experiment setup.
Download Original Figure

바이어스 티 유무에 따른 S-파라미터 그래프는 그림 16과 같으며, 주파수대역 300 kHz 이상에서 바이어스 티 유무에 상관없이 S-파라미터가 동일하게 나오는 것을 볼 수 있다. 이를 통해 VDS전압을 인가하며 기생성분 추출이 가능하다는 것을 확인하였다.

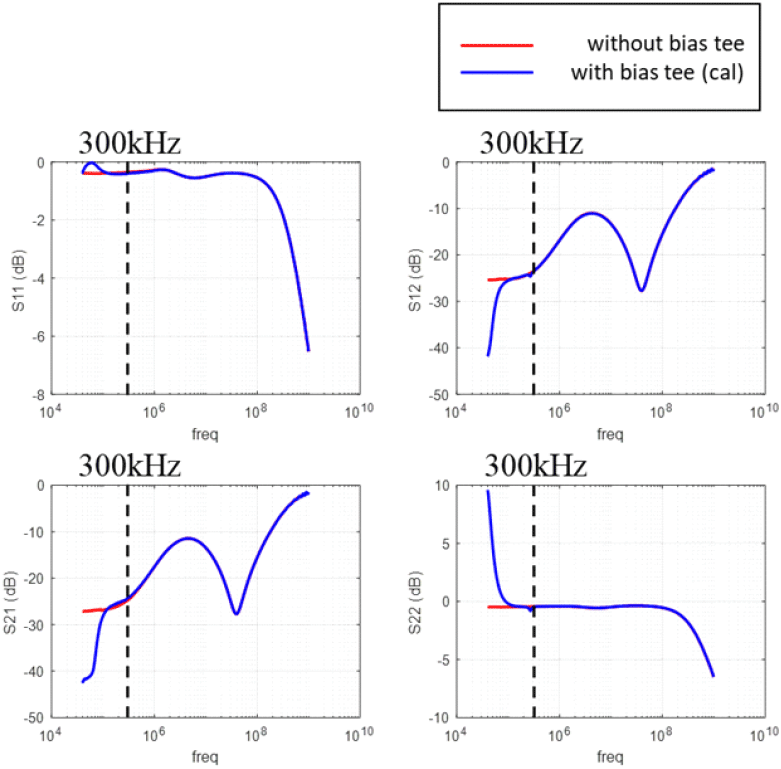
jkiees-34-11-811-g16
그림 16. | Fig. 16. 바이어스 티 유무에 대한 S-파라미터 그래프 | S-parameter graph with and without bias tee.
Download Original Figure

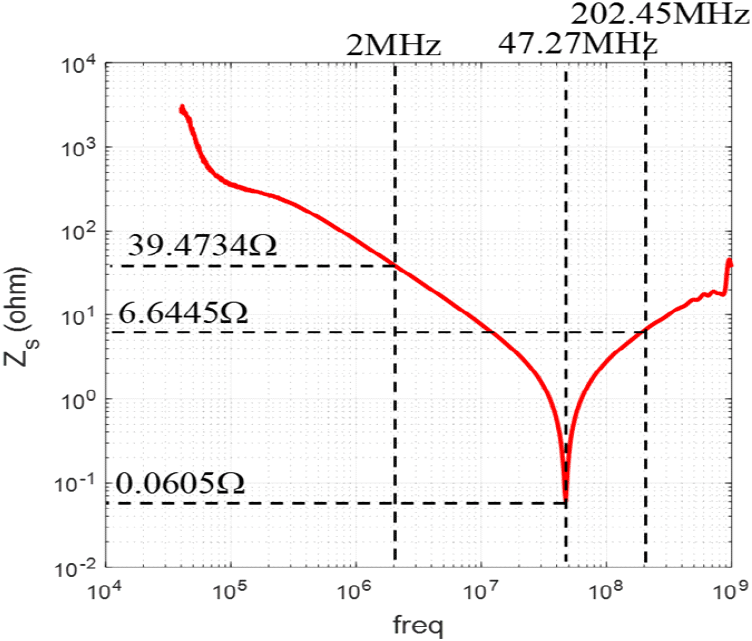
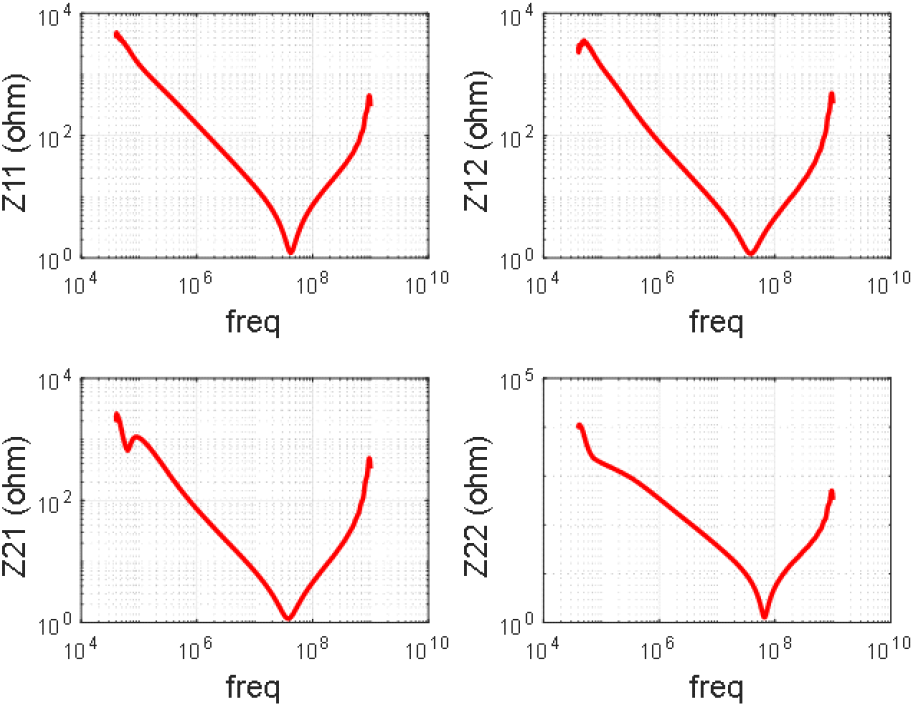
그림 17에 측정된 MOSFET의 Z-파라미터를 나타내었으며, Zd, Zg, Zs를 추출하기 위해 식 (7)을 이용하였다. VDS가 0 V일 때 Zs(=Z11−Z12) 그래프는 그림 18이고, TPA 측정법과 동일하게 커패시턴스 우세한 부분에서 임피던스 및 주파수를 이용해 커패시턴스를 추출하였다. 저항과 인덕턴스의 경우, 공진주파수와 공진 임피던스를 이용하여 구하였다. VDS의 전압을 바꿔가며 측정을 하였으며, 그 결과를 표 1에 나타내었다.

jkiees-34-11-811-g17
그림 17. | Fig. 17. 2-포트 측정을 이용한 MOSFET의 Z-파라미터 | Z-parameter of MOSFET using 2-port measurement.
Download Original Figure
jkiees-34-11-811-g18
그림 18. | Fig. 18. VDS=0 V일 때 Zs 그래프 | Zs graph at VDS=0 V.
Download Original Figure
표 1. | Table 1. 2-포트 측정법으로 추출한 기생성분 | Parasitic components extracted by 2-port measurement method.
VDS [V] Rd [Ω] Rg [Ω] Rs [Ω] Cgd [pF] Cgs [pF] Cds [pF] Ld [nH] Lg [nH] Ls [nH]
0 0.223 1.17 0.061 236.8 882.6 235.4 5.89 8.664 5.681
5 0.498 1.13 0.115 99.47 922 65.9 6.181 8.241 5.766
10 0.649 1.117 0.137 79.92 911.1 46.51 6.168 8.153 5.79
15 0.798 1.11 0.145 69.73 900.9 37.18 6.246 7.929 5.899
20 0.906 1.103 0.156 62.91 892.8 31.74 6.111 8.023 5.914
25 1.007 1.098 0.16 58.25 886.8 27.77 6.037 8.186 5.83
30 1.103 1.095 0.163 54.44 880.9 25.18 5.961 7.986 5.936
Download Excel Table

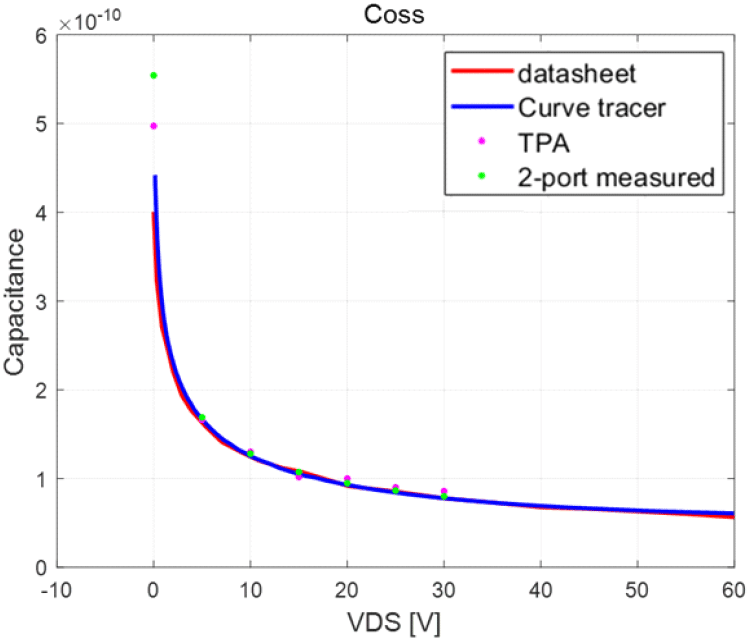
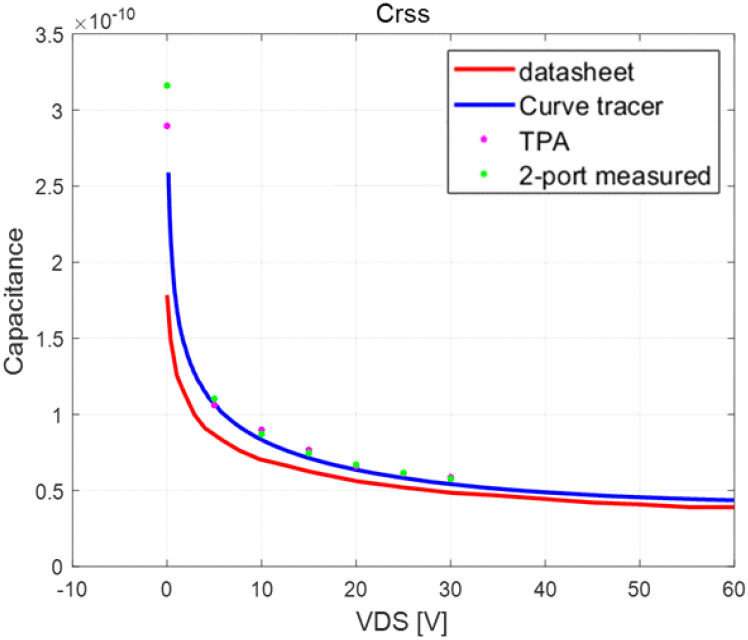
커패시턴스 정확성 검증을 위해 식 (6)을 이용해 데이터 시트, curve tracer, TPA 측정법으로 추출한 결과 비교 그래프는 그림 19~그림 21과 같다. Curve tracer와 TPA의 결과와 잘 일치하여 2-포트 측정법의 유효성을 보였다.

jkiees-34-11-811-g19
그림 19. | Fig. 19. Ciss의 그래프 | Graph of Ciss.
Download Original Figure
jkiees-34-11-811-g20
그림 20. | Fig. 20. Coss의 그래프 | Graph of Coss.
Download Original Figure
jkiees-34-11-811-g21
그림 21. | Fig. 21. Crss의 그래프 | Graph of Crss.
Download Original Figure

TPA와 2-포트 측정법으로 추출한 커패시턴스가 잘 일치하나 TPA 측정법의 경우 고주파에서의 임피던스의 변화가 심하여 커패시턴스만 추출할 수 있다. 하지만 2-포트 측정법의 경우 고주파에서 임피던스의 변화가 심하지 않아 인덕턴스, 저항값도 추출이 가능하여 SPICE 모델에 추출한 기생성분을 적용할 때 파라미터들은 2-포트 측정법으로 추출한 기생성분을 사용하였다.

Ⅳ. 제조사 제공 SPICE 모델의 수정

SPICE 모델은 디바이스 모델과 sub-circuit 모델 2종류로 분류된다. 본 논문의 MOSFET SPICE 모델은 sub-circuit 모델이고, 디바이스 모델의 조합으로 하나의 회로를 객체로 만들어주는 역할을 한다. 주로 SPICE 명령문으로 프로그래밍되며, Keysight사의 ADS(advanced design system) 시뮬레이션을 이용하여 SPICE 명령문을 회로화하여 SPICE 모델을 수정하였다.

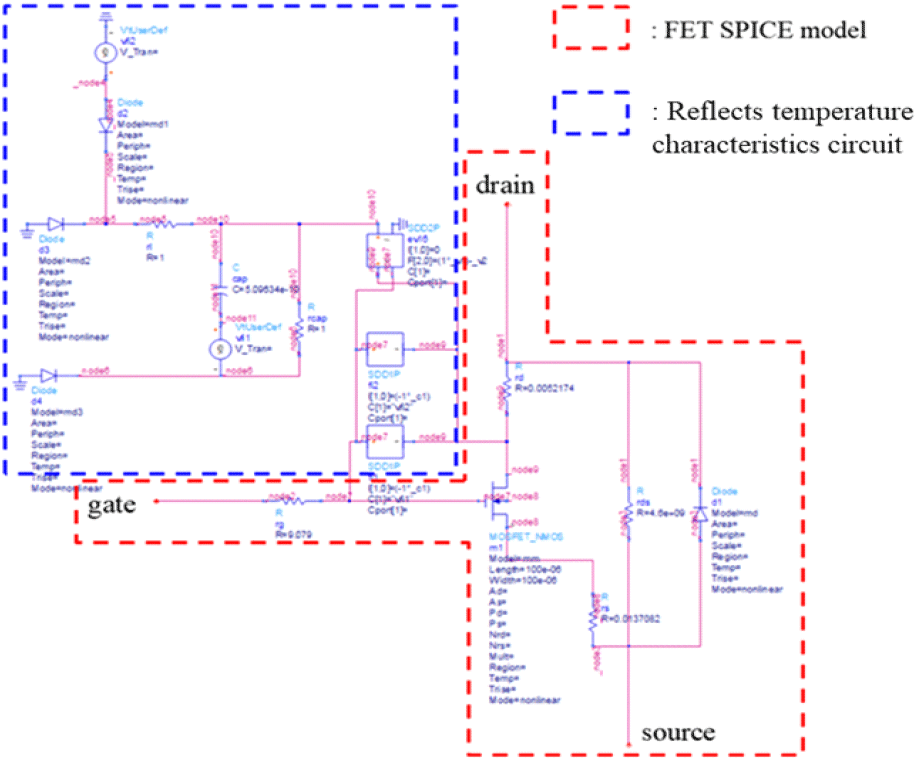
그림 22은 제조사에서 제공된 MOSFET의 기본 SPICE 모델이다. 빨간 네모박스 안 회로는 MOSFET의 기생 성분과 FET 모델이며, 파란 네모박스 안 회로는 온도 특성을 반영해주는 회로이다. 앞서 추출한 기생성분들을 빨간 네모박스 회로에 적용하였으며 그림 23에 나타내었다. SPICE 모델에 반영한 기생성분은 Ⅴ장에서 사용된 스위칭회로의 드레인-소스 전압과 동일하게 5 V일 때 추출한 기생성분을 사용하였다. 추출한 저항은 그림 23의 초록박스 안의 SPICE 모델의 드레인, 소스, 게이트 저항의 값을 변경하였으며, 인덕턴스는 MOSFET의 전극과 MOSFET이 실장되는 PCB 라인의 영향이므로 드레인, 소스, 게이트 단자에 그림 23의 파란박스처럼 추가하였다. Cgs, Cgd의 경우 그림 23의 우측 빨간박스처럼 FET 모델 파라미터에 포함되어 있으며, 채널 폭의 단위 길이당 커패시턴스로 정의가 되어있다. 채널 폭은 MOSFET 심볼에서 확인할 수 있고, 추출한 Cgs, Cgd를 채널 폭의 단위길이당 커패시턴스로 값을 계산하여 SPICE 모델에 적용하였다.

jkiees-34-11-811-g22
그림 22. | Fig. 22. MOSFET의 제조사 SPICE 모델 | Original SPICE model of MOSFET.
Download Original Figure
jkiees-34-11-811-g23
그림 23. | Fig. 23. MOSFET의 물성 파라미터 | MOSFET physical property parameters.
Download Original Figure

그림 24는 MOSFET의 단면도이다. MOSFET의 포트는 주로 바디와 소스가 한 단자로 연결된 형태이다. 따라서 Cds의 경우 바디 다이오드 양단의 임피던스로 나타낼 수 있으며, MOSFET의 SPICE 모델을 확인해본 결과 FET 소자에는 드레인-소스 커패시턴스가 존재하지 않고 다이오드의 임피던스가 커패시턴스로 보이는 것을 확인하였다. 따라서 추출한 Cds를 SPICE 모델에 적용시키기 위해서는 다이오드 모델의 접합 커패시턴스 파라미터를 수정하여야 한다. 다이오드 모델의 커패시턴스 수식은 식 (8)과 같다.

C d i o d e   =   C d i f f   +   C j   +   C d   ×   A r e a C d i f f   =   T f   ×   g d e x p C j   =   A r e a   ×   C j o   ×   1 −   V d V j − M
(8)
jkiees-34-11-811-g24
그림 24. | Fig. 24. MOSFET의 단면도 | Cross section of MOSFET.
Download Original Figure

Vd는 다이오드 양단 전압이며, 물성 파라미터는 다이오드 모델에 정의되어 있다. 물성 파라미터 중 Cjo(접합 커패시턴스)를 수정, 계산하여 Cds를 SPICE 모델에 적용시켰으며, 임피던스를 추출한 결과는 그림 25와 같다. 추출한 기생성분이 SPICE 모델에 잘 적용되었는지 확인하기 위해 그림 26처럼 SPICE 모델과 측정 Z-파라미터를 비교하였다.

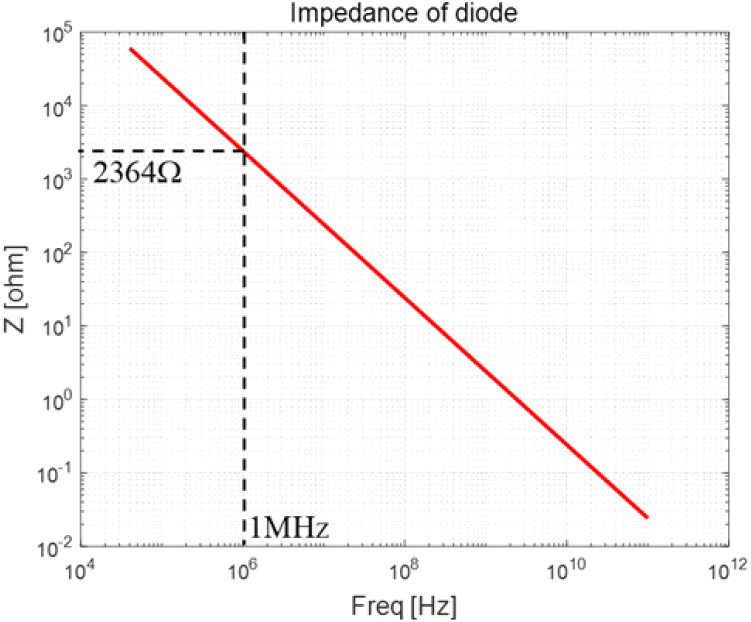
jkiees-34-11-811-g25
그림 25. | Fig. 25. SPICE 모델 내 다이오드의 임피던스 그래프 | Impedance graph of a diode in SPICE model.
Download Original Figure
jkiees-34-11-811-g26
그림 26. | Fig. 26. SPICE 모델과 측정의 Z-파라미터 | Z-parameters of SPICE model and measurement.
Download Original Figure

측정 Z-파라미터는 제조사로부터 제공된 SPICE 모델과 차이가 나는 것을 확인하였으며, 추출한 기생성분을 적용한 SPICE 모델과는 100 kHz~200 MHz에서 잘 일치함을 확인하였다. 200 MHz 이상 주파수에서는 PCB의 기생성분으로 인해 차이가 발생하며, 100 kHz 이하 주파수에서는 바이어스 티에 존재하는 인덕턴스의 영향으로 그림 16에서도 차이를 볼 수 있다.

Ⅴ. 시뮬레이션, 측정 간 정합성 비교

본 장에서는 Ⅳ장에서 튜닝된 SPICE 모델을 이용하여 간단한 스위칭 회로에서 측정과 시뮬레이션의 정합성을 보고자 한다. 실험에 사용할 스위칭 회로는 그림 27과 같다.

jkiees-34-11-811-g27
그림 27. | Fig. 27. MOSFET의 스위칭 회로 | Switching circuit of MOSFET.
Download Original Figure
jkiees-34-11-811-g28
그림 28. | Fig. 28. 스위칭 회로 실험 셋업 | Switching circuit experiment setup.
Download Original Figure

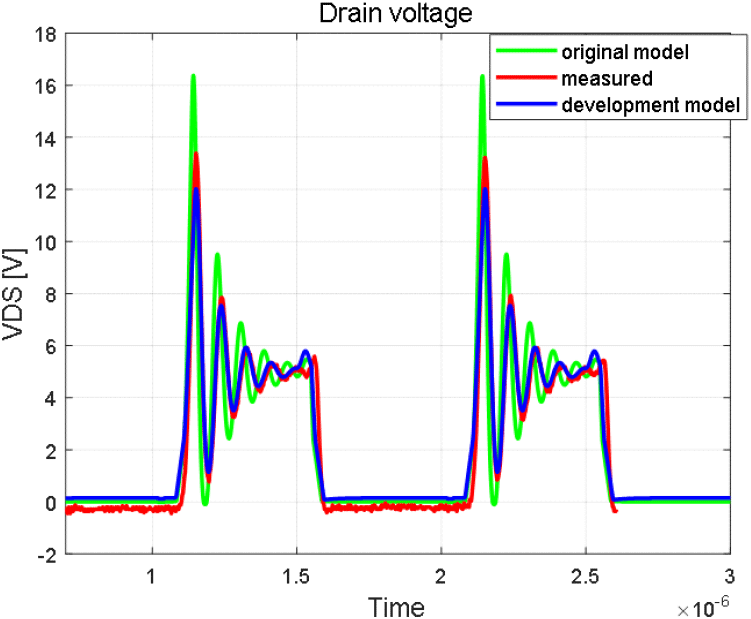
저항은 22 Ω을 사용하였으며 VDD는 5 V, 게이트 바이어스는 주파수 1 MHz, 크기는 0~5 V 구형파를 인가하였다. 시뮬레이션과의 정합성을 높이기 위해 파워 서플라이의 입력 임피던스를 VNA로 추출하여 반영하였다. 회로 시뮬레이션은 Keysight사의 ADS 시뮬레이션을 사용하였고, 회로는 그림 29와 같다. 시뮬레이션과 측정 Vds 및 드레인 전류 비교 그래프는 그림 30 및 그림 31과 같다. 측정의 첫 번째 피크 전압은 13.38 V이며, 기존 모델은 16.37 V, 개발 모델은 12.01 V로 오차율 22.3 %에서 10.2 %로 줄어들었다. 또한 두 번째 피크 전압은 측정이 7.84 V, 기존 모델은 9.51 V, 개발 모델이 7.54 V로 오차율 21.3 %에서 3.8 %로 줄어들었다. 드레인 전류의 상승시간의 경우 측정이 104 ns, 기존 모델은 121 ns, 개발 모델이 103.7 ns로 오차율 16.3 %에서 0.3 %로 줄어들었다. 기존 모델보다 개발 모델이 측정 결과와의 오차가 더 개선된 것을 볼 수 있으며, 이를 통해 MOSFET 패키지의 스위칭 모델의 유효성을 보였다.

jkiees-34-11-811-g29
그림 29. | Fig. 29. 시뮬레이션 회로 | Circuit of simulation.
Download Original Figure
jkiees-34-11-811-g30
그림 30. | Fig. 30. 시뮬레이션과 측정의 Vds 그래프 | Vds graph of simulation and measurement.
Download Original Figure
jkiees-34-11-811-g31
그림 31. | Fig. 31. 시뮬레이션과 측정의 Id 그래프 | Id graph of simulation and measurement.
Download Original Figure

Ⅵ. 결 론

본 논문에서는 제안한 FET 패키지의 고주파 SPICE 모델은 측정한 기생성분을 SPICE 모델에 적용하여 회로 시뮬레이션에서 스위칭 노이즈를 예측할 수 있음을 보였다. 기생성분의 임피던스는 curve tracer와 TPA, 2-포트 측정을 통해 추출하였으며 세 가지 방법의 정합성 비교를 통해 추출된 임피던스의 유효성을 보였다. 이를 SPICE 모델에 반영시키기 위해 다이오드의 커패시턴스 수식을 이용하였으며, 기존 SPICE 모델을 분석하였다. 또한 측정과 시뮬레이션의 오차를 줄이기 위해 2-포트 측정을 이용하여 FET가 실장되는 PCB에 대한 기생성분을 추출하였고 파워 서플라이의 입력 임피던스를 추출하여 시뮬레이션에 반영하였다. 시뮬레이션과 측정을 비교한 결과 높은 정합성을 보였으며, 제안한 FET 패키지의 고주파 SPICE 모델의 유효성을 보였다. 이를 통해 스위칭 노이즈를 예측할 수 있고 설계 이전 스위칭 노이즈에 대한 영향도 예측할 수 있을 것으로 기대된다.

Acknowledgements

이 연구는 성균관대학교와 LG전자(주) 간의 산학협력과제 ‘FET 고주파 해석 모델링 기법 개발’ 연구비 지원으로 연구되었음.

이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2023R1A2C2008116).

References

[1].

Z. Zhao, K. Y. See, W. Wang, E. K. Chua, A. Weerasinghe, and Z. Yang, et al. “Voltage-dependent capacitance extraction of sic power mosfets using inductively coupled in-circuit impedance measurement technique,” IEEE Transactions on Electromagnetic Compatibility, vol. 61, no. 4, pp. 1322-1328, Aug. 2019.

[2].

T. Liu, Y. Feng, R. Ning, W. Wang, T. T. Y. Wong, and Z. J. Shen, “Extraction of parasitic inductances of SiC MOSFET power modules based on two-port S-parameters measurement,” in 2017 IEEE Energy Conversion Congress and Exposition(ECCE), Cincinnati, OH, Oct. 2017, pp. 5475-5482.

[3].

T. Vuttipon, B. Hu, K. Y. See, and F. G. Canavero, “Accurate extraction of noise source impedance of an SMPS under operating conditions,” IEEE Transactions on Power Electronics, vol. 25, no. 1, pp. 111-117, Aug. 2009.

[4].

Z. J. Shen, Y. Xiong, X. Cheng, Y. Fu, and P. Kumar, “Power MOSFET switching loss analysis: A new insight,” in Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, Oct. 2006, pp. 1438-1442.

[5].

H. C. Cheng, Y. H. Shen, and W. H. Chen, “Parasitic extraction and power loss estimation of power devices,” Journal of Mechanics, vol. 37, pp. 134-148, Dec. 2021.

[6].

X. Song, A. Q. Huang, M. Lee, and G. Wang, “A dynamic measurement method for parasitic capacitances of high voltage SiC MOSFETs,” in 2015 IEEE Energy Conversion Congress and Exposition(ECCE), Montreal, QC, Sep. 2015, pp. 935-941.

[7].

L. Middelstaedt, A. Lindemann, M. Al-Hamid, and R. Vick, “Influence of parasitic elements on radiated emissions of a boost converter,” in 2015 IEEE International Symposium on Electromagnetic Compatibility(EMC), Dresden, Aug. 2015, pp. 755-760.

[8].

H. Kim, K. Kim, K. Song, Y. M. Park, S. K. Ryu, and S. Ahn, “Proposal of electromagnetic pulse(EMP) coupling estimation method to power system including load condition and surge protection device(SPD),” in 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity(EMCSI), Reno, NV, Jul.-Aug. 2020, pp. 454-459.

[9].

Č. J. Žlebič, D. R. Kljajić, N. V. Blaž, L. D. Živanov, A. B. Menićanin, and M. S. Damnjanović, “Influence of DC bias on the electrical characteristics of SMD inductors,” IEEE Transactions on Magnetics, vol. 51, no. 1, pp. 1-4, Jan. 2015.

Author Information

홍 영 기 [성균관대학교/석사과정]

jkiees-34-11-811-i1

  • https://orcid.org/0000-0002-9922-6207

  • 2022년 2월: 수원대학교 전자공학과 (공학사)

  • 2022년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 석사과정

  • [주 관심분야] SI/PI, EMI/EMC

최 경 륜 [성균관대학교/박사과정]

jkiees-34-11-811-i2

  • https://orcid.org/0000-0002-3649-0000

  • 2021년 2월: 수원대학교 전자공학과 (공학사)

  • 2023년 2월: 성균관대학교 전자전기컴퓨터공학과 (공학석사)

  • 2023년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 박사과정

  • [주 관심분야] SI/PI, EMI/EMC

양 지 현 [성균관대학교/석사과정]

jkiees-34-11-811-i3

  • https://orcid.org/0009-0003-1342-8559

  • 2023년 2월: 수원대학교 전자공학과 (공학사)

  • 2023년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 석사과정

  • [주 관심분야] SI/PI, EMI/EMC

김 의 혁 [LG전자/책임연구원]

jkiees-34-11-811-i4

  • https://orcid.org/0009-0002-0621-3288

  • 2000년 2월: 중앙대학교 전자공학과 (공학사)

  • 1999년 11월~현재: LG전자 생산기술원 책임연구원

  • [주 관심분야] SI/PI/EMI, 고속신호

김 찬 규 [LG전자/선임연구원]

jkiees-34-11-811-i5

  • https://orcid.org/0000-0001-5470-6824

  • 2015년 2월: 건국대학교 전자공학부 (공학사)

  • 2017년 2월: 한양대학교 정보디스플레이공학과 (공학석사)

  • 2017년 3월~현재: LG전자 생산기술원 선임연구원

  • [주 관심분야] SI/PI/EMI, 고속신호

나 완 수 [성균관대학교/교수]

jkiees-34-11-811-i6

  • https://orcid.org/0000-0002-0315-3294

  • 1984년 2월: 서울대학교 전기공학과 (공학사)

  • 1986년 2월: 서울대학교 전기공학과 (공학석사)

  • 1991년 2월: 서울대학교 전기공학과 (공학박사)

  • 1991년~1993년: SSCL Guest Collaborator

  • 1993년~1995년: 한국전기연구원 선임연구원

  • 1995년~현재: 성균관대학교 전자전기컴퓨터공학과 교수

  • [주 관심분야] SI/PI, EMI/EMC


The Journal of Korean Institute of Electromagnetic Engineering and Science
The Korean Institute of Electromagnetic Engineering and Science, #706, Totoo Valley, 217, Saechang-ro, Yongsan-gu, Seoul, Korea
Tel : +82-2-337-9666 | Fax : +82-2-6390-7550 | kees@kiees.or.kr

Copyright © The Korean Institute of Electromagnetic Engineering and Science. 2024. Powered by Guhmok