Ⅰ. 서 론
방향탐지 기술은 미지의 방향에서 도래한 신호의 입사방향을 추정하는 기술로 1차 세계대전 이후 군사적인 목적을 위해 개발되어 사용되고 있으며, 최근에는 주파수 자원 관리를 수행하는 전파관리국이나 이동 통신 분야 등 다양한 민간 분야에서 사용되고 있다[1]. 방향탐지 방식은 자가 전파 방사 유무에 따라 능동형 방식과 수동형 방식으로 나눌 수 있다. 자가 전파를 송신하지 않는 수동형 방향탐지 방식은 자기 위치 노출의 위험이 없는 장점이 있으며, 수신되는 신호의 특성 중 진폭을 비교하여 방향을 탐지하는 진폭 비교 방식과 위상을 비교하여 방향을 탐지하는 위상 비교 방식으로 나눌 수 있다. 진폭 비교 방식은 수신된 신호세기의 차를 이용하여 방향을 탐지하는 방식으로 정확도는 낮으나 구조가 간단한 장점이 있어 조기경보체계나 전투기 생존체계 시스템에 적용된다. 위상 비교 방식은 수신된 신호의 위상차를 이용하는 방식으로 진폭 비교 방식에 비해 처리해야 하는 데이터양이 많아 빠른 계산속도와 대용량의 메모리가 필요하며, 정확도가 높은 장점이 있다.
방향탐지를 수행하는 장치는 전자전체계를 구성하는 전자지원 장비의 핵심장치이며, 높은 방향탐지 정확도 성능이 요구된다. 도래하는 미상의 신호를 수신하는 방향탐지용 배열 안테나 설계 및 배치가 최종 제작된 장치의 방향탐지 정확도 성능에 큰 영향을 미치기 때문에 안테나 설계 단계에서 안테나 설계에 따른 방향탐지 정확도를 예측 가능하여야 한다. 방향탐지 안테나 설계 시 단위 안테나 간의 연결선인 안테나 베이스라인의 길이 및 형상에 따라 높은 방향탐지 정확도 성능을 내는 주파수 대역 및 방위각이 달라진다[2]. 따라서 광대역 특성의 방향탐지 안테나를 설계하는 경우, 도래하는 신호의 방위각 및 고각에 따른 안테나 간의 위상차 특성을 면밀히 분석하여 안테나 배치를 신중히 결정하여야 한다. 높은 방향탐지 정확도를 위한 이론적인 최적의 안테나 간 거리가 너무 짧거나 긴 경우에는 물리적인 안테나 배치 가능 여부, 단위 안테나 간 커플링 영향, 안테나가 적용될 플랫폼 형상 등을 고려하여 최종 배열 안테나 형상을 결정하여야 한다.
현재까지 방향탐지 알고리즘, 방향탐지 안테나 설계 및 배치에 관한 연구가 활발히 진행되었다[3]∼[7]. 하지만 방향탐지 정확도를 위한 안테나 최적 배치에 관한 연구 또는 방향탐지 안테나 자체 성능에 대한 연구가 대부분이었으며 이론적인 안테나의 최적 배치와 실제 안테나를 배치하였을 때 영향을 모두 고려한 연구에 대한 진행은 미비하다. 또한 정확한 방향탐지를 위해서는 신호의 방위각 및 고각 모두 중요한 요소이나 현재까지 방향탐지 정확도를 산출할 때 신호의 방위각만을 주로 고려하였으며 고각의 영향에 대한 연구가 미비한 상태이다.
본 논문에서는 2차원 위상비교 방향탐지 정확도 산출 프로그램을 이용한 방향탐지용 광대역 배열안테나 설계 기법을 제안하였다. 전방위각에서 일정한 방향탐지 성능을 가지는 원형 배열을 방향탐지 안테나 기본형상으로 선정하였다. 원형 배열 형태의 방향탐지 안테나는 구조가 단순하고 제작이 용이하여 그림 1의 사례와 같이 지상 고정형 또는 차량 탑재형 플랫폼에 주로 사용된다.
도래하는 신호의 방위각/고각 시나리오 및 원형배열 안테나 지름에 따른 방향탐지 정확도 결과를 분석하였다. 방향탐지 정확도 산출을 위해 대표적인 위상 비교 방식 알고리즘인 CVDF(correlative vector direction finding) 방식을 사용하였으며 보다 손쉽고 빠른 분석을 위해 방향탐지 정확도 산출 프로그램을 개발하여 설계에 활용하였다. 또한 광대역 특성을 갖는 단위 다이폴 안테나 및 배열 안테나를 전자기 시뮬레이션 툴을 이용해 설계 및 분석하였다. 본 논문에서 제안된 방향탐지 정확도 산출 프로그램을 이용한 설계 기법을 방향탐지 안테나 설계에 활용한다면 원하는 방향탐지 정확도 성능을 갖는 방향탐지 안테나 설계를 보다 빠르고 정확하게 할 수 있을 것으로 기대된다.
Ⅱ. CVDF 알고리즘
본 논문에서는 배치 안테나의 방향탐지 정확도 산출을 위해 CVDF 알고리즘을 사용하였다[9],[10]. CVDF 알고리즘은 방향탐지 안테나를 구성하는 단위 안테나 간의 위상차를 사용자가 설정한 주파수 및 방위각 및 고각 스텝으로 측정하여 lookup table 형태로 저장한 후 도래하는 신호의 위상차 측정 결과와 lookup table 간 correlation을 계산하여 방향을 결정하는 알고리즘이다. 일반적으로 안테나 개수가 많을수록 정확도가 높아지며, 요구하는 방향탐지 정확도에 맞추어 안테나 개수 및 배치를 결정한다. 본 논문에서는 비용 대 효과가 우수하다고 알려진 5개의 안테나 배치구조를 선택하였다.
그림 2는 5개의 안테나 중심을 기준으로 안테나 소자를 원형으로 배열한 5채널 배열 안테나를 나타낸다. 인접하는 안테나를 제외한 두 안테나 사이의 거리(파란색 실선) D는 식 (1)과 같이 표현된다. 식 (1)에서 R은 중심점에서의 안테나까지의 거리(원형 배열 안테나 반지름)를 나타내며, θ1은 배열 안테나 중심점 기준에서 각 안테나 사이의 각도(5배열의 경우 72도)를 나타낸다. ϕ는 두 안테나(그림 2에서 2번 안테나와 5번 안테나) 사이의 거리 D에 의한 위상차를 의미하며, 식 (2)와 같이 표현된다. 식 (2)에서 λ는 입사 신호의 파장을 의미하며, θ는 입사 신호의 입사각을 나타낸다. 식 (1)과 식 (2)를 통해 알 수 있듯이 입사하는 신호의 주파수와 안테나 간 이격 거리 D를 알고 있을 때, 두 안테나 사이의 위상차를 측정하면 입사 신호의 입사각 θ를 알 수 있다.
그림 2와 같은 5채널의 멀티채널 방향탐지 시스템에서 상관벡터를 이용하는 경우, 방향탐지 성능은 측정된 데이터베이스의 정확도에 종속적이다. 데이터베이스화할 때 모든 입사각과 주파수에 따라 다른 상관벡터가 저장되며, 각각의 안테나 소자에서 수신되는 신호의 세기와 위상정보는 복소벡터로 변환되어 저장된다.
VMi는 새로 측정된 i번째 채널의 복소벡터이고, Vθi는 입사각별로 기존에 저장되어 있는 i번째 채널의 복소벡터로 정의할 경우, 각도 θ에 대한 상관계수인 Rθ는 식 (3)과 같이 산출이 가능하다. 이때 *는 복소수의 conjugate를 의미하며, Rθ는 상관계수 정의에 의해 0∼1 사이의 값을 가지고 1에 가까울수록 상관성이 크다. 기존에 저장되어 있는 0°부터 360°까지의 방위에 대한 위상차값과 새로 측정된 위상차값과의 상관계수 Rθ가 가장 높게 나타나는 방위각을 신호의 도래각으로 추정하는 것이 CVDF 알고리즘의 원리이다.
Ⅲ. 2차원 위상비교 방향탐지 정확도 산출 프로그램
방향탐지 안테나의 최적 배치를 산출하기 위해 본 논문에서는 2차원 위상비교 방향탐지 정확도 산출 프로그램을 개발하여 분석에 활용하였다. 그림 3은 방탐정확도 산출 프로그램의 흐름도를 나타내었다. 방탐정확도 산출 프로그램의 사용방법을 다음과 같이 6단계로 기술하였다.
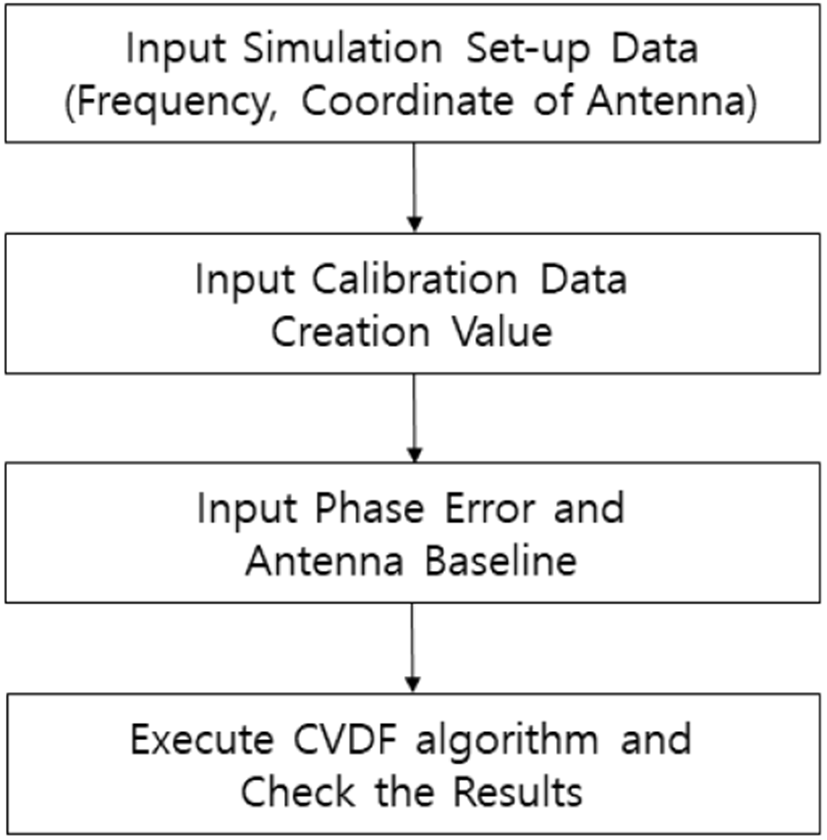
(1단계) 안테나 좌표 및 분석 주파수 범위를 설정, (2단계) 이상적인 방사보정데이터 생성을 위한 설정 값 입력 : 방위각 스텝 입력, 설정 고각 입력, (3단계) 모의 측정 위상차 데이터 생성 시 적용되는 위상차 에러 값 입력, (4단계) 방향탐지 알고리즘 수행 시 사용될 안테나 베이스라인 조합 선택, (5단계) 방향탐지 정확도 시뮬레이션 수행 및 수행결과 분석 수행, (6단계) 주파수 및 방위각별 방향탐지 오차결과 확인 및 최종 오차 RMS 확인.
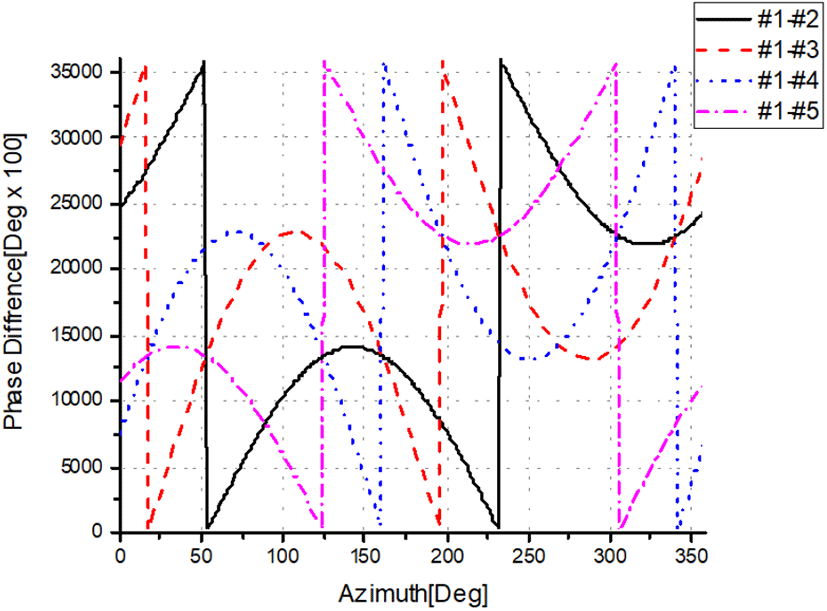
안테나 좌표 및 분석하고자 하는 주파수 범위를 설정하고, 방위각 스텝 및 고각을 입력한 후 방사보정 데이터 생성을 하면 1 MHz 스텝의 이상적인 방사보정 데이터가 생성되며 이는 위상차 에러가 반영된 모의 측정 위상차 데이터와 비교하는 참고값이 된다. 그림 4는 방향탐지 정확도 산출 프로그램으로 계산한 원형 배열 안테나의 이상적인 방사보정데이터를 그래프로 나타낸 결과이다. 그림 4에서 보여주는 위상차 데이터는 1번 안테나와 다른 안테나와의 위상차를 나타낸 것이며, 주파수 및 안테나 배치 및 설정 고각에 따라 변하게 된다.
모의 측정 위상차 데이터에 인가할 위상차 에러값을 입력한 후 안테나 조합을 선택한다. 안테나 조합은 CVDF 알고리즘 수행 시 사용할 안테나 베이스라인을 정하는 것이다. 5개 안테나 배치 시 안테나 베이스라인의 수는 총 10개이며, 그림 5는 10개 베이스 라인을 모두 사용하는 경우의 예를 나타낸 것이다.
이상적인 방사보정 데이터 및 위상차 에러가 반영된 모의 측정 위상차 데이터를 이용하여 방향탐지 정확도 시뮬레이션 및 분석을 수행하면 방위각별 방향탐지 RMS 오차 및 주파수 별 방향탐지 RMS 오차 분석결과를 얻을 수 있다. RMS 오차 Δerr는 ITU-R SM.2097-0에 기술된 RMS 계산을 따르며, 식 (4)와 같다.
Δi는 입사신호의 실제 DOA와 CVDF 알고리즘을 통해 산출된 DOA의 차, N은 시뮬레이션 횟수를 나타낸다.
Ⅳ. 방향탐지 정확도 시뮬레이션 결과
안테나 배치에 따른 방향탐지 정확도 분석을 위해 표 1의 시뮬레이션 파라미터를 이용하여 시뮬레이션을 수행하였다.
표 2는 표 1의 시뮬레이션 파라미터를 입력하여 산출된 원형 배열 반지름 및 고각별 방향탐지 RMS 오차 시뮬레이션 결과를 나타내었다. 배열 반지름이 150 mm인 경우, 해당 주파수 대역에서 고각 평균 방향탐지 정확도가 가장 우수한 것으로 분석되었으며, 반지름이 너무 작거나(50 mm) 큰 경우(250 mm) 방향탐지 정확도 성능이 다른 중간 크기의 배열에 비해 나쁨을 확인할 수 있다.
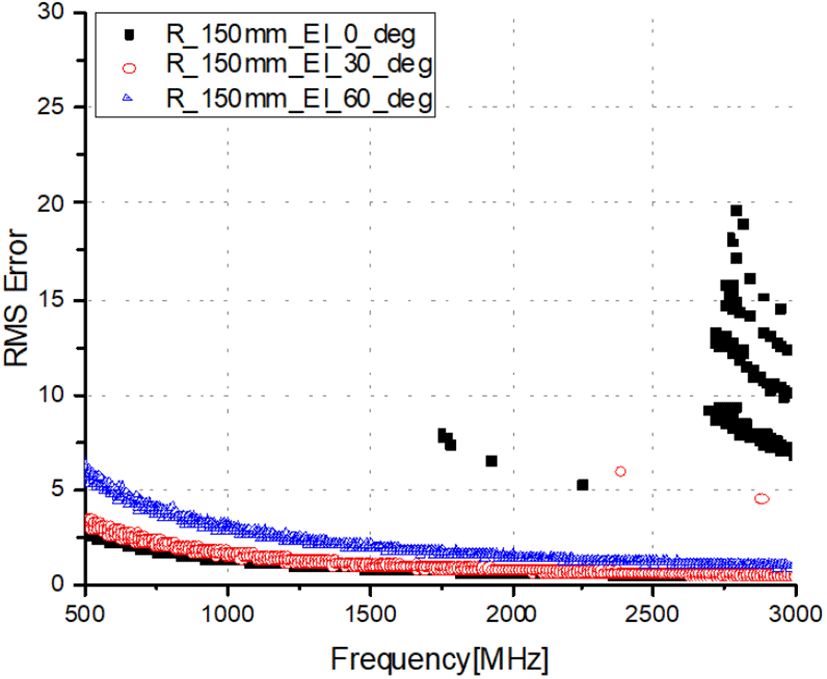
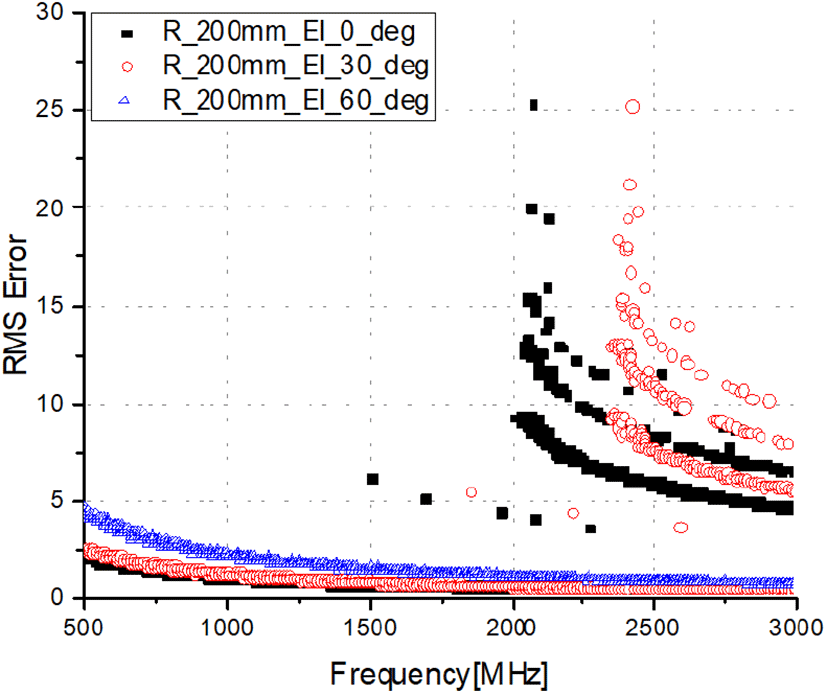
그림 6∼그림 8은 배열 반지름이 100 mm, 150 mm, 200 mm일 때, 고각 0도 및 30도 및 60도에서의 주파수에 따른 방향탐지 RMS 오차를 나타내었다. 배열 반지름이 100 mm인 경우 고각 0도에서 높은 성능을 가지는 반면 고각 60도에서는 베이스라인의 길이가 더욱 짧아져 주파수 대역 전체적으로 성능이 열화됨을 확인할 수 있다. 이와 반대로 배열 반지름이 200 mm인 경우, 고각 0도에서는 베이스라인의 길이가 길어 2 GHz 이상 대역에서 모호성이 발생하지만, 고각 60도에서는 베이스라인의 길이가 짧아져 성능이 좋음을 확인하였다. 따라서 안테나 설계 시 수신하고자 하는 신호의 거리와 위치를 고려하여 배열 안테나의 크기를 결정해야 한다.
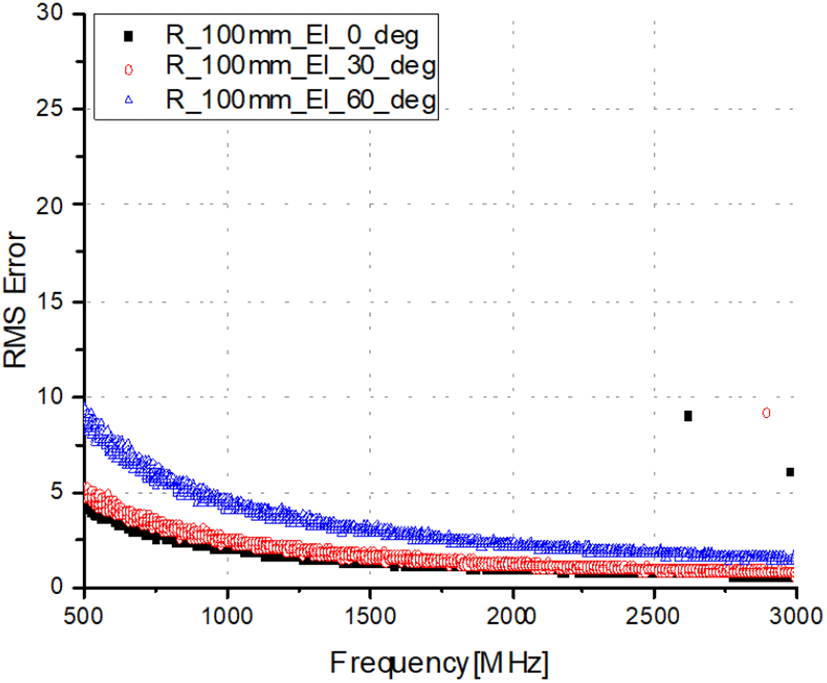
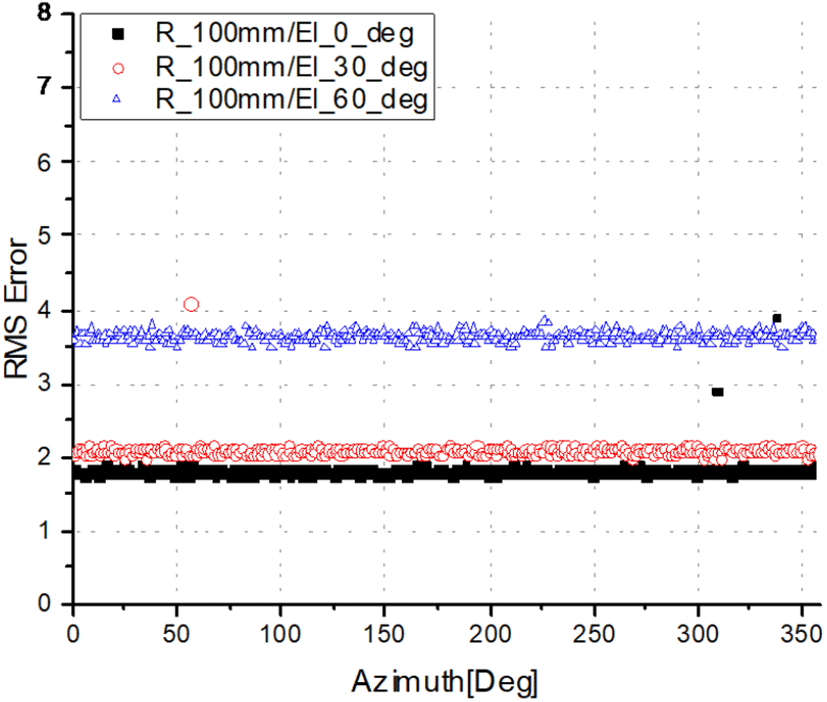
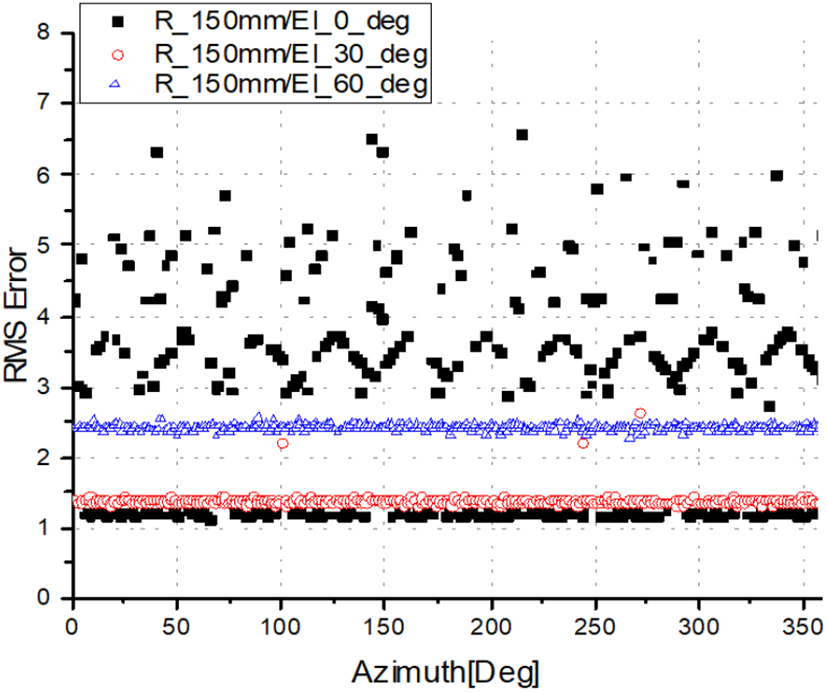
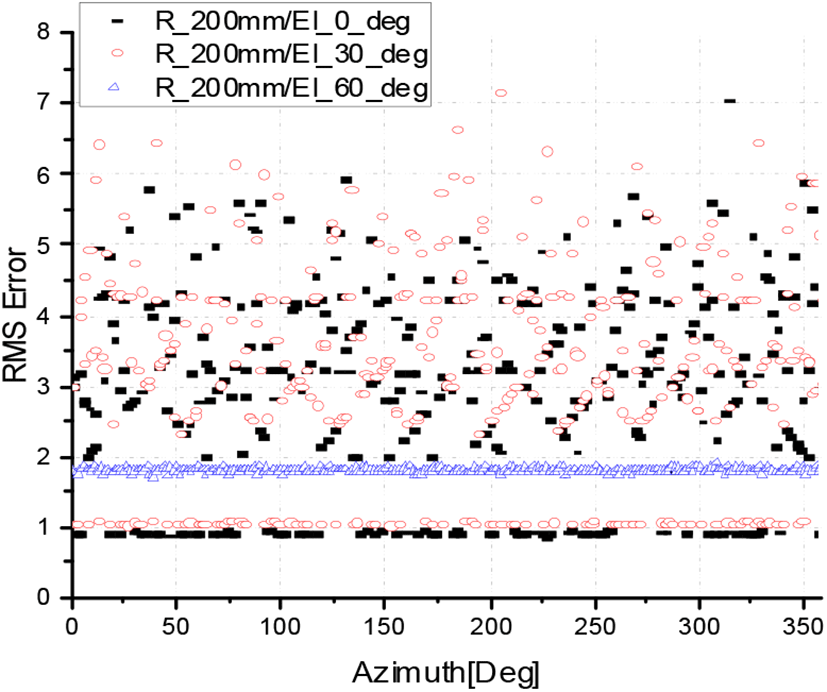
그림 9∼그림 11은 배열 반지름이 100 mm, 150 mm, 200 mm일 때, 고각 0도, 30도, 60도에서의 방위각에 따른 방향탐지 RMS 오차를 나타내었다. 그림에서 알 수 있듯이 안테나를 원형으로 배치하였기 때문에 방위각별 방향탐지 오차는 크지 않음을 알 수 있다. 그림 10 및 그림 11에서 보이는 바와 같이 원형 배열 안테나의 반지름이 길어짐에 따라 모호성이 전 방위각에서 증가함을 알 수 있는데, 이는 안테나 간 베이스라인이 길어짐에 따라 그림 7 및 그림 8에서 분석된 높은 주파수 성분의 모호성이 전 방위각에서 보이기 때문이다.
Ⅴ. 전자기 시뮬레이션 결과
방향탐지 정확도 시뮬레이션 결과를 바탕으로 방향탐지용 배열 안테나를 물리적으로 설계하기 위한 전자기시뮬레이션을 수행하였다. 5배열 안테나를 구성하는 단위 안테나를 설계하였으며, 안테나 형상은 그림 12와 같다. 광대역 임피던스 매칭을 위해 UWB(ultra wide band) 다이폴 구조를 가지며 피드 갭은 1.2 mm이며 두께 1.68 mm의 일반적인 FR-4 유전체 기판에 설계하였다. 그림 13은 단위 안테나의 반사손실을 나타내었다. 단위 안테나는 500∼3,000 MHz 대역에서 −6 dB 이하의 반사손실 특성을 가진다. 그림 14는 단위 안테나의 방사패턴 특성을 나타낸다. 안테나의 수평면인 XZ 면에서 omni-directional한 특성을 가짐을 확인할 수 있다. 단위 안테나의 최대 이득은 500 MHz에서 0.85 dBi, 1,500 MHz에서 4.03 dBi, 3,000 MHz에서 2.68 dBi으로 해석되었다.
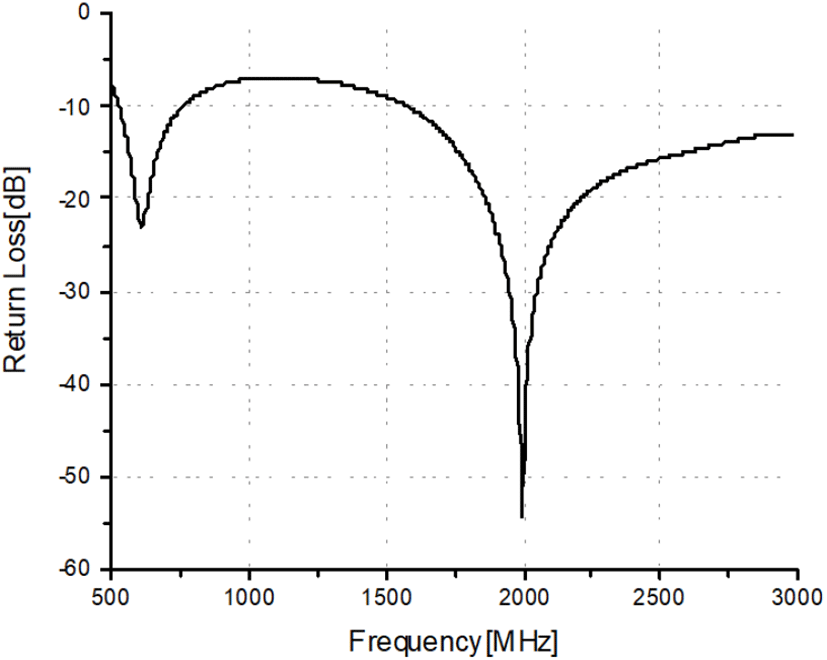
그림 15는 배열 안테나의 원형배열 반지름에 따른 반사손실 특성을 나타낸다. 안테나 간 형상 및 배치가 동일하여 안테나 간의 해석결과가 같으므로 하나의 안테나 해석결과만 나타내었다. 배열 반지름이 작아질수록 안테나 간 전자기 결합의 영향으로 본래의 단위 안테나 반사손실 특성에서 임피던스 매칭이 변화하는 것을 확인할 수 있다. 반지름이 200 mm일 때 원래의 단위 안테나 반사손실 특성과 가장 유사함을 알 수 있다. 평균 방향탐지 정확도 성능이 우수한 반지름 100 mm 배열 안테나와 150 mm 배열 안테나 중 반사손실 특성이 전 대역에서 −6 dB 이하를 만족하는 150 mm 배열 안테나를 선정하였다.
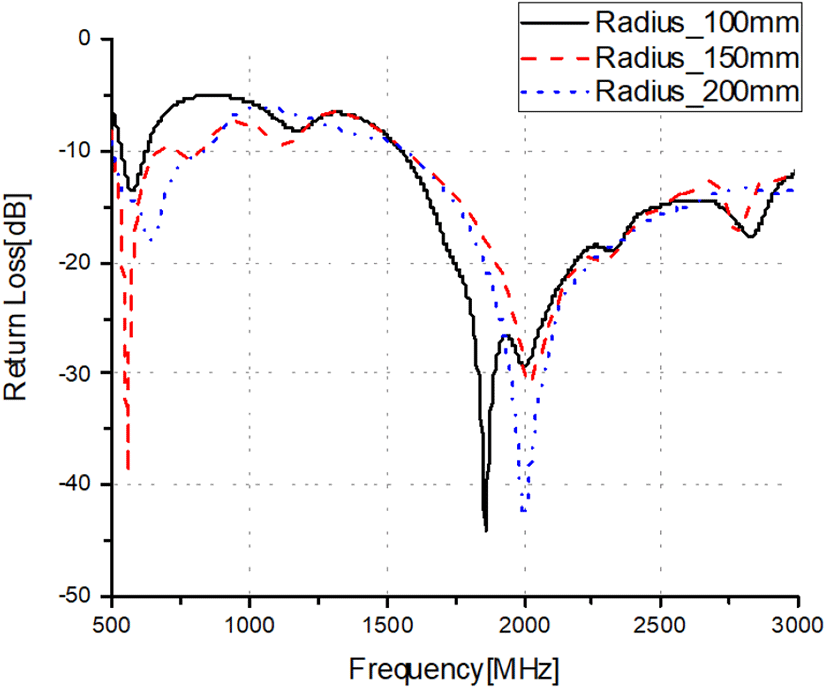
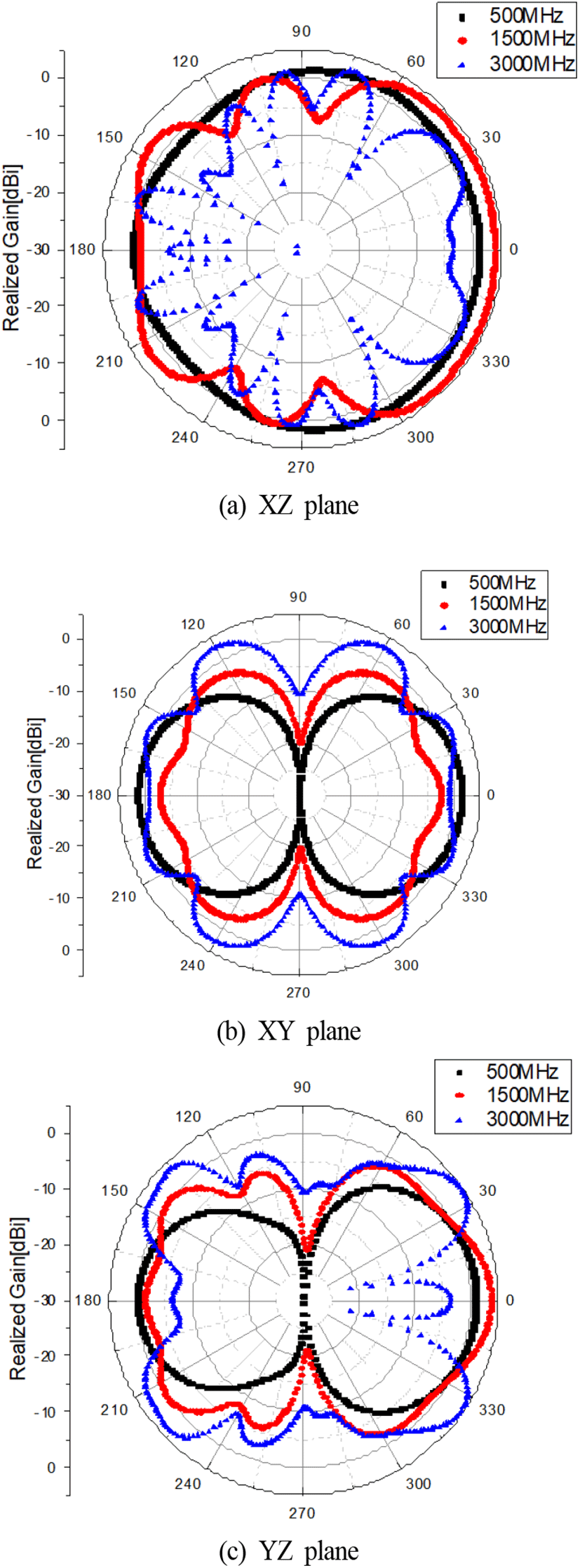
그림 16은 반지름 150 mm 배열 안테나의 방사패턴을 나타내었다. 반사손실과 마찬가지로 방사패턴 또한 안테나 간 해석결과가 동일하므로 하나의 안테나 해석결과만 나타내었다. 안테나의 최대 이득은 500 MHz에서 1.77 dBi, 1,500 MHz에서 3.82 dBi, 3,000 MHz에서 4.68 dBi으로 해석되었다. 안테나의 H-plane에 해당하는 XZ plane의 −180도 방향에 배치한 다른 안테나와의 간섭으로 인해 안테나 후방방사패턴이 영향을 받음을 확인할 수 있다. 안테나 간의 간섭 및 전자기 결합의 영향을 줄이기 위해서는 안테나 간의 거리를 늘려야 하지만 안테나 간의 거리가 길어지면 높은 주파수 대역의 방향탐지 모호성이 증가하는 단점이 있기 때문에 trade-off 관계인 두 가지 면을 모두 고려하여 최종 안테나 형상을 신중히 결정하여야 한다.
Ⅵ. 결 론
본 논문에서는 2차원 위상비교 방향탐지 정확도 산출 프로그램을 이용한 방향탐지용 광대역 배열안테나 설계 기법을 제안하였다. 안테나 배치형태가 방향탐지 시스템 최종 성능에 중요한 영향을 미치기 때문에, 안테나 설계 단계에서 안테나 배치에 따른 방향탐지 정확도를 예측할 수 있어야 한다. 안테나 배치를 결정하기 위해 방향탐지 정확도 산출 프로그램을 이용하여 원형 배열 안테나의 반경 및 입사 신호의 고각을 가변하면서 방향탐지 RMS 오차 결과를 분석하였다. 입사 신호의 고각 변화에 따라 안테나 간 베이스라인의 길이가 변해 정확도 성능에 영향을 주는 것을 확인하였다. 방향탐지 정확도 산출 프로그램의 결과를 토대로 UWB 다이폴 안테나를 단위 안테나로 갖는 5소자 원형 배열 안테나를 전자기 시뮬레이션 툴을 이용하여 설계하였으며, 안테나 간의 전자기 결합 및 간섭에 대한 영향을 분석하였다. 본 논문에서는 5소자 원형배열 형상의 안테나에 대해서만 분석하였지만, 안테나 개수 및 형상을 자유롭게 변경하면서 2차원의 방향탐지 정확도 결과를 신속히 산출 및 분석이 가능하므로 추후 시스템 요구 성능을 만족하는 방향탐지 안테나 개발에 방향탐지 정확도 산출 프로그램을 효율적으로 활용할 수 있을 것으로 기대된다.
















