Ⅰ. 서 론
디지털 오실로스코프는 오실로스코프의 한 종류로서, 측정된 아날로그 신호를 디지털신호로 바꾸는 아날로그-디지털 변환기(analog-to-digital converter: ADC)가 사용된다. 이로 인해 빠르고 복잡한 신호, 단발(single shot) 신호의 측정에 유리하며, 신호 저장 등이 가능하다. 또한, 최근 디지털 오실로스코프는 디지털 회로 또는 디지털 시스템으로부터 입력된 여러 개의 디지털신호를 수집하여 저장하고, 원하는 시점에 표시할 수 있는 로직분석기 기능도 수행할 수 있다. 디지털 오실로스코프는 이와 같은 시간영역 파형 분석뿐만 아니라, FFT 기능이 장착될 경우 스펙트럼 분석기로 사용될 수 있다. 과거 디지털 오실로스코프는 낮은 주파수에 주로 사용되었으나, 최근 디지털 오실로스코프는 사용주파수가 110 GHz에 이르는 것도 보고되고 있다[1].
특히 디지털 오실로스코프는 고속 디지털 신호처리와 함께 관심을 끌고 있는 지터(jitter) 측정에 유용하다. 지터는 주기적인 기준신호의 주기와 실제 신호의 주기성으로부터의 편차를 의미하며, 지터는 거의 모든 통신 링크의 설계에서 중요하다. 이러한 중요성을 고려하여 지터에 대한 정의 및 분류는 최근 IEEE에서 표준화된 바 있다[2]. 그러나 지터는 디지털 오실로스코프로 측정할 수 있지만, 측정 결과를 가공하여야만 얻을 수 있다. 일부 디지털 오실로스코프는 전용 지터 측정기능이 장착되어 사용자가 별도로 측정 결과를 가공하지 않고 직접 측정이 가능하게 된다[3].
지터는 응용에 따라 규격화하는 방법이 달라지며, 여러 가지 정의가 있다. 그중 위상잡음과 관련되는 것은 TIE(time interval error)이다. TIE는 시간영역에서 파형의 상승단 또는 하강단이 이상적인 파형에서 벗어난 정도를 시간 단위로 나타내는데, 이것은 위상 흔들림 또는 위상 오차와 비례관계에 있게 된다. 단 위상오차는 연속적인 함수이나, TIE는 이와 같은 연속적인 위상오차를 반주기마다 샘플한 것이다. 위상잡음은 위상오차를 스펙트럼 영역에서 측정한 것이다. 따라서 TIE는 위상오차를 샘플한 것이기 때문에, TIE를 스펙트럼 영역으로 변환하면 위상잡음을 얻을 수 있게 된다[2].
위상잡음(phase noise) 성능은 통신 시스템 구성 시 필수적으로 고려하여야 하는 중요한 규격 중 하나이다. 위상잡음 전용 측정 계측기로는 키사이트(Keysight)사의 E5052B[4], 로데슈바르즈(Rohde & Schwarz)사의 FSPN[5]이 있으나, 대량생산용 장비로 사용되기에는 매우 고가의 장비이다.
반면 고가의 위상잡음 전용 측정 계측기에 비해 디지털 오실로스코프는 대량생산용 장비로 적절한 가격을 가진다. 또한, 지터 측정기능이 장착된 최근 디지털 오실로스코프는 지터 측정기능과 함께 보통 위상잡음 측정기능도 제공한다. 이것은 앞서 설명한 TIE를 위상잡음 측정에 사용한 것이다. 좀 더 정밀한 위상잡음은 동일한 신호를 분기하여 두-채널에 입력하고, 두 채널에서 얻어진 TIE를 교차상관(cross correlation)하여 개선하여 얻고 있다. 그러나 이처럼 얻어진 위상잡음은 ADC를 이용하여 디지털신호로 변환 시 추가된 ADC 클럭-지터 잡음을 포함하고 있어, ADC 클럭-지터 잡음이 클 때 얻어진 위상잡음은 오차를 보이게 된다.
본 논문에서는 지터 측정기능이 장착되지 않은 디지털 오실로스코프를 이용, 새로운 위상잡음 측정방법을 제안한다. Labview를 이용하여 디지털 오실로스코프로 파형을 읽어 들이고, 읽어 들인 파형으로부터 TIE를 얻고, TIE에 포함된 ADC 클럭-지터 잡음을 보상한 뒤, 교차상관을 통하여 개선된 위상잡음을 얻는 방법이다. 또한, 본 논문에 제안된 방법으로 얻어진 위상잡음 측정결과와 기존의 디지털 오실로스코프를 이용한 위상잡음 측정결과와 비교하여, 본 논문 방법의 우수성을 보였다.
Ⅱ. TIE를 이용한 위상잡음 측정방법
그림 1에 TIE 정의[2]를 설명하기 위한 그림을 보였다. 측정된 파형(measured waveform)의 0점(그림 1의 Z1,…,Zn)은 일반적으로 샘플된 측정값으로부터 보간(interpolation)하여 얻게 된다. 주목할 것은 측정된 0점 Z1,…,Zn은 정확히 주기마다 반복하지 않게 된다. 측정된 0점으로부터 측정된 모든 0점에 가장 가까운 이상적인 정현파형(ideal waveform)을 얻을 수 있고, 이때 얻어진 이상적인 정현파형과 측정된 파형의 0점들 간의 차이(그림 1의 t1,…,tn)를 TIE라고 한다. 따라서 TIE는 반주기마다 나타나는 이산파형이 된다.
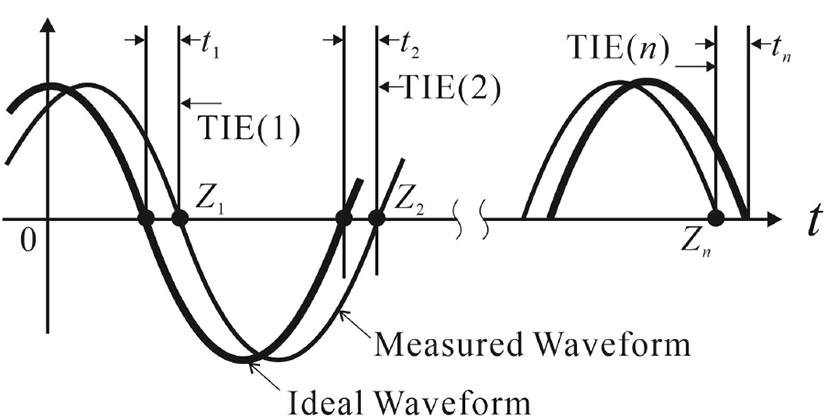
그림 1에서 정현파의 주파수를 ωo=2πfo라고 할 때 샘플된 위상 파형 ϕ은 식 (1)과 같다.
식 (1)의 ϕ는 불규칙하게 흔들리게 된다. 이때 ϕ의 Fourier 변환을 통해 전력스펙트럼밀도(power spectral density) Sϕ(fm)을 얻을 수 있다. 여기서 fm은 오프셋-주파수를 나타낸다. 얻어진 Sϕ(fm)으로부터 위상잡음 L(fm)은 식 (2)와 같이 얻을 수 있다.
그림 2는 본 논문에서의 TIE를 이용한 위상잡음 측정 셋업(setup)을 보였다. 위상잡음을 측정하고자 하는 신호 s(t)는 그림 2와 같이 전력이분기(power divider)를 통해 분기되어 각각 디지털 오실로스코프 Ch1 및 Ch3 두 채널로 입력된다. 이와 같이 s(t)를 전력이분기로 분기하여 디지털 오실로스코프의 두 채널로 입력하는 것은 디지털 오실로스코프 채널에서 발생한 잡음이 신호 s(t)의 위상잡음에 나타나는 것을 제거하기 위한 것이다. 즉 단일 채널 s(t)의 TIE를 측정하고 이를 이용하여 위상잡음을 계산할 경우 채널에서 발생된 잡음은 신호 s(t)의 위상잡음에 나타나게 된다. 그러나 두 채널로 입력된 신호를 교차상관할 경우 각 채널에서 발생한 잡음은 독립이므로, 채널에서 발생한 잡음의 신호 s(t)의 위상잡음에의 기여는 사라지게 된다. 그러나 위상잡음에는 여전히 ADC 클럭-지터 잡음을 포함하고 있다. 그림 2에서 볼 수 있듯이 동일한 ADC 클럭-지터 잡음이 ADC로 샘플된 출력에 나타나게 된다.
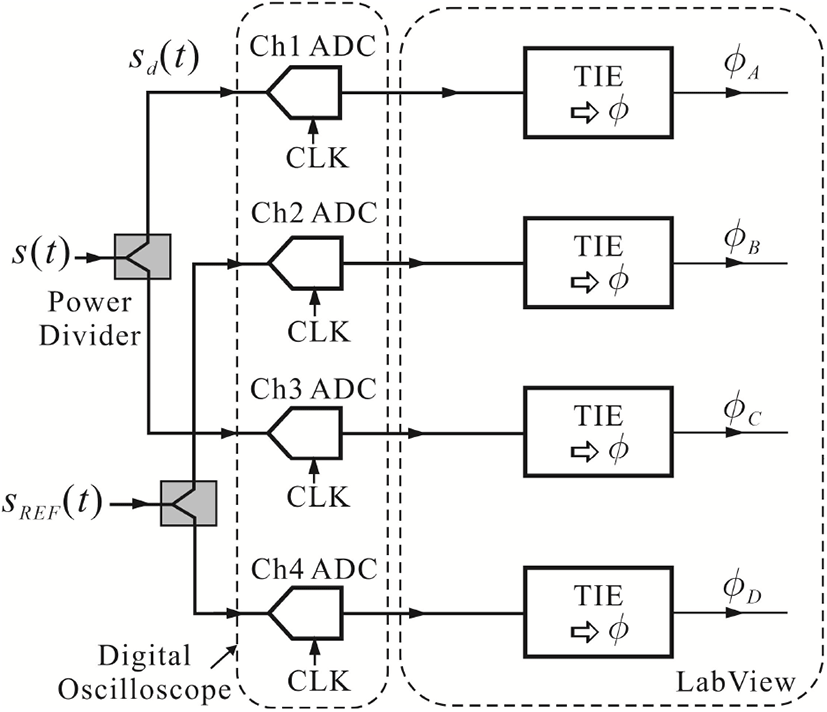
그림 2의 기준신호 sREF(t)는 ADC 클럭-지터를 제거하기 위한 것으로, 신호 s(t)와 동일하게 전력이분기를 통해 분기되어 디지털 오실로스코프로 Ch2 및 Ch4 두 채널로 입력된다. 디지털 오실로스코프로 샘플된 신호는 National Instrument사의 Labview를 통해 읽어 들이며, 읽어 들인 신호의 0점을 찾아, 식 (1)과 같이 위상변화로 바꾼다. 디지털 오실로스코프에 TIE를 측정하는 기능이 있다면 TIE를 읽어 들이고, 식 (1)을 이용, 위상변화로 변환하면 된다. 본 논문에서는 디지털 오실로스코프 지터 측정기능이 없다고 가정하였다.
그림 2의 ϕA, ϕB 및 ϕC는 식 (3)과 같이 나타낼 수 있다 [6].
식 (3)에서 ϕd 및 ϕref는 각각 신호 s(t) 및 기준신호 sREF(t)의 위상 흔들림(fluctuation)을 나타낸다. ϕ1, ϕ2 및 ϕ3은 ADC의 양자화 잡음 및 열잡음에 의한 위상 흔들림이며, 상호독립적 잡음이라고 볼 수 있다. ϕs는 ADC 클럭의 위상잡음으로 인한 잡음이며, 상수 a 및 b는 식 (4)의 관계를 갖는다.
식 (4)의 fd 및 fref는 각각 신호 s(t) 및 기준신호 sREF(t)의 주파수를 나타낸다. 식 (3)으로부터, 식(3a)만 이용하여 위상잡음을 구할 경우, 잡음 ϕ1 및 ϕs의 영향을 포함하고 있어, 부정확한 위상잡음이 얻어지게 된다.
식 (3a) 및 (3c)에 보인 ϕA 및 ϕC의 교차상관 스펙트럼을 식 (5)와 같이 정의한다.
식 (5)에서 F(·)은 Fourier 변환을 나타내고, 는 공액을 나타낸다. 식 (3a) 및 (3c)에서 ϕ1, ϕ3, ϕd, ϕs는 독립인 확률변수이다. 또한 ϕA및 ϕC의 공통 인자는 ϕd+aϕs이다. 따라서 ϕA 및 ϕC를 교차상관하여 스펙트럼을 얻고 평균횟수 M을 증가시킬 경우, ϕA 및 ϕC의 교차상관 스펙트럼은 식 (6)과 같다.
식(6)에서 <·>는 평균 연산을 나타내고, 첨자 M은 평균횟수를 나타낸다. 따라서 잡음 ϕ1의 영향은 사라지고, 개선된 위상잡음 결과를 얻게 된다. 그러나 여전히 ADC 클럭-지터의 영향을 포함하고 있다. 이것이 보통 디지털 오실로스코프에서 교차상관을 통하여 위상잡음을 계산하는 방법이다. 본 논문에서는 식 (6)에 나타나는 ADC 클럭-지터의 잡음의 영향도 제거하는 방법을 제안하고자 한다.
본 논문에서 제안하는 방법을 그림 3에 보였다. 기존의 방법이 ϕA와 ϕC의 교차상관을 구하여, ϕ1, ϕ3의 영향을 제거하는 것인데 비해, 본 논문에서는 그림 3과 같이 ϕB및 ϕC를 이용하여 ADC 클럭-지터로 인한 ϕs의 영향을 제거하는 것이다. 그림 3에서 ϕγ는
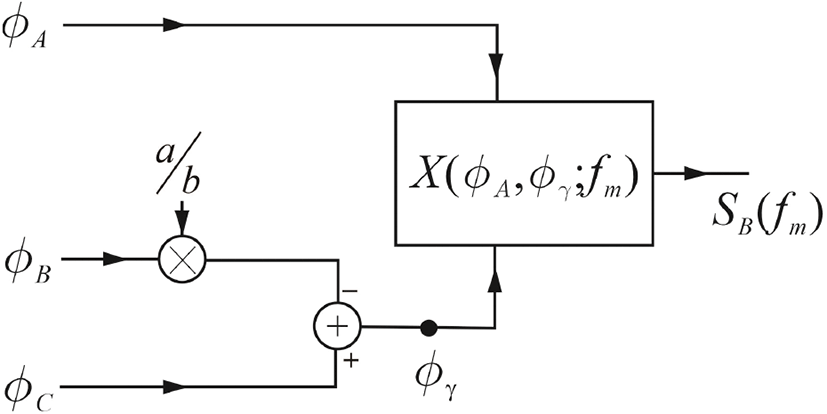
를 얻게 된다. 식 (7)과 식 (3a)를 비교하면 공통잡음은 ϕd뿐인 것을 알 수 있고, 나머지 항들은 독립인 것을 알 수 있다.
따라서 ϕA와 ϕγ의 교차상관은 식 (8)과 같다.
식 (8)로부터 본 논문의 방법을 통하여 잡음 ϕ1 및 ϕs의 영향이 제거된 위상잡음을 구할 수 있음을 알 수 있다.
본 논문에서 디지털 오실로스코프에 지터 측정기능이 없다고 가정하였기 때문에, 읽어 들인 파형으로부터 TIE를 계산하는 것은 Labview 애드-온 지터-해석 툴-키트(tool kit)를 이용하여 구현하였다. 구현할 때 문제가 되는 것은 신호 s(t)와 기준신호 sREF(t)의 주파수가 다르다는 점이다. 따라서 0점들은 다르게 나타나며, 결과적으로 ϕA, ϕB의 샘플 간격이 차이를 갖게 된다. 이를 극복하기 위하여 ϕA, ϕB를 새로운 샘플 간격으로 재-샘플(re-sample) 하는 것이 필요하다. 이것은 Labview의 Resample Waveforms (single shot). vi를 이용하여 구현하였다. 재-샘플 시 선형 보간을 선택하였다. 또한 ϕA, ϕB를 재-샘플을 하더라도 길이가 다르게 된다. 길이는 Align Waveforms(single shot). vi를 사용, 구현하였다.
Ⅲ. 측정결과
위상잡음 측정결과를 비교하기 위하여 키사이트사의 E8257D 신호발생기를 신호원 s(t)로 사용하였다[7]. 주파수와 전력은 1.4151 GHz, 9 dBm으로 선정하였다.
이와 같이 s(t)의 주파수와 전력을 결정한 것은 우선 기존의 디지털 오실로스코프로 측정된 결과와 비교를 용이하게 하기 위해서이다[8]. 두 번째로 사용된 디지털 오실로스코프 MXR608A의 성능을 고려한 것이다. MXR608A는[1] 최대 샘플링 속도가 16 GSa/sec이기 때문에 측정 가능한 입력주파수는 6 GHz로 제한된다. 또한, ADC 클럭-지터를 제거하기 위해서는 별도로 기준신호가 필요한데, 기준신호의 주파수는 s(t)의 주파수보다 높게 선정되면 ADC 클럭-지터를 제거하는 데 바탕 위상잡음을 열화시키지 않는다. 따라서 MXR608A를 사용 측정 가능한 주파수는 약 4 GHz로 제한되게 된다. 그리고 입력 전력의 경우 MXR608A로 측정 가능한 전압은 43 μV(약 −73 dBm)이므로 이것보다 높은 입력 전력을 필요로 한다. MXR608A의 ENOB는 9 bit여서 적절한 전압은 −19 dBm보다 큰 입력 전력을 가져야 할 것이다. 따라서 여유를 준다면 −15 dBm보다 큰 입력전력이 필요하다. 이러한 면에서 채널 입력 전력 3 dBm(9 dBm 입력전력은 저항성 전력이분기에 의해 이분되어 채널 입력 전력은 3 dBm이 된다)으로 설정하였다.
사용된 디지털 오실로스코프는 키사이트사의 8-채널 MXR608A이며, 이것의 최대 샘플링 주파수 16 GHz이다. 우선 E8257D 신호발생기의 위상잡음을 키사이트사의 신호분석기 E5052B를 사용하여 측정하였다. E5052B로 측정된 위상잡음은 그림 4에 보였다. 그림 4에 보인 바와 같이 E8257D의 위상잡음은 fm=10~100 kHz에서 약 −130 dBc/Hz를 가지며, fm=1~10 MHz에서 약 −150 dBc/Hz를 갖는 것을 알 수 있다. 또한, 그림 4에는 평균횟수 M=10,000일 때 단일-채널 TIE로 계산된 위상잡음을 보였다. 단일-채널 TIE로 계산된 위상잡음은 fm=10~100 kHz에서 약 8 dB의 차이를 보이며, fm=1~10 MHz에서 약 −15 dB의 차이를 보이는 것을 알 수 있다.
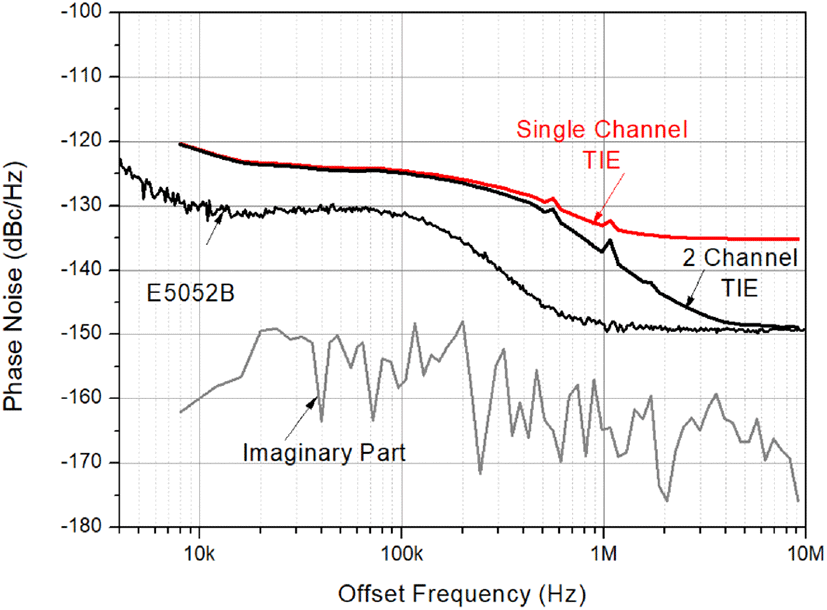
그림 4에 또한 동일 신호에 대해 계산된 두 TIE를 교차상관하여 측정된 위상잡음을 보였다. 교차상관 TIE를 이용해 계산된 위상잡음은 단일 채널 TIE로부터 계산된 위상잡음보다 개선된 것을 알 수 있다. 교차상관 TIE로부터 얻어진 위상잡음은 fm=1~10 MHz에서 E5052B로 측정된 위상잡음과 근접하나 fm=10~100 kHz에서 약 6 dB의 차이를 보이는 것을 알 수 있다. 그림 4의 허수부는 교차상관 TIE로 위상잡음 계산 시 상관관계가 없는 잡음의 평균을 보인 것이다. 따라서 교차상관을 통하여 TIE로 계산된 위상잡음은 개선된 결과를 보이나, 여전히 만족스럽지 않은 것을 알 수 있다. 이것은 ADC 클럭-지터의 잡음 영향에 의한 것이다.
그림 4에 보인 바와 같이 본 논문의 방법은 fm=1~10 kHz의 측정결과를 제공하지 못한다. 이것은 디지털 오실로스코프로부터 Labview로 읽어 들일 수 있는 파형 샘플 수의 제한 때문이다. 그림 4에서 Labview로 읽어들일 수 있는 파형의 샘플 수는 4 M으로 제한된다. 이때 얻어지는 0점의 개수는 약 700 k이다. 따라서 가장 낮은 fm,min은
이다. 여기서 최소 평균횟수를 10으로 설정하였다. 따라서 Labview의 처리능력으로 인해 약 fm=10 kHz 이하의 위상잡음 측정 결과를 제공하지 못하게 된다.
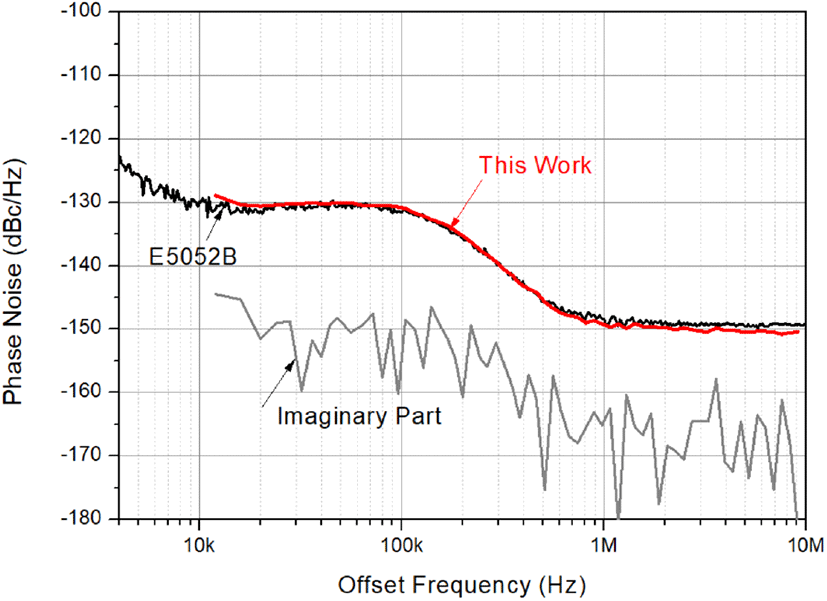
그림 5에는 본 논문에 제시된 방법으로 측정된 위상잡음과 E5052B를 사용하여 측정된 위상잡음의 비교를 보였다. 기준신호 sREF(t)는 별도의 신호발생기 E4438C를 사용하여 공급하였다. 주파수와 전력은 각각 2.41 GHz, 9 dBm으로 설정하였다. 주목할 것은 E4438C 신호원의 위상잡음은 E8257D보다 약 5~10 dB 높다. 그러나 식 (7)에 보인 것과 같이 측정된 s(t)의 위상잡음은 기준신호 sREF(t)의 위상잡음의 영향을 받지 않는다는 것을 알 수 있다. 단지 기준신호 sREF(t)는 ADC 클럭-지터 잡음을 제거하기 위한 것이다. 그림 5에서 알 수 있듯이 본 논문에 제시된 방법으로 측정된 위상잡음은 정확하게 E5052B를 사용하여 측정된 위상잡음에 일치된 결과를 보여주는 것을 알 수 있다. 표 1에는 오프셋-주파수 범위에 따른 두 측정 결과의 평균 차이를 보였다. 표 1에서 오프셋-주파수 10 kHz~1 MHz 범위에서 평균 0.2 dB의 차이를 보이는 것을 알 수 있다. 이것은 E5052B의 위상잡음 측정값의 불확실성을 고려할 때 근접한 결과임을 알 수 있다.
| fm | Mean difference (dB) | E5052B uncertainty |
|---|---|---|
| 10∼100 kHz | 0.53 | 2 dB |
| 100 kHz∼1 MHz | −0.075 | |
| 1∼10 MHz | −0.83 | |
| Mean | −0.2 |
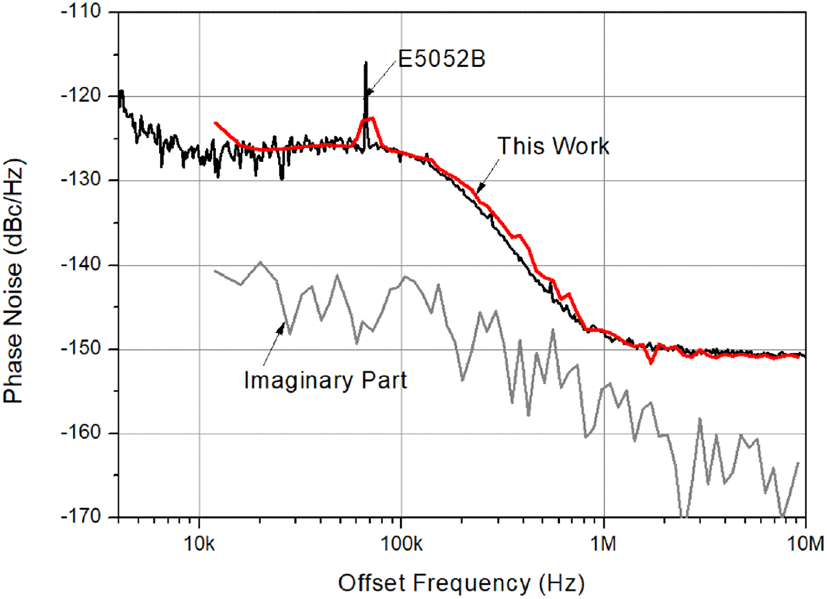
본 논문의 측정방법에 대한 다른 예로 그림 6에 신호발생기 E4438C로 생성된 2.41 GHz 신호에 대해서, 본 논문에 제시된 방법으로 측정된 위상잡음과 E5052B를 사용하여 측정된 위상잡음의 비교를 보였다. E4438C로 생성된 2.41 GHz 신호는 그림 5의 sREF(t)로 사용된 신호이다. 2.41 GHz 신호의 전력은 동일하게 9 dBm으로 설정되어 채널당 입력전력은 약 3 dBm이 된다. 이때 sREF(t)는 E8257D를 사용하여 인가하였고, 주파수와 전력은 각각 4 GHz, 9 dBm이다. 그림 6에서 sREF(t)의 주파수가 높아서 앞서 설명한 바와 같이 약 fm=20 kHz 이상에서 E5052B의 위상잡음과 일치된 결과를 주는 것을 알 수 있다.
Ⅳ. 결 론
본 논문에서 디지털 오실로스코프로 용이하게 측정가능한 TIE(time interval error)를 이용한 위상잡음 측정방법을 제안하였다. 제안된 TIE 교차상관을 이용한 위상잡음 측정방법은, 기존 TIE 교차상관을 이용한 위상잡음 측정방법으로 제거하지 못했던 ADC 클럭-지터에 의한 위상잡음을 효율적으로 제거할 수 있었다. 제안된 방법으로 측정된 위상잡음의 정확성을 보이기 위하여, E5052B로 측정한 키사이트사의 E8257D 신호발생기의 위상잡음과, 본 논문에서 제안된 위상잡음 측정방법을 이용하여 측정한 위상잡음을 비교하였다. 비교 결과, 두 측정 결과는 일치된 결과를 보였다.
본 논문으로 측정 가능한 신호의 위상잡음은 디지털 오실로스코프의 성능에 따라 제한된다. MXR608A를 사용한 위상잡음 측정범위는[1], 기준신호까지 고려한다면 신호 입력범위는 주파수 4 GHz, 입력전력 −15 dBm까지 측정할 수 있다. 위상잡음의 측정 가능 범위는 −160 dBc/Hz로 예상된다. 또한, 본 논문 방법의 정확도 평가는 더욱 많은 연구가 필요하다.
본 논문에서 제안된 방법을 디지털 오실로스코프에 내장할 경우, 디지털 오실로스코프의 위상잡음 측정기능을 향상할 수 있으며, 디지털 오실로스코프의 범용성을 높일 수 있을 것으로 생각된다.









