Ⅰ. 서 론
위상잡음(phase noise)은 신호원 위상의 시간에 따른 불규칙한 흔들림을 의미하며, 위상잡음 성능은 통신 시스템 구성시 필수적으로 고려하여야 하는 중요한 규격 중 하나이다.
2009 IEEE 기준에[1] 따르면 위상잡음은 식 (1)과 같이 정의된다.
A=Power density in one phase noise modulation side band, per Hz
B=Total signal power
식 (1)은 이상적인 스펙트럼-분석기로 용이하게 설명된다. 측정하고자 하는 신호원(SUT: source under test)을 스펙트럼분석기에 인가하고, 반송파전력(Ps) 및 반송파(carrier)의 오프셋-주파수 fm에서 단위-대역폭 당 스펙트럼 잡음전력(Pn)으로 계측될 때, 위상잡음 L(fm)은 L(fm)=Pn/Ps로 정의된다. 그러나 실제 스펙트럼-분석기의 경우 스펙트럼-분석기 바탕잡음(noise floor)과 스펙트럼-분석기 내 LO 신호의 위상잡음으로 인해 낮은 위상잡음을 갖는 SUT의 경우 정확한 측정을 수행할 수 없다.
다른 방법으로 위상검출기(PD: phase detector)를 이용한 방법이 있다[2],[3]. PD는 이상적 승적기(multiplier)와 유사하며, 두 개의 입력 신호의 곱에 비례하는 출력을 생성한다. PD를 사용 위상잡음을 측정하기 위해서는 두 개의 PD 입력 포트 중, 한 포트에 SUT를 입력하고, 다른 입력 포트에는 SUT와 같은 주파수, 90° 위상차를 갖는, 위상잡음이 SUT에 대해 무시할 수 있는 기준(reference) 신호를 인가한다. 이때 PD 출력-포트에 검출된 저주파 잡음신호의 전력스펙트럼 밀도(PSD: power spectral density) Sϕ(fm) 는 위상잡음이 된다. PSD Sϕ(fm)은 일반적으로 0 < fm <∞에서 정의된다. 식 (1)의 L(fm)은 Sϕ(fm)과 다음의 관계를 갖는다.
스펙트럼-분석기 방법과 달리 PD 방법은 낮은 위상잡음을 갖는 SUT에도 적용할 수 있으나, SUT와 같은 주파수를 갖는 기준신호원이 필요하다. 또한 앞서 설명한 바와 같이 SUT보다 충분히 낮은 위상잡음을 갖는 기준신호원이 필요하다. 기준신호원의 주파수가 SUT의 주파수와 같도록 만들기 위해서 일반적으로 위상잠금회로(PLL: phase locked loop)을 사용한다. 이 때 PLL에서 위상잠금은 PLL 내의 루프-필터에 의해 달성되는데, 루프-필터의 대역폭은 측정하고자 하는 fm보다 충분히 좁아야 한다. 루프-필터의 대역폭이 일부 낮은 fm을 포함할 경우, 루프-필터의 대역폭에 포함된 낮은 fm에서 측정된 위상잠음은 PLL 루프-필터 보상 문제를 동반한다. 따라서 낮은 위상잡음을 갖는 SUT의 위상잡음 측정을 위한 PD 방법은 낮은 위상잠음을 갖는 기준신호원, 기준신호원 PLL 때문에 구현하기 어렵게 된다.
이와 같은 아날로그 방법 이외에 디지털 기술의 발전과 더불어 디지털 기술을 이용한 위상잡음 측정 방법이 개발되었다[4]~[7]. 이 방법은 입력된 신호의 위상 ϕ를 얻기 위하여, 그림 1과 같이, 우선 ADC (analog-to-digital converter)를 통하여 디지털신호로 변환하고, 변환된 신호를 두 개의 직교하는 디지털-하향변환기(DDC: digital down converter)를 사용 cosϕ 및 sinϕ를 얻는 것이다. 뒷단 CORDIC(coordinate rotation digital computer)은 반복을 통하여 cosϕ 및 sinϕ로부터 ϕ를 얻는 디지털 회로이다. 특히 CORDIC은 FPGA(field programmable gate array)로 용이하게 구현되며, 구현 방법은 널리 알려져 있다.
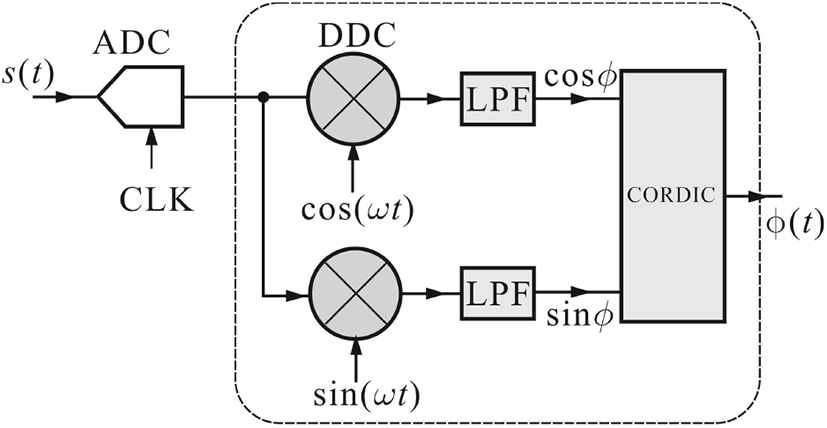
주목할 것은 그림 1의 ϕ는 시간영역 함수이고, ϕ의 주파수 영역에서 PSD가 Sϕ (fm)이며, Sϕ (fm)으로부터 식 (2)에 의하여 위상잡음 L(fm)을 얻게 되는데, L(fm)은 그림 2와 같이 일반적으로 log scalefm에 대해 도시한다. 따라서 반복적으로 ϕ를 Fourier 변환하여 얻어진 Sϕ(fm)을 평균하는 것이 필요하다. 그러나 일반적인 방법으로 ϕ를 FFT 변환 후, 평균을 취할 경우, 수렴된 Sϕ(fm)을 얻는데 참을 수 없는 정도의 긴 시간을 소요하게 된다. 이것을 보이기 위하여 그림 2에 ϕ(t)의 FFT로 얻어진 Sϕ(fm)을 보였다.
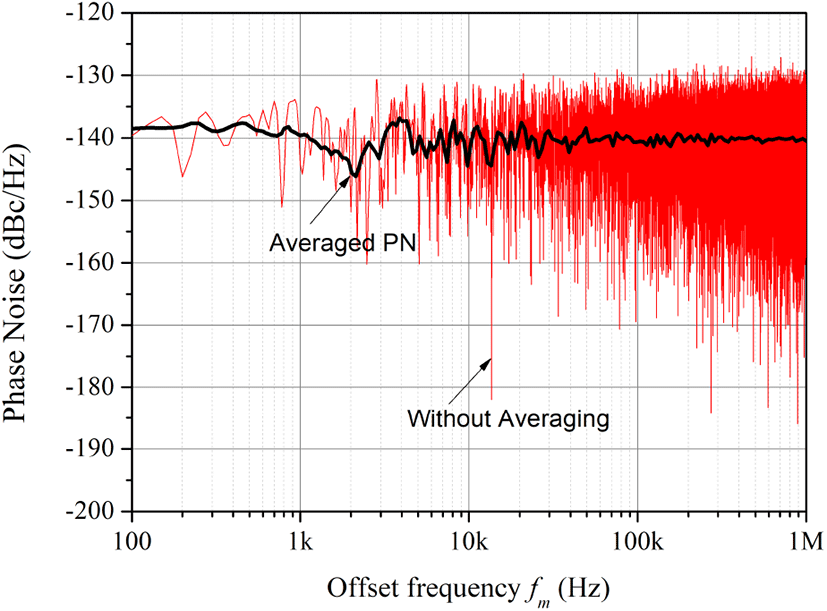
그림 2의 Sϕ(fm)은 주파수 15 MHz, 진폭 1 V, 위상 0°인 정현파에, 진폭이 [−700 μV, 700 μV]의 균일한 분포를 갖는 잡음이 추가된 파형을 s(t)로 정의하고, s(t)를 ADC로 100 MSa/sec 로 샘플 후, 샘플된 s(nΔt')에 대해 그림 1의 수신부를 이용 ϕ(nΔt)를 구한 뒤(Δt=10Δt'), FFT 연산하여 계산된 결과이다. 이와 같은 조건에서 주파수 영역 스펙트럼은 fmin~fmax에서 나타나는데, fmin=1/(4 M × 0.1 μsec)=25 Hz, fmax=5 MHz 가 된다. 그림 2는 fmin~fmax중 일부 fm에 대하여 도시한 것이다. 그림 2에서 Sϕ(fm)의 요동(fluctuation)은 fm에 따라 비례하여 커지는 것을 알 수 있다. 이러한 요동은 fm에 따른 Sϕ(fm) 값을 파악하기 어렵게 한다. 따라서 Sϕ(fm) 요동을 제거하기 위해서는 다수의 s(nΔt') 집합에 대해 얻어진 Sϕ(fm)에 대해 평균 작업을 수행하여야 한다. 그림 2에 평균을 취하여 Sϕ(fm)의 요동이 충분히 제거된 결과를 보였다. 주목할 것은 높은 fm에서 Sϕ(fm)의 요동을 충분히 제거하기 위해서는 많은 수의 Sϕ(fm) 집합에 대하여 평균을 요구하여, 경우에 따라서는 위상잡음을 얻는데 참을 수 없는 정도의 긴 시간을 소요하기도 한다.
그림 2와 같은 높은 fm에서 Sϕ(fm) 요동을 제거하기 위해서는 직접 입력샘플에 대한 FFT를 수행하는 대신에, 그림 3과 같이 입력 샘플을 샘플-길이 NF=2,000개로 이루어진 반복적인 샘플 집합으로 생각하여 순차구조 (decimating structure) FFT를 수행하면, 고주파에서 Sϕ(fm)의 요동이 제거된 결과를 얻게 된다.[8]그림 3에서 Δt=0.1 μsec (fs=10 MHz)이고, 그림과 같이 샘플-길이 n=4 M일 때 예를 보였다.
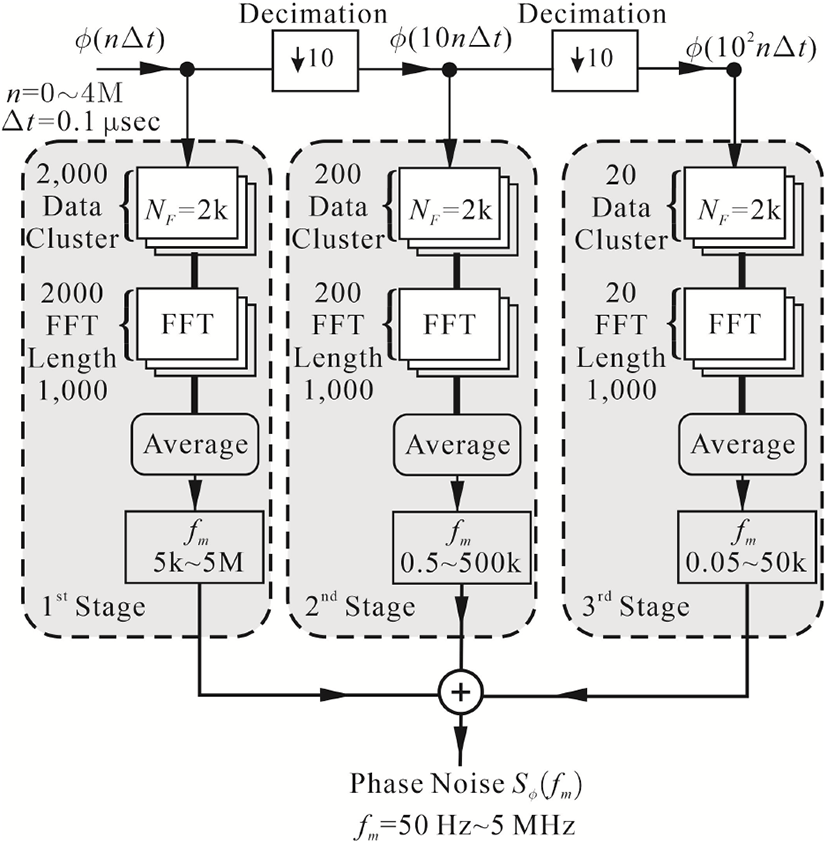
그러면 길이 4 M를 갖는 1개의 샘플은 길이 NF=2,000개를 갖는 2,000개 샘플들의 집합이 된다. 길이 NF= 2,000개를 갖는 샘플에 대해서 FFT할 경우, 스펙트럼은 앞서 설명한 바와 같이 주파수 영역 fmin~fmax를 계산하면 5 kHz~5 MHz가 된다. 길이 NF=2,000개를 갖는 동일한 샘플이 2,000개 있기 때문에 각 샘플에 대해 스펙트럼을 구한 뒤 평균하면 fm=5 kHz~5 MHz 스펙트럼을 2,000번 평균한 것이 된다. 이것을 표 1에 정리하였다.
다음 ϕ(nΔt)을 decimation할 경우, decimation된 ϕ(10nΔt)의 샘플-수는 400k가 되는데, 이것 또한 샘플-길이 NF인 샘플들로 분해하면, 샘플-길이 NF인이 샘플이 200개 얻어진다. 이 집합에 대해 PSD를 구하면, fm=0.5~500 kHz 스펙트럼을 200번 평균하여 얻은 결과가 된다. 마찬가지로 진행하면 3단에서는 fm=50 Hz~50 kHz의 스펙트럼을 20번 평균한 것을 얻게 된다. 주목할 것은 샘플-길이 NF 선택에 따라 여러 가지 주파수 대역 선택이 가능하다. 결론적으로 그림 3 구조는 fm이 높아질수록 평균회수는 증가하여 그림 2에 보인 높은 fm에서 요동을 제거하는데 효과적이다. 순차구조(decimating structure) FFT 구조는 FPGA를 이용 실시간(real time)으로 위상잡음을 구할 때 보편적으로 널리 사용되며, 비교적 짧은 시간에 높은 fm에서 충분히 요동이 제거된 위상잡음을 얻는 것을 가능하게 한다.
이와 같은 디지털 방법을 사용 Sϕ(fm)을 측정할 때Sϕ(fm)의 측정가능범위는 주로 ADC의 SNR(signal to noise ratio)에 의해 결정되게 된다. 이상적인 샘플링을 가정할 경우 ADC의 SNR은 식 (3)과 같이 결정된다.[9]
식 (3)에서 B는 ADC bit-수, fs는 샘플링-주파수를 나타낸다. 물론 식 (3)은 신호의 스펙트럼에 대한 SNR이고, 위상잡음 Sϕ(fm)을 나타내지는 않는다. 그러나 높은 fm에서 식 (3)으로 주어지는 SNR은 앞서 설명한 스펙트럼-분석기로 정의되는 위상잡음 L(fm)에 해당한다. 따라서 식 (3)에 의하여 높은 fm에서 바탕 위상잡음을 평가할 수 있다.
식 (3)을 이용 범용 디지털 오실로스코프에 널리 사용되는 10-bit ADC에 대해서 SNR을 계산하면 fs=100 MHz 에서 약 −140 dB가 된다. 이 SNR은 일반적인 VCO (voltage controlled oscillator)를 고려하면 적절하지만, 매우 낮은 약 −170 dBc/Hz 정도의 위상잡음을 갖는 수정발진기를 고려하면 충분하지 않은 SNR이다. 또한 ADC의 샘플링-clock은 불완전하며, 샘플링 clock도 위상잡음을 가지고 있어, 샘플링-clock 위상잡음의 영향을 고려하면 식 (1)로 예상한 SNR보다 작은 값을 얻게 된다[10]. 식 (1)로부터, ADC의 SNR 개선 방법은 ADC bit-수 증가나, 샘플링 주파수 fs를 높이는 방법이 있다. 현실적으로 ADC bit-수는 18-bit 정도가 한계이다.
ADC bit-수 증가나, 샘플링 주파수 fs를 높이는 방법 이외에 교차상관 후 이의 평균을 이용하는 방법이 있다. 일반적으로 그림 4와 같이 ADC로 샘플링된 data를 동시에 공급하여 여러 채널을 통해 ϕ를 얻을 수 있다. 각 채널의 ADC에 의해 발생된 열잡음은 독립이기 때문에 그림 4의 ϕA 및 ϕC에 포함된 열잡음은 독립이 된다. 따라서 ϕA, ϕC의 교차평균을 구할 경우, ADC에 의해 발생된 열잡음은 0으로 수렴시킬 수 있다. 교차상관 (cross correlation) 회수M의 증가에 따른 두 개의 독립잡음 ϕ1및 ϕ2의 교차상관 PSD는 감소되는 것으로 알려져 있다[11].
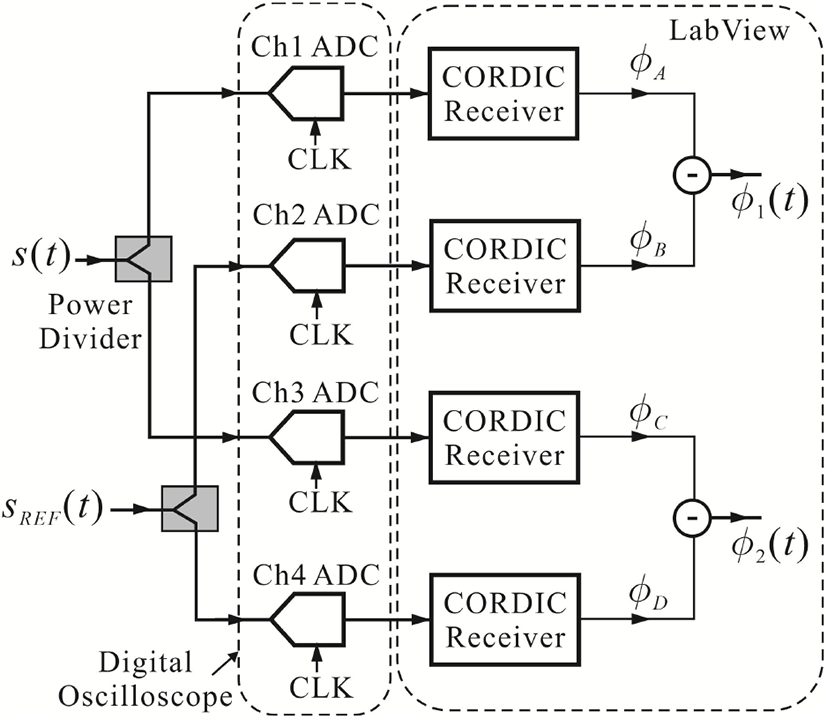
그러나 ADC로 샘플링할 때 들어온 clock 위상잡음은 공통이어서 이와 같은 간단한 교차 상관의 평균으로는 제거되지 않게 된다. 그림 4는 4-채널 오실로스코프를 이용하여 교차상관에 필요한 두 개의 위상을 얻기 위한 4-채널 측정 구조를 보였다. 그림 4에서 s(t)는 SUT이며, sREF(t)는 낮은 위상잡음을 갖고 위상잡음이 알려진 기준신호이다. 그림 4의 CORDIC 수신기(receiver)는 그림 1의 점선 친 부분을 나타낸다. 그림 4에서 ADC의 잡음과 clock (CLK)-잡음까지 고려하여[10], ADC1 및 ADC2를 통하여 얻어진 위상 ϕA 및 ϕB는 각각 식 (4) 및 식 (5)와 같이 나타낼 수 있다.
식 (4)와 (5)에서 ωm, ωREF, ωs는 s(t), sREF(t) 및 CLK의 각-주파수를 나타내며, 사전에 알고 있는 양이 된다. 또한 같은 CLK를 사용 샘플하였기 때문에, 동일한 잡음 ϕCLK가 ϕA 및 ϕB에 나타나게 된다. 여기서 ωm=ωREF 일 때 위상 ϕ1은
와 같다. 유사하게 ϕ2는
식 (6)과 식 (7)에서 ϕp=ϕADC1-ϕADC2와 ϕq=ϕADC3-ϕADC4 는 상관관계는 거의 없다고 알려져 있다[6]. 여기서 ϕ1, ϕ2의 스펙트럼을 각각 ω1, ω2라고 정의하면, ϕ1, ϕ2의 교차상관 PSD은 이 된다. 시행회수 M에서 교차상관 PSD의 평균값은
이 된다. 따라서 ϕp, ϕq가 독립이라고 가정하면, 시행회수 M→∞일 때 교차상관 PSD의 극한값은 Sϕ(fm)+SREF(fm)이 된다. 따라서 SREF(fm)이 이미 결정된 값이기 때문에, 미지의 Sϕ(fm)은 M→∞일 때 교차상관 PSD로 부터 결정할 수 있게 된다. 보통 기준발진기로 SREF(fm)이 매우 작은 발진기를 사용하기 때문에 SREF(fm)=0으로 근사하게 된다. 따라서 M→∞일 때 식 (6)의 교차상관 PSD의 극한값은 위상잡음 Sϕ(fm)이 된다. 이러한 교차상관 방법을 사용할 경우 −170 dBc/Hz 의 위상잡음도 측정할 수 있는 것으로 알려져 있다.[6]
그림 4의 ϕ1및 ϕ2를 받아서 교차상관을 수행하는 구조는 ϕ1및 ϕ2에 대해서 그림 5와 같은 2개의 병렬구조를 구성하고, 교차상관 스펙트럼은 그림 5와 같이, 같은 주파수에서 얻어진 스펙트럼 결과를 곱하여 얻게 된다. 주목할 것은 그림 5의 구조는 그림 3과 같이 순차구조 FFT이며, 동시에 ϕ1및 ϕ2 교차상관을 수행하여 높은 fm에서 요동을 제거하는 구조이기도 하다. 디지털방법으로 위상잡음 측정시 그림 4의 구조와 그림 5 구조를 병합하여 사용된다.[8]
앞서 설명한 그림 4와 그림 5를 병합한 구조는 FPGA를 사용 구현되게 된다. FPGA를 사용할 경우, 실시간으로 위상잡음을 측정할 수 있는 장점을 가지고 있다. 또한 샘플링에 사용하는 clock의 선정에 있어 위상잡음이 적은 OCXO를 사용할 수 있어, 식 (4) 및 식 (5)에 나타나는 clock의 위상잡음효과를 크게 줄일 수 있다.
본 논문에서는 FPGA 대신 그림 4에 보인 4-채널 ADC는 주파수 8 GHz까지 동작하는 Keysight사의 MSO804A 디지털 오실로스코프[12]를 이용하고, CORDIC 수신기 및 그림 5의 교차상관 decimating FFT 구조를 NI-사의 Labview™를 이용 구현하려고 한다.
이러한 구현의 단점은 FPGA와 달리 bit-stream으로 연산하지 않고, 샘플링된 파형에 대하여 연산하기 때문에 실시간에서 동작하지 않게 된다. 따라서 앞서 FPGA보다는 위상잡음 측정 속도는 분명히 느리게 된다. 또한 ADC bit수는 디지털 오실로스코프의 bit-수로 제한되고, clock의 위상잡음 효과가 FPGA clock 선정과 같이 최적화 된 것은 아니기 때문에, 크게 나타나게 되어 FPGA 구현보다 SNR이 나빠지게 된다. 결과적으로 낮은 위상잡음을 갖는 SUT 측정에 제한이 있다.
반면, 장점은 디지털 오실로스코프는 보편적인 계측기이므로 난이한 FPGA 프로그래밍을 피하고, Labview™를 PC에서 설치하여 위상잡음을 용이하게 계측할 수 있게 된다. 단점으로 제기된 SNR의 개선은 식 (3)에서 보인바와 같이 디지털 오실로스코프의 샘플링 주파수를 가변하여 해결할 것이다.
본 논문의 기여로는
-
1) 위상잡음측정기 구현에 있어 이와 같은 구현은 본 논문에서 처음으로 제시하는 것이 된다. 이 결과로 보급이 용이한 위상잡음측정기 구현이 가능하다.
-
2) 높은 fm에서 위상잡음 요동을 제거하기 위해서 FPGA에서는 필연적으로 그림 5와 같은 순차구조 교차상관 구조를 사용하여야 한다. 그러나 Labview™를 이용할 경우 높은 fm에서 위상잡음 요동을 제거하기 위해서 꼭 그림 5와 같이 구현할 필요가 없게 된다. 본 논문에서는 그림 5와 같은 순차구조 교차상관 구조 대신 보다 구현이 용이한 LBA(logarithmic bandwidth averaging) 기법을 사용 구현할 것이다.
-
3) 다음 문제로 구현된 디지털위상잡음 측정방법으로 측정된 위상잡음의 정확도 평가문제가 있다. 이것을 평가하기 위하여 Keysight 사의 33600A[13], E8257D[14], 그리고 VCO[15]의 위상잡음을 본 논문에 구현된 측정방법으로 측정하고, E5052B[16] 결과와 비교하여 구현된 방법의 정확도를 보일 것이다.
-
4) 또한 본 논문에서는 수 GHz의 높은 주파수를 갖는 신호원에 대해서 전술한 디지털 위상잡음 측정방법을 적용하려고 한다. 이때 ADC 샘플링 주파수 fs는 Nyquist 샘플링 주파수에 비해 일반적으로 낮게 설정된다. 그러나 위상잡음은 그림 6과 같이 반송파주파수 주변 매우 좁은 주파수 영역에 나타나기 때문에, 위상잡음은 그림 6의 하향변환된 첫 번째 Nyquist 대역 내 반송파에 그대로 나타나게 된다. 이러한 샘플링은 언더-샘플링(under-sampling)으로도 알려져 있다. 본 논문에서는 첫 번째 Nyquist 대역 내 반송파의 위상잡음을 측정하여 SUT의 위상잡음을 얻을 수 있게 된다. 따라서 본 논문에서는 언더-샘플링을 이용하여 RF에서 주파수 하향변환 없이 SUT의 위상잡음을 측정하는 방법을 제안한다.
Ⅱ. Labview™를 이용한 위상잡음측정기 구현
앞서 서론에서 설명한 바와 같이, 본 연구의 위상잡음측정기는 디지털 오실로스코프와 Labview™ 프로그램으로 구성된다. 본 논문의 Labview™은 National Instruments사의 Labview 2015이다. Labview™은 디지털 오실로스코프로부터 SUT의 샘플 파형을 읽어 들이는 것과, 읽어 들인 파형으로부터 위상잡음을 계산하는 것이다. SUT 샘플신호파형으로부터 위상잡음은 그림 4의 CORDIC 수신기와 FFT를 계산 후 LBA를 통해 높은 fm에서 위상잡음 요동을 제거한다. 그림 5의 순차구조 교차상관 구조는 사용되지 않는다. 본 절에서는 그림 4와 LBA(logarithmic bandwidth averaging)의 Labview™ 구현에 대해 설명할 것이다.
이 두 가지 구조 구현에 앞서 그림 4의 ADC CLK 주파수와 ADC로부터 읽어 들일 최소 샘플-수의 결정이 필요하다. SUT의 위상잡음은 보통 오프셋-주파수 fm< 10 MHz에서 측정된다. 이것은 CLK 주파수에 따라 다르다. 우선 CLK 주파수는 100 MHz 기준으로 계산하였다. 샘플 속도가 약 100 MSa/sec일 때 읽어 들일 최소 샘플-길이 N은 > 4 MSa로 결정하였다. N= 4 MSa일 경우, fm> 25 Hz의 위상잡음만 측정 가능하다. 보다 많은 N이 가능할 경우, 측정 가능한 fm은 25 Hz보다 낮출 수 있다. 이것을 표 2에 정리하여 보였다.
| Sampling rate | 100 MSa/sec |
| Minimum number of sample length | > 4 MSa |
그림 1의 DDC는 Labview™에서 단순히 샘플된 파형간의 곱으로 구현할 수 있다. 따라서 Labview™에서 DDC는 이상적인 승적기(multiplier)를 이용하여 구현하였다. 그림 1에 보인 DDC LO 신호 cosωt 및 sinωt는 Labview™의 정현파 신호생성기를 통하여 구현하였다. 신호생성기의 주파수 ω를 결정하기 위하여, ADC를 통하여 받은 신호에 대해 FFT 연산 후 결정된 주파수를 사용하였다. 따라서 본 논문에서 Labview™을 통한 위상잡음 측정은 RF-하드웨어를 이용한 측정에서와 달리 입력주파수를 얻기 위하여 PLL을 구성할 필요가 없다. 디지털 하드웨어(hardware)를 이용한 위상잡음측정도 RF 측정에서와 마찬가지로 PLL을 통한 주파수합성기를 필요로 한다. 비록 정현파원을 NCO(numerically controlled oscillator)를 이용하여 구현하지만, 이것도 ADC로 들어온 신호의 입력주파수와 같아져야 하기 때문에 PLL을 필요로 한다. 그러나 본 방법과 같이 프로그램을 이용할 경우, 별도의 PLL을 필요로 하지 않는다.
DDC의 출력에는 주파수 2ω에 해당하는 신호가 나타나게 되는데, 그림 1의 저역여파기(LPF: low pass filter)는 주파수 2ω에 해당하는 신호를 제거하는 역할을 한다. 본 논문에서 측정하려고 하는 위상잡음 최대 오프셋-주파수 fm을 < 2.5 MHz로 설정하였다. 이에 준하여 LPF 대역폭은 5 MHz로 설정하였다.
LPF는 디지털-IIR(infinite impulse response) 저역여파기로 구현하였다. IIR 여파기는 FIR(finite impulse response) 여파기에 비해 적은 단수로 원하는 주파수 선택도를 얻을 수 있다. FIR 여파기는 선형 위상특성을 가지고 입력 위상을 왜곡시키지 않는 출력을 제공하는 장점이 있다. 그러나 FIR 여파기는 원하는 주파수 선택도를 얻기 위하여 많은 탭(tap)-수를 요구한다. 이러한 면에서 본 논문에서는 디지털-IIR 여파기를 선택하였다. 표 3에는 Labview™ 으로 구현한 디지털-IIR 여파기 규격을 요약하였다. 또한 그림 7에는 Labview™으로 계산된 디지털-IIR 여파기의 전달함수 H(jω)를 보였다. 그림 7의 특성으로부터 설계된 대역폭 5 MHz 디지털-IIR 저역여파기는 대역폭 내에서 선형적인 위상을 주는 것을 알 수 있다.
| Type | Elliptic |
|---|---|
| Order | 16 |
| Passband frequency | 5 MHz |
| Passband ripple | −0.1 dB |
| Attenuation at 10 MHz | −120 dB |
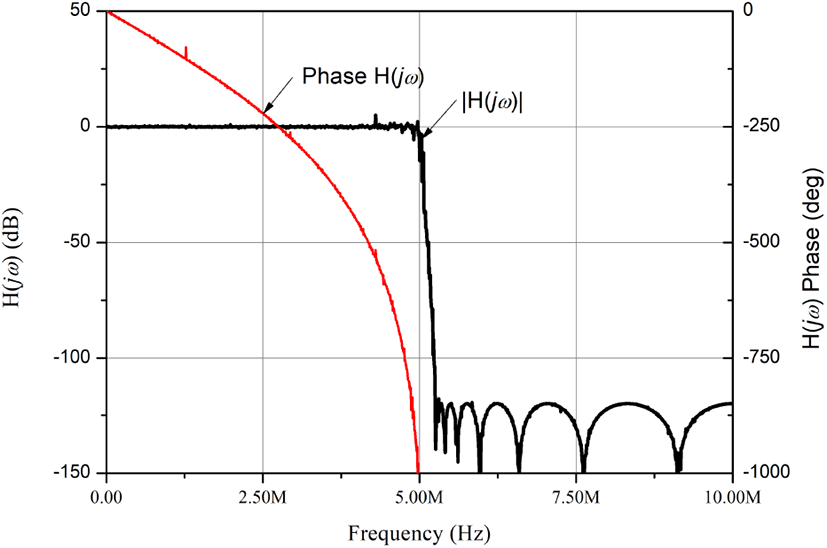
디지털-IIR 저역여파기 출력신호는 샘플속도에 비해 상당히 천천히 변하는 신호이다. 그러나 LPF 출력은 여전히 입력과 같은 샘플속도 100 MSa/sec를 가지게 된다. 이 경우, LPF 출력신호를 다운-샘플하여 다음에 필요한 FFT 계산량을 줄일 수 있게 된다. 또한 하드웨어 면에서 다음 단의 CORDIC은 몇 차례 반복연산을 통하여 cosϕ 및 sinϕ로부터 ϕ를 얻기 때문에 다운-샘플은 필요하게 된다. 본 논문에서 선정된 LPF 대역 폭은 5 MHz이고, 샘플속도는 100 MSa/sec이므로 데시메이션(decimation)에 의해 샘플속도를 1/10로 줄이는 것이 가능하다. 이러한 데시메이션은 CORDIC으로 계산된 ϕ에 영향을 줄 수 있다. 따라서 데시메이션 영향 검토가 필요하다. 시뮬레이션 결과 설정된 1/10 데시메이션은 ϕ에 영향을 주지 않는 것을 확인하였다. 따라서 본 논문에 Labview™으로 구현된 CORDIC 수신기는 CORDIC-부 앞 두 경로에 데시메이터가 삽입되었다.
그림 1의 cosϕ 및 sinϕ로부터 ϕ를 얻는 CORDIC의 FPGA 구현은 널리 알려져 있다. 그러나 Labview™ 프로그램에서는 별도의 CORDIC 구현은 필요하지 않다. Labview™에서 CORDIC은 atan-함수를 사용하여 구현하였다. 구현된 CORDIC 수신기에 Labview™으로 위상잡음이 없는 진폭 1 V, 주파수 15.1 MHz, 위상 90°를 갖는 표 2와 같이 샘플속도 100 MSa/sec로 샘플된 정현파 입력신호를 입력하였다. 이때 샘플-수 4 M으로 두고 시뮬레이션 하였다. 계산된 위상잡음 결과는 오프셋주파수 fm에 관계없이 약 < −250 dBc/Hz 였다. 따라서 이 위상잡음 값은 Labview™ 프로그램을 사용 이론적으로 구할 수 있는 가장 작은 위상잡음 값이 된다.
또한 일반적으로 그림 1의 ADC 출력은 순수한 정현파 가 아니고, 2차 및 3차 고조파를 포함하게 된다. 따라서 그림 1의 수신기 입력에 2차 및 3차 고조파를 제거하기 위한 고조파제거 여파기 추가 여부를 고려할 필요가 있다. 그림 1의 수신기를 보통의 혼합기(mixer)를 사용 하드웨어로 구현할 경우, 2차 및 3차 고조파 주변의 잡음 또한 하향 변환된 스펙트럼에 추가 되어, 검출된 위상잡음 값에 오차를 주게 된다. 따라서 일반적인 하드웨어로 구현된 수신기의 경우 필수적으로 2차 및 3차 고조파를 제거하기 위한 여파기 추가하여야 한다. 그러나 그림 1의 DDC는 Labview™ 프로그램을 이용 구현된 이상적인 선형 혼합기여서 2차 및 3차 고조파 주변의 잡음의 영향은 없게 된다. 따라서 그림 1의 수신기에서 추가적인 고조파제거 여파기는 필요 없게 된다. 고조파주변 잡음의 영향은 CORDIC 수신기 입력에 별도의 고조파 제거 여파기를 삽입하지 않고 잡음이 추가된 1-톤(tone) 신호원과 고조파를 반영한 3-톤 신호원에 동일한 잡음이 추가된 합성 신호원을 인가하고, 시뮬레이션하여 위상잡음의 변화를 확인하였다. 두 위상잡음 결과는 동일하였다. 따라서 예상한 바와 같이 CORDIC 수신기 입력에 별도의 고조파 제거 여파기는 필요하지 않은 것을 확인하였다.
본 절에서는 그림 5의 순차구조 교차상관 FFT를 대신할 LBA(logarithmic bandwidth averaging) 방법의 Labview™ 구현에 대해 설명한다. 본 논문에서는 순차구조 교차상관 FFT 대신에 직접 샘플-수 4 M에 대한 교차상관 FFT를 수행하고, 얻어진 결과에 대해 LBA를 수행하여, log-scale fm에 대한 교차상관 스펙트럼을 구했다. 설명에 있어 그림 5의 복잡성을 피하기 위해, 이보다 간단한 구조인 그림 3을 이용하여 설명한다. 그림 3에서, 각 단에서 FFT 후 주파수 간격은 1/(NF Δt),1/(10NF Δt), 1/(102NF Δt)로서, 계산하면 5 kHz, 500 Hz, 50 Hz가 된다. 주목할 것은 계산된 주파수 간격 5 kHz, 500 Hz, 50 Hz는 주파수 대역폭 BW 에 해당하게 된다. 따라서 이때 FFT를 통해 얻어진 결과 값은 각 단별로 BW 5 kHz, 500 Hz, 50 Hz에서의 잡음전력의 평균값이라고 볼 수 있다. 결과로 그림 5의 순차구조 교차상관 FFT 구조는 fm이 높아지면 보다 넓은 BW 에서 평균값을 제공하고, 넓은 BW 에서 잡음전력의 평균은 그림 2와 같은 높은 fm에서 Sϕ(fm)의 요동을 줄일 수 있게 된다.
이 점에 착안하여 직접 샘플-수 4 M에 대한 교차상관 FFT를 수행하고, 교차상관 FFT로 결정된 fm대신에 새로이 log 주파수 간격을 갖는 fm을 설정하고, 주파수 대역폭 BW 를 식 (9)와 같이 설정한다.
식 (9)에서 Q는 상수로 공진기의 정의에 사용되는 Q와 같은 의미를 갖게 된다. 본 논문에서는 Q=20으로 설정하였다. 이와 같이 설정하면 fm이 높아지면 넓은 BW 를 갖게 되고, fm에 따라 결정된 BW 에서, BW 내에 있는 샘플-수 4 M에 대해 계산된 교차상관 FFT 값을 평균하면, 높은 fm에서 Sϕ(fm)의 요동을 제거할 수 있게 된다. 이것을 본 논문에서는 LBA 라고 명명한다. FPGA같은 하드웨어의 경우, 그림 5와 같은 순차구조 교차상관 FFT는 구현에 용이성을 주지만, Labview™ 프로그램 내에서는 구현에 용이성을 주지 못하며, FPGA 시뮬레이션 이상 의미를 갖지 못한다. 따라서 본 논문에서는 순차구조 교차상관 FFT 대신에 LBA를 사용하였다.
교차상관스펙트럼은 Labview™의 크로스-스펙트럼 함수를 이용하여 구현하였다. 본 논문에서 시간영역 파형의 윈도우는 스펙트럼 누설이 가장 적은 7항-Blackman 윈도우를 선택하였다[17]. 다음으로 ϕ1, ϕ2의 스펙트럼을 각각 ω1, ω2라고 정의하면, 교차상관 스펙트럼은 로 복소수 ωr+jυi가 된다. 여기서 실수부 ωr은 ϕ1, ϕ2의 스펙트럼을 각각 ω1, ω2라고 정의하면, 상관관계가 있는 ϕ1, ϕ2의 스펙트럼이 되고, 반면 허수부 ωi는 상관관계가 없는 ϕ1, ϕ2의 스펙트럼을 나타낸다. 따라서 교차상관스펙트럼 결과에서 실수부만 선택하게 된다. 교차상관 스펙트럼으로부터 잡음신호의 PSD(power spectral density) 계산은 윈도우에 따라 달라진다. 계산결과, 7항-Blackman 윈도우의 ENBW(equivalent noise bandwidth)는 2.63191이고, 계산된 잡음전력은 ENBW로 나누어 PSD를 계산하였다. LBA의 구현은 Labview™을 사용 직접 구현하기는 어렵다. 따라서 Matlab으로 프로그램을 작성 후 Labview™ 내의 MATLAB script에 입력하여 구현하였다.
Ⅲ. 위상잡음 측정 및 평가
본 논문의 디지털 오실로스코프와 Labview™으로 구현된 위상잡음 측정기 평가를 위해서 위상잡음이 알려진 SUT가 필요하다. 이를 위해서 본 논문에서는 Keysight사의 함수발생기 33,600A[13], SSG(synthesized signal generator) E8257D[14], Z-Comm사의 VCO는 CRO2170B-LF[15]3가지 SUT에 Keysight 사의 E5052B[16] SSA(signal source analyzer)[17]로 위상잡음을 측정하였다. 다음 구현된 위상잡음 측정방법을 사용하여 측정된 위상잡음과 비교하였다.
우선 함수발생기 33600A를 이용, 주파수 15.1 MHz, 9 dBm 전력을 가지는 정현파를 생성하였다. 전력을 9 dBm으로 설정한 것은 E5052B로 측정된 전력과 같도록 만들기 위해서이다. SSA로 측정시 33600A의 측정된 전력은 약 4.8 dBm이다. 그리고 그림 4의 전력이분기(power divider)는 주파수 15.1 MHz에서 약 4 dB의 손실을 갖는다. 따라서 9 dBm으로 설정시 채널에 입력되는 전력은 약 5 dBm으로 SSA 측정시 전력과 거의 같게 된다.
다음 디지털 오실로스코프의 샘플링 주파수를 1 GHz 설정하였다. 디지털 오실로스코프의 샘플링 주파수를 1 GHz로 높게 설정한 이유는 식(3)으로 주어진 바탕 잡음을 낮추기 위한 것이다. 샘플링 주파수를 1 GHz일 때 바탕잡음은 약 −129 dBc/Hz로 나타났다. 따라서 −150 dBc/Hz의 위상잡음을 얻기 위해서는 약 M=10,000의 교차상관이 필요하게 된다.
그리고 기준입력을 SSG E8257D를 사용하여 인가하였다. 기준입력의 주파수는 1.4151 GHz, 9 dBm으로 설정하였다. 이와 같이 기준입력의 주파수를 설정한 이유는 식 (4)와 식 (5)에서 CLK 잡음을 소거하면
와 같다. 따라서 기준입력의 위상잡음 및 ADC 잡음의 기여가 적게 나타나게 된다. 이러한 점을 고려하여 기준주파수를 충분히 높은 1.4151 GHz로 설정한 것이다.
디지털 오실로스코프는 bit-수 제한 그리고 샘플링 clock의 위상잡음을 조절할 수 없기 때문에 최적화된 위상잡음측정 동작을 위해서는 전술한 바와 같이 디지털 오실로스코프의 샘플링 주파수 그리고 기준입력의 주파수 설정이 필요하다.
그림 8에는 E5052B로 측정된 함수발생기 33600A의 위상잡음을 보였다. 또한 본 논문의 방법으로 교차상관회수 M=10,000 (측정시간 약 1 day)일 때 측정된 위상잡음을 보였다. 보다 개선하기 위해서는 M을 증가시켜야 하지만, 현실적으로 이것이 최대 M이라고 생각된다. M=100,000 으로 할 경우 약 5 dB 개선을 보이게 되는데, 측정시간은 10 day에 가깝게 된다. 그러나 M=10,000일지라도 두 결과는 근접한 것을 알 수 있다. 그리고 측정된 결과의 신뢰성을 보이기 위해서 측정된 교차상관 스펙트럼의 허수부를 보였다. 이 허수부는 앞서 설명한 바와 같이, 허수부의 크기는 충분히 작을 경우 측정된 결과는 정확하다고 추론된다.
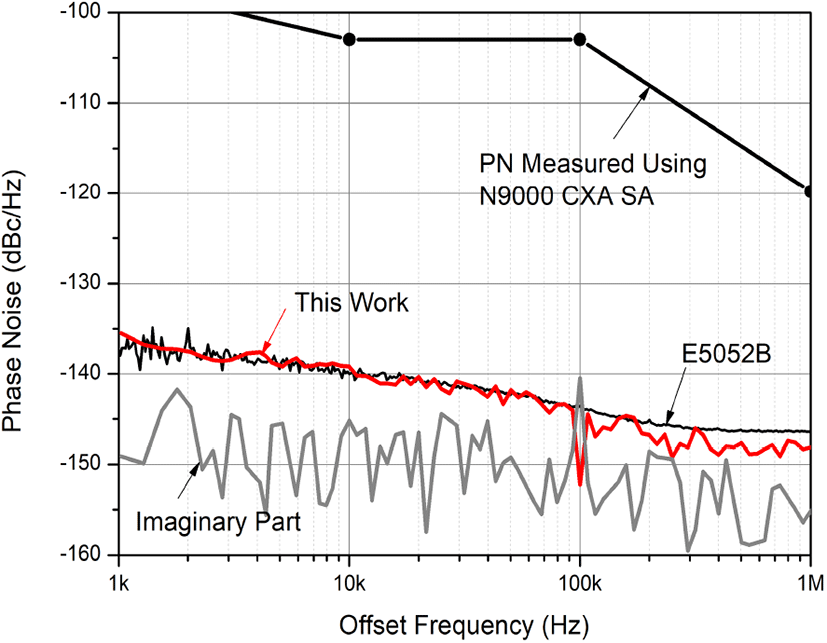
그림 8에 보인 33600A의 위상잡음을 측정하는 데는 상당히 정밀한 위상잡음 측정 계측기가 필요하다. 이것을 보이기 위하여 상용 스펙트럼 분석기 Keysight사의 N9000A CXA Signal Analyzer[18]로 33600A 위상잡음을 측정하였다. 설치된 option은 Option 503으로서 직접 위상잡음을 측정하는 기능이 없어, 스펙트럼 분석기로 fm에서 잡음전력을 측정하여 위상잡음을 계산하였다. 이것을 그림 8에 보였다. 이것은 참고문헌 [18]에 있는 규격과 거의 같다. 그림 8로부터 33600A의 위상잡음을 측정하는 데는 상당히 정밀한 위상잡음 측정 계측기가 필요함을 알 수 있다. 또한 이와 같은 정밀한 위상잡음 측정을 본 논문의 방법으로 수행할 수 있음을 알 수 있다.
우선 측정하고자 하는 SSG E8257D의 주파수 1.4151 GHz 전력 4 dBm으로 두고, SSA E5052B로 위상잡음을 측정하였다. 측정된 결과는 그림 9에 보였다. 본 논문의 방법으로 E8257D의 위상잡음을 측정하기 위하여 디지털 오실로스코프의 샘플링 주파수를 10 GHz로 설정하였다. 샘플링 주파수가 10 GHz일 경우, 바탕 위상잡음은 −140 dBc/Hz로 나타났다. 이것은 함수발생기 33600A를 측정할 때 샘플링 주파수를 1 GHz로 설정하였고, 얻어진 바탕 위상잡음이 약 −129 dBc/Hz임을 고려하면 예상 가능한 결과라고 볼 수 있다. 따라서 교차상관회수 M=10,000 으로 할 경우, fm=1 MHz에서의 측정 가능한 위상잡음은 약 −160 dBc/Hz 일 것이다. 그리고 위상잡음은 −160 dBc/Hz는 그림 9에 보인 E5052B로 측정된 위상잡음을 고려할 때, 충분히 E8257D의 위상잡음을 측정할 수 있음을 알 수 있다.
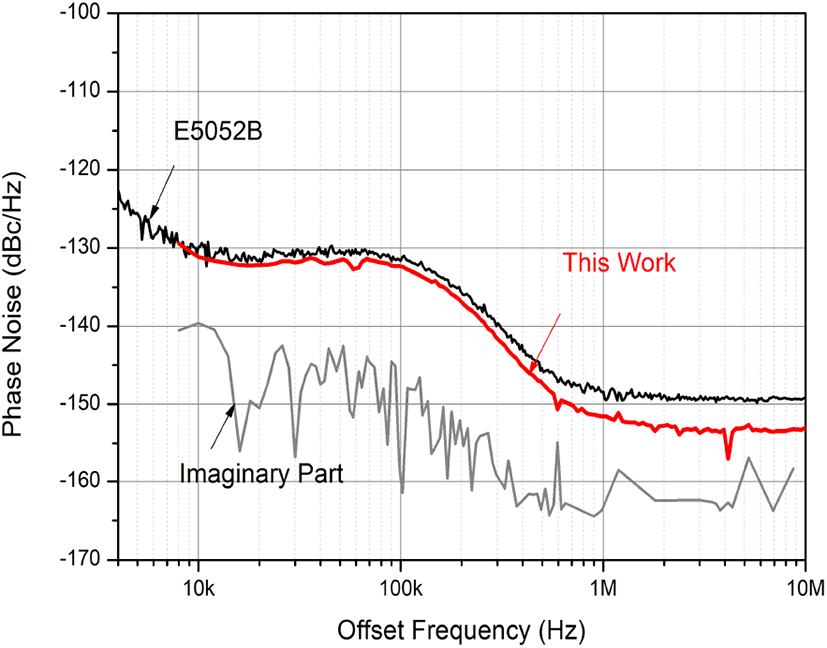
다음으로 기준입력의 주파수는 2.41 GHz로 설정하였다. 기준입력은 별도의 SSG E4438C를 사용 인가하였다. 식(10)에서 보인 바와 같이, 주파수 2.41 GHz는 clock 위상잡음을 제거할 때 큰 바탕 잡음의 변화를 가져오지 않게 된다(식 (10)에 의하면 바탕잡음은 약 1.5배로 커지게 된다).
SUT E8257D의 전력은 10 dBm으로 설정하였다. 주파수 1.41 GHz에서 전력이분기의 손실은 약 4.3 dB로 채널에 인가되는 전력은 5.7 dBm이 된다. 그림 9에 본 논문의 방법으로 측정된 전력 보상 위상잡음을 보였다. 또한 교차상관 스펙트럼의 허수부도 동시에 보였다. 허수부는 충분히 낮아진 것을 알 수 있고, 실수부로 측정된 위상잡음은 신뢰할 만하다고 생각된다. 또한 두 결과는 근접한 것을 알 수 있다.
이 절에서 Z-Comm사의 VCO를 SUT로 선정하고, 본 논문의 방법을 이용하여 위상잡음 측정하였다. Z-Comm사의 VCO는 CRO2170B-LF[15]로서 조정전압 0 V에서 약 1,934 MHz의 발진주파수를 갖는다. 조정전압을 0 V로 선정한 것은 DC 전원 공급기를 이용 조정전압을 인가할 때, DC 전원 공급기의 잡음이 추가되기 때문에, 이의 영향을 배제하기 위한 것이다.
그림 10에는 SSA E5052B로 측정된 위상잡음을 보였다. 그림 10에서 E5052B로 측정된 위상잡음은 fm=1 MHz에서 약 −140 dBc/Hz를 갖는 것을 알 수 있다. 그리고 E5052B로 측정시 입력 전력은 약 2.6 dBm이었다. 교차상관회수 M=10,000으로 고려할 경우, 앞서 함수발생기 33600A의 위상잡음 측정 설정을 고려하면 함수발생기 33600A의 디지털 오실로스코프의 샘플링 주파수와 같게 하면 적절할 것이다. 따라서 디지털 오실로스코프의 샘플링 주파수 1 GHz 설정하였다. 이와 같은 설정이면 교차상관회수 M=10,000, fm=1 MHz에서 위상잡음 약 −150 dBc/Hz 까지 측정할 수 있을 것이다.
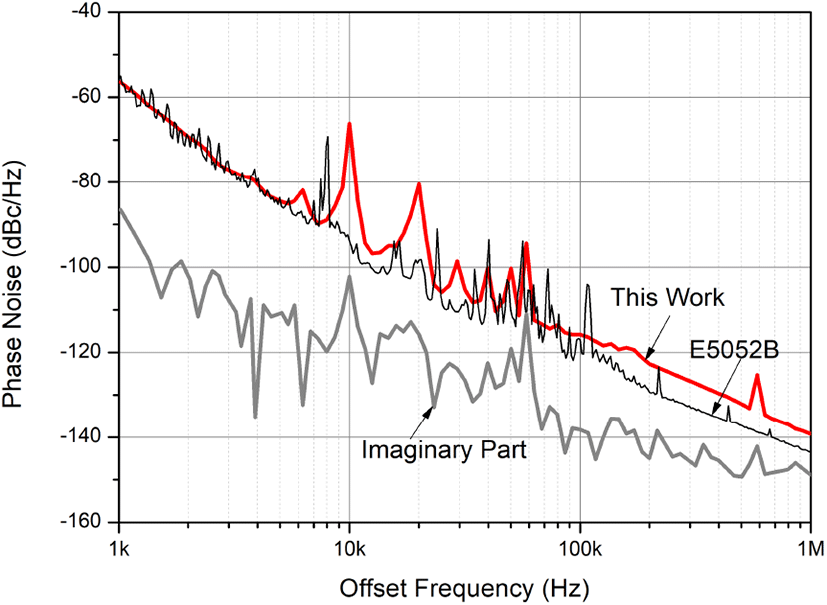
다음 기준입력의 주파수 2.01 GHz 10 dBm으로 하였다. 기준입력은 E8257D SSG를 이용하여 인가하였다. 식(10)에 의하면 이 경우 바탕잡음은 최대 3 dB(2배) 커지게 되는데, 이와 같은 증가를 상쇄하기 위해서는 교차상관회수를 약 4배 증가시켜야 된다. 따라서 바탕잡음의 증가는 교차상관회수를 크게 증가시키지 않는 것을 알 수 있다.
그림 10에 본 논문에서 제시한 방법으로 측정된 결과와 Keysight 사의 E5052B Signal Source Analyzer[16]로 측정된 결과를 보였다. 그림 10에서 볼 수 있듯이, 두 결과는 낮은 fm에서는 근접한 것을 알 수 있다. 이로서 본 논문에서 제시한 방법을 이용 위상잡음 측정한계 범위에 있는 SUT의 위상잡음을 정확하게 측정할 수 있는 것을 알 수 있다.
Ⅳ. 결 론
본 논문에서 4-채널 10-bit 디지털 오실로스코프 MSO804A와 Labview™을 이용한 새로운 위상잡음 측정 방법을 제안하였다. 제안된 방법으로 측정한 위상잡음의 정확성을 평가하기 위하여, Keysight 사의 33600A, E8257D, Z-comm사의 2 GHz VCO 3가지 SUT에 대해 측정한 위상잡음 결과와 Keysight 사의 E5052B Signal Source Analyzer측정결과를 비교하여 평가하였다. 측정된 위상잡음 결과는 E5052B 위상잡음 측정기 결과와 근접함을 보였다. 오차는 약 ± 3 dB 정도이다. 정밀도가 높은 위상잡음측정기는 상당히 고가이며, 범용적이지 않다. 반면, 디지털 오실로스코프가 범용적인 계측기인 점을 고려하면, 본 방법을 적용한다면 저가의 범용적인 위상잡음측정기 구현이 가능하다고 사료된다. 또한 추후 심화 연구를 통하여 본 방법을 개선할 경우, 수정발진기의 위상잡음 측정도 가능하다고 본다.
표 4는 본 논문의 결과와 다른 문헌의 디지털 위상잡음 측정 결과를 비교한 것이다. 본 논문의 ADC bit-수는 다른 문헌에 비해 적지만(bit-수 감소로 약 20 dB 이상의 바탕 위상잡음 열화 예상), 본 논문의 바탕 위상잡음은 다른 문헌과 비교할 때 동등 이상이다. 특히, 다른 문헌의 결과보다 대역폭이 넓어 위상잡음 측정 장비로서의 장점이 있다. 또한 미래에 예상 가능한 디지털 오실로스코프 하드웨어의 ADC 비트 수와 대역폭의 발전을 고려할 때, 본 논문의 제시된 방법이 가치 있다고 생각된다.
| Items | [4] | [6] | [19] | This work |
|---|---|---|---|---|
| ADC bits | 14 | 14~15 | 16 | 10 |
| Bandwidth (MHz) | NA | 1~30 | 80±7.5*1 | 8,000 |
| HW implementation | ADC, FPGA | ADC, FPGA | Data capture | Data capture |
| Sampling clock implementation | External source | ? | OCXO | Internal clock |
| fs (MHz) | 65 | 75~105 | 100 | ~20 GHz*2 |
| Sampling clock PN compensation | No | Yes | No | Yes |
| PN floor (dBc/Hz) | −125 | −173 | −155 | −160*3 |











