Ⅰ. 서 론
CIWS(close-in weapon system) 레이다가 해면 저고도(sea-skimming)로 비행하는 대함 미사일을 격추가 가능한 수준으로 탐지 및 추적하기 위해서는 아주 낮은 오차를(ex. 1 mrad 미만의 오차) 가지고 표적의 위치각(고각/방위각)을 측정하여야 한다. 낮은 오차로 표적의 위치각을 측정하기 위해서는 우선 안테나 빔 폭이 작아야 한다. 그러나 보통 안테나 크기의 제한 등으로 안테나 빔 폭을 아주 작게 만들기 힘들다. 그리고 해면의 큰 반사계수의 영향으로 다중경로(multipath) 신호가 모노펄스 처리에 의한 모노펄스 값의 추출을 방해하여 표적의 고각 추출을 어렵게 한다. 해면 저고도 표적을 탐지/추적하기 위하여 해면의 다중경로 환경에서 표적의 고각을 측정하는 것은 오래된 주제이며, 다양한 방법들이[1]~[3] 연구되었다. 본 논문은 그 다양한 방법들 중에서 Eckersten이 연구한 “복소수 각(complex angle)”의 구현[1]을(표적 고각에 따라 해면 다중경로 신호에 의한 모노펄스 고각 오차 신호의 복소수 값에 나타나는 특징적 변화를 이용한 표적 고각 측정법) 기반으로 CIWS 레이다의 해면 저고도 표적의 고각 측정 방법을 연구하였다. Eckersten의 방법의 성능은 해면 상태의 반사계수 값 및 해면에 대한 지표각(grazing angel)에 의존적이라는 특성 등의 여러 한계점들을 파악하고, 이런 한계점들을 개선 및 극복하여 CIWS의 레이다에 Eckersten의 방법의 구체적인 적용 및 확장을 설계하였다. 본 논문은 CIWS의 레이다가 안테나의 제한된 빔 폭 조건에서 해면 저고도 표적의 고각을 정확하고 효과적으로 측정하는 방법을 제시한다. 제시한 방법을 적용하여 다양한 안테나 빔 폭 및 송신주파수 조건에서 시뮬레이션을 통해 그 결과를 기술하고, 그 성능을 평가한다.
Ⅱ. 해면 다중경로 환경에서 해면 저고도 표적 탐지
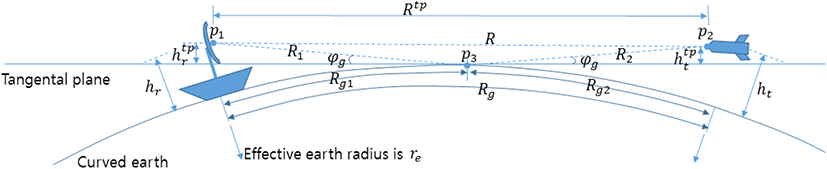
그림 1은 해면 다중경로 환경에서 레이다 신호의 전파에 관한 기하학적 표현 및 기호 정의를 나타낸다. 바람이 없는 좋은 해상 상태일 때 해면은 거울처럼 높은 반사 계수를 가지며, 해면에서 저고도로 접근하는 표적의 레이다 반사 신호의 지표각은 매우 적기 때문에 다중경로의 반사 신호들이 레이다 장치의 한 거리 셀에 모두 들어오게 된다. 한 거리 셀에 들어온 다중경로 신호들은 서로 상쇄 및 보강 간섭들을 일으키게 되며, 해당 거리 셀의 신호로 전통적인 모노펄스 처리를 하면 제대로 된 표적의 고각을 측정할 수 없다. 그래서 다중경로의 간섭 신호들을 제거하는 방법들이 연구되거나, 다중경로 신호들의 간섭 효과를 이용한 고각 측정 방법들이 연구되기도 한다[1]~[3]. 본 논문은 해면 다중경로 신호들의 간섭 효과를 이용한 고각 측정 방법을 기술한다. 해면의 반사는 정반사(specular reflection)와 확산반사(diffuse reflection)로 구분할 수 있으며, 잔잔하고 평평한 해면에서는 순수하게 정반사만 존재한다고 볼 수 있다. 해상 상태가 거칠어지면 확산반사가 존재하지만 표적 탐지에 확산반사의 영향은 미미하며, 정반사가 크게 영향을 미친다. 먼저 그림 1에서 보듯이 해면에서 지표각 φ_g를 가지는 레이다 반사(정반사) 신호를 고려하면 레이다에 들어오는 다중경로 수신 신호들의 경로는 p1→p2→p1, p1→p2→p3→p1, p1→p3→p2→p1 그리고, p1→p3→p2→p3→p1이다. 해면에서 정반사에 의한 효과는 수직편파 신호에 나타나며, 수직편파 신호의 지표각이 φg일 때 해면의 반사계수는 다음과 같다.
여기서 ϵ는 로서 해면의 복소 유전율 상수이다[4]. 곡면 지구 발산 계수, D와 해면 상태의 표면 거침 정도, S_r을 같이 고려하면 해면 반사계수는 다음과 같다.
여기서, D=(1+(2Rg1Rg2)/(reRg(sin(φg)))−1/2, Sr=e−2z, z= (2πhrmssin(φg)/λ)2 그리고 re는 유효지구반경, λ는 신호의 파장이다. 또 hrms는 해면 높이의 표준편차이며, 해상상태, σ에 따라 hrms=0.031σ2과 같이 표현된다[5]. 여기서 σ는 해면의 파고에 따라 0에서 9까지의 정수 값을 가진다. 모노펄스 채널을 이용한 각도 측정에서는 고각오차신호, Del/∑의 실수 부분 Re[Del/∑]을 이용하는데 다중경로 신호 환경에서는 다중경로 신호의 간섭으로 Re[Del/∑]을 이용하는 각도 측정이 어렵다(모노펄스 처리를 위한 안테나 수신채널[1]에서 ∑는 합 채널 신호, Del는 고각 방향 차 채널 신호임). 해면 저고도 표적의 다중경로 신호 환경에서 고각오차신호의 허수부, Im[Del/∑]는 다음 식의 n에 대한 유용한 곡선 패턴을 형성한다[1].
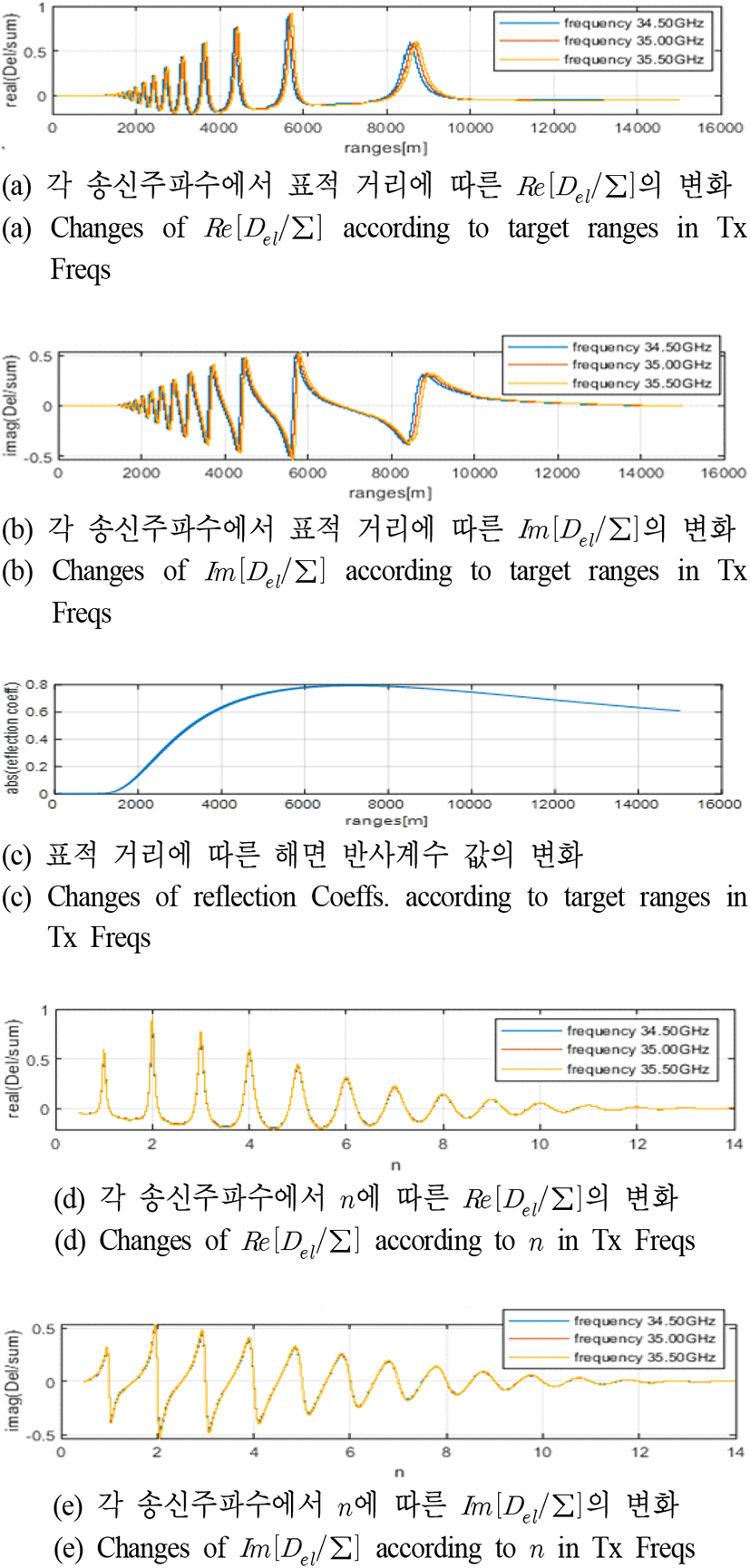
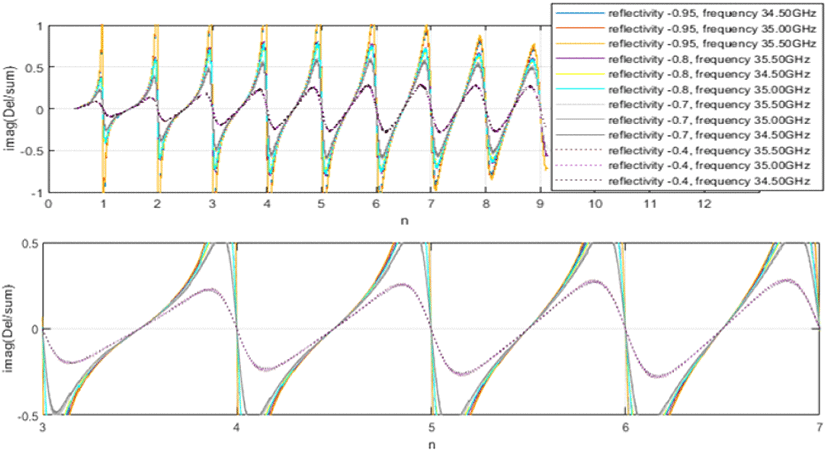
해면 저고도 표적에서 R≈Rtp 이므로 로 사용할 수 있다. 그림 2는 해면 저고도 표적에 대한 시뮬레이션으로 다중경로 레이다 반사 신호의 Re[Del/∑]과 Im[Del/∑] 및 해면 반사계수 변화를 나타내었다. 그림 2의 시뮬레이션에 대한 시나리오는 레이다 해면고도는 10 m이며, 표적이 최초 거리 15 km에서 표적 속도 640 m/s 및 해면고도 10 m로 표적 거리 85 m까지 다가오는 경우이다. 레이다 빔은 시나리오 진행 중에 항상 표적을 지향한다. 전송주파수 34.5, 35.0 및 35.5 GHz에서의 결과들을 그림 2의 각 그래프에 같이 나타내었다. 그림 2(a)에서 보듯이 Re[Del/∑]의 값으로 모노펄스 처리를 하면 측정 오차가 커짐을 알 수 있다. 그러나 그림 2(b)에서 보듯이 Re[Del/∑]의 값은 특정 거리 구간에서 유용한 패턴이 형성되는 것을 알 수 있다. 그림 2(a)와 그림 2(b)에서 보듯이 거리에 따른 Re[Del/∑]와 Im[Del/∑]의 값은 전송주파수에 따라 다른 것을 알 수 있다. 그림 2(c)는 현 시나리오의 시뮬레이션에서 반사계수 값을 나타내었다. 표적 거리가 가까워져(약 1.5 km 이내) 해면 반사계수의 절대 값이 작아지면 다중경로 신호의 간섭이 작아져서 Re[Del/∑] 의 값을 이용한 모노펄스 처리의 측정 오차가 사용가능할 만큼 작아진다. 참고로 1.5 km 이내에서는 반사계수의 절대 값이 거의 0이라서 그림 2(b)의 Im[Del/∑]가 거의 0의 값을 가지는 것을 볼 수 있으며, 그림 2(a)의 Re[Del/∑]가 1.5 km 이내에서 거의 0의 값을 가지는 것은 레이다 빔의 중심이 표적을 지향하기 때문이다. 그림 2(d)와 그림 2(e)에서 보듯이 n에 따른 Re[Del/∑]와 Im[Del/∑]의 값은 전송주파수에 따라 차이가 거의 없는 것을 볼 수 있다. n에 관해 표현하면 일종의 정규화(normalization) 효과를 나타내는 것으로 보이며, 이 효과는 주파수 차이가 주파수 밴드들의 주파수 차이만큼이나 나면 사라진다. 한 주파수 밴드 내에서 1 GHz 범위 정도의 주파수 차이는 이런 정규화 효과를 나타낸다. 그리고 그림 2(e)에서 볼 수 있듯이 n에 따라 Im[Del/∑]의 값의 유용한 패턴이 만들어진다. 참고문헌 [1]의 내용처럼 n에 따른 Im[Del/∑]의 값의 패턴을 이용해 표적의 고도 및 고각을 측정할 수 있다(식 (3)의 n에서 표적 고도를 구할 수 있다). 참고로 저고도 표적에서 표적거리가 가까워지면 n의 값은 커지게 되고, 표적거리가 가까워지면 해면 반사계수의 절대 값이 작아지게 된다. 그러므로 그림 2(d)와 그림 2(e)에서 n이 10 이상일 때에 표적거리가 가까워지고, 해면 반사계수의 영향이 점점 사라지게 되어 Re[Del/∑]와 Im[Del/∑]의 값이 0에 수렴하게 되었다. 그림 3은 고정된 해면 반사계수(식 (2)) 값을 가정했을 때 n과 Im[Del/∑]에 대한 그래프이다. 시나리오는 그림 2와 동일하며 해면 반사계수 값만 고정하였다. 그림 3의 첫 행 그래프의 일부 영역을 확대해서 그린 그래프가 그림 3의 두 번째 행 그래프이다. 그림 3의 그래프에서 볼 수 있듯이 n의 값이 정수가 되는 영역 근처를 제외하면 반사계수 −0.95, −0.8 및 −0.7을 가지는 곡선 그래프들은 거의 유사해서 반사계수에 상관없이 하나의 곡선 그래프로 나타낼 수 있음을 확인할 수 있다(전송주파수 차이는 곡선차이를 유발하지 않음). 그러나 반사계수 −0.4인 곡선 그래프는 다른 곡선들과 차이가 있음을 확인할 수 있다. 그림 2(c)와 그림 2(b)에서 확인할 수 있듯이 해면 반사계수의 절대 값이 커서 다중경로 신호의 영향이 크게 나타나는 상황들(해면 반사계수의 절대 값이 0.7 이상)에서는 n과 Im[Del/∑]에 대한 대표 곡선을 이용해 표적의 고도 및 고각을 구할 수 있다.
Ⅲ. 해면 저고도 추적 표적의 고각 측정법 설계
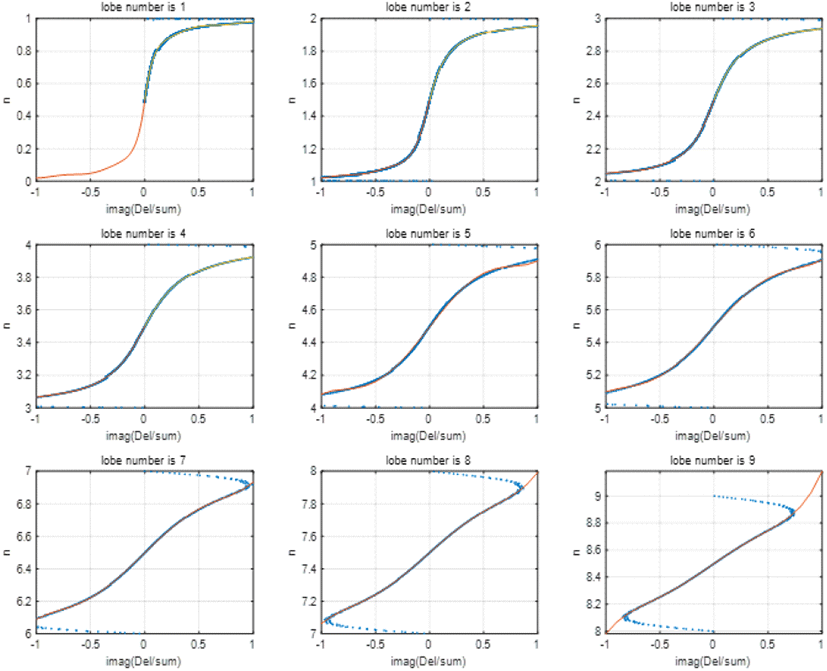
그림 3의 설명에서 언급한 것처럼 해면 저고도 표적의 고각 측정을 위해 n과 Im[Del/∑]에 대한 곡선을 이용한다. 다음 그림 4는 그림 3에서 해면 반사계수 −0.95일 때의 n과 Im[Del/∑]에 대한 곡선 패턴을 기준으로 n의 각 구간별로 Im[Del/∑]과 n에 피팅 곡선(fitting curve)을 구한 것이다. 그림 4의 피팅 곡선은 첫 행, 최 좌측부터 차례로 n이 1 이하일 때(nlobe=1일 때), n이 1에서 2까지 일 때(nlobe=2일 때), 그리고 n이 2에서 3까지일 때(nlobe=3일 때) 등이다. n의 구간 및 Im[Del/∑]의 값을 알면, 그림 4의 피팅 곡선으로 n의 값을 구하여 표적의 고도 및 고각을 구할 수 있다. 그림 5는 그림 4의 피팅 곡선을 이용한 해면 저고도 표적의 고각 측정법 설계를 나타낸다. 그림 5에서 측정된 표적거리 Rmeasure와 레이다 해면 고도 및 초기 고각 측정치 θinitMP를 이용하여 표적의 해면 고도를 식 (4)로[6] 계산한다(최초 계산은 θt=θinitMP로 시작). θinitMP는 모노펄스 처리를 이용하여 구한 표적의 고각 측정치로서 해면 다중경로 신호 때문에 측정 오차가 크다.
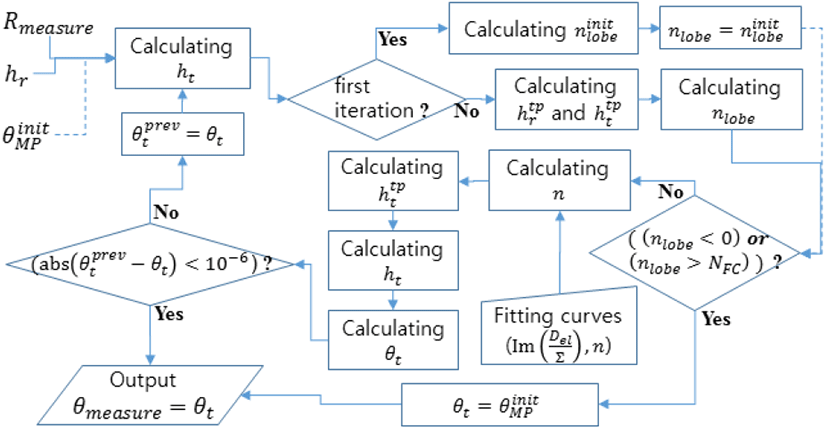
설계한 고각 측정법은 반복 계산을 통해 수렴하는 표적의 고각 및 해면 고도를 구한다. 반복 계산의 최초 고각은 θinitMP을 사용하고, 피팅 곡선 선택을 위한 최초 nlobe의 값은 nlobeinit을 사용한다. nlobeinit 는 식 (5)와 같이 구한다.
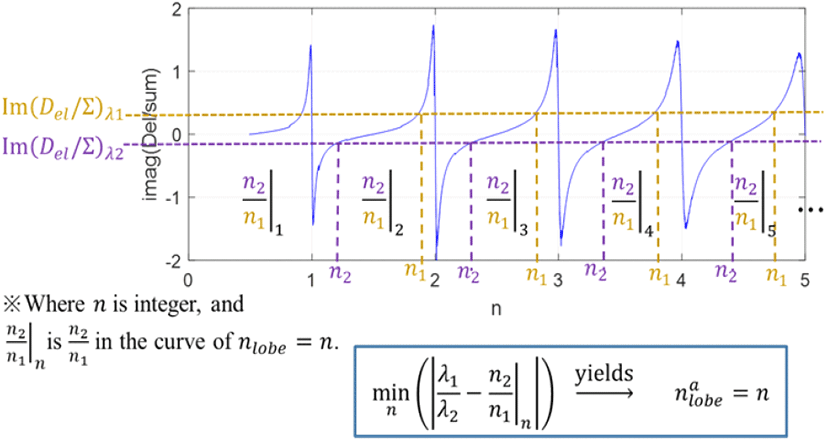
여기서 SNR은 표적 신호의 dB 스케일 신호 대 잡음비를 나타내며, max(A ,B)는 A와 B중에서 큰 값을, nlobea는 그림 6과 같이 두 개의 송신주파수에서 얻은 표적 신호의 Im[Del/∑] 값들을 이용하여 구한 nlobe의 값을 나타낸다. 송신파장 λ1에서의 Im[Del/∑]의 값을 Im[Del/∑]λ1, 송신파장 λ_2에서의 그 값을 Im[Del/∑]_λ2이라 할 때, 각 nlobe의 곡선에서 Im[Del/∑]_λ1과 Im[Del/∑]_λ2에 대응되는 n1과 n_2들을 구하고, (λ1/λ2-n2/n1)의 절대 값이 최소가 되게 하는 nlobe의 정수 값 n을 nlobea로 한다. 그림 6의 방식으로 구한 nlobe의 값인 nlobea는 표적 신호의 신호 대 잡음비가 40 dB 이상일 때만 유효한 값을 나타내며(경험적 수치임), 신호 대 잡음비가 낮으면 그림 6의 방식은 제대로 동작하지 않는다. 그림 5의 반복 계산에서 최초 nlobe의 계산이 아니면, 식 (3)을 이용하여 식 (6)과 같이 nlobe을 계산한다.
여기서 floor(A)는 A보다 작거나 같은 정수를 나타내며, htpr과 htpt는 식 (7)과 같이 계산한다[4,7].
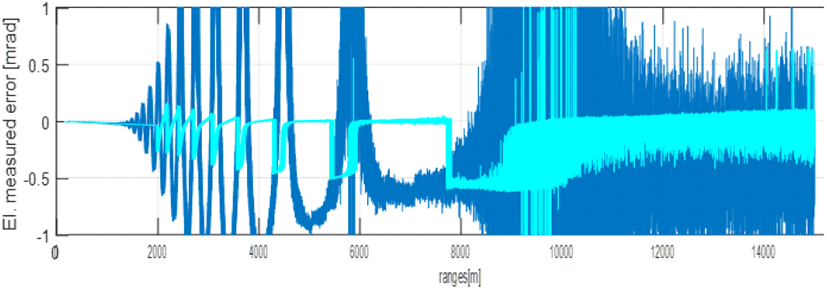
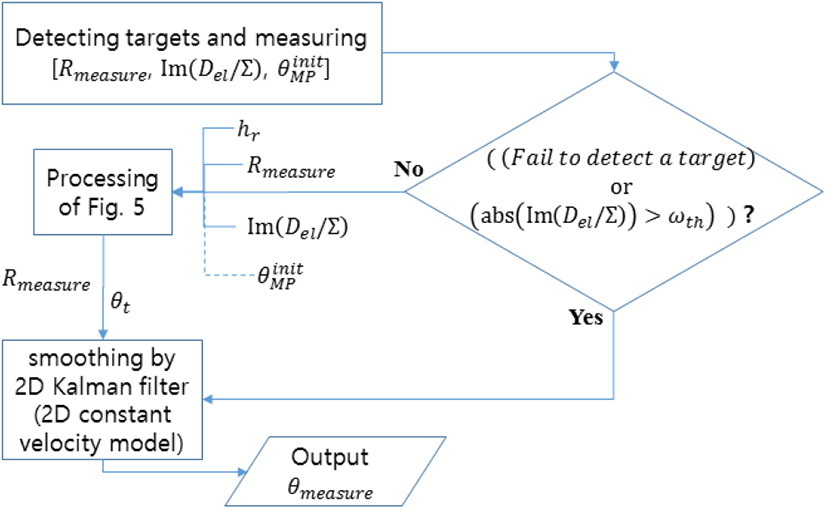
만약 계산한 nlobe 값이 0보다 작거나 피팅 곡선의 개수 NFC보다 크면 최종 측정치로서 표적 고각 θinitMPɛ를 출력하여 마치며, 만약 그렇지 않으면 계산한 nlobe 값으로 그림 4에서 피팅 곡선을 선택하고, 선택한 피팅 곡선에서 Im[Del/∑] 값을 이용하여 n 값을 구한다. 계산한 n 값과 식 (3)으로 http를 다시 계산하고, 식 (7)로 h_t를 다시 계산한다. 그리고 식 (4)로 θt를 다시 계산한다. 그 다음으로 현재 반복 계산에서 구한 표적 고각 θt와 그 전 반복 계산에서 구한 표적 고각 θtprev과의 차이의 절대 값이(10^(-6) 보다) 작아서 수렴하였으면 최종 측정치로서 표적 고각 θt를 출력한다. 수렴하지 않았으면 다시 식 (4)부터 시작하여 표적 고각 계산 수행을 반복한다(보통 3번 이하의 반복 수행으로 수렴한다). 그림 7은 그림 5에서 설계한 방법으로 고각 측정 시뮬레이션을 행한 결과이다. 시나리오는 그림 2와 동일하게 하였다. 다만 안테나 빔이 표적을 거의 정확하게 조향하는 것을 가정하였으며(매번 빔 조향 오차가 약 0.017° 정도 되도록 함), 반복 계산의 최초 고각은 θinitMPɛ이 아니라, 빔 조향 고각으로 설정하였다. 이것은 빔 조향 및 반복 계산의 최초 고각을 최적으로 설정하여 레이다를 운영한 것을 가정한 것이다. 그림 7에서 어두운 색 실선 그래프는 모노펄스 처리를 통해 구한 고각 측정치와 실제 고각과의 오차를 나타내며, 밝은 색 실선 그래프는 그림 5의 제안한 방법으로 구한 고각 측정치와 실제 고각과의 오차를 나타낸다. 그림 7에서 보듯이 n의 값이 정수가 되는 영역 근처를 제외하면 측정값 오차는 0.2 mrad 이하인 것을 볼 수 있고, n의 값이 정수가 되는 영역을 포함하더라도 측정값 오차가 0.65 mrad 이하인 것을 볼 수 있다(가끔씩 측정오차가 아주 크게 튀는 것은 제외하였다). n의 값이 정수가 되는 영역 근처에서 오차가 큰 이유는 그림 3에서 보듯이 n의 값이 정수가 되는 영역 근처에서 반사계수에 따른 그래프 변화가 큰 영역이기 때문이며, 이것 때문에 −0.95의 반사계수를 이용한 그림 4의 피팅 곡선이 반사계수 차이에 따라 n의 값이 정수가 되는 영역 근처에서 실제 값과의 오차를 유발한다. 설계한 반복 계산을 통한 각도 측정 방법은 반복 계산의 최초 고각 설정 값이 실제 nlobe의 값을 잘 반영하여 찾아내면 좋은 측정 성능을 보임을 그림 7의 시뮬레이션 결과에서 확인할 수 있다. 그러나 측정값에서 튀는 현상이 있어서 측정값을 평활화(smoothing)하여 사용해야 한다. 그래서 본 논문에서는 측정값의 평활화를 위해 표적의 거리와 고각에 관한 2차원 등속 모델의 칼만 필터(Kalman filter)를 사용하였다. 그림 8은 그림 7의 방법과 칼만 필터에 의한 평활화를 포함하는 본 논문에서 설계한 해면 저고도 표적의 고각 측정법을 나타낸다. 그림 8에서 먼저 표적의 탐지와 (abs(Im[Del/∑])>ωth)의 여부를 확인한다. 표적을 탐지하고 (abs(Im[Del/∑])≤ωth)을 만족하면 그림 5의 처리와 칼만 필터에 의한 평활화 처리 과정을 거쳐서 표적의 고각 측정 값 θmeasure을 출력한다. 만약 표적이 탐지 되지않았으면 칼만 필터에 의한 표적 거리와 고각의 예측치 값을 사용하여 필터를 갱신하고, 표적 고각을 출력한다. 또한 (abs(Im[Del/∑])>ωth)일 때도 마찬가지로 필터 예측치 값으로 필터를 갱신하고, 표적 고각을 출력한다. 여기서 abs(A)는 A의 절대 값을 나타내며, >ωth는 그림 5의 방법이 사용 가능한지를 판단하기 위한 임계값이다. (abs(Im[Del/∑])>ωth)을 이용하면 n의 값이 정수가 되는 영역 근처에 속해 있는지를 판단할 수 있다. 즉, 그림 3과 그림 7에서 언급한 피팅 곡선을 사용할 수 없고, 그림 5의 방법을 사용했을 때 측정오차가 커지는 영역을 (abs(Im[Del/∑])>ωth)로 판단하여, 그림 5의 처리를 하지 않고(오차가 큰 측정치를 사용하지 않고) 필터 예측치 값으로만 필터를 갱신하여 표적 고각을 구하는 것이다(그림 3을 참고하여 본 논문은 >ωth=0.5로 설정함).
Ⅳ. 시뮬레이션과 결과
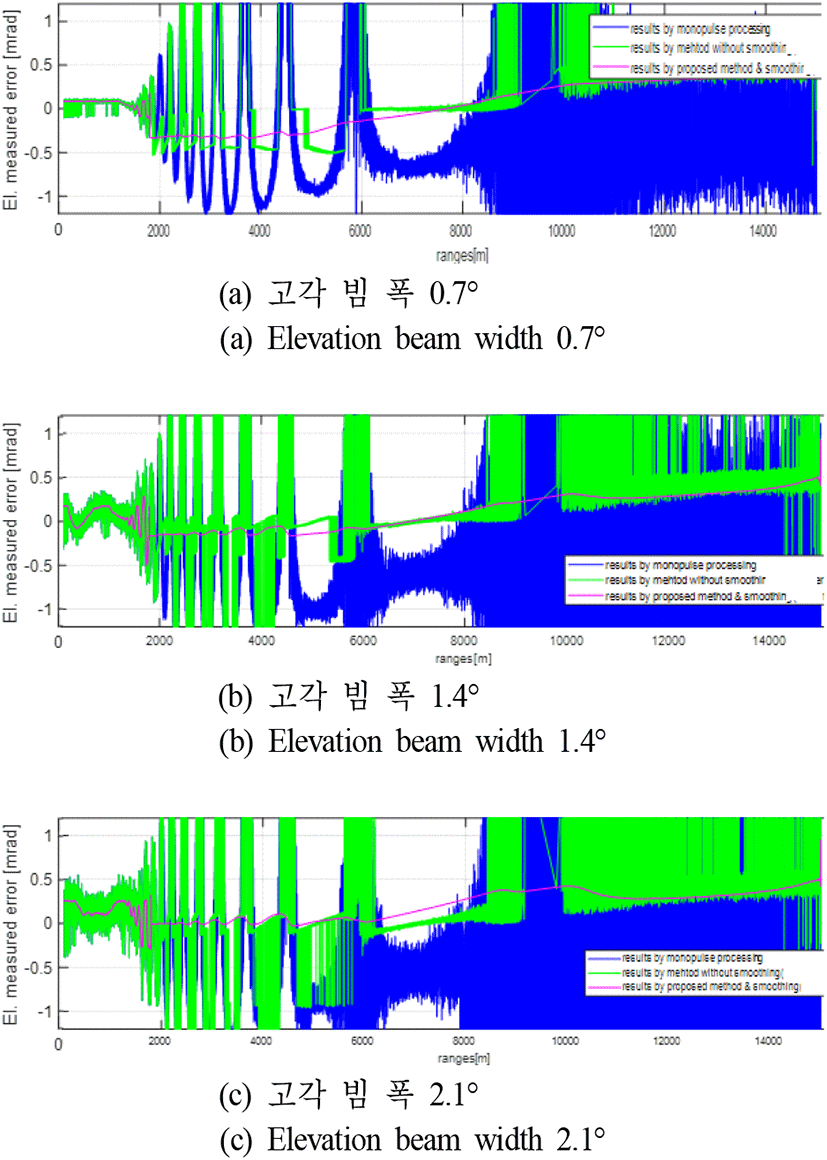
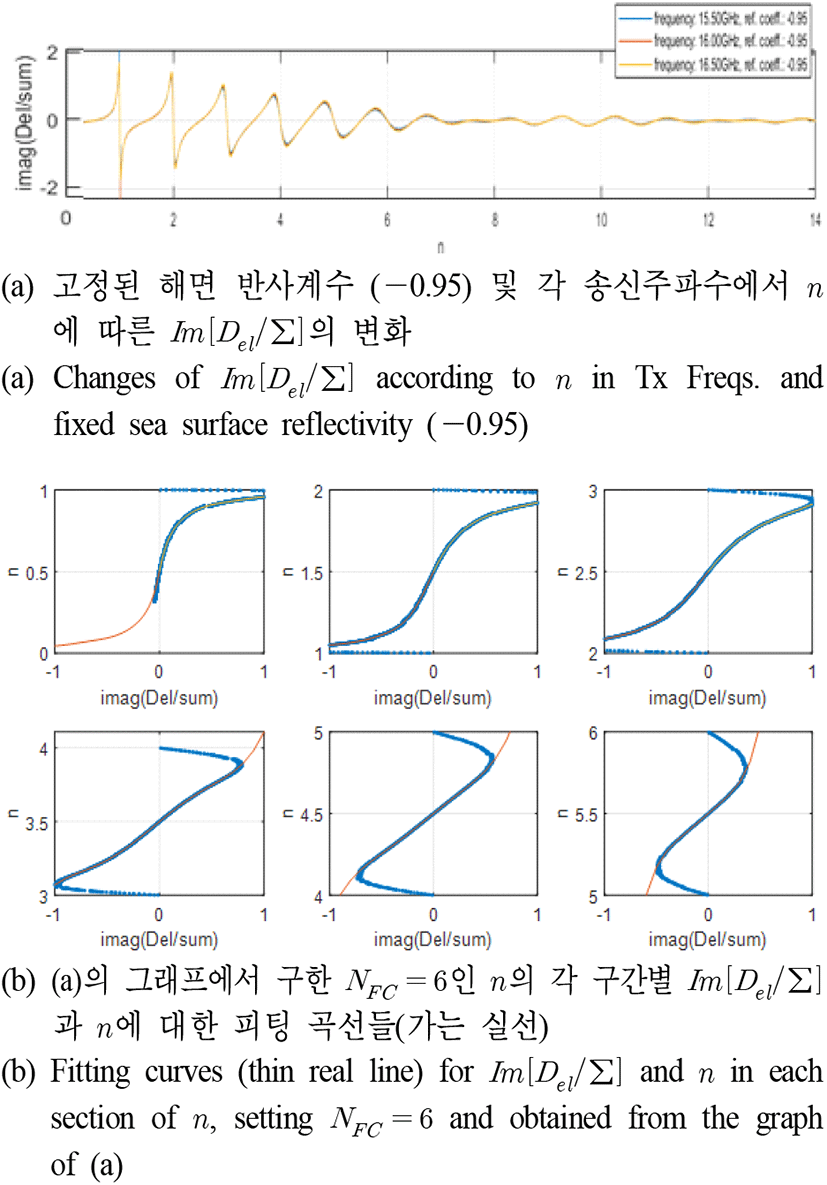
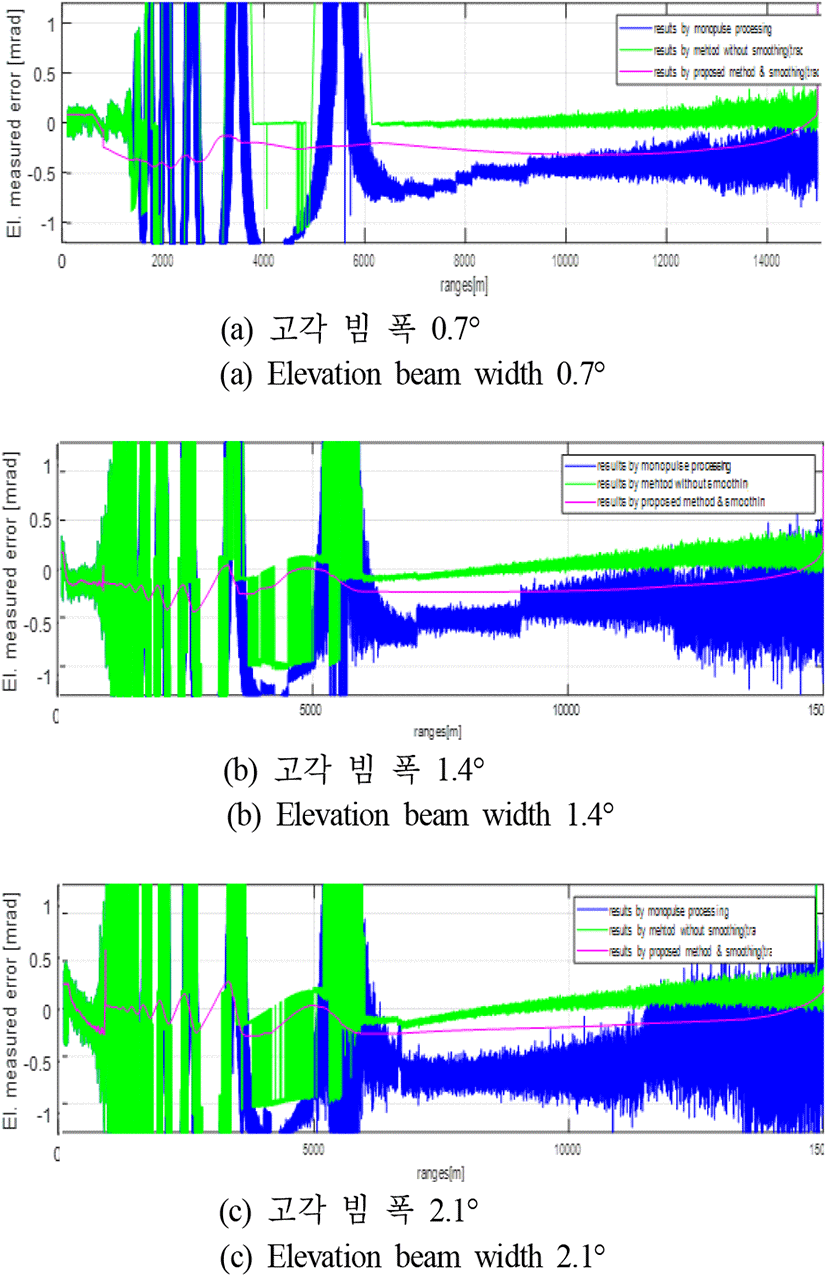
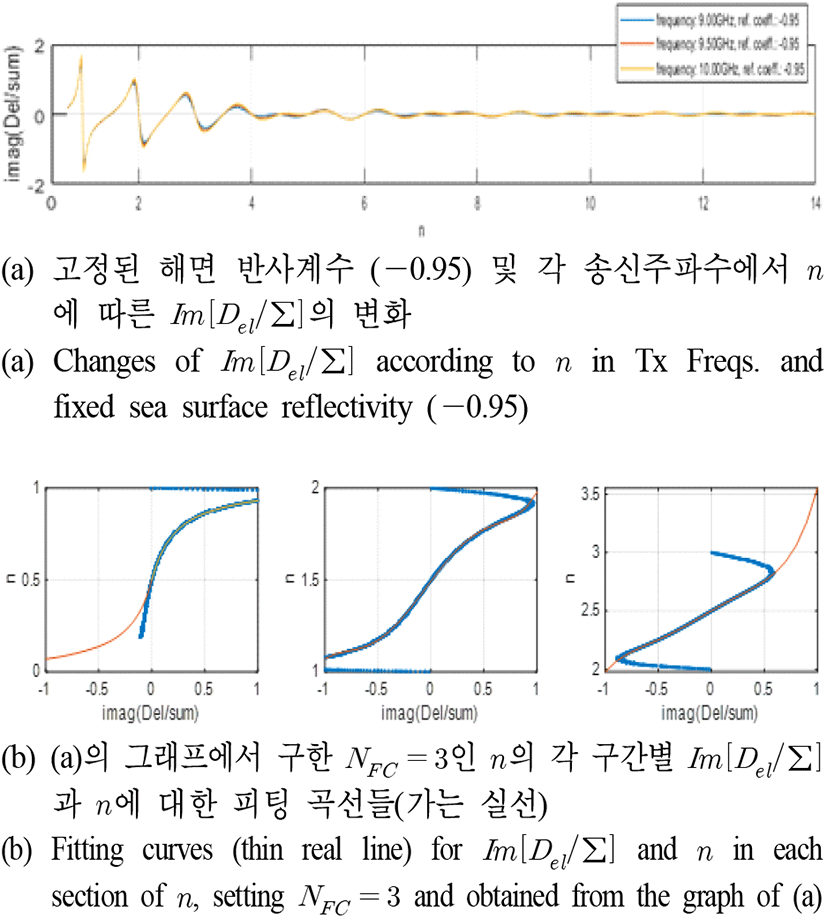
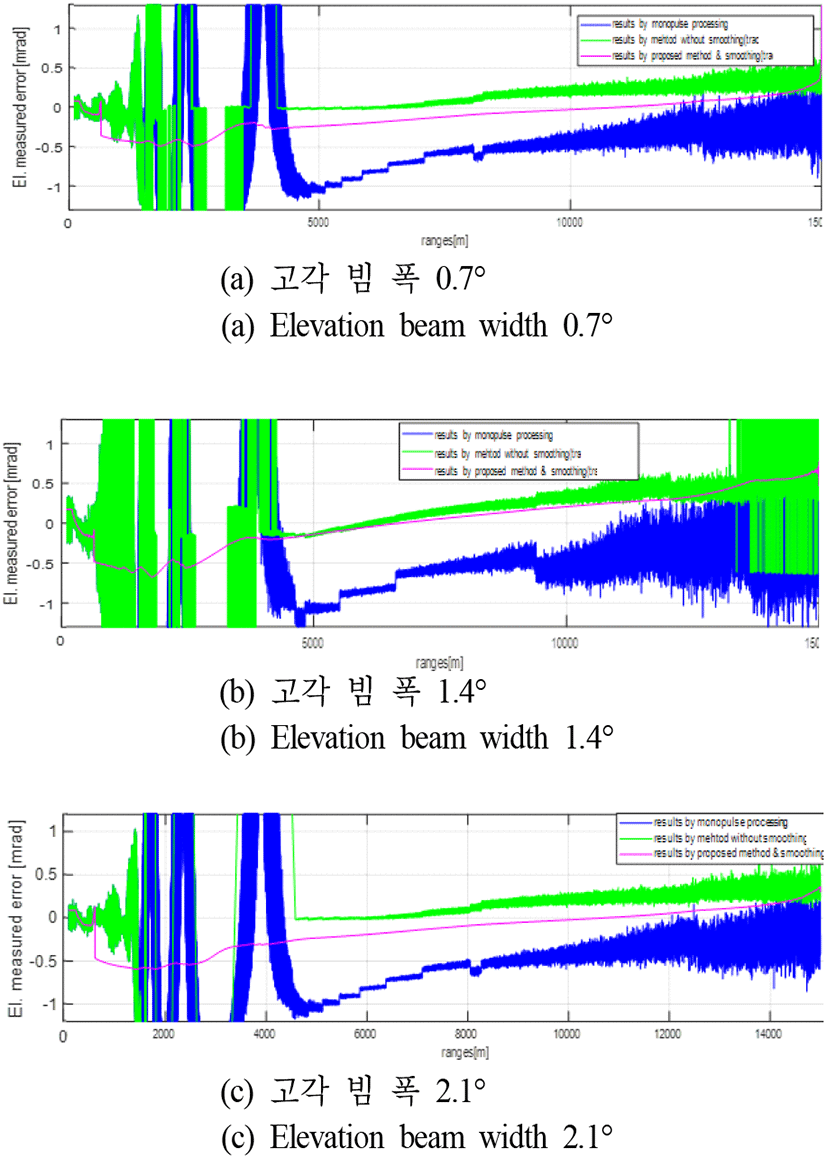
시뮬레이션을 통해 본 논문에서 설계한 그림 8의 해면 저고도 표적의 고각 측정법을 실험하고 성능을 확인한다. 표 1은 시뮬레이션 시나리오 및 레이다 파라미터이다. 레이다는 모노펄스 처리가 가능하며, ∑과 Del채널을 가지고 있다. 표 1에서 보듯이 표적은 최초 15 km 거리 및 해면 고도 10 m에서 상대속도 640 m/s로 접근한다. 그리고 표적이 레이다에 85 m까지 가까이 오는 동안에 표적의 해면 고도는 5 m와 10 m 사이를 오가며 바뀐다. 표적의 SNR은 표적이 접근하는 동안에 15 dB에서 45 dB까지 변하도록 하였다. 해상 상태는 2로 가정하였다. 실험은 표 1의 시나리오에서 표 1의 각 송신주파수 대역 및 안테나 고각 빔 폭별로 행하였다. 그리고 각 주파수대역에서 실험할 때 송신주파수 값 3개를 연달아 바꾸어 가면서 운영하여 그림 6의 계산이 가능하도록 하였다. 그림 9는 그림 4의 피팅 곡선(Ka 대역)을 사용하여 Ka 대역에서 각 안테나 빔 폭 별로 본 논문의 방법을 실험한 결과를 나타내었다. 그림 9(a)의 그래프에서 가장 큰 고각 측정 오차를 보이는 것은 모노펄스 처리에 의한 결과이고 그 다음으로 큰 측정 오차를 보이는 것은 제안한 방법에서 칼만 필터를 이용한 평활화를 적용하지 않은 결과이다. 그리고 가장 작은 측정 오차를 보이는 부드럽게 연결된 실선 그래프는 제안한 방법에 의한 결과이다. 그림 9(b)와 그림 9(c)도 그림 9(a)와 같은 방식으로 나타내었다. 그림 9의 결과에서 보듯이 제안한 방법은 고각 측정 오차 측면에서 안테나 빔 폭에 따른 성능 차이는 별로 없는 것을 확인할 수 있다. 다만 해면에서의 다중경로 효과가 거의 없어지는 약 1.8 km 이후에는 전적으로 모노펄스 처리에 의지하게 되므로 안테나 빔 폭과 성능과의 관계를 보이고 있다. 그리고 그림 9와 동일한 시나리오로 운영하여 얻은 그림 2(c)의 반사계수 값의 변화와 비교하여 확인할 수 있듯이 반사계수의 절대 값이 0.7보다 작아지는 영역(1.5 km에서 4 km의 영역)에서 다소 고각 측정 오차가 커지는 경향을 확인할 수 있다. 이것은 그림 4의 피팅 곡선이 그림 3에서 확인할 수 있듯이 반사계수의 절대 값이 0.7 이상인 경우에 잘 부합하기 때문이다. 그러므로 기상 상태가 좋지 않아서 해상 상태의 수가 높아지면 반사계수의 절대 값이 작아지는 상황이 발생할 것이고, 그러면 제안한 방법의 성능이 떨어지는 경향을 보일 수 있을 것이다. 제안한 방법은 Ka 대역의 실험에서 표적의 고각 측정 오차가 최대 0.5 mrad 이하로 들어오는 성능을 보임을 확인할 수 있다. 그림 10(a)는 Ku 대역에서 그림 3과 같은 방식으로 해면 반사계수(식 (2)) 값을 −0.95로 고정하여 n과 Im[Del/∑]에 관한 그래프를 그려 본 것이다. 그림 10(a)의 결과로부터 Ku 대역에서는 피팅 곡선의 개수 NFC를 6으로 설정하였다. 그림 10(b)는 그림 10(a)의 n과 Im[Del/∑]에 대한 곡선 패턴을 기준으로 NFC=6개인 n의 각 구간별로 피팅 곡선을 구하여 그림 4와 같은 방식으로 나타내었다. 그림 10(b)의 피팅 곡선을 이용하여 Ku 대역에서 각 안테나 빔 폭 별로 본 논문의 방법을 실험한 결과를 그림 11에 그림 9와 같은 방식으로 나타내었다. 그림 11에서 보듯이 고각 측정 오차 측면에서 안테나 빔 폭에 따른 성능 차이는 별로 없고 반사계수의 절대 값이 0.7보다 작아지는 영역(표적 시나리오는 그림 2 때와 동일하므로 거리에 따른 반사계수 변화는 그림 2(c)와 유사하며, 거리 약 2.6 km 이하에서 반사계수 절대 값이 0.7보다 작아짐)에서 다소 고각 측정 오차가 커지는 등의 Ka 대역의 결과와 유사한 결과를 보인다. 제안한 방법은 Ku 대역의 실험에서 표적의 고각 측정 오차가 최대 0.7 mrad 이하로 들어오는 성능을 보임을 확인할 수 있으며, 해면 반사계수의 절대 값이 0.7 이상인 구간에서는 최대 측정 오차가 0.5 mrad 이하인 것을 확인할 수 있다. 그림 12(a)는 X 대역에서 그림 3과 같은 방식으로 해면 반사계수(식 (2)) 값을 −0.95로 고정하여 n과 Im[Del/∑]에 관한 그래프를 그려 본 것이다. 그림 12(a)의 결과로부터 X 대역에서는 피팅 곡선의 개수 NFC를 3으로 설정하였다. 그림 12(b)는 그림 12(a)의 n과 Im[Del/∑]에 대한 곡선 패턴을 기준으로 NFC=3개인 n의 각 구간별로 피팅 곡선을 구하여 그림 4와 같은 방식으로 나타내었다. 그림 12(b)의 피팅 곡선을 이용하여 X 대역에서 각 안테나 빔 폭별로 본 논문의 방법을 실험한 결과를 그림 13에 그림 9와 같은 방식으로 나타내었다. 그림 11에서 보듯이 고각 측정 오차 측면에서 안테나 빔 폭에 따른 성능 차이는 별로 없고, 반사계수의 절대 값이 0.7보다 작아지는 영역(표적 시나리오는 그림 2 때와 동일하므로 거리에 따른 반사계수 변화는 그림 2(c)와 유사하며, 거리 약 1.8 km 이하에서 반사계수 절대 값이 0.7보다 작아짐)에서 다소 고각 측정 오차가 커지는 등의 Ka 및 X 대역의 결과와 유사한 결과를 보인다. 제안한 방법은 X 대역의 실험에서 표적의 고각 측정 오차가 최대 0.7 mrad 이하로 들어오는 성능을 보이며, 해면 반사계수의 절대 값이 0.7 이상인 구간에서는 최대 측정 오차가 0.5 mrad 이하인 것을 확인할 수 있다.
Ⅴ. 결 론
CIWS의 레이다가 안테나의 제한된 빔 폭 조건 및 해면 다중경로 환경에서 적은 오차로 해면 저고도 표적의 고각을 측정하는 방법을 제시하였다. 제시한 방법의 성능이 해면 다중경로 환경 및 다양한 안테나 빔 폭(0.7°, 1.4°, 2.1°)과 다양한 송신주파수 대역(Ka, Ku, X)에서 시뮬레이션을 이용한 실험을 통해 표적의 최대 고각 측정 오차가 0.7 mrad 이하가 됨을 확인하였다. 제안한 방법은 안테나 모노펄스 수신 채널이 있으면 사용 가능하기에 ABF (adaptive beam forming) 등을 이용해 다중경로의 간섭신호를 제거하여 표적 고각을 측정하는 방법에 비해 비교적 적은 비용으로 간단한 구현이 가능하다는 장점이 있다. 그리고 주파수 변화에 따른 해면 반사 신호의 변화를 이용하는 방법에 비해 비교적 낮은 SNR에서도 잘 동작한다. 그러나 해면의 정반사 현상을 이용하기에 해상의 기상상태가 좋지 않아(해상상태의 수가 높아져서) 정반사 효과를 이용하기 어려워지고 확산반사의 영향이 더 커지면 성능이 저하될 수 있는 단점이 있다.













