Ⅰ. 서 론
최근 고속 전자회로 설계 시스템에서는 레퍼런스 층(reference layer) 사이에 상하 또는 좌우로 인접한 두 전송선로가 평행한 구조를 갖는 듀얼 스트립라인(dual-stripline) 이 많이 사용되고 있다. 이것은 첫째로는 보다 작은 형태의 제품을 원하는 고객의 요구가 갈수록 증가하고 있기 때문에 이것을 충족시키기 위함이고, 둘째로는 스택업(stack-up) 층 수와 두께를 줄여서 사용되는 재료를 줄이고, 공정을 단순화하여 원가를 절감하고자 하기 위함이다.
전송선로 스트립 라인(stripline) 구조는 마이크로 스트립 라인(micro-stripline) 구조와는 달리 균질한 유전체 환경을 가지므로 마이크로 스트립 라인에 비하여 상대적으로 우수한 신호 전달 특성을 보이지만, 설계 층 수 및 두께의 증가로 인하여 원가 상승이 필연적이기 때문에 이것을 줄일 필요가 있다. 또, 제품 설계 관점에서 동일 스택업 상에서 레퍼런스 층을 신호(signal) 층으로 변경함으로써 회로 간격을 증가시키고, 경로 확보를 통한 추가 공간 확보를 통한 설계 유연성을 가질 수 있는 장점 때문에 최근에 상하 레퍼런스 층을 공유하는 듀얼 스트립라인 구조를 산업현장에서 많이 채택하여 사용하고 있다.
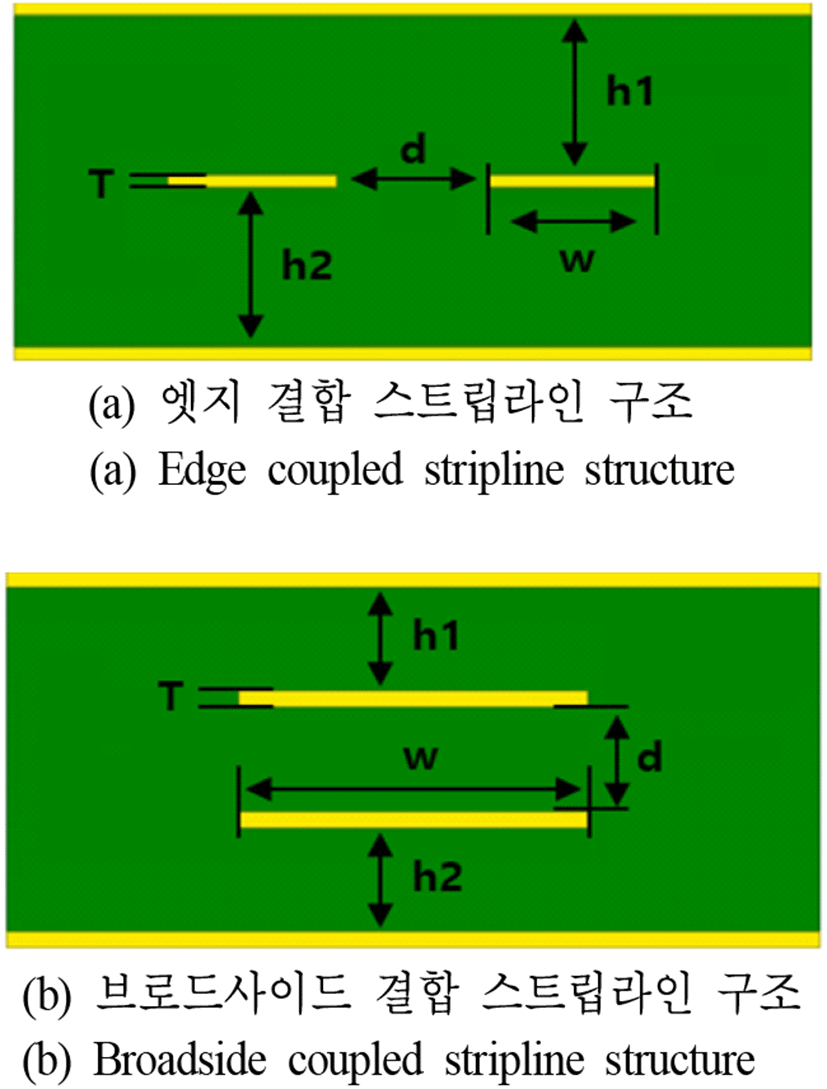
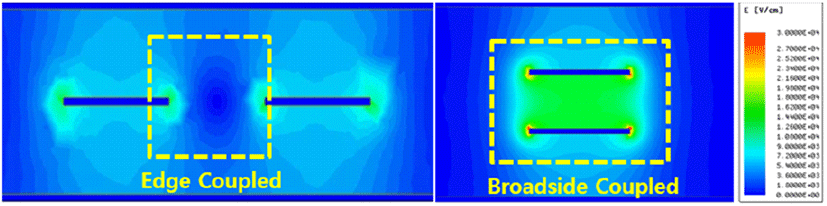
스트립라인은 그림 1(a)와 같이 두 선로가 수평 방향으로 평행한 엣지 결합 스트립라인(edge coupled stripline)과 그림 1(b)와 같이 두 선로가 수직 방향으로 평행한 브로드사이드 결합 스트립라인(broadside coupled stripline)의 두 가지로 나눌 수 있으며, 적용하는 회로 구조에 따라서 각각 적절히 사용될 수 있다. 신호의 누화 관점에서 두 회로의 차이점을 살펴보기 위해서 그림 2에서 선로 단면에서의 E-field 분포를 나타냈으며, 넓은 면을 공유하는 브로드사이트 결합 스트립라인의 구조적 특징으로 인해서 이 경우, 두 선로 간 커패시턴스(capacitance) 간섭이 상대적으로 많이 발생한다는 것을 알 수 있다. 이러한 누화를 완화시키기 위해서 선로 간 거리(d) 및 레퍼런스 층과의 거리(h1,h2)를 조절하는 등 물리적인 방법을 활용한 설계 변경 기법이 현장에서 다양하게 시도되어 왔으나, 주로 파라미터 조절 후 효과분석이라는 일종의 시행착오(trial and error) 방식을 사용하였기 때문에 그 효과가 제한적이었다[1],[2]. 이 경우, 보다 체계적으로 신호 무결성을 향상시키기 위해서는 주어진 형상에서 신호 누화 정도를 예측할 수 있는 방법이 필요하다.
위와 같은 맥락에서 본 연구는 브로드사이드 결합 스트립라인을 대상으로 하고, 이 두 선로가 weak-coupling 되었다는 가정 하에서, 기존에 발표된 선로 누화를 예측할 수 있는 수식들을 정리하고, 이것을 밑바탕으로 하여 브로드사이드 결합 스트립라인의 신호 누화를 저하할 수 있는 체계적인 방법을 제시하고자 한다. Weak-coupling 가정 하에서의 누화 예측 수식 이론은 상당히 복잡하며[2]~[7], 따라서 본 논문에서는 결과 수식을 위주로 기술하고자 한다.
II장에서는 부하단에서의 반사가 없을 때를 상정한 경우와 부하단에서의 반사를 고려한 두 가지 경우에 있어서의 누화 전압 수식을 기술하고, III장에서는 II장에서 기술된 수식을 기반으로 하여 결합 파라미터의 변화, 특히 두 선로 사이의 상호 커패시턴스(mutual capacitance) 변화에 따른 누화 증감에 대한 분석을 수행한다. IV장에서는 신호 누화를 최소화하는 적절한 상호 커패시턴스를, 비균질 매질을 이용하여 구현하는 방법을 제시하고, EM 시뮬레이션을 통해 제시한 방법이 신호 무결성 향상에 유효함을 검증하였으며, V장에서는 본 논문의 결론을 기술한다.
Ⅱ. 선로 이론 기반의 누화 전압 예측
그림 3(a)는 두 개의 선로로 구성된 전송선로의 개념도를 보인다. 이 중 윗 쪽 선로는 신호가 인가되는 aggressor- line을, 아래 쪽 선로는 윗 쪽 선로의 영향을 받는 victim- line을 나타낸다. Victim-line은 전원이 연결되지 않은 상태로 aggressor-line과의 전자기적 결합(coupled)에 기인한 노이즈(noise)가 근단 및 원단에 전달되고[1],[3], 이 때 근단에 전달되는 노이즈를 근단 누화(near end X-talk, NEXT)라고 하며, 원단에 전달되는 노이즈를 원단 누화(far end X-talk, FEXT)라고 한다[1].
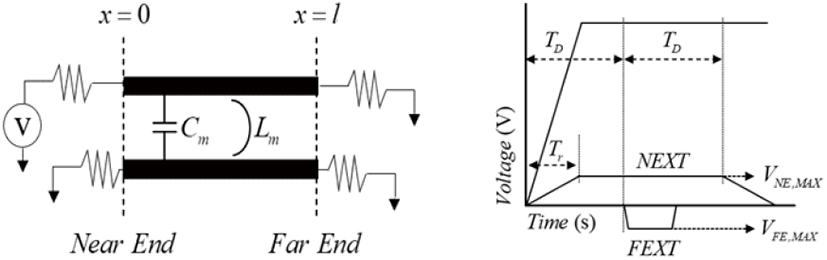
식 (1)[4],[5]과 식 (2)[1]는 해당 근단과 원단 누화가 Jarvis Model[3]을 기반으로 도출된 수식들이며, 이것들은 전송 선로의 양단이 모두 정합되었을 때(matched loads)를 가정할 경우에 해당한다. 식 (1)에서의 x는 양 단의 위치를 의미하며, x=0일 경우는 근단을, x=l일 경우는 원단을 나타내게 된다. Vs(t)는 전원 전압 함수, TD는 시간 지연, Tr은 상승 시간이며, Lm과 Cm은 각각 상호 인덕턴스(mutual inductance)와 상호 커패시턴스를 의미한다. 식 (1)을 이용하면 그림 3(b)와 같이 하나의 aggressor-line 및 하나의 victim-line으로 구성된 2-라인 전송선로에서 victim- line에 유기되는 근단 및 원단 누화의 전압을 거리 및 시간에 따라서 구할 수 있다. 식 (2)는 근단 및 원단 누화 최대 전압값을 나타낸 수식이며, 그림 3(b)에 일반적인 경우에서의 근단 및 원단 누화가 표현되어 있다.
단, , C=Cs+Cm (F), L=Ls(H), , l:Length
한편, 본 논문에서 다루는 브로드사이드 결합 구조 스트립 라인에서는 상호 커패시턴스가 상대적으로 크기 때문에 각 전송 선로의 특성 임피던스가 변하게 되며, 이것으로 인하여 전원단과 부하단에서 임피던스 부정합(unmatched loads)이 나타나게 된다. 따라서 정합되었을 때를 가정하는 식 (1)과 식 (2)는 브로드사이드 결합 스트립라인에서는 적용할 수 없게 된다[6]. 그림 4(a)는 본 논문에서 진행하고자 하는 브로드사이드 결합 스트립라인 모델의 구조를 나타내며, 그림 4(b)는 해당 모델을 기반으로 한 회로 시뮬레이션 조건을, 그리고 그림 4(c)는 임피던스 부정합된 듀얼 스트립라인의 시뮬레이션 결과와 임피던스 정합을 가정하여 얻은 식 (1)과 식 (2)의 비교 결과이다. 여기서 실선은 회로 시뮬레이터를 이용한 해당 모델의 근단 및 원단의 파형을 나타내고, 점선은 식 (1)을 이용하여 나타낸 파형이다. 조건은 부하의 임피던스 50 Ω, 선로의 길이 25 mm, 주파수 1.5 GHz, 상승시간 200 ps이며, 해당 모델의 EM 시뮬레이션 결과로 추출된 각 커패시턴스 및 인덕턴스 요소 값을 식 (1)에 반영하여 추출하였다. 각각 C는 186 pF, Cs는 109 pF, Cm은 77 pF, L은 288 nH, Lm은 117 nH이며, 이때의 부정합된 임피던스는 39.5 Ω이다.
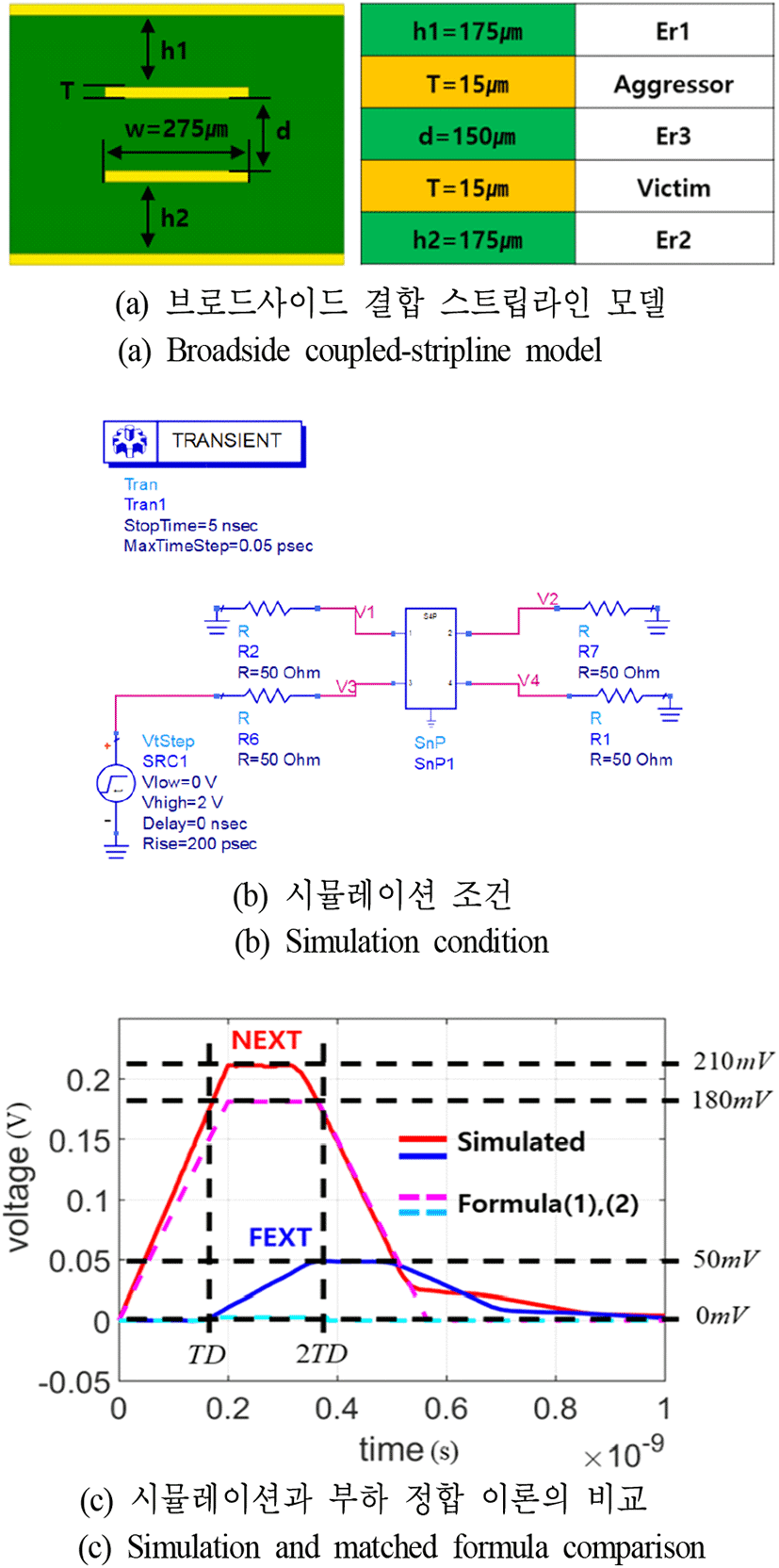
그림 4(c)의 근단 및 원단 누화의 실선 파형은 부하단에서의 반사파의 영향 때문에 그림 3(a)의 파형들과 비교하면 상당한 차이를 보이게 됨을 알 수 있다. 그림에서 알 수 있듯이 실선과 점선은 서로 일치하지 않으며, 이것은 임피던스 정합을 가정하여 유도된 식 (1)이 임피던스 정합이 되지 않은 브로드사이드 결합 스트립라인에서는 사용할 수 없다는 것을 나타낸다. 따라서 브로드사이드 결합 스트립라인에서 사용이 가능한 새로운 수식이 필요하게 된다.
이에 Weak-coupling 가정을 기반으로 하지만 부정합에서의 누화 현상을 포괄할 수 있는 이론을 선행 연구[6],[7]를 통해 확인하였고, 식 (3)~식 (5)와 같은 보완 누화 수식을 활용하여 신호의 반사가 고려된 결과 수식을 추출하였다.
선행 연구[6],[7]의 누화 이론에서는 기존 2-라인 전송선로에서 전자기적 결합으로 기인되는 상호 인덕턴스와 상호 커패시턴스가 victim-line의 부하에 미치는 영향이 상대적으로 무시할만한 수준이라는 가정[1]~[5]을 포함하지 않고, 이것을 영향 요소로 반영함으로써 전자기적 결합이 발생하는 선로의 임피던스가 받는 영향까지 고려하였다. 본 논문에서는 이 이론을 기반으로 하여 체계적으로 누화를 최소화하는 방법론을 정립하고자 한다.
식 (3)은 해당 이론의 페이져 전압(phasor voltage)으로부터 jω → s의 변환을 통해 도출된 주파수 영역에서의 누화 전압 수식을 나타내며, VS(s)는 전원 전압 함수, VNE(s)는 근단 누화 함수, VFE(s)는 원단 누화 함수, MNE, KNE 와 MFE 는 각각 근단과 원단에서의 인덕턴스와 커패시턴스로 유도된 누화 상수, q는 간섭(coupling) 계수, τ는 부하단의 시간 상수, α는 종단 저항과 임피던스의 비례 상수, P는 α로부터 도출된 부하 정합 상수이며, P=1일 경우는 부하의 임피던스와 종단 저항이 정합되었음을 의미한다. X 및 a,b는 주파수 영역으로 변환됨에 따라 유도된 보완 이론 사용 변수들이며, 해당 변수들의 유도 과정은 상당히 복잡하며 선행 연구물[6]을 참고하여 확인할 수 있다.
단,
위 주파수 영역에서의 누화 수식은 라플라스 역변환(laplace inverse transform, e-nsTF(s)=F(t-nT)) 및 테일러 변수(Taylor operator, D-mF(t)=F(t-mT))을 활용하여 시간 영역에서의 누화 함수로 도출할 수 있으며, 이는 식 (4)와 같이 정리할 수 있다[4],[6]. 여기서의 VS(t), VNE(t), VFE(t)는 각각 시간 영역에서의 전원 전압, 근단과 원단 누화 함수이며, 각 함수의 계수 N과 F는 일정한 규칙성을 가지고 유도되었다. 각 단을 기준으로 근단은 짝수 배수, 원단은 홀수 배수의 시간 지연만큼 누화가 누적되는 전원 전압과의 선형 관계가 성립되었으며, 이는 각각의 시간 지연 배수 이후, 부하의 부정합으로 기인되어 각 단으로 되돌아오는 반사파가 반영되었음을 나타낸다.
단,
이때, 근단 및 원단 누화의 최대 전압값은 하기 식 (5)와 같이 정의할 수 있다. 보완된 식 (4) 및 식 (5)가 본 논문의 브로드사이드 결합 스트립라인의 근단 및 원단 특성을 정확하게 표현할 수 있는지를 확인하기 위해 그림 4(a), 그림 4(b)의 조건으로 회로 시뮬레이션과 이론식을 이용한 파형을 그림 5와 같이 결과 비교하였으며, 여기서 실선은 그림 4(c)에서의 실선과 같은 파형을 나타낸다. 한편, 그림 5에서의 점선은 식 (4)와 식 (5)를 이용하여 나타낸 파형이다.
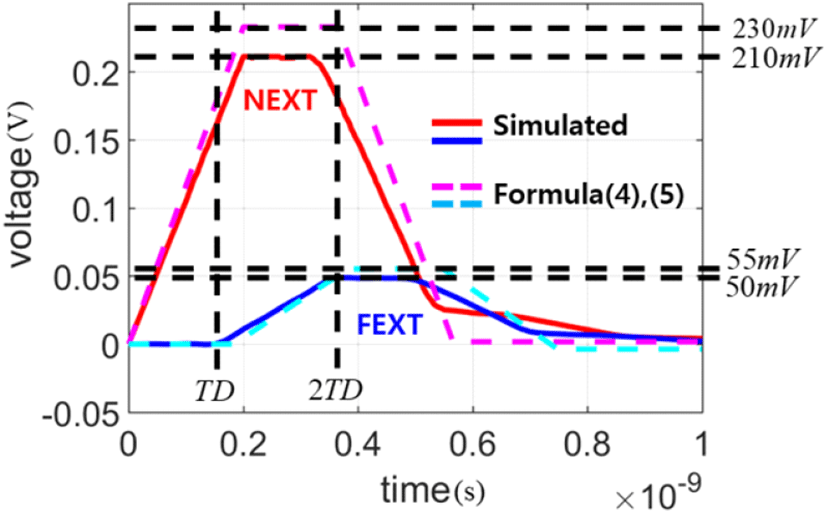
그래프의 실선과 점선을 비교해 보면 약 10 % 정도의 오차(tolerance)를 포함하며, 이것은 수식 유도과정에서 가정한 무손실 선로라는 것, 완벽한 균질 구조를 가진다는 것, 그리고 종단 저항은 순수하게 저항 성분만을 지닌다는 것의 세 가지[6]와 테일러 급수의 근사치에 기인한다고 분석된다. 즉, 식 (4)와 식 (5)는 그림 5와 같이 근단 및 원단 누화가 잘 표현된다는 것을 확인하였으며, 해당 수식들을 기반으로 브로드사이드 결합 스트립라인에서의 누화 성분을 분석하고, 이것을 완화하기 위한 개선 방안을 수립하고자 한다.
Ⅲ. 듀얼 스트립라인 구조에서의 누화 특성
본 논문에서 다루는 두 전송선로의 누화 감소를 간략히 표현하면 식 (5)의 VNE,MAX 및 VFE,MAX 값을 최소화하는 것으로 요약할 수 있다. 이것은 물론 그림 4(a)에서 여러 가지 기하학적 구조를 변화시켜서 원하는 목적을 달성할 수도 있으나, 실제 산업 현장에서는 선로들이 실제로 위치해야 하는 곳이 정해져 있는 등의 제약 조건 때문에 대부분의 경우, 선로 단면의 모양이 이미 정해져 있는 것이 보통이다. 이러한 측면에서 본 논문에서는 단면의 모양을 고정시킨 상태에서 VNE,MAX 및 VFE,MAX 값의 최소화를 모색하고자 한다. 이 경우에 변화할 수 있는 유일한 변수는 스트립라인 주변을 구성하는 절연체의 유전율[8]이며, 따라서 이 유전율(εr)을 변화시키면서 VNE,MAX 및 VFE,MAX 값을 최소화 시키고자 한다. 이 경우, 전송선로의 R-L-G-C 파라미터 중에서 커패시턴스만이 유일하게 변화하게 되며, 따라서 선로의 자기 커패시턴스(C) 및 상호 커패시턴스(Cm)가 변화할 때 VNE,MAX 및 VFE,MAX가 어떻게 변화하는지를 알아볼 필요가 있다.
그림 6은 Cm/C가 변화할 때 VNE,MAX 및 VFE,MAX의 변화를 도출한 그림이다. 그림 6(a), 그림 6(b)의 실선은 부하와의 정합을 가정한 구조에서의 근단 및 원단 누화이며, 이것은 식 (2) 및 식 (5)를 이용하여 구할 수 있다. 그림 6(a), 그림 6(b)의 점선은 부하와의 부정합을 가정한 구조에서의 근단 및 원단 누화이며, 이것은 식 (5)를 이용하여 구할 수 있다.
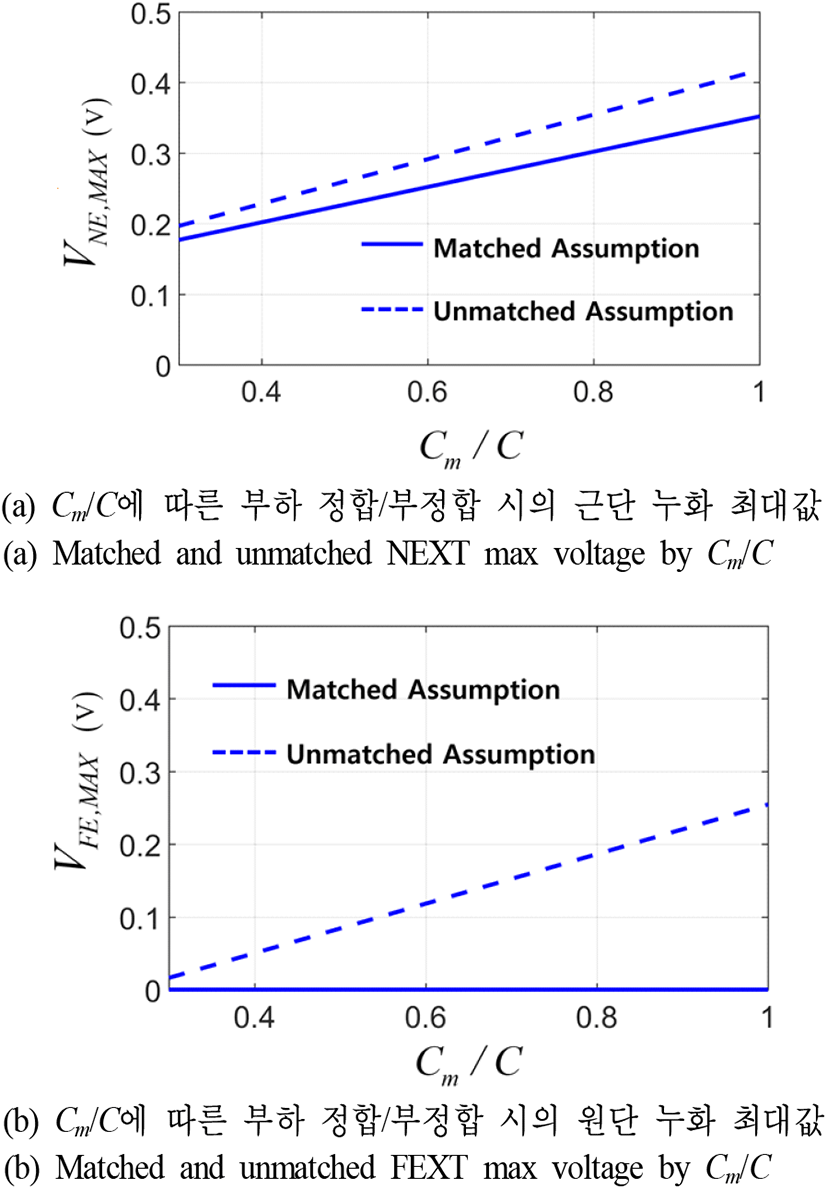
절연체가 하나의 물질로 이루어진 균질한(homogeneous) 구조에서는 상호-자기 커패시턴스 비와 상호-자기 인덕턴스 비가 동일한 값을 가지게 된다[9]. 즉, 균질 매질의 대칭 스트립라인에서는 다음 식 (6)이 성립한다.
단, C, Cm: 각 스트립라인 단위 길이당
자기, 상호커패시턴스
L, Lm: 각 스트립라인 단위 길이 당
자기, 상호인덕턴스
이 조건을 식 (2)에 대입하면 원단 누화는 발생하지 않게 되고, 근단 누화는 커패시턴스 비에 비례한 값을 가지게 된다. 그러나 앞에서 언급했듯이 식 (2)는 선로와 부하 임피던스와의 정합을 가정한 수식이므로 실제와는 차이가 있게 된다. 한편, 그림 6의 점선과 같이 선로와 부하 임피던스와의 부정합을 포함한 경우, 상호-자기 커패시턴스 비가 감소하면서 근단 누화 및 원단 누화 모두 함께 감소하게 된다.
본 논문에서 사용하고 있는 스트립라인 구조에서 상호-자기 커패시턴스 비는 균질 매질일 때 ~0.4 수준이며, 이 때 그림 5에서와 같이 최대 전압값이 50 mV 수준으로 생성됨을 확인할 수 있었으며, 이것은 근단에서의 임피던스 부정합에 기인하게 된다고 볼 수 있다. 이는 균질 매질의 스트립라인에서는 식 (6)이 성립하게 되고, 이 때 임피던스가 정합인 경우의 근단 누화를 나타내는 식 (2)를 이용하면 원단 누화는 0이 되기 때문이다. 즉, 그림 5에서의 50 mV 수준으로 생성된 원단 누화 최대값은 순전히 근단에서의 임피던스 부정합 때문에 생성되었다고 정리할 수 있다.
지금까지의 논의로부터 신호 특성 측면에서 가장 큰 영향성을 미치는 주 요소가 근단 누화라는 것을 알 수 있으므로, 근단 누화를 우선적으로 개선시키고자 한다.
그림 6은 상호-자기 커패시턴스의 비율에 대한 VNE,MAX 및 VFE,MAX 를 표현한 그래프이었으며, 그림 7은 자기 커패시턴스와 상호 커패시턴스 값들이 독립적으로 변화하였을 때 근단 누화의 최대 전압 경향을 나타낸 3차원 그래프이다. 누화 개선에 대한 방향성 수립을 위해서 자기 커패시턴스와 상호 커패시턴스 값을 0에 가까운 값까지 확장하여 표현하는 등, 가능한 넓은 범위에서면 전체에 대한 3-D 그래프를 표현하였다. 누화의 최대치를 감소시키기 위해서는 그림 7의 점선 영역과 같이 결과적으로 x축인 자기 커패시턴스 값 대비 y축인 상호 커패시턴스 값을 작게 해야 한다는 것을 확인할 수 있다. 그러나 적정 커패시턴스 값을 유지하면서 상호 커패시턴스만을 완화시키는 방법은 균질한 매질을 사용하는 구조에서는 유전율 재료의 측면에서 한계가 있기 때문에 비균질 구조를 도입하여 유효 유전율을 변화시키는 방안으로 접근하여야 함을 알 수 있다.
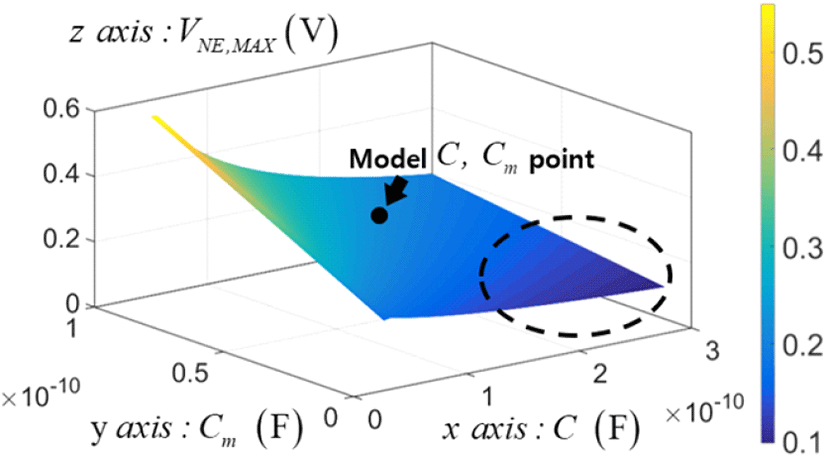
앞에서 언급한 식 (6)의 관계식은 균질 매질에서 성립하지만 비균질 매질에서는 성립하지 않으므로 비균질의 경우까지 확장하기 위해서 비균질 요소(inhomogeneous factor) k를 식 (7)[9]과 같이 도입하였다.
비균질 매질 조건에서,
식 (7)에서 비균질 요소 k가 1일 경우는 균질 구조를 나타내며, 1이 아닌 경우는 비균질의 구조를 나타내게 된다. 즉, k가 변화하면 상호-자기 인덕턴스의 비는 변화하지 않지만 상호-자기 커패시턴스 비가 변화하게 되고, 이 때 근단 누화 최대 전압이 최소값을 갖는 k를 얻고자 한다. 이와 같은 맥락에서 k의 변화에 따른 최대 전압 특성 변화를 확인하기 위하여 그림 8의 2차원 등고선 그래프를 도시화하여 비균질 요소 k 값 변화에 따른 근단 누화의 최대 전압값을 표시하였다.
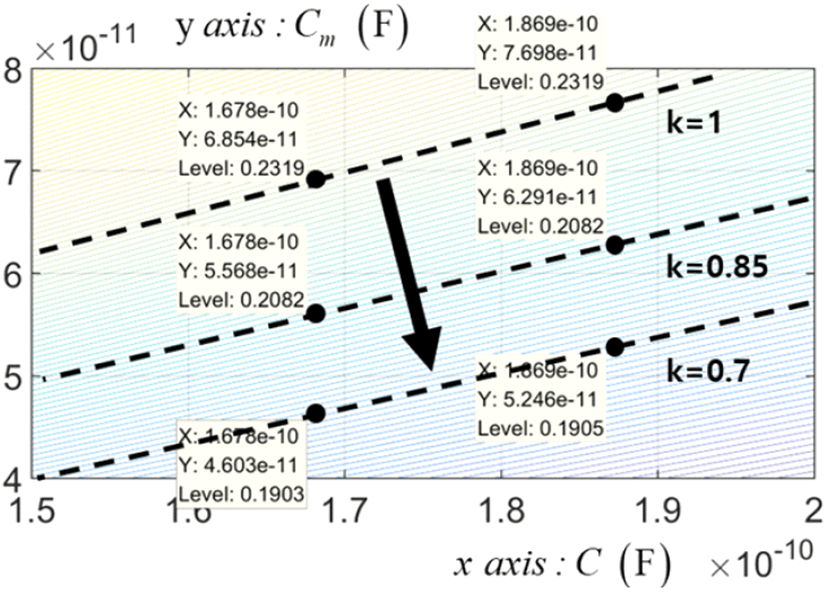
그림 8의 2차원 점선들은 같은 최대 누화 전압값을 갖는 등고선을 나타낸다. k=1을 예로 들면, 해당 점선은 모두 0.2319(V) 값을 갖는 등고선을 나타내게 되며, 화살표와 같이 k 값을 감소시키면 최대 누화 전압값을 감소시킬 수 있음을 보여준다. 적절한 k 값이 주어지면 식 (8)과 같이 상호 커패시턴스 값을 정할 수 있으며, 다음 장에서는 정해진 상호 커패시턴스 값을 실제로 구현하는 방법에 대해서 기술하도록 한다.
Ⅳ. 공극(Airgap)을 활용한 특성 개선 제안
본 장에서는 앞에서 검증된 바를 기반으로 하여 비균질 구조 채용 방안을 모색하고, 유효 유전율과 상호 커패시턴스에 변화를 줄 수 있는 공극 적용 비균질 채용 방안을 발굴하여 제안한다.
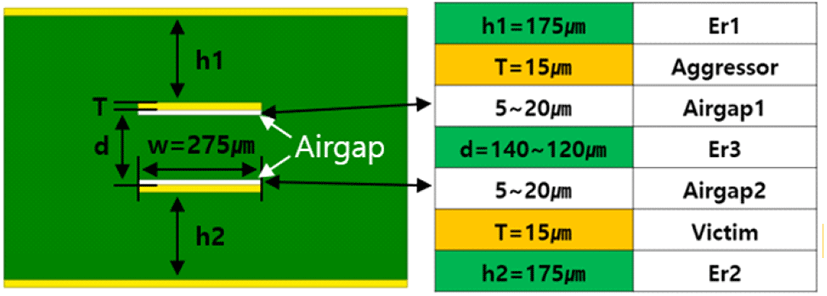
그림 9는 본 논문에서 제안하는 공극 구조에 대해 도시한 것이며, 이는 균질의 듀얼 스트립 구조 내 마주보는 두 신호 층 사이에 얇은 공극을 형성하여, 두 전송 선로 간 발생하는 상호 커패시턴스를 제어하기 위한 유효 유전율 조절이 주 목적이다. 또한, 두께에 따른 비균질의 정도 및 유효 유전율 변화 상관성을 확인하는 등, 실제 특성 개선에 영향을 미치는 요소를 분석하였다. 제안된 방법은 기존의 브로드사이드 결합 스트립라인 구조 내 공극 층을 도입하는 것이므로 폭과 두께를 변수로 설정할 수 있다. 폭의 경우는 전송 선로의 폭과 동일한 수준으로 설정하였으며, 두께를 변화시켜서 누화 최대전압이 감소하는 것을 확인하였다. 그림 10은 ANSYS/Q2D를 사용하여 5/10/ 20/40 μm의 4개의 공극에 대해서 자기 및 상호 커패시턴스 값을 계산한 결과를 그림 8과 동일한 그래프에 4개의 검은 점으로 표현한 것이다. 각 점의 왼쪽 상단에 자기 및 상호 커패시턴스 값, 그리고 누화 최대 전압을 표현하였으며, 오른쪽에는 공극의 두께 및 비균질 요소 k 값을 표시하였다. 그림에서 확인할 수 있듯이 공극의 두께가 두꺼워질수록 비균질 요소 k의 값은 1에서 멀어지는 작은 값을 가지게 되고, 상호 및 자기 커패시턴스 값도 모두 줄어들어, 근단 누화의 최대 전압값도 동시에 완화될 수 있음을 확인할 수 있다. 따라서 근단 누화 전압 최대값을 줄이기 위해서는 공극의 두께가 클수록 좋다는 것을 알 수 있다.
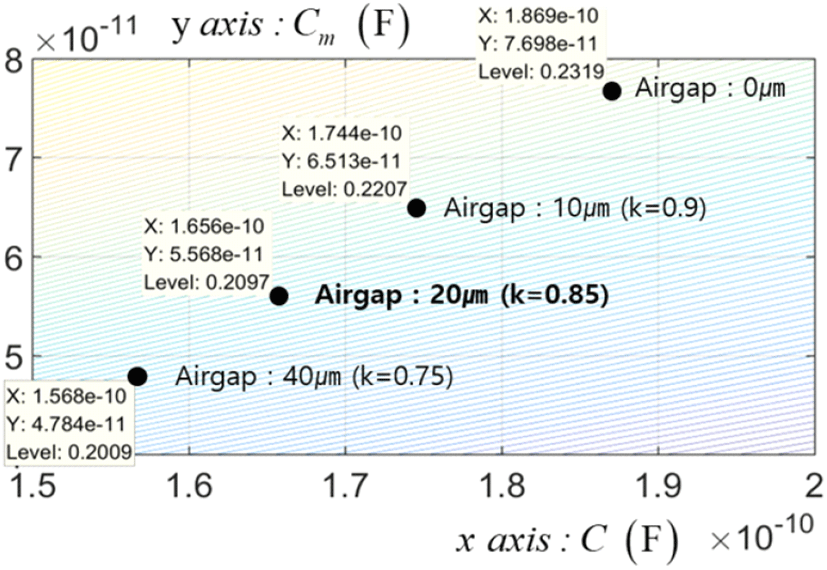
한편, 앞에서도 언급하였지만 근단 누화 최대 전압을 줄이면 원단 누화 최대 전압도 줄어들게 되지만, k 값을 더욱 줄이게 되면 식 (2), 식 (3) 그리고 식 (4)에서 알 수 있듯이 원단 누화 최대 전압은 상승하기 시작한다. 식 (3) 및 식 (4) 수식이 매우 복잡하기 때문에 식 (2)를 통해 살펴보면, 상호-자기 커패시턴스비와 상호-자기 인덕턴스비와의 차이가 커질수록 식 (2)에서의 VFE,MAX가 커짐을 확인할 수 있다. 즉, 비균질 요소 k 값이 균질 구조를 나타내는 값인 1에서 절대 값이 멀어질수록 더 크게 나타나게 된다.
본 논문의 목적은 근단 누화 최대 전압값 개선뿐 아니라, 원단 누화의 최대 전압 값 특성 또한 개선시키는 것이므로 공극 사용을 통한 비균질 매개 채용으로 인해 발생할 수 있는 부작용(trade off)을 감안하여 양 단 모두의 특성을 개선시킬 수 있는 적절한 공극의 두께를 결정하여야 한다. 이에, 공극이 적용되지 않은 기존 구조와 공극이 적용된 구조의 원단 누화 특성 비교를 위해 근단 누화의 최대 전압을 가장 크게 감소시켰던 두께인 20/40 μm를 각각 적용하여 원단 누화 최대 전압의 절대값을 공극 미적용 시의 최대 전압 절대값과 비교하여 그림 11과 같이 차이값(δ)을 확인하였다. 그림 11(a)는 20 μm의 두께를 적용한 공극 구조에서의 원단 누화 특성을 미적용 구조와 비교한 결과이며, 그림 11(b)는 40 μm 두께를 적용한 공극 구조를 비교한 결과이다.
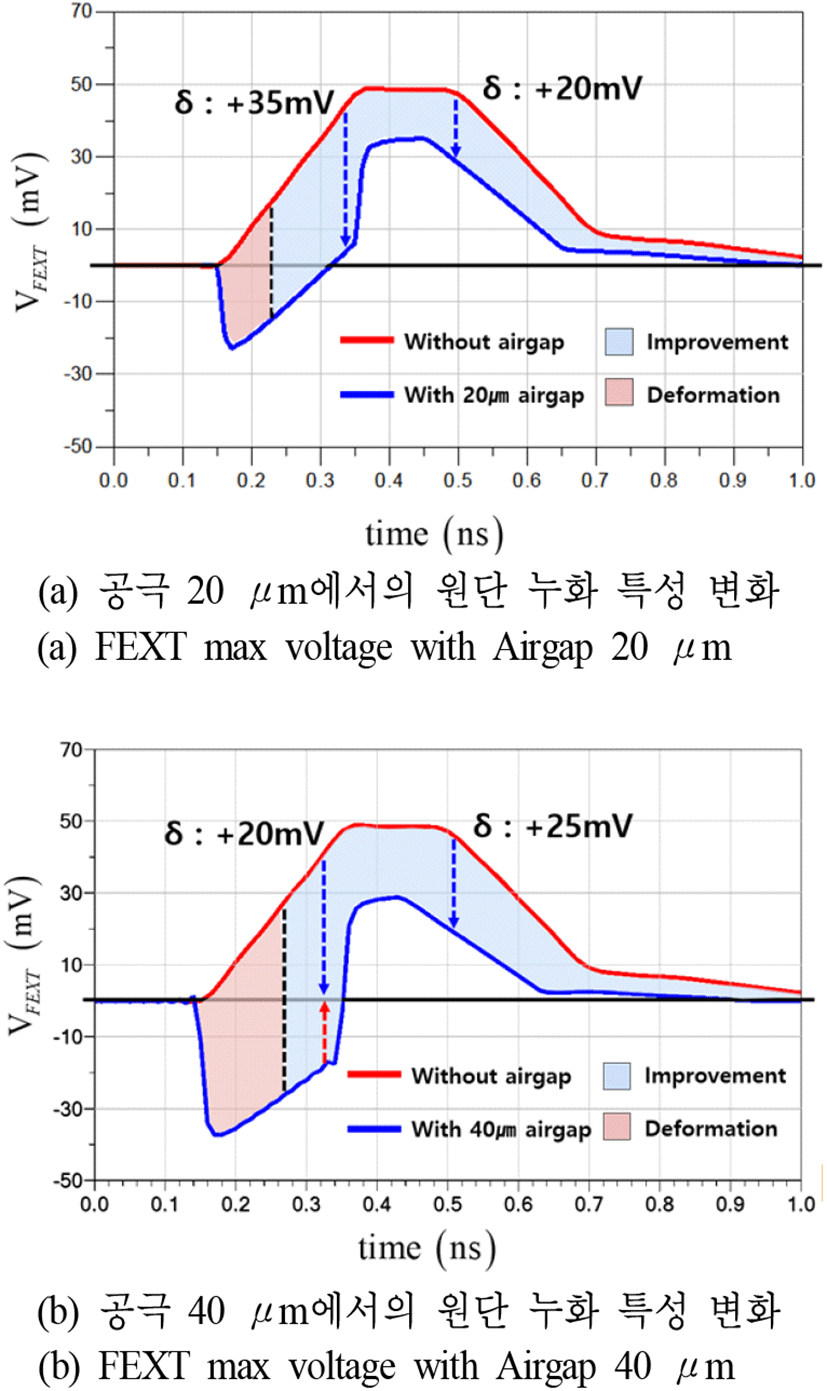
비균질 적용으로 인한 개선 효과 대비 부작용이 더 크게 작용하는 영역을 경계선으로 설정하였고, 20 μm의 공극 두께를 가지는 구조에서는 그림 11(a)에서의 개선 영역이 개악 영역 대비가 넓고 개악의 정도도 낮은 반면, 그림 11(b)의 40 μm의 공극 두께 구조에서는 개선 효과는 20 μm 대비하여 낮으나, 개악 현상은 크게 발생함을 확인하였다. 이에, 근단 및 원단을 모두 개선할 수 있는 최대 공극의 두께를 20 μm로 도출하였다.
공극 적용에 따른 개선 정도를 확인하기 위하여, 공극이 적용되지 않은 그림 4(a)의 구조를 기준으로, 그림 9의 공극 적용 구조에서 최적 두께로 도출된 20 μm를 적용하여 특성 결과를 비교하였다. 각각의 신호 선로에는 레퍼런스 층이 적용되어 있으며, 공극은 대칭 구조를 형성하기 위하여 각각 10 μm로 두 선로에 적용하였다. 목표로 하는 상승 시간 및 주파수는 각각 200 ps와 3 Gbps이다.
우선, 해당 주파수에서의 신호 특성 경향 확인을 위해 S(scattering)-파라미터를 그림 12와 같이 도출하였다. 그림 12(a)는 반사 특성인 S11 및 S22 파라미터이며, 그림 12(b)는 전달 특성인 S12 및 S21 파라미터이다. 그림 12에서 확인할 수 있듯이 목표로 하는 1.5 GHz에서 반사 특성 및 전달 특성 모두가 공극 미적용 대비 적용한 구조가 개선됨을 확인하였다.
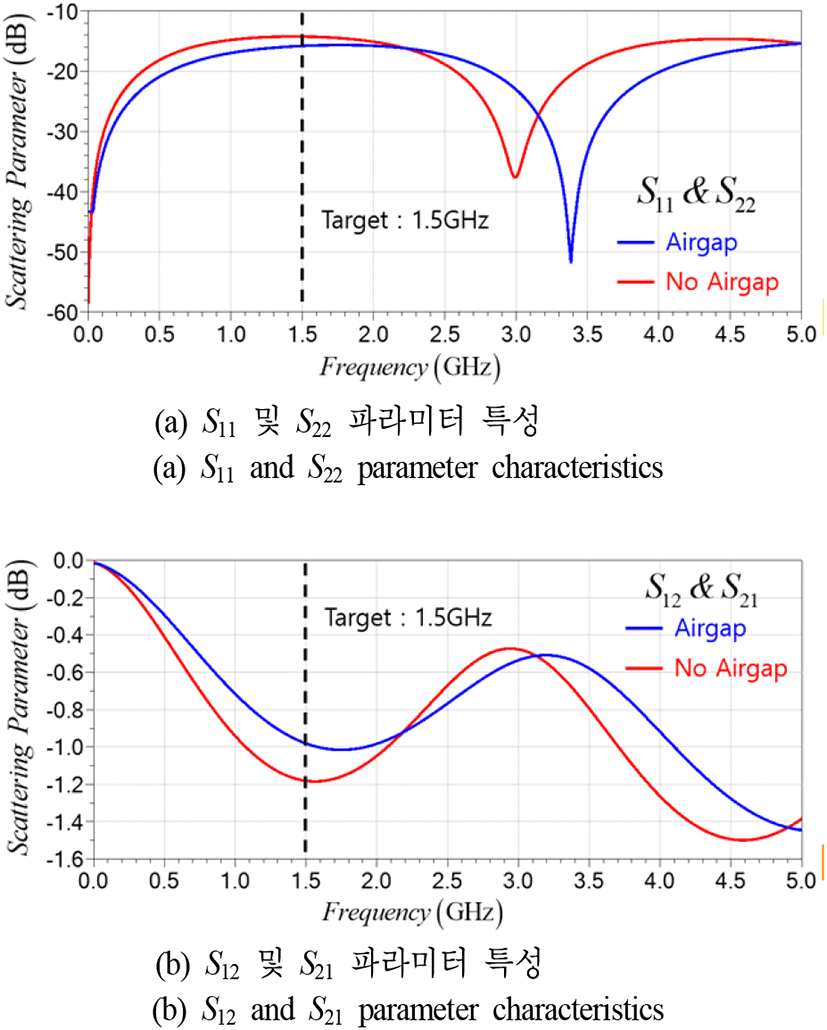
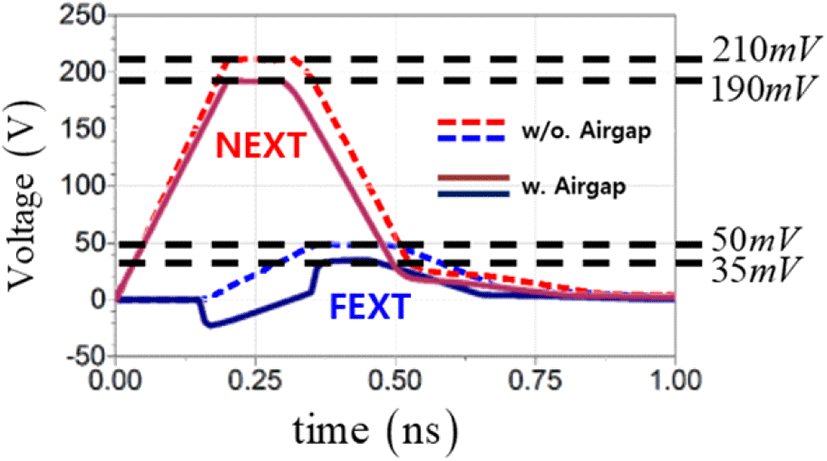
그림 13은 공극 적용에 따른 제안 구조 모델의 근단과 원단의 누화 변화를 전체적으로 나타낸 것이다. 공극을 적용하였을 경우, 커패시턴스 간섭이 약 30 % 완화되고, C는 186 pF에서 165 pF으로, Cm은 77 pF에서 55.6 pF으로 변하게 된다. 이에 따라 단위 커패시턴스 비 감소 및 임피던스 부정합 기인 반사 영향 또한 공극 적용 전 임피던스인 39.5 Ω에서 적용 후 41.8 Ω으로 약 2.3 Ω 개선되어, 근단 누화는 약 20 mV 개선되며, 원단에 미치는 반사 영향 또한 약 15 mV 줄어드는 효과를 얻을 수 있다. 특히 원단에는 균질 구조가 비균질로 변환되어 발생하는 누화에도 불구하고, 비균질로 기인된 누화(−) 성분이 반사파(+) 성분과 중첩되어 상쇄되는 현상이 나타났고, 그림 10(a)에서와 같이 특정 구간에서는 약 30~40(mV)까지 개선되는 결과를 얻을 수 있었다.
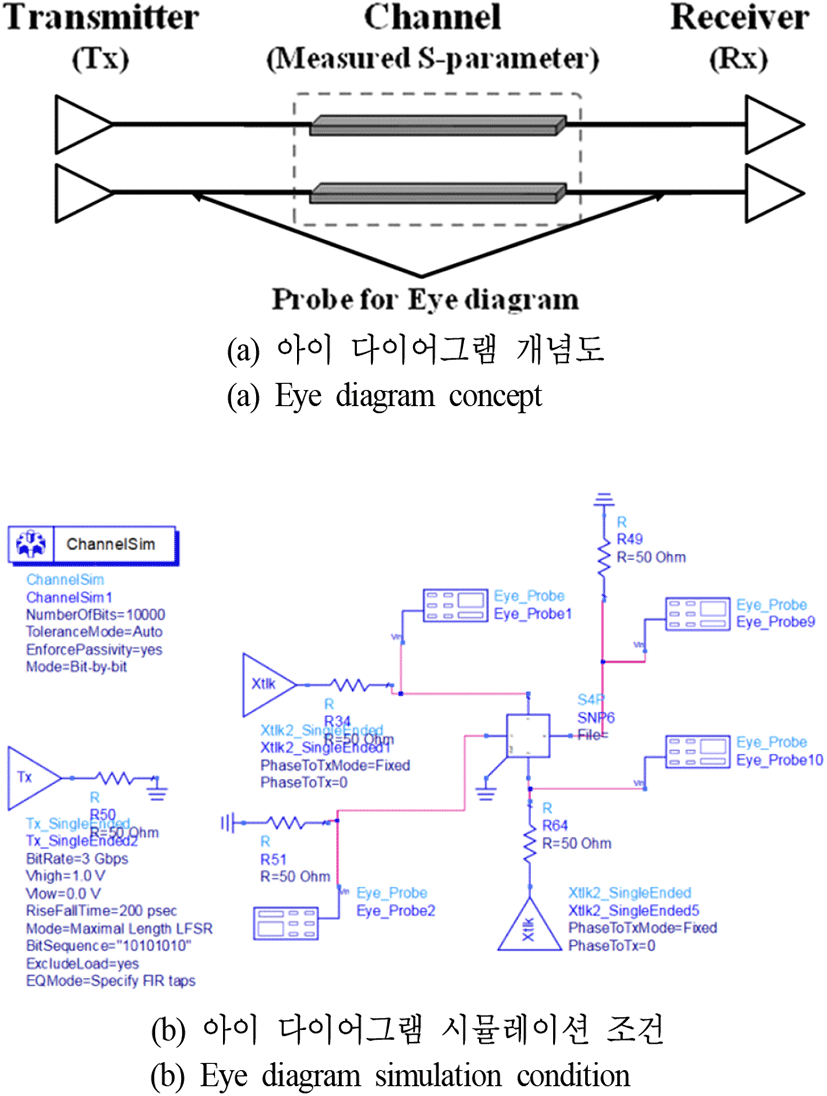
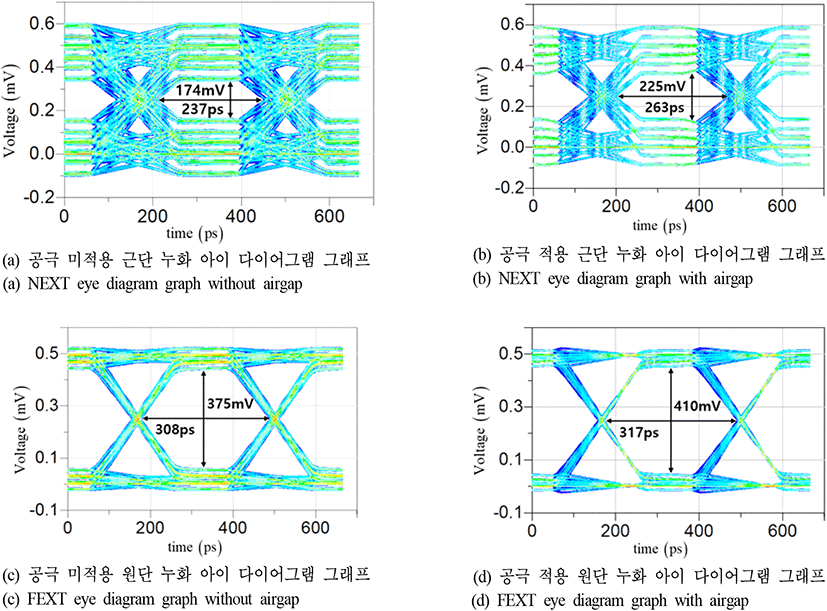
이를 토대로, 제안된 방법의 아이 다이어그램 특성을 확인하기 위해 그림 14와 같은 아이 다이어그램(eye diagram) 시뮬레이션 조건을 수립하고 결과를 확인하였다. 그림 14(a)는 아이 다이어그램 시뮬레이션 조건에 대한 개념도이며, 그림 14(b)는 해당 모델을 기반으로 한 시뮬레이션 조건이다. 아이 다이어그램을 통한 특성 확인은 기존 단일 간섭 구조뿐 아니라, 수직 누화(vertical crosstalk) 및 수평 누화(horizontal crosstalk)의 영향까지 확인하기 위해서 두 가지 누화가 모두 반영된 복수 간섭 구조에서도 공극 적용에 따른 개선 정도를 확인하였으며, 불연속(discontinuity) 구간의 영향 또한 고려하기 위하여 실제 구조를 모사한 모델을 통한 시뮬레이션도 진행하였다. 아이 다이어그램 시뮬레이션은 그림 4(a) 및 그림 9의 구조에서 추출한 S파라미터를 활용하여 최적 두께로 검증되었던 20 μm의 공극을 적용하였고, 적용 전과 후를 각각 비교 분석하였다. 상승 시간 및 목표 주파수는 기존 조건과 동일한 200 ps와 3 Gbps로 설정하였다. 그림 15(a)는 해당 조건에서의 단일 간섭이 발생하는 브로드 사이드 결합 스트립라인에 공극이 없는 본래의 구조를 적용한 근단 누화 결과이며, 그림 15(b)는 단일 간섭이 발생하는 구조에 공극을 적용한 근단 누화 결과이다. 마찬가지로 그림 15(c)는 본래 구조의 원단 누화 결과이며, 그림 15(d)는 공극 적용 구조의 원단 누화 결과이다.
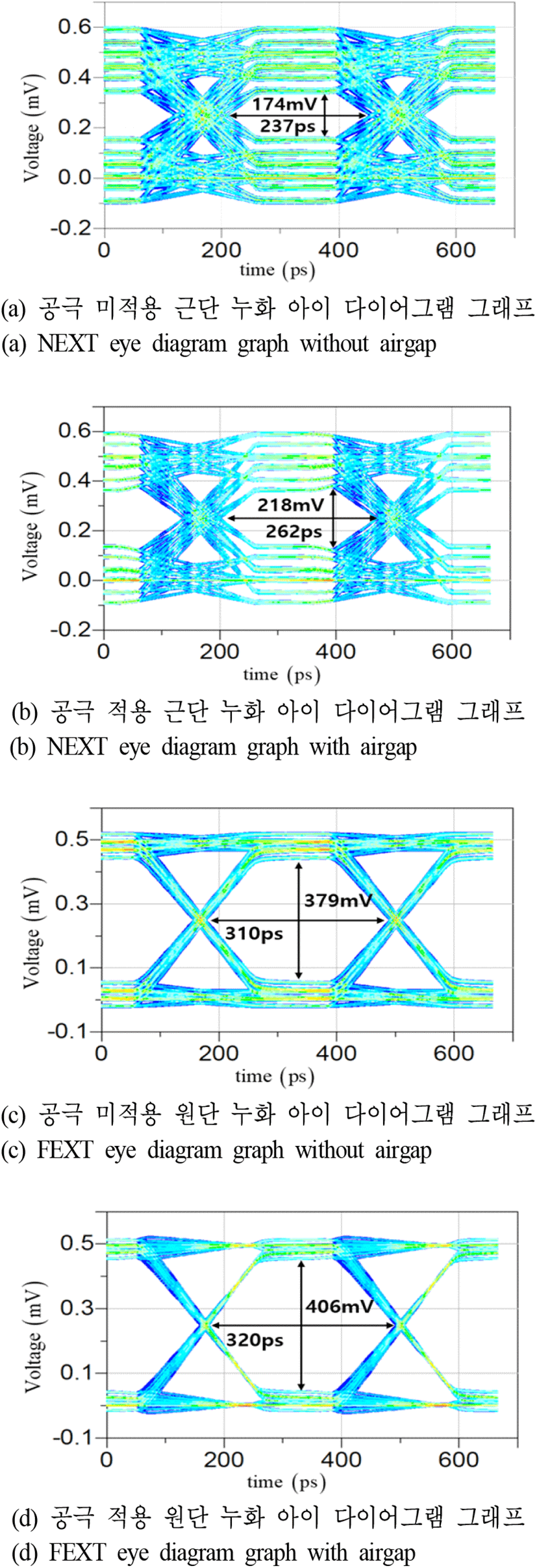
단일 간섭 선로에서의 시뮬레이션 결과, 양 단 모두의 특성이 향상됨을 확인하였고, 드라이버(driver)단에서의 개선 정도는 43 mV / 17 ps이며, 리시버(receiver)단에서는 27 mV / 10 ps 수준 개선되었다.
메모리 모듈 시스템 환경은 data in/out(DQ), clock(CK), command address(CA) 등의 다양한 신호가 스트립라인 구조 내에 수직 및 수평으로 나란히 배치된 구조로 대부분이 설계되어 있다. 이는 듀얼 스트립라인 구조 내에서 수직 누화와 수평 누화가 동시에 발생하는 복수 간섭 구조로 이루어져 있다는 것을 의미한다. 복수 간섭이 반영된 환경에서도 공극의 효과가 나타나는지 확인하기 위해 그림 16과 같은 복수 선로 구조를 구현하였다. 시뮬레이션 조건은 동일하며, 엣지 선로 간의 간섭을 확인하기 위한 수평 거리는 선로의 폭과 비슷한 수준인 250 μm로 설계되었다.
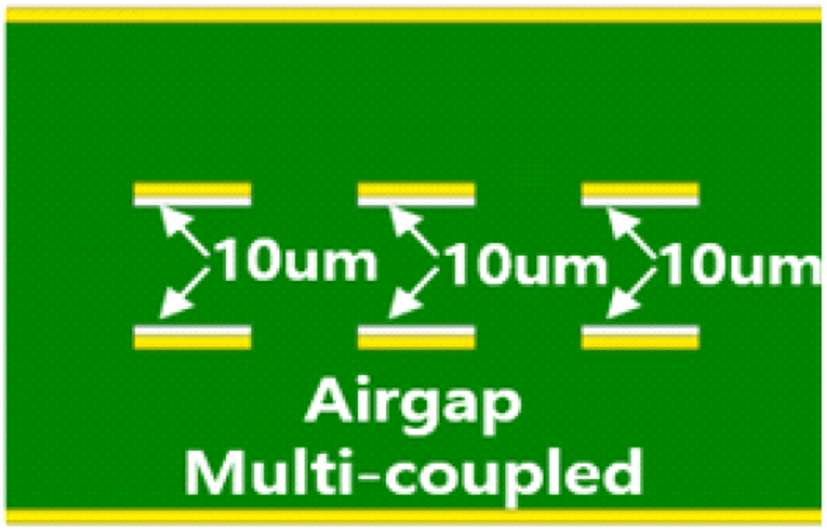
그림 17과 같이 복수 간섭 선로에서의 시뮬레이션 결과, 또한 양 단 모두의 특성이 향상됨을 확인하였고, 드라이버 단에서의 개선 정도는 51 mV / 26 ps이며, 리시버 단에서는 35 mV / 9 ps 수준 개선되었다.
실제 메모리 모듈과 시스템 보드의 인터페이스에서는 비아(via)와 같은 불연속 구간(discontinuity)이 소자와의 연결을 위해 다수 발생하고 있으며, 모듈과 시스템을 연결하게 되는 구간에서는 본 논문 구조와 같은 스트립 선로가 아닌 마이크로스트립라인 선로 또한 사용되고 있다. 실제 구조의 해당 불연속 구간에서도 공극 효과가 동일하게 발생할지를 확인하기 위하여 마이크로스트립 선로와 비아를 반영한 실제 구조를 모사한 모델링을 그림 18과 같이 설계하였다. 단일 간섭 구조와 복수 간섭 구조의 특성 개선 정도의 차이가 제안된 방안의 적용 유무에 따른 결과에 큰 영향이 없는 것을 감안하여 단일 선로로 구성하였으며, 외층에서 비아를 통과한 후 내층 및 비아, 외층의 경로로 전파되는 조건을 모사하였다.
실 구조 모사 환경 시뮬레이션은 Q2D 설계가 아닌 HFSS 3D 환경에서 진행하였으며, 기존 단일 및 복수 간섭 구조와 조건은 동일하다. 실제 구조를 모사한 환경에서도 그림 19와 같이 동일하게 양 단 모두의 특성이 향상 됨을 확인하였다. 드라이버 단에서의 개선 정도는 35 mV / 10ps 이며, 리시버 단에서의 개선 정도는 22 mV / 7 ps 수준이다.
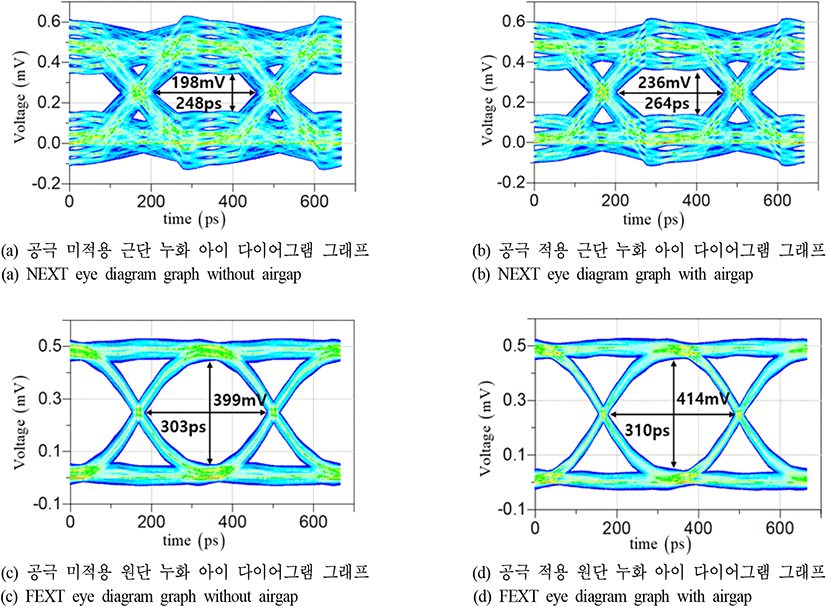
표 1은 단일 및 복수와 실제 구조 모사에 대한 특성 개선 정도를 정리한 것이며, 정리된 바와 같이 공극을 적용할 경우는 드라이버단에서는 단일 간섭 선로 24 %, 복수 간섭 선로 29 %, 실제 모사 구조에서는 17 %의 개선을, 리시버 단에서는 단일 간섭 선로 7 %, 복수 간섭 선로 9 %, 실제 모사 구조에서는 5 %의 개선을 얻을 수 있으며, 듀얼 스트립 브로드사이드 결합에서는 균질 대비 비균질의 구조가 신호 무결성 향상에 효과가 있음을 확인할 수 있었다.
Ⅴ. 결 론
본 논문에서는 브로드사이드 결합 스트립라인 구조 특성상의 커패시턴스 간섭으로 인한 누화 발생을 개선하기 위한 구조 변경 방안을 제안하였고, 이것을 이론적 접근하기 위하여 Weak-coupling assumption unmatched crosstalk을 연구한 선행이론을 기반으로 제안된 방안의 개선 효과 증명 및 개선의 방법론을 수립하였다.
선로 배치 등의 듀얼 스트립 구조 특징을 고려한 설계가 선행되어야 하나, 변경이 불가한 고정된 구조에서는 본 논문에서 제안한 바와 같이 커패시턴스 값을 조절하여 신호 특성 최적화가 가능할 것으로 도출되었으며, 제안된 방안은 공극을 활용하여 비균질 상태로의 전환을 유도하였고, 이것을 이용하여 커패시턴스 간섭 완화 및 누화를 개선할 수 있었다. 비균질로 인한 원단 특성 제약이 존재하였으나, 누화 이론에 기반을 둘 경우, 선로의 길이와 원단 누화는 비례하기 때문에 상대적으로 선로의 길이가 작은 칩(chip) 및 패키지(package) 단위와 같은 경우에는 더 큰 개선 효과를 얻을 수 있을 것으로 예상된다.
본 논문에서 고안된 공극과 비균질 매개 이용 방안의 실적용을 위해 RCC(resin coated copper) 공정 기법을 활용한 필름 삽입 기술, 비균질 유도를 위한 일부 층 저유전율 PPG(prepreg) 사용 등, 가능 공정 기술도 지속 검토하고 있다. 만약 산업 현장에서 유전율을 제어하여 간섭 및 누화를 완화시키는 방안, 혹은 유전율 저하를 위하여 유전체 결합을 활용하는 방안이 적용된다면 본 논문의 방법론이 큰 기여를 하여 폭넓게 활용될 수 있을 것으로 기대된다.













