Convolutional-Neural-Network-Based EBG Structural Design for High-Speed PCB Noise Suppression

Sim, Seongbo; Kim, Myunghoi

doi:10.5515/KJKIEES.2021.32.1.42

J. Korean Inst. Electromagn. Eng. Sci. 2021; 32(1):42-50

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2021.32.1.42

특집논문/SPECIAL EDITION

Convolutional Neural Network 기반 EBG 구조 설계를 통한 고속 PCB 노이즈 저감

심성보¹

, 김명회¹^,^*

Convolutional-Neural-Network-Based EBG Structural Design for High-Speed PCB Noise Suppression

Seongbo Sim¹

, Myunghoi Kim¹^,^*

Author Information & Copyright ▼

¹한경대학교 ICT로봇기계공학부

¹School of ICT, Robotics & Mechanical Engineering, Hankyong National University

^*Corresponding Author: Myunghoi Kim (e-mail: mhkim80@hknu.ac.kr)

© Copyright 2021 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 16, 2020; Revised: Dec 21, 2020; Accepted: Dec 27, 2020

Published Online: Jan 31, 2021

요약

기술이 빠르게 발전하여 디지털 시스템의 동작 주파수는 수 GHz 대역까지 증가했다. 이로 인하여 Simultaneous Switching Noise 문제가 증가했고, 이를 줄이기 위해 Electromagnetic Band Gap(EBG) 구조가 많이 연구된다. EBG 구조 설계에서 중요한 과정 중 하나는 노이즈를 저감하는 Stopband 대역을 예측하는 것이다. 기존에 3차원 전자장 시뮬레이션 프로그램을 이용하는 방법과 Floquet 이론 기반의 수식을 이용하는 방법이 있으나, 한계점이 존재한다. 본 논문에서는 Convolutional Neural Network(CNN)을 이용하여 EBG 구조의 Stopband 대역을 예측하는 새로운 방법을 제안한다. 또한 기본 CNN 구조, GoogLeNet, ResNet, DenseNet과 같은 CNN Architecture 모델을 활용하여 어떤 CNN 구조가 Stopband 대역 예측에 높은 성능을 보이는지 분석한다. 900개의 EBG 구조 모델에 대해서 학습시킨 후 CNN 구조의 mean absolute error를 비교한 결과, DenseNet이 가장 우수한 성능을 보임을 확인하였다.

Abstract

With rapid advances in technology, the operating frequencies of digital systems have increased to several GHz bands. This has led to an increase in simultaneous switching noise(SSN). To reduce SSN, electromagnetic bandgap(EBG) structures have been intensively studied. One of the critical steps in the design of an EBG structure is to predict the stopband that reduces SSN. Existing methods include using a 3D electromagnetic field simulation program or equations based on the Floquet theory. However, these have limitations. In this study, we verified a new method for predicting the stopband using a convolutional neural network(CNN). Specifically, a CNN architectural model was used to compare structures that perform well in predicting the stopband. It was also used to confirm that the DenseNet showed high performance.

Keywords: Simultaneous Switching Noise; Electromagnetic Band Gap; Machine Learning; Convolutional Neural Network

Ⅰ. 서 론

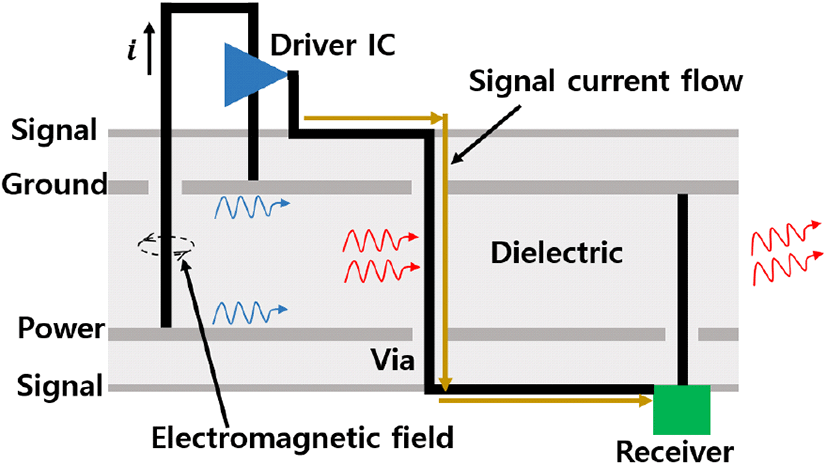
전기·전자·정보 통신 기술이 빠른 속도로 발전하여 디지털 시스템은 대용량의 정보를 빠른 속도로 전송할 수 있게 되었다. 이에 따라 디지털 시스템은 고속화·광대역화 되었으며, 동작 주파수는 수 GHz 대역까지 증가하였다. 하지만 동작 주파수의 증가로 다층 printed circuit board(PCB) 구조에서 simultaneous switching noise(SSN)에 의한 전자파 장해(electromagnetic interference: EMI) 문제가 발생한다. SSN은 PCB에서 전원과 접지 사이의 동시 스위칭 동작이 빠른 속도로 일어나면서 전류가 급격히 변동하여 생긴다. SSN은 인접한 전원 및 신호선에 영향을 주어 오동작을 야기할 수 있다. 그림 1은 SSN의 발생 원리를 나타낸다^[1].

그림 1. | Fig. 1. Simultaneous switching noise 발생과 EMI 방사 | Simultaneous switching noise generation and EMI radiation.

Download Original Figure

수 GHz의 SSN을 저감하기 위해 많은 연구가 이뤄지고 있다. 주목을 받는 연구 중 하나는 electromagnetic band gap(EBG) 구조를 PCB 기판에 적용하는 방법이다. EBG 구조는 특정 주파수 대역에서 높은 임피던스를 가져 해당 대역에서 전파하는 노이즈를 저지하는 특성을 보인다. 이런 특성을 갖는 EBG 구조를 다층 PCB 구조에 적용하여 SSN과 같은 노이즈를 저감하여 최종적으로 EMI 문제를 줄일 수 있다. 많이 연구되고 있는 EBG 구조 중 하나는 그림 2와 같은 inductance-enhanced patch(IEP)가 포함된 EBG 구조다^[2],[5]. IEP-EBG 구조는 power/ground plane과 같은 도체판이 부착된 유전체나 자성체 기판 상에 일정한 주기를 가지고 배치한 도체판(patch)과 이를 power/ ground plane에 연결해 주는 via로 이루어져 있다. 또한, patch에 slot을 만들거나 나선형 등의 모양을 만들어 기존 EBG 구조보다 inductance를 증가시킨 구조다. inductance를 증가시키면 stopband가 낮은 대역에 형성되며, 구조의 크기를 소형화시킬 수 있다.

그림 2. | Fig. 2. Inductance-enhanced EBG 구조와 패치 부분 상세 | Inductance-enhanced EBG structure and patch.

Download Original Figure

EBG 구조를 설계하는 과정에서 중요한 요소 중 하나는 높은 임피던스를 갖는 주파수 대역, 다시 말하면 SSN을 저감할 수 있는 stopband 대역을 예측하는 것이다. Stopband 대역을 예측하는 대표적인 방법으로는 3차원 전자장 시뮬레이션 프로그램을 이용하는 방법과 Floquet 이론 기반으로 도출된 수식을 이용하여 계산하는 방법이 있다. 원하는 stopband 대역을 얻기 위해서는 이런 방법과 유전 알고리즘(genetic algorithm), 입자 군집 최적화(particle swam optimization) 등의 최적화 기법을 결합하여 결과를 도출한다. 하지만 새로운 EBG 구조를 설계하면서 앞의 방법을 이용할 경우 비용 증가, 시간 증대, 수식 계산 로드 증가, 설계 자동화 난이도 증가 등의 한계점이 존재한다. 이런 한계점을 극복하고 원하는 대역에서 노이즈를 저감하는 EBG 구조를 설계하기 위해서는 새로운 Stopband 대역 예측 방법을 연구할 필요가 있다.

따라서 본 논문에서는 EBG 구조의 Stopband 대역 예측을 위해 기계학습(machine learning)을 적용하는 방법을 제안한다. 기계학습은 다량의 데이터와 학습 알고리즘으로 컴퓨터를 학습시켜 스스로 문제를 해결할 수 있는 인공지능을 구현하는 방법이다. 그 중 생물의 뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 기계학습 모델인 인공신경망(artificial neural network)에 집중했다. 그림 3은 인공신경망의 구조를 간단하게 표현한 것이다. 인공신경망은 입력층, 은닉층, 출력층으로 구성되어 있으며, 이를 연결하여 연산을 진행하여 출력을 구하는 방식이다. 인공신경망과 관련된 수많은 연구가 진행되어 convolutional neural network(CNN), recurrent neural network (RNN) 등의 신경망이 발표되었다. 여기서는 특히 이미지 처리에 많은 강점을 보이는 CNN을 활용했다^[3],[4].

그림 3. | Fig. 3. 인공신경망의 구조 | Artificial neural network structure.

Download Original Figure

Ⅱ. Convolutional Neural Network

CNN은 뇌의 시각 피질이 물체를 인식할 때 동작하는 방식에서 착안한 모델이다. 이는 이미지 인식 및 처리 분야에서 강점을 보인다. 그림 4는 CNN의 기본적인 구조를 보여준다. CNN의 중요한 구성요소 중 대표적인 것은 Convolution Layer와 Pooling Layer이며, 일반적으로 CNN은 두 가지 layer를 여러 층으로 쌓아 구성한다. convolution layer는 입력받은 이미지에 대해 특징을 추출하며, pooling layer는 정해진 범위 내에서 최댓값이나 평균값 등의 특정 값으로 압축한다. 두 layer 모두 커널, 스트라이드, 패딩과 같은 하이퍼 파라미터가 존재한다. 커널은 기존의 입력에서 특징을 추출하거나 특정 값으로 압축할 때 기준이 되는 범위, 스트라이드는 이 범위를 이동시키는 거리, 패딩은 layer의 연산을 진행하기 전 데이터 손실을 방지하기 위해 데이터 주변에 0과 같은 특정 값을 입력할 것인지 결정한다^[7],[8].

그림 4. | Fig. 4. Convolutional neural network의 동작 방식 | Convolutional neural network operation method.

Download Original Figure

2-1 CNN Architecture

CNN Architecture는 convolution layer와 pooling layer를 여러 층으로 쌓아 만드는 기본적인 CNN 구조를 변형하여 성능을 향상시킨 모델이다. 보통 이미지 분류 성능을 확인하는 ILSVRC 대회나 컴퓨터 비전 관련 학술대회인 IEEE CVPR에서 발표된다. 본 연구에서는 다양한 CNN Architecture 중 높은 성능을 보여준 모델 중에서 많이 알려진 GoogLeNet, ResNet, DenseNet을 활용하였다.

GoogLeNet은 Inception Module이라 하는 서브 네트워크 구조를 만들어 해당 구조를 여러 층으로 쌓아 만든다. 이전의 구조보다 10배 정도 적은 파라미터를 효과적으로 사용한다. 그림 5는 inception module의 구조를 보여준다. 각 layer의 ‘1×1+1(S)’ 표시는 해당 layer에서 1×1 커널, 스트라이드 1, same 패딩을 사용한다는 의미다. 입력은 4개의 경로로 나뉘어 각 경로의 layer를 지난 뒤 Concatenation 연산을 거친다. 이 연산은 더하는 것이 아니라, 각 출력들을 깊이 방향으로 합치는 연산이다. 다시 말하면, 각 출력들을 위로 쌓아 하나로 만드는 연산이다. GoogLeNet는 inception module을 여러 층으로 쌓아 만든다^[7],[9].

그림 5. | Fig. 5. Inception module의 구조 | Inception module structure.

Download Original Figure

ResNet은 Skip Connection(shortcut connection)을 포함하는 Residual Block이라는 구조를 여러 층으로 쌓은 모델이다. 그림 6은 residual block의 구조를 보여준다. Skip connection은 layer의 입력을 출력과 더해주는 연결을 말한다. Skip connection을 통해 일부 층이 학습되지 않더라도 모델 전체는 학습을 시작할 수 있으며, 입력 신호가 전체 모델에 쉽게 영향을 줄 수 있다^[7],[10].

그림 6. | Fig. 6. Residual block의 구조 | Residual block structure.

Download Original Figure

DenseNet은 그림 7의 Dense Block라 부르는 구조를 여러 층으로 쌓아 만든다. 입력을 출력과 연결하는 것이 ResNet의 skip connection과 비슷하지만 DenseNet에서는 더하는 것이 아닌 Concatenation 연산으로 입출력을 연결한다. DenseNet은 이전의 CNN Architecture보다 훨씬 더 적은 파라미터로도 높은 성능을 낼 수 있다^[11].

그림 7. | Fig. 7. Dense block의 구조 | Dense block structure.

Download Original Figure

Ⅲ. CNN을 이용한 EBG 구조의 Stopband 예측

본 논문에서 제안하는 CNN 기반 EBG 구조의 Stopband 예측을 위해서는 우선 다양한 EBG 구조와 각 구조의 stopband를 입력으로 해서 신경망 모델을 학습시켜야 한다. 데이터 생성은 3차원 전자장 시뮬레이션을 통해서 이루어졌다. 다양한 EBG 구조에 대해서 stopband 데이터를 도출한다. 그리고 EBG 구조의 Patch 이미지를 CNN 모델의 입력으로 사용하며, 도출한 stopband 대역의 하측 차단 주파수와 상측 차단 주파수를 출력으로 설정한다. 그림 8은 학습 데이터 생성을 위해 주로 활용한 IEP-EBG 구조의 Patch 이미지이다. Unit Cell의 가로, 세로 길이는 5.2 mm, 높이 0.354 mm이며, Via는 직경 0.4 mm, 높이 0.2 mm이다. Power/Ground Plane은 가로, 세로 5.2 mm, 두께 0.018 mm이다. EBG Patch의 두께는 0.018 mm이며, 그림 8과 같이 가로, 세로 5mm이다. Patch에는 Slot을 형성해서 EBG 구조가 갖는 등가 inductance를 증가시킨다. 또한 s_x, s_y, g_a, d_g의 길이를 변화시켜 inductance 증가량을 변화시킨다. 그림 9는 학습데이터를 입력하기 위해 사용된 EBG Patch 이미지 모음의 일부를 보여준다. 다양한 Slot 패턴을 가지는 patch를 생성하고 이때, slot의 두께, 개수를 설계 변수로 한다. EBG patch 이미지는 흑백으로 변환된 후 100×100의 크기로 CNN 모델에 입력한다.

그림 8. | Fig. 8. 학습에 주로 이용한 EBG patch 구조 | EBG patch structure mainly used for training.

Download Original Figure

그림 9. | Fig. 9. 학습에 이용된 다양한 EBG patch image | Various EBG patch images used for training.

Download Original Figure

ResNet, GoogLeNet, DenseNet은 참고문헌 [9]~[11]에 표기되어 있는 구조를 활용했으며, 기본적인 CNN 구조를 활용한 모델은 Convolution Layer와 Max Pooling Layer를 여러 층으로 쌓는 구조다. 표 1은 각 모델별 layer의 하이퍼 파라미터를 나타낸다. 모델당 900개의 학습 데이터(training set)를 입력하고, 900개의 학습 데이터를 100회 학습한다. 또한 각 구조 당 100회 학습한 모델을 100개씩 만들어 해당 구조가 여러 번의 학습을 진행할 경우에도 결과에 변동이 없는지 확인한다. 그 후 Training Set과 비슷하게 slot의 설계 변수를 변화하여 생성한 Test Set을 각 모델에 입력하여 학습한 patch와 유사하지만 학습하지 않은 patch에 대한 예측 결과를 확인한다. 그림 10은 해당 Test Set의 일부를 보여준다.

표 1. | Table 1. CNN 모델별 layer의 하이퍼 파라미터 | Hyper parameters in layer by CNN model.

Output size	Basic CNN structure	GoogLeNet	ResNet	DenseNet
50×50	Convolution, 64, 7×7+2(S)
25×25	Max pooling, 3×3+2(S)
	Convolution, 128, 7×7+1(S)	Convolution, 64, 1×1+1(S)	$[64, 3 × 3 64, 3 × 3] × 3$	$[16, 3 × 3 4, 3 × 3] × 6$
	Convolution, 128, 7×7+1(S)	Convolution, 192, 3×3+1(S)	$[64, 3 × 3 64, 3 × 3] × 3$	Convolution, 88, 1×1+1(S)
13×13	Max pooling, 3×3+2(S)	Max pooling, 3×3+2(S)	$[128, 3 × 3 128, 3 × 3] × 4$	Avg pooling, 2×2+2(S)
	Convolution, 256, 7×7+1(S)	$[64, 128, 32, 32 96, 16]$		$[16, 3 × 3 4, 3 × 3] × 12$
	Convolution, 256, 7×7+1(S)	$[128, 192, 96, 64 128, 32]$		Convolution, 136, 1×1+1(S)
7×7	Max pooling, 3×3+2(S)	Max pooling, 3×3+2(S)	$[256, 3 × 3 256, 3 × 3] × 6$	Avg pooling, 2×2+2(S)
		$[192, 208, 48, 64 96, 16]$		Avg pooling, 2×2+2(S)
		$[160, 224, 64, 64 112, 24]$		$[16, 3 × 3 4, 3 × 3] × 24$
	Convolution, 512, 7×7+1(S)	$[128, 256, 64, 64 128, 24]$		$[16, 3 × 3 4, 3 × 3] × 24$
		$[112, 288, 64, 64 144, 32]$		Convolution, 232, 1×1+1(S)
		$[256, 320, 128, 128 160, 32]$		Convolution, 232, 1×1+1(S)
4×4	Max pooling, 3×3+2(S)	Max pooling, 3×3+2(S)	$[512, 3 × 3 512, 3 × 3] × 3$	Avg pooling, 2×2+2(S)
		$[256, 320, 128, 128 160, 32]$		$[16, 3 × 3 4, 3 × 3] × 16$
		$[384, 384, 128, 128, 192, 48]$		$[16, 3 × 3 4, 3 × 3] × 16$
1×1	Global Avg pooling, fully connected

Download Excel Table

그림 10. | Fig. 10. EBG patch image test set | EBG patch image test set.

Download Original Figure

Ⅳ. 예측 결과

표 2와 그림 11, 12는 각 CNN 모델에 Training Set과 Test Set을 입력하여 얻은 stopband 예측 결과( $y^$ )와 3차원 전자장 시뮬레이션에서 얻은 stopband 결과(y)의 mean absolute error(MAE) 오차를 나타낸다. MAE 오차는 두 값의 차이를 구하고 절댓값을 취하여 구한 수치로 식 (1)과 같다.

MAE= 1 n ∑ | y − y^|

(1)

표 2. | Table 2. CNN 모델별 MAE 오차의 평균, 표준편차, 최소, 최대 | Mean, standard deviation, minimum, maximum of MAE by CNN model.

	Training set				Test set
	Avg	Std	Min	Max	Avg	Std	Min	Max
Basic CNN structure	0.1574	0.0494	0.0738	0.3219	0.3342	0.0836	0.1508	0.5897
GoogLeNet	0.0823	0.0367	0.0412	0.2313	0.4168	0.0737	0.2610	0.6556
ResNet	0.2590	0.1487	0.0499	0.9518	0.3582	0.1374	0.1501	0.8076
DenseNet	0.0747	0.0270	0.0379	0.1798	0.1858	0.0323	0.1534	0.2962

Download Excel Table

그림 11. | Fig. 11. Training set을 적용했을 때 출력의 MAE 오차 | MAE of output when training set is applied.

Download Original Figure

그림 12. | Fig. 12. Test set을 적용했을 때 출력의 MAE 오차 | MAE of output when test set is applied.

Download Original Figure

전자장 시뮬레이션에서 예측한 결과와 CNN에서 예측한 Stopband 대역폭 모두 GHz 단위를 사용하므로 둘의 차이를 구한 MAE 오차도 GHz 단위다.

표 2에서 training set을 적용했을 때 MAE 오차의 평균을 살펴보면 4개의 모델 모두 0.3 GHz로 낮은 수치를 보여준다. 하지만 그림 11의 경우, ResNet에서 100개의 모델의 MAE를 살펴보면 학습할 때마다 값의 변동이 크다. GoogLeNet와 DenseNet은 모두 매우 작은 MAE 수치를 보여주고 있으나, DenseNet의 변동 폭이 GoogLeNet보다 더 작다. 학습하지 않았던 Test Set을 입력하여 얻은 결과를 표현한 그림 12를 살펴보면 DenseNet이 가장 작은 MAE 오차를 보여주며, 각 모델당 변동 폭도 다른 3개의 구조보다 훨씬 더 작다.

현재 상태에서 오차 및 여러 번의 학습 시 결과 값의 변동을 줄이기 위해서 가장 접근하기 쉬운 방법으로는 CNN의 각 layer의 하이퍼 파라미터를 변경하는 것이다. 하지만 이 방법은 한계가 있다. 또한, 학습하지 않았던 Test Set을 적용하여 전자장 시뮬레이션 결과와 비교한 그림 12와 13을 살펴보면 일부 patch에 대해서는 다른 patch에 비해 예측 결과가 차이를 보인다. 이는 하이퍼 파라미터를 변동하는 것보다 더욱더 다양한 구조의 EBG 구조를 학습하여야 해결할 수 있는 문제다.

그림 13, 그림 14는 test set에 대하여 전자장 시뮬레이션에서 도출한 stopband 대역의 하측 차단 주파수, 상측 차단 주파수와 CNN 모델에서 예측한 stopband 대역의 결과를 비교한 것이다. CNN 모델에서의 예측값은 마찬가지로 각 구조당 100개의 모델에서 출력한 결과의 평균을 활용하였다. 각 CNN 모델에서 예측한 결과도 전자장 시뮬레이션의 결과 그래프와 비슷한 형태를 보여준다. 다만 일부 patch는 다른 patch들보다 전자장 시뮬레이션의 결과와 차이가 있는 모습을 보여주고 있다. 전체적으로 ResNet와 DenseNet이 전자장 시뮬레이션 결과와 유사하다.

그림 13. | Fig. 13. Test set의 stopband 하측 차단 주파수 예측 결과 | The result of predicting the low frequency of the stopband when a test set is given as an input.

Download Original Figure

그림 14. | Fig. 14. Test set의 stopband 상측 차단 주파수 예측 결과 | The result of predicting the high frequency of the stopband when a test set is given as an input.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 새로운 EBG stopband 예측 방법인 CNN 기반 예측법을 제시하고, 기존 방법인 3차원 전자장 시뮬레이션 방식과 비교 분석하였다. 또한, CNN 기반 stopband 예측법의 정확도 향상을 위하여 CNN 기본 모델과 CNN Architecture 활용 모델들을 모두 적용하였다. 본 논문에서 제안한 CNN 기반 예측법은 3차원 전자장 시뮬레이션 결과와 비교하여 검증하였으며, 비교 결과 매우 우수한 성능을 보여주었다. 특히 DenseNet 기반 예측법의 경우에는 같은 모델을 여러 번 생성했을 때 발생하는 결과 변동이 가장 작으면서 전자장 시뮬레이션 결과와 매우 유사한 성능을 보여주었다. 이는 Layer의 입출력에 Concatenation 연산을 진행하여 초기 입력이 모델의 출력까지 영향을 미치는 DenseNet의 특징에 의한 것이다. GoogLeNet은 Shortcut Connection이 없으며, ResNet의 경우 shortcut connection이 존재하지만 여기서는 입출력을 더하는 연산만을 하기에 DenseNet과는 차이를 보인다.

본 연구의 CNN 모델 학습은 EBG 구조의 가로, 세로 길이 및 높이 등의 다른 설계 변수의 변화에 대한 학습이 반영되지 않았다. 해당 설계 변수의 변화를 반영한 다양한 구조에 대한 학습을 진행하여 Patch의 변화뿐만 아니라, EBG 구조의 unit cell의 변화에 대해서도 정확한 예측을 할 수 있는 기계학습 모델 연구를 추후 진행할 예정이다. 더 나아가, 원하는 stopband 대역을 입력하면 그에 맞는 EBG 구조를 생성할 수 있는 기계학습 기반의 EBG 구조 설계 자동화 방법에 관한 연구도 필요하다.

Acknowledgements

이 연구는 과학기술정보통신부 신진연구지원사업(2019R1C1C1005777) 연구비의 지원으로 연구되었음.

References

[1].

H. G. Kim, “Electromagnetic band gap structure for frequency selective simultaneous switching noise suppression and study on its miniaturization,” M.S. thesis, Sungkyunkwan University, 2017.

[2].

J. H. Kwon, H. D. Choi, “Research trend of electromagnetic interference reduction technology using EBG structure,” The Proceedings of The Korean Institute of Electromagnetic Engineering and Science, vol. 18, no. 1, pp. 32-42, Jan. 2007.

[3].

M. Kim, “A miniaturized electromagnetic bandgap structure using an inductance-enhanced patch for suppression of parallel plate modes in packages and PCBs,” Electronics, vol. 7, no. 5, p. 76, 2018.

[4].

R. Abhari, G. V. Eleftheriades, “Metallo-dielectric electromagnetic bandgap structures for suppression and isolation of the parallel-plate noise in high-speed circuits,” IEEE Transactions on Microwave Theory and Techniques, vol. 51, no. 6, pp. 1629-1639, Jun. 2003.

[5].

T. Kamgaing, O. M. Ramahi, “Multiband electromagnetic-bandgap structures for applications in small form-factor multichip module packages,” IEEE Transactions on Microwave Theory and Techniques, vol. 56, no. 10, pp. 2293-2300, Oct. 2008.

[6].

H. H. Park, D. H. Lee, “Machine learning based EMI/EMC design technology trend,” The Proceedings of The Korean Institute of Electromagnetic Engineering and Science, vol. 31, no. 1, pp. 41-51, Jan. 2020.

[7].

A. Géron, Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, Sebastopol, CA, O'Reilly Media, 2019.

[8].

S. Raschka, V. Mirjalili, Python Machine Learning, Birmingham, Packt, 2017.

[9].

C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, and D. Anguelov, et al., “Going deeper with convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Boston, MA, Jun. 2015, pp. 1-9.

[10].

K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, Jun. 2016, pp. 770-778.

[11].

G. Huang, Z. Liu, L. van der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HI, Jul. 2017, pp. 4700-4708.

Author Information

심 성 보 [한경대학교/석사과정]

jkiees-32-1-42-i1

https://orcid.org/0000-0001-6654-6207
2020년 2월: 한경대학교 전기전자제어공학과 (공학사)
2020년 3월～현재: 한경대학교 ICT로봇기계공학부 석사과정
[주 관심분야] EMI/EMC, Signal/Power Integrity, Machine Learning

김 명 회 [한경대학교/교수]

jkiees-32-1-42-i2

https://orcid.org/0000-0002-4981-4860
2003년 2월: 한국과학기술원 전기 및 전자공학과 (공학사)
2005년 2월: 한국과학기술원 전기 및 전자공학과 (공학석사)
2012년 8월: 한국과학기술원 전기 및 전자공학과 (공학박사)
2005년~2008년: 국방과학연구소 연구원
2012년~2015년: 한국전자통신연구원 선임연구원
2015년 9월~현재 : 한경대학교 부교수
[주 관심분야] EMI/EMC, 고속 패키지/인터커넥트 설계, Signal/Power Integrity