Beamforming Algorithms

Noh, Song; Hyunchae, Chun

doi:10.5515/KJKIEES.2020.31.8.006

J. Korean Inst. Electromagn. Eng. Sci. 2020; 31(8):701-712

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2020.31.8.006

특집논문/SPECIAL EDITION

빔포밍 알고리즘

노송¹

, 전현채¹^,^*

Beamforming Algorithms

Song Noh¹

, Chun Hyunchae¹^,^*

Author Information & Copyright ▼

¹인천대학교 정보통신공학과

¹Department of Information and Telecommunication Engineering, Incheon National University

^*Corresponding Author: Hyunchae Chun (e-mail: hyunchae.chun@inu.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 20, 2020; Revised: Aug 03, 2020; Accepted: Aug 21, 2020

Published Online: Aug 31, 2020

요약

빔포밍 기술은 5세대(5G) 이동통신 구현을 위한 중요한 기술요소이며, 나아가 6G 통신 네트워크에서 고려되는 밀리미터파 및 테라헤르츠 통신 시스템에 높은 대역 효율, 공간 다이버시티, 빔포밍 이득을 제공하기 위해 활발한 연구가 진행되고 있다. 본 논문에서는 빔포밍 알고리즘에 대해 통계적 신호처리 및 최적화 관점에서의 고찰을 통해 빔포밍 기술을 체계적으로 이해하는 데 도움을 주고자 한다. 빔포밍 기술의 이론적인 배경과 빔포밍 기술 특징에 따른 주요 알고리즘을 폭넓게 기술하고자 한다.

Abstract

Beamforming techniques have become an integral part of the fifth-generation(5G) of mobile communication systems and continue to evolve for providing high spectral efficiency, spatial diversity, and beamforming gain in millimeter-wave and terahertz(THz) communication for future 6G networks. This paper presents a comprehensive overview of beamforming algorithms from statistical signal processing and optimization perspectives. The fundamentals of beamforming for wireless communication and several representative beamforming algorithms for single-stream and multi-stream transmission are discussed.

Keywords: Beamforming; 5G; MIMO; Massive MIMO; Millimeter-Wave

Ⅰ. 서 론

빔포밍 기술은 레이다와 음파 탐지, 의료 이미지 등 국방 및 민수 분야에서 널리 쓰이는 기술이다. 특히 이동 통신 분야에서는 LTE 표준 규격에서 빔포밍 기술이 도입된 이후 현재 5세대(5G) 이동통신 시스템에서는 대규모(massive) 다중 입출력(MIMO: multiple-input multiple-output) 안테나 기반의 고용량 데이터 처리 및 초고주파(millimeter-wave) 대역 통신의 빔포밍 이득을 실현하기 위한 주요 기술이 되었다^[1].

이동 통신 시스템에서 빔포밍 기술의 사용 목적은 통신 도달거리 내에 균일하게 신호를 형성하지 않고, 특정 지역에 신호를 집중하기 위해 사용한다. 즉, 특정 사용자에게 높은 전송 용량을 제공하는데 활용될 수 있으며, 공간 빔포밍을 통해 동일한 무선 자원을 사용하는 다수의 사용자를 구분할 수 있는 주파수 효율을 높이는 기술로도 활용된다.

본 논문은 특정 빔포밍 기술에 집중하거나 복잡한 식의 전개를 통해 설명하지 않고, 빔포밍 기술의 이론적인 배경 및 다양한 전송 환경에서 빔포밍 기술 구현에 필수 내용을 요약하여 전달하는데 주목적을 두고 있다. 본 논문은 다음과 같이 구성되어 있다. 서론에 이어 Ⅱ장에서는 고려하는 신호 및 시스템을 설명하고, Ⅲ장과 Ⅳ장에서는 데이터의 통계적 특성을 사용하거나, 이를 사용하지 않는 빔포밍 설계 기법을 설명한다. Ⅴ장에서는 다중 입출력 안테나 시스템에서 빔포밍 기법, Ⅵ장에서는 대규모 다중 입출력 안테나 시스템에서 빔포밍 기법을 소개한다. 마지막으로 Ⅶ장에서는 결론을 맺는다.

Ⅱ. 시스템 모델

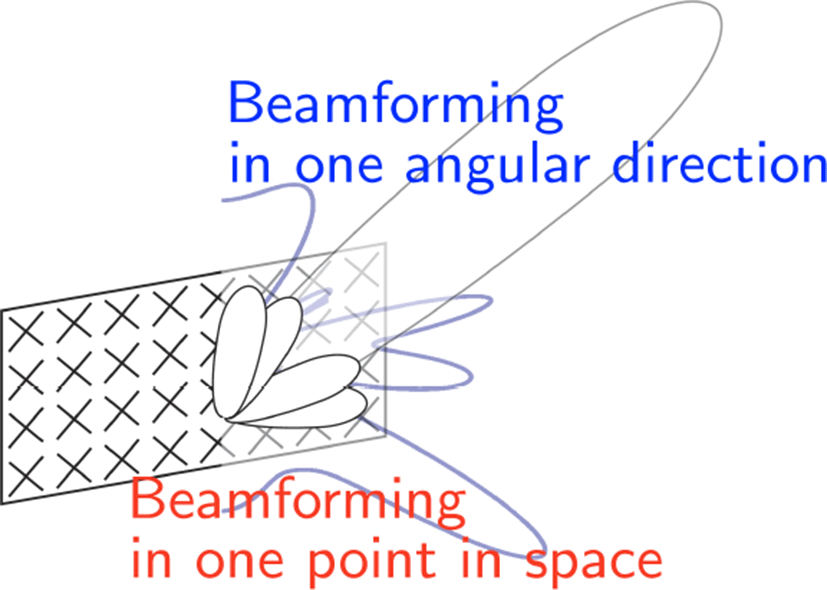
각 안테나는 고정된 방사 패턴을 가지고 있지만, 빔포밍을 통해 주파수/시간/공간적으로 다른 방사 패턴을 나타낼 수 있다. 그림 1에 한정적인 각도 공간에 신호를 집중하여 빔을 형성하는 경우와 중첩된 다수의 빔을 형성하여 특정 공간에 집중되지 않는 빔 설계 예시를 나타냈다.

그림 1. | Fig. 1. 빔포밍 예시 | Illustration of beamforming.

Download Original Figure

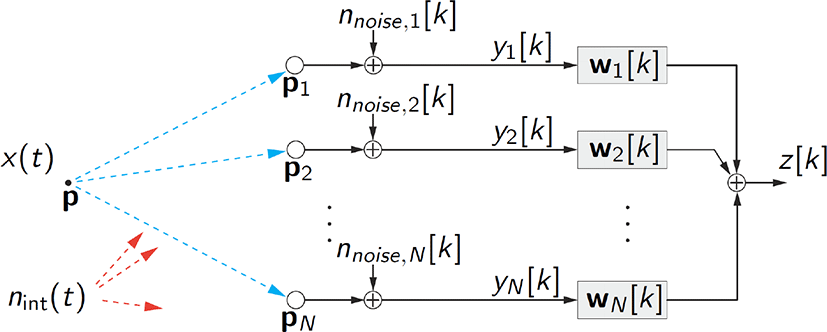
먼저 빔 설계 기법을 설명하기 위해 고려되는 신호 및 빔포밍 시스템 구조를 설명한다(본 논문에서 주로 수신 빔포밍을 고려하며, 소개된 알고리즘은 송신 빔포밍 구조에서도 적용할 수 있다). 그림 2에서 송신 신호 x(t)는 공간벡터 p∈ℝ³로 나타낸 위치에서 발생하고, 수신기 주변 신호의 반향 및 간섭 신호는 n_int(t)로 나타낸다. 공간벡터 p_n에 위치한 각 수신 안테나는 전달된 연속 신호를 일정한 시간 간격 T마다 샘플링하여 이산 신호를 획득하며, 전달지연시간 τ_n을 고려한 식 표현은 식 (1)과 같다.

x n [k] = x (k T − τ n)

(1)

τ n = ‖ p − p n ‖ / c

(2)

그림 2. | Fig. 2. 일반적인 빔포밍 시스템 예시 | Illustration of a general beamformer.

Download Original Figure

식 (2)에서 c는 빛의 속도를 나타낸다. n번째 안테나에서의 수신 잡음 및 간섭 신호의 합은 n_n[k]=n_noise,n[k]+n_int,n[k]로 표현하며, 가우시안 분포 랜덤 변수로 모델링한다(n_n[k]~CN(0,σ²)). 이때 수신 신호는 다음과 같다.

y n [k] = x n [k] + n n [k]

(3)

그림 2에 나타낸 바와 같이, 각 안테나에서 수신한 신호들은 길이 M의 가중치 벡터 w_n[k]를 통해 시간·공간 영역에서 빔포밍 연산을 수행하게 된다. 빔포밍 후 얻은 최종 출력 신호는 z[k]∈ℂ로 표현하고, 전체 시스템 식은 다음과 같다.

z [k] = w H [k] y [k] = w H [k] (x [k] + n [k])

(4)

식 (4)에서 사용된 시간·공간 영역에서의 빔포밍 및 수신 신호 벡터는 다음과 같이 정의된다.

w [k] = [w 1 T, ⋯, w N T] T y n [k] = [y n [k], ⋯, y n [k − M + 1]] T y [k] = [y 1 T, ⋯, y N T] T

(5)

따라서 특정 공간 p에서 발생한 신호에 적합한 수신 빔포밍은, 시간·공간 영역에서 얻은 신호 y[k]에 대해 가중치 벡터 w[k]를 사용하여 여러 안테나에 전달된 신호를 유기적으로 결합하는 것이다. 예를 들어 신호 전달 시 발생하는 지연시간(τ_n)을 적절하게 보상하는 것도 빔포밍 설계 시 고려될 수 있다. 본 논문에서는 간결한 설명을 위해 공간 영역에서의 빔포밍 연산만 고려하기로 한다(M=1).

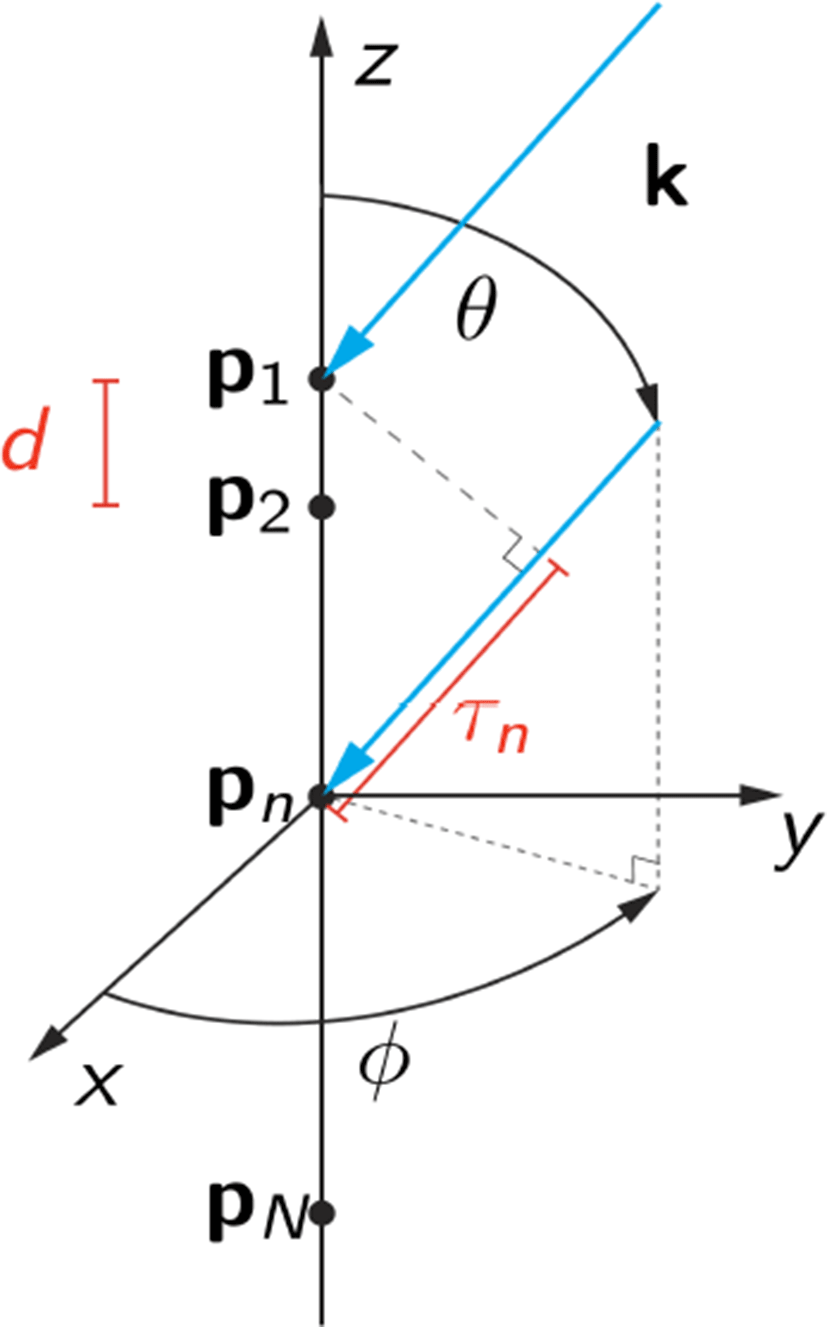
송·수신기의 거리가 충분히 떨어져 있는 원거리장 (far-field)에서의 안테나 동작 특성을 고려하면, 수신기에 전달되는 신호는 동일한 크기와 위상을 갖는 평면파로 근사화하여 나타낼 수 있다. 그림 3에 나타낸 바와 같이, 평면파의 진행 방향은 벡터 k∈ℝ³로 주어지며, 다음과 같이 표현할 수 있다^[2].

k = 2 π λ a (θ, ϕ) = ω c a (θ, ϕ) = ω c [sin θ cos ϕ sin θ sin ϕ cos θ]

(6)

그림 3. | Fig. 3. 균일 선형 배열 안테나 기반 좌표 시스템 | Coordinate system with a ULA.

Download Original Figure

식 (6)에서 λ는 파장, ω는 동작 주파수, 그리고 (θ,ϕ)는 수직 입사각 및 수평 입사각을 나타낸다. 그림 3에서 선형 배열 안테나는 z축 방향으로 균일한 간격 d마다 위치하며, 안테나 첨자값에 비례하여 위치 값이 증가한다고 가정하면, n번째 안테나의 공간 벡터 p_n은 다음과 같다.

p n = [0, 0 (n − 1) d] T

(7)

첫 번째 안테나를 기준으로, n번째 안테나의 전달 지연시간은 다음과 같이 정의할 수 있다.

τ n = a T (θ, ϕ) p n c = (n − 1) d c cos θ

(8)

따라서 송신기에서 복사된 신호는 평면파 모델을 이용하여 다음과 같이 표현할 수 있다.

x n [k] = X^e j (ω k T − k T p n) = X^e j ω k T e − j π (n − 1) cos θ

(9)

식 (9)에서 $X^$ 는 평면파의 크기를 나타내며 간단히 1로 가정한다. 식 (4), (9)를 참조하여, 수신 빔포밍 응답 신호는 가중치 벡터 w[k]와 전달 신호 x[k]의 내적을 통해 나타낸다.

w H [k] x [k] = e j ω k T ∑ n = 1 N w n * [k] e − j π (n − 1) cos θ

(10)

이때 식 (10)을 제곱하여 수신 빔 패턴을 다음과 같이 정의할 수 있다.

B (θ) = | ∑ n = 1 N w n * [k] e − j π (n − 1) cos θ | 2

(11)

식 (11)의 빔 패턴은 가중치 벡터 w[k]가 전달 지연시간 및 수신 각도를 적절히 보상하였을 경우 최대 빔포밍 이득을 나타낸다. 또한, 식 (11)은 정규화된 주파수 ω₀=(ω/c)dcosθ에서 가중치 벡터의 이산 푸리에 변환(DTFT: discrete time Fourier transform) 값으로 해석할 수 있으며, 빔포밍 설계 및 각도 기반의 방향 탐지 기술에서도 주로 사용하는 표현이다.

Ⅲ. 데이터-비의존적 빔포밍 기법

전달 신호의 통계적 특성 정보 및 채널 추정을 위한 파일럿 신호를 사용하지 않을 경우, 수신 빔포밍 설계 기법을 소개한다.

3-1 균일(Uniform) 빔포밍

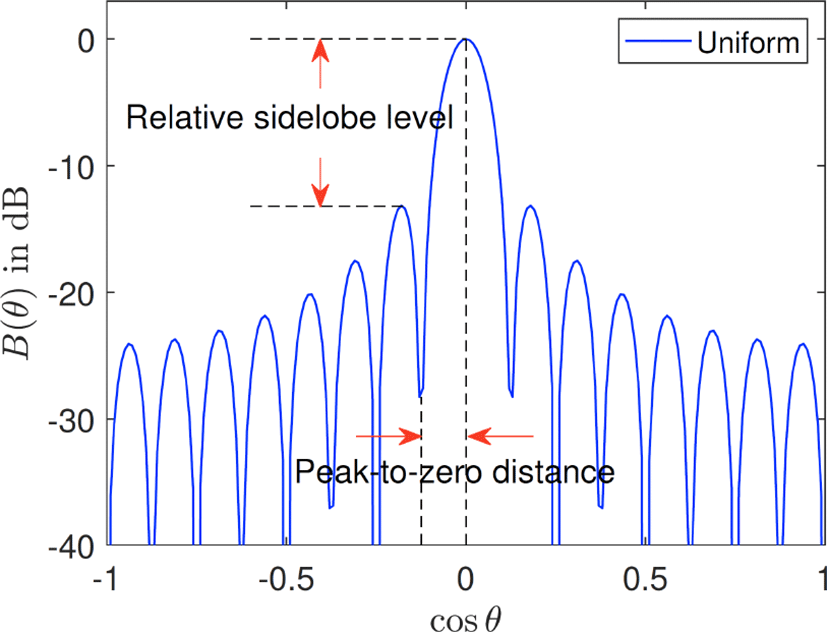
먼저 송신 신호가 특정 방향에서(예: θ=π/2) 발생하는 것을 고려한다. 이때 각 안테나에서 사용하는 가중치는 $w n = 1 / N$ 로 균일하게 주어진다(시간 존속성이 없을 경우, 첨자 [k]를 생략한다). 동작 특성으로는 정규화된 주파수 ω₀=0에서의 신호 성분은 통과시키고, 그 외 주파수 대역 신호 성분은 감쇠시킨다. 그림 4에 N=16 안테나 균일 빔포밍을 통해 얻은 빔 패턴을 나타냈다. 빔 패턴의 주엽(mainlobe) 방향에서 빔포밍 이득이 높게 나타나며, 주엽 방향에서 멀어질수록 빔 패턴의 부엽(sidelobe)에 의해 빔포밍 이득은 점차 감소한다. 이때 사용하는 빔 패턴 성능 측정 방법으로는 최대 빔포밍 이득 대비 일정 부분의 지향성을 보장하는 주 빔폭(main beamwidth)이 있으며, 주 빔폭이 작을수록 빔 지향성을 높일 수 있다. 또한, 주엽의 최대 이득 대비 부엽의 최대 빔포밍 이득의 비율인 상대적인 주엽 크기로 빔 패턴의 성능을 측정할 수 있으며, 비율이 높을수록 주엽 방향 외에서 발생하는 간섭 신호의 영향을 줄이게 된다. 그림 4의 경우, 상대적인 주엽 크기는 약 13 dB 차이가 발생한다.

그림 4. | Fig. 4. 공간 균일 빔포밍 기반 빔 패턴 | Beam pattern of spatial uniform beamforming.

Download Original Figure

3-2 Dolph-Chebyshev 빔포밍

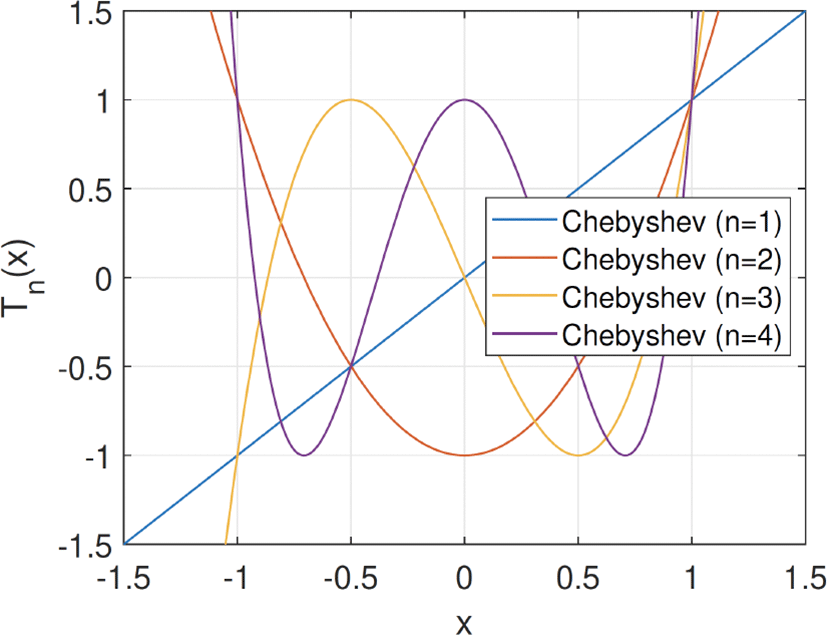
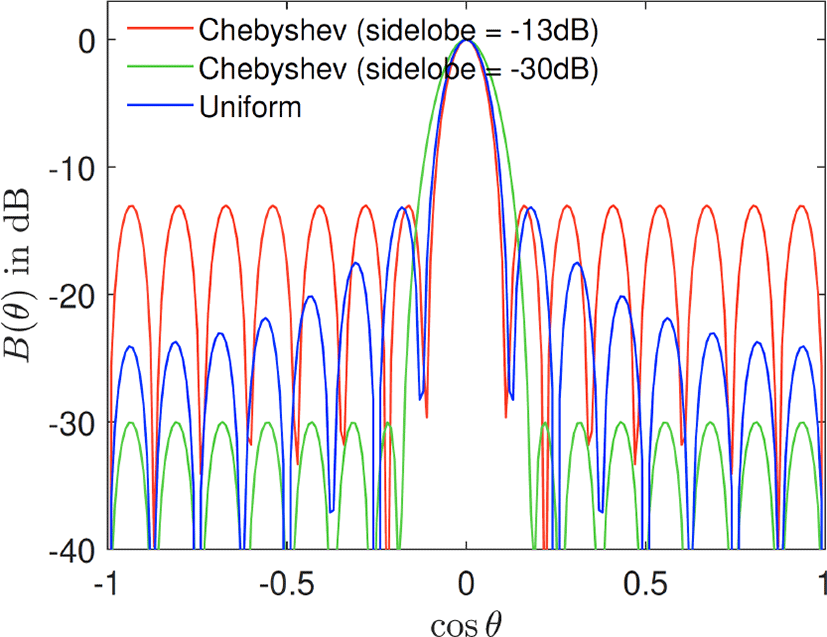
주어진 부엽의 빔포밍 이득 조건 내에서 주 빔폭을 최소화하는 빔포밍 설계 방법이다. 이때 Chebyshev 다항식을 사용하는데, 그림 5에 나타낸 예제를 보면 다항식의 공역이 [−1, 1] 구간일 때 최대값이 1로 제한되는 특징이 있다. 일정한 부엽 크기를 가지는 빔 패턴 설계에 활용하기 위해, 안테나 어레이 팩터(array factor) 표현을 코사인(cosine) 함수의 가중치 합으로 표현하고, 이를 Chebyshev 다항식과의 매칭을 통해 빔포밍 가중치 벡터를 설계한다^[3]. N=16 안테나 균일 빔포밍과 Dolph-Chebyshev 빔포밍의 빔 패턴을 그림 6에 나타냈다. Dolph-Chebyshev 빔포밍의 경우, 부엽 크기 조건(−13 dB, −30 dB)을 일정하게 만족하는 빔 패턴을 생성한다. 특히 −13 dB의 경우, Dolph-Chebyshev 빔포밍과 균일 빔포밍의 상대적인 부엽 크기는 같지만, Dolph-Chebyshev 빔의 주 빔폭이 좁아서 상대적으로 높은 빔 지향성을 확보하게 된다.

그림 5. | Fig. 5. Chebyshev 다항식 예시 | Example of Chebyshev polynomials.

Download Original Figure

그림 6. | Fig. 6. 빔 패턴 비교 | Comparison of beam patterns.

Download Original Figure

Ⅳ. 데이터-의존적 빔포밍 기법

수신부에서 전달 신호의 통계적 특성이나 채널 정보를 이용 가능할 때, 채널의 특성을 활용하는 빔포밍 설계 기법을 소개한다.

4-1 정상성(Stationary) 신호 기반 빔포밍

송·수신기 위치가 고정된 통신 환경에서 채널 및 잡음의 통계적인 특성이 느리게 변하는 경우, 잡음 공분산(covariance) 행렬 및 목적 신호의 입사각 정보를 활용하여 목적 신호의 증폭 및 간섭 신호의 영향을 최소화하는 빔포밍을 설계할 수 있다.

식 (4)에서, 빔포밍 후 출력 신호의 전력은 다음과 같이 나타낸다.

E {| z [k] | 2} = w H E {y H [k]} w = w H R y w

(12)

이에 잡음 및 간섭 신호의 영향을 최소화하는 빔포밍 설계는 식 (12)의 출력 신호 전력을 최소화하는 문제로 접근할 수 있다. 또한, 목적 신호의 입사각 θ₀ 및 간섭 신호의 입사각 ${θ 1, ⋯, θ N c − 1}$ 정보를 이용할 경우, 원하는 빔포밍 이득 조건을 갖도록 제한 조건으로 수식화한다.

C H w = f

(13)

C = [u N (θ 0), u N (θ 1), ⋯, u N (θ N c − 1)] f = [1, 0, ⋯, 0] T u N (θ) = [1, e j 2 π d λ, ⋯, e j 2 π d λ (N − 1) θ] T

(14)

해당 문제는 표 1에 나타낸 LCMV(linearly constrained minimum variance) 빔포밍 설계 기법이며^[4],[5], 라그랑주 승수법(Lagrange multiplier)을 사용하여 주어진 제한 조건을 만족하는 최적의 빔포밍 설계를 얻게 된다.

표 1. | Table 1. 정상성 신호에 대한 빔포밍 기법 | Data-dependent beamformers for stationary signals.

	LCMV beamforming	GSC beamforming
Objective function	min_ww^HR_yw	min_a (w₀+Ba)^HR_y(w₀+Ba)
Objective function	subject to C^Hw=f	min_a (w₀+Ba)^HR_y(w₀+Ba)
Design method	$w o p t = R y − 1 C (C H R y − 1 C) − 1 f$	$w o p t = w 0 + B a o p t = C (C H C) − 1 f − B R y B − 1 p y B = B H y$

Download Excel Table

LCMV 빔포밍의 다른 구현 방법으로, 조건 행렬 C의 열공간(column space) 및 영공간(nullspace)에서 각각 구한 빔포밍 벡터의 합으로 설계할 수 있다. 해당 문제는 표 1에 나타낸 GSC(generalized sidelobe canceller) 기반 빔포밍 기법이며, 조건 행렬 C의 의사역행렬(pseudo inverse) 연산을 통해 고정 벡터 w₀와 C^HB=0 조건을 만족하는 블록 행렬 B를 구한 후, 가중치 벡터 a를 찾는 최적화 문제를 통해 빔포밍 벡터를 얻게 된다. 그 외 빔포밍 설계 조건 및 통신 환경에 맞추어 다양한 최적화 기법이 적용 가능하다^[6].

4-2 비정상성(Non-Stationary) 신호 기반 빔포밍

이동 사용자 환경에서 통신 성능을 열화시키는 채널 특성 및 잡음은 정상성인 경우보다는 시간에 따라 통계적인 특성이 바뀌는 비정상성인 경우를 고려할 수 있다. 즉, 비정상성 잡음의 크기 및 주파수 응답이 일정 시간이 지나게 되면 바뀌게 된다. 따라서 신호의 통계적 특성 검출 성능이 현저하게 떨어질 수 있다. 또한, 정상성 신호의 경우에도 통계적인 특성 정보를 얻기 어려운 경우에는 기존 빔포밍 설계 기법의 성능 열화가 존재한다.

이에 빔포밍을 통해 얻고자 하는 목적은 신호 d[k]와 통계적(stochastic) 출력 신호와의 자승 오차를 최소화하는 문제를 고려하여 다음과 같이 목적 함수를 정의한다.

J [k] = E {| d [k] − w H [k] y [k] | 2}

(15)

식 (15)에서의 목적 신호 d[k]는 훈련 신호를 통해 수신기에서 획득할 수 있다. 이때 다음 단계의 빔포밍 벡터는 기본적으로 현재 빔포밍 벡터 w[k]에 목적 함수의 기울기(gradient)를 ∇J[k] 반대 방향으로 스텝 크기 μ만큼 더하여 갱신하게 된다^[7].

∇ J [k] = R u w [k] − p

(16)

w [k + 1] = w [k] − μ ∇ J [k]

(17)

식 (16)에서 필요한 공분산 행렬 및 기대값은 비정상성 신호의 특성을 고려하여 다음과 같이 근사화하여 얻을 수 있다.

p = E {d * [k] y [k]} ⇒ p^= d * [k] y [k] R y = E {y [k] y H [k]} ⇒ R^y = y [k] y H [k]

(18)

해당 문제는 표 2에 나타낸 LMS(least mean square) 기반 빔포밍 설계 기법이다^[8],[9]. LMS 빔포밍 기법은 비교적 낮은 연산 복잡도를 갖는 장점이 있으나, 공분산 행렬의 고유값(eigenvalue) 분포 및 스텝 크기 μ에 따라 알고리즘의 안정성 및 수렴 속도에 영향을 받는다.

표 2. | Table 2. 비정상성 신호에 대한 빔포밍 기법 | Data-dependent beamformers for non-stationary signals.

	LMS-based beamforming	RLS-based beamforming
Objective function	$J [k] = E {\| d [k] − w H [k] y [k] \| 2}$	$J [k] = ∑ ν = 0 k β v \| d [k − ν] − w H [k − ν] y [k − ν] \| 2$
Design method	$w [k + 1] = w [k] + μ (d [k] − w H [k] y [k]) * y [k] w [0] = 0$	$w [k + 1] = w [k] + R y − 1 [k] y [k] (d [k] − w H [k] y [k]) * w [0] = 0$
Complexity	O(N)	O(N²)
Operation property	The LMS-based algorithm minimizes the weighted sum of the squared error for stochastic signals. The speed of convergence of the LMS-based algorithm depends on the step-size and the eigenvalue spread of R_y(0 < μ < 2/λ_max, λ_max denotes the largest eigenvalue of R_y)	The RLS-based algorithm minimizes the weighted sum of the squared error for deterministic signals. The speed of convergence of the RLS-based algorithm does not depend on the condition number of R_y, which leads to, in general, an order of magnitude faster than that of the LMS-based algorithm.

Download Excel Table

다른 접근방법으로, 목적 신호와 결정적(deterministic) 출력 신호와의 가중치 자승 오차를 최소화하는 문제로 접근할 수 있다. 망각 인자 β∈[0,1]를 통해 현재와 과거에 얻은 오차값에 다른 가중치를 고려한 빔포밍 설계가 가능하다. 다음 단계의 빔포밍 벡터의 갱신을 위해 필요한 공분산 행렬과 기대값은 다음과 같이 재귀적인 연산을 통해 얻을 수 있다^[9]～[11].

R y [k] = ∑ ν = 0 k β ν y [k − ν] y H [k − ν] = β R y [k − 1] + y [k] y H [k] p [k] = ∑ ν = 0 k β ν d * [k − ν] y H [k − ν] = β p [k − 1] + d * [k] y [k]

(19)

해당 문제는 표 2에 나타낸 RLS(recursive least square) 기반 빔포밍 설계 기법이며, 연산 복잡도를 낮추기 위해 공분산의 역행렬 연산도 재귀적으로 얻을 수 있다.

S [k] : = R y − 1 [k] = 1 β (S [k − 1] − G [k] y [k] y H [k] S [k − 1]) G [k] = S [k − 1] / [β + y H [k] S [k − 1] y [k]]

(20)

최종적으로 상기 식 표현을 $w [k + 1] = R y − 1 w [k]$ 에 대입하여 표 2에 나타낸 빔포밍 설계를 얻게 된다. 표 2는 LMS 및 RLS 기반 알고리즘의 연산 복잡도 및 동작 특징을 요약하여 나타낸다^{[4],[12],[13]}. RLS 빔포밍 기법은 LMS 기법에 비해 연산 복잡도를 다소 늘어나지만, 수렴 속도가 증가하게 된다.

또한, 4-1에서 소개한 LCMV 빔포밍 기법도 비정상성 신호에 대해 확장이 가능하다^[5]. 식 (18)의 근사화된 공분산 행렬을 이용한 빔포밍 갱신 방법은 다음과 같다.

w [k + 1] = ω 0 + P (w [k] − μ R y^w [k]) = w 0 + P (w [k] − μ z [k] * y [k]) P = I − C (C H C) − 1 C H

(21)

이떄 알고리즘 초기 빔포밍 벡터 w[0]는 표 1에 나타낸 GSC 빔포밍의 고정백터 w₀로 다음과 같이 설정하며 (w[0]=w₀=C(C^H C)⁻¹f), 이는 적응적 간섭 신호 빔포밍 설계 기법(adaptive interference canceler)과 동일하다^[9],[14].

Ⅴ. 다중 안테나 시스템 기반 빔포밍 기법

다수의 송·수신기 안테나 사용을 고려하는 다중 입출력 안테나 시스템 기반 빔포밍 설계 기법을 소개한다. MIMO 빔포밍 기술은 주로 공간 다중화(spatial multiplexing), 공간 다이버시티(spatial diversity) 및 안테나 이득의 극대화를 통해 전송률 및 비트 오류 성능을 향상하고자 한다. 이론적으로 MIMO 기술은 송·수신기 안테나 수 중 작은 값에 선형적으로 비례하는 채널 용량을 제공한다.

먼저, (N_t,N_r)개의 송·수신 안테나를 고려한 시스템 식 표현은 다음과 같다.

y = H x + n, for H ∈ ℂ N r × N t

(22)

식 (22)에서 채널 행렬 H는 다중 경로 전파와 페이딩 현상을 모델링한다. 수신기 주변에서 반사, 굴절 산란이 충분히 일어나는 이상적인 상황에서는(rich scattering) 동일한 독립 가우시안 확률 분포(i.i.d: independent and identically distributed)를 따르는 분석적 채널로 모델링된다.

H ∼ C N (0, ∑)

(23)

식 (23)에서 Σ는 채널 공분산 행렬을 나타낸다. 또한 가시채널(LoS: line-of-sight) 및 우세한 채널 경로가 존재하는 경우(sparse scattering), 송·수신기 안테나 간 높은 상관성을 가지는 물리적 채널로 모델링된다.

H = ∑ ℓ = 1 L α ℓ u N r (θ r, ℓ) u N t H (θ t, ℓ)

(24)

식 (24)에서 α_ℓ과 (θ_t,ℓ, θ_r,l)은 ℓ번째 전달 경로의 이득 및 출발각/도착각을 나타낸다.

5-1 고유(Eigen)-빔포밍

수신기에서 얻은 피드백 받은 채널 정보를 바탕으로 송신기에 전체 혹은 부분적인 채널 정보를 사용한 폐루프(closed-loop) MIMO 시스템을 고려한다.

이때 채널 용량을 최대화하는 빔포밍 설계 기법은 전체 채널 행렬의 특이값 분해(SVD: singular value decomposition)를 통해 얻게 된다^[15],[16].

H = U Λ V H

(25)

식 (25)에서, U와 V는 좌측 및 우측 특이행렬을 나타내며, 유니타리(unitary) 행렬이다. 이때, 송신 빔포밍 행렬은 W_tx=V 로 주어지고, 수신 빔포밍 행렬은 $W rx H = U H$ 와 같이 얻어진다. 이를 통해 MIMO 전송 시 고유 빔포밍을 사용할 경우, 특이값(singular value) 수 만큼 간섭이 없는 스칼라 가우시안 채널로 분리한다.

y ¯ = U H y = U H (H (V x ¯) + n) = Λ x ¯ + n ¯

(26)

이를 단일 입출력 안테나(SISO: single-input single-output) 시스템과 비교해 보면, 분리된 스칼라 채널의 수 만큼 채널 용량 증가를 얻을 수 있는 장점이 있다. 추가로 MIMO 시스템 채널 용량을 최대화하기 위해 각각의 스칼라 채널에 Waterfilling기법을 사용하여 송신 전력을 적절히 분배하여야 한다.

5-2 LMMSE 빔포밍

수신기에서만 채널 정보에 접근이 가능한 개루프 (open-loop) MIMO 시스템에서, N_r>N_t인 경우, 수신 빔포밍 기법과 유사하게 동작하는 선형 신호 검출 기법을 고려한다.

표 3은 송신 신호 검출을 위한 대표적인 MIMO 수신 신호처리 기법을 요약하여 나타낸다^[17]. 다중 송신 신호를 검출하는 최적의 방법은 최대 우도비 ML 수신기를 사용하는 것이다. 그러나 다중 스트림 전송의 수와 신호 성상도(constellation)에 의해 전달되는 신호 수 N_m이 증가할 경우, 최대 우도비 수신기의 연산 복잡도는 지수적으로 증가한다 $O (N m N t)$ .

표 3. | Table 3. 대표적인 MIMO 신호 검출 기법 | Overview of representative MIMO detectors.

		MIMO detector
Optimum		Maximum likelihood (ML), maximum a posteriori (MAP)
Suboptimum	Linear	Matched filtering (MF), zero-forcing (ZF), minimum mean square error (MMSE)
Suboptimum	Nonlinear	Successive interference cancellation (SIC), sphere decoding (SD), genetic algorithm (GA), semidefinite programming relaxation (SDPR) etc.

Download Excel Table

이에 낮은 복잡도를 가지는 선형 빔포밍 설계 기법은 다음과 같이 최적화 문제를 통해 접근할 수 있다.

min W E {‖ x − x^‖ 2} subject to x^= W H y

(27)

식 (27)을 최적화 문제를 통해 얻은 선형 빔포밍 행렬은 다음과 같다.

W M M S E H = H H (H H + σ 2 I N t) − 1 = (H H H + σ 2 I N t) − 1 H H

(28)

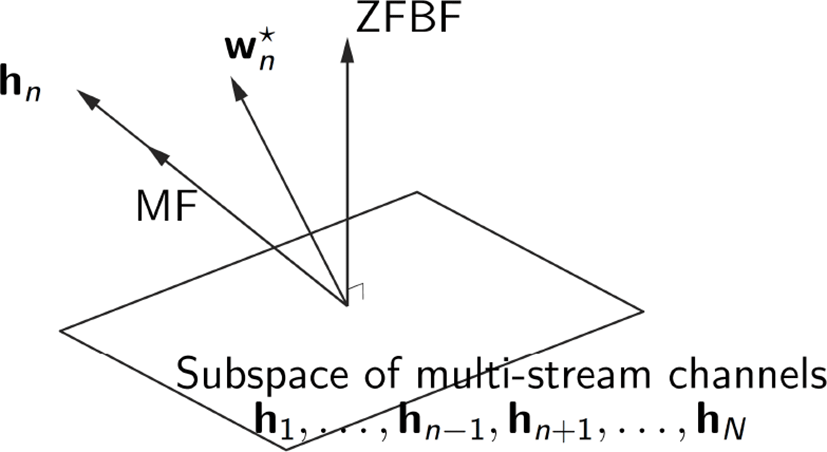
식 (28)의 빔포밍은 수신 신호의 공분산 행렬 정보를 이용하여 간섭 신호를 화이트닝(whitening)한 후 정합 필터(MF: matched filtering) 연산을 수행한다. 그림 7에 나타낸 바와 같이^[18], MMSE 빔포밍은 수신 신호의 증폭(MF)과 간섭 신호의 최소화(ZF: zero-forcing) 사이에 균형을 찾는 설계 기법이다. 이를 위해서 해당 신호에 대한 정보뿐만 아니라, 간섭 신호에 대한 채널 정보도 필요로 한다. 낮은 신호 대 잡음비 영역에서 최적으로 동작하는 MF 빔포밍의 연산 복잡도는 비교적 낮은 O(N_r N_t)이다. 높은 신호대 잡음비 영역에서 최적으로 동작하는 ZF/MMSE 빔포밍은 역행렬 연산으로 인해 $O (N r N t + N r N t 2 + N t 3)$ 의 높은 연산 복잡도를 필요로 한다^[19].

그림 7. | Fig. 7. 선형 MMSE 빔포밍 예시 | Illustration of linear MMSE beamforming

Download Original Figure

Ⅵ. 대규모 안테나 시스템 기반 빔포밍 기법

대규모 안테나 시스템에서는 주로 다수의 안테나 N을 가진 기지국이 보다 적은 다수의 사용자를 지원하는 상황을 가정한다. 단일 안테나 사용자를 가정했을 때, 기지국과 i번째 사용자와의 채널은 벡터 h_i∈ℂ^N로 나타낼 수 있다. 안테나마다 겪게 되는 채널 특성이 독립적인 이상적인 환경을 가정했을 때 여러 사용자의 내적은 다음과 같은 관계를 만족한다^[20],[21].

lim x → ∞ 1 N h m H h n = {1, if m=n 0, if m ≠ n

(29)

식 (29)에 대한 이론적인 이유로는 각 채널 벡터가 평균이 0인 독립적인 확률 변수들로 모델링되었을 때, 이를 내적한 결과는 큰 수의 법칙(law of large numbers)에 따라 기대값에 수렴하게 된다. 즉, 안테나 수가 증가함에 따라 다른 채널 간에 점근적으로 직교성을 가지게 된다. 이러한 대규모 다중 안테나 시스템의 특징은 간단한 선형 빔포밍을 사용하여 다중 사용자 데이터 전송 시 발생하는 간섭 신호를 제거하는데 적용될 수 있다.

그림 8은 상향링크 데이터 전송 경우를 나타내며, 식 표현은 다음과 같다.

[x^1 x^2] = W rx H [h 1 h 2] [x 1 x 2] + [n 1 n 2] W rx = [h^1 h^2]

(30)

그림 8. | Fig. 8. 대규모 다중 입출력 안테나 시스템 기반 상향링크 빔포밍 | Matched filter beamforming for uplink massive MIMO.

Download Original Figure

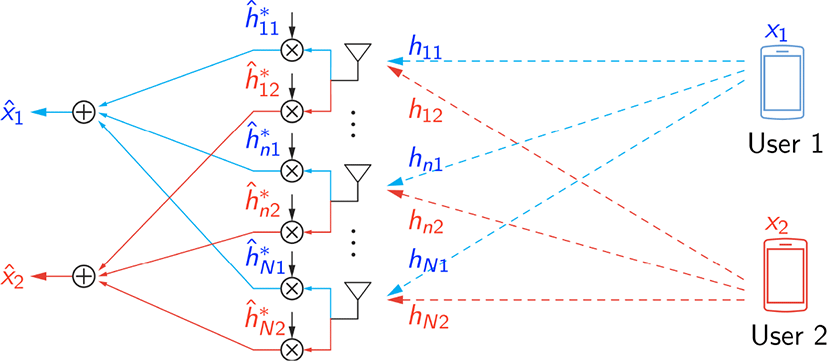
이때 기지국은 추정된 채널 벡터를 사용하여 정합 필터 기반 수신 빔포밍을 수행하고, 식 (29) 관계를 이용하면 사용자 간 간섭 신호와 잡음 신호는 0으로 수렴하게 된다. 따라서 다중 사용자 간 간섭이 없는 단일 스트림 전송 환경으로 동작하게 된다.

그림 9는 하향링크 데이터 전송 경우를 나타내며, 이때 식 표현은 다음과 같이 나타낸다.

그림 9. | Fig. 9. 대규모 다중 입출력 안테나 시스템 기반 하향링크 빔포밍 | Conjugate beamforming for downlink massive MIMO.

Download Original Figure

[x^1 x^2] = [h 1 T h 2 T] W tx [x 1 x 2] + [n 1 n 2] W tx = [h^1 * h^2 *]

(31)

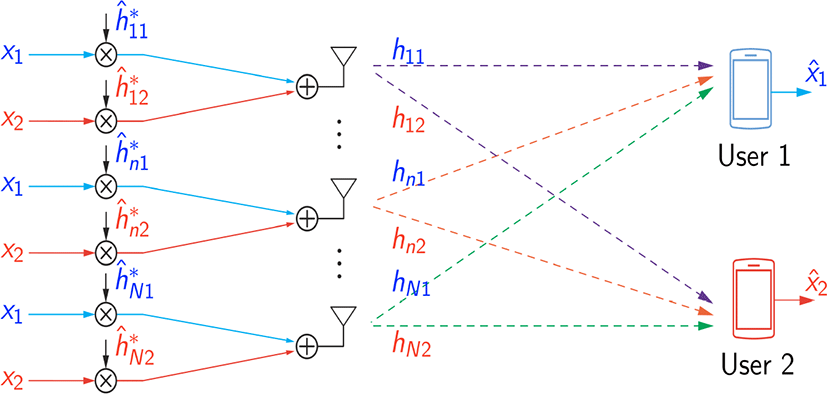
기지국은 상향링크 전송과 동일하게 추정된 채널벡터를 사용하여 송신 빔포밍을 수행한다. 간단한 정합 필터 기반 빔포밍을 통해 이론적으로 사용자 간 간섭 신호의 점근적인 제거가 가능하여, 수신 신호의 전력은 기지국 안테나 수에 따라 선형적으로 증가하게 된다. 해당 빔포밍 구현을 위해서는 안테나마다 RF(radio frequency) 체인을 구성하여 빔포밍 가중치의 크기 및 위상 신호 조절이 가능한 전디지털 빔포밍 시스템이 필요하다.

이에 송·수신기 구현 복잡도를 낮추기 위해 안테나의 수보다 적은 수의 RF체인을 사용하는 하이브리드 빔포밍 시스템의 연구도 진행되고 있으며^[22], 빔포밍 구조는 다음과 같이 위상 제어만 가능한 아날로그 빔포밍 W_analog와 위상 및 크기 제어가 가능한 디지털 빔포밍 W_digital 두 단계로 구성된다.

W = W anal o g W digital

(32)

그림 10에 나타낸 하이브리드 빔포밍 시스템의 빔포밍 표현은 다음과 같다.

그림 10. | Fig. 10. 하이브리드 빔포밍 시스템 예시 | Illustration of hybrid beamfoming systems.

Download Original Figure

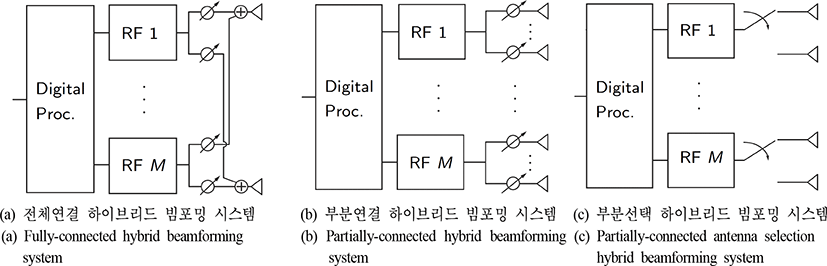
(a) 전체연결 하이브리드 빔포밍 시스템

W ana log = [w 1, ⋯, w M] w m ∈ ℂ N, | w m (n) | = 1 / N

(b) 부분연결 하이브리드 빔포밍 시스템

W analog = [w ¯ 1 ⋱ w ¯ M] where w ¯ m ∈ ℂ N M | w ¯ m (n) | = N / M

W ana log = [e 1 ⋱ e M] where e m ∈ ℂ N M e m (n) ∈ {0, 1}, ‖ e m ‖ = 1

따라서 하이브리드 빔포밍 설계 시, 아날로그 빔포밍 행렬 W_analog의 요소 크기가 고정되어 있고, 위상 제어만 가능한 점이 최적화 문제의 제한 조건으로 포함되어야 한다^[23].

최근에는 초 다수 안테나를 활용한 통신 시스템 분석 및 빔포밍 기술이 활발히 연구되고 있다^[24]. 제한된 영역에 초 다수의 안테나를 설치할 경우, 연속된 안테나로 근사화된 개구면(aperture)의 신호 송수신 과정은 광학 홀로그래픽 영상(optical holographic image) 신호의 수신 및 재형성 과정으로 모델링된다^[25],[26]. 이에 전파의 기록 및 재생을 위한 홀로그래픽 빔포밍 전송 기술이 연구되고 있다^[27]. 또한, 다수의 수동 반사 소자를 사용하여 메타물질 기반 지능형 반사 표면(IRS: intelligent reflecting surface) 시스템이 최근 제시되어, 위상 제어를 통한 정합(coherent) 빔포밍 기법 연구가 진행되고 있다^[28]～[30]. 나아가 넓은 영역에 초 다수의 안테나를 설치할 경우, 분산 안테나 시스템(DAS: distributed antenna system) 및 셀 경계가 없는 Cell-free massive MIMO 기반의 백홀 링크를 활용한 네트워크 및 분산 빔포밍 기술 연구가 필요할 것으로 판단한다^[31].

Ⅶ. 결론 및 연구 방향

본 논문에서는 5G 이동통신 시스템의 핵심 요소 기술 중 하나인 빔포밍 기술에 대해 소개하였다. 이론적인 배경 및 특징에 따라 빔포밍 기술을 분류하고, 핵심 원리 최신 응용까지 다루었다. 또한 빔포밍 기술은 6G 핵심 기술로 주목받고 있는 테라헤르츠 대역(THz) 통신 및 메타물질 기반 안테나 시스템의 실현을 위해 필요한 필수 기술이며, 나아가 초광대역에 적합한 빔포밍 알고리즘 설계, 송수신기 복잡도 문제를 효과적으로 해결하기 위한 연구가 필요하다.

Acknowledgements

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임 (NRF-2019R1G1A1009021, NRF-2020R1F1A1072761).

References

[1].

M. Giordani, M. Polese, A. Roy, D. Castor, and M. Zorzi, “A tutorial on beam management for 3GPP NR at mmWave frequencies,” IEEE Communications Surveys & Tutorials, vol. 21, no. 1, pp. 173-196, Firstquarter 2019.

[2].

3GPP, “Study on channel model for frequencies from 0.5 to 100 GHz,” TR 38.901, V16.1.0, Valbonne, France, Dec. 2019.

[3].

C. L. Dolph, “A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level,” in Proceedings of the IRE, Jun. 1946, vol. 34, no. 6, pp. 335-348.

[4].

W. Liu, S. Weiss, Wideband Beamforming: Concepts and Techniques, Hoboken, NJ, John Wiley & Sons, May 2010.

[5].

O. L. Frost, “An algorithm for linearly constrained adaptive array processing,” Proceedings of the IEEE, vol. 60, no. 8, pp. 926-935, Aug. 1972.

[6].

A. B. Gershman, N. D. Sidiropoulos, S. Shahbazpanahi, M. Bengtsson, and B. Ottersten, “Convex optimization-based beamforming,” IEEE Signal Processing Magazine, vol. 27, no. 3, pp. 62-75, May 2010.

[7].

P. J. Schreier, L. L. Scharf, Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals, Cambridge, Cambridge University Press, 2010.

[8].

B. Widrow, S. D. Stearns, Adaptive Signal Processing, Englewood Cliffs, NJ, Prentice-Hall, 1985.

[9].

J. Bourgeois, W. Minker, Time-Domain Beamforming and Blind Source Separation, New York, NY, Springer, 2009.

[10].

S. S. Haykin, Adaptive Filter Theory, Englewood Cliffs, NJ, Prentice Hall, 1996.

[11].

M. G. Bellanger, Adaptive Digital Filters and Signal Analysis, New York, NY, Marcel Dekker, 1987.

[12].

B. D. Van Veen, K. M. Buckely, “Beamforming: A versatile approach to spatial filtering,” IEEE ASSP Magazine, vol. 5, no. 2, pp. 4-24, Apr. 1988.

[13].

J. Benesty, Y. Huang, Adaptive Signal Processing: Applications to Real-World Problems, London, Springer, 2003.

[14].

X. Guo, L. Chu, and L. I. Baocang, “Robust adaptive LCMV beamformer based on an interative suboptimal solution,” Radioengineering, vol. 24, no. 2, pp. 572-582, Jun. 2015.

[15].

D. Tse, P. Viswanath, Fundamentals of Wireless Communication, Cambridge, Cambridge University Press, 2005.

[16].

M. Vu, A. Paulraj, “MIMO wireless linear precoding,” IEEE Signal Processing Magazine, vol. 24, no. 5, pp. 86-105, Sep. 2007.

[17].

S. Yang, L. Hanzo, “Fifty years of MIMO detection: The road to large-scale MIMOs,” IEEE Communications Surveys & Tutorials, vol. 17, no. 4, pp. 1941-1988, Fourthquarter 2015.

[18].

E. Björnson, M. Bengtsson, and B. Ottersten, “Optimal multiuser transmit beamforming: A difficult problem with a simple solution structure,” IEEE Signal Processing Magazine, vol. 31, no. 4, pp. 142-148, Jul. 2014.

[19].

F. Rusek, D. Persson, B. K. Lau, E. G. Larsson, T. L. Marzetta, and O. Edfors, et al., “Scaling up MIMO: Opportunities and challenges with very large arrays,” IEEE Signal Processing Magazine, vol. 30, no. 1, pp. 40-60, Jan. 2013.

[20].

T. L. Marzetta, “Noncooperative cellular wireless with unlimited numbers of base station antennas,” IEEE Transactions on Wireless Communications, vol. 9, no. 11, pp. 3590-3599, Nov. 2010.

[21].

H. Q. Ngo, E. G. Larsson, and T. L. Marzetta, “Aspects of favorable propagation in massive MIMO,” in 2014 22nd European Signal Processing Conference(EUSIPCO), Lisbon, Sep. 2014, pp. 76-80.

[22].

I. Ahmed, H. S. Khammari, A. Shahid, A. Musa, K. S. Kim, and E. De Poorter, et al., “A survey on hybrid beamforming techniques in 5G: Architecture and system model perspectives,” IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 3060-3097, Fourthquarter 2018.

[23].

T. Lin, J. Cong, Y. Zhu, J. Zhang, and K. B. Letaief, “Hybrid beamforming for millimeter wave systems using the MMSE criterion,” IEEE Transactions on Communications, vol. 67, no. 5, pp. 3693-3708, May 2019.

[24].

Samsung Research, “6G - the next hyper-connected experience for all,” White Paper, 2020.

[25].

A. Pizzo, T. L. Marzetta, and L. Sanguinetti, “Spatially-stationary model for holographic MIMO small-scale fading,” IEEE Journal on Selected Areas in Communications, to be published. doi:

[26].

C. Huang, S. Hu, G. C. Alexandropoulos, A. Zappone, C. Yuen, and R. Zhang, et al., “Holographic MIMO surfaces for 6G wireless networks: Opportunities, challenges, and trends,” IEEE Wireless Communications, to be published. doi:

[27].

W. Saad, M. Bennis, and M. Chen, “A vision of 6G wireless systems: Applications, trends, technologies, and open research problems,” IEEE Network, vol. 34, no. 3, pp. 134-142, May/June 2020.

[28].

S. Gong, X. Lu, D. T. Hoang, D. Niyato, L. Shu, and D. I. Kim, et al., “Towards smart wireless communications via intelligent reflecting surfaces: A contemporary survey,” IEEE Communications Surveys & Tutorials, to be published. doi:

[29].

C. Liaskos, S. Nie, A. Tsioliaridou, A. Pitsillides, S. Ioannidis, and I. Akyildiz, “Realizing wireless communication through software-defined hypersurface environments,” in 2018 IEEE 19th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Chania, Jun. 2018, pp. 14-15.

[30].

Q. Wu, R. Zhang, “Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network,” IEEE Communications Magazine, vol. 58, no. 1, pp. 106-112, Jan. 2020.

[31].

E. Björnson, L. Sanguinetti, H. Wymeersch, J. Hoydis, and T. L. Marzetta, “Massive MIMO is a reality: What is next? Five promising research directions for antenna arrays,” Digital Signal Processing, vol. 94, pp. 3-20, Jun. 2019.

Author Information

노 송 [인천대학교/조교수]

jkiees-31-8-701-i1

https://orcid.org/0000-0002-0106-7106
2008년 2월: 숭실대학교 정보통신전자공학과 (공학사)
2010년 2월: 한국과학기술원 전기및전자공학과 (공학석사)
2015년 12월: 미국 Purdue University Electrical and Computer Engineering (공학박사)
2015년 12월～2018년 7월: 미국 Intel Corp. 시스템 엔지니어
2018년 9월～현재: 인천대학교 정보통신공학과 조교수
[주 관심분야] 신호처리, 무선통신 시스템, 스마트 시스템 설계

전 현 채 [인천대학교/조교수]

jkiees-31-8-701-i2

https://orcid.org/0000-0002-3907-4862
2006년 8월: 고려대학교 전자공학과 (공학사)
2009년 2월: 한국과학기술원 전기및전자공학과 (공학석사)
2011년 5월: LG전자 MC 사업본부 RF 리서치 엔지니어
2016년 1월: 영국 University of Oxford, Engineering Science (공학박사)
2018년 8월: University of Oxford 박사후연구원
2018년 9월～현재: 인천대학교 정보통신공학과 조교수
[주 관심분야] 무선 광통신 시스템, 신호처리, 양자암호통신