Ⅰ. 서 론
최근 몇 년 간, IR-UWB(Impulse Radio Ultra-wideband) 레이다 기술은 사람 계수(people counting), 이미징(imaging), 측위(positioning) 및 추적(tracking) 등의 분야에서 활발하게 연구되고 있다[1]~[8]. IR-UWB 레이다는 초광대역을 사용함으로써 높은 시간 해상도를 가지기에 정밀한 거리 측정이 가능하며, Gaussian 펄스를 송신하기에 낮은 사용률(duty cycle)과 전력 소모를 가진다. 또한 넓은 주파수 대역을 사용함으로써 레이다 환경의 변화에 적은 영향을 받으며 장애물을 투과하여 그 너머를 탐지하는 것에 유리하다.
IR-UWB 레이다의 장애물 투과 능력을 이용하여, 콘크리트나 벽돌 등으로 이루어진 벽 너머의 사람을 탐지하기 위한 많은 연구가 진행되어 왔다[9]~[14]. 특히 근래의 군사 작전이 도심에서 이루어지는 경우가 많은 군사 분야에서 많은 관심을 받고 있으며, 재해 상황의 인명 구조나 침입 탐지 등의 분야에서도 유용하게 쓰일 수 있다.
레이다를 이용하여 벽 너머의 사람을 탐지하는 방법은 크게 주파수 영역에서 호흡이나 움직임을 탐지하는 방법과 거리 영역에서 수신된 신호의 파형으로부터 탐지하는 방법이 존재한다. 주파수 영역에서 표적을 탐지하는 방법은 표적의 움직임이 매우 적거나 일정한 주파수로 움직이는 경우 유용하게 사용된다[15],[16]. 하지만 이 방법은 여러 표적이 동시에 존재하거나, 불규칙적으로 움직일 경우, 표적을 올바르게 탐지하기 어렵다. 거리 영역에서 표적을 탐지하는 방법은 일반적으로 수신된 레이다 신호로부터 MTI(Moving Target Indicator) 필터를 통하여 표적의 신호를 추출하고, CFAR(Constant False Alarm Rate) 알고리즘을 이용하여 표적을 탐지한다. 그러나 벽 투과 환경에서는 벽으로 인한 신호 감쇠 및 다중 경로 효과(multipath effect) 등으로 인하여 일반적인 환경에 비해 레이다 신호로부터 표적의 신호를 명확하게 추출하는 것이 쉽지 않다. 이러한 문제를 해결하기 위하여 다중 CFAR을 이용하여 가까운 거리의 표적을 탐지한 연구 또한 존재한다[17]. 그러나 이 방법은 CFAR을 변경하는 것만으로, 벽으로 인하여 왜곡된 레이다 신호로부터 다양한 상태의 표적을 추출하는 것에는 한계점이 존재한다.
본 연구에서는 IR-UWB 레이다 시스템을 이용하여 벽 너머의 표적들을 탐지하는 레이다 탐지 알고리즘을 제안한다. 벽 너머에서 멈춰 있거나, 천천히 혹은 빠르게 움직이는 표적의 신호를 올바르게 추출하기 위하여 표적의 상태에 따라 표적의 신호를 추출할 수 있는 다중 MTI 필터를 설계하고, 그에 적합한 CFAR 알고리즘 또한 적용한다. 이러한 다중 탐지기를 통하여 탐지된 결과들을 결합하고, 올바르게 탐지된 표적과 벽이나 클러터로 인한 오탐지의 신호 특성 차이를 기계 학습(machine learning) 기법을 이용하여 분류함으로써 높은 탐지율(detection rate)과 낮은 오탐율(false alarm rate)을 가질 수 있도록 설계하였다.
본 논문의 2장에서는 연구에 사용된 벽 투과 레이다 시스템에 대한 간략한 설명과 일반적인 레이다 시스템에서 사용되는 탐지 알고리즘에 대하여 설명하고, 3장에서 제안하는 탐지 알고리즘을 소개한다. 4장에서 실제 시험을 통한 성능 평가를 수행하고, 이에 대한 결론을 5장에서 다룬다.
Ⅱ. 벽 투과 레이다 시스템
본 연구에서 사용한 벽 투과 레이다 시스템은 이전에 진행했던 연구에서 개선된 것으로, 개인이 운반 및 운용이 가능하도록 크기와 무게를 경량화 한 것이다[18]. NOVELDA(Novelda AS, Kviteseid, Norway)에서 제작된 NVA6100 임펄스 기반 레이다 송수신 칩을 사용하였으며, 표 1에서 확인할 수 있듯이 저주파대의 Gaussian 펄스 생성기를 통하여 0.4~3.2 GHz 대역에서 동작한다. 그림 1에서와 같이 생성된 Gaussian 펄스는 필터와 증폭기를 통하여 벽 너머의 표적을 탐지하기 위한 적절한 전력을 얻는다. 전체 시스템의 유효 등방성 복사 전력(effective isotropic radiated power)과 잡음 지수(noise figure)는 각각 40 dBm과 6 dB이다.
| Parameter | Value |
|---|---|
| Central frequency | 1.8 GHz |
| Bandwidth | 2.8 GHz |
| Average transmission power | −14 dBm |
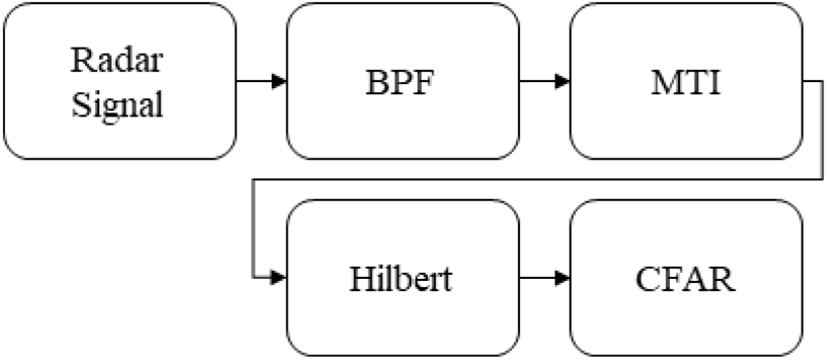
일반적으로 레이다 시스템에서 사용되는 탐지 알고리 즘의 구조는 그림 2와 같으며, 레이다 포착범위(radar coverage)의 상황을 인지하기 위하여 순차적으로 진행된다[18]. 레이다 시스템에서는 일반적으로 재귀적 MTI 필터를 이용하여 수신된 레이다 신호로부터 표적의 신호를 추출한다. 또한 CFAR 알고리즘을 이용한 표적 탐지를 수행하기 위하여 Hilbert 변환을 수행한다. 이러한 구조는 매우 단순하여 낮은 연산량을 가지지만, 벽 투과 등의 환경에서는 적합한 성능을 보여주기 어렵다.
레이다에서 수신된 신호는 식 (1)과 같이 표현할 수 있으며, s(t)는 레이다로부터 송신된 신호를 의미하고, n(t)는 채널 잡음을 뜻한다[19]. 레이다 신호의 거리를 나타내는 지표는 fast time index, 즉 t이며, 시간의 경과에 따른 레이다 신호는 slow time index, k로 나타낸다. 송수신 과정에서 발생한 감쇠와 지연은 각각 αki와 τki로 표현하고, N은 다중 경로 현상(multipath effect)을 의미한다.
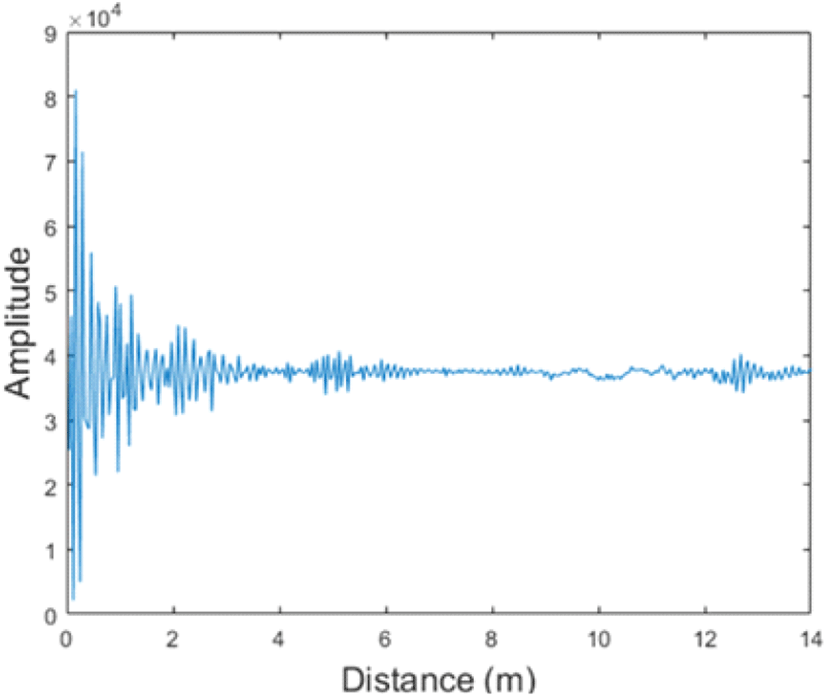
그림 3은 벽 너머에 다섯 명의 표적이 존재하는 상황에서 수신된 레이다 신호로, 이 신호에서 다섯 명의 표적을 구분하는 것은 쉽지 않다. 이러한 상황에서 레이다 신호로부터 표적의 신호를 추출하기 위하여 사용되는 것이 MTI 필터이다.
벽 투과 환경에서 레이다에 수신된 신호에서는 지면에 반사되거나 벽 내부의 다중 반사 혹은 장애물에서 반사된 클러터의 영향이 매우 크다. 일반적으로 사용되는 MTI 필터는 고역 필터(high pass filter)로 정지된 클러터의 신호를 차단하고, 움직임이 존재하는 표적의 신호를 통과시키는 구조로 이루어져 있다. 그림 4는 대표적인 재귀적 MTI 필터의 구조를 나타내며, 이 다이어그램으로부터 식 (2)와 식(3)을 도출할 수 있다[20].
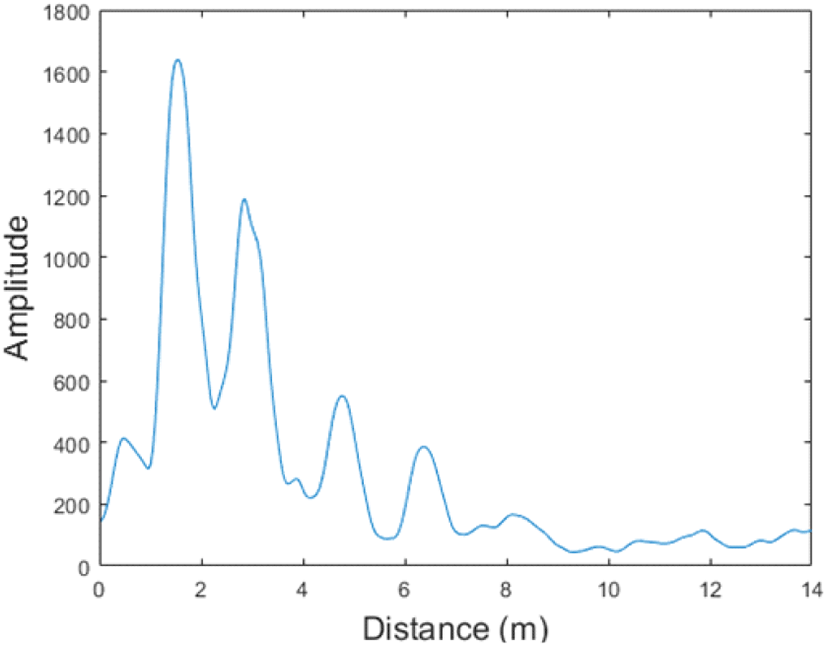
식 (2)의 ck(t)는 k번째 측정 신호에서의 추정된 클러터 신호이며, 이전 k−1번째의 클러터가 제거된 신호인 yk−1(t)와 ck−1(t)를 통하여 생성된다. MTI 필터의 주 파수 응답(frequency response)은 적용 변수인 α를 통하여 조절이 가능한데, 적용 변수의 값이 크다면 클러터가 제거된 신호의 신호 대 잡음비(Signal to Noise Ratio)가 높지만, 레이다 환경에 적합한 클러터 신호를 추정할 때까지 걸리는 시간이 늘어난다. 반대로 적용 변수의 값이 작다면 레이다 환경의 변화에 빠르게 대응하여 움직이는 표적의 신호를 추출할 수 있지만, 신호대 잡음비가 낮아져 CFAR을 이용한 표적 탐지에 어려움을 겪는다. 그림 5는 다섯 명의 표적이 존재하는 상황에서 클러터가 제거된 신호의 Hilbert 변환으로, 그림 3의 레이다 수신 신호와 비교하여 표적이 존재하는 거리를 보다 명확하게 확인할 수 있다. 그러나 8 m 부근에 존재하는 표적은 명확하게 식별하기 어려운데, 이는 표적에서 레이다까지의 거리와 벽으로 인한 영향으로 충분한 신호 대 잡음비를 얻지 못한 것이다.
수신된 레이다 신호로부터 클러터를 제거한 후, MTI 신호로부터 표적을 탐지한다. 레이다 포착범위가 완전히 비어있는 상태이고, 다중 경로 효과를 무시한다면, 채널 잡음만을 고려하여 표적을 탐지할 수 있다. 하지만 현실적으로 표적의 움직임이나 클러터 환경의 변화 등으로 인하여 레이다 환경과 다중 경로 환경이 변한다. 특히나 벽 투과 레이다 시스템에서는 벽으로 인한 감쇠 및 벽 내부의 다중 반사로 인하여 표적 식별이 쉽지 않다. 이러한 상황에서 CFAR은 레이다 신호의 통계적 특성에 따라 탐지 임계값(detection threshold)을 적응적으로 적용하여 일정 한 오탐율을 유지하는 기법으로, 레이다 시스템을 이용한 탐지에서 가장 대중적으로 사용되는 방법이다[21]. CFAR을 이용한 탐지는 일정한 크기의 윈도우를 슬라이드시키며, 윈도우 안에 존재하는 신호의 값들을 이용하여 탐지 임계값을 정한다. 그림 6은 CFAR 탐지 알고리즘의 구조를 나타낸 것으로, CUT의 값이 CFAR을 통하여 구한 임계값보다 크다면 표적이 존재하는 것으로 판단한다.
CFAR의 임계값을 정하는 방법은 여러 가지가 존재하며, 대표적인 것으로 CA(Cell Averaging)와 OS(Ordered Statistics)의 두 가지 방법이 있다. CA-CFAR은 윈도우 안에 존재하는 값들의 평균을 이용하여 임계값을 구하는 방법으로, 레이다 환경이 균일할 때, 좋은 성능을 보여준다. 반면, OS-CFAR은 윈도우 내부의 값들을 정렬(sort)한 다음 k번째 값으로 임계값을 구하는 방법으로, 클러터가 많거나 다중 표적을 탐지하는 환경에서의 성능에 이점을 가진다.
Ⅲ. 표적의 상태에 따른 탐지 알고리즘
본 연구에서는 다중 MTI 필터와 기계 학습을 이용하여 탐지율과 오탐율의 성능을 향상시키는 새로운 레이다 탐지 알고리즘을 제안한다. 제안하는 방법의 구조는 그림 7에 나타나 있으며, 각각의 MTI 필터는 멈춰있는 표적이나 움직이는 표적의 신호를 보다 높은 신호 대 잡음비로 추출할 수 있도록 설계되어 있다.
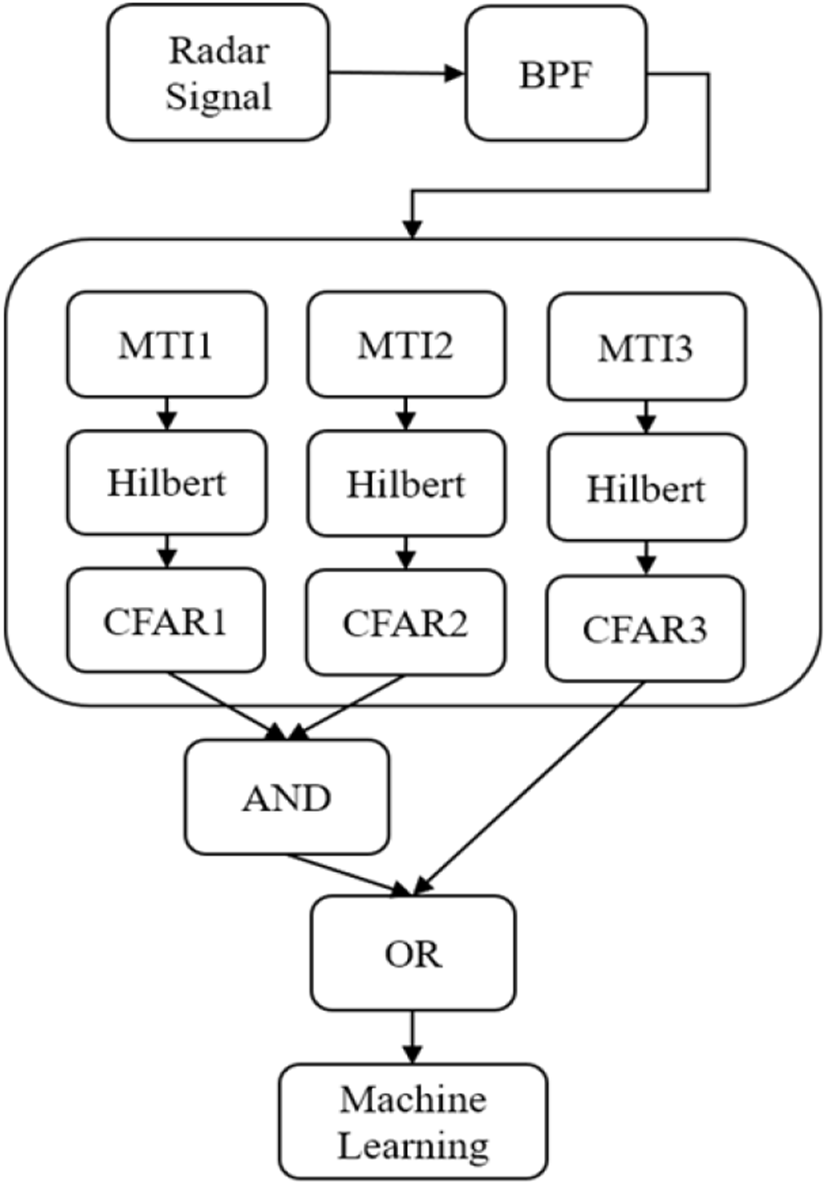
레이다 포착범위에 표적이 존재할 때, 레이다에서 수신된 신호로부터 표적의 신호를 추출해야 하는데, 표적의 움직임 상태에 따라 다중 MTI 필터를 적용함으로써 CFAR 단계에서의 탐지율과 오탐율을 개선할 수 있다. 다 중 MTI 필터는 3개의 MTI 필터로 구성되어 있는데, 첫 번째 MTI 1 필터는 앞서 설명한 가장 대표적인 재귀적 MTI 필터를 적용하여 보편적인 상황에 대응할 수 있도록 하였다.
제안하는 레이다 탐지 알고리즘의 두 번째 MTI 2 필터는 서 있는 표적의 신호를 추출하는데 적합하도록 설계되었다. 그림 8에서 확인할 수 있는 것처럼, 표적이 멈춰있을 때의 레이다 환경의 클러터 신호를 보다 효과적으로 추정하기 위하여 일반적으로 사용되는 재귀적 MTI 필터에 비하여 과거의 신호를 더 많이 반영한다. 이 과정을 식으로 표현하면 아래와 같이 정리할 수 있다.
마지막으로, 레이다 탐지 알고리즘의 세 번째 MTI 3 필터는 Chebyshev 필터를 사용하였으며, 그림 9에서 확인할 수 있다[22]. Chebyshev 필터는 세 개의 지연선(delay line)을 가진 필터로 보다 고주파 대역의 신호를 추출하도록 설계되었으며, 다음과 같은 수식으로 정리할 수 있다.
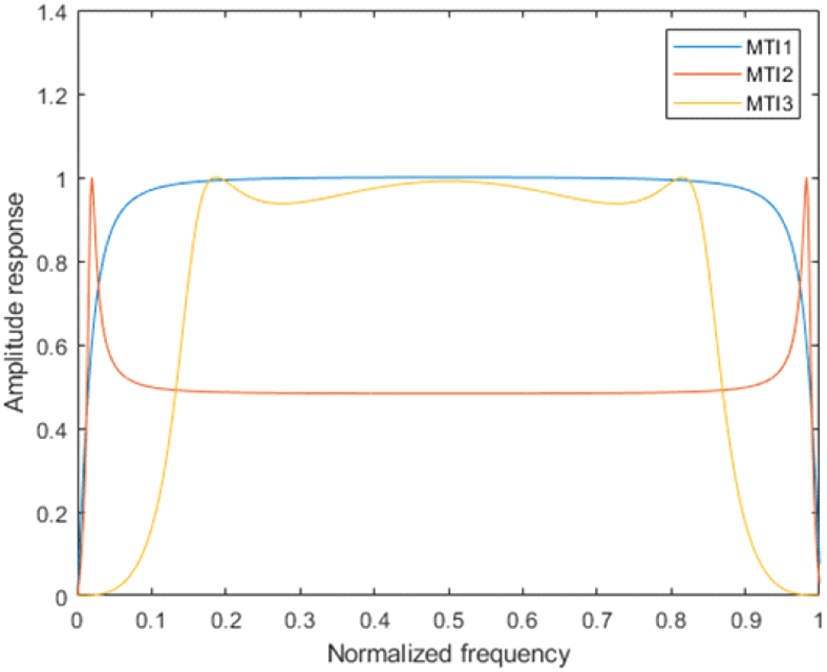
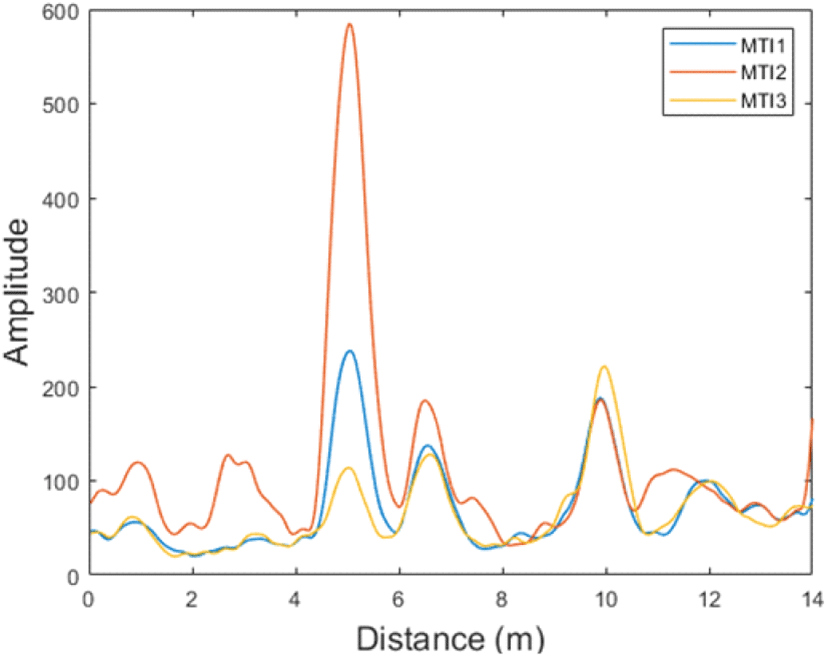
그림 10에서와 같이 다중 MTI 필터들의 주파수 응답은 각 필터의 목적에 맞도록 설계되었다. 일반적으로 레이다 신호에서 클러터로 인한 효과는 시간에 따라 크게 변동하지 않기에 저주파 대역에 대부분의 성분을 가지게 된다. 이와는 대조적으로, 표적은 움직임을 가지고 있기에 보다 높은 대역에 신호가 분포한다. MTI 1 필터는 주파수 응답에서 확인할 수 있듯이, 대부분의 움직임 신호를 추출할 수 있지만, 반대로 그렇기 때문에 높은 신호 대 잡음 비를 가지기 어렵다. MTI 2 필터의 경우, 매우 좁은 주파수 영역에서 동작하도록 설계되었는데, 움직임이 많은 경우에 대해서는 올바르게 동작하기 어렵지만, 표적이 멈춰있거나 움직임이 작은 경우에는 매우 높은 신호 대 잡음비로 표적의 신호를 추출할 수 있다. 마지막으로 MTI 3 필터는 다른 필터들에 비하여 고주파 대역의 신호를 추출하는데, 이는 움직임이 큰 표적을 효율적으로 탐지할 수 있도록 한다. 즉, MTI 2 필터와 MTI 3 필터는 각각 움직임이 적은 표적과 움직임이 많은 표적에 맞추어 동작하며, 이는 그림 11의 결과에서 확인할 수 있다. 그림 11은 약 5 m와 6.5 m에 표적이 서 있고, 약 10 m에서는 표적이 앞으로 움직이고 있는 상황에서의 각각의 MTI 필터들의 결과를 나타낸다. 결과에서 확인할 수 있듯이, 멈춰있는 표적에 대해서는 MTI 2 필터가 가장 명확한 결과를 보여주고, MTI 3 필터는 움직이는 표적에 대하여 좋은 결과를 보여준다. 특히, MTI 3 필터의 경우, 고주파 대역에서 동작하기에 다른 필터들에 비하여 높은 클러터 억제 능력을 가진다. MTI 1 필터는 멈춰있는 표적과 움직이는 표적에 대하여 범용적인 성능을 보여준다.
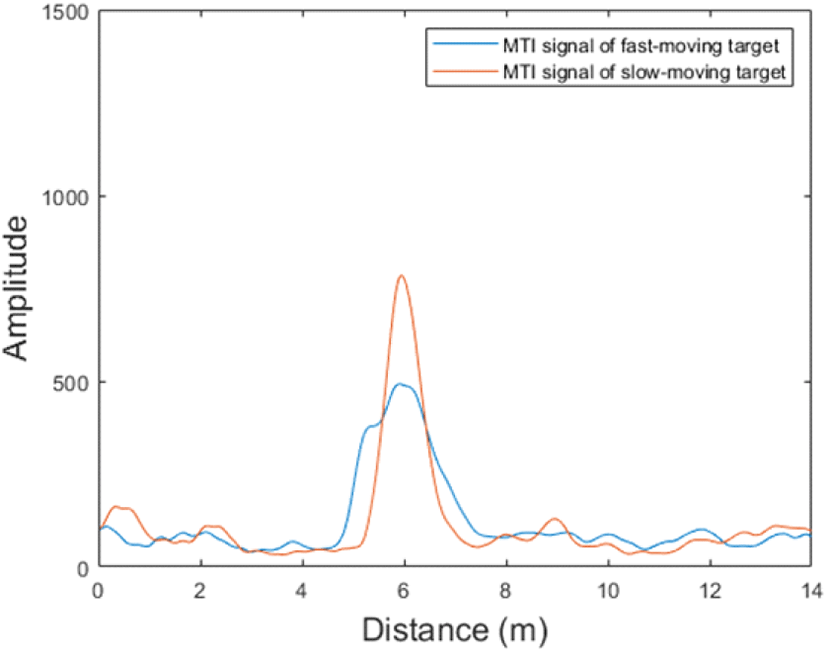
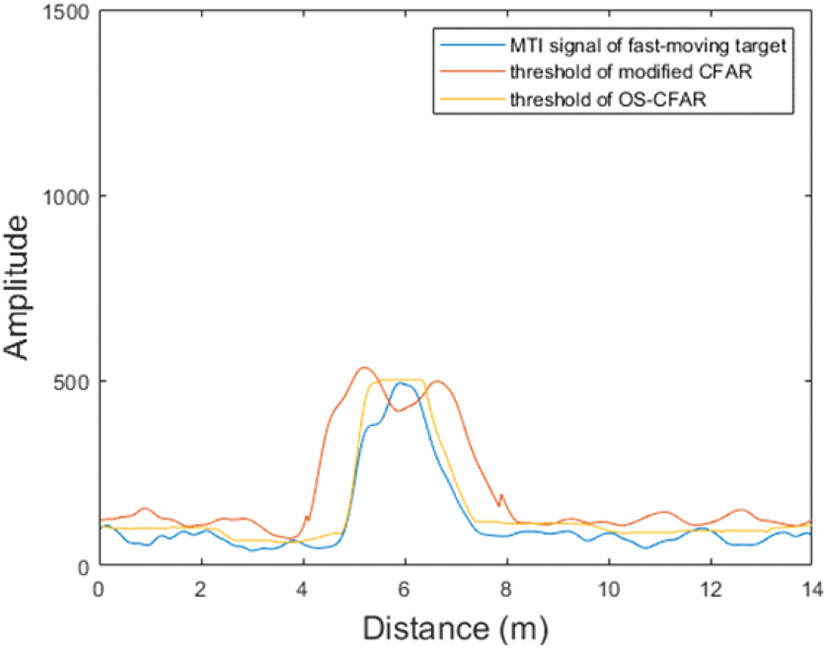
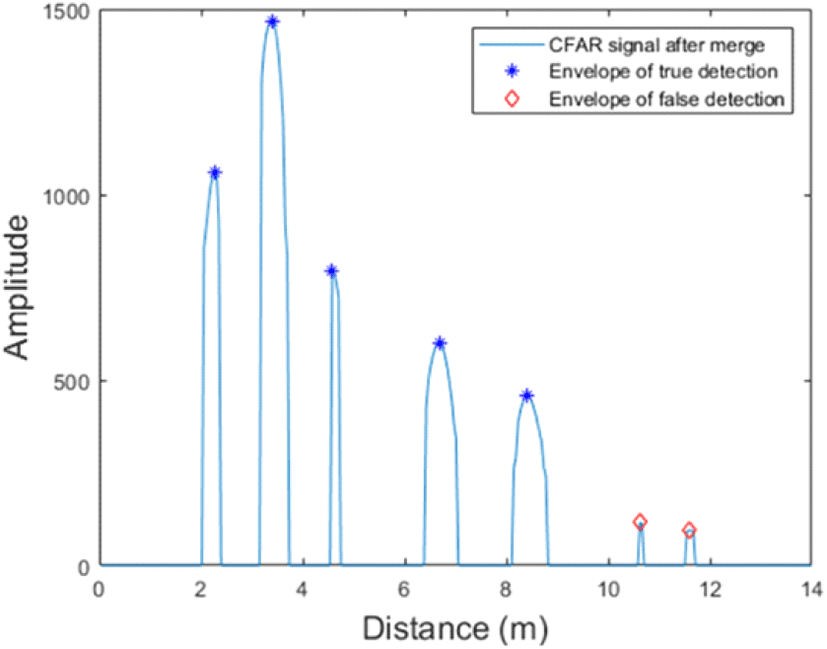
다중 MTI 필터를 이용하여 표적의 신호를 추출한 다음에는, 이 신호들로부터 표적이 존재하는지를 탐지해야 한다. 앞서 언급하였던 것처럼 OS-CFAR은 CA-CFAR에 비하여 클러터의 영향이 큰 환경이나 다중 표적을 탐지하는데 있어 이점을 가지는데, 벽 투과 레이다 시스템에서는 벽으로 인한 다중 반사 및 다중 경로 효과로 인한 영향이 크기 때문에 이러한 환경에서는 OS-CFAR이 보다 적합하다. 따라서 MTI 1 필터와 MTI 2 필터의 결과에는 OS-CFAR을 적용하였으며, 움직임이 큰 표적의 신호를 추출하기 위한 MTI 3 필터의 경우에는 새로운 방식으로 임계값을 구하도록 하였다. 그림 12에서와 같이 빠르게 움직이는 표적의 신호는 멈춰 있거나 천천히 움직이는 표적의 신호에 비하여 낮은 값을 가지며, 넓게 퍼지는 포락선(envelope)의 형태를 가지게 된다. 이는 신호에서 표적의 꼭짓점 근처의 표준 편차(standard deviation)는 낮은 값 을 가지고, 그 외의 표적 신호에서는 상대적으로 높은 값을 가진다는 것을 의미한다. 새로운 방식의 임계값은 이러한 표준 편차의 양상을 이용하여 동작하도록 설계되었으며, 기존의 OS-CFAR과의 비교는 그림 13에서 확인할 수 있다.
본 연구에서 제안하는 탐지 알고리즘은 그림 7의 다이어그램에서와 같이 세 종류의 탐지기와 그 결과들을 결합하는 형태로 이루어져 있다. 그림 14에서와 같이 각각의 MTI 필터와 그에 따른 CFAR을 통한 탐지 결과로부터 실제 표적의 존재 여부를 추정한다. 이 과정은 MTI 1 필터를 사용한 탐지기의 결과와 MTI 2 필터를 사용한 결과 를 AND 연산을 통하여 결합하고, 이를 다시 MTI 3 필터 를 사용한 탐지기의 결과와 OR 연산을 수행하는 것으로 이루어져 있다. AND 연산은 두 가지의 탐지기에서 동시에 표적을 탐지하였을 경우에만 표적이 존재하는 것으로 판단하는 것으로 멈춰있거나 움직임이 적은 표적에 대하여 높은 신뢰도를 가진 결과를 얻을 수 있다. 이러한 AND 연산을 통한 탐지율과 오탐율은 다음과 같이 나타낼 수 있다.
MTI 3 필터를 통한 탐지기의 결과는 AND 결합의 결과와 OR 연산을 수행한다. OR 연산을 사용함으로써 AND 결합에서 얻은 움직임이 적은 표적에 대한 탐지에 더하여 빠르게 움직이는 표적의 탐지를 보완할 수 있다. OR 결합의 탐지율과 오탐율은 MTI 3 필터가 적용된 탐지기와 AND 결합의 결과가 합쳐진 형태로 나타나며, 각각의 탐지기에서 동일한 위치에 오탐지가 일어나지 않는다면 아래와 같은 수식으로 정리할 수 있다.
표 2는 한 명의 표적이 빠르게 움직이는 시험 데이터에 제안하는 탐지 알고리즘을 적용하여 단계별로 출력된 탐지율과 오탐율을 정리한 것이다. 이 결과에서 앞서 언급한 탐지기 설계의 의도대로 MTI 3 필터를 사용하는 탐지 기가 다른 두 개의 탐지기에 비하여 큰 움직임을 가진 표적에 대하여 더욱 효과적으로 동작하는 것을 확인할 수 있다. 또한 AND 및 OR 연산을 이용한 결합을 통하여 보다 높은 탐지율을 얻을 수 있음을 알 수 있다. 그럼에도 불구하고, 다중 MTI 필터의 결과를 결합하는 과정에서 오탐율 또한 증가하는데, 이를 해결하기 위하여 제안하는 방법의 마지막 단계인 기계 학습을 적용하였다.
| Step | Detection rate (%) | False alarm rate(%) |
|---|---|---|
| MTI 1 | 58.9 | 16.3 |
| MTI 2 | 72.4 | 23.4 |
| MTI 3 | 89.1 | 9.25 |
| Merge(AND) | 46.9 | 9.9 |
| Merge(OR) | 90.6 | 17.1 |
제안하는 탐지 알고리즘의 기계 학습은 표적을 탐지한 것과 클러터 및 잡음으로 인한 오탐지를 구분함으로써 오탐율을 억제하도록 설계되었다. 표적과 그렇지 않은 것을 구분하는 것은 이진 가설검정(binary hypothesis test)으로 볼 수 있다[23]. 다만, 레이다 신호의 특성상 표적과 그렇지 않은 것에서 추출할 수 있는 특성(feature)들이 전부 독립적인 것은 아니기에, 일반적인 가설검정을 적용하는 것은 매우 복잡하다. 따라서 제안하는 방법에서는 기계 학습을 이용하여 표적과 클러터 및 잡음을 학습시킴으로써 이 문제를 보다 효과적으로 접근하였다.
그림 15에서와 같이 다중 MTI 필터를 통하여 탐지된 신호들의 각각의 포락선으로부터 시간 영역(time domain)과 주파수 영역(frequency domain)에서 특성들을 추출한 다. 또한 MRMR(Minimum Redundancy Maximum Relevance) 기법을 이용하여 추출된 특성들 사이의 중복성과 계산 복잡성을 줄이도록 하였다. MRMR 기법은 상호 정보량(mutual information)을 통하여 특성들의 중요도를 판별한다[24]. 탐지기를 통하여 탐지된 신호에서 추출한 특성들은 표 3과 같으며, MRMR 기법을 통하여 판별한 특성들의 중요도 는 그림 16과 같다. 이러한 과정을 거쳐 추정된 특성들의 중요도에 따라 포락선의 다중 꼭짓점의 여부, 포락선의 길이 및 넓이 등을 포함한 상위 15개의 특성을 사용하였다.
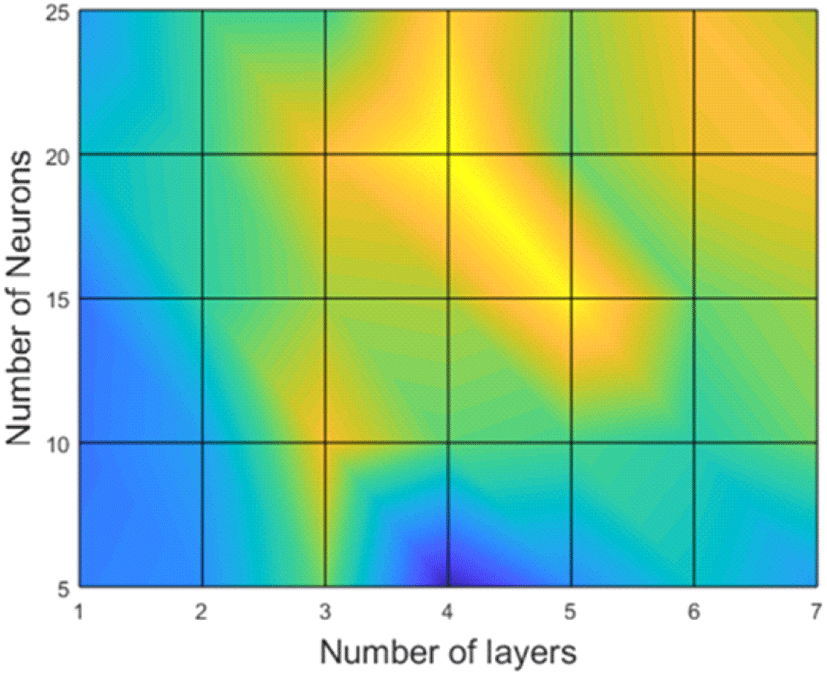
MRMR 기법을 이용하여 선택된 특성들은 신경 회로망(neural network)을 통하여 탐지된 신호가 실제 표적인지 아닌지를 판별한다. 신경 회로망을 통한 판별의 성능을 향상시키기 위하여, 신경 회로망을 구성하는 레이어(layer)와 뉴런(neuron)의 수에 따른 성능을 그림 17과 같이 분석하였다. 이 결과는 실제 표적을 올바르게 판별한 경우인 TP(True Positive)의 비율을 나타낸 것으로, 4개의 레이어와 20개의 뉴런을 사용하였을 때, 가장 높은 성능을 보인다. 본 논문에서 제안하는 탐지 알고리즘의 기계 학습은 이 결과에 따라 레이어와 뉴런을 배치하고, 각 레 이어에서 탄젠트 시그모이드 전달 함수(tangent sigmoid transfer function)를 사용하여 입력 값을 계산 후, 출력하는 형태로 설계되었다. 제안하는 방법에서 사용하는 신경 회로망의 목적은 실제 표적의 탐지율을 유지하면서 오탐율을 감소시키는 것이기에, 오탐지를 판별하는데 가중치를 두어 설계하였으며, 그 결과는 그림 18과 같다.
Ⅳ. 시험 결과
설계된 벽 투과 레이다 시스템의 탐지 성능을 평가하기 위하여 김천 시험장에서 현장 시험을 수행하였다. 그림 20에서와 같이 시나리오에 따른 표적들은 15 m의 벽으로 둘러싸인 사각형 모양의 건물 내에 위치하며, 벽 너머에 레이다를 설치하였다. 벽 투과 레이다 시스템의 탐지 성능을 검증하기 위하여 일반적인 레이다로는 투과하기 어려운 벽을 이용하여 시험을 수행하였다. 시험장의 벽은 총 22 cm의 두께로 10 cm의 벽돌과 12 cm의 콘크리트로 이루어져 있다[25].
벽 투과 레이다 시스템의 탐지 성능을 평가하기 위하여 수행한 시험 시나리오는 표 4에 정리되어 있다. 시험 시나리오들은 단일 표적과 다중 표적이 멈춰 있거나 움직이는 표적까지 다양한 상황에서의 성능을 평가할 수 있도록 하였다. 또한 기존의 CA-CFAR과 OS-CFAR의 결과와 제안하는 탐지 알고리즘의 결과를 비교하였다.
시험 결과는 탐지 단계에서의 탐지율과 오탐율로 나타내었다. 탐지율은 실제 존재하는 표적의 수 대비 올바르게 탐지된 표적의 수를 의미하며, 오탐율은 오탐지된 표적의 수를 오탐지가 일어날 수 있는 기회의 수로 나눈 값을 의미한다[26].
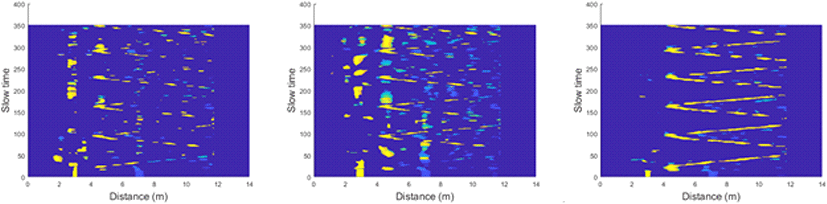
그림 21은 한 명의 서 있는 표적에 대한 탐지 방법에 따른 결과를 보여준다. 제안하는 알고리즘의 결과의 빨간 점은 다중 MTI 필터가 적용된 탐지기들의 결합 단계에서의 결과이며, 파란 점은 회로 신경망을 이용하여 오탐지를 제거한 결과이다. 제안하는 탐지 알고리즘의 최종 결과인 회로 신경망의 결과와 다른 두 가지의 기존 탐지 방법의 가장 큰 차이점은 탐지된 신호의 특성을 이용하여 오탐지를 제거한다는 것이다. 그림에서 확인할 수 있는 것처럼, 일반적인 탐지 방법으로는 벽으로 인한 신호의 왜곡을 오탐지하는 경우가 많지만, 제안하는 방법의 결과는 이러한 오탐지를 대다수 제거하였다. 다음으로 같은 상황에서 표적이 자리에 앉아있을 때의 결과는 그림 22와 같다. 표적이 앉아 있게 되면 레이다 반사 면적(radar cross section)이 줄어들게 되고, 이에 따라 일반적인 탐지 방법의 탐지율 또한 감소하나, 제안하는 방법의 경우 다중 탐지기의 결합을 이용하여 탐지율을 유지하는 것을 확인할 수 있다.
그림 23, 그림 24 그리고 그림 25는 (0, 4)m에서 (0, 13) m까지 이동하는 표적의 속도에 따른 결과를 보여주는데, 이 경우 벽과 거리로 인한 전파 손실(propagation loss)로 인하여 약 11.5 m가 최대 탐지 거리인 것을 알 수 있다. 다른 시나리오들과 마찬가지로 회로 신경망을 통하여 오탐지를 상당수 제거할 수 있으며, 특히, 표적이 빠르게 움직이는 시나리오에서 제안하는 방법의 결과가 다른 두 탐지 방법에 비하여 현저히 좋다는 것 또한 확인할 수 있다.
그림 26은 한 명의 표적이 (−1.5, 2.5) m를 원점으로 하는 반경 0.5 m의 원을 그리며 움직이고 있고, 다른 한 명의 표적이 (−1.5, 6) m에 서 있는 시나리오의 결과이 다. 이 경우, 레이다 시스템 가까이에서 크게 움직이는 표적의 존재로 인하여, 뒤에 있는 표적의 탐지에 영향이 나타나는 것을 볼 수 있다. 그림 27은 두 명의 표적이 거리상에서 교차하게 움직이는 상황으로, 두 표적이 매우 근접하였을 때는 표적의 신호들이 겹쳐지면서 CFAR을 이용한 탐지가 어려워지는 것을 확인할 수 있다. 이 경우, 신호의 양상은 표적이 빠르게 움직이면서 넓게 퍼지는 형태와 비슷한데, 그렇기 때문에 제안하는 탐지 방법이 기 존의 것들에 비하여 상대적으로 좋은 결과를 보여준다.
그림 28은 세 명의 표적이 정해진 위치에 앉아 있을 때의 결과이다. 다중 표적이 앉아 있는 상황에서는 앞서 언급하였듯이, 레이다 반사 면적이 줄어들고, 표적 간의 다중 경로 효과가 발생한다. 이러한 상황에서는 OS-CFAR이 CA-CFAR에 비하여 좋은 결과를 보여준다는 것을 확인할 수 있으며, 제안하는 탐지 방법은 다른 두 방법에 비하여 더욱 좋은 성능을 가진다. 그림 29에서는 두 명의 표적이 서 있고 다른 한 명이 움직이는 것으로, CFAR을 이용한 탐지에서는 움직이는 표적으로 인한 오탐지가 매우 빈번하다. 하지만 신호의 특성을 반영한 신경 회로망을 통하여 이러한 오탐지를 상당수 제거할 수 있다는 것을 재차 확인할 수 있다. 마지막으로 다섯 명의 표적에 대한 결과는 그림 30과 같다. 이 경우에서도 다른 시나리오들 과 유사한 결과를 확인할 수 있으며, 특히 다중 표적으로 인하여 발생하는 오탐지가 효과적으로 억제되는 것을 알 수 있다.
시험 시나리오에 대한 수치적 결과는 표 5에 정리되어 있다. 대부분의 시나리오에서 제안하는 탐지 방법은 기존의 CA-CFAR과 OS-CFAR을 이용한 탐지에 비하여 높은 탐지율과 낮은 오탐율을 가진다. 특히, 빠르게 움직이는 표적에 대한 결과의 경우, 기존 탐지 방법으로는 좋은 결과를 얻기 힘들지만, 제안하는 방법의 경우 이러한 표적에 대한 고려가 포함되었기에 상대적으로 높은 성능을 보여준다. 다중 표적이 존재하는 환경에 대해서도 신경 회로망을 이용한 오탐지 제거가 유효하기에, 상대적으로 높은 탐지율과 낮은 오탐율을 얻을 수 있다는 것을 알 수 있다.
Ⅴ. 결 론
본 논문에서는 새로운 방식의 레이다 표적 탐지 알고리즘을 제안하고, 벽 투과 레이다 시스템을 이용한 현장 시험을 통하여 그 성능을 평가하였다. 수신된 레이다 신호로부터 표적의 신호를 추출하는 과정에서 표적의 움직임에 맞추어 동작할 수 있도록 다중 MTI 필터를 사용하였으며, 빠르게 움직이는 표적을 올바르게 탐지할 수 있도록 신호의 표준 편차에 따른 임계값을 사용하도록 하였다. 다중 탐지기의 결과를 결합함으로써 높은 탐지율을 가질 수 있도록 설계함과 동시에, 결합으로 인하여 증가하는 오탐율을 표적 신호의 특성을 이용한 신경 회로망을 이용하여 억제하였다. 제안하는 방식의 타당성을 검증하기 위하여 다양한 시나리오의 현장 시험을 수행하고, 그 결과를 기존에 일반적으로 사용되는 CA-CFAR과 OS-CFAR을 이용한 탐지기와 비교하였다.































