해상 클러터 환경에서의 표적 거리, 속도 추정 알고리즘

Ⅰ. 서 론

레이다에서 쏜 신호가 해상에 있는 표적 이외의 다른 물체에 맞고 들어오는 레이다 수신 신호를 해상 클러터라 한다. SCR(Signal to Clutter power Ratio)이 낮은 환경에서 CA-CFAR 방법을 이용하여 표적을 탐지할 경우^[1], 해상 클러터 신호의 크기가 상대적으로 크기 때문에 레이다 수신 신호의 크기만을 이용하여 표적을 탐지하는 것은 어렵다. 또한, 해상 클러터의 도플러 파워 스펙트럼을 보면, 낮은 도플러 주파수에 대부분의 파워가 존재하기 때문에^[2], 속도가 느린 표적은 해상 클러터와 구분하기가 어렵다.

해상 클러터 환경에서 표적을 탐지하는 방법은 다기능 레이다를 사용하는 경우 해상 클러터 모델링과 표적 탐지 방법^[3], 공중레이다에서 STAP(Space-Time Adaptive Processing) 방법을 이용하여 낮은 SCR의 느린 표적을 탐지하는 방법^[4] 등의 연구들이 진행 중이다. 또한 참고문헌 [5]는 표적과 클러터의 펄스 간 상관관계의 차이를 이용하여 표적 거리를 추정하는 방법을 설명하였다.

해상 클러터는 파도 높이, 바람 세기 등의 파라미터로 정해지는 평균 파워에 해당하는 텍스쳐(texture) 성분과 클러터 패치에 균등하게 존재하는 여러 개의 산람점에 대한 신호인 스펙클(speckle) 성분으로 구성되어 있다. 텍스쳐 성분은 감마 확률분포를 따르고, 스펙클은 가우시안 분포를 따른다. 두 가지 성분으로 구성된 해상 클러터의 크기를 K 확률분포를 표현할 수 있다. 그리고 해상 클러터의 도플러 스펙트럼은 가우시안 분포의 형태를 따른다^[2]. 또한, 텍스쳐 성분의 시간적 상관관계는 스펙클의 상관관계보다 상대적으로 길다. 그리고 각 거리 빈끼리 스펙클 성분의 공간적 상관관계는 독립적이기 때문에 텍스쳐 성분의 공간적 상관관계에 의해 클러터의 공간적 상관관계가 나타난다^[6]. 이러한 클러터의 크기, 도플러 스펙트럼 및 상관관계 특징을 이용하여 코히어런트 펄스를 사용하는 펄스 도플러 레이다에서의 클러터를 SIRV (Spherically Invariant Random Vector)로 모델링할 수 있다^[7].

기존 연구^[5]의 방법은 표적이 있는 거리만 추정하는 알고리즘을 제시하고, 표적의 속도는 추정하지 못하는 단점이 있다. 본 논문에서는 펄스 도플러 레이다를 사용하여 얻은 데이터를 표적과 해상 클러터의 상관관계, 속도 특징의 차이를 이용하여 낮은 RCS의 느린 표적의 거리와 속도를 추정하는 방법을 제시한다. 정합 필터를 통과한 펄스 축으로의 클러터에 대한 공분산 행렬을 구한 후, 고유값 분해(eigen value decomposition: EVD)를 하여 구한 고유값을 이용하여 클러터를 억제할 수 있다. 또한 이산 푸리에 변환 행렬을 통해 클러터와 표적의 속도 성분의 차이를 알 수 있다. 모의실험을 통해 제안된 알고리즘의 성능을 SCR에 대한 표적의 거리와 속도에 대한 평균 제곱근 오차(root mean square error: RMSE)와 표적 탐지 확률(detection probability)로 알고리즘의 성능을 확인한다.

Ⅱ. 해상 클러터 환경에서의 레이다 신호처리

2-2 정합필터

레이다 수신신호에서 표적의 거리를 찾기 위해 정합필터를 수행한다. 우선, 식 (1)의 수신 신호를 샘플링 간격 t_s로 샘플링한 후 신호 처리한다.

$$r^m\left[n\right]=r^m\left(n\times t_s\right)$$

(6)

정합필터 h 는 SCR(Signal to Clutter power Ratio)를 최대화하도록 설계한다.

$$h=R_h^{-1}{s}_r^H$$

(7)

여기서은 $s_r={\left[\begin{array}{cccc}{s}_N& s_{N-1}& \text{L}& s_1\end{array}\right]}^T$송신 신호를 시간 전한신호, [·]^H는켤레전치, t_P는 펄스너비, $N=round\left(\frac{t_p}{t_s}\right)$은펄스 너비의 샘플 개수를 의미한다. R_h는 클러터 수신 신호의 공분산 행렬이고, 클러터의 공간적 상관관계를 이용하여 R_h를 구할 수 있다.

공간적 상관관계는 거리 빈의 신호로 결정된다. 스펙클의 공간적 상관관계는 거리 빈끼리 독립적이기 때문에 서로 다른 거리 빈에 존재하는 스펙클의 상관관계는 0이 된다. 따라서 p번째 거리 빈에 존재하는 클러터와 q번째 거리 빈에 존재하는 클러터의 공분산은 식 (8)이다.

$$\begin{array}{c}E\left[a_{c,p}^m{\left(a_{c,q}^m\right)}^{*}\right]=E\left[\sqrt{{\rho }_{c,p}^m}\sqrt{{\rho }_{c,q}^m}{z}_{c,p}^m{\left(z_{c,q}^m\right)}^{*}\right]\\ =\{\begin{array}{ll}E\left[\rho \right]\hfill & p=q\hfill \\ 0\hfill & p\ne q\hfill \end{array}\end{array}$$

(8)

m 번째 펄스의 수신 신호에 대해 그림 1, 식 (8)을 이용하여 i번째 수신 신호 샘플(식 (9))과 j번째 수신 신호 샘플(식 (10))의 공분산(식 (11), 식 (12))을 구해보면,

$$r_i^m=s_N{a}_{c,i}^m+s_{N-1}{a}_{c,i+1}^m+\text{L+}{s}_1{a}_{c,i+N-1}^m$$

(9)

$$r_j^m=s_N{a}_{c,j}^m+s_{N-1}{a}_{c,j+1}^m+\text{L+}{s}_1{a}_{c,j+N-1}^m$$

(10)

$$\begin{array}{c}E\left[r_i^m{\left(r_j^m\right)}^{*}\right]=E\left[r_i^m{\left(r_{i+k}^m\right)}^{*}\right]\\ =E\left[\left(s_N{a}_{c,i}^m+\text{L+}{s}_1{a}_{c,i+N-1}^m\right){\left(s_N{a}_{c,i+k}^m+\text{L+}{s}_1{a}_{c,i+k+N-1}^m\right)}^{*}\right]\\ =E\left[\left(s_{N-k}{a}_{c,i+k}^m\right)\left(s_N{a}_{c,i+k}^m\right)+\text{L+}\left(s_1{a}_{c,i+N-1}^m\right){\left(s_{1+k}{a}_{c,i+N-1}^m\right)}^{*}\right]\\ =s_{N-k}{s}_N^{*}E\left[a_{c,i+k}^m{\left(a_{c,i+k}^m\right)}^{*}\right]+\text{L+}{s}_1{s}_{1+k}^{*}E\left[a_{c,i+N-1}^m{\left(a_{c,i+N-1}^m\right)}^{*}\right]\\ =E\left[\rho \right]\left(s_{N-k}{s}_N^{*}+\text{L+}{s}_1{s}_{1+k}^{*}\right)\end{array}$$

(11)

그림 1. | Fig. 1. m 번째 펄스의 수신 신호에 대한 샘플 | Samples of received signal for the m th pulse.

Download Original Figure

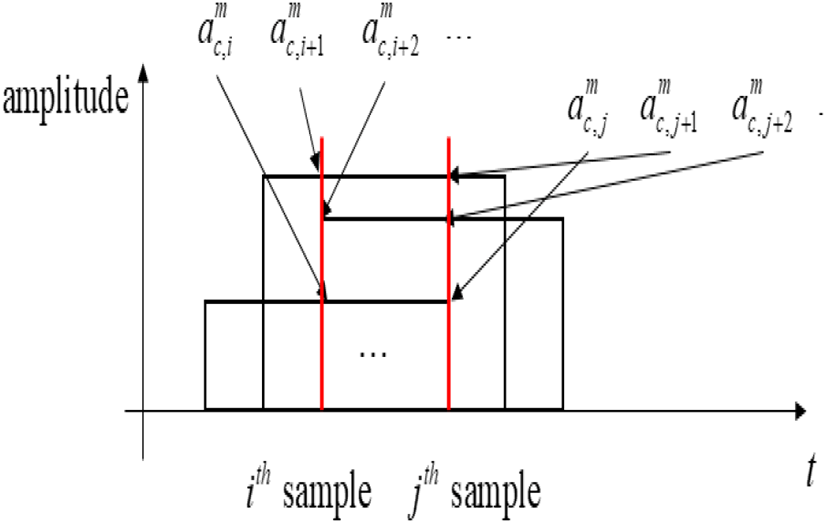
여기서 i번째 수신신호 샘플과 j번째 수신신호 샘플간의 간격을 k로 정의한다. 만약 i=j라면, 이다.

$$\begin{array}{c}E\left[r_i^m{\left(r_i^m\right)}^{*}\right]=E\left[\left(s_N{a}_{c,i}^m+\text{L+}{s}_1{a}_{c,i+N-1}^m\right){\left(s_N{a}_{c,i}^m+\text{L+}{s}_1{a}_{c,i+N-1}^m\right)}^{*}\right]\\ =E\left[\left(s_N{a}_{c,i}^m\right){\left(s_N{a}_{c,i}^m\right)}^{*}+\text{L+}\left(s_1{a}_{c,i+N-1}^m\right){\left(s_1{a}_{c,i+N-1}^m\right)}^{*}\right]\\ =s_N{s}_N^{*}E\left[a_{c,i}^m{\left(a_{c,i}^m\right)}^{*}\right]+\text{L+}{s}_1{s}_1^{*}E\left[a_{c,i+N-1}^m{\left(a_{c,i+N-1}^m\right)}^{*}\right]\\ =E\left[\rho \right]\left({\left|s_1\right|}^2+{\left|s_2\right|}^2+\text{L+}{\left|s_N\right|}^2\right)\end{array}$$

(12)

Ⅲ. 클러터 억제 알고리즘

표적이 없고 해상 클러터만 있는 상황에서 얻은 수신 신호를 정합 필터에 통과시킨 결과는 C_r ∈ £^M×L 이다.

C_r의 펄스 축으로의 클러터 표본 공분산 행렬을 구한다.

식 (14)의 공분산 행렬에 대해 고유값 분해(Eigen Value Decomposition)를 한다.

여기서 U: 고유벡터 행렬, S: 고유값의 대각행렬이다.

식 (14)에서 구한 고유값 중 가장 작은 고유값에 해당하는 고유벡터를 u_s라 한다. 고유벡터 u_s와 펄스축로의 클러터 벡터와 내적하면 거리-도플러 맵에서 클러터를 억제할 수 있다.

또한, 표적은 등속도로 움직이고 있고, 해당 표적이 있는 거리 빈에 대해 펄스 축으로 푸리에 변환을 하면 표적 속도에 해당하는 특정 주파수에서 피크 값을 가진다. 본 논문에서는 표적의 속도를 찾기 위해서 제로 패딩을 이용하여 세밀한 주파수를 가진 이산 푸리에 변환 행렬(D)을 이용한다.

표적과 클러터의 시간적 상관관계와 속도의 차이를 고려한 제안된 알고리즘을 사용하면, 특정 거리 빈에 표적이 있을 경우, 나머지 거리 빈에 대해서는 식 (14)에서 구한 고유벡터 u_s를 내적하여 클러터를 억제시키고, 동시에 해당 거리 빈에서는 이산 푸리에 변환 행렬 D를 곱하여 표적의 거리와 속도를 동시에 찾을 수 있다.

그림 2. | Fig. 2. 제안된 알고리즘의 흐름도 | Flow chart of proposed algorithm.

Download Original Figure

Ⅳ. 모의실험

중심 주파수 f₀=10⁹[HZ], 대역폭 BW=2.4×10⁶[HZ], 펄스 너비 t_p=5×10⁻⁶[sec]인 선형 주파수 변형 송신 신호를 사용하였다. 그리고 펄스 반복 주기는 T_r=40×10⁻⁶[sec], 샘플링 간격은 t_s=1.6×10⁻⁶[sec]이다. 그리고 펄스 너비의 샘플 개수는 N=30, 역치에 사용되는 α=N×0.8를 사용하였다.

클러터는 SIRV로 생성한다^[7]. 텍스쳐는 감마 확률분포를 따르고, 모양 파라미터 a=2, 크기 파라미터 b=1을 가진다. 스펙클은 가우시안 확률분포를 따른다.

클러터의 공간적 상관관계는 그림 3, 클러터의 시간적상관관계는 그림 4의 상관관계를 가진다.

그림 3. | Fig. 3. 해상 클러터의 공간적 상관관계 | Spatial correlation of sea clutter.

Download Original Figure

그림 4. | Fig. 4. 해상 클러터의 시간적 상관관계 | Temporal correlation of sea clutter.

Download Original Figure

표적은 거리 R_tgt=10,000[m], 속도 v_tgt=10[m/s]이다. 그리고 표적의 복소 반사계수의 실수, 허수 각각 평균이 ${\overline{x}}_{tgt}$이고 공분산이 σ²I인 가우시안 확률 분포$\left(N\left({\overline{x}}_{tgt},{\sigma }^{2}I\right)\right)$를 따른다.

식 (15)는 평균 SCR이고, 여기서 P_s는 표적 신호의 파워, P_c는 클러터의 파워, a, b는 K 분포에서의 모양 파라미터, 크기 파라미터이다.

SCR=−3[dB]일 경우, 정합 필터 결과를 통과한 신호에 대해 클러터를 억제하기 전(그림 5)과 클러터 공분산 행렬에서 가장 작은 고유값에 해당하는 고유 벡터 u_s를 내적하여 클러터를 억제한 결과(그림 6)를 표현했다. 고유 벡터 u_s와 내적하면 클러터 공분산에서의 가장 작은 고유 값에 해당하는 값을 가지게 되기 때문에 클러터가억제되어 표적의 위치를 찾을 수 있다.

그림 5. | Fig. 5. 해상 클러터를 억제하기 전 결과 | The results before suppressing sea clutter.

Download Original Figure

그림 6. | Fig. 6. 해상 클러터를 억제한 후의 결과 | The results after suppressing sea clutter.

Download Original Figure

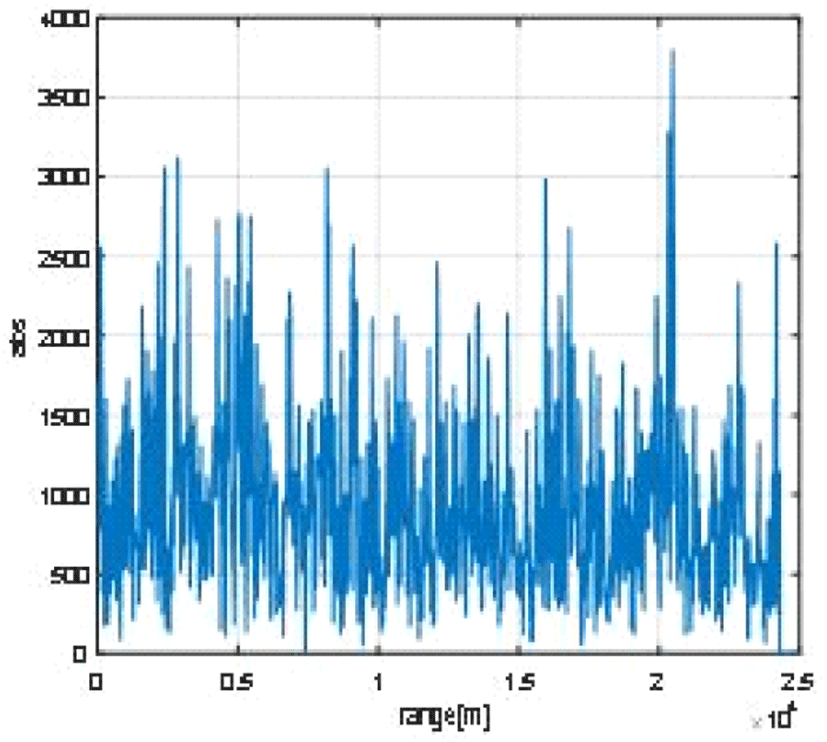
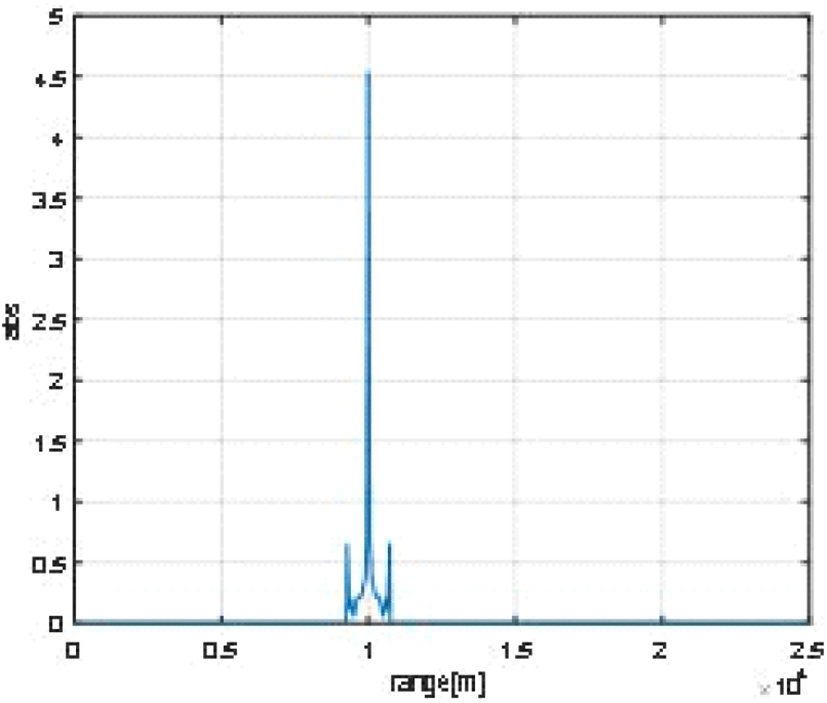
그림 7은 그림 6에서 가장 큰 크기에 해당하는 거리에서 이산 푸리에 변환 행렬을 수행한 결과이다. 표적의 속도는 등속도로 움직이고 있다고 가정하였기 때문에 이산 푸리에 변환 행렬과 내적하면 표적의 도플러 주파수에 해당하는 값에서 피크 값을 가지게 되고, 이를 이용하여 피크 값에 해당하는 도플러 주파수로 표적의 속도를 추정할 수 있다.

그림 7. | Fig. 7. 이산 푸리에 변환 행렬을 수행한 결과 | Result of DFT matrix.

Download Original Figure

거리-도플러 맵에서 CA-CFAR^[1] 방법을 사용할 경우, 테스트 셀에 표적을 탐지하기 위해서 8개의 가드 셀, 15개의 주위 셀을 사용하여 알고리즘을 진행하였다. CA-CFAR 방법은 테스트 셀의 주위 셀을 이용하여 역치를 구하고, 테스트 셀의 값이 역치보다 클 경우에 표적이있다고 판단한다.

그림 8, 그림 9는 CA-CFAR 방법과 제안된 알고리즘을수행하였을 경우, 표적의 거리와 속도의 평균 제곱근 오차를 나타냈다. 각 그래프에서 빨간색 그래프는 CA-CFAR 방법을 이용하여 표적의 거리, 속도를 추정하였을 경우 평균 제곱근 오차를 나타냈고, 파란색 그래프는 제안된 알고리즘을 사용하여 구한 표적의 거리, 속도를 추정하였을 경우 평균 제곱근 오차를 표현했다. 낮은 SCR 환경에서 CA-CFAR 방법을 사용하면 거리-도플러 맵에서 해당 셀 주위의 값들이 상대적으로 크기 때문에 표적의 거리, 속도를 추정하는데 많은 오차가 발생하게 된다. 이에 반해 제안된 알고리즘을 사용하면 클러터를 억제시키고 표적의 정보를 추정하기 때문에 상대적으로 적은 오차가 발생한다. 제안된 알고리즘으로 표적의 거리와 속도를 추정하였을 경우, SCR이 −15 dB일 경우 표적의 거리와 속도의 오차가 상대적으로 크지만, SCR이 높아질수록 표적 거리와 속도의 RMSE 값이 줄어드는 것을 확인하였다.

그림 8. | Fig. 8. 표적 거리의 RMSE | RMSE of the target range.

Download Original Figure

그림 9. | Fig. 9. 표적 속도에 대한 RMSE | RMSE of the target velocity.

Download Original Figure

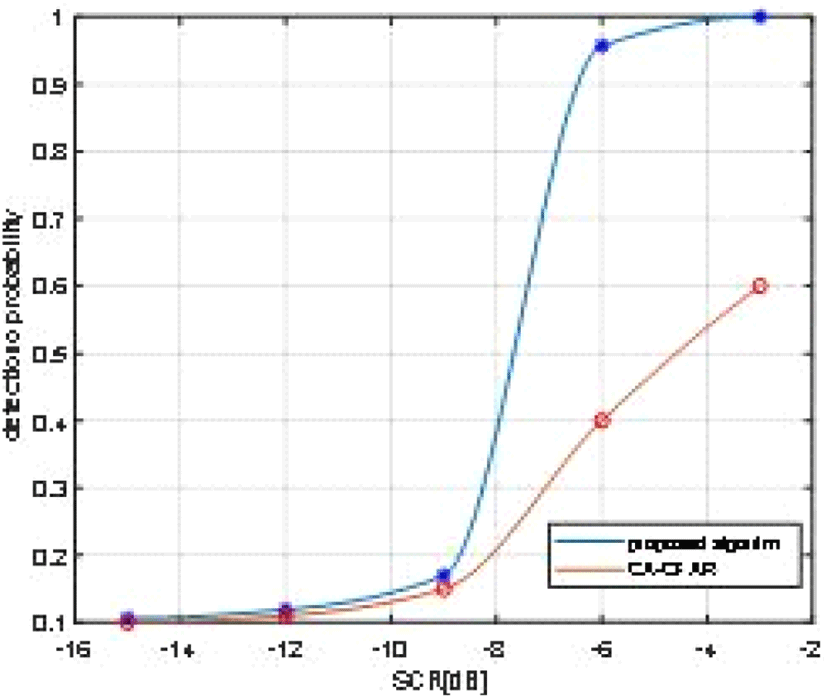
그림 10은 오경보 확률을 0.1일 경우에 Monte Calro 방법을 수행하여 얻은 SCR에 따른 탐지 확률을 구하였다. 빨간색 그래프는 기존 CA-CFAR를 사용하였을 경우 탐지 확률, 파란색 그래프는 제안된 알고리즘을 사용하였을 경우 탐지 확률이다. 낮은 SCR에서는 CA-CFAR 방법을 이용하면 주위 셀 값으로 구한 역치가 높기 때문에 표적 탐지 확률이 낮다. 하지만 제안된 알고리즘으로 구한 탐지 확률은 CA-CFAR를 이용하여 구한 탐지 확률보다 훨씬 높은 탐지 확률을 가지는 것을 확인할 수 있다.

그림 10. | Fig. 10. SCR에 따른 표적 탐지 확률 | Detection probability with respect to SCR.

Download Original Figure

Ⅴ. 결 론

해상 클러터와 표적의 상관관계, 속도의 차이를 이용하여 바다 위에 있는 표적 탐지 및 거리, 속도를 추정할 수 있는 알고리즘을 제안하였다. 제안된 알고리즘을 수행한 결과, 기존 CA-CFAR로 표적을 탐지할 경우보다 월등히 높은 탐지 확률을 가지는 것을 확인하였다.