Ⅰ. 서 론
최근 자율 주행 기술의 발전과 더불어 자동차 내부에서는 핏콕(peacock), 헤드업 디스플레이 등의 다양한 AVN (audio video navigation) 서비스가 발전함에 따라, 이를 제어하기 위한 새로운 사용자 인터페이스의 필요성이 증가하고 있다. 특히 큰 부피를 갖거나 두 개 이상의 스크린을 제어하기 위해서는 기존의 터치 기능은 사용하기 불편하고, 음성 인식기능은 사용 환경에 따라 적용이 제한적이다. 따라서 새로운 사용자 인터페이스는 비접촉식이어야 하며, 운전자가 자유로운 환경에서 적용할 수 있어야 한다. 이러한 환경에서 미세한 비접촉 손동작 조작은 적용이 쉽고 좁은 환경에서 사용할 수 있어 차세대 사용자 인터페이스가 될 수 있다. 기존 손동작 인지 방법에는 카메라를 이용하는 방법이나 라이다를 이용하는 방법 등이 있다[1],[2]. 하지만 카메라를 사용하는 방법은 사생활 보호 측면에서 사용이 제한적이며, 어둠 속에서는 성능이 떨어진다. 이에 비해 레이다를 이용한 손동작 인지 기술은 차량 내부 디자인에 영향을 미치지 않으면서 초소형 제작이 가능하고 양산시 단가를 절감할 수 있는 장점이 있다. 따라서 최근 인공지능 기술 발전과 함께 레이다 기반 손동작 인지 기술의 연구가 활발히 되고 있다.
레이다를 이용하여 손동작을 인지하는 연구는 초기에 도플러 레이다를 기반으로 수행되었으나, 속도 정보만을 이용하기 때문에 인식률 및 인식할 수 있는 손동작 수는 제한적이다[3]~[5]. 또한, 초기에 사용한 ISM(industry science medical) 대역 24 GHz FMCW 레이다는 250 MHz 비교적 좁은 대역폭을 이용하여 낮은 거리 해상도를 갖기에 미세한 손동작 인지를 할 수 없다. 따라서 정밀한 손동작 인식을 위해서는 60 GHz FMCW 레이다를 이용하여 속도와 미세한 거리 정보를 추출하여 손동작 인지하는 연구가 진행되고 있다[6].
기존 연구로 엔비디아의 24 GHz FMCW 레이다 기반 손동작 인지에서는 배경 제거 기법(background subtraction) 을 이용한 MTI(moving target indicator) 필터를 사용하여 클러터 신호를 제거하였고[5], 다른 연구는 고역 통과 무한 임펄스 응답 필터 기반 MTI 필터를 이용하였다[7]. 이러한 MTI 필터를 사용할 경우, 속도 해상도 단위의 최소치보다 낮은 속도의 손동작은 감지될 수 없는 문제점이 있다. 60 GHz FMCW 레이다를 이용한 Google 솔리 프로젝트는 거리-속도-시간 3차원 정보를 추출하여 이를 CNN + LSTM(long short-term memory) 딥러닝 모델로 손동작을 인지하였다[6]. 3D 데이터는 큰 메모리가 요구되며, 이는 엣지 컴퓨팅 측면에서 효율적이지 않다는 문제점이 있다.
본 논문에서는 미세 손동작을 감지하기 위해서 높은 거리 해상도를 갖는 60 GHz FMCW 레이다를 사용하였다. 상체 클러터 신호와 사람의 다양한 손 크기로 인해 인지 정확성이 낮아지는 점을 해결하기 위해 주파수별 가중치를 갖는 MTI 필터를 적용하고, 정규화 기법을 도입하였다. 수신된 레이다의 3차원 데이터를 2차원 데이터로 변환하고, 이를 경량 CNN에 적용하여 레이다 기반 손동작 인지 가능성을 실험적으로 확인하였다.
논문의 구성은 다음과 같다. 2장에서는 미세 손동작을 감지하기 위한 FMCW 레이다 시스템의 파라미터와 시스템 구성도에 따른 신호 흐름을 서술한다. 3장에서는 새롭게 제안하는 클러터 신호 제거를 위한 주파수 가중 MTI 필터와 메모리 절감을 위해 적용한 데이터 압축 기법을 기술한다. 4장에서는 제안한 알고리즘과 CNN을 이용하여 개선된 인지 성능을 고찰하고, 5장에서 결론을 맺는다.
Ⅱ. 레이다 시스템 구성도
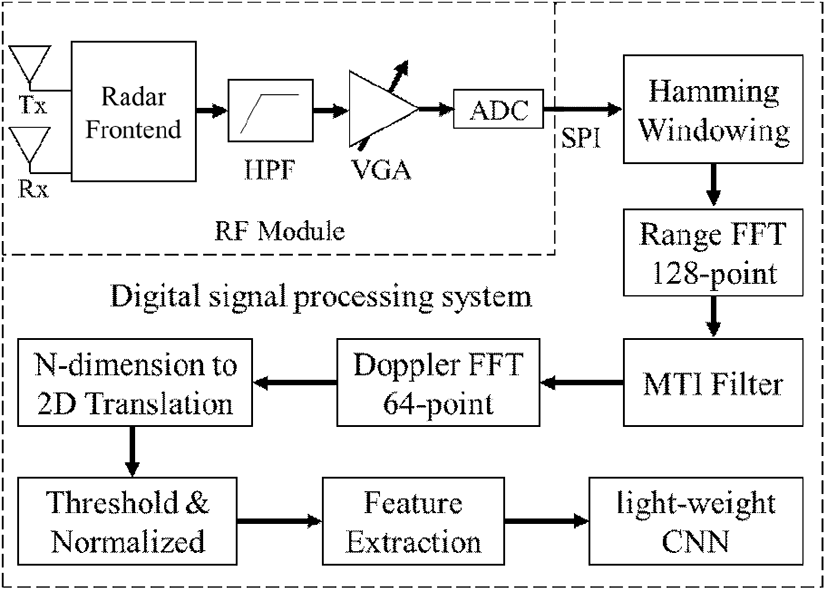
본 연구에서 사용한 FMCW 레이다 시스템의 구성도는 그림 1과 같다. 레이다 센서 칩은 독일 인피니언사의 칩 (BGT60TR13C)을 이용한 60 GHz 대역 FMCW 레이다 모듈을 사용하였으며, 레이다 센서 칩 사양과 레이다의 시스템 파라미터는 표 1과 같다.
사용한 FMCW의 파형은 고속 톱니파이며, 한 프레임은 64개의 첩 신호 파형으로 구성된다. 이 방식은 톱니파의 지속 시간이 매우 짧기에 저속 이동 표적의 경우 다중 첩 신호 중에서 표적의 위치가 동일 비트 주파수로 발생한다[8]. 표적의 속도는 다중 첩 신호 간의 동일 비트 주파수 내에서 도플러 효과에 따라 위상변화로 나타난다. 따라서 1차 Real-FFT를 통해 거리 정보를 알 수 있고, 1차 FFT 결과에서 얻은 각 주파수 별 위상 정보를 이용해 2차 Complex-FFT를 통해 도플러 주파수를 추출하고, 표적의 속도를 구할 수 있다[9]. 또한, 톱니파의 주파수 변조 대역폭이 6 GHz로 매우 넓기 때문에, 거리 해상도가 2.54 cm로 매우 높아 미세한 손동작의 차이를 구분할 수 있다.
신경망의 정확성을 높이기 위해 2차 FFT를 수행하기 전 MTI 필터를 통해 정지된 클러터를 감쇄시키는 입력 데이터 전처리를 수행하였다. 그 후, 3차원 데이터를 차원 압축 기법을 사용하여 시간 도메인 기준 거리-시간, 속도-시간 2차원 데이터 2개로 변환하였다. 변환된 2차원 데이터 각각에 대해 잡음 제거와 목표 객체 검출을 위하여 정규화한 후, CNN을 사용해 손동작을 인지하였다.
Ⅲ. 레이다 기반 손동작 인지 기법
본 논문은 FMCW 레이다 시스템에서 새로운 신호처리 기법을 통해 이전보다 낮은 메모리 부하와 높은 정확성을 달성하도록 하는 손동작 인지 기법을 제안한다.
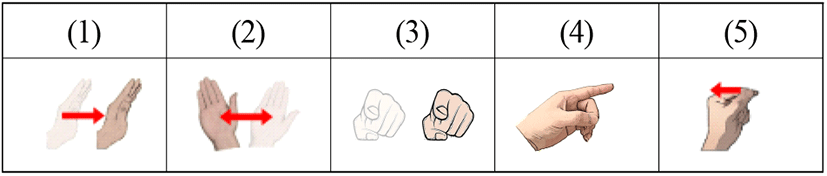
구분하고자 하는 손동작은 표 2와 같으며, 본 절에서는 손동작 인지 기법을 제안하는 MTI 필터와 2차원 데이터 변환 및 신호 정규화로 나누어 설명한다(그림 2).
손동작 감지를 위해서는 정지된 배경 객체에 의한 클러터 신호를 감쇄하고, 표적으로 하는 손동작만 감지하기 위한 MTI 필터가 요구된다. 이는 손동작보다 뒤에 존재하는 사람의 상체 및 의자와 같은 주변 물체로 인한 클러터 신호는 신경망 네트워크에서 손동작 인지 정확성을 감소시키기 때문이다.
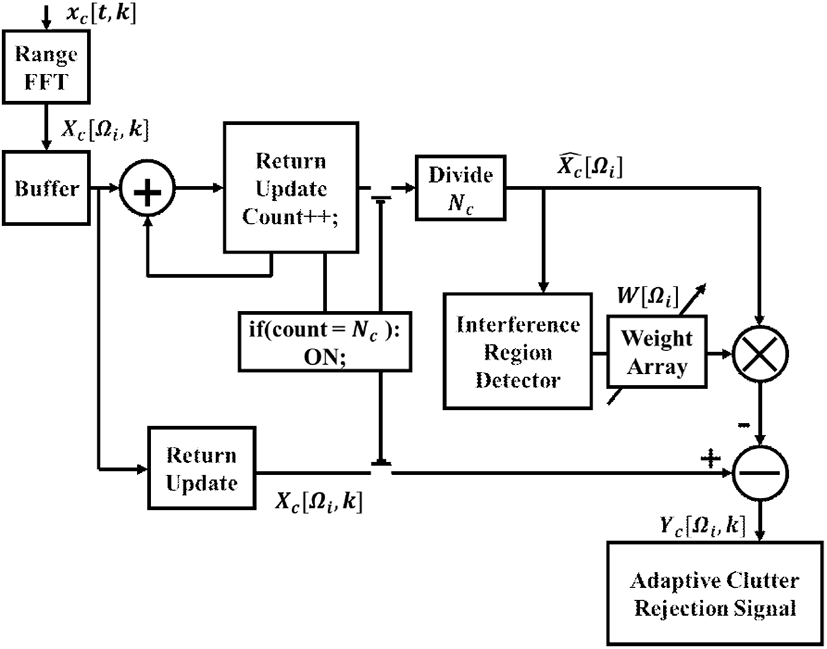
FMCW 레이다에서 MTI 필터는 PRF(pulse repetition frequency) 간격으로 수집하는 표적 정보의 비트 주파수 간의 상관성 특성을 이용한다[10],[11]. 기존 FMCW 레이다의 MTI 프로세싱은 비트 신호에 존재하는 배경 클러터 (background clutter)를 추출하여 제거하는 배경 제거 기법과, 유한 임펄스 응답 필터 또는 무한 임펄스 응답 필터를 이용하는 기법이 연구되었다[12]. 본 논문에서는 그림 2와 같이 복잡성이 낮고 효율이 우수한 주파수 가중 MTI 기법을 제안한다.
제안하는 손동작 감지 레이다 시스템에서 Xc [Ωi,k]는 Nc개 첩 파형의 표적 반사 신호로 구성된 수신기 출력의 2차원 프레임 데이터이며, t는 한 첩 내의 시간 인덱스이고, k는 첩 인덱스이다. Xc [t, 0]은 현재 첩의 반사 신호를 뜻한다. FFT 이후 데이터를 표현한 그림 2와 달리 시간 영역에서는 FMCW 레이다에서 정지된 객체의 반사 신호는 Nc개 반사 신호의 평균값인 되고, 이러한 배경 클러터 신호는 식 (1)과 같이 나타낼 수 있다[13].
이는 시간 영역에서 수행하는 배경 제거 기법으로, 이를 고속 첩 FMCW 레이다의 주파수 영역에서 해석하면, 정지 객체는 각 첩에서 동일 주파수에 나타난다. 반면, 이동 객체는 고속 첩의 특성에 따라, 동일 주파수 Bin 내에서 위상 천이로 나타나기 때문에 각 첩 FFT의 평균을 취하면 시간 영역과 동일한 결과로 나타난다. 따라서 주파수 영역에서 보면 식 (1)은 식 (2)로 나타낼 수 있다.
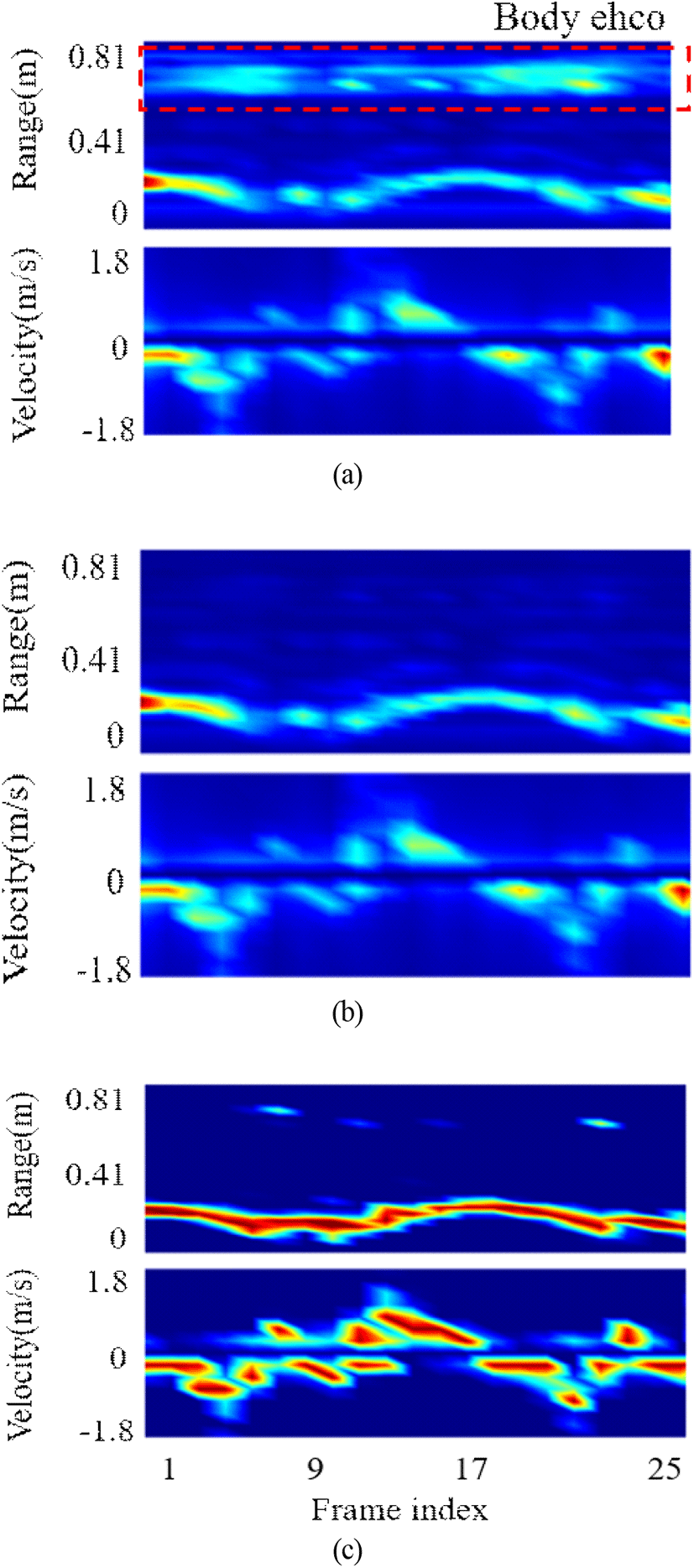
그림 3은 손동작 표 2에서 손동작 (5)번 유형의 동작을 하였을 때의 수신 신호의 결과이다. 그림 3으로 나타낸 데이터 Xc [Ωi,0]는 한 첩 신호의 FFT 결과이며, 별모양 마크 데이터는 식 (2) 평균 FFT 결과인 이다. 그림 3 (a)에서 두 번째 피크는 Xc [Ωi,0]에만 나타나는데, 이는 이동 표적에 해당하며, 두 데이터에 공통으로 나타나는 피크 값들은 정지 객체에 해당한다.
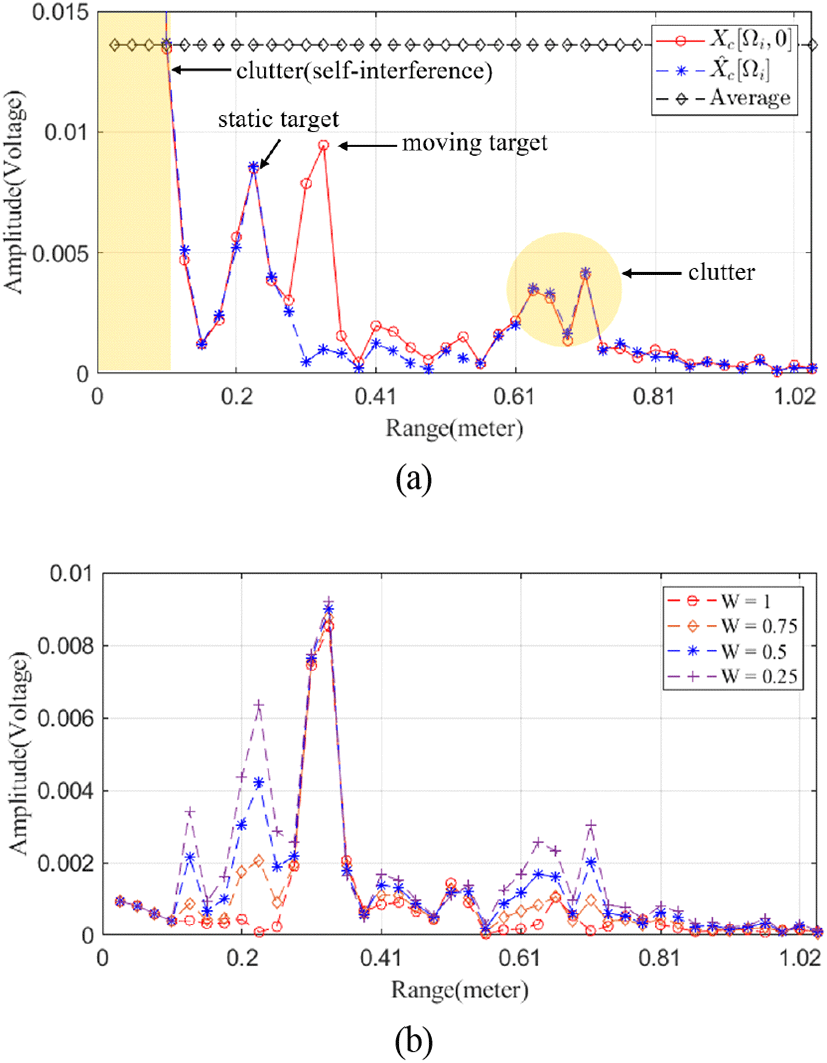
고속 톱니파 FMCW 레이다는 송수신 안테나의 격리도 부족과 주파수 급변 구간에서 나타나는 스파크 신호로 인해 자기 간섭(self-interference)의 클러터 신호가 발생하는 문제점이 있다[14]. 이러한 자기 간섭 클러터 신호는 그림 3(a)에서 볼 수 있듯이 DC 부근의 큰 신호로 나타난다. 그러나 이러한 클러터의 주파수 대역을 특정하여 제거할 수는 없기 때문에, 본 연구에서는 실험 데이터의 특성을 분석하여, 그림 3(a)에서 신호의 평균 세기보다 큰 값을 갖는 주파수 대역을 자기 간섭 클러터 신호의 주파수 대역으로 판단하였다. 이를 구분하는 신호 세기 값으로 정지 객체 FFT 출력의 평균값을 임계치로 이용하였고, 이는 식 (3)과 같고, 결과는 그림 3(a)의 평균 데이터이다.
식 (3)은 주파수별 가중치 W[Ωi]를 정하는 방법을 나타낸다. 식 (3)에서 NS =64로 첩 신호 내 ADC 샘플의 절반 값으로 FFT 포인트의 절반 값과 같다. W[Ωi]는 정지 객체 FFT 출력값 의 각각 주파수별로 곱해지는 64개의 가중치 값을 갖는 가중치 배열이다.
평균 신호 세기보다 큰 신호 세기를 갖는 주파수 대역을 DC 부근 자기 간섭 신호로 판단하였고, W[Ωi] 배열에서 가중치 1을 두고 해당 성분들은 식 (4)와 같이 제거하였다. 식 (4)는 주파수 가중 MTI 필터링 후 도플러 FFT 이전 데이터인 Yc [Ωi,k]를 나타낸 것이다. 식 (4)에서 k은 한 프레임 내의 첩 인덱스이다. 또한, 그림 3(a)의 측정 데이터를 보면 자기 간섭 클러터 신호 외에도 여러 개의 정지 객체 신호가 존재한다. 그림 3(a)에서 이동 표적보다 높은 주파수에 나타나는 객체는 상체 및 팔에 의해 반사되는 신호 추정되면, 넓은 주파수 범위에 걸쳐 분포하고 있다. 손동작에서 가장 큰 정보를 갖는 부분은 이동 객체 정보이나, 부분적으로 손동작 간 정적 객체 정보도 손동작을 구분하는 정보를 포함하고 있다. 기존의 MTI 기법(W=1)을 적용하면 그림 3(b)에서 이동 객체만 남게 된다. 그런데, 이러한 기법은 (5)번 손동작에서 정지된 손에 해당하는 정보, 즉 그림 3(a)에서 정적 표적 객체의 값에 해당하는 손의 위치 정보도 제거하게 되어, 다른 손동작과의 차별성을 감소시키는 요인이 된다. 즉, 손동작을 구분하기 위해서는 자기 클러터는 전면 제거해야 하지만, 신체에 해당하는 정지 객체는 선택적으로 제거해야 한다. 하지만, 사람마다 다른 손 크기와 상체의 크기로 인하여 손동작과 상체를 구분하기 어렵다. 따라서 자기 간섭 신호 이외 신호는 가중치를 달리하여 신호를 감쇄하였다. 이는 식 (3)과 같이 신호 세기의 평균값보다 작은 신호의 세기를 갖는 주파수 대역은 W[Ωi] 배열에서 1보다 작은 가중치 값을 갖도록 하였다. 그림 3(b)는 Xc [Ωi,0]에 가중치 값을 [0.25, 0.5, 0.75, 1]로 달리하여 MTI를 적용한 결과이다. 가중치 값을 0.25로 사용하였을 경우 상체 클러터 신호를 적절히 제거하지 못하는 점을 그림 3(b)에서 볼 수 있다. 이러한 가중치 값은 사람에 따른 손동작과 상체 크기의 차이로 인해서 최적화하기 어려운 면이 있다. 본 연구에서는 손동작에서 얻은 전파 기반 이미지의 구조 유사도 지수(SSIM: structural similarity index method) 를 성능 척도로 이용하였고, 이를 통해 가중치 값을 최적화하였다. 가중치 값에 따른 성능은 그림 4와 같다. 가중치 값에 따른 성능을 비교하기 위해서 동일 손동작의 데이터 2개를 무작위로 선정하여 구조적 유사성 지수를 측정하였다. 이때, 비교하는 이미지는 후술하는 거리 프로파일과 도플러 프로파일의 2차원 이미지다. 그림 4에서 SSIM 측정값은 두 이미지 간의 유사성을 측정하는 지수이다[15]. 그림 4에서 녹색으로 도시한 SSIM 측정값은 동일 가중치에서 5가지 손동작의 SSIM 측정값을 평균한 것이다.
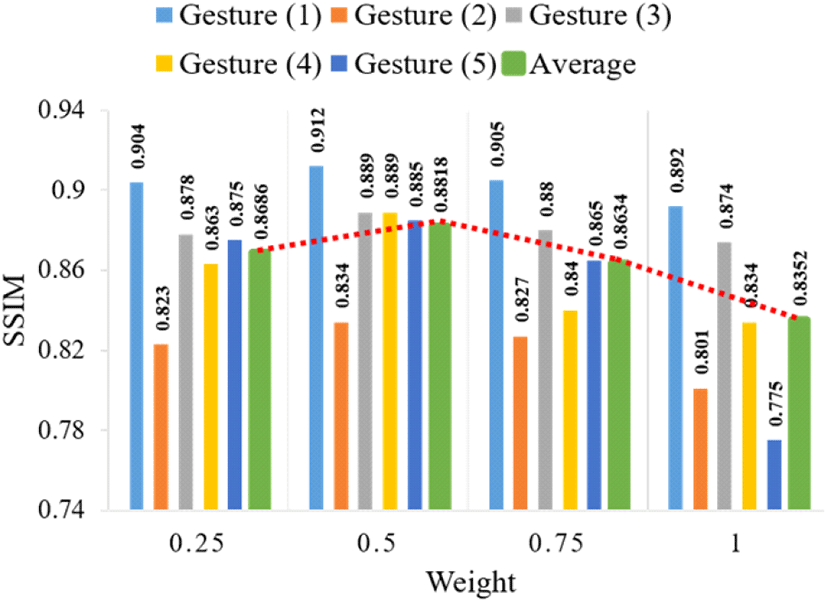
결과적으로 MTI 가중치를 달리하였을 때 가중치 값 0.5에서 가장 높은 유사도 지수를 나타내는 점을 알 수 있다. 이는 MTI 필터링을 통하여 사람마다 달리 존재하는 상체 클러터 신호를 제거하여 사람 간 차이를 줄인 결과이다. 따라서 본 연구에서는 자기 간섭 클러터를 제외한 정적 객체에 대해서는 가중치를 0.5로 낮추어 부분적으로 제거해 사용하였다.
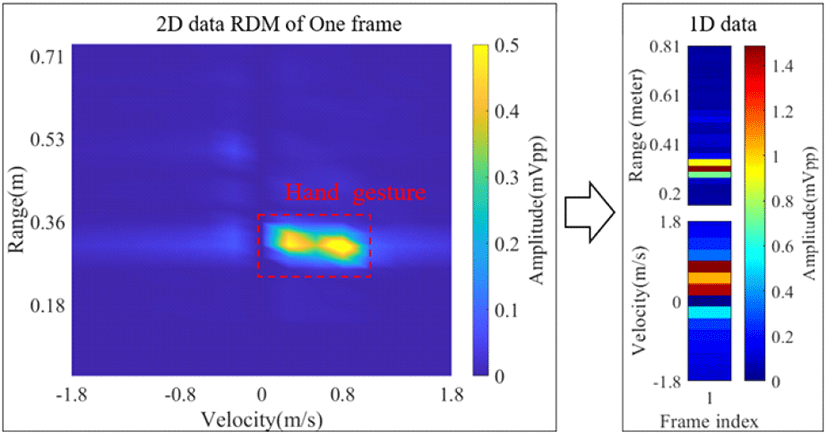
기존 FMCW 레이다 신호처리는 2D-FFT를 통하여 64 첩으로 구성된 한 프레임마다 RDM(range-doppler map) 이라는 2차원 데이터를 얻을 수 있다[16]. 손동작 인식에 사용한 데이터는 25개 프레임으로 구성되어 3차원 데이터가 된다. 신경망 네트워크의 연산 복잡성은 데이터 크기의 제곱으로 증가하고, 메모리도 데이터 크기에 비례해 증가한다. 신경망 커널의 복잡도와 메모리가 증가하는 문제점을 해결하기 위해 본 연구에서는 식 (5), 식 (6)과 같이 거리-속도-시간 3차원 데이터를 거리-시간, 속도-시간의 2차원 데이터 변환하여 연산 및 메모리 사용량을 축소하는 기존 구조를 채택하였다[6]. 식 (5)는 같은 시간 영역을 갖는 속도 및 거리로 표현된 3차원 데이터 RVT(r, ν, T)를 속도 영역의 모든 성분을 합하여 평균하는 식이다.
여기서 r 은 RDM에서 거리 Bin을 뜻하고, v 는 도플러 Bin, T는 프레임 인덱스이다. NS =64로 첩신호 내 ADC 샘플의 절반 값, Nc =64로 한 프레임에 반복되는 첩 신호의 수이다. 속도 성분만 남은 데이터VT(v,T)는 식 (6)과 같이 동일 방식으로 구한다. 그림 5는 한 프레임의 2차원 데이터를 1차원 데이터로 축소한 결과이다. 기존 연구[6]에 이와 같은 방식으로 데이터를 축소하였다. 본 연구에서는 10 KHz의 고속 PRF를 갖는 기존 연구[6]에 반하여 첩 신호 간 25 μs 휴지 시간을 갖도록 첩 사양을 PRF 6.45 KHz로 결정하였다. 이에 따라 낮은 속도 해상도를 갖지만 보다 적은 데이터로 메모리 부하를 절감하였다.
축소한 1차원 데이터를 CNN 입력 데이터로 사용하기 전 전처리를 하였다. 전처리로 손동작에 의한 전파 신호에서 잡음을 제거하고, 각기 다른 손동작 크기에 따른 신호 세기의 스케일 차이를 줄이기 위하여 정규화를 진행하였다. 식 (7)은 앞서 계산한 식 (5)의 결과로 얻은 RT(r,T) 거리 프로파일의 평균값인 mi 을 구한 것이다. 식 (8)은 이러한 mi 값에 RT(r,T)의 분산 값을 더하여 임계치 값 Thri 로 사용하였다. 계산된 Thri 값을 최소값으로 이용하고 RT(r,T)를 프레임 인덱스 T마다 프레임 내 최대 수신 신호 세기를 최대값으로 이용하여 식 (9)와 같이 최소최대 정규화를 진행하였다. 이와 같은 방식으로 VT(ν, T)도 프레임 단위별 임계치를 적용하였다. 이러한 일반적인 정규화 기법을 이용하여 데이터 스케일 분포를 일정하게 만들고, 임계치를 통하여 잡음을 제거함으로써 인지 정확성을 높일 수 있다. 이러한 정규화에 따른 결과는 4장에서 고찰하였다.
이처럼 정규화를 거친 RT(r,T), VT(v,T) 2개의 1차원 정보는 하나의 프레임 시간 단위마다 출력된다. 본 연구에서 인지하려는 손동작은 1초 이하의 손동작이다. 따라서 0.78초 동안 25개의 프레임 데이터를 수집하였다. 수집된 데이터는 25개의 1차원 데이터로 구성된다. 이는 RT(r,T)와 VT(v,T)로 나뉘어 2개의 2차원 데이터이다. 본 연구에서는 이러한 2개의 2차원 데이터를 하나의 이미지로 간주하여 경량 2차원 CNN 입력 데이터로 사용하였고, 이를 통해 손동작을 분류 인지하였다. 경량 신경망 네트워크는 Binary Weight Layer(BWL), Binarized Layer (BL)[17], Quantizated Layer(QL)[18]로 구성된 맞춤형 네트워크를 사용하였다. 네트워크는 합성 곱 층으로 구성된 특징 추출과 선형 층으로 구성된 분류기로 이루어져 있다.
Ⅳ. 레이다 모듈 및 측정 결과
본 논문에서는 그림 6과 같이 레이다 모듈에서 1 개의 송신 안테나와 1 개의 수신 안테나를 사용하였고, 30 cm 전방에서 손동작을 취하였다. 또한, 기존 연구들의 팔을 움직이거나 손을 크게 움직이는 손동작 대신 미세 손동작을 인지하였다. 미세 손동작을 결정하기 위해서 최종 사용자의 편리성과 각기 다른 손동작 간의 거리 정보와 속도 정보가 명확히 구분되어야 하는 점을 고려하였다.
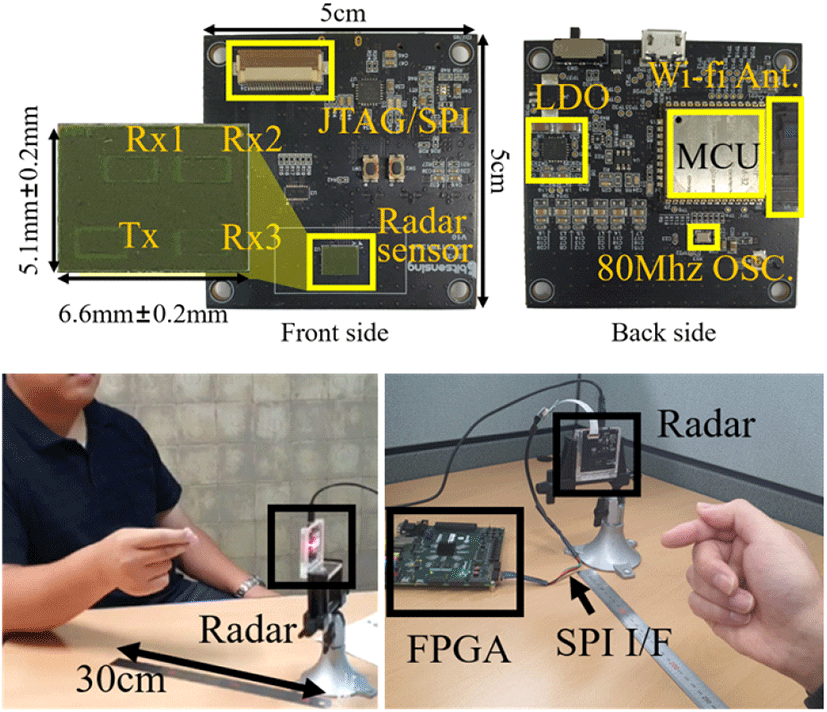
손동작은 표 2와 같이 (1) 손바닥을 전진하는 손짓, (2) 좌우로 이동하는 손짓, (3) 검지를 우측으로 움직이는 손짓, (4) 검지로 원을 그리는 손짓, (5) 엄지를 검지를 타고 위로 올리는 손짓 총 5가지로 구성되어 있다.
그림 7은 표 2에서 2번 손동작의 단계별 데이터를 도시한 것이다. RT(r,T)와 VT(v,T)에 주파수 가중 MTI 필터 적용한 결과는 그림 7(b)와 같고, 정규화를 적용한 결과는 그림 7(c)와 같다. 정규화를 통해 신경망 분류 시 발생하는 참가자의 서로 다른 손 크기 및 손동작 속도, 상체 크기 등에 의해 발생하는 특징 차이 문제점을 해결하였다. 신호처리를 통해 손동작 특징 차이를 줄였다.
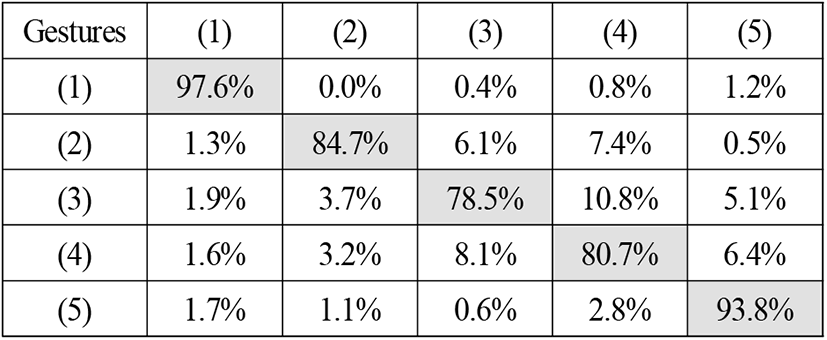
본 연구에서 제안된 신경망의 성능을 측정하기 위하여 손동작 인지 정확성 수치를 이용하였다. 손동작에 따라 수집된 전파 기반 데이터의 90 %로 신경망 네트워크를 학습하였고, 10 %는 교차검증에 활용하였다. 검증용 손동작 데이터는 경량 합성 곱 신경망 분류기의 입력으로 사용하였고, 5개의 손동작에 해당하는 스펙트로그램을 무작위로 일치시켰다. 경량 합성 곱 신경망 분류기의 교차검증은 표 3과 같고, 평균 정확도는 87.1 %이다. 손동작 (1), (5)에 비해 (2), (3), (4)의 인식률이 떨어지는 이유는 레이다의 특성상 종 운동에 비해 횡 운동의 변별력이 떨어지는 문제점에 기인한 것으로 판단된다. 이를 해결하기 위해서는 횡적 운동의 차별성을 획득하는 레이다 구조가 필요할 것이다. 기존 연구와 비교한 표 4의 결과는 본 연구와 서로 다른 조건에서 얻어진 것이므로 정확한 정량적 비교는 아니다. 그러나 표 4의 비교 연구들은 검증용 사용자의 손동작이 학습데이터에 포함되지 않으면 낮은 정확도를 갖는 반면, 본 연구 결과는 상대적으로 우수한 정확도를 보이고 있음을 알 수 있다. 이러한 특정 개인에 국한되지 않는 정확도는 기존 연구에서 서술되어 있듯이 실제 성능을 측정하는 중요한 수치이다[6].