Ⅰ. 서 론
AESA(Active Electronically Scanned Array) 레이다는 기존의 MSA(Mechanically Scanned Array) 레이다와는 달리 원하는 시점에 원하는 방향으로 전자적 빔 조향이 가능하기에 표적 하나 하나에 대해 필요로 하는 정보를 선택적으로 얻어낼 수 있도록 하는 선택적 빔 운용이 가능하다. 따라서, AESA 빔 운용의 장점을 고려하여 위협 표적 정보를 추출하기 위한 효율적인 빔 운용 설계가 필요하다. 레이다는 위협 표적의 위치, 속도, 그리고 방향 정보를 탐지하는 센서로써, 적보다 먼저 표적을 탐지한 후 위협에 대응할 수 있도록 지원해야 한다. 이를 위하여 레이다는 주어진 자원 하에서 가능한 먼 거리의 위협 표적을 탐지할 수 있는 파형의 설계가 필요하다.
본 논문은 AESA 레이다의 하드웨어 성능이 동일한 조건 하에서 장거리 위협 표적을 효율적으로 탐지하도록 하는 선택적 빔 운용 설계와 각 빔 운용 별 파형 설계 방법에 대해 제시한다. 기술된 설계 방법은 하드웨어의 구현 가능성을 고려하였으며, 설계 방법에 수반되는 레이다 성능 제약과 이에 따른 고려사항들을 제시하였다.
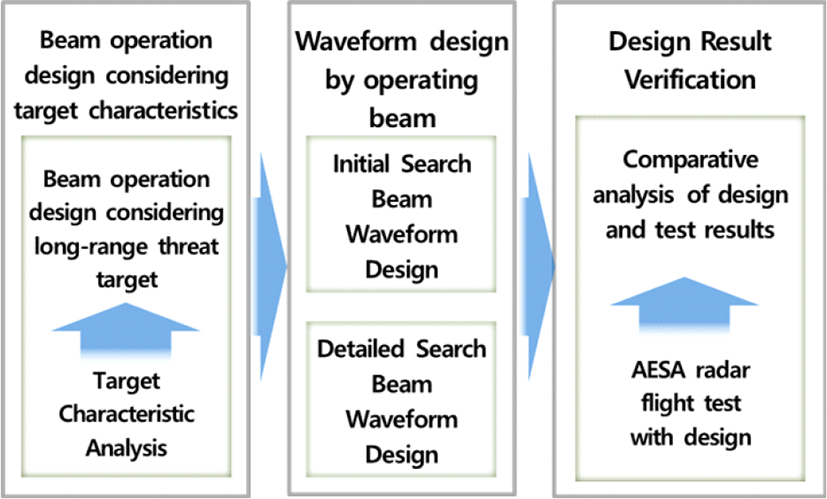
본 논문은 그림 1과 같이 구성된다. Ⅱ장에서는 탐지하고자 하는 장거리 위협 표적의 특성을 기반으로 설계 요구조건을 도출하고, 도출된 요구조건을 만족시키기 위한 빔 운용 설계를 기술하였다. Ⅲ장과 Ⅳ장은 운용 빔별 파형 설계 방법과 고려사항, 그리고 성능 제약에 대해 논의하였다. Ⅴ장에서는 비행 시험으로 얻은 결과를 설계결과와 비교 분석함으로써, 설계의 타당성을 확인하였고, 마지막으로 Ⅵ장에서는 본 논문의 결론을 기술하였다.
Ⅱ. 장거리 위협 표적 특성을 고려한 빔 운용 설계
장거리 위협 표적은 크게 하기의 3가지 표적특성을 갖는다.
표적 특성 1: 일반적으로 레이다에서 판단하는 표적의 위협도는 자함까지의 도달 시간을 기준으로 평가하기에 위협 표적은 높은 방사상의 속도를 보유함.
표적 특성 2: 표적이 장거리에 존재하기에 표적반사 신호의 전력이 낮음.
표적 특성 3: 전투기 연료를 효율적으로 사용하며, 공격 및 침투 지역으로의 진입을 위해 저 기동 상태로 이동.
장거리 위협표적 탐지에 특화된 빔 운용 설계는 표적특성 1을 고려하여, 저속이거나 멀어지는 표적들을 저 위협 표적으로 분류시켜 무시하고, 방사상의 접근속도가 위협 표적으로 분류되는 속도영역 표적들만을 선택적으로 탐지하도록 설계할 수 있다. 또한, 표적 특성 2와 같이 낮은 표적 반사 신호를 갖는 장거리 표적들을 효율적으로 탐지해 내기 위해서는 표적 반사 신호가 지상 클러터 반사 신호에 의해 영향을 받지 않도록 설계되어야 한다. 이를 위하여 본 논문에서는 HPRF(High Pulse Repetition Frequency) 파형을 사용하여 위협 속도영역의 표적에 대해 클러터가 없는 도플러 영역에서 탐지될 수 있도록 하고, 우수한 속도 및 거리 분해능을 가지면서 거리상에 모호성 없이 표적을 탐지할 수 있도록 파형을 설계하였다.
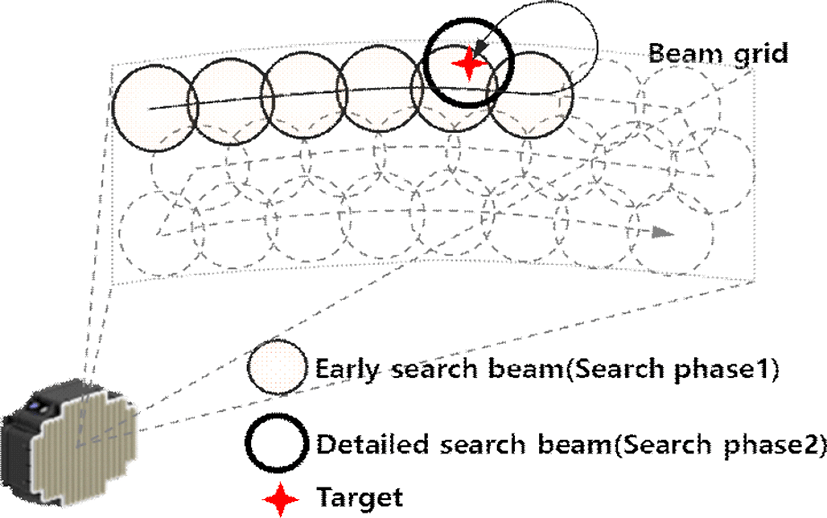
장거리 위협 표적은 표적 특성 3을 갖는 저 기동 표적이기에 비교적 긴 시간 동안 RCS(Radar Cross Section) 특성에 유사성을 지닌다. 이러한 표적 특성은 레이다가 표적을 향해 비교적 긴 시간 동안 빔을 조사하여 파형 위상의 coherent integration 이득을 높게 확보할 수 있도록 함으로써 장거리 표적탐지에 유리하다. 또한, AESA 레이다의 기민한 전자 빔 조향 능력을 통해 표적 RCS의 유사성이 유지되는 시간 동안 하나의 표적에 이종의 빔을 할당함으로써 표적탐지 확률은 유지시키며, 이종의 표적 정보를 조합하여 한 표적에 대한 정보를 완성시킬 수 있다.
그림 2는 본 논문에서 제시한 이종의 탐지 빔 조합을 통한 표적정보의 추출 과정을 보인다. AESA 레이다는 관심영역 내에 존재할 수 있는 장거리 위협 표적을 찾기 위해 그림 2와 같이 빔 그리드를 형성시켜 탐색을 수행하며, 각 드웰 영역에 대해 초기 탐색 빔(탐색 1 단계)만을 운용하며, 위협 속도영역 내에 표적의 존재 유무를 빠르 게 검사한다. 검사 중 특정 드웰 방향의 위협 속도 영역에서 표적 속도가 탐지되면, 해당 드웰에 상세 탐색 빔(탐색 2단계)을 즉시 할당함으로써 표적의 거리 정보를 추출하도록 하였다. 이러한 빔 운용 방식은 1단계 빔 운용에서 표적속도가 탐지된 조건 하에서만 2단계 빔 운용 자원을 할당하기에 장거리 위협 표적의 빠른 탐지와 시간 자원의 효율적 운용을 가능하게 해준다.
Ⅲ. 초기 탐색 빔 파형 설계
초기 탐색 빔은 장거리에서 접근하는 위협 표적에 대해 속도성분 추출만을 수행하기에 거리 분해능 증진을 위한 펄스압축 기술의 적용 없이 펄스열만을 사용하여, 펄스압축 신호처리에서 발생하는 거리 윈도우 손실을 제외시켰다[1]. 또한, HPRF 파형을 통해 클러터가 없는 도플러 영역에서 높은 SNR(Signal to Noise Ratio)을 가지며, 표적탐지할 수 있도록 설계하였고, 표적 RCS(Radar Cross Section) 특성의 유사성이 유지되는 시간과 처리장치의 FFT (Fast Fourier Transform) 연산능력을 고려하여 표적 신호의 위상을 최대로 coherent integration 하도록 파형의 CPI(Coherent Processing Interval) 시간과 펄스 개수를 설계하였다[1],[2]. 그림 3은 이동 플랫폼에서 AESA 레이다 운용 시 기존 HPRF 설계 방법에 따른 도플러 스펙트럼을 나타내며, 주엽 클러터를 영 속도로 이동시킨 이후의 스펙트럼을 보인다.
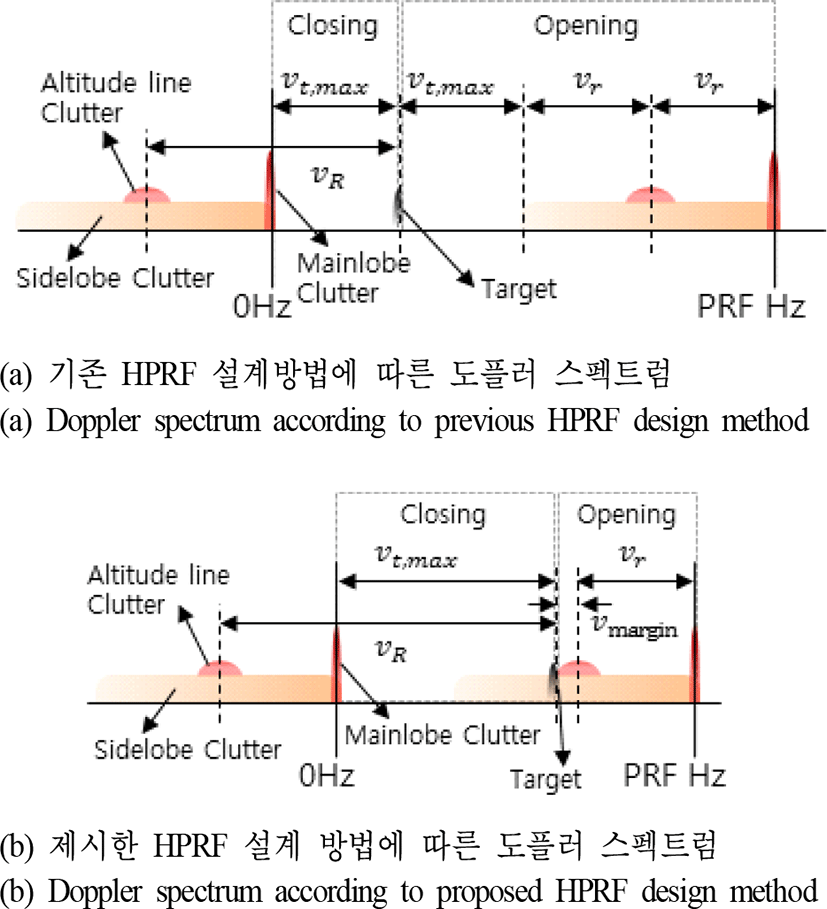
기존의 지상 레이다들은 주엽과 부엽 그리고, 고도 클 러터가 모두 영 속도에 존재하기에 식 (1)을 통해 HPRF를 설계해도 접근속도와 퇴각 속도 영역을 동일하면서 크게 설계할 수 있었지만, 전투기 등의 이동플랫폼에서의 스펙트럼은 그림 3(a)와 같이 자함 속도에 의해 표적의 접근속도 영역이 현저히 줄어들고, 위협 표적이 존재하지 않는 퇴각속도 영역만 비대해진다. 또한, 큰 값의 PRF 설계가 요구되어, 하드웨어의 듀티 증가로 인한 시스템 불안정성을 유발시킨다. 본 논문에서 Ⅱ장에서 기술한 장거리 위협 표적 특성 1을 고려하여 퇴각속도 영역의 표적은 무시하고 위협 표적이 존재할 수 있는 접근속도 영역을 극대화 하도록 식 (2)를 적용하여 그림 3(b)와 같은 스펙트럼을 설계한다.
여기서, vr은 자함의 속도[m/s]를 나타내고, vt,max는 탐지하고자 하는 위협 표적의 최대 관심속도[m/s]를 나타내며, vR은 자함과 표적간의 방사상 상대속도[m/s]를 나타내고, vmargin은 고도 클러터에 영향을 받지 않도록 추가하는 속도 마진[m/s]를 나타낸다. 그리고, λ는 파장[m]을 나타낸다.
이러한 설계 방법은 식 (1)에서 큰 비중을 차지하는 2(vt,max+vr)/λ 성분을 제거시킴으로써, 기존 대비 절반 정도의 HPRF 사용만으로도 표적특성 1을 만족시킨다.
제안한 설계의 예로써, 펄스폭 1.2 us에 듀티 14 %를 사용하는 레이다로 vmargin을 70 m/s 갖도록 116.7 kHz의 HPRF를 설계하면 자함 속도를 최대 마하 2까지 운용하며, 최대 관심 표적속도 1,000 m/s까지를 안정적으로 탐지해 낼 수 있다. 그림 3(b)는 일부 접근속도 영역에 부엽 클러터 성분을 포함하고 있어서 장거리의 저 SNR 표적탐지에 어려울 듯 보이지만, 본 영역은 클러터 반사 신호가 거의 수신되지 않는 안테나 후방방사 영역이어서 장거리 표적탐지에는 문제가 없다.
Ⅳ. 상세 탐색 빔 파형 설계
상세 탐색 빔은 초기 탐색 빔을 통해 탐지한 속도 표적의 확인과 동시에 거리 정보를 획득하기 위해 운용한다. 표적의 RCS 특성이 유사한 시간 동안에 유사한 탐지확률로 표적을 탐지해 내기 위해, 초기 탐색 빔에서 사용한 동일 HPRF로 설계하며, 거리를 추출하기 위해 LFM(Linear Frequency Modulation) Ranging 기법을 적용하였다. 또한, LFM Ranging의 낮은 거리 분해 성능을 보완하기 위해 펄스압축 파형을 조합하여 설계하였다.
LFM Ranging은 신호처리 단위인 한 버스트 시간에 대해 식 (3)과 같은 선형 주파수 변조 신호를 송신한 뒤, 표적 거리만큼 시간 지연된 수신 신호를 de-chirp 처리하여, 송수신 신호 간의 주파수 차이를 거리 정보로 환산하는 기술이다.
여기서, LFM ranging을 통해 수신되는 주파수 fD는 fD,LFM와 로 구성된다. fD,LFM는 선형 주파수 변조에 의해 표적거리 R [m] 만큼 발생하는 송수신 신호 간의 주파수 차이이고, ξ는 한 버스트 시간 동안 적용되는 선형 주파수 변조율 [Hz/s]을 나타내며, c는 전파속도 [m/s]를 나타낸다. 자함과 표적이 이동하는 운용환경 하에서의 fD는 도플러 변화에 의한 주파수 가 추가적으로 섞여 들어오기에, 식 (5) 및 식 (6)과 같이 2개의 주파수 변조율을 사용하여, 표적의 거리와 속도 정보를 분리시켜 획득한다.
여기서, fD1와 fD2는 각각 선형 주파수 변조율 ξ1 [Hz/s]와 ξ2 [Hz/s]를 사용하는 송수신 신호 간 주파수 차이이고, 두 개의 선형 주파수 변조율(ξ1, ξ2)에 의해 얻어지는 Δf12를 통해 식 (6)과 같이 표적의 거리와 속도를 획득할 수 있다. LFM Ranging을 통해 2개 이상의 표적을 거리에 대해 분해하기 위해서는 표적 신호가 식 (7)[3]과 같이 최소 1 개 이상의 도플러 필터 차이를 두고 수신되어야 하며, 도플러 필터의 대역폭은 하나의 버스트 시간(TCPI)에 사용한 주파수 변화의 양으로 결정된다.
여기서, ΔR은 한 버스트 내에서 거리상으로 분리 가능한 두 표적 간의 거리 [m]이고, δR은 도플러 필터의 대역폭인 Δfbin과 이종의 선형 주파수 변조율(ξ1, ξ2)에 의해 결정되는 거리 분해능을 나타낸다.
본 논문에서는 이후 절에서 기술한 방법들을 적용하여, 클러터가 없는 영역에서 표적을 탐지하면서도 가능한 우수한 거리분해능을 갖도록 식 (8)을 이용하여, 이종의 선형 주파수 변화율을 설계하였다.
여기서, k는 1 이상의 정수이고, 두 선형 주파수 변조율(ξ2, ξ3) 간의 차이는 (k+1)/k에 의해 최대 2배에서 1/k 배까지이며, 거리 분해능은 식 (7)에 의해 cΔfbin/(2|ξ1|)에서 kcΔfbin/(2|ξ1|)까지 설계 가능하다. 상세 탐색 빔에는 선형 주파수 변조율을 사용하지 않는 버스트(ξ3=0)를 추가로 사용하여 다수 표적들데 대한 도플러 정보를 획득하고, 이종의 선형 주파수 변조율을 갖는 두 개의 버스트(ξ1, ξ2)를 통해 표적정보를 획득한 뒤, 하기의 모호성 해결 절차를 거침으로써 한 드웰 내에 존재하는 다수의 표적 정보를 모호성 없이 분해하도록 설계하였다.
여기서, fD3은 주파수 변조율을 사용하지 않는 버스트의 수신 주파수로써, 표적의 도플러 주파수()가 탐지된다.
LFM ranging은 비교적 적은 양의 주파수를 한 버스트 시간에 걸쳐 선형 주파수 변조에 사용하기에 세밀하지 못한 거리 분해능을 제공한다. 본 절에서는 거리 분해능의 향상을 위해 LFM ranging과 펄스압축 기술[1],[2]의 접목 방법을 보이고, 거리 모호성 없이 표적 거리를 산출하기 위한 선형 주파수 변조율의 설계 하한 조건에 대해 기술한다.
여기서, RT는 레이다를 통한 거리 측정 시, 노이즈에 의한 측정오차를 무시할 때 가정할 수 있는 실제 표적의 거리이며, m은 PRI(Pulse Repetition Interval) 내의 거리 게이트 수이고, RT(modulo m)는 RT을 m으로 나눠 만들어진 나머지이다. LFM ranging 기술과 펄스압축 기술의 접목을 통해 우수한 거리 분해능을 갖는 표적 거리 RT를 얻기 위해서는 거리분해능이 좋지 못한 LFM ranging을 통해 N 값(RT를 m으로 나누어 만든 정수)을 찾아내고, 각 펄스마다 높은 LFM(Linear Frequency Modulation)을 적용시켜, 우수한 거리분해능을 통해 RT(modulo m)을 측정해낸 후 이미 알고 있는 m을 식 (10)과 같이 이용하여 표적거리를 산출한다. 이를 위해 상세 탐색 빔 파형 중 선형 주파수 변조를 하지 않는 버스트에 대하여 PRI 내에 m개의 거리게이트를 갖도록 펄스압축 파형을 적용시켜, RT(modulo m)을 측정하도록 하였다. N 값의 측정은 식 (11)과 같이 LFM ranging으로 측정되는 표적거리 Rc를 이용하여 정수 형태의 Int[Rc,m]을 얻은 후, 펄스압축 파형(버스트 시간에 대해 선형 주파수 변조 없이 펄스압축 파형[1],[2]을 적용)을 통해 Int[Rc,m]번째 PRI와 Int[Rc,m]−1번째 PRI에서 측정된 거리게이트 중 Rc와 가까운 거리게이트가 속한 PRI를 구함으로써 N 값을 정한다.
그림 4는 모호성 없는 N 값을 갖도록 하는 LFM ranging의 거리분해능 조건을 송수신 신호의 예를 통해 보인다. 10 개(m)의 거리 게이트를 갖는 PRI를 사용하고, 표적 반사 신호가 거리 게이트 8번에서 PRI 주기(m)로 수신되는 예를 도식화하였다. δT > PRI/2인 경우에는 n번째 PRI의 2번째 부터 n+1번째 PRI의 4번째 거리게이트까지 LFM ranging 파형을 통한 측정신호가 수신될 수 있다. 만약 n번째 PRI의 2번째 거리게이트에서 Rc가 측정되었다고 가정하면, 펄스압축 파형을 통해 Int[Rc,10]=n번째 PRI와 Int[Rc,m]−1=n−1번째 PRI에서 측정된 거리게이트 중 Rc와 가까운 n−1번째 PRI를 N 값으로 모호하게 판단할 수 있다. N 값이 모호하면, 식 (10)의 m에 의해 최소 1 PRI 만큼의 큰 거리오차가 발생할 수 있다.
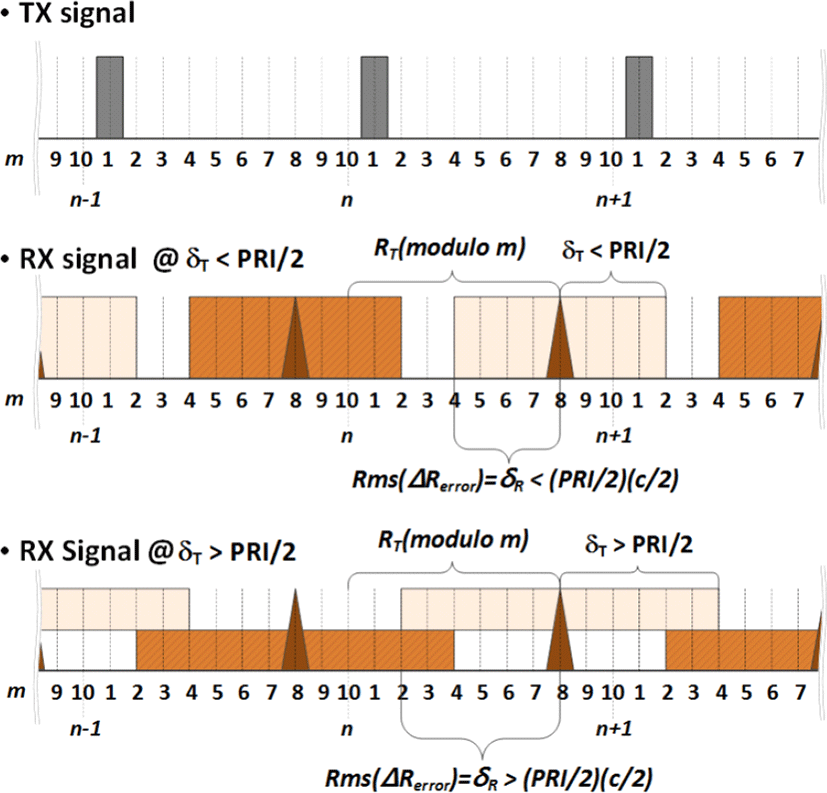
LFM Ranging의 거리 분해능에 대한 조건식 (13)[4]을 적용하면, 그림 4에서와 같이 ΔRerror가 PRI/2에 해당하는 거리 이상을 넘지 않기에 모호성 없는 N 값 측정이 가능해진다.
여기서, ΔRerror은 표적거리 RT와 LFM Ranging으로 측정된 RC와의 거리오차이고, δR와 δT은 LFM Ranging의 거리분해능에 해당하는 거리와 시간이다.
여기서, P은 상세 탐색 빔에서 하나의 버스트 시간을 구성하는 펄스의 개수이고, α는 도플러 분해능을 향상시켜 ξ의 하한 조건이 완화되도록 도플러 신호처리 시 추가해주는 제로패딩(Zero Padding)의 개수이다. 식 (14)는 식 (13)을 만족시키기 위해 LFM ranging에서 설계되어야 하는 선형 주파수 변조율의 하한 조건식을 나타낸다.
HPRF 파형을 사용하는 상세 탐색 빔은 버스트 시간 동안 상승(+)과 하강(−) 그리고 영(0)의 선형 주파수 변조율을 통해 LFM ranging 기법을 설계할 수 있으며, 그림 5는 3가지 선형 주파수 변조율을 갖는 HPRF 파형에 대해 도플러 속도 퍼짐 현상을 시뮬레이션한 결과이다.
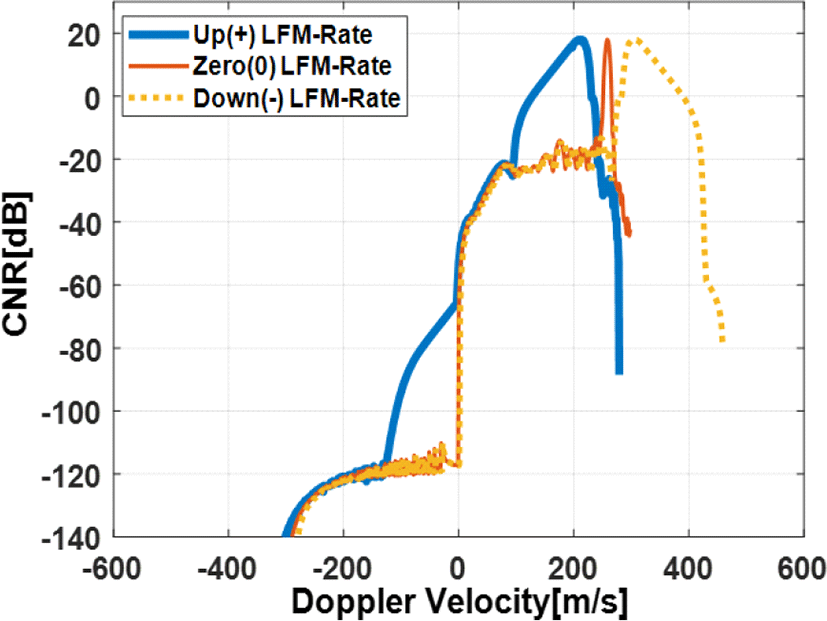
시뮬레이션은 자함의 고도 6 km, 이동속도 300 m/s, 빔 조향 방위각 30°, 고각 −2.4°, 그리고 클러터 모델 Constant gamma 0.1 기준에서 수행되었다. LFM ranging 파형을 수신하여 dechirp 처리하면, 식 (4)와 같이 거리에 대해 송신과 반대 부호의 선형 주파수 변조율(ξ)을 가지며, 도플러 스펙트럼이 퍼지게 된다. 하강(−) 선형 주파수 변조율을 사용하면 그림 5와 같이 관심 속도영역 내로 다량의 클러터 반사 신호가 유입되기에, 본 논문에서는 장거리 표적탐지 시에 우수한 SCR(Signal to Clutter Ratio) 성능을 확보하도록 상승(+)과 영(0)의 선형 주파수 변조율을 LFM Ranging 설계에 사용하였다.
그림 6은 선형 주파수 변조율 +5 MHz/s 운용에 대한 거리와 도플러 차트의 시뮬레이션 결과이다. 상승과 영의 선형 주파수 변조율 사용 시, 표적신호(fD)를 클러터신호(fc)보다 양의 방향으로 크도록 만들어, 표적이 클러터 없는 영역에서 탐지되도록 식 (15)[4]와 같이 설계한다.
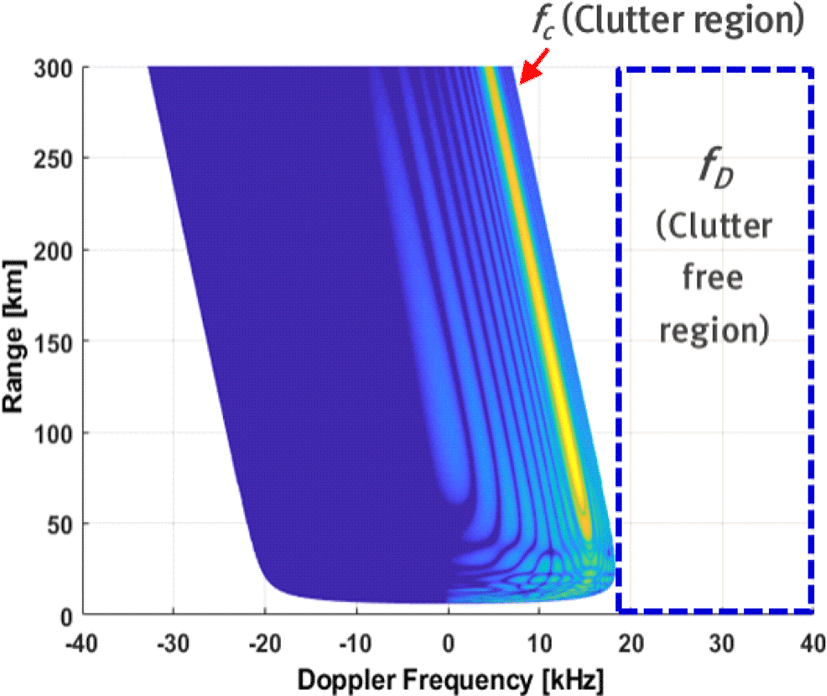
LFM ranging의 거리분해능 향상을 위한 선형 주파수 변조율의 상한 조건식 (14)와 클러터 없는 영역에서 표적탐지를 위한 하한 조건식 (15)를 조합하여 식 (16)의 최종 조건식을 도출할 수 있다.
접근속도 55 m/s 표적을 최대 300 km의 거리까지 클러터 없는 영역에서 탐지하기 위해서는 선형 주파수 변조의 상한선이 1.83 MHz/s가 되어 LFM ranging을 위한 PRF는 P+α가 8,192 개일 때 86.7 kHz 미만으로 선택될 수 있다. 하지만, 그림 3과 같이 설계할 때, 86.7 kHz의 PRF는 위협 표적으로 간주되는 최대 표적접근속도(일반적으로 1,000 m/s)와 자함의 최대 이동속도까지를 만족시키며 운용하기에는 부족한 값이다. 따라서 장거리에 위치한 저 위협 표적(저속표적)에 대해서는 탐지성능에 손해를 가져가면서, 우수한 거리 분해능으로 장거리 위협 표적을 탐지하도록 하는 선형 주파수 변조율의 최적화 설계가 필요하다.
그림 7은 식 (16)을 통해 유도되었으며, 선형 주파수 변조율에 따라 가용한 PRF 도출과 성능 제약의 예시를 나타낸다. 그림 7(a)의 점선은 선형 주파수 변조율에 따라 운용 가용한 최대 PRF 값을 나타내고, 실선은 접근 속도 55 m/s를 갖는 표적에 대해 클러터 신호의 간섭 없이 탐지 가능한 최대거리를 나타낸다. 상세 탐색 빔의 HPRF와 선형 주파수 변조율의 설계는 앞선 각 절들에서 기술되어진 하기의 3가지 고려사항들을 포괄적으로 만족하도록 그림 7의 가용한 PRF와 선형 주파수 변조율들로부터 최적의 값을 찾는다.
고려사항 1: 위협 표적에 대한 관심속도 범위와 작전 시 운용 가능해야 할 자함의 최대속도
고려사항 2: 탐지 표적에 대한 거리 분해능과 표적 탐지거리를 고려한 LFM Ranging의 선형 주파수 변조율
고려사항 3: 저 위협 표적에 대한 탐지성능 열화
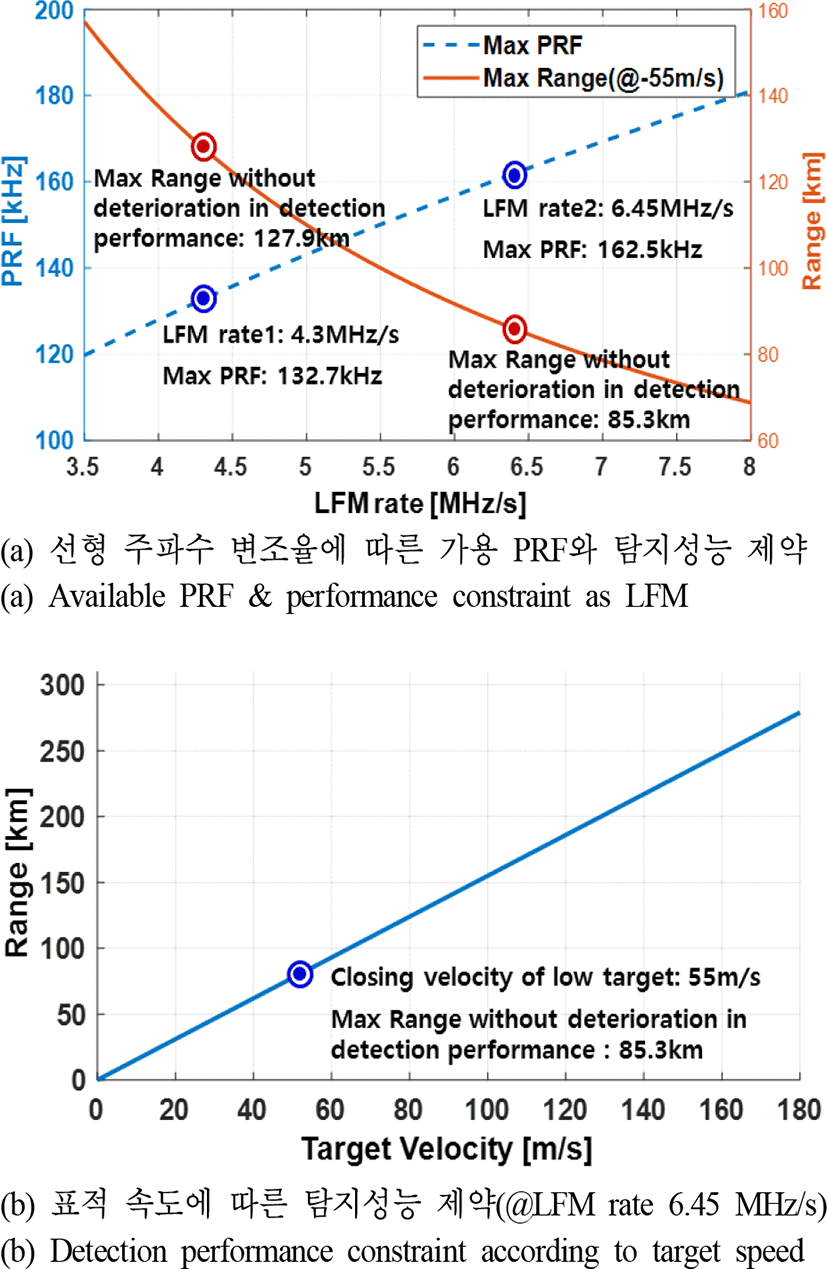
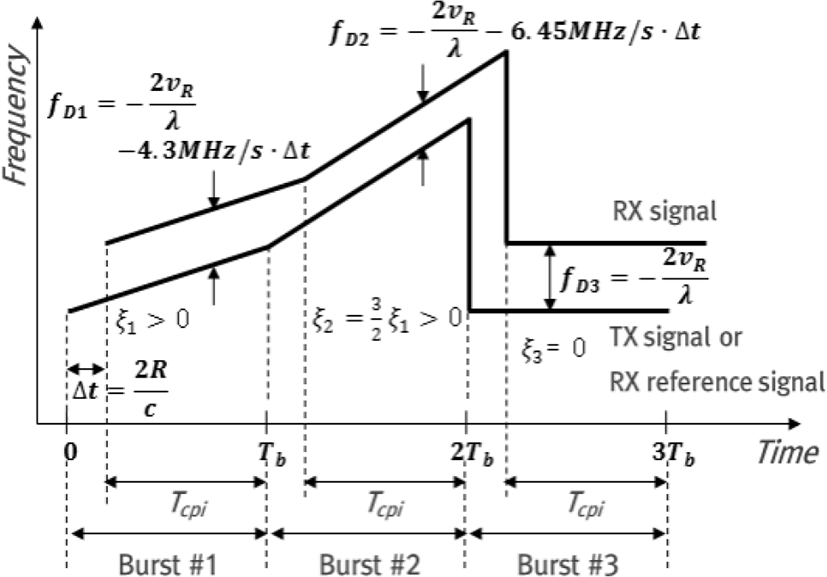
최적의 선형 주파수 변조율의 예로써 식 (8)에 의해 4.3 MHz/s(ξ1)와 6.45 MHz/s(ξ2)를 선정할 수 있으며, 공통적으로 가용한 130 kHz의 HPRF를 선정하여 운용 가능하다. 그림 7(b)는 선형 주파수 변조율 6.45 MHz/s 사용 시 클러터에 의한 간섭 없이 탐지 가능한 최대거리를 보이며, 접근속도 55 m/s의 저속표적은 85.3 km까지이다. 또한, 속도가 높은 위협 표적일수록 클러터 영향 없이 탐지 가능한 최대거리는 증가한다. 그림 8은 예로써 설계된 상세 탐색 빔의 최종 파형으로써 3종의 선형 주파수 변조율을 나타낸다.
그림 8에서 Δt는 표적 거리에 의한 시간 지연이고, TCPI는 동기 신호처리 구간(coherent processing interval)의 시간으로써, dechirp 신호 처리 후 도플러 처리하는 시간 구간이며, Tb는 버스트 시간을 나타낸다.
Ⅴ. 비행 시험을 통한 설계 검증
본 논문에서 제시한 설계 방법을 항공기용 AESA 레이 다에 구현하여 그림 9와 같이 수송기(C-130H)의 램프 도어에 탑재한 후 레이다 후방방사를 통해 표적 탐지 시험을 수행하였다. 시험조건은 해상 클러터 환경 하에서 수송기를 고도 2.5 km에서 −72 m/s의 속도로 이동시켰고, 표적기는 방위각 0 ° 방향에서 고도 2.5 km를 유지하며, 거리 65 km부터 −250 m/s의 속도로 접근시켰다.
레이다 후방방사 환경 하에서 측정한 HPRF 파형의 도플러 스펙트럼은 전방 방사를 기준으로 설계한 그림 3(b)와는 달리 그림 10(a) 형태로 만들어진다. 자함의 레이다가 퇴각속도를 갖기에 주엽클러터 성분은 음의 주파수 성분을 갖는다. 신호처리를 위해 주엽클러터 성분을 0 Hz로 이동시키면 부엽클러터 성분들이 저속의 관심속도영역을 침범하게 되어 시험환경에 의한 성능제약이 발생한다.
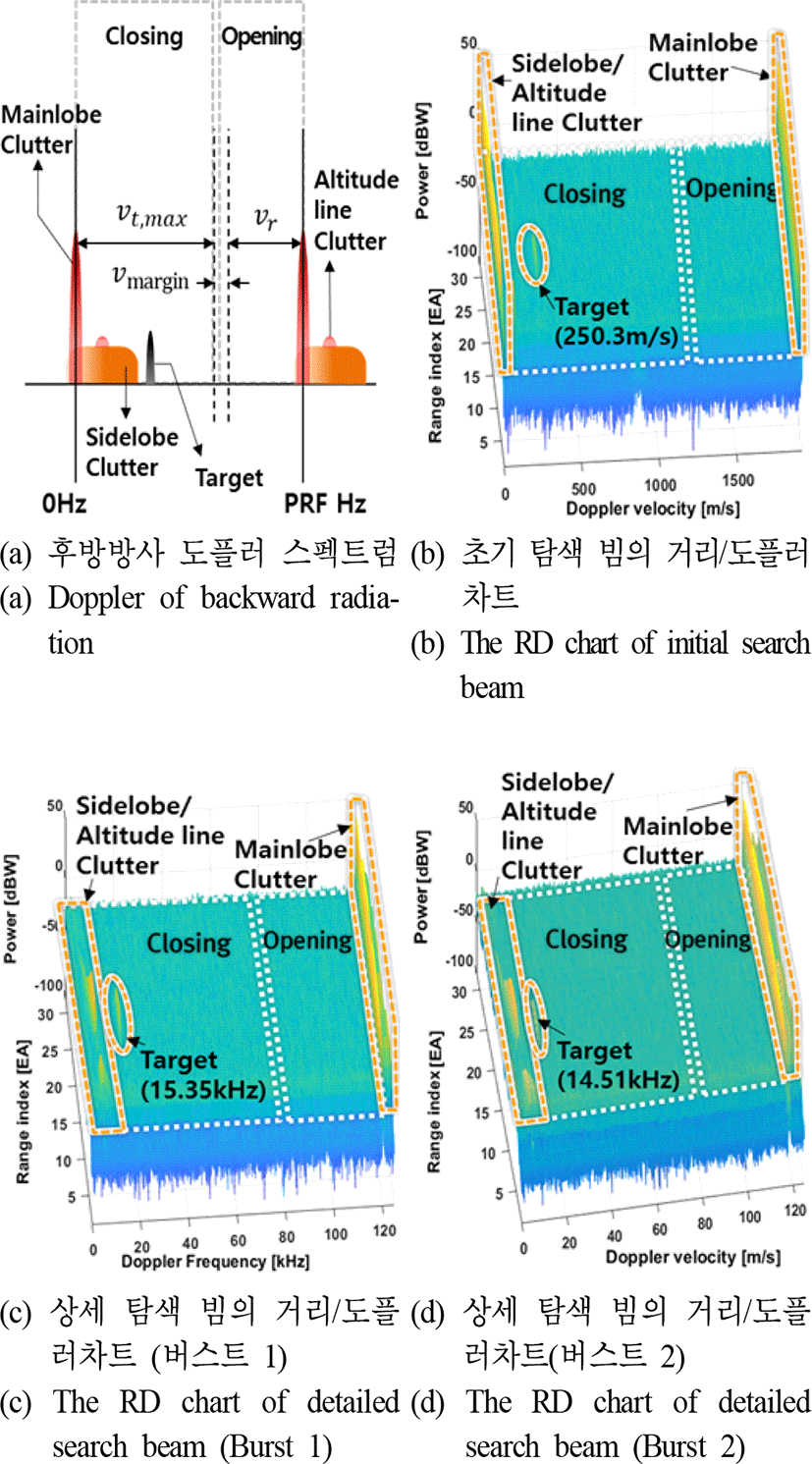
설계 의도에 부합하는 시험 수행을 위해, 부엽클러터에 영향이 없는 속도영역에서 표적기를 운용시켜 시험하였고, 그림 10은 초기 탐색 빔과 상세 탐색 빔의 시험결과를 거리 대 도플러 차트로 보인다. 초기 탐색 빔은 설계된 파형 특성대로 그림 10(b)와 같이 클러터가 없는 도플러 영역에서 −250.3 m/s의 표적기 속도 성분을 탐지하였고, 레이다는 즉각적으로 상세 탐색 빔을 할당하여 그림 10(c) 및 그림 10(d)와 같이 표적을 탐지하였다. LFM ranging을 사용하는 상세 탐색 빔의 첫 번째와 두 번째 버스트 결과를 통해 식 (6)을 이용하여 63 km 이상에서 표적을 성공적으로 탐지하였고, 펄스압축 기술의 접목을 통해 기준 이상의 거리 분해능이 확보됨을 확인하였다. 또한, 그림 10(b)와 그림 10(c)의 클러터 스펙트럼 분포를 비교하여, LFM ranging에 의한 클러터 스펙트럼의 기울어짐 현상이 그림 5의 시뮬레이션 결과와 부합됨을 확인함으로써, 설계된 양의 선형 주파수 변조율을 사용할 시에 클러터 신호의 간섭 없이 표적의 탐지가 가능함을 확인하였다. 또한, 장거리 위협 표적에 대한 빠른 탐지와 클러터 간섭 없는 영역에서의 모호성 없는 정보 추출, 그리고 표적의 반사 신호에 대한 신호처리 결과인 거리 대 도플러 차트가 비행시험 시나리오에 따른 예측 값과 일치됨을 확인함으로써, 본 논문에서 제시한 빔 운용 방식과 탐지 파형의 설계 방법이 유효함을 확인하였다.
Ⅵ. 결 론
본 논문은 효율적으로 장거리 위협 표적을 탐지하도록 하는 빔 운용 설계와 각 빔 운용 별 파형 설계 방법에 대해 제시하였다. 이를 위하여 탐지하고자 하는 장거리 위협 표적의 특성을 기반으로, 초기 탐색 빔에서 표적의 도플러 속도와 각도 정보를 빠르게 얻고, 초기 탐지 빔에서 표적이 존재하는 드웰에 대해서만 상세 탐색 빔으로 표적의 거리 정보를 확보함으로써, 자원의 효율적 운용을 통해 장거리 위협 표적을 빠르게 탐지하는 빔 운용 정책을 제시하였다. 클러터 간섭 없이 노이즈 간섭만 존재하는 환경 하에서 장거리의 낮은 SNR 신호를 탐지하도록 LFM ranging 기술을 이용한 HPRF 파형을 설계하였고, 거리 분해능 향상을 위한 펄스압축 기술의 접목 방법과 HPRF 값 및 LFM ranging 선형 주파수 변조율의 최적화된 설계 방법을 사용하였다. 수송기(C-130H)를 이용한 비행 시험을 통해 위협 표적으로 인식되는 관심 속도영역 표적의 탐지 시험을 수행하였고, 시험결과와 설계치를 분석하여 제시된 설계 방법의 유효성을 검증하였다. 논문에서는 항공기 AESA 레이다를 예로 하여 설계 방법을 제시하였으며, 이는 공중에서 빠르게 이동하는 플랫폼 하의 AESA 레이다가 파형 설계 시 가장 고려할 점이 많기 때문이다. 따라서 제시된 빔 운용 및 파형 설계 방법은 지상과 해상의 이동 또는 고정 플랫폼에 설치되어 운용하는 AESA 레이다에도 공통적으로 적용할 수 있다. 본 논문은 하드웨어 성능이 동일한 상태에서, 장거리의 위협 표적을 빠르고 효율적으로 탐지함으로써 장거리 표적에 대한 교전 능력을 향상시킬 것으로 판단한다.












