PDF Download
PubReader
Export Citation
Email the Author
Share Facebook
Share Twitter
Cited by 7 Articles
Metrics (View:6,496)
Ⅰ. 서 론
최근 무기 기술 체계의 발달과 함께 스텔스 항공기의 생존성 향상을 위한 전자기 산란 특성 연구의 중요성이 확대되고 있으며, 항공기의 피탐지 성능의 사전 확보를 위해 레이다 단면적(radar cross section: RCS)을 측정하거나 전자기 수치해석을 통해 계산하는 연구가 활발히 진행되고 있다[1]～[4].
전자기 수치해석의 경우, RCS를 알고자 하는 표적의 CAD 모델이 있다면 간편하게 시뮬레이션을 진행할 수 있는 장점이 있고, 현재 Method of Moment(MoM), Multilevel Fast Multipole Method(MLFMM)[5], High-Order Basis Function(HOBF)[6],[7] 등의 고성능 알고리즘이 개발 및 상용화되어 있다. 하지만 전자기 수치해석 문제의 특성상 해석 대상의 전기적 크기가 커질수록 연구실 단위의 컴퓨팅 자원으로는 계산하는 데에 한계가 있으며, 고주파 대역에 특화된 광선 추적법[8]과 같은 근사 방법이 사용되지만, 정확도를 보장할 수 없는 단점이 존재한다.
반면에 RCS 측정은 Vector Network Analyzer(VNA)와 안테나의 가용 대역이 적합하다면 주파수에 따라 측정 시스템의 수정 없이 수행할 수 있다. 항공기의 경우, 크기가 크고 복잡하여 원거리장 측정을 위해 야외에서 넓은 범위의 측정 환경을 구축해야 하며, 주변 지형, 물체 등에 의한 산란 영향을 제어해야 한다[9].
이에 대한 대안으로 항공기 축소 모형을 이용한 RCS측정이 제안되어 실험실 단위에서 복잡한 설비 없이 측정을 수행할 수 있다[10]. 그러나 축소 모형의 경우, 축소 비율의 제곱에 비례해 RCS 값이 감소하여 실측 상황에서 측정값이 매우 낮아지게 되어 정확한 측정이 어렵다[11]. 또한, 산란파의 대부분이 되돌아오는 평판[12]과 달리 항공기는 산란원이 다양하고 일정하지 않은 복잡한 구조이므로 전자파 무반사실(anechoic chamber)과 같이 주변 환경의 산란 영향과 잡음을 제거할 수 있는 시설을 구축해야 하는 어려움이 있어, 측정의 자유도와 오류 보정 측면에서 개선이 필요하다.
본 논문에서는 비 챔버 환경에서 복잡한 구조의 축소 모형에 대한 모노스태틱 RCS의 측정 시스템 구성 및 측정 방법을 제시한다. 기존 RCS 측정 시스템이 필연적으로 가지는 정확도에 대한 한계를 코히어런트 적분, 코히어런트 뺄셈, 시간 게이팅의 후처리 과정을 통해 개선하였다. 실크기 항공기의 MLFMM을 이용한 수치해석 계산 결과와 1/30배 축소 모형의 비 챔버 환경에서의 측정결과, 잡음 및 간섭 신호가 보정된 챔버 환경에서의 측정결과를 통해 측정의 정확도를 비교하였다.
Ⅱ. 측정이론 및 원리
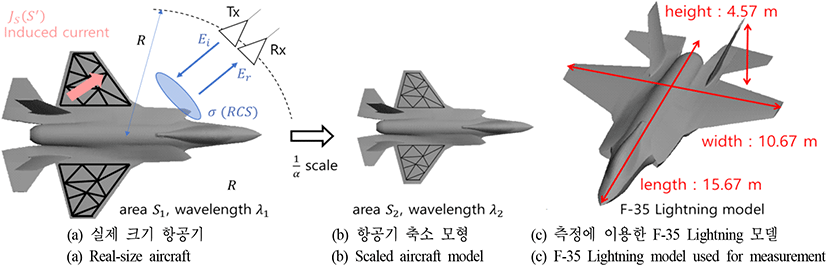
그림 1과 같이, 1/α배 비율 축소 모형을 표적 주파수 대역보다 α배 높은 주파수에서 측정하면 파장 대비 물체의 크기 비율이 동일하므로 전기적으로 동일한 문제로 치환할 수 있고, 평판 모형의 경우 식 (1)과 같이 RCS를 정의할 수 있다.
|Ei|, |Er|은 각각 입사파와 산란파의 전기장 크기를, R은 측정 거리를, JS(S')은 전기장에 의해 유도된 전류를, k는 파수(=2π/λ)를, η는 공기의 고유 임피던스를 의미한다. 이때, 모형이 1/α배 축소되고, 주파수가 α배 증가하면, 파장(λ)이 α배 되고 면적이 1/α2배 되므로 식(1)에 의해 RCS는 1/α2배 되어 줄어들게 된다.[11]
본 논문에서는 1/30배 축소 모형을 사용하므로 RCS는 1/900배가 되어 실제 크기 모형에 비해 측정상황에서 VNA를 통해 측정되는 S 파라미터 값이 29.54 dB 낮아지게 된다. 이에 따라 표적에 의한 전자기 산란 신호가 주변 잡음이나 간섭의 영향에 취약해지며, 실험 장비 및 구성의 하드웨어적인 한계점을 극복하기 위해 측정 시스템 구성상의 추가적인 보완이 필요하다.
RCS 측정은 식 (2)의 레이다 방정식[13]에서 수신 전력 Pr(f)와 RCS σ(f)의 관계를 이용한다. VNA를 통해 수신 단에서 측정되는 복소 신호 크기 Vr(f)와 RCS 값 σ(f)의 관계를 복소 보정 벡터 vcal(f)로 정의한다. vcal(f)는 상대적인 S 파라미터 값인 Vr(f)를 절댓값인 σ(f)로 변환해주는 변수로, 이론적인 RCS 값을 알고 있는 calibration 대상(3차원 물체의 경우, 일반적으로 구)의 측정값(Vr,cal(f))과 이론값(σcal(f))의 크기 차이만큼을 측정 대상의 측정값에 보상하여 RCS의 절댓값을 도출한다[13].
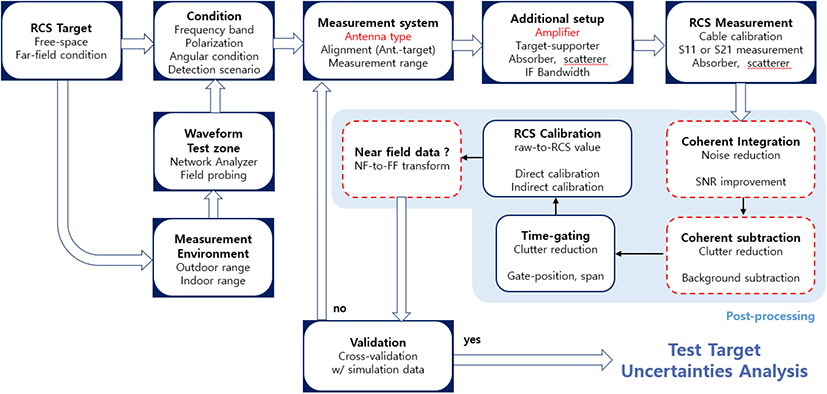
그림 2는 본 논문에서 제안하는 축소 모형의 RCS 측정 과정을 나타낸 개념도이다. 비 챔버 환경의 경우, 잡음 신호 레벨이 챔버 환경에 비해 높고, 천장, 바닥, 그 외 요인에 의한 산란 영향이 존재한다. 항공기 축소 모형은 모노스태틱 측정 환경에서 입사파 대부분이 산란되어 되돌아오지 못하므로 다른 산란체의 영향에 의해 측정값이 실 제와 크게 다를 수 있다. 따라서 측정 신호의 잡음 대비 신호 크기(signal-to-noise ratio, SNR)를 향상시키고, 주변 산란 체의 영향을 제거하는 후처리 과정이 중요하다.
본 논문에서 제안하는 후처리 과정의 구성은 그림 2의 파란색 배경으로 표시하였다. 기존 RCS 측정 시스템의 후처리 과정인 시간 게이팅(time-gating)과 RCS calibration(파란 실선 테두리)에 코히어런트 적분, 코히어런트 뺄셈, 원거리장 변환의 세 단계(빨간 점선 테두리)를 추가하였다. 후처리 과정을 적용하기 위한 MATLAB 코드는 직접 구현하였다.
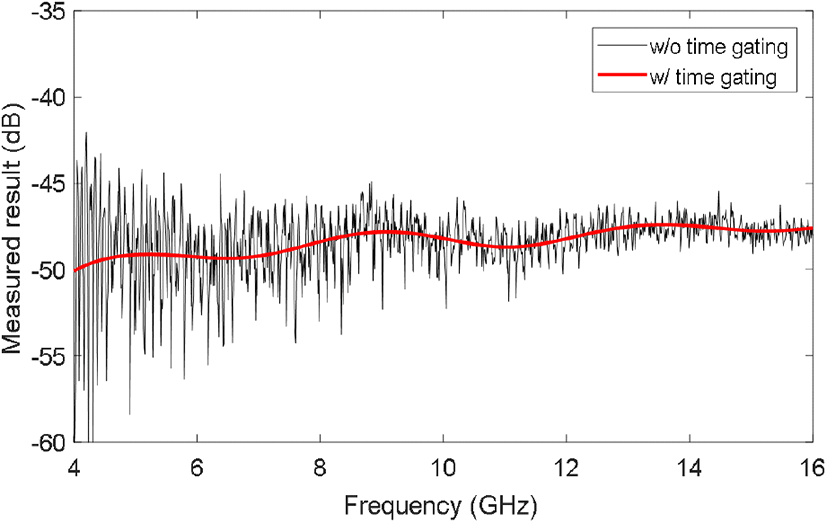
코히어런트 적분은 측정 신호의 SNR을 향상하기 위해 반복 측정한 신호를 더해주는 것으로 잡음에 의해 흔들리는 신호를 안정화하고 정확도를 향상한다. 시간 게이팅은 물체가 놓인 거리 영역의 측정값만 필터링하여 다중 반사 및 표적 외 거리의 산란체 영향을 제거한다[14]. 그림 3과 같이 주파수 영역에서 시간 게이팅된 결과를 보면 주변 잡음의 영향이 줄어 측정값의 편차가 감소하는 것을 알 수 있다. 하지만 측정 대상과 동일한 거리에 있는 산란 체의 영향은 시간 게이팅으로 제거할 수 없으므로 코히어런트 뺄셈을 통해 시간(또는 거리)영역에서 복소수 뺄셈을 해줌으로써 제거할 수 있다. 원거리장 기반의 개념인 RCS를 측정하기 위한 compact range 챔버의 경우에는 평면파를 인위적으로 만들어 원거리장을 구현하지만[11] 실험실 단위의 비 챔버 환경에서는 근거리장 측정이 일반적이므로 원거리장 변환을 적용하였다[9],[14].
Ⅲ. 측정결과 및 분석
그림 4는 측정에 사용한 항공기 축소 모형과 측정 환경을 나타낸 것으로, 측정상의 편의를 위해 1/30배 항공기 축소 모형(52.2 cm×35.6 cm×15.2 cm)을 500 MHz～9 GHz, 10 MHz 간격의 주파수 범위에서 측정하여 실크기 항공기의 VHF 대역 모노스태틱 RCS를 도출하였다. 모노스태틱 측정 환경은 송신 및 수신 안테나의 위치가 동일하므로 측정 물체에 대해 송수신 안테나가 나란하게 위치하여 S_21 값을 측정하였다[15].
안테나는 500 MHz～3GHz(DRH-500M-003G, MTG사), 2 GHz～18 GHz(DRH-002G-018G, MTG사)의 두 종류의 double ridged horn 안테나를 사용하였다. 측정 편파는 V-V 편파로 고정하였고, 입사 각도는 0°(정면) - 180°(후면), 5° 간격의 범위로 설정하였다. RCS 계산에 사용한 calibration 물체로는 30 cm 반지름의 구를 사용하였다. 측정 신호의 SNR 향상을 위해 증폭기(ZVA-403GX+, Minicircuit사)를 이용하였고, 3.6 m의 거리에서 측정한 근거리 장 결과를 원거리 장 결과로 변환하였다[14].
본 절에서 항공기 정면 기준 주파수 영역 모노스태틱 RCS 결과 및 특정 주파수에서의 입사 방향에 따른 모노스태틱 RCS 결과를 도출하였다.
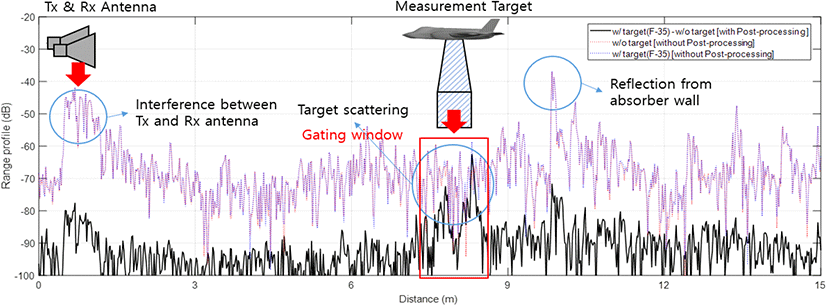
그림 5는 본 논문에서 제안한 후처리 과정의 효과를 비 교하기 위해 제안한 후처리 과정을 사용하지 않은 경우(시간 게이팅, RCS calibration만 포함)와 사용한 경우(5단계 모두 포함)의 거리 영역 측정값을 비교한 것이다. 주파수 영역에서의 측정값을 역 푸리에 변환하여 시간 영역 측정값을 구한 후 시간 축에 광속을 곱하여 거리영역을 나타내었다.
제안한 후처리 과정을 사용하지 않은 경우에는 측정 대상이 존재하는 위치에서의 산란된 전자파의 측정값이 약 -65 dB로 안테나 간에 직접적으로 간섭되는 신호나 주변 물체에 의한 산란 영향보다 약 20～25 dB 정도 낮게 나타난다. 이는 2-1절에서 언급한 축소화에 의한 RCS 감소 효과이고, 산란되어 수신 안테나로 되돌아온 신호 중에서 표적에 의한 신호가 다른 간섭 신호에 묻혀버려 표적 대상의 유무에 관계없이 측정값에 변화가 없음을 확인할 수 있다.
제안한 후처리 과정을 적용하면 그림 5의 검정색 실선과 같이 측정 대상을 제외한 다른 요인에 의한 간섭이나 잡음의 영향이 감소하고, 측정 대상에 의한 수신 신호의 크기를 가장 크게 만들어 간섭, 잡음 대비 신호의 크기(signal-to-interference and noise ratio: SINR)를 향상할 수 있다. 후처리한 결과에서 측정 대상의 위치에 시간 게이팅 함수를 적용하여 물체에 의한 RCS 영향을 도출할 수 있다.
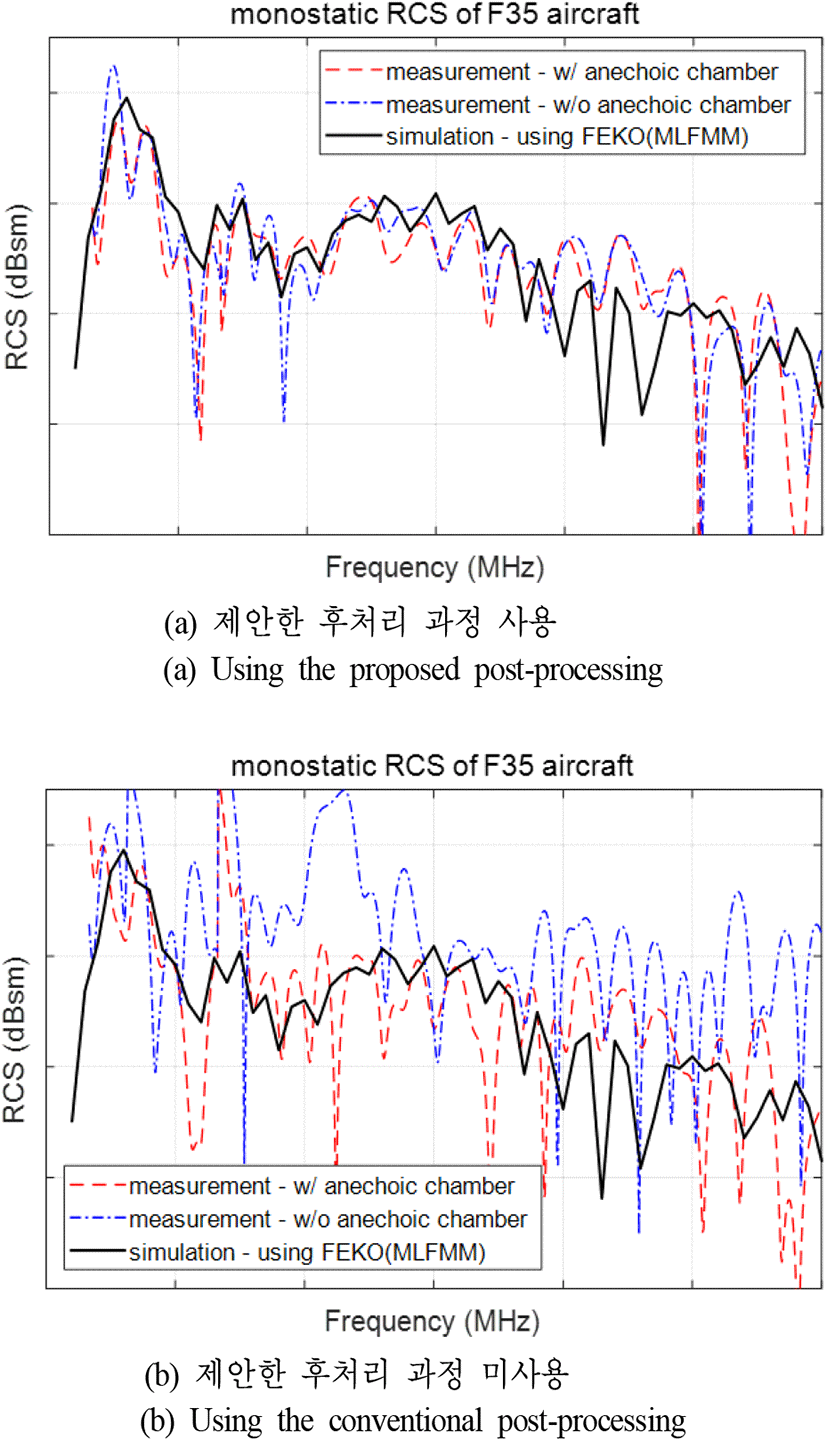
그림 6은 앞서 시간 게이팅한 결과를 주파수 영역으로 푸리에 변환한 후 RCS calibration을 적용해 RCS 값을 도출한 최종 결과이다. 그림 6(a)는 제안한 후처리 과정을 사용한 것으로, 챔버 유무에 관계없이 시뮬레이션 해석 값과 유사한 결과를 도출할 수 있다. 반면에 그림 6(b)는 제안한 후처리 과정을 사용하지 않은 결과로, 챔버 환경에서의 측정 결과가 비 챔버 환경에 비해 간섭 영향이 적어 시뮬레이션 결과에 비교적 일치하지만 큰 오차를 가진다. 다수의 간섭원의 영향이 측정 대상에 비해 상대적 으로 매우 커서 수신된 전력의 대부분이 간섭 신호에 의한 것이다. 따라서 시간 게이팅 단계에서 간섭 신호의 영향을 제거하면 측정 대상에 의한 신호의 크기가 매우 작아서 잡음의 크기와 구분되지 않는다. 이로부터 그림 6(b)와 같이 측정값이 부정확하게 된다.
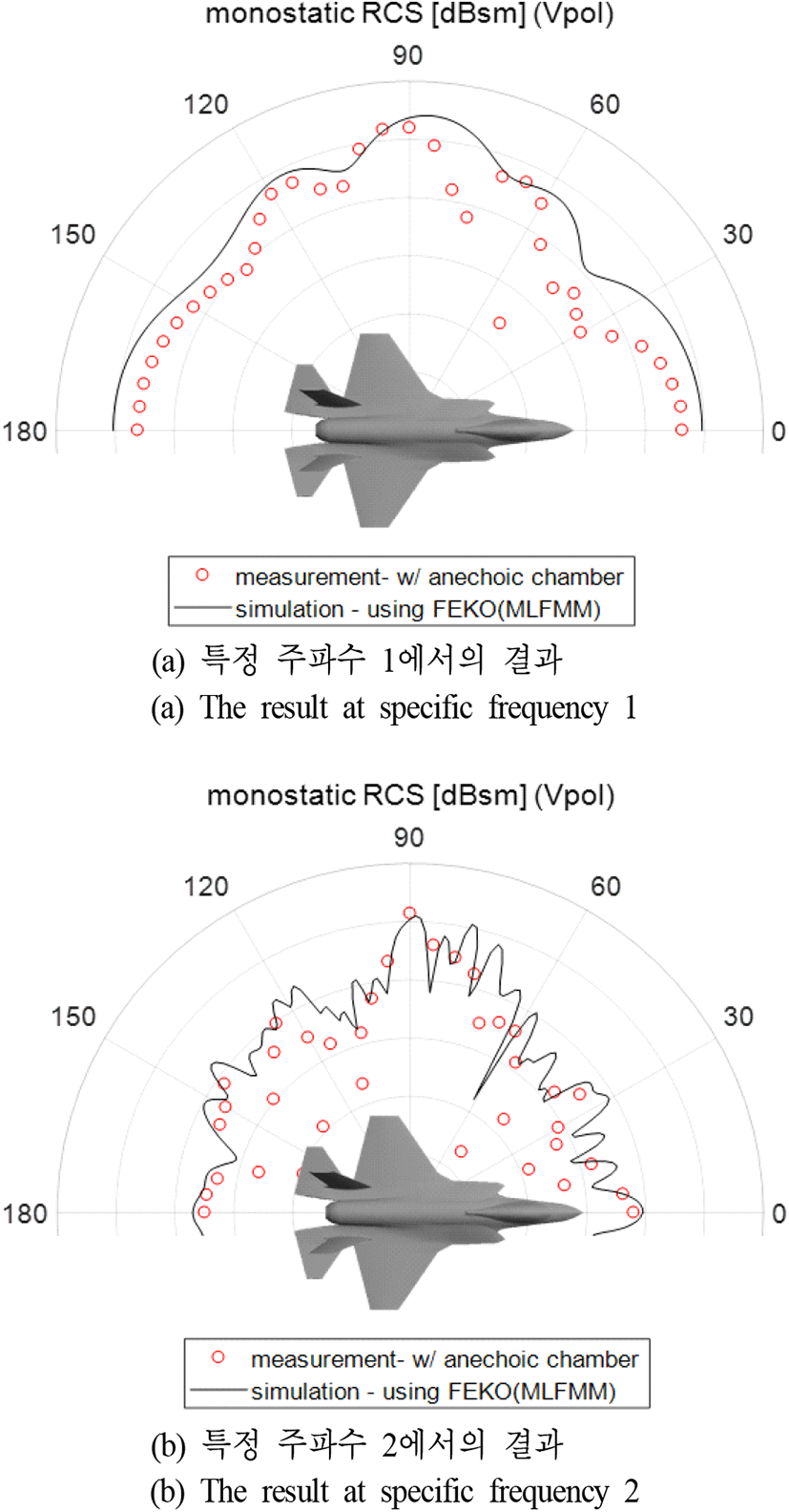
그림 7은 본 논문에서 제안한 후처리 과정을 적용해 특정 주파수에서 여러 입사방향별 모노스태틱 RCS를 측정 한 결과이다. 측정하는 항공기 모델의 각도를 변화하며, 앞선 측정과 동일한 과정과 방법으로 진행하였다. 특정 주파수에서의 측정 결과와 시뮬레이션 결과를 비교해 보면 높은 일치율을 보인다. 이는 주파수와 입사 방향에 따라 크게 달라질 수 있는 산란 특성의 경향성을 높은 정확도로 측정해 낼 수 있음을 의미한다.
Ⅳ. 결 론
본 논문에서는 실험실 단위의 비 챔버 환경에서 잡음 및 간섭 요인의 영향을 감소하기 위한 후처리 과정을 제안하여 복잡한 구조를 가지는 항공기 축소 모형의 모노스태틱 RCS 측정 방법을 제시하였다. 해당 방법을 통해 항공기 축소 모형이 복잡한 구조와 낮은 RCS를 가져 상대적으로 작은 전자기 산란 경향을 가짐에도 불구하고, 높은 측정 정확도를 도출하였다. 이를 이용하면 전기적 거대 구조의 축소 모형 측정뿐만 아니라, 드론, 무인 항공기 등의 작은 RCS를 갖는 물체의 측정과 수치해석으로 풀 수 없는 고주파수 대역에서의 산란 특성 분석에도 활용할 수 있다.
