Ⅰ. 서 론
차량용 레이다는 차량 주변 사물의 존재를 파악해 주차에 도움을 주거나, 자동 긴급제동 시스템(autonomous emergency braking: AEB)에 사용될 수 있으며 관통하는 성질이 있으므로 교차로에서 교차하는 차량을 발견할 수 있으므로 교차 차량 알림(Cross Traffic Alert: CTA)에 활용될 수 있다. 특히, 라이다(lidar) 및 광학 감지기(카메라 등) 와 비교했을 때 날씨에 영향을 받지 않기 때문에 비 혹은 안개에 의해 전방 관측이 어려운 상황에서도 동작할 수 있다는 장점이 있다.
차량용 레이다는 최근에 연구되기 시작했지만, 레이다 영상 기법은 군용으로 널리 사용됐다. 기존의 합성개구레이다(Synthetic Aperture Radar: SAR)는 주로 측방 관측(side-looking)을 통해 영상 형성을 수행한다[1]. 그 이유는 전방 관측(forward-looking)은 분해능이 현저히 떨어지기 때문이다[2]. 따라서 바이스태틱(bistatic) 합성개구레이다를 통해 분해능을 키우거나[3]~[9] 빔 폭(beam width)이 좁은 실개구레이다(real aperture radar: RAR)로 기계적 조향을 통해 전방을 관측하는 스캐닝 레이다(scanning radar)[10]~[15]가 연구된 바 있다. 그러나 스캐닝 레이다의 특성상 거리 방향의 분해능은 송신하는 신호의 대역폭에 의해 제한되며, 거리 방향에 수직인 방향의 분해능은 빔 폭에 의해 결정된다는 단점이 있다.
이동하면서 전방의 지면을 탐색하기 위한 스캐닝 레이다가 군용으로 쓰인 바 있는데, 예를 들어 고해상도 Frequency Modulated Continuous Wave(FMCW)를 활용한 브림스톤(brimstone) 미사일을 꼽을 수 있다[16]. 여기서도 역시 거리 방향 분해능은 FMCW의 대역폭을 조절하여 개선시킬 수 있지만, 거리 방향에 수직인 방향의 분해능은 안테나의 방위각 방향 빔 폭에 의해서 결정된다. 따라서 거리 방향과 비교하면 그에 수직인 방향의 분해능은 현저히 떨어진다.
본 논문에서는 전방 관측 특히, 곡선운동을 하는 차량용 전방 관측 역산란 합성 영상 형성에 대해 다룬다. 선형 주파수 변조(linear frequency modulated) 펄스 열 신호를 그림 1과 같이 차량의 앞부분으로 송신하는 것을 가정하였다. 그림에서 검은색 점은 점 표적을 나타내고, 파란색 점은 레이다의 장착 위치를 나타낸다. 또한, 반원으로 표시된 영역은 레이다의 빔 폭을 나타낸다. 빔 폭이 넓어 그림에 표시된 점 표적들이 누적 시간(integration time) 동안에는 항상 빔 안에 들어와 있음을 가정하였다. 이러한 곡선운동을 하는 상황에서의 합성개구레이다에 관한 연구가 진행된 바 있다[17]~[20]. 참고문헌 [17]은 완전한 원형의 경로로 진행할 때 합성개구레이다 영상 형성에 대해 다뤘고, 참고문헌 [18]~[20]은 곡선운동을 할 때 합성개구레이다 영상 형성의 가능성 및 영상 형성 알고리즘을 제시하였다. 하지만 직선운동이 아닌 상황에서 전방 지면에 대한 영상을 형성하는 차량용 영상레이다는 아직 연구가 진행되지 않았다.

본 논문에서는 영상 형성을 위해 시간 영역 상관관계(time domain correlation: TDC) 기법이 사용되었다. 이 기법을 제안하는 이유는 다른 기법들에 비교해 계산량이 많지만, 그만큼 영상의 거리 및 각도 분해능을 최대한으로 개선할 수 있기 때문이다. 모의실험 결과에서는 직선운동을 했을 때 같은 기법을 적용한 영상 결과와의 비교를 통해 곡선운동에서도 영상이 형성됨은 물론 전방 관측이 가지는 한계점인 좌우의 구별도 가능하게 됨을 확인할 수 있다.
Ⅱ. 전방 관측 영상레이다 신호 모델링
그림 1과 같이 차량이 곡선운동을 하면서 전방의 바닥 면을 관측할 때 단일 안테나를 가진 레이다가 차량의 앞 부분에 장착되어 선형 주파수 변조(linear frequency modulated) 신호를 펄스 반복 주기(pulse repetition interval: PRI)마다 송수신하여 측정 데이터를 얻는다고 가정하였다. 이때, 레이다의 빔 폭은 차량이 움직이는 동안 모든 표적에 대해 신호를 수신할 수 있을 정도로 넓다고 가정하였다. 그림 2에 송신하는 신호를 시간-주파수 축에 도시하였다. S는 펄스 폭, B는 대역폭 Tp는 펄스 반복 주기를 나타낸다. p번째로 송신하는 신호를 수식으로 나타내면 다음과 같다.
위에서 K=B/S를 나타내고, fc는 반송 주파수, t̃p는 다음과 같다.
위에서 연속 시간 변수 t가 가지는 범위는 p번째 펄스에 대해 다음과 같다.
p번째 펄스를 송신한 다음 다수의 표적으로부터 반사되어 돌아왔을 때 잡음 없이 수신된 신호는 다음과 같다.
위에서 g(xk,yl)는 지면이 격자로 이루어져 있다고 가정했을 때 격자의 x, y 위치에 따른 반사율을 나타내며, X, Y는 각각 표적이 존재하는 위치의 x축 방향의 격자 수, y축 방향의 격자 수를 의미한다. 여기서 xk, yl은 지면을 격자로 나눈 위치를 나타내므로 표적이 존재하는 위치를 의미하지는 않는다. 만약 해당하는 격자에 표적이 존재하면 g(xk,yl)의 값이 0이 아니지만 아무런 표적이 존재하지 않는다면 해당하는 g(xk,yl)의 값은 0이다. 또한, τ는 표적에 맞고 돌아오는 왕복 시간을 의미하고, 아래와 같이 표적의 위치 xk, yl에 대한 함수로 표현될 수 있다.
위에서 R(t,xk,yl)는 레이다와 표적 간의 거리를 나타낸다. 표적은 고정되어 있어서 움직이지 않는다고 가정했을 때 레이다가 장착된 차량이 곡선 운동하기 때문에 거리가 시간에 의한 함수로 표현된다. 이 논문에서는 차량의 주행기록계가 정확하여 차량의 위치는 안다고 가정한 상태로 차량 전방 지면의 영상을 얻는다.
수신기의 믹서를 통과한 다음 샘플링된 후에 얻어진 신호 z0 (tf,p)결과는 다음과 같다.
위에서
를 의미하고, 이산화된 시간 tf,p 및 왕복 시간 τ는 아래와 같다.
tf는 이산화된 fast-time이고, f번째 샘플의 시간을 가리킨다. tf가 가지는 시간의 범위는 샘플링을 시작하는 시점으로부터 송신하는 펄스가 끝나는 시간까지인 S까지 이다. 샘플링을 시작하는 시점은 영상을 형성하고자 하는 영역을 고려해서 2Rmax/c(여기서 Rmax는 영상에서 나타날 가장 먼 표적과의 거리를 나타내며 c 펄스의 전달속도를 나타낸다)로 정한다. 또한 tf의 길이는 F라고 가정한다.
위의 k, l, f, p는 모두 이산 변수들이므로 위의 식과 더불어 잡음 벡터 n을 고려하면 아래의 식과 같이 행렬과 벡터의 곱과 합으로 나타낼 수 있다.
위에서 벡터 z=[z(t1,1),...,z(tF,1,), z(t1,2),..., z(tF,P)]T는 잡음이 더해진 상태의 측정치를 나타내며, P는 송신하는 펄스의 총 개수를 나타낸다. 또한, 벡터 g=[g(x1,y1),..., g(xX,y1), g(x1,y2),..., g(xX,yY)]T는 각각의 위치 격자에 해당하는 반사율을 나타낸다. 만약 격자에 표적이 없다면 0의 값을 가진다. 행렬 A는 다음과 같다.
위에서
를 나타낸다. 따라서 벡터 z의 크기는 FP×1이고, A의 크기는 FP×XY이며, 벡터 x의 크기는 XY×1이 되는 것을 알 수 있다. 또한, 위의 식과 같이 믹서를 통과한 측정치를 벡터와 행렬의 꼴로 나타내면 벡터 g를 벡터 z를 통해 추정하는 것으로 생각할 수 있다.
Ⅲ. 시간 영역 상관관계를 통한 역산란 합성 영상 형성
본 논문에서는 시간 영역 상관관계(time domain correlation: TDC) 기법[2]을 통해 곡선운동을 하는 상황에서 전방 관측 역산란 합성 영상을 형성한다. 이는 합성개구레이다 영상 기법 중 비교적 덜 알려진 기법이지만, 계산량이 큰 대신 영상의 분해능을 최대한 개선시킬 수 있다는 장점이 있다. 시간 영역 상관관계 기법은 정합 필터링을 공간변화 시스템(space-variant system)에 대하여 콘볼루션이 아닌 상관관계(correlation)로 구현한 기법이다. 잡음이 고려된 연속 시간의 p번째 송신한 펄스로부터 얻은 측정 치를 zp (t)라고 하면 시간 영역 상관관계로부터 얻은 x, y위치에 따른 영상 ĝ(xk,yl)는 다음과 같이 얻어진다.
위에서 는 xk, yl에 반사율 1을 가진 단일의 점 표적이 존재한다고 가정했을 때의 측정치를 모사한 것으로, 측정된 zp (t)와 켤레복소수를 취하여 곱하고, 시간에 대하여 적분함으로써 상관관계를 계산한다. 또한, 총 P개의 펄스를 송신하여 측정치를 얻기 때문에 각 펄스에 대한 상관관계의 총합을 얻는다. 따라서 모사된 측정치와 다수의 표적으로부터 형성된 측정치와의 상관관계의 절댓값이 클수록 큰 반사율을 가진 표적이 xk, yl에 존재함을 알 수 있으며, 반대로 그 값이 작다면 해당하는 위치에는 표적이 존재하지 않음을 알 수 있다. 측방관측의 상황에서는 가 k와 l 즉, 표적의 위치에 따라 거의 바뀌지 않기 때문에 식 (13)이 콘볼루션으로 표현되므로 공간 불변 시스템(space-invariant system)에 대한 정합 필터링을 적용할 수 있다. 하지만 전방 관측에서는 위치에 따라 측정치가 크게 바뀌므로 위치에 맞는 측정치를 모사하여 상관관계를 구함으로써 정합 필터를 공간변화 시스템에 대해서 구현할 수 있다.
위에서 설명된 식 (13)을 이산화된 시간 축에 대해서 표현하면 식 (10)~식 (12)에 의해 다음과 같이 간단하게 벡터 g를 얻기 위한 정합 필터링 결과를 얻어낼 수 있다.
위에서 (·)H는 켤레 전치를 의미한다.
전방 관측 영상 형성을 위해 각 위치에 대한 측정치 각각에 대해서 모두 상관관계를 계산하여 영상을 얻어내는 시간 영역 상관관계 기법도 한계가 존재한다. 전방을 관측할 때 좌우 대칭으로 표적이 존재한다면 그 두 표적은 완전히 일치된 측정치를 제공하기 때문에 구별할 수 없다. 즉, 끼리 일치하기 때문에 같은 상관관계 값으로 계산된다. 하지만 차량이 곡선운동을 한다면 좌우의 측정치가 다르므로 구별할 수 있으므로 영상에서 좌우의 구별이 가능하다. 따라서 차량의 곡선운동에 대한 경로가 주어져 있다고 가정한다면 앞선 절에서 나타난 A 행렬을 레이다 측정치 없이 만들 수 있으므로 곡선운동의 상황에서도 영상 형성이 가능하다. 또한, 곡선운동을 할 시에는 직선운동을 하는 상황에 비교해 좌우 구별이 가능하므로 분해능이 개선된다. 시간 영역 상관관계는 정합 필터링이 공간변화 시스템에 적용된 기법이기 때문에 신호처리 이후의 신호 대 잡음 비를 최대화한다. 따라서 신호와 같은 크기의 잡음이 주어진 상황(0 dB의 신호 대 잡음 비를 가진 잡음), 잡음이 신호보다 강한 상황(−10 dB의 신호 대 잡음 비를 가진 잡음)에서도 영상이 형성되는 것을 모의실험에서 확인할 수 있다.
시간 영역 상관관계의 계산 복잡도는 점근 표기법으로 O(FPXY)을 따른다[21]. 따라서 영상화하고자 하는 표적 영역이 넓을수록, 측정치 벡터의 길이가 길수록 계산량이 기하급수적으로 증가하게 된다.
Ⅳ. 모의실험 결과
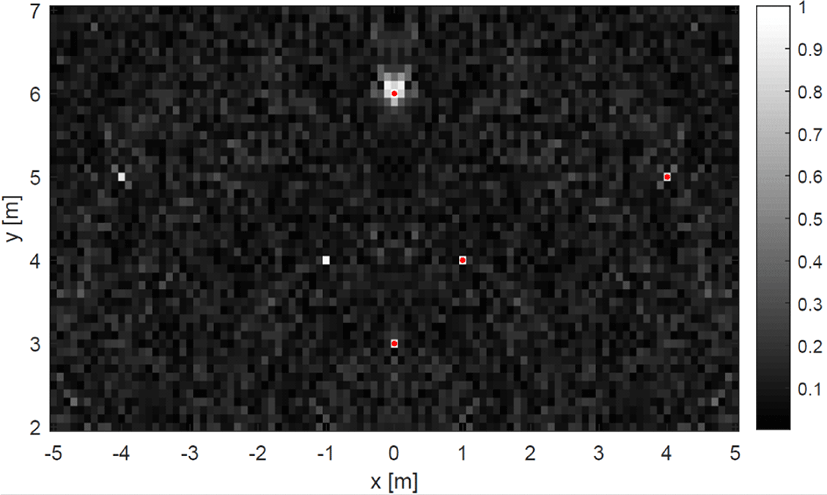
본 논문에서는 점 표적 네 개를 차량 주변에 배치한 다음 그림 3과 같이 직선 주행할 때와 곡선 주행할 때 각각에 대해 제안하는 기법인 시간 영역 상관관계 기법을 적용하여 얻은 결과 영상을 비교한다. 그림 3에서 푸른색 원은 직선 주행할 때 차량의 경로를 나타내며, 붉은색 원은 곡선 주행할 때 차량의 경로를 나타낸다. 이전 절에서 제시된 이산화 된 시간인 tf,s에 따라 경로를 도시하였다. 또한, 검은색 사각형으로 점 표적을 표시하였다.
x축은 차량이 레이다를 작동시키는 순간의 우측으로 향하는 축으로 정의하였고, y축은 차량이 향하는 방향으로 정의하였다. 따라서 z축은 지면을 뚫고 나오는 방향이다. 레이다의 위치를 (0,0,0)이라고 했을 때 점 표적의 z축 방향 위치는 레이다의 장착 높이가 h일 때 표적들은 바닥에 놓여있음을 가정하면 -h가 된다. 점 표적들의 (x,y)위치는 각각 (0,3), (1,4), (4,5), (0,6)으로 정하였다.
모의실험에서 쓰인 파라미터들이 표 1에 제시되었다. 제시된 파라미터에 따라 fast-time 샘플의 수 F 및 송신하는 펄스의 개수 P가 결정된다.
영상 형성 알고리즘은 이전 절에서 언급한 바와 같이 시간 영역 상관관계가 사용되었으며, 측정치가 각각 잡음이 적은 상황(10 dB의 신호 대 잡음 비를 가진 잡음)과 신호와 같은 크기의 잡음이 주어진 상황(0 dB의 신호 대 잡음 비를 가진 잡음) 잡음이 신호보다 강한 상황(−10 dB의 신호 대 잡음 비를 가진 잡음)에 대해 영상 결과를 얻었다.
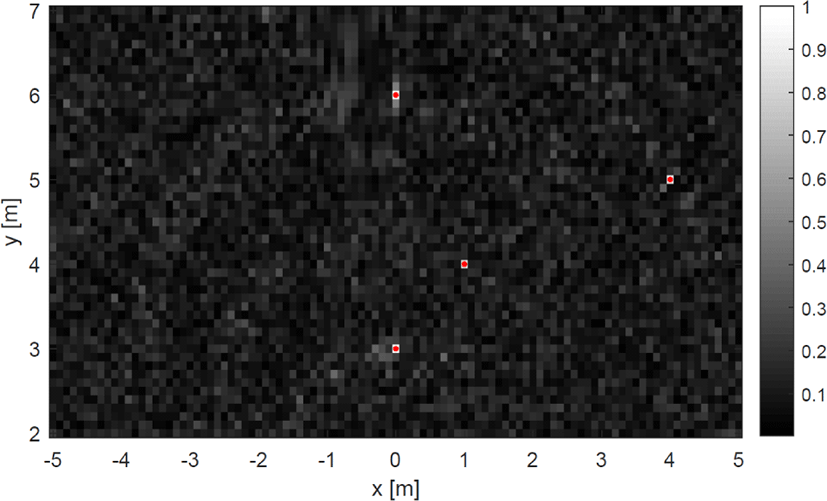
그림 4 및 그림 5는 측정치의 신호 대 잡음 비가 10 dB 일 때 차량의 움직임에 따른 영상 결과를 나타낸다. 붉은색 점으로 점 표적의 실제 위치를 영상과 함께 표시하였으며, 정규화된 영상이기 때문에 가장 큰 값을 가지는 픽셀값이 1이다. 따라서 1에 가까운 큰 값을 가질수록 표적이 그 부분에 존재함을 나타내며, 0에 가까운 값을 가질수록 그 부분에는 표적이 없음을 나타낸다. 또한, 레이다의 빔 폭은 차량이 움직이는 동안 모든 표적에 대해 신호를 수신할 수 있을 정도로 넓다고 가정하였다. 직선운동을 할 때는 좌우의 표적이 같은 거리변화를 가지기 때문에 좌우를 구별할 수 없다. 따라서 그림 4에서 좌측에는 점 표적이 존재하지 않는데도 있는 것으로 영상이 밝게 나타나 영상이 좌우가 대칭되어 나타나는 것을 확인할 수 있다. 반면에 곡선운동을 할 때는 좌우의 구별이 가능해진 것을 그림 5를 통해 확인할 수 있다. 특히, (0,6)에 존재하는 표적이 직선운동을 할 때보다 곡선운동을 할 때 해상도가 눈에 띄게 개선된 것을 확인할 수 있다. 정량적으로 해상도의 개선 정도를 분석하기 위해 (0,6)에만 표적이 존재할 때의 x축 방향으로의 점 분산 함수(point spread function : PSF)를 직선운동할 때와 곡선운동할 때 얻어 그림 6에서 비교하였다. y축 방향으로는 거리 해상도에 의해 해상도가 결정되어 두 점 분산 함수가 비슷하므로 x축에 대한 점 분산 함수만 비교하였다. 검은색 점선이 직선운동을 할 때 얻은 점 분산 함수이고, 빨간색 실선이 곡선운동을 할 때 얻은 점 분산 함수이다. 곡선운동을 할 때 주엽(main-lobe)의 두께는 작아져서 해상도가 개선되지만, 부엽(side-lobe)의 크기는 커지게 됨을 확인할 수 있다. 주엽의 −3 dB 폭은 직선운동을 할 때는 0.24 m이지만, 곡선운동할 때 0.015 m로 향상되었다. 또한, 점 분산 함수가 비대칭으로 나타난 이유는 좌측으로 회전하기 때문에 좌우가 다른 상관관계 값을 가지기 때문이다.
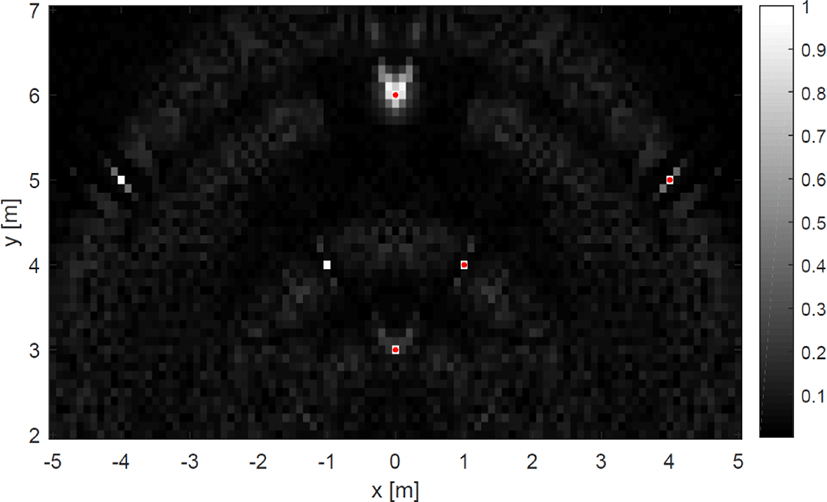

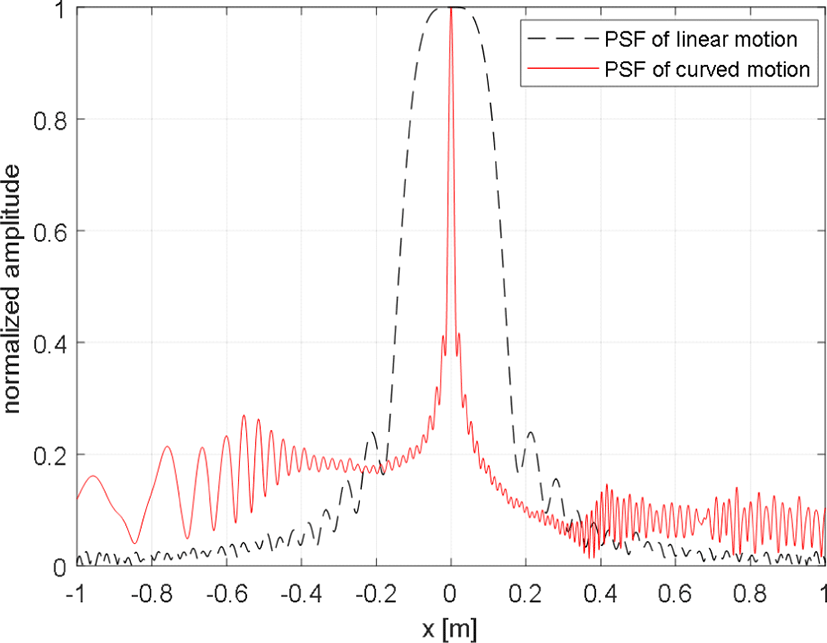
그림 7 및 그림 8은 측정치의 신호 대 잡음 비가 0 dB일 때 차량의 움직임에 따른 영상 결과를 나타낸다. 신호와 잡음이 같은 수준임에도 불구하고, 신호 대 잡음 비가 10 dB일 때와 흡사한 영상 결과를 얻을 수 있었다. 이것은 시간 영역 상관관계가 정합 필터이기 때문에 필터링 후의 신호 대 잡음 비가 최대화되기 때문이다. 따라서 시간 영역 상관관계는 잡음에 강건함을 알 수 있다.
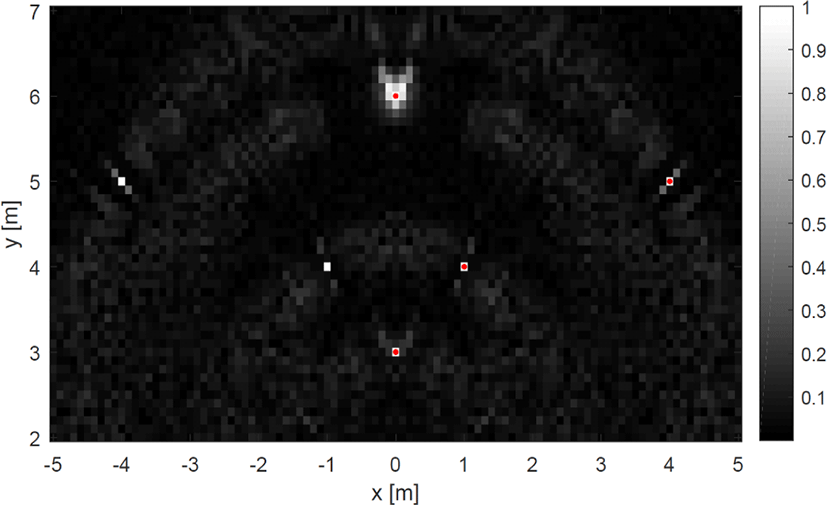
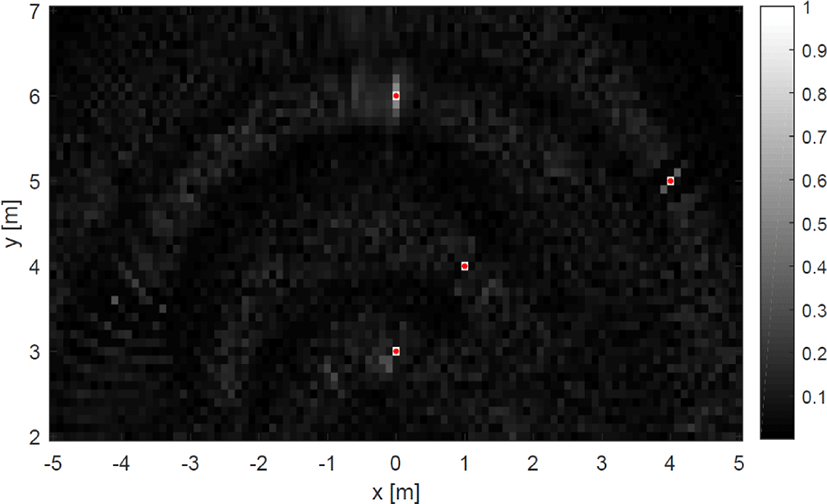
그림 9 및 그림 10은 측정치의 신호 대 잡음 비가 −10 dB 일 때 차량의 움직임에 따른 영상 결과를 나타낸다. 여기서도 역시 직선운동일 때보다 곡선운동일 때 시간 영역 상관관계를 적용한 것이 해상도도 개선되며, 좌우의 구별이 가능한 것을 확인할 수 있다. 그러나 잡음이 신호보다 큰 상황에서는 곡선운동일 때 형성된 영상에서 잡음의 영향이 더 크게 나타남을 알 수 있다. 즉, 차량이 곡선 주행할 시에는 정합 필터링을 거친 다음 나타나는 주엽의 두께는 작아서 해상도는 개선되지만, 부엽의 크기는 직선운동일 때보다 조금 더 높은 레벨을 가지기 때문에 잡음이 커질수록 부엽의 크기에 의한 영상의 성능 저하가 더욱 두드러져 나타난다. 하지만 측정치의 신호 대 잡음 비가 −5 dB 이상만 되어도 이런 문제점은 크게 완화되기 때문에 곡선운동을 하는 상황일지라도 여전히 잡음에 강건하다고 할 수 있다.
또한, 평균 계산시간 및 영상의 엔트로피 값을 구하기 위해 몬테 카를로(Monte Carlo) 모의실험을 10,000회 수행하여 평균값을 취했다. 3.00 GHz, 6개 코어인 CPU의 PC에서 MATLAB을 통해 영상을 얻는데 평균적으로 0.6939초가 소요되었다. 이 계산 시간은 단순히 AH를 z에 곱하는 시간뿐만 아니라, A행렬을 생성하는 시간도 포함한다. 엔트로피값의 계산 결과가 비교가 표 2에 제시되었다. 영상의 엔트로피는 다음과 같이 식 (14)에서 구한 ĝ의 함수로 정의된다[22].
| Motion\SNR | −10 dB | 0 dB | 10 dB |
|---|---|---|---|
| linear motion | 7.8155 | 7.1155 | 6.8827 |
| curved motion | 7.9880 | 7.5979 | 7.4433 |
위에서 이며, ĝ(k)는 벡터 ĝ의 k번째 원소를 의미한다. 모의실험 결과, 신호 대 잡음 비가 클수록 차이가 더 두드러지며, 항상 곡선운동할 때 만들어진 영상의 엔트로피가 큰 것을 알 수 있다. 이는 앞서 점 분산 함수의 비교, 분석을 통해 알 수 있듯이 곡선운동 시에는 주엽의 −3 dB 빔 폭은 작아지지만, 부엽의 크기가 커지기 때문에 영상의 픽셀이 가지는 절댓값이 0에서 0.2 사이의 값을 가지는 픽셀이 많아지면서 엔트로피가 증가한다.
Ⅴ. 결 론
본 논문에서는 곡선운동을 하는 차량용 전방 관측 역산란 합성 영상 형성에 대해 다뤘다. 시간 영역 상관관계 기법을 사용함으로써 기존의 합성개구레이다가 가지는 전방 관측의 낮은 해상도를 개선할 수 있었다. 또한, 직선운동 상황에서는 좌우가 구별되지 않는 문제점이 있지만, 곡선운동 상황에서는 좌우가 구별된다는 장점이 있으며, 점 분산 함수의 비교를 통해 해상도가 개선되는 것을 확인하였다. 그러나 영상의 엔트로피 측면에서는 부엽의 크기가 커지기 때문에 엔트로피가 증가하게 된다.
TDC는 분해능을 높이는 대신에 계산량이 크다는 단점이 있다. 행렬 A의 크기는 측정치의 길이와 지면을 나누는 격자 수에 의해 결정되기 때문에 실시간 영상생성을 위해서는 계산 복잡도를 고려한 파라미터 설정이 필요하다. 긴급제동 시스템의 경우, 특히 더 빠른 연산이 요구되는데, 처음에는 넓은 영역에 적은 격자 수로 저해상도 영상을 얻은 다음 반사율이 높은 표적이 존재하는 부근에만 격자 수를 늘려 원하는 부분만 고해상도 영상을 얻는 계층적 격자 수 변화 알고리즘과 같은 연구가 앞으로 이루어져야 한다. 또한, 영상에서 표적의 위치에 따라 표적 주변으로 상이 퍼지는 방향이 다름과 동시에 해상도 역시 다른 것을 확인할 수 있는데, 이것에 대한 분석 및 차량의 곡선 주행 방향과 각속도에 따른 해상도의 변화에 관한 분석연구가 이뤄져야 할 것으로 보인다. 더불어, 본 논문에서는 차량 전방의 바닥 영상을 획득하는 2차원 영상만을 다뤘기 때문에 3차원으로 확장하여 3차원 영상을 얻는 연구가 앞으로 이뤄져야 할 것이다.














