Learning-Based People Counting System Using an IR-UWB Radar Sensor

Choi, Jae-Ho; Kim, Ji-Eun; Kim, Kyung-Tae

doi:10.5515/KJKIEES.2019.30.1.28

J. Korean Inst. Electromagn. Eng. Sci. 2019; 30(1):28-37

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2019.30.1.28

특집논문/SPECIAL EDITIONS

IR-UWB 레이다 센서를 이용한 학습 기반 인원 계수 추정 시스템

최재호, 김지은, 김경태^†

Learning-Based People Counting System Using an IR-UWB Radar Sensor

Jae-Ho Choi, Ji-Eun Kim, Kyung-Tae Kim^†

Author Information & Copyright ▼

포항공과대학교 전자전기공학과

Department of Electrical and Electronic Engineering, Pohang University of Science and Technology

^†Corresponding Author : Kyung-Tae Kim (e-mail: kkt@postech.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 14, 2018; Revised: Dec 12, 2018; Accepted: Dec 24, 2018

Published Online: Jan 31, 2019

요약

본 논문에서는 임펄스 무선-초광대역(impulse-radio ultra wideband: IR-UWB) 레이다를 이용하여, 특정 공간 내 존재하는 인원들의 계수를 실시간으로 추정하는 시스템을 제안한다. 제안된 시스템은 정확한 인원 계수 추정을 수행하기 위해 학습 기반의 분류 기법을 사용한다. 즉, 인원수에 의해 달라지는 반사 신호의 패턴에 따라 특징 벡터 데이터베이스(feature vector database)를 형성하고, 형성된 데이터베이스를 이용하여 분류기(classifier)를 학습시킨다. 학습된 분류기를 통해 새로운 신호 수신 시 자동으로 인원 계수 추정을 수행할 수 있다. 실내 환경에서 0명부터 10명까지 변하는 사람들을 실시간으로 추정함으로써, 본 논문에서 제안된 시스템의 효용성을 검증하였다.

Abstract

In this paper, we propose a real-time system for counting people. The proposed system uses an impulse radio ultra-wideband(IR-UWB) radar to estimate the number of people in a given location. The proposed system uses learning-based classification methods to count people more accurately. In other words, a feature vector database is constructed by exploiting the pattern of reflected signals, which depends on the number of people. Subsequently, a classifier is trained using this database. When a newly received signal data is acquired, the system automatically counts people using the pre-trained classifier. We validated the effectiveness of the proposed algorithm by presenting the results of real-time estimation of the number of people changing from 0 to 10 in an indoor environment.

Keywords: IR-UWB Radar; People Counting; Feature Extraction; Classification

Ⅰ. 서 론

최근 사물 인터넷(Internet of Things: IoT) 기술의 발전에 따라 이를 스마트 시티(smart city) 구축에 활용하려는 연구가 활발히 진행 중에 있다^[1]. 그중에서 센서(sensor) 기술은 주변 상황에 대한 정보를 자동적으로 획득할 수 있게 하는 기술로서, 스마트 시티의 환경 구축을 위한 핵심 요소 중 하나이다. 예를 들어, 센서를 이용한 도로 위 교통 정보 파악을 통해 지능형 교통 체계(intelligent transportation system: ITS) 구축이 가능하다^[2]. 또한 특정 공간 내 사람들의 재실․부재 여부 혹은 밀도 정보를 감지함으로써 전등, 에어컨 등 실내 에너지 자원을 효율적으로 사용할 수 있다^[3].

이중, 실내 환경에서의 인원 계수 추정 및 밀도 감지는 다양한 센서를 통해 수행될 수 있다. 대표적으로 영상 센서 및 열선 감지(passive infrared: PIR) 센서를 활용한 연구가 존재한다^[4]～[6]. 그러나 영상 센서의 경우 주위 환경에 의해 성능이 좌우되며, 사생활 침해의 문제로 인해 사용자들에게 불쾌감을 주는 단점이 있다. 또한 PIR 센서는 높은 오경보율(false alarm probability)과 낮은 거리 해상도(range resolution)로 인하여 다수 사람의 밀도 감지에 적합지 못하다^[7],[8].

그에 반해, IR-UWB 레이다는 넓은 대역폭을 사용하여 정밀한 거리 해상도를 보유한 센서로, 주위 환경에 상관없이 일정한 성능을 유지하는 장점을 가지고 있다^[9]. 또한, 사생활 침해의 문제로부터 자유롭다는 점으로 인해 최근 IR-UWB 센서를 활용한 인원 계수 추정 연구가 활발히 이루어지고 있다. 대표적으로, 사람 신호 추출을 통한 인원 계수 추정 기법이 존재한다^[10]～[12]. 상기 기법은 레이다 수신 신호로부터 각 사람들의 반사 신호를 탐지하고, 탐지된 신호 군집의 개수를 계산하여 인원 계수를 추정한다. 그러나 이는 신호 탐지에 필요한 최적의 임계값(threshold)들을 정하기가 매우 어려우며, 사람들이 임의로 움직일 경우 정확한 추정이 불가능하다. 이러한 문제점들을 해결하기 위해 심층 신경망(deep neural network: DNN)^[13] 및 최대 우도 추정(maximum likelihood estimation: MLE) 기반 기법^[14] 등이 연구되었으나, 이들은 매우 많은 양의 표본 데이터(training data)를 요구하므로 실제 적용에 어려움이 있다.

본 논문에서는 특징 벡터 추출 및 학습 기반의 식별 과정을 통해 적은 양의 표본 데이터로도 높은 정확도를 보이는 인원 계수 추정 시스템을 제안한다. 제안된 시스템은 크게 전 처리, 특징 벡터 형성, 분류기 학습, 인원 계수 추정의 단계로 이루어져 있다. 먼저, 레이다 수신 신호로부터 클러터(clutter) 신호를 제거하고, 거리에 따른 신호 감쇠 보상을 수행하여 전 처리를 수행한다. 다음으로, 추출 알고리즘을 사용하여 전 처리된 신호로부터 사람 신호를 추출한다. 이 과정에서 특정 단일 임계값을 사용하여 사람 신호를 추출하는 기존 기법과 달리, 제안된 시스템은 다양한 임계값에 따라 사람 신호를 추출한 후, 각각의 추출된 신호로부터 사람 수에 의존하는 신호 정보들을 계산한다. 이후, 신호 정보들 간의 잉여 정보를 차원 감소 과정을 통해 제거함으로써 특징 벡터(feature vector)를 형성할 수 있다. 마지막으로, 형성된 특징 벡터 데이터베이스(database)를 이용하여 분류기를 학습시킨다. 학습된 분류기를 이용함으로써, 새로운 신호의 특징 벡터가 입력될 시 학습 기반의 인원 계수 추정이 가능하다.

제시한 시스템의 효용성 검증을 위하여 실제 실내 환경에서의 실험을 진행하였다. 실험은 반지름 9.5 m의 반원 공간에서 진행되었으며, 최소 0명에서 최대 10명까지의 사람들이 자유롭게 활동하는 상황에서 실시간 인원 계수 추정을 수행하였다. 각 사람 수 당 약 3분에 해당하는 8,640개의 수신 펄스(pulse)를 획득하고, 이로부터 특징 벡터 데이터베이스를 형성하여 분류기를 학습하였다. 학습된 분류기는 ±1명의 오차 감안 시 100.0 %의 정확도로 인원수를 추정할 수 있었다.

Ⅱ. 신호 전 처리

본 절에서는 획득한 IR-UWB 레이다 수신 신호에 전 처리를 수행하여 특징 벡터 형성에 적합한 형태로 가공하는 과정을 설명한다. 세부적으로, 신호 전 처리는 이동 평균 기법(running average method), 정합 필터링(matched filtering), 적응 이득 제어(adaptive gain control: AGC)의 과정들로 이루어져 있다.

2-1 수신 신호 모델

IR-UWB 레이다는 임펄스(impulse) 신호를 송신한 뒤 사람 및 주위 환경으로부터 반사된 P개의 신호를 수신한다. 특정 시간 t에 대한 k번째 레이다 수신 펄스 r_k (t)은 다음의 식 (1)과 같이 지연된 송신 신호의 선형 결합(linear combination) 형태로 정의된다^[7].

r k (t) = ∑ i = 1 P a i s (t − τ i) + N (t),

(1)

여기서 s(t)는 레이다의 송신 신호, a_i는 반사체의 레이다 단면적(Radar Cross Section: RCS)에 따른 반사 계수(reflectivity), τ_i는 거리에 따른 지연 시간(time delay), N(t)는 잡음(noise) 신호를 나타낸다. k는 슬로우 타임(slow time) 방향의 인덱스(index)로서, 펄스 반복 주파수(pulse repetition frequency: PRF)에 따른 시간 정보를 의미한다.

2-2 이동 평균 기법

식 (1)의 IR-UWB 레이다 수신 신호는 벽, 천장, 기둥 등 사람이 아닌 물체로부터 반사되어 발생하는 클러터(clutter) 신호로 인해 사람 신호가 가려진다. 이 때, 클러터는 움직임이 거의 없기 때문에 사람 신호에 비해 시간에 따른 변화가 미비한 특징을 가진다. 이동 평균 기법은 이러한 특성을 이용하여 시간 당 변화가 적은 클러터 신호를 억제하는 기법으로 식 (2)와 같이 정의된다^[14].

c k (t) = α c k − 1 (t) + (1 − α) r k (t), y k (t) = r k (t) − c k (t),

(2)

여기서 c_k (t)는 k번째 펄스에 대한 클러터 신호로서 이전 펄스의 클러터 신호와 현재의 수신 신호 펄스를 이용하여 계산할 수 있다. α는 가중 인자로서 시간 당 변화가 적은 신호를 어느 정도 클러터 신호로 간주할지의 비율을 결정한다. c_k (t)를 계산하고 이를 레이다 수신 신호 r_k (t)로부터 차분함으로써 이동 평균 필터가 적용된 y_k (t)를 얻을 수 있다.

2-3 정합 필터링

수신 신호에 이동 평균 기법을 적용하여 클러터 신호를 제거한 후, 정합 필터링(matched filtering)을 수행함으로써 신호 대 잡음 비(Signal to Noise Ratio: SNR)를 더욱 상승시킬 수 있다. 정합 필터링은 송신 신호와의 콘벌루션(convolution) 연산을 통해 구현되며, 식 (3)과 같다.

m k (t) = y k * (− t) * s (t),

(3)

여기서 m_k (t)는 y_k (t)로부터 정합 필터링을 수행한 신호이며 s(t)는 레이다 송신 신호이다.

2-4 적응 이득 제어

IR-UWB 레이다 신호는 거리에 따른 신호 감쇠가 존재하기 때문에, 레이다로부터 사람의 위치가 멀어질수록 반사 신호의 세기가 약해지게 된다. 따라서 제안된 인원 계수 추정 시스템에서는 적응 이득 제어(adaptive gain control: AGC) 과정을 통해 상기 문제점을 보상해줌으로써 신호의 거리 의존성을 최소화한다. AGC 과정은 식 (4)와 같이 m_k (t)에 거리 보상 신호 q(t)를 곱하여 줌으로써 수행된다.

p k (t) = m k (t) ⋅ q (t) . q (t) = (c t 2) β .

(4)

여기서 p_k (t)는 적응 이득 제어 과정을 통해 최종적으로 전 처리가 수행된 k번째 펄스를 의미한다. c는 빛의 속도, β는 신호 세기 감쇠 정도를 조절하는 상수이다.

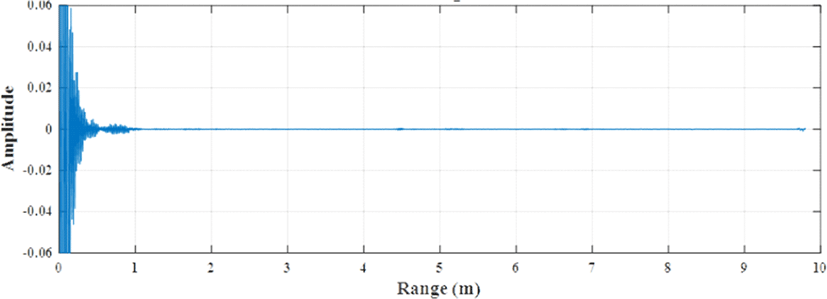
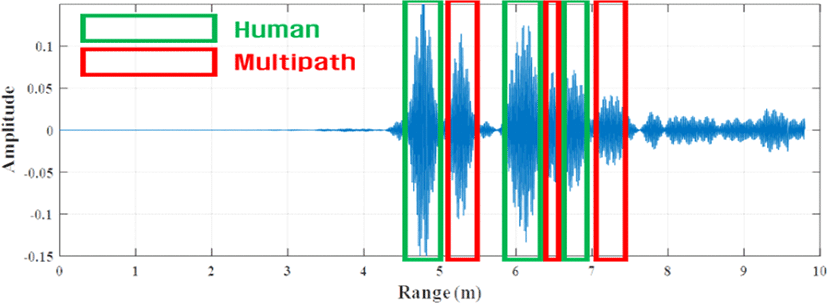
그림 1과 그림 2는 공간 내 3명의 사람들이 존재하는 상황에서 수신된 IR-UWB 레이다 원 신호(raw signal) 및 전 처리된 신호를 나타낸다. 그림 1의 원 신호(raw signal)에 전처리를 수행할 시, 그림 2와 같이 사람 신호가 드러나게 됨을 확인할 수 있다. 최종적으로, 전 처리된 IR-UWB 레이다 신호는 사람 신호, 멀티패스(multipath) 신호, 잡음 신호로 이루어져 있다. 이러한 멀티 패스 및 잡음 신호는 정확한 계수 추정을 방해하는 요인이 되므로 이를 해결하기 위한 추가적인 처리 과정이 필요하다.

그림 1. | Fig. 1. 전 처리 수행 전의 IR-UWB 레이다 신호 | IR-UWB radar signal before applying signal preprocessing.

Download Original Figure

그림 2. | Fig. 2. 전 처리 수행 후의 IR-UWB 레이다 신호 | IR-UWB radar signal after applying signal preprocessing.

Download Original Figure

Ⅲ. 특징 벡터 추출 및 분류기 학습

본 절에서는 전 처리된 신호 펄스를 묶어 프레임을 구성한 후, 형성된 각 프레임으로부터 특징 벡터를 형성하는 과정을 설명한다. 먼저 임계값을 변화시켜 가며, 변형된 CLEAN 알고리즘을 사용하여 사람에 의해 발생된 신호 피크(peak)를 탐지한다. 다음으로, 형성된 피크를 묶어 프레임(frame)을 구성한 후, 이로부터 특징 벡터를 형성한다. 마지막으로, 최소 0명부터 최대 10명까지 각각의 사람 수에 대해 특징 벡터를 계산하고, 구축된 데이터베이스를 훈련 데이터로 사용함으로써 분류기를 학습한다.

3-1 변형된 CLEAN 알고리즘

전 처리된 신호에 존재하는 멀티패스 신호 및 잡음 신호는 인원 계수 추정에 있어 오차를 발생시키므로 이들을 최대한 억제하고, 사람 신호만을 추출하는 과정이 필요하다. 변형된 CLEAN 알고리즘은 기존 CLEAN 알고리즘을 수정하여, 입력 신호로부터 사람에 의해 발생된 피크만을 탐지하는 기법이다. 상기 알고리즘은 사람 신호 근방에 위치한 멀티패스 신호를 제거하고, 특정 세기 이하의 신호를 잡음으로 간주함으로써 사람 피크를 탐지한다. 상세한 알고리즘은 그림 3과 같다^[10].

그림 3. | Fig. 3. 변형된 CLEAN 알고리즘 순서도 | The flowchart of modified CLEAN algorithm.

Download Original Figure

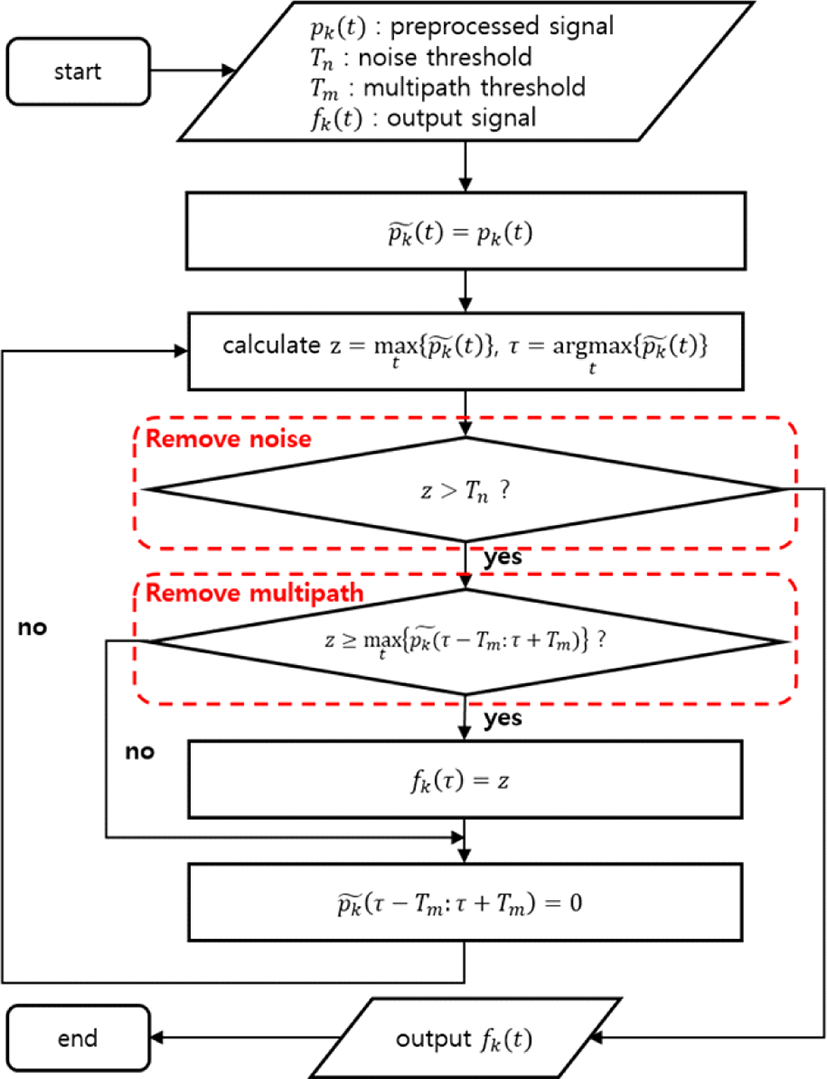
상기 과정에서 가장 중요한 점은 적절한 임계값 T_n과 T_m을 통해 잡음 신호 및 멀티패스 신호를 제거하는 것이다. 그러나 사람들이 임의로 움직이는 상황에서 정확한 사람 신호 추출을 가능케 하는 최적의 임계값 설정은 거의 불가능하다. 그림 4를 확인하여 보면 T_n을 증가시킬 시 더욱 많은 잡음 신호를 제거할 수 있지만, 신호 세기가 작은 사람 신호 또한 제거될 수 있다. 반면, T_n을 감소시킬 시 작은 세기의 사람 신호를 탐지할 확률이 증가하지만, 잡음 신호 또한 탐지될 가능성이 증가한다. 멀티패스 신호의 경우 T_m이 증가하게 된다면 더욱 효과적으로 멀티패스 신호를 제거할 수 있지만, 서로 가까이 위치한 사람들의 신호를 분리할 수 없게 된다. 반대로 T_m을 감소시킬 시 가까이 위치한 사람들을 정확히 분리할 수 있는 반면, 멀티패스 신호 또한 탐지되게 된다. 결론적으로, T_n과 T_m 각 값의 증가와 감소 사이에 존재하는 트레이드오프(trade-off) 관계는 최적의 값 설정을 어렵게 한다.

그림 4. | Fig. 4. 변형된 CLEAN 알고리즘의 임계값 설정 | Threshold settings of modified CLEAN algorithm.

Download Original Figure

3-2 특징 벡터 추출을 통한 훈련 데이터베이스 형성

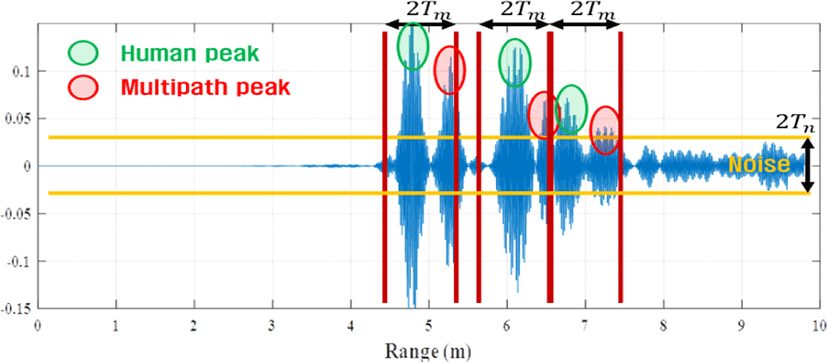
제안한 알고리즘은 단일 임계값이 아닌 다양한 임계값을 사용하여 사람 신호를 추출한다. 또한, 이 과정에서 발생하는 잉여 정보를 추후 차원 감소 연산을 통해 제거함으로써 상기 문제점을 해결한다. 먼저, 평균 잡음 신호 수준 th_noise에 맞추어 T_n을 [0.4th_noise, 0.7th_noise, th_noise, 1.3th_noise, 1.6th_noise]으로 변화시켜가며 사람 신호를 추출한다. 이와 동시에 평균적인 멀티패스 신호 발생 지점 th_mpath 에 맞추어 T_m을 [0.4th_mpath, 0.7th_mpath, th_mpath, 1.3th_mpath, 1.6th_mpath]으로 변화시켜가며 추출 알고리즘을 수행한다. 해당 과정을 통해 다양한 상황에 대한 사람 신호 추출이 가능하며, 최종적으로, 총 25번의 추출 알고리즘이 수행된다.

임계값을 변화시켜가며 추출된 사람 신호로부터 알고리즘은 슬로우 타임 방향으로 W 개의 신호를 사용하여 1 프레임을 형성한 후, 이로부터 특징 벡터를 추출한다. W를 고려하여 n번째의 슬로우 타임 인덱스에 대한 프레임 F^(T_n,T_m) [n]은 다음의 식 (5)와 같이 표현된다.

F (T n, T m) [n] = [f n (T n, T m) [1] f n + 1 (T n, T m) [1] ⋯ f n + W − 1 (T n, T m) [1] f n (T n, T m) [2] f n + 1 (T n, T m) [2] ⋯ f n + W − 1 (T n, T m) [1] ⋮ ⋮ ⋱ ⋮ f n (T n, T m) [N p] f n + 1 (T n, T m) [N p] ⋯ f n + W − 1 (T n, T m) [N p]]

(5)

여기서 $f k (T n, T m) [i]$ 는 임계값 (T_n,T_m)을 사용하여 추출된 사람 신호를 의미하며, k는 슬로우 타임 인덱스를, i는 패스트 타임(fast time) 인덱스를 의미한다. N_p는 샘플링(sampling)된 수신 신호의 펄스 크기를 나타낸다.

형성된 각 프레임으로부터 오로지 사람 수에 의존하는 신호 변수를 정의할 수 있다. 첫 번째로, 사람의 수가 증가할수록 추출된 신호의 피크(peak) 개수가 증가한다. 따라서 프레임 내 0을 제외한 피크의 개수를 계산하여 $C 1 (T n, T m)$ 을 정의한다 (식 (6)). 두 번째로, 사람의 수가 증가할수록 시간에 따른 신호 피크의 분산 값이 증가한다. 따라서 거리 값을 고정 후 시간에 따른 신호 피크의 분산 값을 계산하고, 거리 별로 획득된 각 분산 값의 평균을 계산함으로써 $C 2 (T n, T m)$ 을 정의한다 (식 (7)). 최종적으로 각 프레임으로부터 $C 1 (T n, T m)$ 과 $C 2 (T n, T m)$ 을 계산함으로써 프레임 별 특징 벡터를 형성할 수 있다.

C 1 (T n, T m) = Count i, k (f k (T n, T m) [i] > 0),

(6)

C 2 (T n, T m) = ∑ i = 1 N i Var k [f k (T n, T m) [i]] N i .

(7)

앞서, T_n=[0.4th_noise, 0.7th_noise, th_noise, 1.3th_noise, 1.6th_noise], T_m = [0.4th_mpath, 0.7th_mpath, th_mpath, 1.3th_mpath, 1.6th_mpath] 총 25개 조합의 임계값에 걸쳐 사람 신호를 획득하였으므로 각 펄스 신호마다 25개의 프레임을 획득하게 된다. 또한, 상기 수식을 통해 1 프레임 당 2 개의 특성 변수를 계산할 수 있으므로, W 개의 신호로부터 총 50 개의 특성 변수를 계산할 수 있다. 최종적으로 각 특성 변수를 요소(element)로 하는 특징 벡터를 형성할 수 있으며, 이는 식 (8)과 같이 정의된다.

v= [d 1, d 2, …, d 50] T,

(8)

여기서

d 1 = C 1 (0.4 t h n o i s e, 0.4 t h m p a t h), d 2 = C 2 (0.4 t h n o i s e, 0.4 t h m p a t h), d 3 = C 1 (0.7 t h n o i s e, 0.4 t h m p a t h), ⋮ d 49 = C 1 (1.6 t h n o i s e, 1.6 t h m p a t h), d 50 = C 2 (1.6 t h n o i s e, 1.6 t h m p a t h),

을 만족한다.

최종적으로, Q개의 프레임 데이터로부터 각각 특징 벡터를 형성함으로써 식 (9)와 같이 훈련 데이터베이스를 만들 수 있다.

V = [v 1 v 2 … v Q] . = [v 11 v 12 … v 1 Q v 21 v 22 … v 2 Q ⋮ ⋮ ⋱ ⋮ v 50, 1 v 50, 2 … v 50, Q],

(9)

여기서 V는 50×Q 크기의 행렬이며, v_ij는 데이터베이스 행렬 V의 i번째 열, j번째 행의 요소이다.

3-3 주성분분석 기법을 통한 차원 감소

앞서 획득한 각 특성 변수들은 서로 중복성을 갖고 있으므로 잉여 정보가 발생한다. 이는 정확도는 상승시키지 않은 채 분류기의 계산량 만을 증가시킨다^[15]. 상기 문제점을 해결하기 위해 주성분분석(principal component analysis: PCA) 기법을 적용하여 훈련 데이터 V의 차원을 감소시킴으로써 잉여 정보를 제거한다^[16]. V의 공분산 행렬로부터 변환 행렬 Ρ를 형성할 수 있으며, 이로부터 식 (10)과 같이 특징 벡터의 차원을 50×1에서 10×1으로 감소시킬 수 있다.

V ¯ = P T V . = [v ¯ 11 v ¯ 12 … v ¯ 1 Q v ¯ 21 v ¯ 22 … v ¯ 2 Q ⋮ ⋮ ⋱ ⋮ v ¯ 10, 1 v ¯ 10, 2 … v ¯ 10, Q],

(10)

여기서 Ρ는 10×50 크기의 변환 행렬이며, 차원 감소 후의 훈련 데이터베이스 V̅는 10×Q의 크기를 갖는다.

마지막으로, V̅의 각 요소가 0과 1사이의 크기를 갖도록 조정하여준다. 이는 식 (11)의 정규화(normalization) 과정을 통해 이루어질 수 있다.

v ˜ i j = v ¯ i j − v ¯ i, min v ¯ i, max − v ¯ i, min, i = 1, 2, …, 10, j = 1, 2, …, Q

(11)

여기서

v ¯ i, min = min j (v ¯ i j), j = 1, 2, …, Q v ¯ i, max = max j (v ¯ i j), j = 1, 2, …, Q

를 만족한다. 최종적으로 형성된 훈련 데이터베이스는 다음과 같다.

V ˜ = [v ˜ 11 v ˜ 12 … v ˜ 1 Q v ˜ 21 v ˜ 22 … v ˜ 2 Q ⋮ ⋮ ⋱ ⋮ v ˜ 10, 1 v ˜ 10, 2 … v ˜ 10, Q] .

(12)

3-4 다층 퍼셉트론 분류기

다층 퍼셉트론(multi-layer perceptron: MLP)은 뉴런(neuron)의 조합으로 이루어지며, 역전파 알고리즘(backpropagation algorithm)을 통해 가중치를 학습함으로써 분류를 수행한다. 최종적으로 형성된 특징 벡터 ṽ_j는 10개의 요소를 가지므로 각각의 값을 10개의 뉴런으로 구성된 입력 층(input layer)에 대응시킨다. 또한 0명부터 10명까지 11 클래스 식별을 수행하여야 하므로 각 인원수에 해당하는 11개 뉴런을 이용하여 출력 층(output layer)을 구성하였다. 그림 5는 최종적으로 구성된 MLP 분류기를 나타낸다. 훈련된 분류기에 10×1 크기의 특징 벡터를 입력하고, 출력 노드(node)를 확인함으로써 학습 기반의 인원 계수 추정을 수행할 수 있다.

그림 5. | Fig. 5. 다층 퍼셉트론 분류기 | The multi-layer perceptron classifier.

Download Original Figure

Ⅳ. 실험 결과

본 절은 제안된 시스템의 성능을 검증하기 위하여, 0명부터 10명까지 인원수가 변화하는 사람들에 대한 계수 추정 결과를 제시한다. 상기 시스템은 Xethru(社)의 X4M03 IR-UWB 레이다를 사용하였으며, 레이다의 사양은 표 1에 정리되어 있다.

표 1. | Table 1. IR-UWB 레이다 사양 | The specification of an IR-UWB radar.

Carrier frequency	8 GHz
Frequency bandwidth	1.5 GHz
Azimuth beamwidth	65〫
Elevation beamwidth	65〫
Maximum detectable range	10 m

Download Excel Table

실험은 일반적인 실내 환경 내에서 수행하였다. 두 곳의 장소에서 실험을 진행하였는데, 첫 번째는 주변이 트인 환경에서 진행하였으며(그림 6), 두 번째는 벽, 천장 등 으로 사방이 막힌 공간에서 실험을 진행하였다(그림 7).

그림 6. | Fig. 6. 실험 장소 1(트인 실내 공간) | Place of experiment 1(open indoor space).

Download Original Figure

그림 7. | Fig. 7. 실험 장소 2(막힌 실내 공간) | Place of experiment 2(closed indoor space).

Download Original Figure

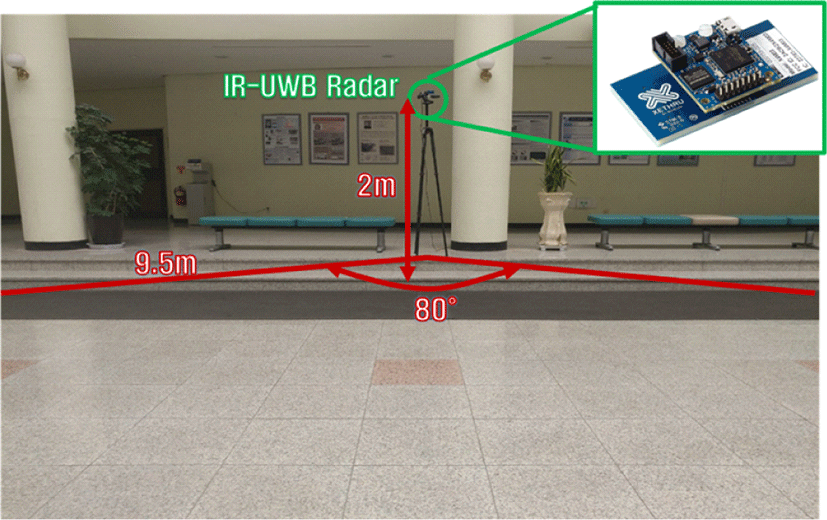
장소를 제외하고는 첫 번째 실험과 두 번째 실험 모두 같은 조건에서 진행되었다. 실험은 반지름 9.5m, 중심각 80°의 부채꼴형 공간에서 진행되었으며, 부채꼴의 꼭짓점 높이 2 m 부근에 한 대의 IR-UWB 레이다를 설치하였다.

다음으로 최소 0명에서 최대 10명까지 각각의 인원수 당 레이다 수신 신호를 획득하여 특징 벡터 데이터베이스를 형성하고, MLP 분류기 학습을 수행하였다. 이 때, 각각의 사람들은 실험 공간 내에서 자유롭게 거동하되, 서로 붙어서 움직이는 상황은 배제하였다. 학습을 위해 각 사람 수 당 획득한 수신 펄스는 8,640개이며, 48 펄스 당 1개의 프레임을 구축해 180개의 프레임을 형성하였다. 1 프레임 당 1개의 특징 벡터를 형성할 수 있고, X4M03 레이다는 1초에 48 펄스를 송·수신 할 수 있으므로 각 인원수 당 180초, 즉 3분에 해당하는 수신 신호를 사용하여 분류기 학습이 수행된다. 훈련 데이터 양은 분류기의 추정 성능에 영향을 미치므로, 더욱 많은 데이터를 통해 학습을 수행할수록 추정 정확도는 상승할 것이다^[17]. 그러나 학습 데이터의 증가에 따른 정확도 상승은 선형적이지 않으며, 데이터 수집에는 시간 및 에너지가 소모되므로 적절한 표본 수를 선택하여야 한다.

실험 환경 내 설치된 IR-UWB 레이다는 탐지 반경 내 존재하는 사람들로부터 실시간으로 수신 신호를 획득하고, 획득한 데이터를 연결된 컴퓨터로 전송한다. 다음으로, MATLAB을 이용하여 제안된 알고리즘에 따라 수신 신호 프레임으로부터 특징 벡터를 계산한다. 최종적으로, 특징 벡터를 사전에 학습된 MLP 분류기에 입력시킨 후 출력된 결과를 확인함으로써 실시간 인원계수 추정을 수행할 수 있다. 실험은 그림 8과 같이, 레이다 탐지 반경 내 자유롭게 움직이는 0명부터 10명까지의 사람 수를 실시간으로 추정하였다. 그림 9와 그림 10은 각각 트인 환경과 막힌 환경에 대한 인원 계수 추정 결과를 보여준다. 오차 행렬의 파란색 부분은 실제 공간 내 존재하는 사람들의 수를 시스템이 정확히 추정한 경우의 비율을 나타낸다. 또한 행렬의 초록색 부분은 실제 인원에 비해 +1명 혹은 −1명으로 추정된 비율을 나타낸다.

그림 8. | Fig. 8. 실시간 인원 추정 | Real-time people counting.

Download Original Figure

그림 9. | Fig. 9. 트인 실내 공간에서의 계수 추정 오차 행렬 | Confusion matrix of people counting in open indoor space.

Download Original Figure

그림 10. | Fig. 10. 닫힌 실내 공간에서의 계수 추정 오차 행렬 | Confusion matrix of people counting in closed indoor space.

Download Original Figure

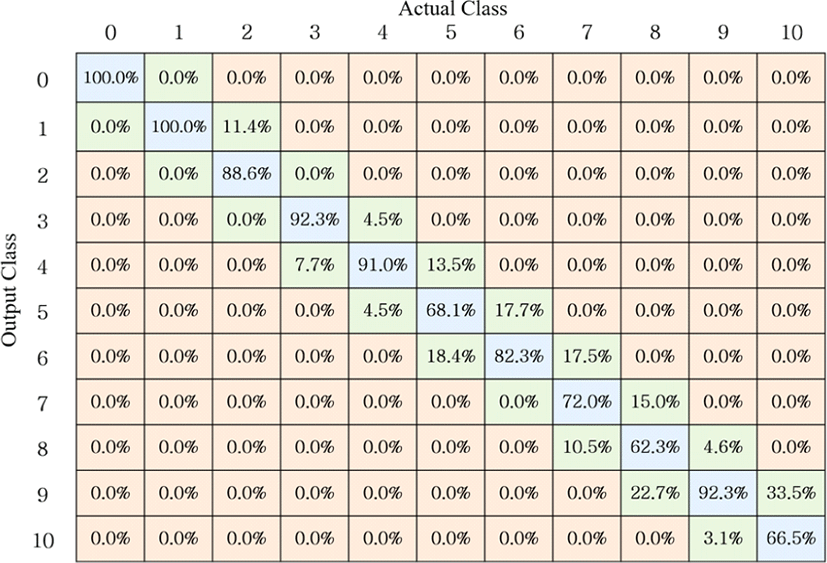
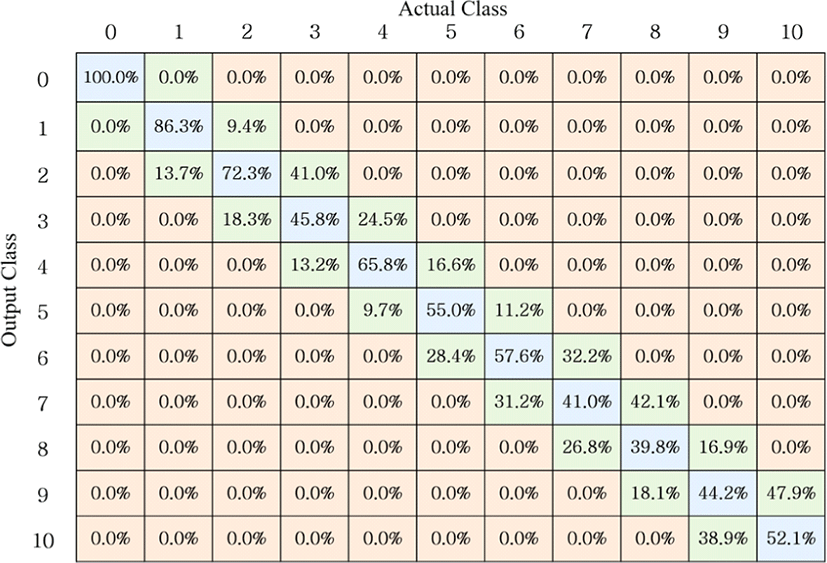
결과를 보면, 첫 번째 장소에서의 실험과 두 번째 장소에서의 실험 모두 ±1명의 오차 감안 시, 100.0 %의 확률로 인원 계수를 추정할 수 있었음을 확인할 수 있다. 따라서 제안된 시스템이 트인 환경 및 닫힌 환경에서 모두 비교적 정확한 계수 추정을 수행한다고 할 수 있다.

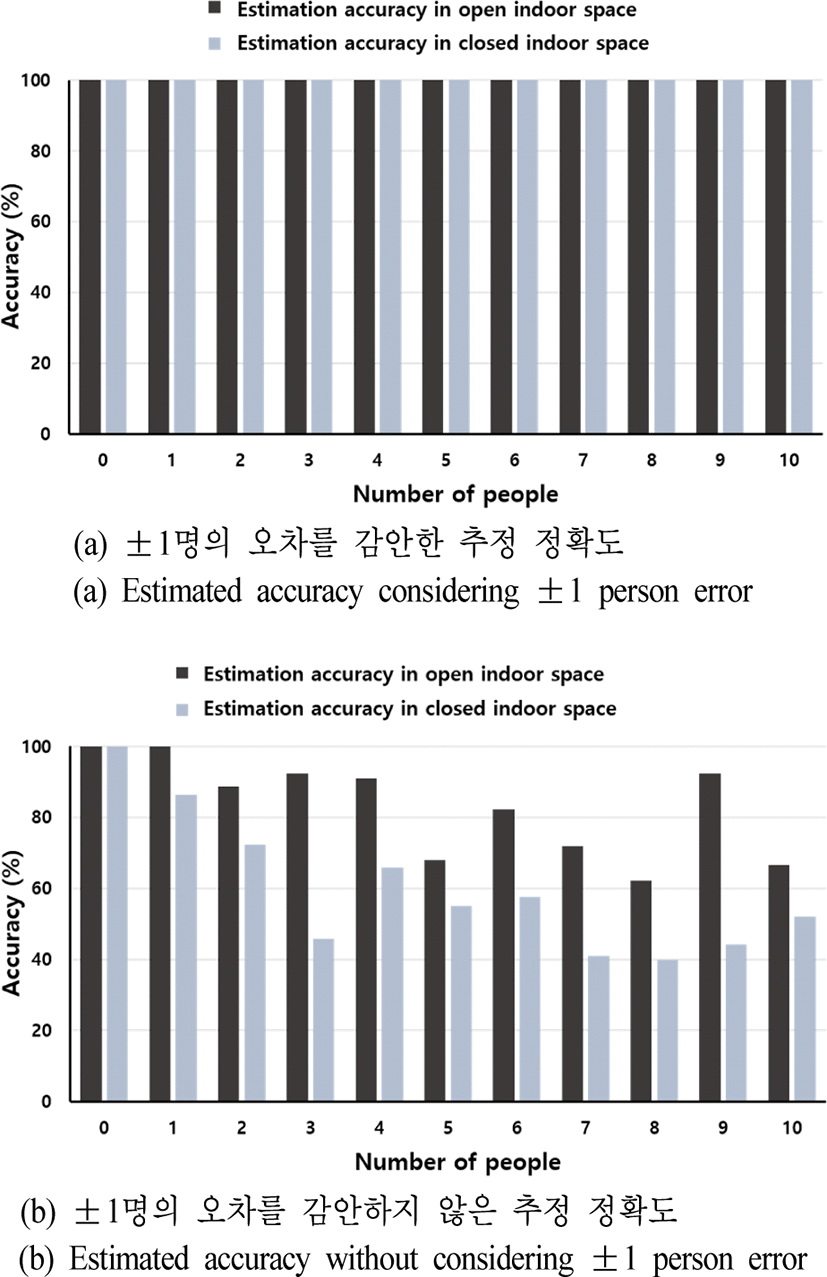
±1명의 오차를 감안하지 않을 시, 첫 번째 실험의 경 우, 평균 83.2 %, 두 번째 실험의 경우 평균 60.0 %의 추정 정확도로 두 번째 실험 환경에 비해 첫 번째 실험 환경이 더욱 높은 정확도를 보였다. 실제로 그림 11의 요약된 계수 추정 결과를 확인하여 보면, 모든 인원수에 대해서 첫 번째 실험의 추정 정확도가 두 번째 실험의 추정 정확도보다 높음을 확인할 수 있다. 이는 트인 실내 환경의 경우 천장이 높으며 사방이 트여 있어 클러터 신호와 멀티패스 신호의 영향이 적은 이상적 환경인 반면, 닫힌 실내 환경의 경우 주변이 벽과 거울 등으로 막혀 있으며, 천장이 낮아 클러터와 멀티패스 신호의 영향이 매우 큰 환경이기 때문이다. 클러터 신호와 멀티패스 신호의 영향력은 정확한 사람 신호 추출에 영향을 미쳤을 것이고, 이는 결 국 추정 정확도에 영향을 미칠 것이다.

그림 11. | Fig. 11. 트인 환경과 닫힌 환경에서의 계수 추정 결과 | The result of people counting in open and closed environment.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 IR-UWB 레이다 수신 신호를 이용하여 인원 계수 추정을 수행하는 알고리즘을 제안하였다. 기존의 사람 탐지 기법을 통한 인원 계수 추정의 경우, 단일 임계값을 사용하기 때문에 최적의 임계값 설정이 어려우며, 멀티패스 신호와 잡음 신호로 인한 정확도 감소 문제가 존재한다. 제안된 알고리즘은 다양한 임계값을 사용하여 사람 신호를 추출하여 특징 벡터를 형성함으로써 최적 임계값 설정의 문제점을 해결하였으며, 해당 과정에서 발생하는 잉여 정보를 PCA 기법을 사용하여 제거하였다. 이후, 특징 벡터를 통해 형성된 훈련 데이터베이스를 이용하여 분류기를 학습하고, 학습 기반의 인원 계수 추정을 수행하였다. 트인 환경과 닫힌 환경에서의 실시간 실험 결과를 통해 제안된 학습 기반의 인원 계수 추정 기법이 적은 양의 훈련 데이터를 사용함에도 불구하고, ±1명 내의 오차 감안 시 100.0 %의 확률로 정확하게 인원 계수를 추정할 수 있었음을 확인할 수 있었다.

Acknowledgements

「본 연구는 ㈜ 삼성전자의 지원을 받아 연구되었습니다.」

References

[1].

A. Zanella, N. Bui, A. Castellani, L. Vangelista, and M. Zorzi, "Internet of things for smart cities," IEEE Internet of Things Journal, vol. 1, no. 1, pp. 22-32, Feb. 2014.

[2].

W. Balid, H. H. Refai, "On the development of self-powered IoT sensor for real-time traffic monitoring in smart cities," 2017 IEEE Sensors, Glasgow, Oct. 2017, pp. 1-3.

[3].

T. Joseph, R. Jenu, A. K. Assis, V. A. S. Kumar, P. M. Sasi, and G. Alexander, "IoT middleware for smart city: An integrated and centrally managed IoT middleware for smart city," in 2017 IEEE Region 10 Symposium(TENSYMP), Cochin, Jul. 2017, pp. 1-5.

[4].

C. Zeng, H. Ma, "Robust head-shoulder detection by PCA-based multilevel HOG-LBP detector for people counting," in 2010 20th International Conference on Pattern Recognition, Istanbul, Aug. 2010, pp. 2069-2072.

[5].

Y. L. Hou, G. K. H. Pang, "People counting and human detection in a challenging situation," IEEE Transactions on Systems, Man, and Cybernetics—Part A: Systems and Humans, vol. 41, no. 1, pp. 24-33, Jan. 2011.

[6].

C. N. Padole, H. Proenca, "Periocular recognition: Analysis of performance degradation factors," in 2012 5th IAPR International Conference on Biometrics(ICB), New Delhi, Mar. 2012, pp. 439-445.

[7].

J. W. Choi, X. Quan, and S. H. Cho, "Bi-directional passing people counting system based on IR-UWB radar sensors," IEEE Internet of Things Journal, vol. 5, no. 2, pp. 512-522, Apr. 2018.

[8].

F. Wahl, M. Milenkovic, and O. Amft, "A distributed pir-based approach for estimating people count in office environments," in 2012 IEEE 15th International Conference on Computational Science and Engineering, Nicosia, Dec. 2012, pp. 640-647.

[9].

J. D. Taylor, Introduction to Ultra-Wideband Radar Systems, Boca Raton, CRC Press, 1994.

[10].

J. W. Choi, S. S. Nam, and S. H. Cho, "Multi-human detection algorithm based on an impulse radio ultra-wideband radar system," IEEE Access, vol. 4, pp. 10300-10309, Jan. 2017.

[11].

J. W. Choi, J. H. Kim, and S. H. Cho, "A counting algorithm for multiple objects using an IR-UWB radar system," in 2012 3rd IEEE International Conference on Network Infrastructure and Digital Content, Beijing, Sep. 2012, pp. 591-595.

[12].

J. W. Choi, S. H. Cho, "A crowdedness measurement algorithm using an IR-UWB radar sensor," in International Conference on Future Communication, Information and Computer Science(FCICS), Beijing, May 2014, pp. 119-122.

[13].

X. Yang, W. Yin, and L. Zhang, "People counting based on CNN using IR-UWB radar," in 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, Oct. 2017, pp. 1-5.

[14].

J. W. Choi, D. H. Yim, and S. H. Cho, "People counting based on an IR-UWB radar sensor," IEEE Sensors Journal, vol. 17, no. 17, pp. 5717-5727, Sep. 2017.

[15].

K. T. Kim, D. K. Seo, and H. T. Kim "Efficient radar target recognition using the MUSIC algorithm and invariant features," IEEE Transactions on Antennas and Propagation, vol. 50, no. 3, pp. 325-337, Mar. 2002.

[16].

R. O. Duda, P. E. Hart, and D. G. Stork, Pattern Classification, New York, NY, John Wiley & Sons, 2012.

[17].

C. M. Van der Walt, E. Barnard, "Data characteristics that determine classifier performance," SAIEE Africa Research Journal, vol. 98, no. 3, pp. 87-93, Nov. 2006.

Author Information

최 재 호 [포항공과대학교/석사과정]

jkiees-30-1-28-i1

2017년 2월: 고려대학교 컴퓨터·통신공학부 (공학사)
2017년 2월～현재: 포항공과대학교 전자전기공학과 석사과정
[주 관심분야] 레이다 신호 처리 및 영상, 사람 탐지

김 지 은 [포항공과대학교/석·박사 통합과정]

jkiees-30-1-28-i2

2012년 2월: 경북대학교 전자공학과 (공학사)
2012년 2월～현재: 포항공과대학교 전자전기공학과 석박사 통합과정
[주 관심분야] 레이다 신호 처리 및 영상, 레이다 표적 탐지 등

김 경 태 (포항공과대학교/정교수)

jkiees-30-1-28-i3

1994년 2월: 포항공과대학교 전자전기공학과 (공학사)
1996년 2월: 포항공과대학교 전자전기공학과 (공학석사)
1999년 2월: 포항공과대학교 전자전기공학과 (공학박사)
2002년 3월～2011년 2월: 영남대학교 전자공학과 교수
2011년 3월～현재: 포항공과대학교 전자전기공학과 교수
2012년 9월～2017년 12월: 레이다/IR 표적식별 특화연구실실장
2018년 1월～현재: 국방R/D 전략 및 기술협력 센터장
2018년 1월～현재: 무인감시정찰기술연구센터장
[주 관심분야] 레이다 신호 처리 및 영상, 레이다 표적인식 및 패턴인식, 전자기수치해석 및 RCS 측정