Ⅰ. 서 론
Inverse synthetic aperture radar(ISAR) 영상 형성은 이동하는 표적의 레이다 수신 신호를 이용하여 2차원의 고해상도 영상을 만드는 기법을 의미한다[1]~[5]. ISAR 영상을 이용하면 전파 회절에 의해 결정되는 산란점 분포를 이차원에서 확인 가능하므로 자동표적인식(Automatic Target Recognition: ATR) 및 non-cooperative target recognition (NCTR)을 통한 표적의 피아 식별을 보다 더 효율적으로 수행할 수 있게 된다.
ISAR 영상 형성 시 이동하는 표적의 운동 성분은 병진운동(Translational Motion: TM)과 회전운동(Rotational Motion: RM)으로 나눌 수 있다. 병진운동은 레이다와 표적사이의 거리를 변화시키는 성분이고, 회전운동은 표적이 회전축을 중심으로 회전하는 성분이다. 병진운동은 ISAR 영상 형성 시 보상되어야 하는 성분이므로 병진운동 보상(Translational Motion Compensation: TMC) 기법을 이용하여 제거해야 한다. 반대로 표적의 선형 회전운동 성분은 ISAR 영상을 형성하기 위해 필요한 성분이다. 그러나 고기동 표적의 경우 표적의 회전성분이 비선형적으로 변하게 되고, 이는 회전성분은 ISAR 영상의 초점(focus)을 흐리게 하는 요소가 된다. 따라서 비선형 회전 성분이 존재하는 경우 회전운동 보상기법(Rotational Motion Compensation: RMC)을 이용한 보상 과정이 ISAR 영상 형성 시 필수적으로 수행되어야 한다.
비선형 회전 성분을 보상하는 대표적인 기법 중 하나인 prominent point processing(PPP)[4]~[7]은 보간법(interpolation)을 이용하여 coherent processing interval(CPI) 동안 수신된 레이다 신호가 선형 회전성분을 가지도록 재배치함으로써 RMC를 수행하는 기법이다. 이는 개념적으로 쉽고 구현이 간단하기 때문에 ISAR 응용분야에서 널리 활용되고 있다. 여기서 PPP 기반 회전운동 보상을 수행하기 위해서는 단일 산란점의 위상정보 추정이 필수적이다. 상기 목적을 달성하기 위해 참고문헌 [6]에서는 지배적 산란점이 존재한다는 가정하에 phase unwrapping and linear regression(PU-LR)을 적용하여 위상정보를 추정하였다. PU-LR 기법의 경우 지배적 산란점이 존재한다면 빠르고 정확하게 위상정보를 획득할 수 있다. 그러나 실제 환경에서 지배적 산란점이 존재하지 않는 경우 잘못된 위상정보 추정으로 인해 회전운동 보상기법 수행 오류를 야기할 수 있다. 또 다른 방법인 adaptive joint-time frequency(AJTF)[4]기법은 위상성분을 추정하기 위한 다차원의 비용함수(multi-dimensional cost function)를 설정하여 최적의 해를 찾는 기법이다. AJTF 기법은 지배적 산란점이 존재하지 않는 환경에서 산란점의 위상정보를 추정할 수 있지만, 전역 탐색(exhaustive search)으로 위상정보를 추정하기 때문에 시간이 오래 걸리는 문제가 있다. Particle swarm optimization(PSO) 기법은 반복(iteration) 학습을 수행하여 비용함수의 최적의 해를 찾음으로써 상기 AJTF 기법의 연산량 문제를 개선하였다[5]. 그러나 반복 학습을 통한 다차원의 변수 추정과정은 여전히 높은 연산량을 요구한다.
본 논문에서는 지배적 산란점이 존재하지 않는 환경에서 빠른 속도로 높은 품질의 ISAR 영상을 형성하기 위한 PPP 기법을 연구하였다. 먼저, 표적이 존재하는 레인지 빈을 선택 후, integrated cubic phase function(ICPF)[8]을 이용하여 산란점의 위상 정보를 추정하였다. 여기서 ICPF는 linear frequency-modulated(LFM) 신호의 변수를 추정하는 방법 중 하나로, 1차원 영역(domain)에서 최댓값을 찾음으로써 빠른 연산시간 내 위상함수의 추정을 가능하게 한다. 또한 ICPF는 위상신호가 중첩되어 있는 경우에도 변수 추정이 가능하게 한다는 특징이 있다[8]. 추정된 위상정보를 이용하여 PPP 기반 회전운동 보상 기법을 수행함으로써 성공적으로 ISAR 영상을 획득하였다.
Ⅱ. ISAR 신호 모델
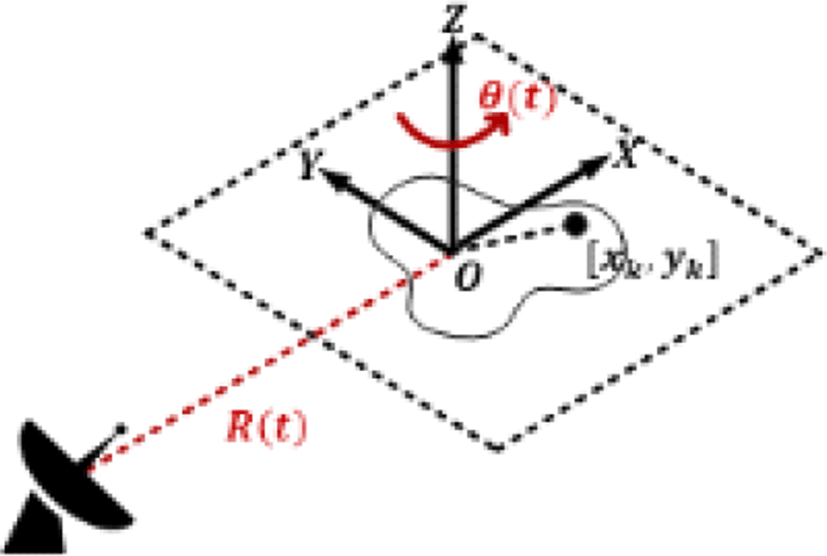
ISAR 영상을 형성하기 위한 기하 구조는 그림 1과 같다. 그림 1에서 X축은 거리방향, Y축은 교차 거리방향이다. 표적의 수신 신호에 거리방향 압축과 거리정렬을 수행하여 모든 산란점들이 각 레인지 빈에 위치한 경우, n(n=1,2,…,N)번째 레인지 빈에서의 레이다 신호는 식 (1)과 같다.
상기 식 (1)에서, k=1,2,…,Kn은 n번째 레인지 빈 내 존재하는 산란원의 인덱스, Kn은 n번째 레인지 빈에 있는 표적의 산란원 개수, Ak는 산란원의 크기, fc는 레이다의 중심 주파수 그리고 c는 빛의 속도이다. xk와 yk는 XY좌표계에서의 위치정보, R(t)는 XY좌표의 원점 O와 레이다 사이의 거리, θ(t)는 Z축을 중심으로 회전한 표적의 회전 각도를 나타낸다. 거리정보 R(t)와 회전정보 θ(t)는 식 (2) 및 식 (3)과 같이 각각 표현될 수 있다.
여기서, 식 (2)는 병진운동 성분 그리고 식 (3)은 회전운동 성분으로 각각 정의된다.
동일한 레인지 빈에 있는 산란점은 X축 방향의 거리가 같으므로 가 된다. 전체 관측각도의 변화량이 작고 병진운동 보상기법을 수행하여 R(t)성분이 제거된다면, 식 (1)은 식 (4)와 같이 근사된다[9].
식 (3)에서 회전성분을 이차항으로 근사하고 식 (4)에 대입하면 다음과 같이 표현될 수 있다.
식 (5)에서 상수항 은 t의 성분이 아니므로 무시하였다. 식 (5)에서 t에 대한 함수를 식 (6)과 같이 간단하게 재정의할 수 있다.
식 (6)에서 αk.1는 2f0yrΩ/c이고, αk.2는 f0Ω′/c이다.
Ⅲ. ICPF를 이용한 PPP 수행 기법
ICPF는 신호의 상관함수를 이용하여 위상성분의 이차항을 추정한다. 이때, 참고문헌 [8]의 연구 결과에 따르면 상관함수 s(t+τ)s(t−τ)는 다음과 같다.
식 (7)에서, τ는 시간 t의 지연성분이고, Rauto(t,τ)는 각 산란점의 위상신호에 대한 자기상관(autocorrelation) 함수, Rcross(t,τ)는 서로 다른 두 산란점[p번째 산란원과 q번째 산란원(p ≠ q)]의 위상신호 간 상호상관(cross-correlation) 함수이다.
상관함수 Rs(t,τ)를 τ2에 대해 푸리에 변환하는 기법을 cubic phase function(CPF)이라 하고 다음과 같이 표현한다.
여기서 CPFauto(t,fτ)와 CPFcross(t,fτ)는 각각 Rauto(t,τ)와 Rcross(t,τ)의 CPF 수행 결과이다. 위 식에서 δ(fτ-αk.2)에 의해 fτ=αk.2인 지점에 크기가 인 첨두값이 발생하므로, 식 (9)를 이용하여 |CPF(t,fτ)|의 최댓값을 찾는 과정을 수행함으로써 의 크기가 가장 큰 k=r번째 산란점의 이차항 성분 αr.2를 추정할 수 있다. 식 (9)를 이용한 이차항 추정 과정에서 시간 t는 첨두값 의 형성 위치에 영향을 주지 않으므로 임의의 시간 t0에 대한 |CPF(t0,fτ)|의 최댓값을 찾음으로써 동일한 결과를 도출할 수 있다. 하지만 CPF는 다수의 산란점 정보가 중첩되는 경우 CPFcross(t,fτ) 성분에 의해 기만 첨두치(spurous peak)가 발생한다. 기만 첨두치는 상기의 최댓값을 이용하여 αr.2를 추정하는데 오차를 야기한다. 이를 해결하기 위해 참고문헌 [8]에서 제안한 ICPF는 CPF(t,fτ)의 절댓값에 제곱을 수행한 다음, 모든 시간 t에 대해 더하는 기법으로 다음과 같이 표현된다.
식 (10)에서 TCPI는 측정 시간이다. 식 (9)를 식 (10)에 대입한 결과는 다음과 같다.
상기 식 (11)에 있어, ICPFauto(fτ)는 동일한 위치 fτ=αk.1에서 중첩적으로 신호값을 더하게 되므로, ICPFauto(αk.2) ≫ ICPFcross(αk.2)가 되어 ICPFcross(αk.2)는 ICPFauto(αk.2)와 비교했을 때 무시할 수 있다[8]. 따라서 ICPF의 과정을 이용하면 CPFcross(fτ)에 의한 기만 첨두치 문제를 최소화 함으로써 r번째 산란점에 대한 이차항 성분 αr.2를 추정할 수 있다.
추정된 이차항 성분 αr.2의 복소공액 신호 exp(−j2παr.2t2)을 수신신호 s(t)에 곱한 다음 푸리에변환을 수행함으로써 r번째 산란원의 일차항 성분 αr.1을 다음과 같이 추정할 수 있다.
식 (12)에 식 (6)을 대입한 결과는 식 (13)과 같다.
식 (13)에서 Δαk.2는 αk.2-αr.2가 되므로 k ≠ r인 k번째 산란원의 신호는 시간 t에 대하여 첩(chip)신호이다. 따라서 푸리에 변환을 수행하여도 특정 주파수에 에너지가 집약되지 않는다. 반면 r번째 산란원은 Arδ(ft-αr.1)에 의해 주파수 αr.1에서 첨두값을 형성함으로 최종적으로 r번째 산란원의 일차항을 추정할 수 있다.
ICPF를 이용하여 추정한 r번째 산란원의 위상변수는 다음과 같다.
여기서, hr(t)는 아래 식 (15)와 같이 정의된다.
표적의 회전운동 성분 중 ISAR 영상의 초점을 흐리게 하는 것은 비선형성분(t의 이차항 성분)이므로 이를 제거해야 한다. 식 (13)에서 보는 바와 같이 단순히 exp(−αr.2t2)을 수신신호 s(t)에 곱하는 것은 r번째 산란점을 제외한 다른 산란점의 이차항 성분을 제거하지 못한다.
따라서 본 논문에서는 추정된 hr(t)를 이용하여 모든 산란원들의 회전성분이 선형화 되는 t′을 정의한 후, 수신 신호를 t′에 재배치함으로써 회전운동 보상 기법을 수행하였다. 먼저, hr(t)를 이용하여 다음의 식 (16)을 만족하는 시간변수 t′을 획득한다.
여기서 Ar은 hr(t′)의 비례상수이다. q(q ≠ r)번째 산란점의 함수가 hq(t)일 때 r번째 산란점과의 관계는 다음과 같다.
식 (17)에서 보는 바와 같이 함수 hr(t)와 함수 hq(t)는 선형적인 관계에 있다. 따라서 함수 hr(t)가 일차함수가 되도록 시간 t를 t′으로 재배치하게 되면 hq(t′) 역시 다음과 같은 일차항의 함수가 된다.
따라서 r번째 산란원의 위상정보를 이용하여 t′을 획득한 후, 보간법을 이용하여 레이다 수신 신호를 t′의 방향으로 보간한다면, 모든 산란원들의 회전운동 성분이 선형적으로 보상되게 된다.
Ⅳ. 시뮬레이션 결과
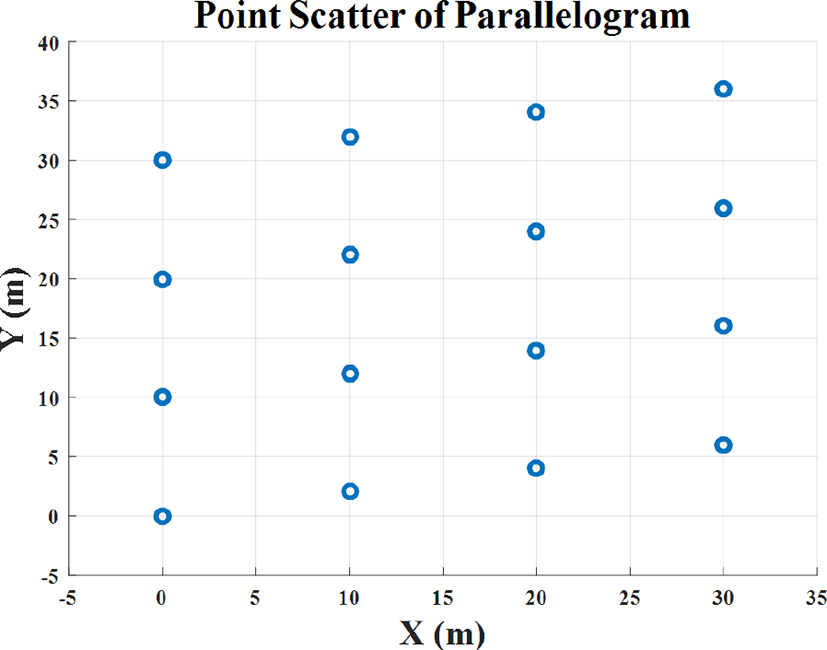
본 절에서는 PU-LR, AJTF, PSO 그리고 본 논문에서 제안된 ICPF 기반의 회전운동 보상 알고리즘의 성능을 비교 분석한다. 본 시뮬레이션에서는 25개의 점산란원으로 구성된 평행사변형 형태의 점산란원 모델을 사용하였으며(그림 2). 첩신호를 송신하는 레이다를 가정하였다. 레이다의 시뮬레이션 조건은 표 1과 같고, 표 2에는 기동하는 표적의 시뮬레이션 환경을 명시하였다. 여기서, 표적은 각속도뿐만 아니라 각가속도까지 함께 존재하는 비선형 회전운동을 겪기 때문에, 회전운동 보상 기법을 수행하지 않을 경우 ISAR 영상의 초점이 흐려지게 된다.
| Center frequency | 30 GHz |
| Bandwidth | 500 MHz |
| Pulse repetition interval | 600 Hz |
| Measured time | 1 sec |
| Radar position | [0, 0, 0] km |
| Initial position | [100, 100, 0 ] km |
| Moving direction | [1, 0, 0] |
| Velocity | 50 m/s |
| Acceleration | 3 m/s2 |
| Angular velocity | 5.6×10−3 rad/s |
| Angular acceleration | l.ll×10−2 rad/s |
ISAR 영상의 품질을 정략적으로 평가하기 위해 엔트로피(entropy)를 이용하였다. 여기서 엔트로피가 높을수록 무질서하다는 것을 의미하므로 엔트로피가 낮은 영상이 일반적으로 품질이 좋은 영상이라 판단한다[10]. 엔트로피의 정의는 다음과 같다.
여기서, I(m,n)은 거리-도플러 방향에서 형성된 ISAR 영상이고 S는 다음과 같다.
여기서 m과 M은 각각 도플러 축의 인덱스와 전체 도플러 빈의 개수이고 n과 N은 각각 레인지 빈의 인덱스와 전체 레인지 빈의 개수이다.
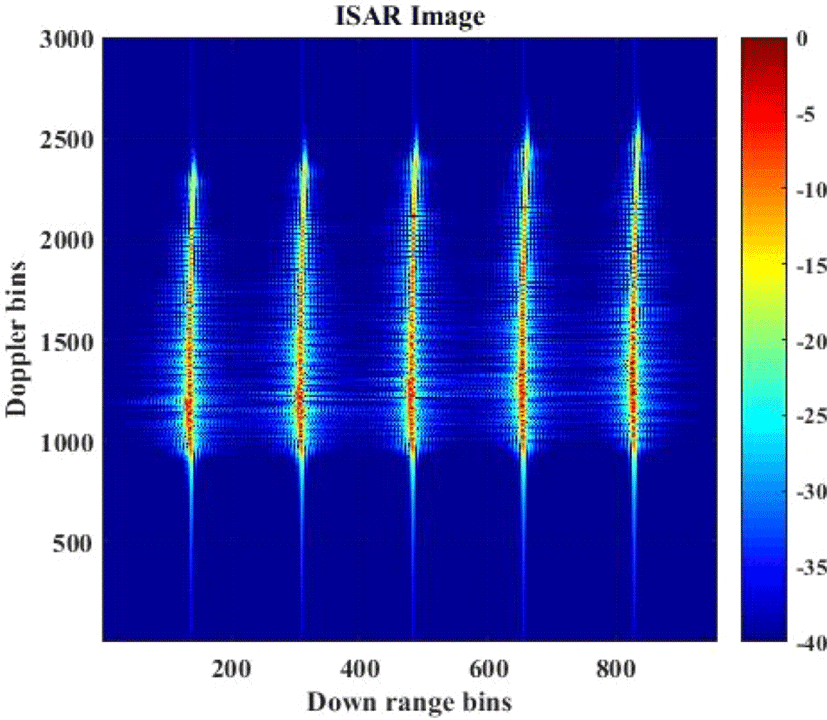
표 2에 명시된 조건으로 기동하는 표적의 수신 신호에 펄스압축을 수행한 다음, 거리정렬[10] 및 병진운동 보상 기법[6]을 수행하였다. 앞서 언급한 바와 같이 표적의 회전성분이 비선형이므로 회전성분 보상 기법을 적용하지 않고 획득한 ISAR 영상(그림 3)은 초점이 맞지 않는 것을 확인할 수 있으며, 이때의 영상 엔트로피는 11.12이었다.
기존에 존재하는 기법인 PU-LR, AJTF 그리고 PSO 기반의 회전운동 보상을 수행 후 형성된 ISAR 영상들은 각각 그림 4(a)~그림 4(c)와 같다. PU-LR을 이용하여 회전성분 보상 기법을 수행하는데 걸리는 시간은 0.302초로 매우 빠른 시간에 회전운동 보상을 수행하는 것을 확인할 수 있다. 그러나 본 시뮬레이션에서 사용된 표적의 경우 그림 2와 같이 어떤 레인지 빈에서도 지배적 산란원 없이 다중산란원들이 존재하기 때문에, PU-LR을 이용할 경우 정확한 위상 추정을 할 수 없게 된다. 이는 PU-LR을 기반하는 PPP 수행 시 회전성분을 적절하게 보상할 수 없게 하므로 PU-LR을 이용하여 획득한 ISAR 영상(그림 4(a))은 초점이 맞지 않았으며, 엔트로피 역시 10.38로 보상 전 결과(그림 3)에 비해 크게 개선되지 않았다.
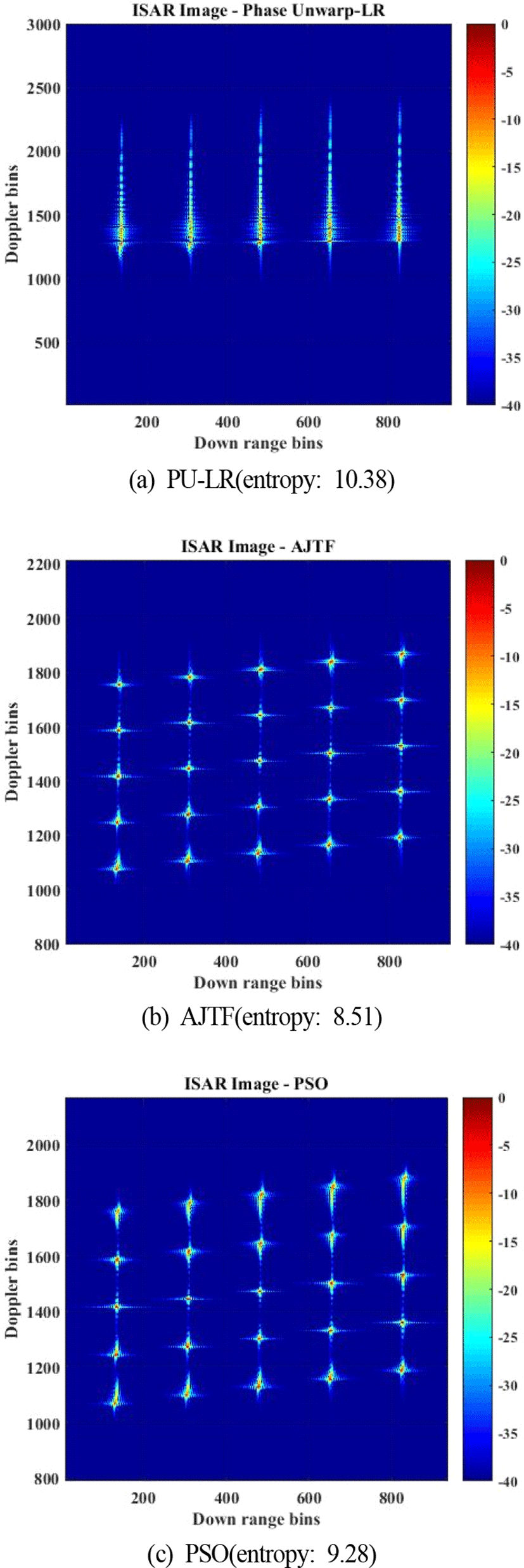
반면 AJTF와 PSO 기법은 다중산란점이 존재하는 환경에서도 단일 산란점의 위상 정보를 찾을 수 있으므로, AJTF 및 PSO 기법을 이용하여 PPP를 수행하면 적절한 회전운동 보상이 수행될 수 있다. 따라서 AJTF와 PSO를 이용하여 획득한 ISAR 영상(그림 4(b)와 그림 4(c))의 엔트로피는 각각 8.51과 9.28로 초점이 잘 맞는 것을 확인할 수 있었다. 하지만 AJTF의 수행 시간은 21.21초로 매우 느렸고, PSO의 경우 AJTF보다는 수행 시간이 개선되었지만 2.22초로 여전히 수초 이상이 걸렸다. 여기서 하나의 ISAR 영상을 획득하기 위해 수초 이상이 걸릴 경우 실시간 영상 획득이 요구되는 환경에서의 적용이 불가능하므로, PSO 기반의 회전운동 보상 기법의 경우 계산 시간에 대한 추가적인 개선이 필요하다.
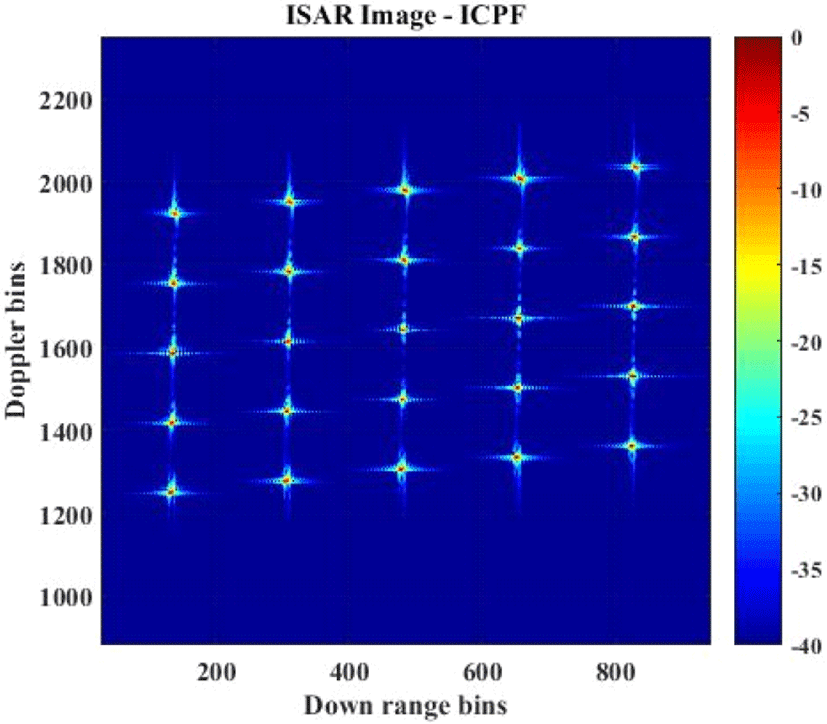
반면 본 논문에서 제안된 ICPF 기법의 경우 상호상관 성분을 제거함으로써 지배적 산란점이 존재하지 않는 환경에서 산란원의 위상정보를 추정할 수 있었다. 이에 대한 결과로 획득된 위상정보를 이용하여 회전보상 기법을 수행함으로써 엔트로피가 8.6인 우수한 품질의 ISAR 영상(그림 5)을 형성할 수 있었다. 뿐만 아니라 제안된 기법의 수행 속도는 0.62초로 실시간 영상 획득이 가능한 수준의 성능을 보였다.
각 기법의 수행 시간 및 ISAR 영상의 엔트로피는 다음 표 3과 같다. 정리하면 PU-LR 기법은 실시간 영상 획득이 가능한 수준의 수행 속도를 보였지만, 지배적 산란점이 존재하지 않는 환경에서 초점이 맞지 않는 ISAR 영상을 형성하였다. 반면, AJTF와 PSO 기법은 지배적 산란점이 존재하지 않는 환경에서도 초점이 잘 맞는 ISAR 영상 형성이 가능하였다. 하지만 ISAR 영상을 형성하기 위해 많은 연산시간이 요구되므로 실시간 영상 형성을 요하는 환경에서는 사용되기 힘들다. 상기의 기법들과는 반대로 본논문에서 제안한 기법의 경우 지배적 산란점이 존재하지 않는 환경에서도 매우 빠른 연산시간 내 성공적인 회전운동 보상을 수행할 수 있었다. 따라서 제안된 기법을 이용할 경우, 기존의 기법들에 비해 보다 더 실질적이고 효율적인 회전운동 보상을 가능하게 한다는 것을 확인할 수 있다.
| Tmie(sec) | Entropy | |
|---|---|---|
| PU-LR | 0.302 | 10.38 |
| AJTF | 21.21 | 8.51 |
| PSO | 2.22 | 9.28 |
| Proposed method | 0.62 | 8.6 |
Ⅴ. 결 론
본 논문에서는 기존의 PPP 기반 운동성분 보상 기법을 개선하는 방법을 제안한다. 제안된 기법은 ICPF 기법을 이용하여 산란점의 위상성분을 추정한 다음 PPP 기반 회전성분 보상 기법을 적용하여 ISAR 영상을 획득하였다. 제안된 기법은 기존의 PPP 기반 회전운동 보상 기법들의 한계점을 보완함으로써 지배적 산란점이 존재하지 않는 환경에서 우수한 품질의 ISAR 영상을 획득할 수 있었다. 이와 더불어 빠른 속도로 회전운동 보상 기법을 수행함으로써 실시간 ISAR 영상 획득이 가능하였다.
하지만 실제 측정 환경에서는 표적의 기동을 예상할 수 없을 뿐만 아니라 잡음과 클러터가 존재할 수 있기 때문에 시뮬레이션 환경에서 예상하지 못한 문제가 실제 측정 시 발생할 수 있다. 현재 본 연구의 저자들은 추가적인 연구를 통해 실제 측정데이터를 이용하여 제안된 기법을 검증할 계획이다.