Ⅰ. 서 론
공대지 GMTI(Ground Moving Target Indication) 모드는 항공기 레이다가 지면을 조사하여 지면 클러터가 항상 존재하는 상황에서 지면위에 움직이는 표적을 탐지하기를 요구한다. 지면 위의 움직이는 표적은 표적의 속도가 낮은 경우, 도플러 처리를 하더라도 주엽클러터가 존재하는 영역에 표적이 존재한다. 주엽클러터 영역에 존재하는 표적은 표적 신호의 수신 전력이 주엽클러터 전력보다 높지 않고서는 탐지되지 못한다. 그러므로 주엽클러터 영역에 존재하는 지면의 낮은 속도의 표적은 주엽클러터를 제거하여 표적을 탐지하여야 하며, 이런 GMTI 기술은 아주 도전적인 영역으로 인식되어지고 있다.
초기 GMTI 기술은 SLR(Side Looking Airborne Radar) 시스템에서 시작되었으며, 제한된 조건에서 동작하는 DPCA(Displaced Phase Center Antenna) 외에도 DPCA보다 개선된 adaptive DPCA, 그리고 Yadin의 방법[1], STAP(Space Time Adaptive Processing) 등 다른 다양한 시스템 환경 조건에서 동작하는 새로운 기술들이 개발되었다. 특히 STAP 기반 방법은 시스템에 의한 제한조건에 덜 영향을 받으면서 적용이 가능하며 만족할 만한 성능을 가진다[2].
STAP 처리는 훈련 데이터량과 처리 시간을 고려하여, FD(Full-Dimensional) STAP에 비해 감소된 훈련 데이터의 양과 처리 시간을 요구하는 D/B(post-Doppler/Beamspace) 영역에서의 RD(Reduced Dimension) STAP을 사용할 수 있다[2]. 본 논문에서는 항공기 레이다의 안테나 수신 채널(Σ, Δ 채널)을 고려하여 D/B 영역에서의 RD STAP 중에서 sigma-delta STAP(Σ-Δ STAP)의 항공기 레이다 GMTI 모드에 적용 방법 제안 및 시뮬레이션을 행하였다. 성능 평가 시뮬레이션에서는 ICM(Internal Clutter Motion) 환경을 고려하여 클러터를 모의하고 제안 방법으로 적용된 STAP의 성능을 평가하였다.
Ⅱ장에서 Σ-Δ STAP과 GMTI 모드에의 적용을 기술하고, Ⅲ장에서는 ICM 환경을 고려한 클러터 모의 방법을 기술한다. Ⅳ장에서는 시뮬레이션 클러터 환경에서 본 논문에서 적용한 Σ-Δ STAP의 성능을 분석 및 평가하고, V장에서 결론을 맺는다.
Ⅱ. GMTI 모드와 Sigma-Delta STAP
이 장은 본 논문에서 고려하는 GMTI 모드의 시나리오 및 요구 기준 그리고 Σ-Δ STAP에 대해 설명한다.
보통 항공기 레이다는 Sum(Σ)과 Difference(Δ) 안테나 수신 채널을 이용하여 클러터를 제거 및 지상 이동 표적을 탐지한다. Guard 채널 등의 추가적인 안테나 수신 채널이 있는 레이다는 클러터 제거 능력 및 표적 탐지 성능을 높일 수 있다[1]~[3]. 본 논문의 항공기 레이다는 Σ(Sum), Δa(Diff. Azimuth, Δ Azimuth), Δe(Diff. Elevation, Δ Elevation, ), Λ(Guard) 채널을 가진 것을 고려하며, 이 4개의 안테나 수신 채널을 가지고 GMTI를 수행한다. 표 1에 따라 시뮬레이션을 행하고, 제안한 STAP 방법의 성능을 평가한다. 참고로 표 1의 감마(Gamma)는 상수 감마(constant gamma) 클러터 반사계수 모델에서 감마의 값을 나타내며, 주엽클러터 거리는 안테나 빔의 중심이 바라보는 지면과 항공기 사이의 거리이다.
| 파라미터 | 값 | 파라미터 | 값 |
|---|---|---|---|
| 중심 주파수 | 10 GHz | CPI 펄스 개수 | 128 |
| PRF | 1.88 kHz | 항공기 고도 | 6,000 m |
| 샘플링 주파수 | 5 MHz | 항공기 속도 | 200 m/s |
| 안테나 빔 폭 | 3.6 ° | Gamma | 0.1 |
| 송신 펄스폭 | 40 μsec | 주엽클러터 거리 | 50 km |
Σ-Δ STAP은 Σ 채널과 Δa 또는 Δe 채널을 이용하여 STAP 알고리즘을 적용한 것이다. 그림 1(a)는 Σ-Δ STAP에 의한 GMTI 처리 흐름을 나타낸다. Σ-Δ STAP에서 Σ와 Δa 채널을 사용하거나, Σ와 Δa, Δe 채널을 사용할 수 있다. 그림 1(b)는 Σ와 Δa, Δe 채널을 사용할 경우에 STAP 처리를 위해 형성하는 데이터 입방체의 형태이다.
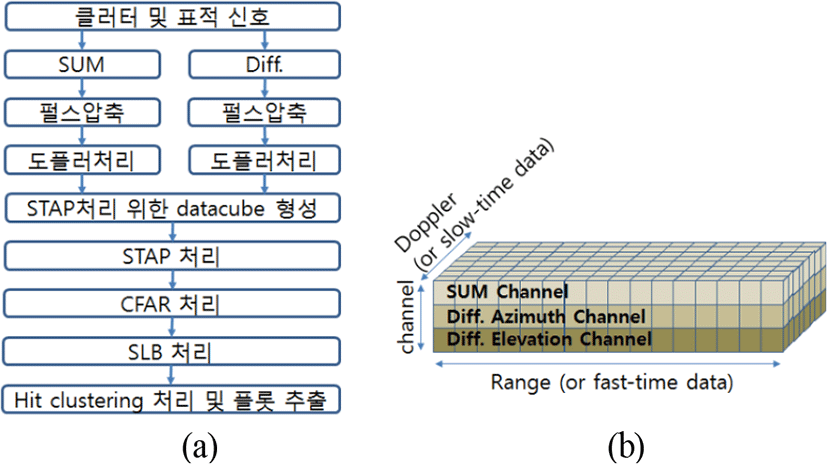
본 논문의 Σ-Δ STAP은 JDL(Joint-Domain Localized)[3] 방법과 비슷하며, JDL의 특별할 경우로 볼 수 있다. JDL 은 D/B 영역의 LPR(Localized Processing Region) 내의 신호로 간섭 신호를 억압한다. 본 논문의 Σ-Δ STAP에서 LPR은 그림 2와 같이 3 가지로 설계했다. 3가지의 차이는 도플러 채널 및 안테나 수신 채널을 STAP 처리에 어떻게 이용하는가의 차이이다. 그림 2에서 색인 n,k지점의 처리될 데이터 x(n,k)는 식 (1)과 같다.
위 식의 xc,n(k)에서 c는 안테나 수신채널 색인, n은 도플러 채널 색인, k는 거리(range) 색인을 나타낸다. 그림 2의 첫째 행 경우는 식 (1)에서 N = 0이며, 둘째 행 그림은 N=0, 셋째 행 그림은 N = 1이다. 또한, x(n,k)에 대해 STAP 처리하기 위한 훈련 데이터는 식 (2)와 같다.
여기서 A = W+G, B = G+1이며 W는 그림 2에서처럼 처리될 데이터 주위의 훈련 데이터를 취하는 거리 셀(cell) 크기, G는 처리될 데이터와 연관된 정보를 취하지 않고 간섭 신호만을 훈련 데이터로 취하기 위해 두는 훈련 데이터 수집을 막는(guard) 셀의 크기이다. 훈련 데이터로부터 공분산 매트릭스(matrix)는 다음과 같다.
여기서 XH는 X의 허미티안 행렬 전치(Hermitian transpose)를 나타낸다. 그리고 W의 크기는 x(n,k) 벡터의 원소 개수에 비래하여 설정어여야 한다[2]. 구한 공분산 매트릭스를 이용해 처리될 데이터에 적용될 연산 가중치 및 연산은 다음 식과 같다.
w는 MVDR(Minimum Variance Distortionless Response) 알고리즘[4]에 의한 필터 가중치이며, z(n,k)는 필터 출력으로서 최종적으로 STAP 처리된 결과이다. 식 (4)에서 Rcov의 역행렬 적용 전에 Rcov에 대해 DL(Diagonal Loading, Rcov=Rcov+λI)을 적용하고, 역행렬을 구하여 사용하도록 한다. 그러면 훈련 데이터 개수의 제한 등에 의해 생길 수도 있는 역행렬 이상 현상 예방과 강건한(robust) 가중치 형성이 이루진다[4]. t의 값은 그림 2의 3가지 설계된 방법에 따라서, 각각 첫째 및 둘째, 셋째 행 그림의 방법에 대해 t = [1,0]T, t = [1,0,0]T, t = [0,0,0,1,0,0,0,0,0]T로 설정한다. 그림 1(a)에서 보듯이, GMTI 모드는 관심 거리/도플러 영역의 z(n,k)들에게 CFAR 처리 단계를 적용한다. 설계한 Σ-Δ STAP의 3가지 처리 방법들(방법 1 : 그림 2의 1행의 방법, 방법 2 : 그림 2의 2행의 방법, 방법 3 : 그림 2의 3행의 방법)의 성능 차이는 나중에 시뮬레이션을 통해 확인한다.
Ⅲ. ICM 환경을 고려한 클러터 모의
Σ-Δ STAP은 균질한(homogeneous) 클러터 특성을 이용한다. 파도나 나뭇가지의 흔들림에 의한 클러터의 시간적 특성 변화(ICM: Internal Clutter Motion)에 의한 클러터 반사율의 시간적 변화는 시간적으로 수집한 훈련 데이터 들의 상관관계 저하를 유발하고, 이로 인해 Σ-Δ STAP의 클러터 제거 능력이 저하될 수 있다. 따라서 ICM 환경에서 설계한 Σ-Δ STAP의 3가지 처리 방법의 성능을 확인하기 위하여 클러터의 ICM 모의가 필요하다[2]. 이 장은 본 논문에서 사용한 ICM 환경 클러터 모의에 대해 설명한다[5].
Billingsley ICM 모델은 STAP 시뮬레이션에 널리 사용된다[2]. BLS(Billingsley) 모델은 바람의 속도(mph, mile per hour) 및 전송 주파수에 의해 정해지는 파라미터를 가지는 클러터의 시간적 전력 스펙트럼을 정의하고 있다. 바람의 속도에 따라 흔들리는 숲/바다와 같은 다양한 지형들로부터 획득한 데이터를 이용하여, 바람 속도와 지형에 따른 BLS 모델의 파라미터 값을 구해 놓고 있다[5]. 본 논문에서는 Mountcastle[5]이 제시한 BLS ICM을 반영한 모의 데이터 생성 방법을 사용한다. Mountcastle[5]은 백색 가우시안 랜덤 프로세스를 적당한 선형 시불변 필터에 통과시킴으로써 BLS ICM을 반영한 시퀀스를 생성했다. 선형 시불변 필터의 입력이 백색 가우시안 랜덤 프로세스이면 출력은 유색 가우시안 랜덤이다. 선형 시불변 필터의 전력 스펙트럼이 BLS ICM 모델의 전력 스펙트럼 모양을 따르도록 필터를 설계한다.
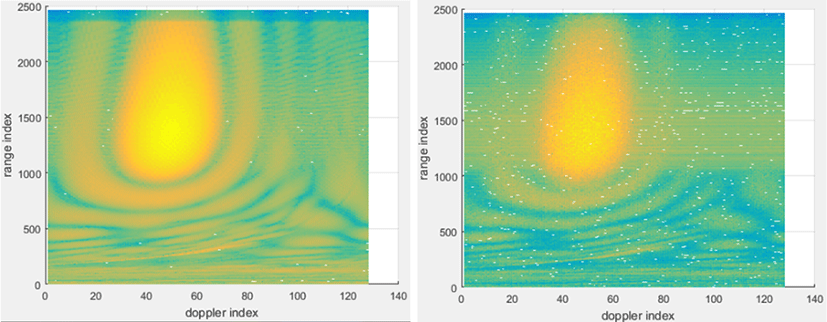
그림 3은 ICM 모의를 첨가한 경우와 하지 않은 경우의 모의 클러터 신호의 거리/도플러 맵을 비교하여 보여준다. 그림 3에서 거리 및 도플러 색인(rangle/Doppler index)은 거리 및 도플러 셀에 대한 색인이다. 그림 3의 ICM 모의에서 바람 속도는 6 mph로 하였다. 그림 3의 우측에서 보듯이, ICM 효과에 의한 클러터 반사율의 변화로 클러터 전력이 도플러 방향으로 퍼진 것을 볼 수 있다. 본 논문은 클러터 모의에 ICM 모의도 첨가하여 제시한 STAP 처리 방법의 성능을 비교한다.
Ⅳ. 시뮬레이션 결과 및 분석
본 장에서는 시뮬레이션을 통해 본 논문의 3가지 Σ-Δ STAP 방법의 성능을 비교한다.
STAP 처리 결과, 확인을 위한 클러터 모의는 표 1의 파라미터에 따라 시간 영역에서 지상클러터를 생성했다[6].
먼저 ICM 모의를 첨가하지 않은 모의 클러터의 R/D 맵(거리/도플러 맵)은 그림 4이다. 그림 4는 각 채널의 공간상에서 클러터 분포의 특징을 나타내며, 각 채널의 다른 클러터 분포 특징이 STAP에서 클러터 제거에 이용된다.
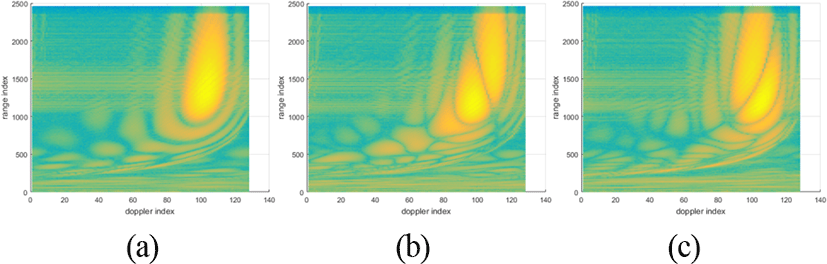
그림 5는 표 1의 시나리오 및 표적 RCS 10 m2, 표적 거리 50 km, 표적 속도 2 m/s, 표적 방위각 약 20°, 빔조향 방위각 약 20°의 시나리오 상황에서 Σ-Δ STAP의 처리 결과이다. 그림 5의 좌측 그림들은 R/D 맵들을 나타내며, 우측 그림들은 각 행의 좌측 R/D 맵을 도플러/전력 평면에 대해 수직인 방향에서 바라본 3차원 뷰(view)이다. 그림 5에서 1행은 Σ-Δ STAP 처리 결과와 비교를 위해 Σ-Δ STAP 처리전 R/D 맵을 보였다. 그림 5의 1행 그림에서 보듯이, 주엽클러터 영역 안에 위치한 표적 신호가 보이지 않고 있다. 그림 5의 시뮬레이션은 도플러 처리를 행할 때 신호의 도플러 방향 부엽성분 억제를 위한 WD (windowing)를 하지 않았으며, 이 결과들은 도플러처 처리를 행할 때 WD를 한 경우의 결과(그림 6)와 비교될 것이다. 그림 5의 2행의 결과를 보면, 방법 1에 의해 클러터 제거는 이루어졌으나, 표적 신호를 탐지하기에 충분하지 않아 보인다. 그림 5의 3행은 도플러 색인 110에 위치한 표적 신호를 방법 1보다 방법 2가 더 잘 탐지하도록 클러터를 제거함을 보여준다. Σ와 Δa의 두 채널만을 사용하는 것보다 Σ와 Δa, Δe의 세 채널을 사용하는 것이 보다 더 많은 채널 공간에서 클러터 정보를 이용함으로 클러터를 제거하고 SINR(Signal to Interference Ratio)을 높이는 데 유리함을 보여준다. 그림 3의 4행에서 방법 3에 의한 결과는 방법 1 및 2보다 도플러 색인 110에 위치한 표적 신호의 SINR이 훨씬 높음을 보여준다. 더 많은 채널 공간의 클러터 정보 및 인접 도플러 영역의 클러터 정보를 이용하는 것이 식 (4)와 같은 클러터를 제거하는 필터의 가중치를 형성하는 데 좋다는 것을 보여준다. 거리 방향 훈련데이터 개수(그림 2 참조)는 많이 가져갈수록 좋을 수 있다 그러나 거리 방향 훈련데이터 개수가 증가할수록 STAP 처리시간이 증가하고, 훈련데이터 내에 클러터의 이질적(heterogeneous) 특성이 더 증가하게 되어 클러터 제거 능력에 역효과가 발생할 수 있다. 그러므로 Σ-Δ STAP 처리성능 및 처리시간을 고려하여 훈련데이터를 적절히 정해야 한다. 그림 2에서 볼 수 있듯이, 거리 방향에서 처리될 데이터를 중심으로 양쪽으로 훈련데이터를 수집하며, 논문의 모든 시뮬레이션들에서 훈련데이터를 수집할 때 거리방향 셀 수는 200개로 하였다.
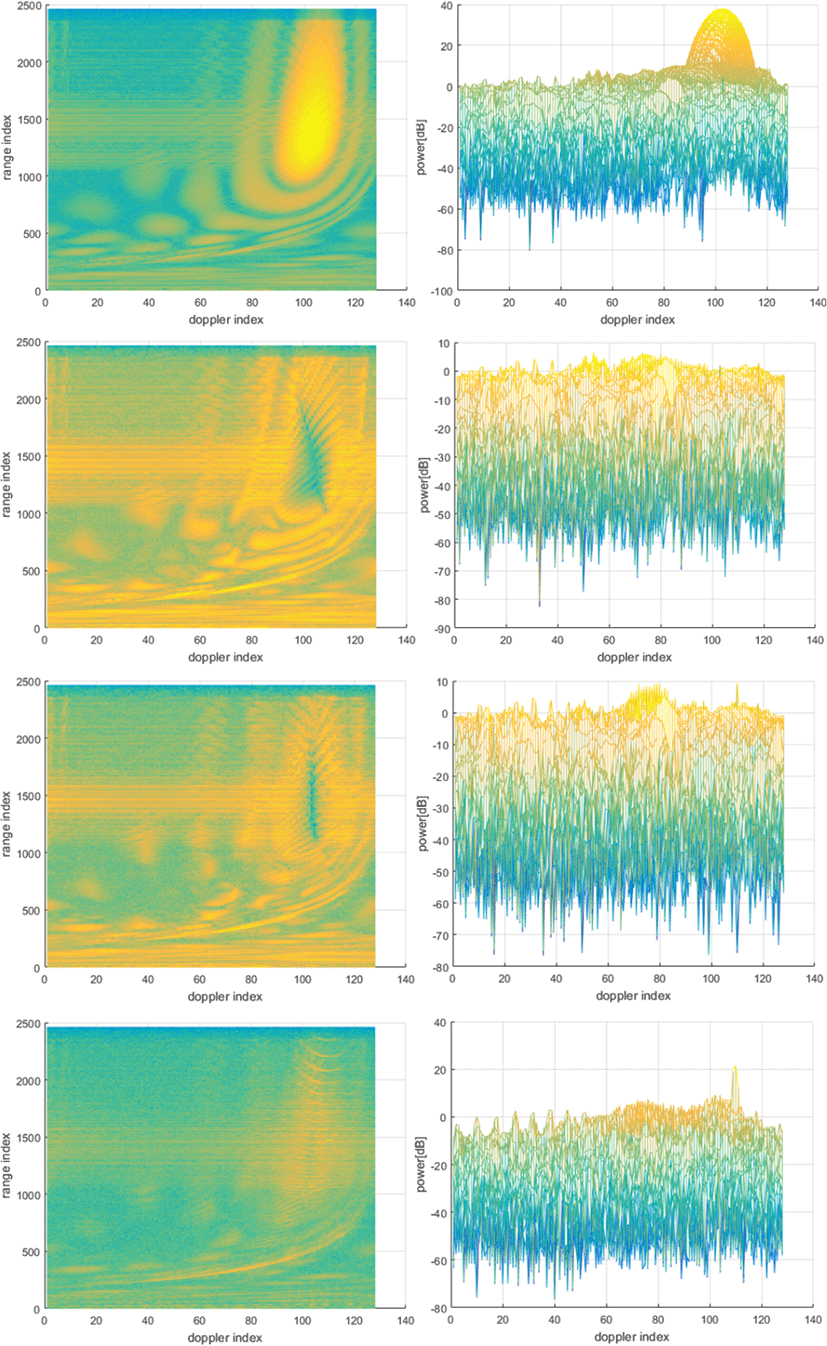
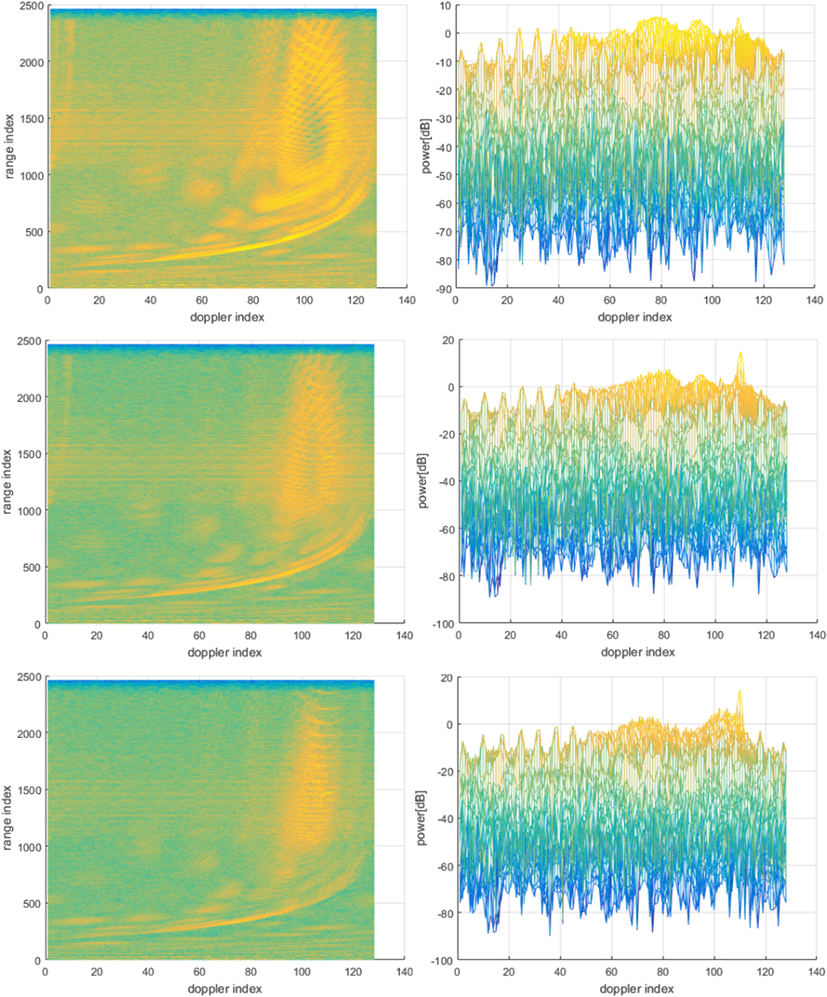
그림 6은 그림 5와 같은 모의데이터에 대해 Σ-Δ STAP을 수행한 것이며, 그림 5와 동일한 방식으로 결과들을 보여준다. 그림 6과 그림 5는 도플러 처리에서 WD를 안한 것(그림 5)과 부엽 85 dB 테일러 윈도우(Taylor window)로 WD를 한 것(그림 6)이라는 차이가 있다. 차례로 그림 5의 2행과 그림 6의 1행, 그림 5의 3행과 그림 6의 2행, 그리고 그림 5의 4행과 그림 6의 3행을 비교하면, 그림 6의 Σ-Δ STAP 처리 결과의 표적 SINR이 대체로 높은 것을 볼 수 있다. 이런 결과의 이유는 WD로 클러터의 도플러 방향 부엽 레벨(level)을 낮추어서 한 도플러 성분의 클러터의 부엽이 다른 도플러 영역에 영향을 덜 미치게 되어, 각 도플러 성분의 클러터의 정보가 일관성을 더 보장받는 효과를 받게 되기 때문으로 보인다. 즉, WD가 Σ-Δ STAP의 성능 향상에 도움을 주는 효과를 가져온다. 그러므로 Σ-Δ STAP 처리를 할 때에 도플러 처리에서 WD를 하는 것이 더 좋은 것으로 보인다. 다만 그림 5의 4행과 그림 6의 3행의 비교에서 볼 수 있듯이, 방법 3의 Σ-Δ STAP에서는 WD에 의한 앞에 기술한 효과가 SINR을 높이는 데에 크게 도움이 되지 않는 것으로 보인다.
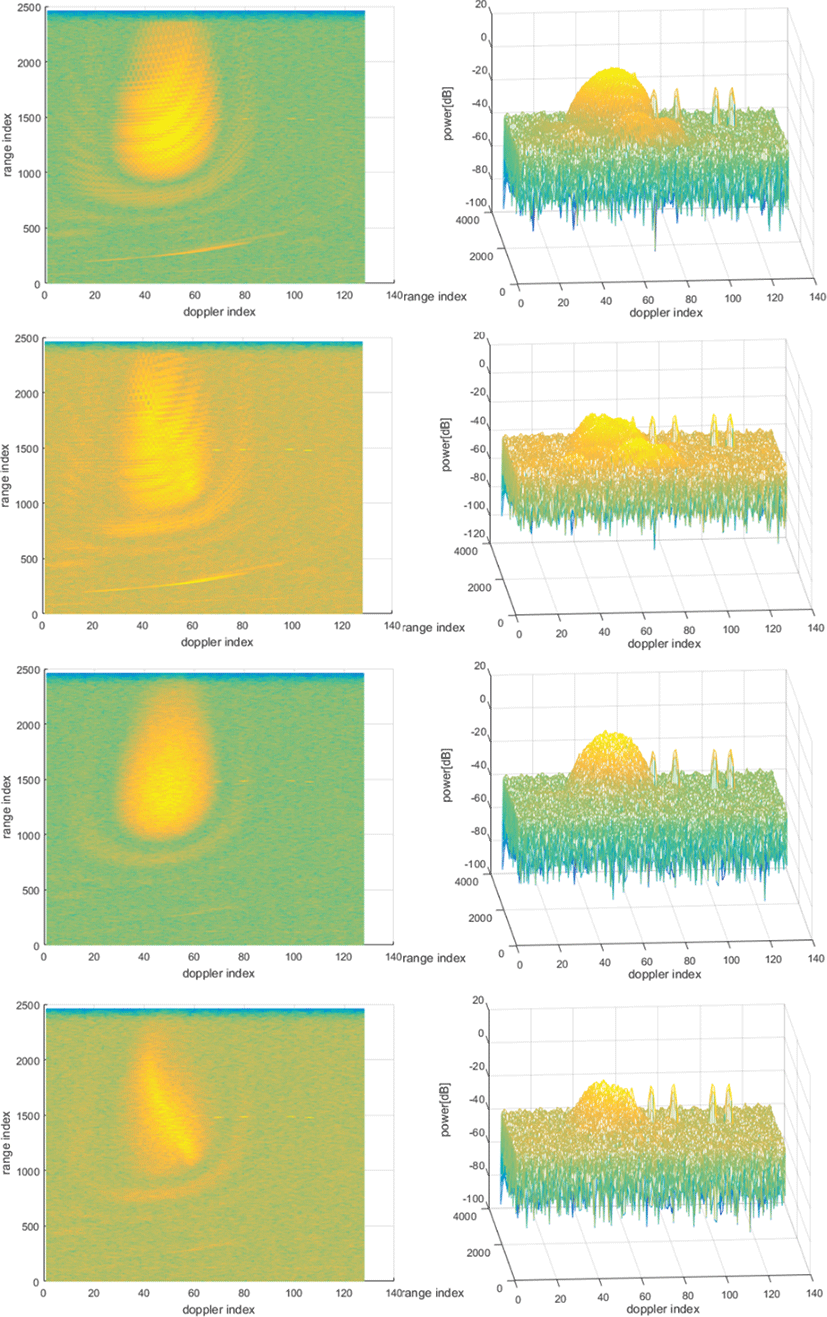
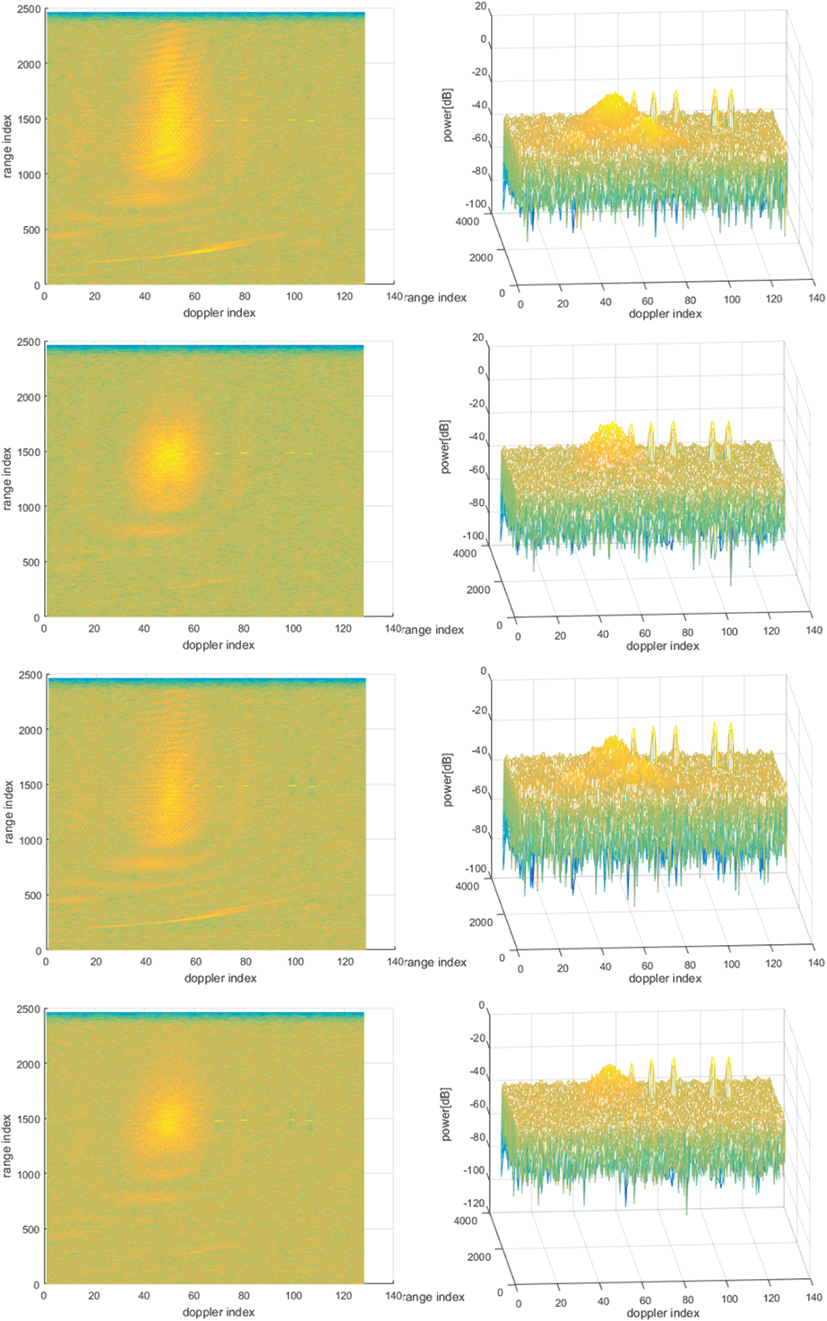
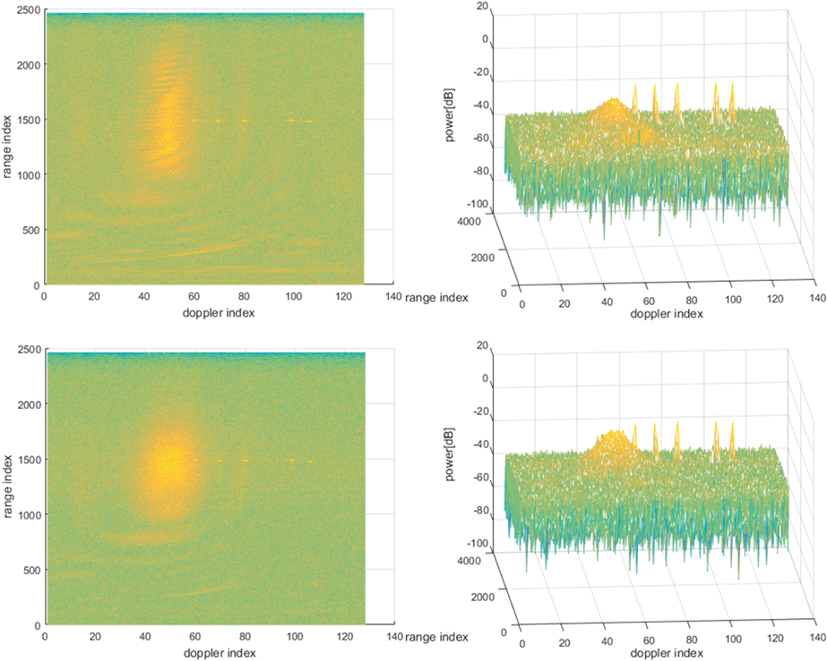
고정적이지 않은(non-stationary) 클러터의 특성을 반영한 ICM 모의를 첨가한 모의클러터에 대한 Σ-Δ STAP의 성능도 비교하였다. 그림 7은 표 1의 시나리오 및 지면 풍속 6 mph(ICM 모의를 첨가한 경우에 사용), 표적 RCS 10 m2, 표적 거리 약 50 km, 표적 속도 2~50 m/s, 표적 방위각 약 25°, 빔조향 방위각 약 25°의 시나리오 상황에서 방법 1의 Σ-Δ STAP의 처리 결과이다. 그림 7은 그림 5와 같은 방식으로 표현되어 있으며, 다만 그림 7의 우측그림들은 표적과 클러터 전력 비교가 잘 나타나도록 적절한 방향에서 바라본 R/D 맵의 3차원 뷰이다. 그림 7의 1행과 3행은 Σ-Δ STAP 처리 결과와 비교를 위해 각각 ICM을 첨가 안한 경우와 첨가한 경우의 Σ-Δ STAP 처리전 R/D 맵을 보였다. 도플러 처리에서 WD를 행하였다. 그림 7의 2행과 4행의 결과를 비교하면 ICM에 의해 Σ-Δ STAP의 성능이 조금 저하되는 것을 볼 수 있다. 그림 8은 그림 7과 동일한 시나리오 상황에서 방법 2와 방법 3의 Σ-Δ STAP의 처리 결과이다. 도플러 처리에서 WD를 행하였다. 그림 8은 그림 7과 동일한 방식으로 표현되어 있다. 그림 8의 1행과 2행을 비교 및 그림 8의 3행과 4행을 비교해서 보면 ICM에 의해 Σ-Δ STAP의 성능 저 하가 극히 적은 것을 볼 수 있다. 즉, ICM에 의한 Σ-Δ STAP의 성능 저하가 SINR의 측면에서 극히 작은 것을 볼 수 있다. 그림 9는 그림 7과 동일한 시나리오 상황 및 도플러 처리에서 WD를 하지 않은 조건에서 방법 3의 Σ-Δ STAP 처리 결과이다. 그림 9는 그림 8과 동일한 방식으로 표현되어 있다. 그림 9의 1행과 2행을 비교하면 ICM에 의해 Σ-Δ STAP의 성능 저하가 SINR 측면에서 극히 적은 것을 볼 수 있다. 방법 3의 Σ-Δ STAP은 도플러 처리에서 WD를 하지 않아도 SINR이 좋아지는 결과를 얻을 수 있는 것으로 보인다.
Σ-Δ STAP의 성능 평가에서 MDV(Minimum Detectable Velocity)를 지표로서 많이 사용된다[2]. 본 절은 본 논문의 3가지 Σ-Δ STAP 방법의 MDV 성능을 구하여 본다.
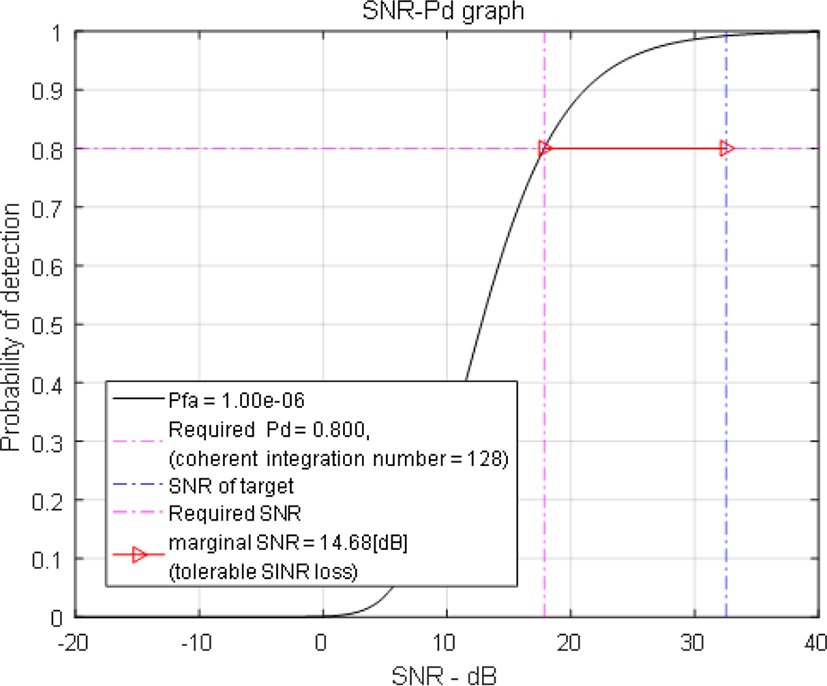
MDV를 구하기 위해서는 먼저 허용가능(tolerable) SNR (Signal to Noise Ratio) 손실을 구하여야 한다. 허용가능 SNR 손실은 요구되는 Pd(detection probability)와 Pfa(false alarm probability)를 만족하기 위해 시스템이 성취해야 하는 SNR에 비해 어떤 시스템이 여유롭게 SNR을 성취할 수 있을 때, 그 부가적으로 남는 SNR 차이 값으로 정의된다. 그림 10은 본 논문에서 사용한 시스템 파라미터로 구한 허용가능 SNR 손실을 보여준다. MDV 성능 평가를 위해 본 논문에서 사용한 시스템 파라미터 및 요구 성능은 표 1의 파라미터 및 RCS=10 m2, Pd=0.8, Pfa=10−6, 표적탐지거리=50 km 등이다. 그림 10은 SNR-Pd 그래프로서 실선은 요구되는 Pfa=10−6일 때 요구되는 SNR과 성취 가능한 Pd를 나타낸다. 최 우측 세로점선은 현 시스템이 앞에 언급한 파리미터 상황에서 성취되는 표적의 SNR을 나타낸다. 요구되는 Pd=0.8를 성취하기 위해 필요한 SNR을 최 좌측 세로점선이 나타내고 있다. 즉, 그림 10에서 볼 수 있듯이, y축 0.8 위치의 가로 실선의 폭(최 좌측세로 점선과 최 우측세로 점선 사이의 SNR 차이)이 현 시스템이 가진 여유 SNR이며, 이 여유 SNR이 허용가능 SNR 손실로 정의된다. 그림 10은 허용가능 SNR 손실이 14.68 dB임을 보여주고 있다.
다음으로 SINR 손실을 계산하여야 한다. SINR 손실(SINRloss)은 다음과 같이 정의된다.
그림 11은 표 1의 시나리오의 클러터 상황에서 SINR 손실 그래프이다. 빔 조향 중심이 지면과 만나는 거리(표 1이 주엽클러터 거리, 50 km)에서 빔 조향 방향을 중심으로 표적 속도에 대한 SINR 손실을 계산하여 그린 것이 그림 11의 각 행에서 점선으로 표시된 종 모양의 그래프이다. 그리고 표 1의 시나리오 및 ICM이 첨가된 클러터 상황에서 도플러 처리에서 부엽 85 dB 테일러 윈도우를 사용하고, 논문의 3가지 Σ-Δ STAP 방법으로 클러터 제거를 하여, 마찬가지로 표적 속도에 대한 SINR 손실을 계산하여 그린 것이 그림 11의 각 행에 실선으로 표시된 그래프이다. 최종적으로 허용가능 SNR 손실(y축의 −14.68 dB에 위치한 가로 점선)과 클러터 간섭신호에 의한 SINR 손실 그래프가 만나는 두 지점(속도 0을 중심한 양쪽 두 끝 지점)의 속도 절대 값 중에서 작은 값을 MDV로 정의한다.
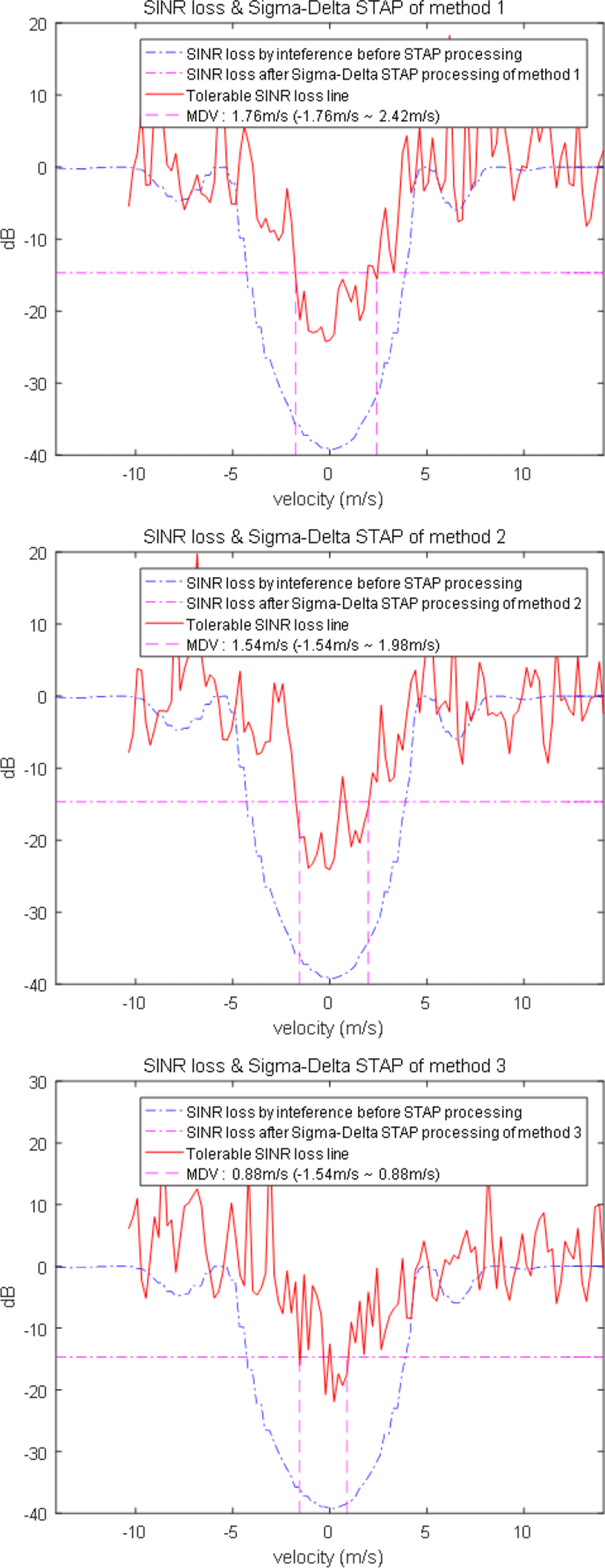
그림 11에서 각 행의 점선의 종 모양 그래프는 클러터 제거 전의 SINR 손실을 나타내며, Σ-Δ STAP 처리 전의 MDV는 약 4.3 m/s 정도임을 볼 수 있다. 이에 비하여, 각 행의 실선의 그래프는 각각 차례로 방법 1, 방법 2 및 방법 3의 Σ-Δ STAP 처리 후의 SINR 손실을 나타낸다. 그림 11에서 볼 수 있듯이 방법 1의 Σ-Δ STAP 처리 후에 MDV는 1.76 m/s, 방법 2의 Σ-Δ STAP 처리 후에 MDV는 1.54 m/s, 그리고 방법 3의 Σ-Δ STAP 처리 후에 MDV는 0.88 m/s이라는 시뮬레이션 결과를 얻었다. 방법 3의 Σ-Δ STAP이 가장 좋은 MDV 성능을 보인다.
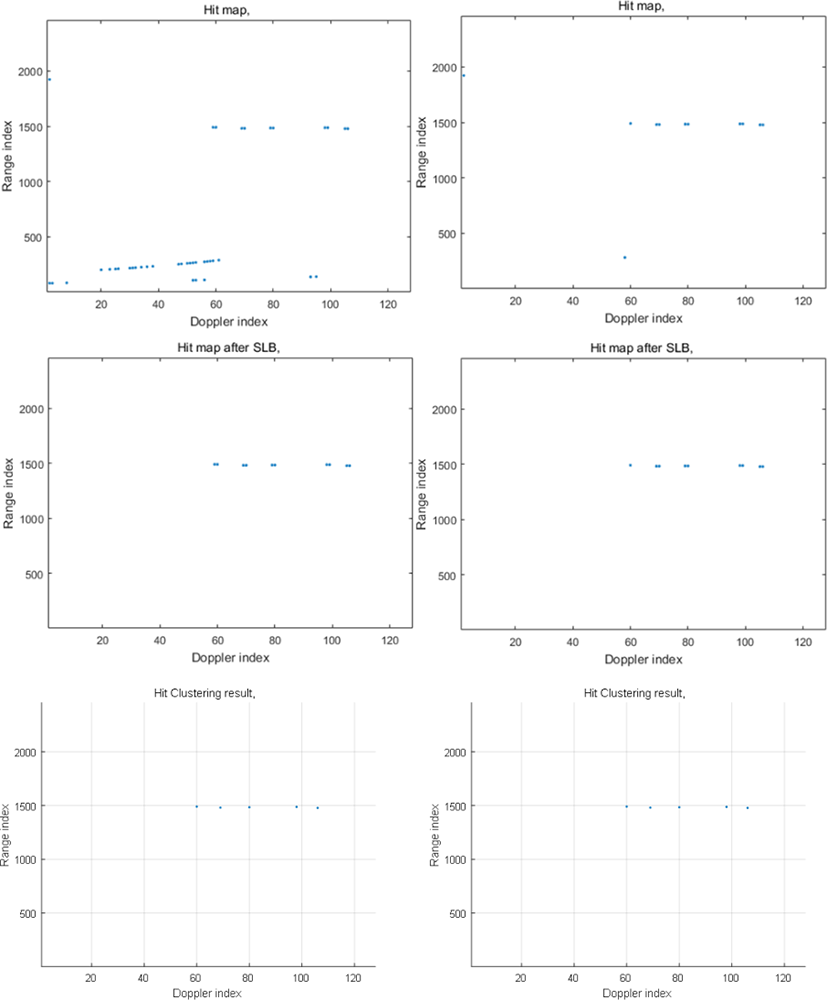
이 절에서는 그림 1(a)에 제시한 Σ-Δ STAP에 의한 GMTI 처리 흐름에 따라 지상이동물체 탐지 시뮬레이션을 행한 결과를 보여준다. 그림 8의 1행과 2행의 시뮬레이션 결과에 추가로 그림 1(a)에서 설명한 Σ-Δ STAP 처리 이후의 GMTI 처리 단계를 적용하여 보았다. 그림 12의 좌측의 1행에서 3행까지의 그림들은 그림 8의 1행의 결과에 차례로 CFAR(Constant False Alarm Rate) 처리, SLB (Sidelboe Blanking) 처리, 그리고 HIT clustering를 행한 결과들이다. CFAR 처리에서 표적뿐만 아니라, 부엽클러터까지 추출된 것을 볼 수 있다. 그러나 SLB 처리에서 부엽클러터는 지워지고, Hit clustering에서 5개의 표적만이 정확하게 탐지되는 것을 볼 수 있다. GMTI 처리에서 SLB 채널 신호가 부엽의 오표적을 줄이는 데 효과를 보임을 알 수 있다. 그림 12의 우측의 그림들은 그림 8의 2행의 Σ-Δ STAP 처리결과 이후에 나머지 GMTI 처리 단계를 적용한 결과로 좌측의 그림과 동일한 양상을 보인다. 그러므로 Σ-Δ STAP의 성능 및 STAP 처리에 필요한 연산 시간, 그리고 SLB 처리가 가능한 레이다 시스템이냐에 따라 제안한 3가지 방법 중에서 적절한 Σ-Δ STAP 처리 방법을 선택할 수 있을 것이다.
Ⅴ. 결 론
Σ, Δ 및 Λ 수신 채널을 가진 항공기 레이다의 GMTI 모드에서 지상이동물체 탐지를 위한 주엽클러터 제거 방법으로 3가지의 Σ-Δ STAP 처리 방법을 제시하였다. 또한, 제시한 Σ-Δ STAP 처리 방법을 GMTI 처리에 적용하는 흐름을 제시하고, GMTI 처리 과정을 시뮬레이션하여 효과적으로 오표적이 적게 표적 추출이 됨을 확인하였다. ICM 등의 환경을 고려한 시뮬레이션을 통해 제시한 3가지 Σ-Δ STAP 처리 방법의 클러터 제거 성능이 우수함을 보였고, 3가지 방법의 성능을 비교하였다. 3가지 Σ-Δ STAP 처리 방법 모두 MDV 측면에서 좋은 성능을 보였으며, 방법 3의 Σ-Δ STAP 처리 방법이 최고의 성능을 보였다. 시뮬레이션 과정 중에 도플러 처리에서 WD 처리가 Σ-Δ STAP의 클러터 제거 성능에 영향을 미침을 확인하고, 도플러 처리에서 WD 처리를 해주는 것이 Σ-Δ STAP에 의한 SINR 향상에 좋음을 알았다.
처리시간에 있어서는, 주엽클러터 영역에 대하여 클러터 억제를 위해 제시한 3가지의 Σ-Δ STAP 처리 방법들을 Intel core i5-3470 CPU(3.2 GHz)에서 MATLAB 코드로 처리했을 때, 방법 3, 방법 2, 방법 1의 순으로 각각 처리시간 38초, 23.5초, 22.5초가 걸렸다. 이 결과는 처리속도 최적화가 되지 않은 MATLAB 코드에 의한 결과다. 실제 구현에서는 DSP(Digital Signal Processor) 보드 등에 병렬처리 코딩 및 C 코드 등에 대한 처리속도 최적화를 통해 실시간 처리가 되도록 구현해야 한다. 현재 레이다 신호처리에 많이 사용되고 있는 DSP의 능력으로 3가지 방법 모두 충분히 실시간 처리가 가능하도록 구현할 수 있다. STAP 처리가 시스템의 제약 사항을 적게 받는 특징이 있으며, 본 논문에서 제시한 Σ-Δ STAP 처리 방법 및 GMTI 처리 방법들은 특정 항공기 레이다 시스템에 의한 제약 사항에 덜 영향을 받으면서 실제 적용이 용이하다.












