Ⅰ. 서 론
최신의 위협 유도 미사일들은 모노펄스 추적 방식(monopulse tracking)을 이용하여 표적의 각도 및 거리를 추정할 수 있다. 모노펄스 추적 방식은 오직 하나의 전자기 펄스를 송/수신하여 표적 추적을 수행하기 때문에 여러 펄스를 통해 전파방해를 수행하는 특정 전자기 기법에 대하여 강인성을 지닌다. 이에 대응하기 위해 모노펄스 추적 방식에 대한 여러 전자 방해책(electronic countermeasure: ECM) 기법들이 많이 개발되어 왔으며, 그에 대한 대전자 대책(electronic counter countermeasure: ECCM) 또한 활발히 연구되어 왔다[1],[2]. 본 연구에서는 다양한 모노펄스 ECM 기법들 중 점 잡음 재밍(spot noise jamming) 기법에 대해 다루도록 하며, 단순히 재머 대 신호비(jammer to signal ratio: JSR)에 따른 탐지율 및 각도 추정 오차 값 비교 등의 분석이 아닌 실제 유도 미사일 시스템(missile guidance system: MGS) 모델링을 통해, MGS에 대한 점 잡음 재밍 기법의 실용적인 효과도 분석이 가능하도록 하였다.
본 연구에서 다룬 모노펄스 센서로서의 MGS를 더욱 자세히 살펴보면 우선, 미리 설정한 펄스 반복 주기(pulse repetition interval: PRI)마다 펄스를 반복 송/수신한 후 일정 오경보율(constant false alarm rate: CFAR) 탐지기[3]를 사용하여 표적을 탐지하도록 하였다. 표적에 대한 CFAR 탐지가 성공하면 진폭 비교 모노펄스(amplitude comparison monopulse: ACM) 기법의 수행을 통해 표적의 각도 정보를 추출하도록 하였다. 그 후, 추정한 표적의 정보들에 의한 미사일의 자세각 변화를 PRI마다 반복적으로 갱신하여 별다른 재밍 신호가 존재하지 않는 경우, 표적에 원활하게 도달할 수 있도록 하였다[4],[5].
위와 같이 MGS를 모델링한 후, 표적에 잡음 재머가 탑재된 경우를 가정하여 잡음 신호를 적용하기 전과 후에 대한 모노펄스 각도 추정 결과 및 유도 미사일의 궤적 변화를 비교하였다. 이를 통해 실제 확인하기 어려운 잡음 재밍 환경 내에서의 유도 미사일 궤적을 보다 쉽게 눈으로 비교할 수 있었으며, 결과적으로 다양한 MGS 운용 시나리오 및 잡음 재밍 조건에 대해서 점 잡음 재밍 기법의 효과적이고 실용적인 성능 분석이 가능하였다.
Ⅱ. 유도 미사일 시스템 모델링
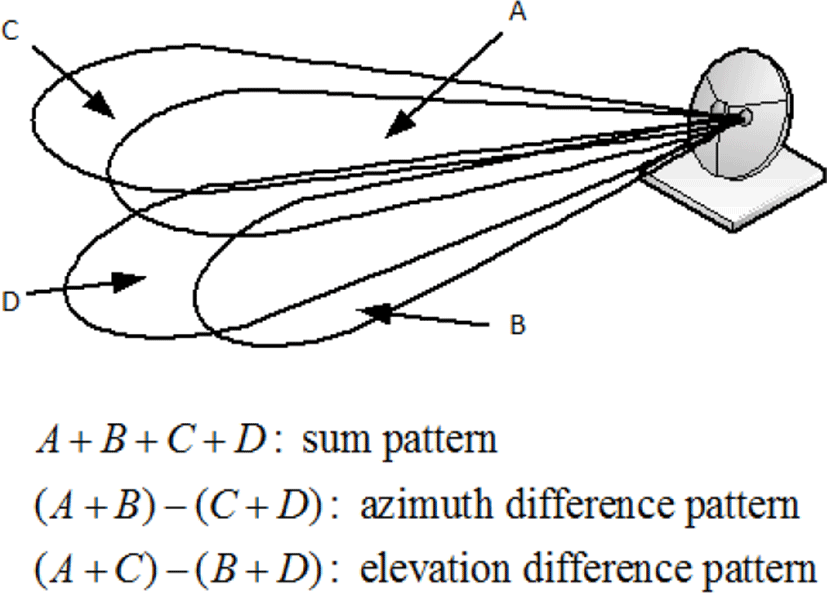
본 절에서는 잡음 재밍 효과도 분석을 위해 구현한 MGS의 전체적인 구조를 설명한다. 시스템 내의 전체적인 신호처리 과정을 그림 1로 정리할 수 있다. 표적의 추 적을 위한 MGS 내의 ACM 레이다는 네 개의 스퀸트 빔을 이용하여 합 패턴(sum pattern)과 차 패턴(difference pattern)을 형성한 후(그림 2), 이로부터 합 채널과 차 채널에서 신호를 수신한다. 그 후, 수신한 표적의 반사 신호는 베이스밴드(baseband)로 전환되어 퓨리에 변환을 통한 정합 필터링(matched filtering) 과정을 거침으로써 높은 신호 대 잡음 비(signal to noise ratio: SNR)를 확보할 수 있도록 한다. 정합 필터링 수행 후 각 채널에서의 반사 신호는 표적이 존재하는 위치에서의 피크(peak) 신호로 나타나며, 해당 피크 신호는 CFAR 탐지를 이용해 쉽게 탐지할 수 있다.
본 시스템에서는 피크 신호 탐지를 위해 여러 CFAR 탐지기 중 평균 일정 오경보율(cell-averaging CFAR: CA-CFAR) 탐지기를 사용하였다. CA-CFAR 탐지기에 대한 구성도는 그림 3과 같다. 그림 3에 나타나 있는 훈련 셀(training cell)은 해당 탐지 지점(cell under test)에 대한 문턱 값(threshold)을 결정해주는 샘플들이며, 가드 셀(guard cell)은 탐지 지점 주변으로 문턱 값의 결정에 영향을 주지 않도록 지정한 영역 내의 샘플이다. CA-CFAR 탐지기를 이용해 도출한 각 샘플 지점마다의 문턱값 T는 아래의 식과 같이 결정한다[3].
위에서 β는 크기 계수(scaling factor)이며, Pn은 잡음 측정 값이다. Pn은 훈련 셀들에 의해서 아래와 같이 결정한다.
위의 식에서 Nr과 xn은 훈련 셀들의 개수와 해당 신호 값들을 나타낸다. 식 (1)의 β는 아래와 같이 Nr과 오탐지율(false alarm rate) Pfa에 대한 식으로 주어진다.
위와 같이 각 샘플마다 문턱 값을 결정한 뒤, 신호 값이 문턱 값 이상으로 나온 샘플 지점에 대해 표적이 위치하는 곳으로 인식한다. 만약 피크 신호에 대하여 CFAR 신호 탐지가 가능하였다면 탐지 지점 신호 값을 이용하여 표적의 방위각 및 고각 정보를 추출하도록 한다. 이는, 탐지된 합 신호와 차 신호를 이용하여 합-차 신호비(sum-difference ratio)를 형성한 후, 아래와 같이 추정할 수 있다[1].
위의 식들에서 θaz와 θel은 표적의 방위각과 고각을 나타내며, s, daz, del은 합 채널, 방위각 방향 차 채널, 고각 방향 차 채널에서의 신호 탐지 값이다. km은 표적의 각도와 모노펄스 합-차 신호비간의 선형적인 관계를 나타내는 상수이며, 다음과 같이 결정된다.
식 (6)에서, kd는 차 패턴의 축상(on-axis)에서의 기울기, θbw는 빔 폭, s0는 합 패턴의 축상에서의 신호 값을 나타낸다.
일반적인 MGS는 표적의 방위각 및 고각을 추정한 후, 이를 이용하여 유도 미사일의 자세각을 변화시켜 별도의 방해 신호가 없는 경우 미사일이 표적의 위치에 도달할 수 있게 한다[4]. 이와 같은 MGS의 동작 매커니즘을 본 절에서 간략히 소개한다.
우선, 미사일의 자세각에 의해 결정되는 국부 직교 좌표계(local orthogonal coordinate(Xb,Yb,Zb))와 미사일의 자세각에 상관없이 존재하는 전역 직교 좌표계(global orthogonal coordinate(Xe, Ye, Ze))를 정의한다. 여기서, Ze=0을 만족하는 평면을 지면으로 간주한다. 그리고 국부 직교 좌표계와 전역 직교 좌표계에 의해 결정되는 오일러 각(Euler angle: 롤 각(roll angle, ϕ), 피치 각(pitch angle, θ), 그리고 요 각(yaw angel, ψ)) 또한 정의한다(그림 4). 이와 같은 미사일 자세각 모델을 6축 자유도 모델(six degrees of freedom model: 6-DOF model)로 명칭하며, 위 모델에 대한 자세한 설명은 참고문헌 [5]에 수록되어 있다.
본 연구에서 다루는 MGS는 매 PRI(ti)마다 추정한 표적의 방위각 및 고각에 대해 미사일의 자세각을 변화시키며, 이때의 오일러 각 변화(Δϕ, Δθ, Δψ)는 아래와 같다.
위의 식들에서, P는 롤 각 방향으로 가해지는 각속도, g는 중력 가속도, Ub는 국부 직교 좌표계의 Xb방향으로의 미사일 속도이며(그림 4 참고), θaz와 θel은 탐색기로부터 추정한 표적의 방위각과 고각이다. N은 양의 상수로서 크기가 클수록 추정한 각도에 더욱 민감하게 미사일의 자세각이 변화하도록 제어한다. 여기서 중요한 사실은 미사일의 자세각 변화는 표적의 방위각과 고각에 비례한다는 점이며, 이에 따라 MGS는 미사일이 진행하는 방향이 표적이 위치하는 지점과 맞닿도록 미사일의 자세각을 조정한다.
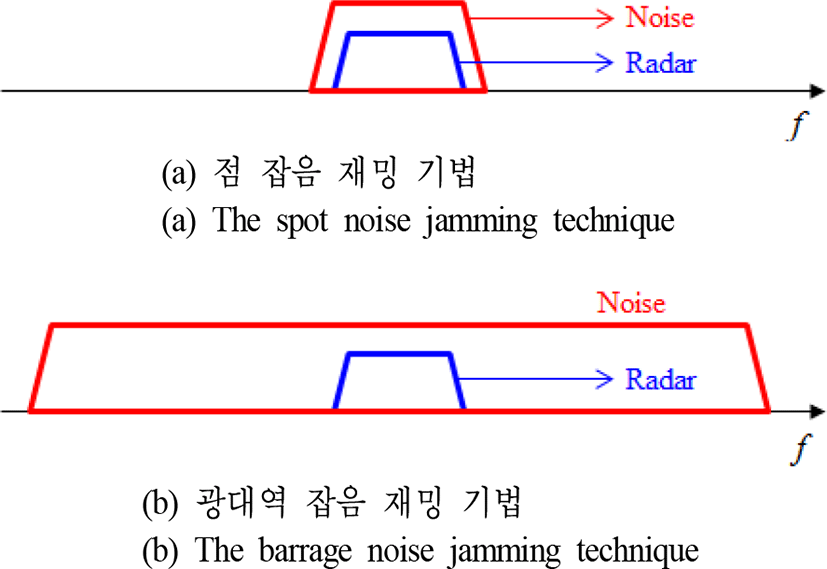
본 절에서는 위에서 소개한 MGS에 부가적으로 가해지는 잡음 재밍 신호에 대해 다루도록 한다. 일반적으로, 잡음 재밍 신호는 잡음 신호를 가하는 특정한 주파수 대역폭이 존재하며, 대표적으로 점 잡음 재밍(spot noise jamming)과 광대역 잡음 재밍(barrage jamming) 기법이 존재한다. 점 잡음 재밍 기법은 레이다 펄스 신호의 대역보다 약간 큰 대역의 잡음 신호를 사용함으로써 광대역 잡음 재밍 기법에 비해 동일한 잡음 신호 파워에 대하여 비교적 큰 잡음 효과를 얻을 수 있는 기법이다. 이와는 달리, 광대역 잡음 재밍 기법은 점 잡음 재밍 기법에 비해 넓은 주파수 대역을 사용함에 따라 잡음 재밍 기법의 ECCM 기법 중 하나인 주파수 호핑(frequency hopping)에 대하여 강인한 성질을 지닌다(그림 5).
본 연구에서는 잡음 재밍 기법들 중 가장 기본적인 점 잡음 재밍 기법에 대한 재밍 효과도 분석을 수행하였으며, 해당 잡음 신호는 미리 정해진 잡음 신호의 주파수 대역과 잡음 신호의 파워에 해당하는 랜덤 신호(random signal)를 주파수 영역에서 가하는 방식으로 생성하였다. 만약, 잡음 재머가 일정한 파워로 잡음 신호를 송신하는 경우, 각 PRI마다의 JSR은 아래와 같이 주어진다.
식 (10)에서 PJ와 PT는 각각 재밍 신호와 레이다 신호의 송신 파워, GJ와 GT는 잡음 재머 안테나와 탐색기 안테나의 송신 이득(gain)이며, R은 표적과 미사일 간의 거리, σ는 표적의 레이다 단면적(radar cross section: RCS) 값이다. 이와 같이 JSR은 MGS 내에서 각 PRI마다 위의 파라미터들에 대한 고유한 값으로 주어진다.
Ⅲ. 시뮬레이션 결과
본 연구의 시뮬레이션에서는 잡음 재밍 신호의 송신 파워를 변경시켜가며 다양한 잡음 재밍 시나리오 내에서의 모노펄스 각도 추정 결과와 유도 미사일 궤적 등의 시뮬레이션 결과를 제시하였다.
모노펄스 레이다가 송신하는 신호는 선형 주파수 변조(linear frequency modulation: LFM) 펄스이며, 주파수 대역은 Ku band, 펄스 폭은 5 μs, PRI는 0.1 ms, PTGT=60 dB로 설정하였다. ACM 각도 추정을 위해 구성한 안테나는 방위각 방향과 고각 방향 모두에 대해 반 파장 간격으로 떨어져 있는 안테나 소자(element)로 이루어진 12×12 정사각형 2차원 배열 안테나이다. 위의 배열 안테나를 사등분하여 네 개의 스퀸트 빔을 구성하였으며, 이때의 스퀸트 각도는 0.5°로 설정하였다. 또한, CA-CFAR 탐지를 위해 가드 셀과 훈련 셀의 개수를 탐지 지점을 중심으로 양쪽에 동일하게 4개와 50개로 배치하였으며, 오탐지율은 10−6으로 설정하였다.
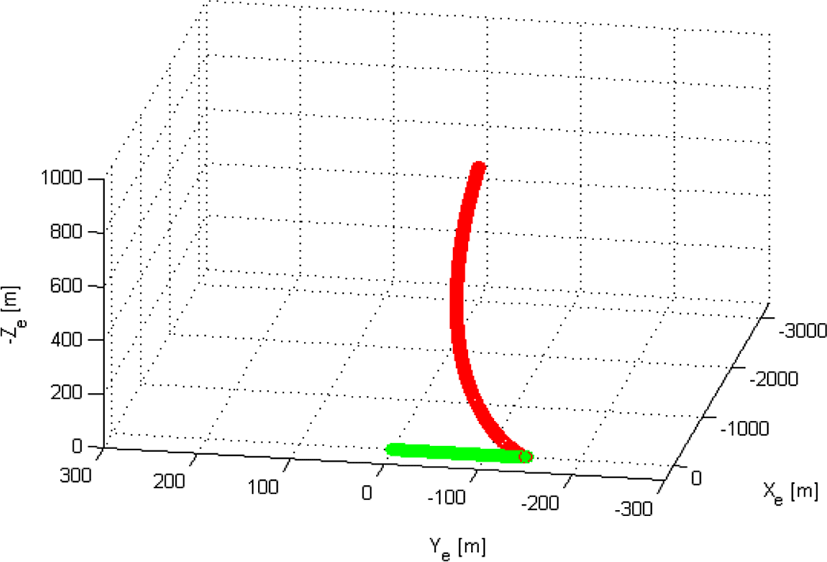
이렇게 설정한 모노펄스 레이다를 장착한 MGS는 전역 직교 좌표계 방향(Xe,Ye,Ze)으로 (−3, 0, −0.5) km의 위치에서 Xe의 방향으로 200 m/s의 속도로 움직이도록 하였으며, 미사일의 추진력, 양력, 공기 저항력은 무시하였다. 또한, 미사일의 자세각 변화를 위해 설정한 식 (8), (9)의 N은 8이었다. 재머가 장착된 표적은 점 표적(point scatterer)인 경우를 가정하였으며, 전역 직교 좌표계의 원점 위치에서 Ye의 방향으로 −10 m/s의 속도로 움직이도록 설정하였다(그림 6).
우선, 잡음 재밍 신호가 존재하지 않는 시나리오에 대해서 MGS가 정확한 표적의 위치를 알아낼 수 있는지에 대해 알아보기 위한 시뮬레이션을 수행하였다. 그림 7과 그림 8은 유도 미사일이 표적에 도달하는 동안 각 PRI마 다 기록한 모노펄스 추정 각도와 전역 좌표계 내의 미사일과 표적의 자취를 나타낸다. 표적과 미사일의 거리가 점차 가까워지면서 추정한 표적의 방위각과 고각에 따라 미사일의 자세각 변화가 이루어졌으며, 결과적으로 표적의 방위각과 고각은 0°로 점차 수렴하였다. 이 구간 동안에는 표적이 위치한 지점은 미사일의 Xb축에 근접함을 의미한다(그림 4 참고). 시뮬레이션 말미에는 미사일이 표적에 가깝게 접근함에 따라 PRI마다의 표적의 방위각과 고각 변화가 상대적으로 커져 표적의 위치는 Xb축과 다소 벗어났지만, 이 경우에도 표적의 위치에 대한 모노펄스 각도 추정이 원활히 수행됨에 따라 표적의 위치를 정확히 추적해 낸 것을 알 수 있다.
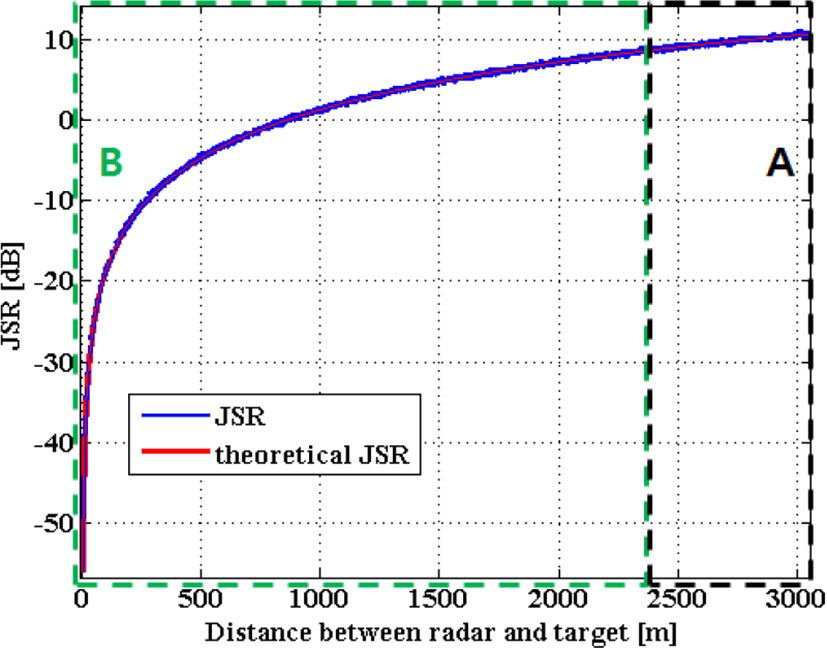
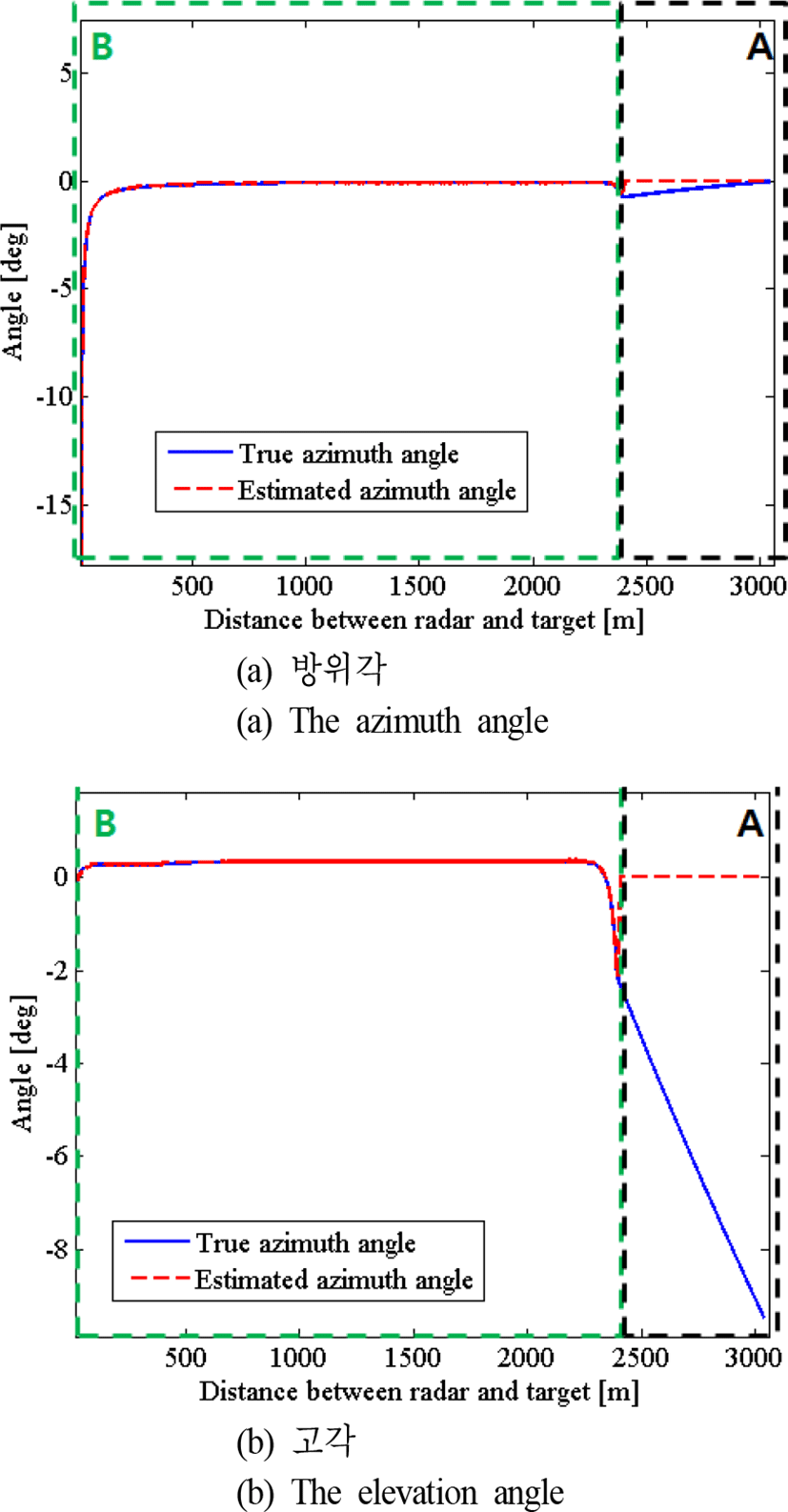
하지만, 위와 달리 PJGJ=30 dB의 잡음 재밍 신호를 부가적으로 가했을 경우, 모노펄스 수신 채널에서는 표적에 대한 반사 신호뿐만 아니라, 잡음 재밍 신호가 동시에 수신된다. 이때의 잡음 신호의 주파수 대역은 20 MHz로 설정하였다. 그림 9에는 시뮬레이션을 진행하면서 기록한 각 PRI마다의 JSR을 나타내었다. 시뮬레이션 초기의 A구간에서는 높은 JSR에 따라 표적의 신호가 CA-CFAR 탐지가 불가능하였으며, 이에 따라 표적의 각도 정보를 추출할 수 없었다(그림 10). 그러나 그림 9를 통해 알 수 있듯이, 시뮬레이션을 진행하면서 미사일과 표적의 거리 가 가까워지면서 JSR이 점차 감소하였으며, 미사일과 표적 사이의 거리가 약 2.4 km일 경우 표적에 대한 탐지가 가능하였다. 이 때의 JSR을 식 (10)을 이용해 얻어낸 결과 약 8.6 dB 이었다. 이 시점 이후의 시뮬레이션 구간을 B구간으로 칭하였으며, B구간에서는 모노펄스 각도 추정 수행이 가능하였고, 결과적으로 추정 각도를 이용한 미사일의 자세각 변화 또한 가능함에 따라 표적의 위치를 원활히 추적할 수 있었다(그림 11).
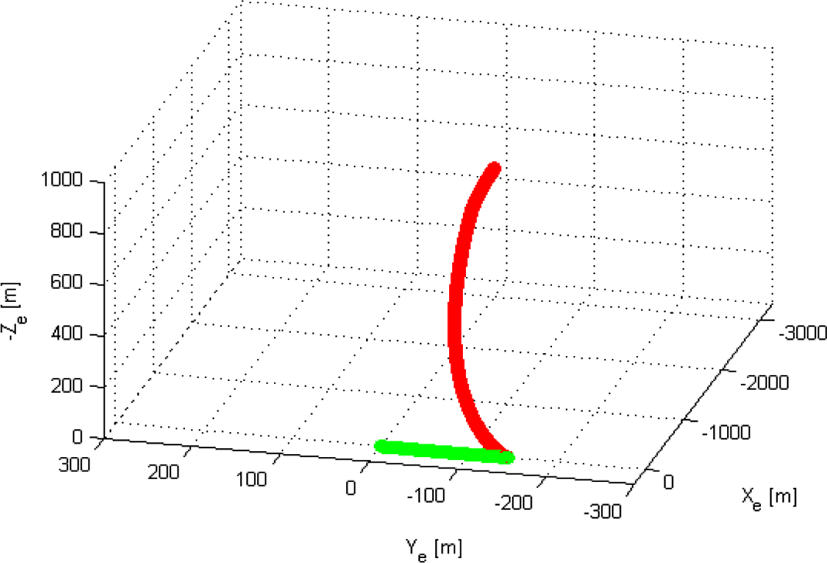
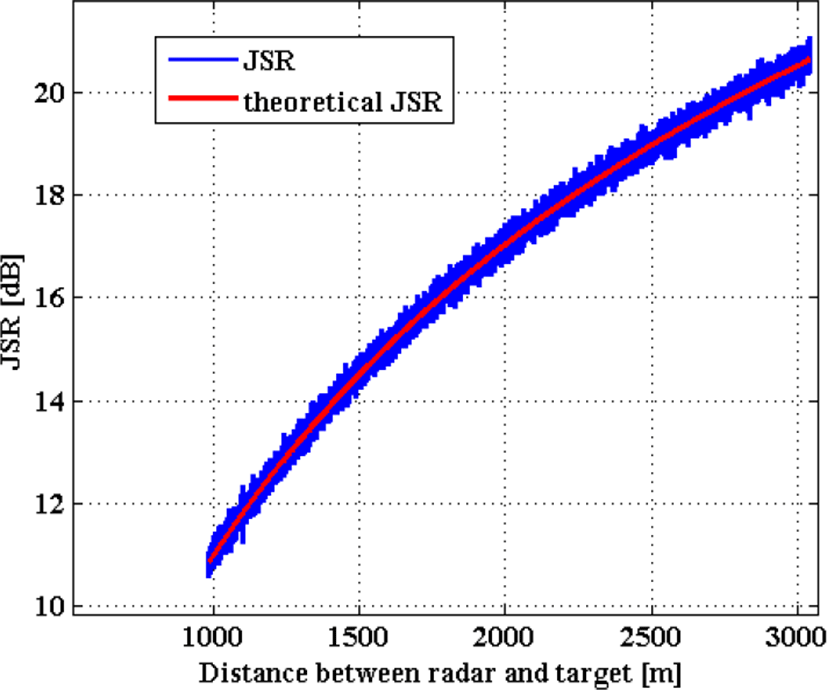
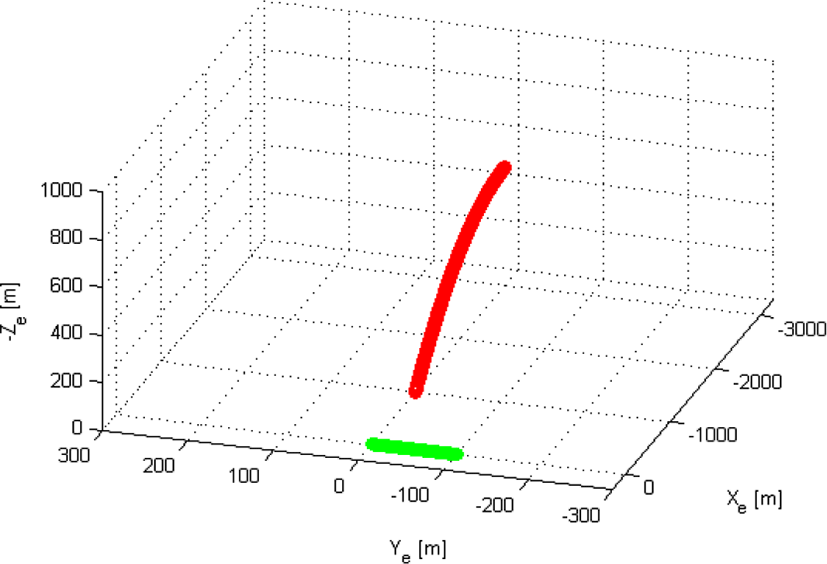
마지막으로, 잡음 신호의 파워를 이전보다 조금 높여 PJGJ=40 dB로 설정한 후 시뮬레이션을 수행하였다. 이 경우, JSR은 식 (10)에 따라 PJGJ=30 dB인 경우와 비교하여 동일한 표적과 미사일 간의 거리에서 약 10 dB 정도가 상승하였다(그림 12). 여기서, 미세한 JSR 변동은 미리 설정한 식 (10)의 JSR에 해당하는 잡음 신호를 주파수 영역의 랜덤 신호로 생성하였기 때문에 일어난 현상이다. 그림 12에서 주목할 점은 미사일이 중력에 의해 낙하하여 지면에 도달하는 경우까지 JSR은 표적의 탐지가 가능하였던 기준(대략 8.6 dB)보다 높았다. 이에 따라, 모든 PRI에 대하여 표적에 대한 탐지가 이루어지지 않았고, 결과적으로 표적의 위치 추적이 불가능하였다(그림 13).
위의 시뮬레이션 결과들을 통해 결론지을 수 있는 사실은 JSR이 일정 수준 이하가 되면 표적의 탐지가 가능함에 따라 원활한 표적 위치 추적이 가능하지만, 잡음 신호의 파워가 증가한다면 표적의 탐지가 불가능하여 미사일이 지면으로 추락하는 경우가 발생할 수 있음이다. 이와 같은 환경을 유도하기 위해서 잡음 재머는 유도 미사일이 지면으로 추락하기 전까지 최소한 8.6 dB 이상의 JSR을 확보할 수 있도록 잡음 신호를 송신하여야 할 것이다.
Ⅳ. 결론 및 향후 연구 방향
본 논문은 ACM 방식으로 표적을 추적하는 MGS를 모델링하여, 부가적인 방해 신호가 없는 경우 표적에 대한 원활한 추적이 가능하도록 모델링하였다. 그 후, 여러 점 잡음 재밍 시나리오에 대한 시뮬레이션을 진행하여 MGS의 각도 추정 결과 및 운동 궤적을 통한 잡음 재밍 성능의 분석을 수행하였다. 제시한 시뮬레이션 결과들은 유도 미사일이 지면으로 추락하기 전까지 잡음 재머는 최소한 8.6 dB 이상의 JSR을 확보할 수 있도록 잡음 신호를 송신하여야 효과적인 잡음 재밍이 가능함을 보여주었다. 향후 연구에서는 잡음 재밍 기법뿐만 아니라, 그 외의 여러 모노펄스 ECM 기능을 위의 MGS에 적용하여 다양한 방해 신호에 대한 효과도 분석을 목표로 할 것이다.




















