Ⅰ. 서 론
모노펄스 레이다에서 표적 신호에 간섭신호가 포함되는 경우 모노펄스 성능 왜곡을 일으키며, 특히 레이돔 플래쉬 부엽(flash lobe)[1]에 의한 클러터 간섭이 존재하는 경우 간섭 신호의 통계적 특성을 이용한 모노펄스 성능 왜곡 보상은 더욱 어렵다[2],[3]. 최근 제안된 GSC(Generalized Sidelobe Canceller) 구조의 모노펄스 시스템은 이를 해결하기 위해 제안되었으나, 표적신호와 플래쉬 부엽 클러터 간섭의 입사 방향이 충분히 떨어진 경우가 아니면 공간 도메인상에서 두 성분의 상관관계(correlation)가 커져클러터 간섭 억제에 한계가 있었다[4]. 이를 극복하기 위해서 시공간 도메인을 모두 이용하는 모노펄스 방식이 제안되었다. Fante는 시공간(space-time) 데이터에 대해 추정된 표적의 방위각과 도플러를 제한조건으로 STAP(Space-Time Adaptive Processing) 신호처리를 적용해서 모노펄스 MR (Monopulse Ratio) 커브를 선형화할 수 있는 차 빔(difference beam)의 가중치를 유도하였다[5]. 또한 Chen Gong은 도플러 추정 에러에 강인하도록 Fante의 알고리즘을 확장하였다[6]. 이들 연구 결과는 시공간 공분산행렬을 이용하는 알고리즘이다.
본 논문에서는 시간 도메인에서 일차적으로 클러터 간섭을 억제한 후 공간 프로세싱을 적용하는 시공간 신호처리 과정을 통해서 클러터 간섭 환경에서 기존 시공간 공분산행렬을 이용하는 알고리즘에 비해 연산량이 적으면서 방향 추정 성능이 우수한 모노펄스 방식을 제안한다. Ⅱ장에서 시스템 구조 및 시공간 신호처리 과정을 제시하며, Ⅲ장에서 시뮬레이션 결과를 보인다.
Ⅱ. GSC 구조 모노펄스 시스템
그림 1은 본 논문에서 제안하는 GSC 기반 모노펄스 시스템을 나타낸다. 시간 도메인 프로세싱부가 전처리 과정으로 포함되는 구조로 시간 도메인 프로세싱부는 각 배열소자에 대응하는 시간 도메인 GSC 필터를 갖는 필터뱅크 구조를 갖는다. 제안 시스템의 신호처리 과정 설명을 위해 본 장에서는 2차원 고각 방향 추정 중심으로 기술하였으며, 시스템은 3차원으로 확장 가능하다.
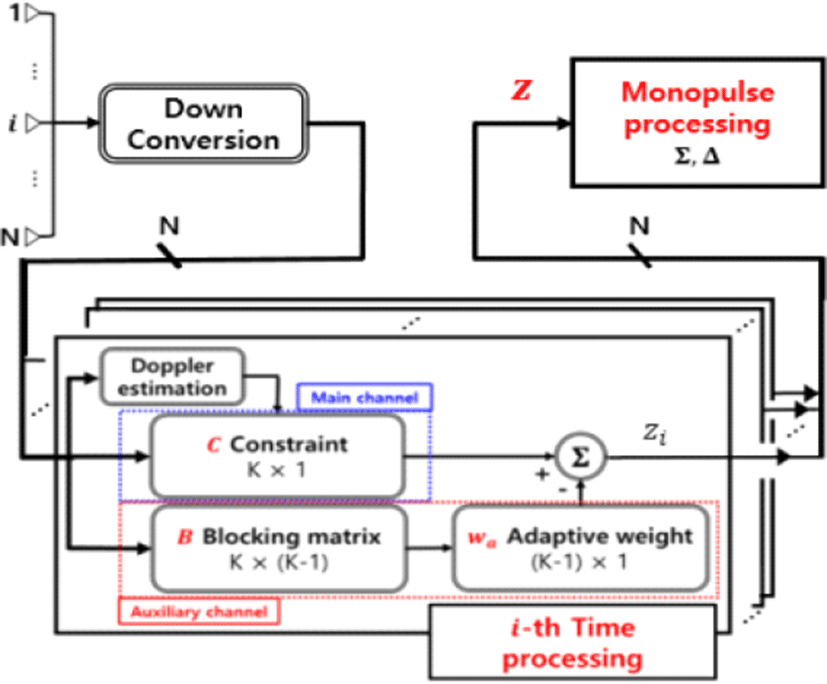
배열 안테나 소자 간격이 λ/2인 경우 i번째 안테나에 수신된 표적신호는 다음과 같이 나타낼 수 있다.
여기서 θt는 표적의 고각 입사 방향이며 st(t)는 시간 도메
인 레인지 프로파일로서 샘플링 시점에 따라 다른 레인지 빈(range bin)을 나타낸다. PRI(Pulse Repetition Interval) 주기 Tp로 K번 샘플링 된 프로세싱 구간의 특정 레인지 빈에 대한 신호벡터는 다음과 같이 나타낼 수 있다.
여기서 ai는 진폭을 나타내며 표적과의 거리가 충분히 먼 경우 i에 관계없이 상수 값을 갖는다고 가정할 수 있다. St는 [1 exp(j2πTP fd,t) ⋯ exp(j2π(K−1)TPfd,t)]T, 첨자 T는 전치 행렬을 나타내고, fd,t는 표적신호의 도플러 주파수를 나타낸다. 식 (2)에서 ai는 특정 레인지 빈에 해당하는 표적 산란원(scatterer)의 반사계수에 비례하는 값으로 본 제안 방식에서는 프로세싱 구간 KTp가 크지 않다고 가정하여 ai는 프로세싱 구간에서 상수로 가정하였다. 추정한 표적의 도플러 주파수가 라고 할 때, K개로 구성된 필터 탭(tap)의 가중치 C0는 다음과 같다.
여기서 fd,t와 가 동일하다면 주 채널(main channel)의 출력은 다음과 같이 얻어지게 된다.
동일한 과정에 의해 i번째 채널에 수신된 클러터 간섭의 샘플링 된 클러터 간섭 벡터는 다음과 같다.
여기서 Ct는 [1 exp(j2πTPfd,c)⋯exp(j2π(K−1) TPfd,c)]T, θc는 플래쉬 부엽에 의한 클러터 간섭 입사 방향, fd,c는 클러터 간섭의 도플러 주파수이다. 보조 채널(auxiliary channel)의 B는 도플러가 가 아닌 성분만을 필터링하는 차단행렬(blocking matrix)로서 주 채널 탭 가중치 C0에 직교공간을 스팬(span)하는 행렬이다. B의 열벡터(column vector)는 그람-슈미트 직교화(Gram-Schmidt orthogonalization)나 SVD(singular value decomposition) 등으로 찾을 수 있다. 보조 채널의 적응형 가중치 벡터 wi는 MVDR(Minimum Variance Distortionless Response) 조건 인 을 만족하도록 다음 식 으로 얻을 수 있다[7].
여기서 첨자 H는 에르미트(Hermitian) 연산자를 나타내며, Ri은 i번째 채널로 수신되는 신호 Xi의 공분산행렬이다. 이때 GSC 필터 출력 zi는 다음과 같이 나타낼 수 있다.
또한 N개 채널의 출력 벡터 z는 다음과 같이 구성된다.
출력된 벡터 z는 공간 필터링만을 하는 전통적인 모노펄스 프로세싱부에 입력되어 합 빔과 차 빔 가중치 벡터와 연산되어 모노펄스 출력을 얻게 된다.
제시된 시스템을 요약해 보면 시간 프로세싱부는 GSC 구조로 구성되며, 시간 도메인에서 표적 성분을 필터링하여 클러터 간섭 성분을 최대로 억제하는 역할을 한다. 이를 위해 시간 도메인 프로세싱부는 표적에 대한 도플러 사전 정보가 주워져야 하며, 편의상 그림 1에서는 도플러 추정부가 있고, 여기서 추정된 도플러 정보가 주 채널필터에 입력되어 표적 성분을 추출하게 된다. 실제 시스템에서 도플러 추정부와 주 채널 필터는 도플러 필터뱅크에 의해 구현 가능하다. 하지만 다음 Ⅳ장에서 제시되는 결과에 따르면 주 채널 필터의 탭 개수가 커서 대역폭이 좁게 되면 추정 도플러 오차에 민감해서 성능을 더 열화시키므로 그림 1에서처럼 두 개의 모듈로 구성하는 것이 효과적이다.
Ⅲ. 시뮬레이션
본 장에서는 두 가지의 기존 방법과의 비교를 통해 제안 알고리즘 성능을 평가하였다. 기존 방법 1(Conventional Method 1)은 수신신호로부터 시간 필터링 없이 공간 필터만 통과하는 보통의 모노펄스 시스템이다. 기존 방법 2는 도플러 필터 뱅크로 시간 프로세싱을 하고 난 후 공간 필터링을 하는 시스템으로 그림 1에서 보조채널 없이 주 채널만 사용하는 시스템이다.
성능평가를 위하여 다음과 같은 시뮬레이션 환경을 설정하였다. 송신 펄스의 중심 주파수는 10 GHz, PRI는 50μs, 수신안테나는 64개의 배열 소자를 갖는 선형 안테나로 가정하였다. 수신 안테나는 0°를 조향하고 있고, 표적신호는 0.1°에서 클러터는 3.5°에서 각각 입사되고 SCR (Signal-to-Clutter Ratio) 0 dB로 정했다(그림 2의 ‘input signal’ 스펙트럼에서 확인 가능).
그림 2는 도플러 추정 오차가 없는 경우, 제안한 GSC 구조 시스템의 여러 지점에서의 출력 벡터를 FFT한 결과를 나타낸다. 주 채널을 통과한 클러터 간섭(‘main channel’로 나타냈음)이 보조 채널에서 적응적 추정을 하여 최종 출력(GSC output)에는 클러터 간섭 성분이 상당히 제거된 것을 확인할 수 있다.
그림 3은 안테나 조향 및 클러터 간섭 입사방향은 위와 동일하게 하고, 표적방향만 −2°에서 2°까지 변화시키며 획득한 MR커브이다. 기존 방법 1의 경우 MR커브가 크게 왜곡되었으며, 도플러 추정 오차가 없다면 기존 방법 2는 기존 방법 1에 비해 MR커브 왜곡을 크게 개선시켰고, 제안한 방법을 적용한 경우 클러터 없는 경우(‘clutter-free’)와 유사할 정도로 MR커브 왜곡이 최소화되었다.
그림 4와 그림 5는 주 채널 필터 탭 개수 K 및 도플러 추정 성능에 따른 방향 추정 오차 성능을 나타낸다. 안테나는 0°를 조향하고 있으며, 11° 부근에서 플래쉬 로브에 의한 클러터 간섭이 입사하는 환경을 가정하였다. CNR은 0 dB부터 30 dB까지 변화시켰고, 3 dB 빔폭안(오차각 산출범위 : ±0.7°)에서 표적 위치를 변화시키면서 몬테카를로 기법에 의해 방향 추정 오차의 MAE(Mean Absolute Error)를 계산하였다.
K가 3인 경우 도플러 오차가 5 % 존재하여도 제안한 방법은 0.2° 이하의 MAE 값을 가졌다. CNR이 큰 경우에도 기존 방법 1과 기존 방법 2에 비해 우수한 방향 추정 성능을 보였다. K가 8의 경우는 주 채널 필터의 통과 대역폭이 좁아 제시된 방식은 도플러 오차에 민감하였다. CNR이 큰 일반적인 환경에서 제안 방법이 가장 우수한 성능을 보였지만, 예외적으로 도플러 오차가 있으면서 CNR이 낮은 일부 구간에서는 제안 방법이 기존 방법 2보다 성능이 떨어졌다. 그 이유는 제안 방법의 경우 보조 채널로 유입되는 표적성분과 잡음이 증가해서 MAE 값을 증가시켰기 때문이다.
Ⅳ. 결 론
본 논문에서는 전처리 과정으로 GSC 기반 시간 프로세싱부가 포함된 모노펄스 시스템을 제시했다. 제시된 시스템은 CNR이 큰 일반적인 레이더 환경에서 기존 방법에 비해 방향추정 성능이 우수하였다. 하지만 주 채널 탭 개수 K에 따라 결정되는 필터 대역폭에 따라 도플러 추정 오차 민감도가 결정되므로 이를 고려한 적절한 K 설정이 필요하다. 또한 보조 채널의 사용은 잡음 전력을 증가시키므로 잡음 전력 증가에 대한 분석을 통해 제안 시스템이 기존 도플러 프로세싱을 사용하는 시스템보다 개선된 성능을 보여줄 수 있는 최소 CNR 값을 찾는 연구가 필요하다.











