Ⅰ. 서 론
최근 표적의 탐지 성능을 향상시키기 위하여 공간(spatial)과 시간(temporal)으로 2차원 이득을 얻을 수 있는 레이다 시스템이 각광을 받고 있다. 이러한 레이다 시스템은 표적에 대한 탐지성능뿐만 아니라, 공간과 시간신호를 이용하여 클러터를 효과적으로 제거할 수 있으며, 이러한 신호처리 방식을 시-공간 적응처리(Space-Time Adaptive Processing: STAP)라고 한다[1]. 시-공간 적응처리 기술의 핵심은 cell-under-test(CUT)에 해당하는 클러터를 추정하는데 있다[2]. RMB 룰은 Homogeneous 클러터 환경에서 최적필터(optimal filter)보다 3 dB 이내의 손실(loss)을 얻기 위해서 IID 가정하에 ‘2×소자 수×펄스 수’ 만큼의 secondary 데이터가 요구됨을 보였다[3]. 하지만 이론적으로 요구되는 이 secondary 데이터량은 지나치게 방대하고 특히 Non-homegeneous 클러터 환경에서는 IID한 샘플 수가 부족하여 secondary 데이터에 의한 클러터 추정에 한계가 있다[2]. 이를 해결하기 위해 secondary 데이터를 줄이기 위한 연구가 다양하게 진행되었다[2],[4]~[6]. 하지만 이들 방법은 실제 환경에서 발생하는 비정상적이고 비균질한 특성을 지닌 클러터에 대해서 제한적인 성능을 보임에 따라 사전정보를 이용한 클러터 억제 기술이 새롭게 제안되었다[7],[8]. 참고문헌 [9], [10]은 Bayesian 접근방법을 이용하여 사전정보와 secondary 데이터를 적절히 가중합(weighted-sum)하여 클러터의 공분산 행렬을 추정하는 방식으로 SINR과 MSE 기준으로 최적의 가중치를 제안하였다. 참고문헌 [11]은 스칼라(Scalar)인 가중치를 벡터(vector)로 확장하여 클러터의 subspace 각각에 가중치를 적용하여 효과적으로 클러터의 공분산 행렬을 추정하는 방법을 제시하였다.
위의 여러 가지 연구들은 사전정보를 이용하지만, 여전히 secondary 데이터가 요구되므로 복잡한 구조의 클러터 환경에서는 한계점이 존재한다. 이것을 해결하기 위해 참고문헌 [12]는 CUT의 데이터로 크기와 위상 추정(Amplitude and Phase Estimation: APES) 필터를 적용하여 클러터의 공분산 행렬을 추정하는 방식을 제안하였다. 하지만 클러터의 ICM(Intrinsic Clutter Motion)에 의해서 클러터 스펙트럼이 퍼지는(spreading) 환경에서는 APES 필터의 성능이 제한된다.
본 논문에서는 바이스태틱 레이다 환경에서 CUT에 대하여 사전정보만을 이용하여 ICM이 포함된 클러터를 추정함으로써 secondary 데이터 없이 클러터를 억제하는 알고리즘을 제시한다. 마지막으로 시뮬레이션을 통해 제시하는 클러터 억제 알고리즘에 의해서 클러터가 적절히 제거되는 것을 보인다.
Ⅱ. 신호 모델링
레이다의 송신단에서 방사된 송신신호는 그림 1과 같이 표적과 더불어 동일 거리에 존재하는 클러터 성분들에 산란되어 레이다의 수신부로 수신된다.
레이다와 l 번째 클러터 패치가 이루는 도플러 주파수 fl는 레이다 송신단과 수신단의 속도벡터 vtx와 vrx, 그리고 l 번째 클러터 패치와 송신단 수신단이 이루는 단위벡터 ctx,l와 crx,l각각의 이동에 의해서 다음과 같이 얻을 수 있다.
위의 식 (1)에서 λ는 파장(wavelength)을 의미한다. M개의 펄스를 사용하고 N개의 소자로 구성된 선형 배열 안테나로 수신되는 신호 x는 다음식과 같다[13].
여기서 w는 백색 잡음으로 CN(0,σ2)을 따르고, 아래첨자 T는 표적을 의미하며, 표적과 동일 거리에 있는 클러터 패치는 Nc개라고 가정하였다. ⊗는 Kronecker 연산이고, b(fl)와 a(θl)는 도플러(Doppler) 지향(Steering) 벡 터와 공간(spatial) 지향 벡터로서 다음식과 같다.
여기서 θl와 prx,n은 l번째 클러터 패치에 의해서 송신단에 수신되는 신호의 입사각과 송신단의 위치벡터를 각각 의미한다.
실제 클러터는 비정상성과 비균질한 특성을 갖기 때문에 클러터의 진폭 αl은 Log-normal 분포를 따르고, 클러터의 ICM에 의해서 생기는 도플러 특성을 Gaussian 스펙트럼으로 모델링 하였으며[14], 표적신호의 진폭 αT는 Swerling 1 모델을 가정하였다[15].
따라서 식 (2)의 첫 번째 항은 표적신호이고, 두 번째 항은 표적과 동일 거리에 존재하는 클러터를 나타낸다.
레이다의 송수신 위치 정보와 이동에 대한 운용정보를 사전정보로 활용하면 CUT의 클러터 xc는 다음과 같이 이론적으로 모델링하여 계산할 수 있다.
이때 클러터 진폭의 통계적 특성은 알 수 없으므로 αn = 1이라고 가정하였다.
Ⅲ. 클러터 억제 알고리즘
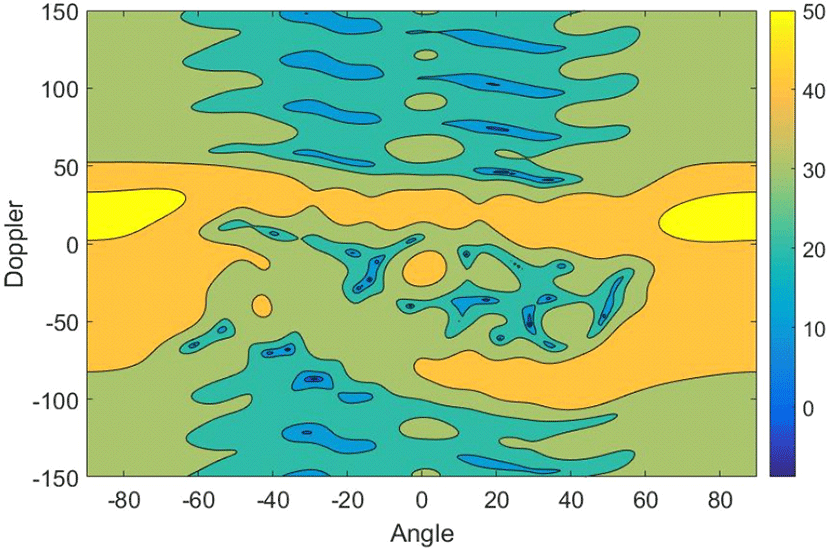
수신 신호 x에 포함된 클러터는 레이다와 Iso-range에 존재하는 클러터와의 거리, 레이다 송수신기의 위치, 그리고 레이다 송수신기의 속도벡터에 의해서 결정되며, angle-Doppler 평면에서 보면 연속된 릿지(ridge) 형태를 갖는다. 그림 2는 표적 신호가 포함된 특정 CUT로 부터 수신된 신호의 angle-Doppler 평면에서의 스펙트럼을 나타낸다.
여기에 사용된 시뮬레이션 환경 파라미터 값들은 IV. 절 표 1에 나타내었고 그림 2의 오른쪽에 있는 그라데이션 바(Gradation bar)는 신호의 파워를 표현한 것으로 단위는 [dB]이다.
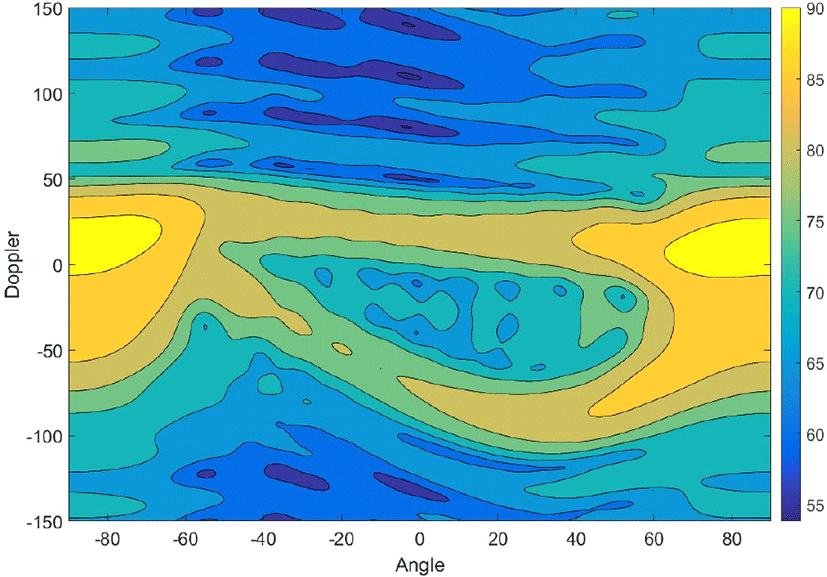
클러터의 스펙트럼은 클러터 패치의 RCS 값에 따라서 클러터 릿지를 이루는 각각의 angle-Doppler 지점들의 진폭값이 변하며, 또한 클러터의 ICM에 의해서 클러터 릿지의 퍼짐(Spread) 현상이 발생한다. 그림 3은 표 1에 주워진 사전정보로부터 식 (5)를 이용해서 계산한 CUT의 클 러터 xc의 angle-Doppler 스펙트럼이다. 그림 2와 비교해 보면 클러터 릿지의 형태는 유사하지만, 퍼짐 정도나 각 클러터 패치마다 다른 RCS는 적절히 보여주지 못함을 확인할 수 있다. 따라서 클러터 릿지를 이루는 angle-Doppler 지점들의 진폭과 클러터 릿지의 퍼짐 정도를 적절히 추정하여 클러터를 억제하는 과정이 필요하다. 이를 위해 제안 방법에서는 우선 클러터 릿지 후보군 생성 및 실제 수신신호와의 상관관계를 이용해서 클러터를 생성하고, 이어서 고유치 해석 과정을 통해서 클러터 성분을 제거하는 두 단계 과정을 진행한다.
3-1 클러터 신호 추정
그림 2와 그림 3을 비교해 보면 사전 정보로 부터 얻어진 클러터 릿지는 수신 신호의 클러터 릿지와 동일 위치에 있으나, ICM이 포함되어 있지 않아서 대체로 퍼짐 정도가 적다. 그러므로 사전 정보로 얻어진 클러터 릿지로부터 도플러 주파수만 증감된 클러터 릿지를 생성한다면 실제 클러터 환경을 반영한 후보군이 될 수 있다. 즉, 식 (5)를 이용해서 계산한 클러터 xc의 도플러 주파수 fl을 fl±nΔf로 적절히 대체함으로써 다음과 같이 후보군 클러터 릿지를 생성할 수 있다.
위 식에서 Δf는 쉬프트(shift)시키고자 하는 도플러 주파수 간격이고, i는 음수를 포함한 정수값을 갖는다. 또한 이때 i의 범위는 다음 식 (7)의 조건으로부터 결정된다.
여기서 γ는 설계 변수로써 x와 가 갖는 상관도 (correlation)의 경계값(threshold)이고 ‖ ‖는 norm 연산을 의미한다. 식 (7)의 조건은 후보 클러터가 실제 수신 신호에 포함된 클러터 와 유사한 정도를 판별하는 것으로 i가 커지면 후보 클러터 도플러가 실제 클러터 도플러 범위를 벗어나게 되어 후보군에서 제외시켜야 한다. 식 (6)은 백로브(backlobe)로 입사되는 신호를 고려하지 않고 후보 클러터 릿지를 생성시키는 경우로서, 만약 백로브를 고려해야 한다면 angle-Doppler 평면에서 특정 angle 당 두 개의 도플러가 존재하게 되어 식 (6)보다는 복잡한 도플러 증감 과정이 필요하다.
3-2 클러터 억제 알고리즘
사전정보를 이용하여 얻은 클러터 의 공분산 행렬 Ri는 고유값 분해에 의해 다음과 같이 표현된다.
위의 식에서 H는 hermitian 연산이고, vi,1vi,2⋯ vi,NM는 고유벡터(Eigen-vector)이며, λi,1 λi,2 … λi,NM는 고유치(eigen-value)이다. 는 noise free이므로 Rank(Ri)=Ki ≤ NM이고, vi,1vi,2⋯ vi,Ki, ∀i의 성분들을 수신신호 x에서 다음식과 같이 제거한다.
위의 식 (9)로부터 사전정보 신호로부터 추정한 클러터 성분들 vi,1vi,2 ⋯ vi,Ki, ∀i을 수신 신호 x에 내적하여 제거하는 과정을 통해 클러터의 진폭에 대한 정보를 추정하는 것을 확인할 수 있다.
Ⅳ. 시뮬레이션
본 절에서 바이스태틱 레이다의 시뮬레이션 파라미터는 표 1과 같다.
그림 4는 식 (6)에서 i 범위 결정을 위한 x와 의 상관도를 나타낸 것이다.
i가 증가할수록 의 릿지가 커지기 때문에 수신 신호 x와의 상관도가 감소한다. 이와 반대로 i가 감소할수록 마찬가지로 상관도가 감소하지만, 다시 상관도가 반등하는 구간을 그림 4에서 확인할 수 있다. 이것은 생성된 클러터 릿지 일부가 angle-Doppler 평면에서 fT = −15 Hz에 존재하는 표적 신호와 유사하게 된 것으로 표적이 제거되지 않기 위해서는 표적 신호와의 상관도보다 크도록 γ를 설정해야 함을 확인할 수 있다. 따라서 와 표적과의 상관도가 0.5~0.6 정도에 위치하므로 γ가 표적과의 상관도보다 충분히 크도록 γ = 0.7로 정하고, 시뮬레이션을 진행하였다.
그림 5는 γ = 0.7을 만족하는 i의 일부인 i =−4, …, 0 에 대해서만 적용하여 클러터 억제 알고리즘을 적용한 출력 신호의 angle-Doppler 스펙트럼이다.
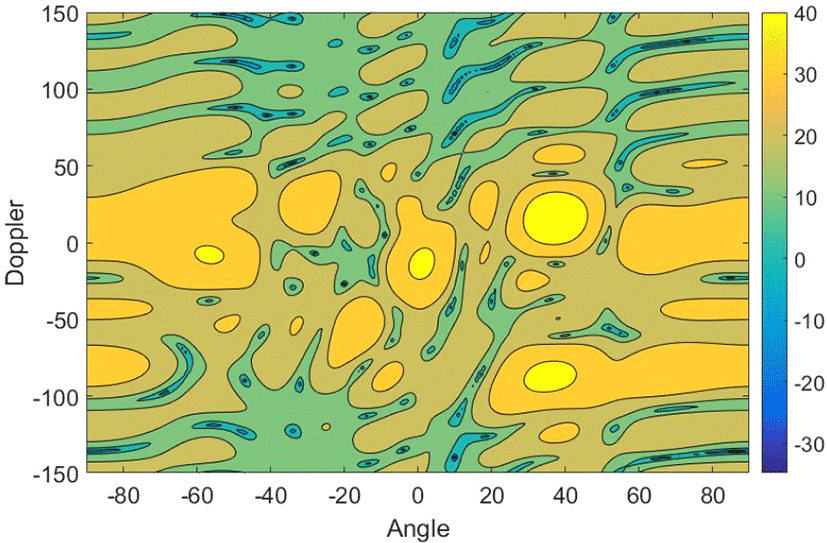
일부 클러터는 제거되었지만, 여전히 상대적으로 신호 세기가 강한 클러터가 남아 있는 것을 확인할 수 있다. 이것은 ICM에 의해서 ICM이 없는 환경의 클러터 릿지보다 좁아진 영역(i =−4, …, 0)의 클러터는 억제가 되었지만, 그 이외의 영역에 대해서는 , i =−4, …, 0로부터 수신신호 x가 갖고 있는 클러터 신호 공간을 추정할 수 없기 때문에, 클러터 성분들을 완전히 제거하지 못한 결과로 해석할 수 있다.
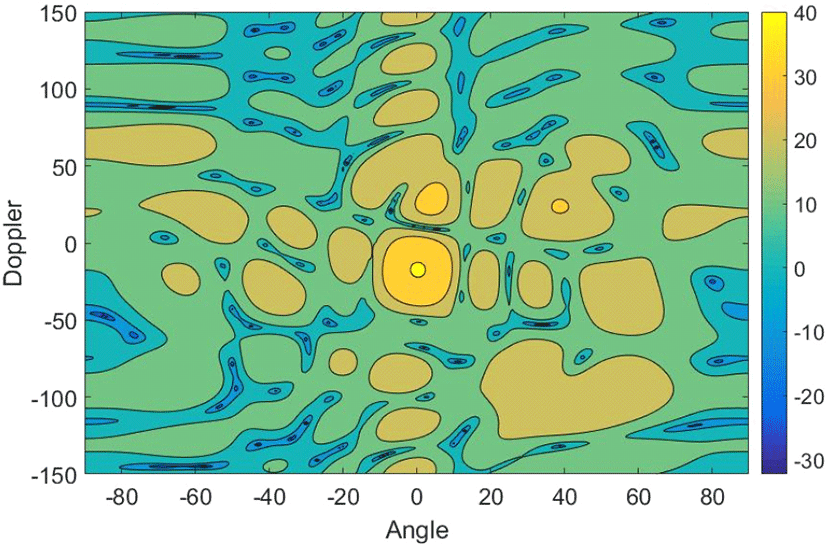
그림 6은 γ = 0.7을 만족하는 모든 i에 대하여 클러터 억제 알고리즘을 적용한 결과를 angle-Doppler 스펙트럼으로 나타내었다.
그림 6으로부터 표적 신호는 정확히 남고, 클러터 신호만 적절히 제거됨을 확인할 수 있다.
Ⅴ. 결 론
본 논문은 바이스태틱 레이다 환경에서 발생하는 비-균질한 클러터에 대하여 angle-Doppler 스펙트럼상에 나타나는 클러터 릿지 구조에 대해 분석하고, 클러터를 억제하는 알고리즘을 제시하였으며, 수학식 유도 및 시뮬레이션을 통해 클러터가 제거됨을 보였다. 실제 수신신호에 포함된 클러터를 사전정보로부터 주파수가 변이된 클러터를 생성하여 ICM에 의해 퍼진 클러터 신호 공간들을 추정하였고, 추정된 신호 공간들을 수신신호에서 내적하여 제거함으로써 진폭 성분이 추정되는 것을 보였다. 본 논문에서 제시한 클러터 억제 알고리즘은 CUT 데이터만을 사용하기 때문에 IID한 secondary 데이터 부족 문제를 해결할 수 있고, 여러 가지 형태의 클러터로 이루어진 복잡한 환경에서도 활용이 가능할 것으로 기대한다.















