잡음 공분산 추정 방식을 적용한 칼만필터 기반 지면밀착 접근표적 추적기법

Ⅰ. 서 론

근거리 미사일/로켓 방어시스템은 탐지추적레이다와 열상추적기를 이용해 적으로부터 발사된 미사일/로켓의 궤적 및 속도에 따른 기동특성을 파악하여 위협체의 움직임을 예측하고, 대응탄과 위협체가 특정 위치에서 조우 할 수 있도록 대응탄을 계산된 시점에 발사하여 대응탄은 조우 위치에서 전면으로 파편을 분사함으로써 위협체를 무력화 시킨다^[1].

최근 연구에 따르면 대응탄 파편의 위협체에 대한 타격 정확도 향상을 위해 대응탄 전면에 RF(Radio Frequency) 근접센서를 적용하여 위협체를 감지하는데, 전면에 위치한 근접센서는 지면으로부터의 클러터 영향을 최소화하기 위해 빔폭이 제한된 안테나를 이용해 위협체를 감지하도록 설계한다^[2]. 그런데 안테나의 제한된 빔폭으로 인해 그림 1과 같이 빔폭 범위 밖으로 위협체가 지나가게 되면 탐지정보가 소실되어 위협체가 파편 분산 범위에 들어오는 순간에 위협체를 감지하기는 쉽지 않다.

그림 1. | Fig. 1. 대응탄과 대전차 위협체의 조우 개념 | The encounter concept of the countermeasure with the target.

Download Original Figure

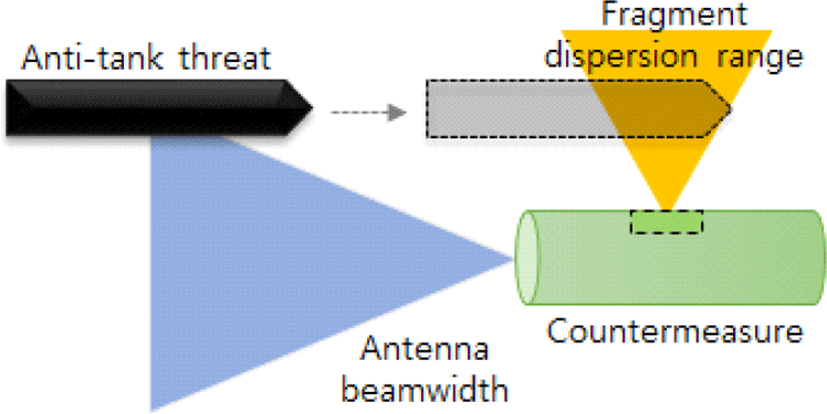
또한 근접센서는 위협체 탐지 및 추적을 위한 거리와 속도정보를 획득하기 위해 FMCW(Frequency-Modulated Continuous-Wave)와 CW(Continuous-Wave)를 이용하는데, 복잡한 지상 환경에서 획득되는 위협체의 거리와 속도정보는 열잡음뿐만 아니라 ,주변의 바위, 나무, 지면 등과 같은 클러터 정보를 포함하게 된다. 이로 인해 근접센서는 위협체 반사신호가 아닌 단발성으로 획득되는 주변의 지형지물의 반사신호를 위협체로 판단하는 오류를 범할 수 있다. 따라서 접근하는 위협체와 클러터를 구분하고, 조우 시점에 빔폭 밖으로 벗어나는 위협체를 추적하여 대응탄 파편 분산 범위 내에서 정확한 기폭 출력을 위해서는 대응탄의 운용환경에 적합한 추적필터를 적용해야 한다.

기존에 빠른 속도로 움직이는 목표물을 추적하기 위해 잡음 공분산을 지속적으로 갱신하는 적응형 칼만필터(Adaptive Kalman Filter)^[3]를 적용하는 경우, 필터 추적값에 대한 신뢰성을 얻기 위해서는 많은 횟수의 필터 갱신이 필요하다. 이 때문에 원거리부터 목표물을 탐지하여 충분한 갱신 정보를 얻고, 고속 연산을 수행하는 고성능 지상 추적 레이다^[4]에서는 적응형 칼만필터의 적용이 가능하지만, 전차로부터 발사되어 비행 중 근거리에서 위협체를 감지하고, 수초 이내에 빠른 기폭 판단을 수행하는 근접센서는 지속적인 연산과 갱신이 필요한 적응형 칼만필터의 적용이 불가능하다.

따라서 근접센서에는 적응형 칼만필터 대신에 고정된 잡음 공분산에 기반한 칼만필터를 이용한 추적필터를 적용할 필요가 있다. 그런데 고정된 잡음 공분산으로 위협체의 거리와 속도정보를 정확하게 추적하기 위해서는 초기 잡음 공분산의 정확한 입력이 필요하다. 이를 위해 본 논문에서는 칼만필터^[5]∼^[7]에 기반한 접근표적 추적기법을 연구하고, 근접센서의 거리와 속도정보 추적 정확도 향상을 위해 실제 위협체 발사 시험으로 근접센서의 측정 오차를 획득하여 해당 오차를 반영하는 칼만필터 잡음 공분산 행렬의 추정 방식을 제안한다.

본 논문의 2-1장에서는 칼만필터의 시스템 모델 설계를 위한 모델 상세구성을 기술하고, 2-2장은 칼만필터의 추적 성능 향상을 위한 잡음 공분산 행렬 추정 방식을 제안한다. 3장에서는 발사시험을 통해 획득한 위협체의 거리와 속도정보를 기반으로 추적필터로써의 칼만필터 성능 검증을 수행하고, 본 논문에서 제안한 방식으로 추정한 칼만필터 잡음 공분산 행렬의 타당성을 검증한다.

Ⅱ. 접근표적 추적기법 연구

2-1 기존 칼만필터 시스템 모델 분석

접근하는 위협체의 거리와 속도정보 추적을 위한 칼만필터를 설계하기 위해서는 위협체의 기동 특성에 대한 모델이 우선 분석될 필요가 있다. 그림 2에 근접센서가 대상으로 하는 위협체의 시간에 따른 속도 변화를 도플러 레이다로 측정한 결과를 나타내었다. 그림 2에서 x축은 시간, y축은 위협체의 속도 정보를 나타낸다.

그림 2. | Fig. 2. 위협체의 시간에 따른 속도 변화 | Velocity of the target.

Download Original Figure

그래프에 나타난 바와 같이 위협체는 발사와 동시에 1차 추진을 시작하고, 일정 시간 가속 후 2차 추진을 진행하여 큰 기동변화 없이 일정한 가속도를 가지고 접근하는 것을 확인할 수 있다.

근접센서는 위협체의 2차 추진 이후 시점에 발사되어 위협체의 거리와 속도정보를 획득하기 때문에, 본 연구에서는 위협체의 2차 추진 시점 이후의 기동특성만을 칼만필터 시스템 모델에 반영한다. 따라서 칼만필터 적용을 위한 위협체의 시스템 모델로서 일정한 가속도로 큰 기동 특성이 없는 Piecewise Constant White Acceleration^[8]를 기반으로 칼만필터를 구성할 수 있다. 위협체의 기동특성을 반영한 칼만필터의 시스템 모델은 다음과 같다.

$$X_k^{-}=F{X}_{k-1}+Gw(k)$$

(1)

$$X_k=\left[\begin{array}{l}{p}_k\\ u_k\end{array}\right]$$

(2)

여기서 $X_k^{-}$는 위협체의 거리와 속도정보에 대한 예측값을 나타내는 상태변수이며, w(k)는 모델 오차에 해당하는 잡음으로써 평균은 0, 분산은 ${\sigma }_w^2$인 백색 가우시안 잡음으로 가정한다. 시스템 모델의 상태천이 매트릭스 F와 입력 매트릭스 G는 아래와 같이 정의하며, dt는 샘플링 시간을 나타낸다.

$$F=\left[\begin{array}{ll}1\hfill & -dt\hfill \\ 0\hfill & 1\hfill \end{array}\right],G=\left[-\frac{d{t}^2}{\begin{array}{l}2\\ dt\end{array}}\right]$$

(3)

예측값과 측정값의 추정 오차에 대한 기준 파라미터인 오차 공분산 $P_k^{-}$에 대한 예측 모델은 아래와 같다. 여기서 Q는 Piecewise Constant White Acceleration 모델에 기반한 시스템 잡음 공분산 행렬을 나타낸다.

$$P_k^{-}=F{P}_{k-1}{F}^T+Q$$

(4)

$$Q=E\left[Gw(k)w(k)G^T\right]={\sigma }_w^2\left[\begin{array}{ll}\frac{d{t}^2}{4}\hfill & \frac{-d{t}^3}{2}\hfill \\ \frac{-d{t}^3}{2}\hfill & d{t}^2\hfill \end{array}\right]$$

(5)

위협체의 거리와 속도정보에 대한 칼만필터의 예측값과 근접센서에서 측정한 위협체 거리와 속도정보의 시스템 모델 반영에 필요한 칼만필터 이득은 다음과 같이 계산한다.

$$K_k=P_k^{-}{H}^T{\left(H{P}_k^{-}{H}^T+R\right)}^{-1}$$

(6)

$$H=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],R=({\sigma }_r^2,{\sigma }_v^2)$$

(7)

여기서 R은 잡음 공분산 행렬, H는 측정행렬을 나타낸다. 칼만필터의 예측값과 근접센서의 측정값 통합 및 다음 상태 예측에 필요한 오차공분산은 다음과 같이 나타낼 수 있다.

$$X_k=X_k^{-}+K_k(Z_k-H{X}_k^{-})$$

(8)

$$P_k=P_k^{-}-K_{k}H{P}_k^{-}$$

(9)

위 식에서 Z_k는 근접센서로부터 입력되는 위협체에 대한 거리와 속도 행렬을 의미하며, X_k는 칼만필터에서 최종적으로 산출해낸 위협체의 거리와 속도를 나타낸다.칼만필터를 통해 추적한 위협체의 거리와 속도에 대한 최종 산출값은 식 (8)과 같이 근접센서 측정값과 칼만필터 예측값의 비율로 결정된다.

여기서 칼만 이득 K는 측정값과 예측값의 반영 비율을 결정하는 값으로 식 (6)과 같이 표현되며, 잡음 공분산 행렬에 의해 그 값이 결정된다. 하지만 근접센서의 잡음 공분산 행렬은 실제 알려져 있지 않은 값으로 가정을 통 해 초기값을 설정할 필요가 있다.

2-2 잡음 공분산 행렬 추정 방식 연구

본 연구에서는 칼만필터를 적용한 시스템에서의 센서 측정잡음이 일반적으로 양자화 오차(quantization error)^[9]로 인해 발생한다고 가정한다. 양자화 오차에 의한 측정잡음은 그림 3과 같이 균일 분포(uniform distribution)를 따르기 때문에 근접센서의 잡음 공분산 행렬을 식 (10)과 같이 나타낼 수 있다.

$${\sigma }_{QNoise}^2=E(e^2)={\displaystyle {\int }_{\frac{-△}{2}}^{\frac{△}{2}}\frac{1}{△}}{e}^{2}de=\frac{{△}^2}{12}$$

(10)

그림 3. | Fig. 3. 양자화 오차에 의한 측정잡음 | Measurement noise by quantization noise.

Download Original Figure

여기서 σ_QNoise는 양자화 잡음, e는 양자화 오차, Δ는 근접센서의 속도와 거리의 해상도를 나타낸다. 이와 같은 방법으로 잡음 공분산 행렬을 설정하는 것은 근접센서의 측정 해상도만을 고려한 것으로, 실제 환경에서 발생하는 열잡음이나 클러터 등에 의한 속도와 거리 오차를 반영하지 못한다. 따라서 양자화 오차만을 반영하여 초기 잡음 공분산 행렬을 설정하면, 실제 모델과 차이나는 칼만이득 K가 계산되고, 이로 인해 위협체에 대한 속도와 거리 추적 정확도가 크게 저하된다.

이를 해결하기 위해 본 연구에서는 실제 위협체 발사 시험으로 근접센서의 거리와 속도정보를 획득하여 획득 정보를 최소자승법으로 1차와 2차 함수로 각각 변환하여 획득 거리와 속도의 편차 분석을 통해 잡음 공분산 행렬을 정확히 추정하고자 한다.

이를 위해 먼저 시험을 통해 획득한 근접센서의 속도정보 측정 편차 분석을 위해 위협체의 속도를 최소자승 법으로 식 (11)과 같이 1차 함수로 근사화한다. 식 (12)는 식 (11)을 산출해내기 위한 과정을 나타낸다.

$$f(x_i)=a{x}_i+b$$

(11)

$$X^2={\displaystyle \sum _{i=1}^n{\left(Y_i-f(x_i)\right)}^2={\displaystyle \sum _{i=1}^n{\left(Y_i-\left(a{x}_i+b\right)\right)}^2}}$$

(12)

위 식에서 X²는 잔차(Residual)의 제곱 합, x_i는 i번째 측정된 위협체 속도의 측정 시간(sampling time), Y_i는 근접센서에서 i번째 측정된 위협체의 속도를 나타내며, f(x_i)는 Y_i와 차이의 제곱(X²)이 최소가 되는 모델을 나타낸다. 식 (12)의 a와 b에 대한 편미분을 통해 식 (12)가 최소가 되는 a와 b값을 아래와 같이 구할 수 있다.

$$\left[\begin{array}{l}a\\ b\end{array}\right]={\left[\begin{array}{cc}{\displaystyle \sum _{i=1}^n{x}_i^2}& {\displaystyle \sum _{i=1}^n{x}_i}\\ {\displaystyle \sum _{i=1}^n{x}_i}& n\end{array}\right]}^{-1}\left[\begin{array}{c}{\displaystyle \sum _{i=1}^n{x}_i{Y}_i}\\ {\displaystyle \sum _{i=1}^n{Y}_i}\end{array}\right]$$

(13)

근접센서의 속도에 대한 잡음 공분산은 최소자승법을 통해 근사화한 속도 1차 함수와 근접센서로 획득한 위협체 속도 정보의 차이에 대한 분산으로서 아래와 같다. 여기서 n은 획득된 위협체 속도정보의 수를 나타내며, v_i는 i번째 획득된 위협체의 속도 정보를 의미한다. 이를 통해 실제 환경의 오차요소들이 포함된 위협체에 대한 속도 분산을 확인할 수 있다. 그림 4에 근접센서로 측정한 위협체의 속도(*)와 최소자승법을 통해 위협체의 속도를 1차 함수(Δ)로 근사화한 그래프를 나타내었다.

$${\sigma }_v^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(f(x_i)-v_i\right)}^2}$$

(14)

그림 4. | Fig. 4. 위협체 측정 속도(*), 1차 함수 변환 속도(Δ) | Measured velocity of the target and transformed velocity of the target by a linear equation.

Download Original Figure

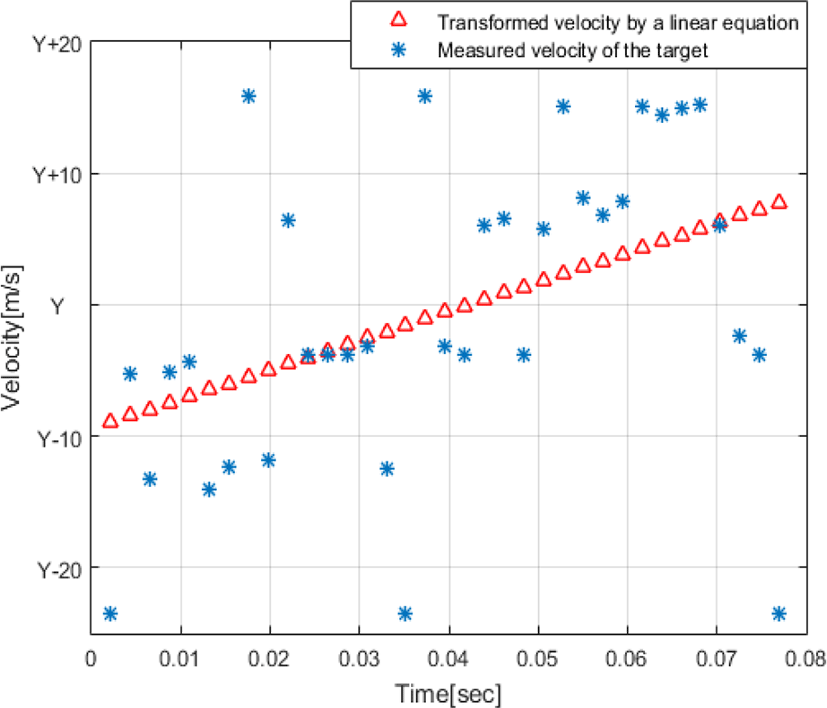
그림 4에 나타낸 바와 같이 근접센서로 측정한 위협체의 속도(*)는 증가하는 추세와 동시에 센서 측정 오차가 포함되어 약 Y±20 m/s 이내의 산발적인 속도 편차를 나타내고, 측정 속도(*)를 최소자승법을 통한 1차 함수로 근사화한 결과(Δ)는 위협체가 일정한 가속도를 가지고 접근하는 특성으로 나타나고 있다.

다음으로 위협체의 이동거리 특성은 일정한 가속도로 접근하는 위협체를 고려하여 2차 함수로 근사화할 수 있다. 따라서 근접센서로 획득한 위협체의 거리를 최소자승법을 통한 2차 함수로 근사화하고, 2차 함수와 위협체 거리정보의 차이에 대한 분산을 잡음 공분산으로 정의한다. 위협체 거리에 대한 2차 함수는 아래와 같이 나타낸다.

$$f\left(x_i\right)=a{x}_i^2+b{x}_i+c$$

(15)

$$\begin{array}{c}{X}^2={\displaystyle \sum _{i=1}^n{(Y_i-f(x_i))}^2}\\ ={\displaystyle \sum _{i=1}^n{\left(Y_i-\left(a{x}_i^2+b{x}_i+c\right)\right)}^2}\end{array}$$

(16)

위 식에서 각 변수의 의미는 식 (11), (12)와 동일하며 Y_i는 근접센서에서 i번째 측정된 위협체의 거리를 나타낸다. 식 (16)의 a, b, c에 대한 편미분을 통해 식 (16)이 최소가 되는 a, b, c는 식 (17)과 같이 나타낸다.

근접센서의 거리에 대한 잡음 공분산은 최소자승법을 통해 근사화한 거리 2차 함수와 근접센서로 획득한 위협체 거리정보의 차이에 대한 분산으로서 식 (18)과 같다. 여기서 n은 획득된 위협체 거리정보의 수를 나타내며, p_i는 i번째 획득된 위협체의 거리정보를 의미한다. 그림 5에 근접센서로 획득한 위협체의 거리(*)와 최소자승법을 통해 위협체의 거리를 2차 함수(Δ)로 근사화한 그래프를 나타내었다.

$$\left[\begin{array}{l}a\\ b\\ c\end{array}\right]=\left[\begin{array}{ccc}{\displaystyle \sum _{i=1}^n{x}_i^4}& {\displaystyle \sum _{i=1}^n{x}_i^3}& {\displaystyle \sum _{}^n{x}_i^2}\\ {\displaystyle \sum _{i=1}^n{x}_i^3}& {\displaystyle \sum _{i=1}^n{x}_i^2}& {\displaystyle \sum _{i=1}^n{x}_i}\\ {\displaystyle \sum _{i=1}^n{x}_i^2}& {\displaystyle \sum _{i=1}^n{x}_i}& n\end{array}\right]=\left[\begin{array}{c}{\displaystyle \sum _{i=1}^n{x}_i^2{Y}_i}\\ {\displaystyle \sum _{i=1}^n{x}_i{Y}_i}\\ {\displaystyle \sum _{i=1}^n{Y}_i}\end{array}\right]$$

(17)

$${\sigma }_p^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(f(x_i)-p_i\right)}^2}$$

(18)

그림 5. | Fig. 5. 위협체 측정 거리(*), 2차 함수 변환 거리(Δ) | Measured range of the target and transformed range of the target by a quadratic equation.

Download Original Figure

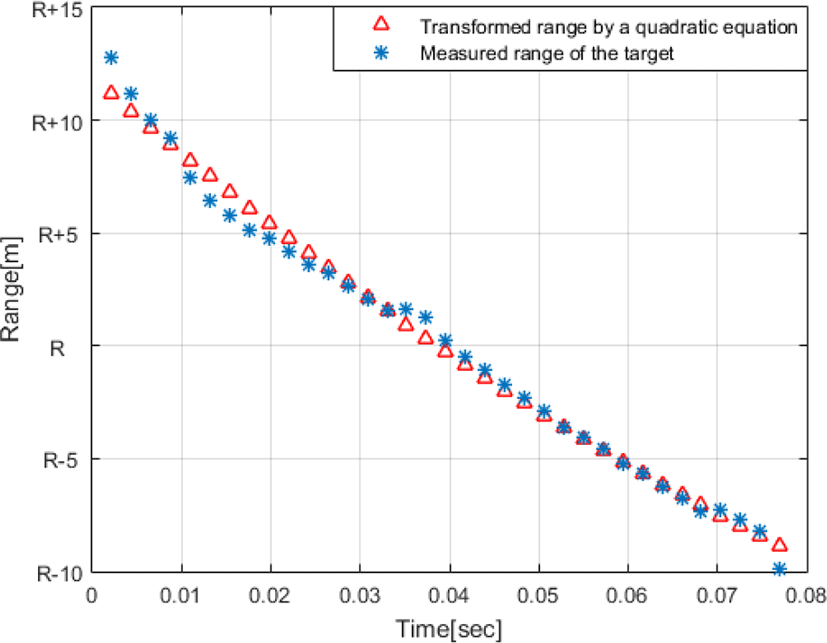
그림 5에 나타낸 바와 같이 근접센서로 측정한 위협체의 거리(*)는 센서 측정 오차가 포함되어 위협체의 속도가 증가와 감소 특성을 가지며 다가오는 거리 특성을 보이고, 측정 거리(*)를 최소자승법을 통한 2차 함수로 근사화한 결과(Δ)는 위협체가 일정한 가속도를 가지고 접근하는 특성으로 나타나고 있다.

이처럼 본 연구에서는 식 (14), 식 (18)과 같이 칼만필터의 잡음 공분산 행렬에 위협체 발사시험을 통해 획득 한 속도와 거리정보의 측정 오차를 포함시킴으로써 양자화 잡음에 대한 오차요소뿐만 아니라, 실제 위협체 발사환경에서 발생할 수 있는 근접센서의 측정 오차를 시스템 모델에 반영하여 속도와 거리 추적에 대한 정확도를 향상시킬 수 있다.

Ⅲ. 위협체 발사시험 및 결과검증

제안하는 추적기법의 성능 평가를 위해 그림 6과 같이 야외시험장을 구성하여 시험데이터를 수집하였다. 지면클러터를 반영하기 위하여 위협체는 약 1.5 m에서 발사하여 약 3 m 높이에 탄착하는 것으로 설정하였고, 위협체와 근접센서의 조우 순간을 촬영하기 위해 측면에 초고속카메라를 설치하였다.

그림 6. | Fig. 6. 시험데이터 수집을 위한 발사시험장 구성 | Field test environment for data acquisition.

Download Original Figure

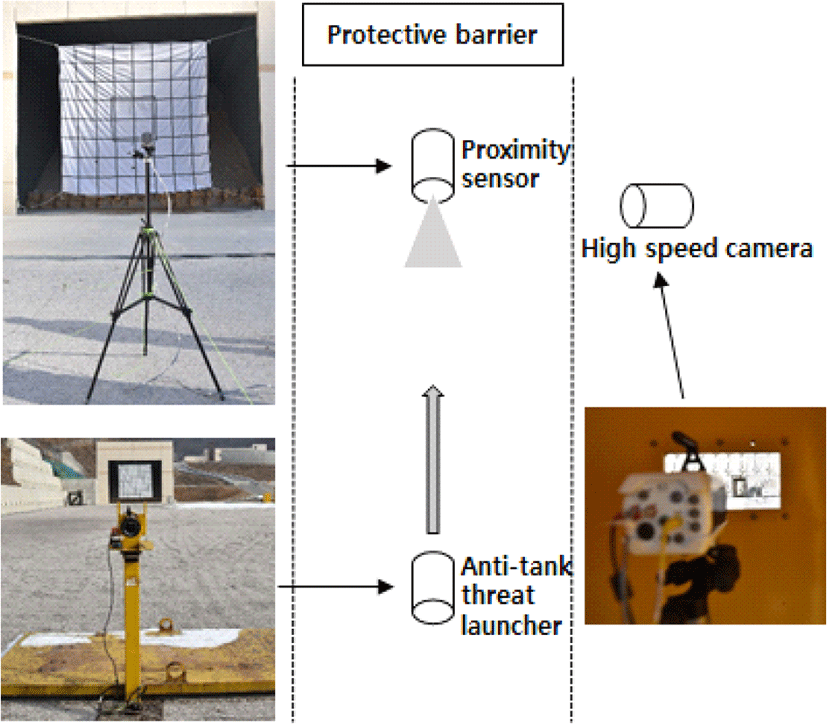
그림 7에 위협체가 근접센서를 지나가는 순간 고속카메라로 촬영한 장면을 나타내었다. 근접센서와 위협체 간 이격거리는 1 m 수준으로 측정되었고, 근접센서에서 획득한 위협체에 대한 데이터는 DSP(Digital Signal Processing)의 FFT(Fast Fourier Transform)를 통해 획득한 비트 주파수를 이용하여 위협체 거리와 속도정보로 변환하였다^[2].

그림 7. | Fig. 7. 근접센서와 위협체의 조우장면 | The encounter scene of the proximity sensor with the target.

Download Original Figure

획득한 위협체의 속도정보를 기존 칼만필터와 제안하는 잡음 공분산 행렬을 적용한 칼만필터의 입력 데이터로 설정하였고, 그 결과를 도플러 레이다를 통해 계측한 위협체의 속도정보와 비교하였다. 그림 8에 본 연구에서 제안하는 잡음 공분산 행렬을 적용한 칼만필터의 위협체 속도 추적 결과(Δ), 기존 칼만필터의 위협체 속도 추적 결과(□), 근접센서로 획득한 위협체의 속도(*), 도플러 레이다로 측정한 위협체의 속도(○)를 나타내었다.

그림 8. | Fig. 8. 위협체의 측정 속도와 필터 추적 속도 비교 | Comparison of the measured velocity and filter tracking velocity.

Download Original Figure

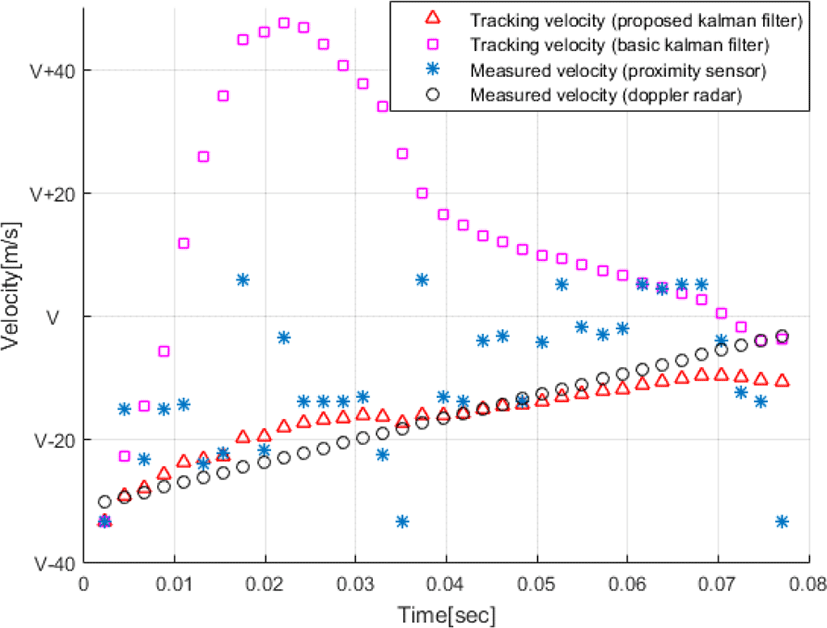
그림 8에서 잡음 공분산 행렬에 단순한 초기 오차만을 설정한 기존 칼만필터(□)는 위협체에 대한 속도 추적이 초반에 발산하는 경향을 보인 뒤 안정화 되지만, 실제 발사 환경에서 발생할 수 있는 오차를 고려하여 잡음 공분산 행렬을 적용한 칼만필터(Δ)의 속도 추적 결과는 위협체 추적시점부터 종료시점까지 속도에 대해 안정적인 추적경향을 나타내며, 도플러 레이다로 측정한 참조값과 유사한 결과로 우수한 추적 성능을 보여준다.

위협체 속도에 대한 추적 성능 비교를 위하여 도플러레이다로 정확하게 측정한 위협체 속도를 기준으로 제안하는 잡음 공분산 행렬을 적용한 칼만필터의 추적 속도, 근접센서를 통해 획득한 위협체 속도, 기존 칼만필터의 추적 속도를 표 1과 같이 RMSE(Root-Mean Squared Error)로 비교하였다.

표 1에 나타낸 바와 같이 근접센서로 측정한 위협체의 속도는 도플러 레이다 계측 결과와 비교하였을 때 12.45 m/s의 RMSE 값을 나타내는데, 이는 근접센서의 기본적인 측정오차가 포함된 결과이다. 반면에, 근접센서에서 획득한 위협체의 속도를 기존 칼만필터에 적용하여 비교한 RMSE 값은 38.74 m/s로 근접센서 측정 속도 오차 대비 211 % 증가하였으나, 제안하는 기법을 적용하여 비교한 RMSE 값은 3.34 m/s로 근접센서 측정 결과인 12.45 m/s보다 73 % 감소하여 속도 추적 정확도가 향상되었음을 확인할 수 있다.

그림 9에 제안하는 잡음 공분산 행렬을 적용한 칼만필터의 위협체 거리 추적 결과(Δ), 기존 칼만필터의 위협체 거리 추적 결과(*), 근접센서로 획득한 위협체의 거리(○)를 나타내었다.

그림 9. | Fig. 9. 위협체 측정 거리와 칼만필터 추적 거리 비교 | Comparison of the measured range and Kalman filter tracking range.

Download Original Figure

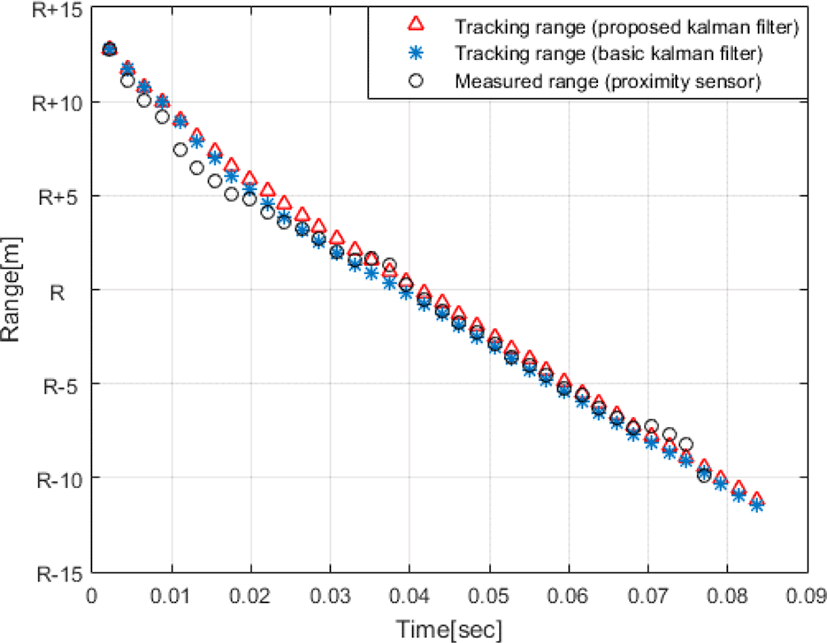
그림 9와 같이 근접센서로 측정한 위협체의 거리는 일정하게 증가하는 가속도 값을 갖는 위협체의 기동특성으로 볼 수 없는 S자의 불규칙한 형태를 나타내고 있다. 이러한 결과는 근접센서에서 주위 클러터를 위협체로 인식하거나, 일정 길이를 갖는 위협체의 다중지점에서의 반사신호 때문에 나타난 결과로 판단된다.

특히 위 그림에서 0.07초 부근에서는 위협체의 탄두가 아닌 탄미로 예측되는 부분이 측정되어 근접센서의 측정 결과(○)만으로 대응탄의 기폭 시점을 판단하기는 쉽지 않다. 하지만 근접센서 측정값에 본 연구에서 제안하는 잡음 공분산 행렬을 적용한 칼만필터의 추적결과(Δ)에서는 위협체가 일정하게 접근하는 결과를 확인할 수 있다. 이는 칼만필터의 시스템 모델이 위협체의 모델 특성을 잘 반영하고 있음을 나타낸다.

다만 제안하는 기법을 적용한 칼만필터의 추적 정확도는 위협체 거리에 대한 명확한 참값 데이터가 존재하지 않기 때문에, 판단하기 어려운 한계가 있다. 하지만 위협체 거리와는 달리 위협체 속도에 대한 참값 데이터는 알고 있고, 표 1과 같이 제안하는 기법을 적용한 칼만필터가 기존 칼만필터보다 더 나은 속도 추적 성능을 나타냄을 확인할 수 있다. 따라서 시스템 모델(식 (1)∼(3))에 의해 속도 추적 성능이 반영되는 거리 추적 성능 또한 제안하는 기법을 적용한 칼만필터가 기존 칼만필터보다 우수할 것으로 판단된다.

그림 10에는 제안하는 기법을 적용한 칼만필터의 성능 비교를 위해 칼만필터의 위협체 거리 추적 결과(Δ), LS (Least Square) 필터의 위협체 거리 추적 결과(*), 근접센서로 획득한 위협체의 거리(○)를 나타내었다. 그림 10과 같이, 제안하는 기법을 적용한 칼만필터(Δ)와 LS 필터(*)는 서로 일정 오차를 가지고 위협체를 추적한다. 근접센서의 위협체 거리 획득 범위를 벗어난 이후 지점(약 0.08초)부터의 칼만필터(Δ)와 LS 필터(*) 사이의 추적 오차는 평균 약 1 m를 나타낸다.

그림 10. | Fig. 10. 위협체 측정 거리, 칼만필터 및 LS 필터 추적 거리 비교 | Comparison of the measured range, Kalman filter tracking range and 2^nd LS filter tracking range.

Download Original Figure

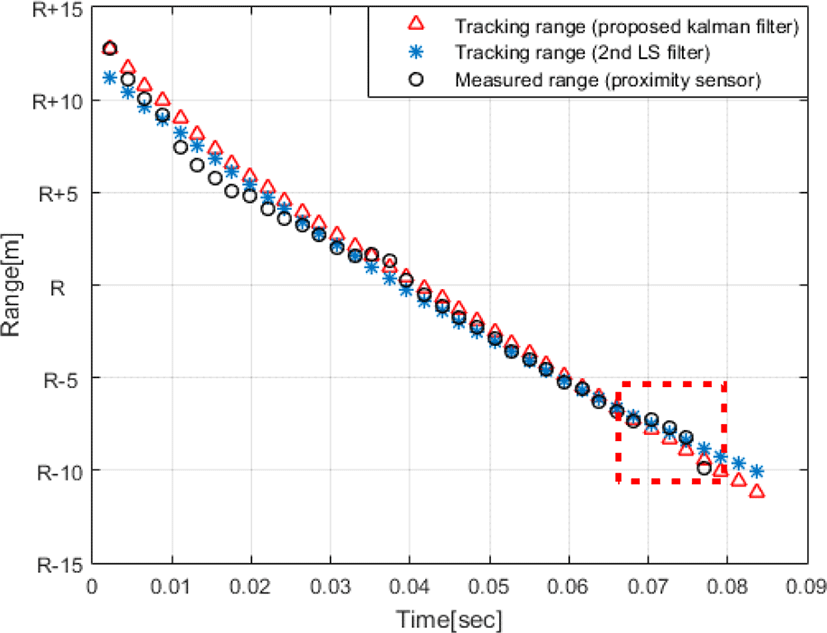
LS 필터(*)는 근접센서의 위협체 거리 획득 시작 시점부터 위협체가 빔폭을 벗어나 거리 획득이 종료된 시점까지의 거리 정보들을 통해 2차 함수 모델을 생성한다. 그러나 그림 10의 붉은 점선의 사각형 부분과 같은 근접한 거리에서는 위협체의 탄미로 예측되는 부분(○)의 거리 정보가 탄두 정보와 함께 그대로 2차 함수 모델 생성에 혼용된다. 따라서 실제 위협체의 거리로 예측되는 지점보다 먼 거리로 위협체를 추적하는 오류를 범할 수 있다.

반면에, 제안하는 기법을 적용한 칼만필터(Δ)의 경우에는 원거리부터 접근하는 위협체의 움직임 및 속도에 대한 경향을 칼만필터의 시스템모델에 반영하기 때문에, 근거리에서 위협체의 탄미로 예측되는 부분(○)이 획득되더라도 속도 정보 연산을 통해 해당 오차가 어느 정도 보정되므로 더 신뢰할 수 있는 위협체 추적 결과를 얻을 수 있다.

표 2에 근접센서 위치를 기준으로 다가오는 위협체에 대한 상세거리 수치를 나타내었다. 표 2에서 근접센서를 기준으로 위협체는 R-9.87 m 지점까지 탐지가 되었고, 이 후 지점부터는 빔폭을 벗어나 더 이상 위협체를 탐지할 수 없음을 확인할 수 있다. 이후 지점부터 칼만필터는 근접센서에서 측정되는 측정값 없이 칼만필터의 예측값만으로 위협체 거리를 추정한다. 따라서 추정된 거리는 위협체가 대응탄의 파편 분산범위에 들어왔는지에 대한 판단정보로 사용될 수 있다.

Ⅳ. 결 론

본 논문에서는 접근표적의 위치를 정확하게 추정하기 위해 최소자승법 기반의 잡음 공분산 행렬을 적용한 칼만필터를 제안하고, 실제 표적 발사시험을 통해 시험 결과를 분석하고, 그 타당성을 검증하였다.

근접센서의 대상 표적에 대한 칼만필터의 시스템 모델을 설계하고, 속도와 거리 추적 정확도 향상을 위해 잡음 공분산 행렬 추정 방식을 새롭게 적용하였다. 실제 위협체 발사시험으로 측정한 위협체의 속도와 거리정보에 제안하는 잡음공분산을 적용한 칼만필터를 통해 근접센서 안테나 빔폭 밖의 지점에서도 위협체를 추적하여 대응탄 측면 파편 분산 범위에서 기폭 시점을 추정할 수 있음을 확인하였다.

향후에는 본 연구에서 제안하는 잡음 공분산 행렬을 적용한 칼만필터를 근접센서에 적용하여 위협체를 정밀하게 무력화 시킬 수 있는 최적의 기폭 시점을 산출하기 위한 연구를 지속적으로 수행할 예정이다.