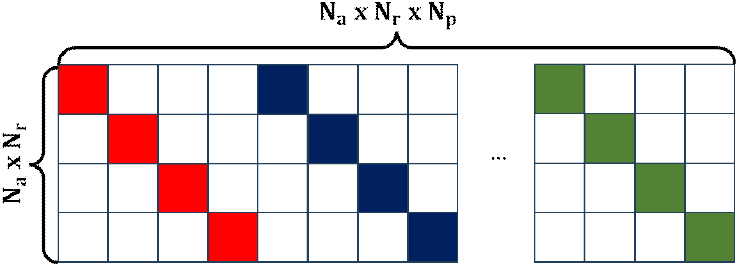I. 서 론
합성 개구 레이다(SAR, synthetic aperture radar)는 주·야간 및 다양한 기상 조건에서 고해상도 원격 탐사가 가능하여 현재 널리 활용되는 영상 획득 기법 중 하나이다[1]. SAR 시스템은 송신기와 수신기의 배치 방식에 따라 모노스태틱(monostatic)과 바이스태틱(bistatic) 모드로 구분될 수 있다. 모노스태틱 모드는 송신기와 수신기가 동일 플랫폼에 탑재되어 표적 탐지 및 추적하는 방식이며, 바이스태틱 모드는 물리적으로 분리된 송신기와 수신기를 통해 서로 다른 관측 각도에서 표적 정보를 수집하기 때문에, 상대적으로 레이다 유효 단면적(RCS, radar cross section)이 작은 표적을 탐지하는 데 유리하다[2]. 코너 리플렉터(corner reflector)의 경우 모노스태틱 SAR 환경에서는 수신 신호가 포화되어 주변 신호를 관측하기 어려워질 수 있지만, 바이스태틱 SAR 기하에서는 관측 각도 차이에 의해 동일 반사체에서 발생하는 응답 세기가 분산된다. 이로 인해 포화 수준이 낮아지므로, 주변 영역의 세부 정보를 보다 효과적으로 획득할 수 있다[3]. 또한 DRFM(digital radio frequency memory) 기반 재밍이 발생하더라도, 바이스태틱 레이다는 일부 채널에서 안정적인 수신 신호를 확보하여 재밍으로 인한 데이터 손실을 부분적으로 회피할 수 있다는 장점이 있다[4]. 이러한 특성 때문에 최근 전자전 분야에서 스텔스(stealth) 기술 및 재밍 기법이 확산되면서 바이스태틱 레이다가 다시 주목받고 있으며, 활용 가치 또한 재조명되고 있다[5],[6]. 그러나 바이스태틱 모드를 효과적으로 운용하기 위해서는 수신 신호 전력 감쇠, 거리 해상도 저하, 송·수신기 간 동기화 문제, 복잡한 기하 정합 등 여러 기술적 난제를 해결해야 한다. 이에 따라 높은 동기화 정밀도와 함께 차별화된 신호 처리 기법이 필수적이다.
최근 플랫폼 운용 시스템이 발전하면서 SAR 영상 품질이 고도화됨에 따라, 방대한 데이터를 저장·처리해야 하는 부담이 점점 커지고 있다. 이러한 문제를 해결하기 위해 여러 데이터 압축 및 복원 기법이 제안되어 왔으며[7], 특히 연산 가속화를 위해 주파수 영역에서 신호를 처리를 구현하는 방식이 널리 적용된다. 그러나 바이스태틱 SAR 영상 복원의 경우, 복잡한 기하학적 정합이 요구되므로 시간 영역에서 정합을 수행하는 편이 더 적합할 때가 많다. 시간 영역에서 수신 신호를 각 픽셀에 직접 합산하여 영상을 재구성하는 BPA(back-projection algorithm)은 추가적인 기하 가정이 필요하지 않고 높은 복원 정확도를 확보할 수 있으나, 연산 비용이 매우 큰 단점이 있다. 한편, 압축센싱(CS, compressive sensing) 기법은 Nyquist 이론에서 요구되는 샘플 수보다 적은 측정치만으로도 영상을 복원함으로써 연산과 데이터 저장 부담을 완화하는 이점이 있다[8]. 실제로 데이터 손실이나 품질 저하가 발생한 환경에서도 제한된 신호만으로도 고품질의 SAR 영상을 복원하는 사례들이 보고되고 있다[9].
BPA와 CS는 각각 SAR 영상 처리 분야에서 이미 잘 알려져 있으나, 두 기법을 직접 결합하면 연산량이 기하급수적으로 증가하기 때문에 실제 적용 사례는 매우 드물다. 특히 바이스태틱 환경에서 동기화가 불충분할 경우 거리 오차나 에일리어싱이 발생하여 영상 품질이 크게 저하될 수 있다. 본 논문에서는 이러한 문제를 해결하기 위해 주파수 변조 연속파(FMCW, frequency modulated continous wave) 레이다로 획득한 바이스태틱 SAR 영상을 효과적으로 복원할 수 있는 병렬 구조의 BPA-CS 알고리즘을 제안한다. BPA-CS 과정에서 발생하는 막대한 연산 부담을 줄이기 위해 블록 단위 병렬 처리와 CS 알고리즘을 병행하였으며, 모의실험과 실제 바이스태틱 환경에서 획득한 데이터를 통해 성능을 검증하였다. 이를 통해, 기존 BPA-CS 대비 연산 시간을 크게 단축하면서도 우수한 영상 복원 정확도를 유지함을 확인하였다. 나아가 본 논문에서 제시하는 병렬 구현 방식과 무선 동기화 기반 실측 데이터 적용 사례는 향후 군집 위성 SAR나 무인기 체계에서도 높은 활용 가능성을 시사한다.
II. 본 론
FMCW 레이다의 송신 신호 St(t)는 식 (1)과 같이 운용 주파수 f0와 주파수 변조율 kr을 이용해 톱니파 형태의 시간 t에 대한 주파수 변조 신호로 나타낼 수 있다[10]. 이때의 수신 신호 Sr(t)는 목표물로부터 반사되는 지연 시간 τR를 이용해 식 (2)와 같이 표현할 수 있다.
본 논문에서는 송신기와 수신기는 레이다 신호 주파수 대비 1/2의 주파수를 가지는 국부 발진(LO, local oscillation) 신호 기반 무선 송수신 방식으로 동기화되며, 수신기에서 수신한 LO 신호 sLO,r(t)는 식 (3)와 같이 표현된다.
여기서 τLO는 레이다 신호가 송신기/수신기 간 간격 RLO만큼 전파되느라 지연된 시간이다. 수신 단에서 LO 수신 신호와 레이다 수신 신호를 주파수 혼합기를 통해 주파수 하향 변환(down converter)하고, 두 신호의 차에 해당하는 비트 주파수(beat frequency) 성분을 수신한다[11]. 이러한 과정을 거친 신호는 송신기와 수신기 플랫폼 간의 간격 가 존재하는 TanDEM 모드와 유사한 Azimuth-Invariat 바이스태틱 SAR 수신 신호로 정의되고 식 (4)과 같이 근사적으로 표현할 수 있다. 이때 바이스태틱 지연 시간 τ는 목표물 위치 (xn, yn)와 안테나의 위치 u, 각 전파 지연 시간을 합산하여 식 (5)와 같이 정의된다.
시간 영역에서 수행되는 BP 알고리즘은 각 측정 지점에서 수신된 신호를 이용하여 영상 임의의 픽셀 (xi, yi)에서의 반사도 I를 재구성한다[12]. 구체적으로, 거리 압축 데이터를 대상으로 송∗수신 안테나와 픽셀 지점 간의 거리와 이에 대응하는 지연 시간(td)을 계산하여 보간하고, 모든 측정 지점에서의 수신 신호를 합산하여 최종 SAR 영상을 형성한다. 바이스태틱 환경에서의 BP 알고리즘은 송·수신 안테나와 표적 사이의 거리를 바탕으로 다음과 같이 지연 시간 td식 (6)을 계산한다.
식 (6)에서 Rr와 Rt는 각각 송∗수신기와 표적까지의 거리를 나타내며, c는 빛의 속도이다. 이후 식 (7)에 의해 거리 압축된 신호 Src는 dechirp 과정을 거친 SAR 수신 신호에 대한 거리 방향 푸리에 변환으로 표현되며, 표적까지의 왕복 지연 시간을 반영하여 반사도 I를 식 (9)와 같이 계산한다[13].
여기서 TP는 펄스 지속 시간, fr은 거리 주파수 성분을 의미하며 Φrc는 식 (8)과 같다.
최종적으로 영상의 모든 픽셀 지점에 대해 식 (10)과 같이 반사도를 획득하여 최종적인 SAR 영상을 획득한다.
압축센싱은 신호의 희소성(sparsity)을 기반으로 Nyquist 샘플링 한계보다 적은 측정치만으로도 원 신호를 복원할 수 있는 기법이다. 본 논문에서는 레이다 신호 방정식을 식 (11)와 같이 정의한다. y는 측정 신호, A는 측정 행렬, x는 복원하고자 하는 신호, z는 잡음을 나타낸다.
그림 1은 BPA 기반 압축센싱(BPA-CS) 알고리즘의 개념적 블락도를 보여준다. 본 연구에서는 희소 신호의 복원 기법으로서 식 (12)와 같이 BPDN(basis pursuit de-noising) 알고리즘을 적용하였다[14]. y는 바이스태틱 원시 신호를 거리 방향으로 압축하고 보간을 적용한 후의 측정값, A는 측정 행렬이다. 는 방위 방향 랜덤 샘플링 행렬, 은 방위 방향 합성 행렬이다[15]. 이때 는 Ψazimuthsum의 역행렬이며 Na는 방위 방향 샘플 수, Nr는 거리 방향 샘플 수이며 Np는 측정 펄스 수이다.
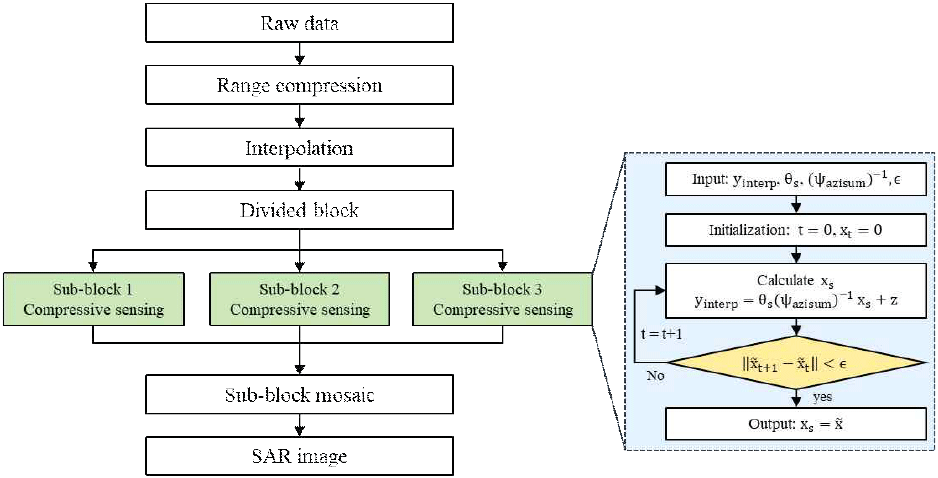
여기서 ‖ · ‖1은 l1 − norm이며, σ는 잡음 경계값으로, 이를 통해 일정 수준의 잡음을 허용하면서도 신호를 복원할 수 있다. 따라서, 신호 손실이나 영상 품질 저하가 발생하기 쉬운 바이스태틱 구조에서도 안정적인 복원이 가능하다.
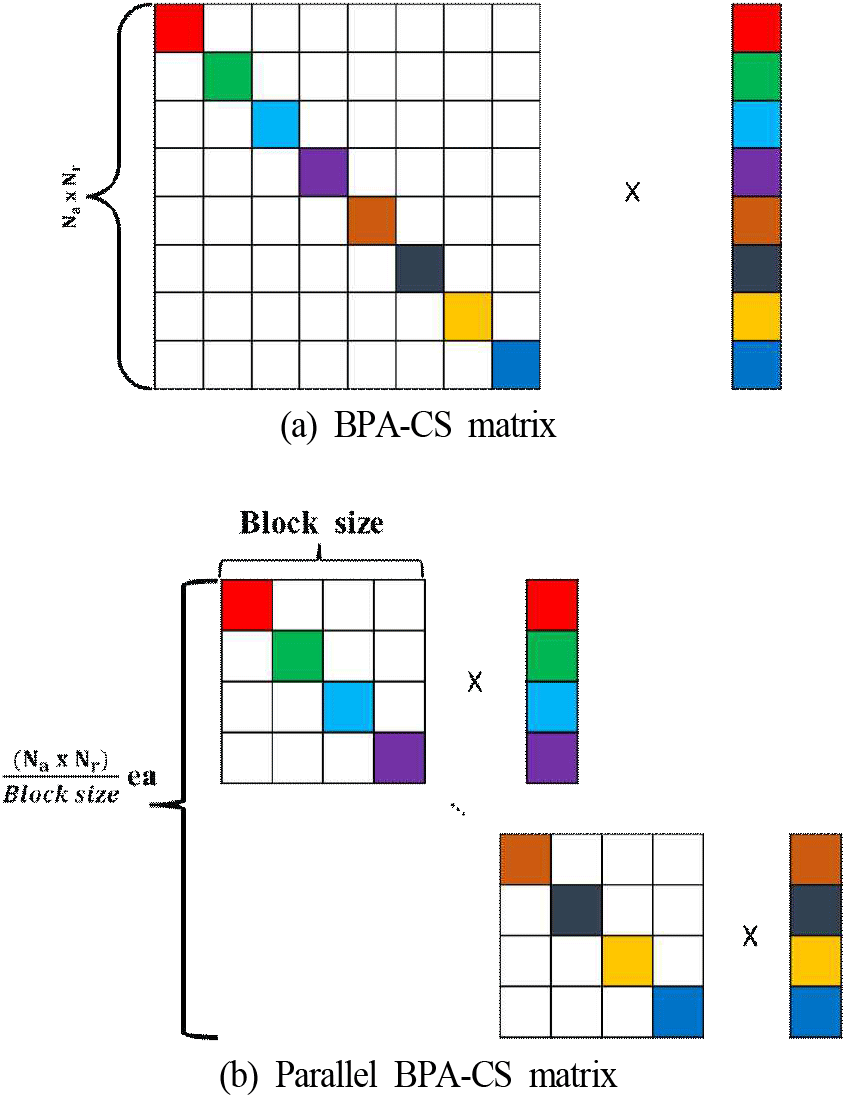
그림 2는 Ψazisum의 행렬 크기를 나타내며, 영상 해상도가 높아질수록 행렬의 크기와 연산량이 기하급수적으로 증가함을 보여준다. 이러한 연산 복잡도를 완화하기 위해 본 논문에서는 BPA-CS의 연산 가속화를 위한 병렬 BPA-CS를 제안한다. 그림 3(a)에서 측정 행렬을 펄스 단위로 분할 하면 대각 행렬 형태의 특성을 갖게 되며, 이때 그림 3(b)와 같이 일정한 블록 크기로 행렬을 나눈 후 병렬 연산을 수행한 결과가 직렬 연산과 동일해진다. 이러한 특성을 통해서 행렬을 블록 크기 나눈 후 Θparallel∊ℂblock size × block size와 같은 작아진 행렬의 크기를 통해서 기존 O(N3)에 해당하던 연산량이 블록 크기 B를 도입함으로써 O(NB2) 수준으로 크게 감소하게 된다.
III. 실험 및 결과
본 논문의 병렬 BPA-CS 기법을 적용하기 위해 Gotcha 데이터를 사용하였다[16]. 블록 크기를 100×100과 400×400로 설정하여 각각 병렬 PBA-CS를 수행하였다. 이렇게 서로 다른 블록 크기를 적용함으로써, 연산 시간 단축과 영상 복원 성능 간의 균형이 어떻게 달라지는지 확인하고자 하였다. 그림 4(a)는 Gotcha 데이터의 4°를 사용한 BPA 영상 결과이며, 그림 4(b)는 BPA-CS 영상 결과이다. 그림 4(c) 및 그림 4(d)는 병렬 BPA-CS 영상 결과이며, 그림 4(c)의 블록 크기는 100×100, 개수는 400개이며, 4(d)의 블록 크기는 400×400, 개수는 100개이다. 그림 4에서 BPA-CS 적용 시 신호 손실률은 50 %, 신호 복원을 위한 알고리즘은 BPDN을 사용하였다. 본 모의실험에서는 알고리즘 성능을 평가하기 위해 PSNR(peak signal-to-noise ratio)과 연산 시간을 주요 지표로 활용하였다. 모의실험 블록 크기에 따른 연산 속도 및 PSNR 성능을 표 1에 나타내었다. 연산 시간 측정에 사용된 컴퓨터는 Intel Core i7 13700F이다. 일반적인 BPA-CS는 연산 시간이 길다는 단점이 있으나, PSNR이 약 39.8 dB로 측정되었다. 반면, 제안된 병렬 BPA-CS 방식을 적용할 경우, 블록 크기의 적절히 조정을 통해 연산 시간이 기존 대비 수 분대로 크게 단축되었으며, PSNR은 약 39.6~39.7 dB로 수준으로 기존과 거의 동일하게 유지되었다. 이는 병렬 연산 구조를 통해 연산 효율성을 크게 향상시키는 동시에, 영상 품질 저하가 최소화됨을 보여준다.
| Algorithm | Block size | Time | PSNR [dB] |
|---|---|---|---|
|
Non Parallel BPA-CS (BPDN) |
40,000×40,000 1 ea |
24 h | 39.8 |
|
Parallel BPA-CS (BPDN) |
400×400 100 ea |
500 s | 39.7 |
|
100×100 400 ea |
297 s | 39.6 |
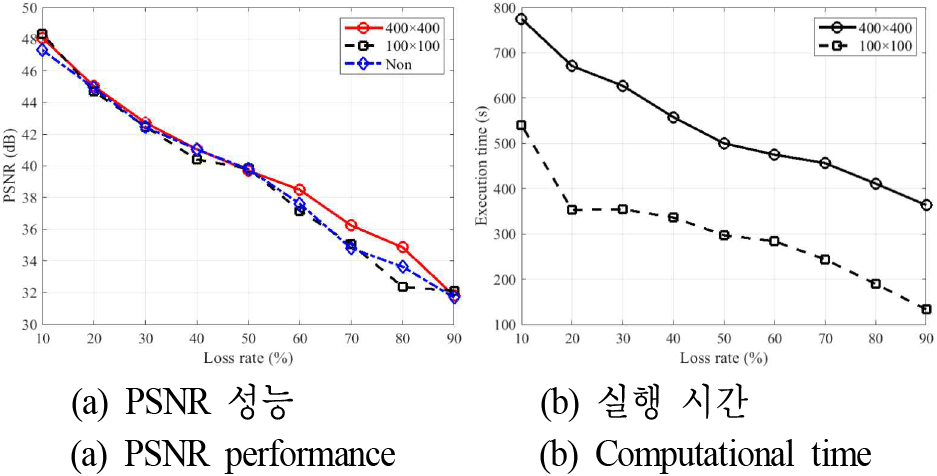
그림 5는 서로 다른 블록 크기와 데이터 손실률에 대해 측정한 PSNR과 연산 시간을 보여준다. 실험 결과, 블록 크기가 작아질수록 연산 속도가 향상되는 경향이 관찰되었으나, 데이터 손실률이 증가할수록 PSNR은 상대적으로 낮아지는 양상을 보였다.
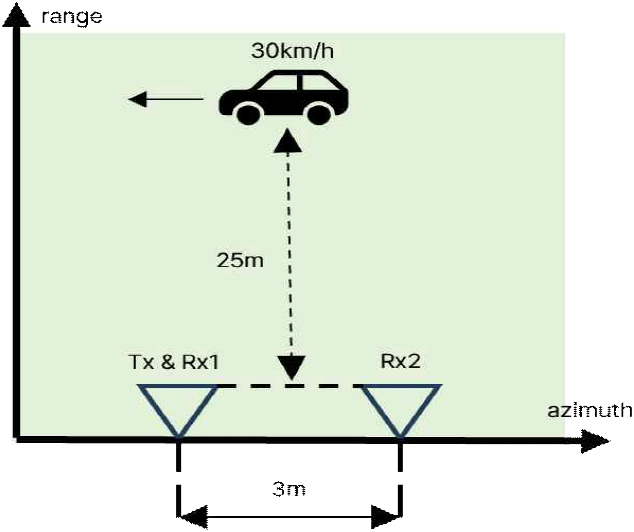
본 연구에서는 그림 6의 기하 구조와 표 2의 파라미터를 적용하여 바이스태틱 구조에 대한 모의실험을 수행하였다. 낮은 PRF와 측정 손실이 존재하는 환경에서 BP 알고리즘과 BPA-CS 알고리즘을 각각 적용하여, 모노스태틱/바이스태틱에서 발생하는 에일리어싱 현상의 완화 정도를 비교 및 분석한다. 압축센싱 기법 적용 시, 50 %의 데이터 손실률과 BPDN을 사용하였다. 그림 7은 모의실험을 진행한 결과이며, 그림 7(a) 및 그림 7(b)는 각각 모노스태틱/바이스태틱 데이터의 BPA 영상 결과이며, 그림 7(c) 및 그림 7(d)는 데이터 손실률 50 % 상황에서의 BPA 영상 결과, 그림 7(e) 및 그림 7(f)는 BPA-CS 영상 결과이다.
| SAR system parameters | Value |
|---|---|
| Center frequency | 9.9 GHz |
| Bandwidth | 400 MHz |
| Beam width | 20° |
| Pulse width | 0.004 s |
| PRF | 249.95 Hz |
| Effective radar velocity | 30 km/h |
| Bistatic baseline | 3 m |
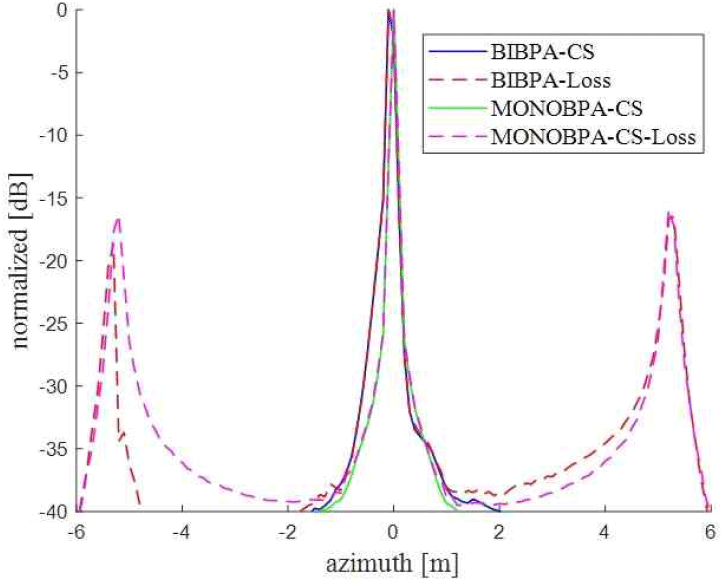
본 모의실험을 기반으로 계산된 도플러 대역폭(Doppler bandwidth)은 약 90 Hz로, Nyquist 이론을 만족하기 위해서는 최소 180 Hz 이상의 PRF가 필요하다. 그러나 본 논문에서는 데이터 손실을 50 %로 설정함에 따라 PRF가 125 Hz에 불과해 에일리어싱이 발생한다. 그림 8은 이러한 손실 환경에서 모노스태틱/바이스태틱 BPA 영상의 방위 방향 프로파일을 도시한 것으로, 단일 표적임에도 불구하고 에일리어싱으로 인해 방위 방향에 추가적인 응답이 나타나는 것을 확인할 수 있다. 반면, 압축센싱 기법을 적용한 BPA-CS 알고리즘 결과에서는 Nyquist 이론을 엄밀히 충족하지 않더라도 표적을 단일 개체로 복원할 수 있음을 확인하였다. 이는 PRF가 부족하고 측정 손실이 존재하는 환경에서도 압축센싱을 활용함으로써 에일리어싱을 효과적으로 억제하고 영상 품질을 유지할 수 있음을 시사한다.
바이스태틱 모드의 실제 데이터를 획득하기 위해 현장 실험을 진행하였다. 운동장에서 차량을 운행하면서 데이터를 획득하였으며 데이터 획득일은 2024년 10월 16일이다. 그림 9는 본 실험 현장 사진이며, 표 2는 실험에서 사용된 SAR 시스템 파라미터를 보인다. 그림 10은 모노스태틱/바이스태틱 실험 데이터를 처리한 결과로 그림 10(a) 및 그림 10(c)는 각각 모노스태틱/바이스태틱 데이터의 BPA 영상 결과이며, 그림 10(b) 및 그림 10(d)는 데이터 손실률 50 % 상황에서의 BPA-CS(BPDN) 영상 결과이다.
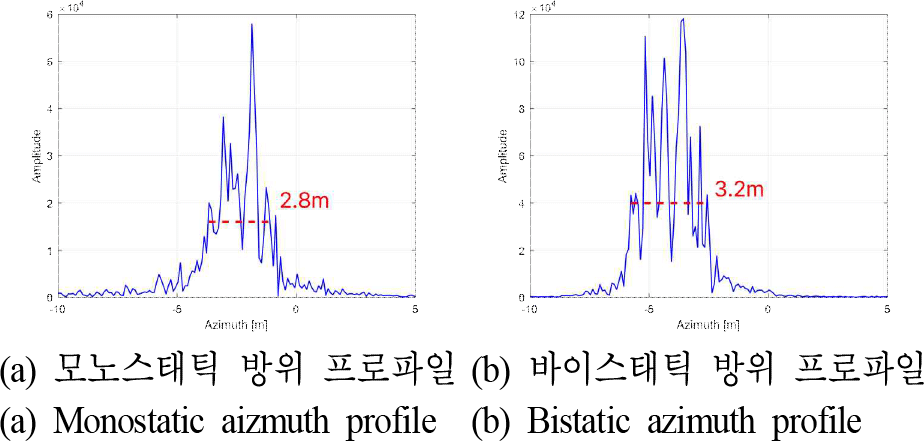
그림 11은 그림 10에 제시된 영상의 방위 방향 프로파일을 나타낸다. 실제 실험에서 사용된 차량의 길이는 약 3.5 m이며, 측정된 차량의 길이는 모노스태틱에서 약 2.8 m, 바이스태틱에서 약 3.2 m로 확인되었다. 이러한 결과는 바이스태틱 SAR 시나리오에서 모노스태틱 대비 더 많은 표적 정보를 수집할 수 있음을 시사하며, 특정 분야에서 바이스태틱 레이다의 활용 가능성을 뒷받침한다.
IV. 결 론
본 논문에서는 바이스태틱 SAR의 기하 정합 복잡성과 데이터 손실 가능성이라는 주요 문제를 해결하기 위해 BPA를 기반으로 한 압축센싱(BPA-CS)을 적용하고, 이를 병렬 구조로 확장하여 연산 효율성을 극대화하였다. 연구 결과, BPA는 바이스태틱 SAR 시스템에서 기하 정합의 복잡성을 효과적으로 처리할 수 있는 필수적인 기법임을 확인하였으며, 데이터 손실 상황에서도 압축센싱 기법을 활용하여 표적 복원이 가능함을 입증하였다. 특히, 병렬 BPA-CS 구조를 통해 블록 크기를 조절함으로써 연산을 병렬화하여 기존 BPA 대비 연산 속도를 대폭 향상시켰으며, 동시에 영상 품질 지표를 손실 없이 유지할 수 있었다.
본 연구는 바이스태틱 SAR 환경에서 BPA-CS의 필요성과 효용성을 분석하였으며, 이를 통해 데이터 손실 및 연산 비용 문제를 극복할 수 있는 접근법을 제시하였다. 향후 연구에서는 제안된 기법을 다양한 실제 환경에 적용하여 추가적인 성능 검증과 최적화를 진행할 예정이다.