The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(3):291-303

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.3.291

논문/REGULAR PAPERS

멀티스태틱 SAR에서 공통 희소성 기반 압축센싱을 이용한 영상 복원 성능 향상

이희우

, 유용선

, 정지환

, 이찬희^*

, 이우경^†

Joint Sparsity-Based Compressive Sensing for Improved Target Detection in Multistatic SAR Imaging

Hee-Woo Lee

, Yong-Sun Yoo

, Ji-Hwan Cheong

, Chan-Hee Lee^*

, Woo-Kyung Lee^†

한국항공대학교 항공전자정보공학과

^*한국과학기술원 전기 및 전자공학부

Department of Electronic and Information Engineering, Korea Aerospace University

^*School of Electrical Engineering, Korea Advanced Institute of Science and Technology

^†Corresponding Author: Woo-Kyung Lee (e-mail: wklee@kau.ac.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jan 09, 2025; Revised: Jan 21, 2025; Accepted: Mar 09, 2025

Published Online: Mar 31, 2025

요 약

본 논문에서는 다중 플랫폼을 운용하는 멀티스태틱 SAR(synthetic aperture radar) 영상의 활용도를 높이고, 효율적인 표적 식별을 수행하기 위해 공통 희소 신호 기반의 압축센싱 복원 알고리즘을 적용한다. TanDEM 모드 활용을 위한 근사적 SAR 영상 생성 기법을 제시하고, 확보된 멀티스태틱 영상에서 산재 표적을 추출하기 위해 SMV-CS 및 MMV-CS 기법을 적용하여 복원 과정에서 기대할 수 있는 표적 복원 및 잡음 억제 성능 효과를 분석한다. 점 표적 기반 SAR 영상 모의실험을 통해 제안 알고리즘의 정량적 성능을 평가하고, 이를 검증하기 위해 차량 기반 SAR 실험을 수행하여 확보한 실측 데이터에 적용한다. 실험적으로 확보한 다중 멀티스태틱 SAR 영상에 MMV-CS 기법을 적용함으로써 표적 식별의 신뢰도를 개선할 수 있음을 보인다. 이를 통해 향후 군집 위성과 같은 다중 플랫폼 SAR 운용 체계에서 생성되는 복수의 멀티스태틱 SAR 데이터를 통합함으로써 얻을 수 있는 이점을 제시한다.

Abstract

This study explores the application of a joint sparse recovery compressive sensing algorithm to the multistatic synthetic aperture radar (SAR) imaging and efficient target identification. An approximate SAR image reconstruction algorithm is proposed for the TanDEM mode operation to improve the target recovery and noise suppression by applying SMV-CS and MMV-CS. The feasibility of the proposed algorithm was evaluated using simplified multistatic SAR simulations. For validation, an experimental raw data has been produced by using vehicle-based multistiatic SAR test-bed. It is demonstrated that integrating multistatic SAR images with the MMV-CS algorithm can be used for the enhanced target identification. This study highlights the potential benefits of multi-platform SAR operation systems such as satellite constellations for improved target detection and identification.

Keywords: Synthetic Aperture Radar; Multistatic SAR; Bistatic SAR; Compressive Sensing; Multiple Measurement Vector

I. 서 론

합성 개구 레이다(SAR, synthetic aperture radar)는 위성, 항공기, 드론 등의 탑재체에 장착되어 표적이나 관심 영역의 반사도를 기반으로 영상을 형성한다^[1],[2]. 광학 센서와 달리 SAR는 주·야간 및 기상 조건과 무관하게 관측할 수 있는 특성을 가지며, 이러한 강점으로 인해 국방 및 민수 분야에서 폭넓게 활용되고 있다. 최근에는 복수의 군집 위성 체계를 기반으로 한 SAR 시스템이 도입되면서 이를 활용한 다양한 모드가 시험 운용되고 있다. 일반적으로 단일 플랫폼의 모노스태틱(monostatic) 모드가 운용되나, 최근에는 복수의 위성에서 송·수신 레이다가 독립적으로 운용되는 바이스태틱(bistatic) SAR 모드가 시연되면서 높은 관심을 받고 있다. 이러한 추세를 바탕으로 향후에는 복수의 송·수신 레이다가 상호 결합하여 운용되는 멀티스태틱(multistatic) 시스템 개발이 활발해질 것으로 기대된다. 모노스태틱 SAR 모드에서는 표적 정보 획득 구간 및 관측각이 제한되어 표적에 대한 다양한 정보 획득이 어렵다. 하지만 송신기와 수신기가 서로 다른 플랫폼에 탑재된 바이/멀티스태틱 구조에서는 다양한 각도에서 지표면 정보를 수집할 수 있어 모노스태틱 SAR 영상과 차별된 추가 정보를 제공할 수 있다^[3]. 바이/멀티스태틱 SAR 시스템 구현을 위해서는 송·수신기의 상대적 위치 및 궤적 변화 등의 기하학적 정보가 정확히 확보되어야 하며 송수신기 간의 신호 동기화가 보장되어야 한다. 따라서 군집 SAR 시스템을 실제 위성이나 항공기, 드론 등에 구현하기 위해서는 플랫폼 궤도 운용과 신호 동기화라는 핵심 기술의 확보가 필수적이다. TanDEM 모드는 군집 운용 모드를 단순화하여 두 플랫폼이 진행 방향을 공유하면서 한 플랫폼이 일정한 간격으로 다른 플랫폼을 따라가는 구조로, 수신신호의 방위 방향 성분 변화를 최소화하는 바이스태틱 SAR 시나리오이다. 송·수신기 간의 물리적 이격을 최소화하여 모노스태틱 모드와의 유사도를 높일 수 있으나, 여전히 위치 정보 및 신호 동기화 오차로 인해 영상 품질 저하가 발생할 가능성이 있다. 따라서 멀티스태틱 SAR 영상의 장점을 극대화하기 위해서는 표적 식별 및 영상 품질 개선 방안이 보완되어야 한다.

압축센싱(CS, compressive sensing) 알고리즘은 신호의 희소성(sparsity)을 기반으로 Shannon-Nyquist 샘플링 이하로 확보된 데이터라도 원신호의 정보가 산재하게 분포하는 경우, 이를 높은 확률로 복원할 수 있는 방안을 제공한다^[4]. 신호 손실이 발생하는 환경에서 한정된 표적을 복원하는 목적으로 사용될 수 있으며, 데이터 수집 과정에서 발생한 손실에 대응할 수 있는 장점이 있다. 기존의 압축센싱 기반 SAR 신호처리 연구는 주로 모노스태틱 SAR 시나리오에서 고해상도 영상 획득 및 산재 표적 신호 복원 목적으로 제안되었다^[5]. 압축센싱 알고리즘은 일부 데이터 손실이 발생하더라도 고해상도 영상 복원을 가능하게 한다는 점에서, 복잡한 기하학적 구조와 신호 모델을 가진 바이/멀티스태틱 SAR 시스템에서 발생할 수 있는 신호 손실 및 품질 저하에 대응하기 위해 사용될 수 있다. 모노스태틱 SAR는 단일 수신기만을 사용하므로 단수 측정 벡터(SMV, single measurement vector) 신호를 입력 신호로 하는 복원 방식을 기반으로 한다. 반면 군집 SAR 운용 체계가 도입될 경우, 다중 수신기의 데이터가 주어지게 되며 복수 측정 벡터(MMV, multiple measurement vector) 신호를 입력 데이터로 사용하여 복원 성능의 신뢰도를 높일 수 있을 것이다^[6]. 복수 측정 벡터 기반 압축센싱(MMV-CS) 알고리즘은 다중 수집 데이터에서 0이 아닌 희소 성분들의 집합을 공통으로 공유하는 시나리오에서 해당 희소 데이터를 복원하는 문제를 다룬다^[7].

본 논문은 복수의 수신기 데이터를 통합하는 MMV-CS 기법을 통해 멀티스태틱 SAR 영상에서의 표적 복원 성능을 개선하는 것을 목적으로 하며, 이를 통해 군집 SAR 시스템의 효율적인 운용과 고해상도 영상 복원을 위한 실질적 해결 방안을 제시하고자 한다. 압축센싱 복원 과정은 복잡한 재귀 연산 과정을 반복적으로 수행하기 때문에, 연산 효율을 높이기 위해서는 연산식을 단순화하는 것이 중요하다. TanDEM 모드로 운용되는 바이스태틱 SAR 시스템은 기하 거리를 모노스태틱 거리로 근사화하는 BEM(bistatically equivalent monostatic) 방식을 적용할 수 있다^[8]. 이를 통해 정합 과정이 단순해지면 TanDEM 모드로 운용되는 복수의 독립된 시스템에서 독립된 SAR 영상을 획득하는 과정에서 공통 희소(joint sparsity) 성분을 추출하여 표적 정보에 대한 복원 신뢰도를 개선할 수 있다.

본 논문에서는 모의실험을 통해 단수 측정 벡터 기반 압축센싱(SMV-CS) 기법과 MMV-CS 기법을 비교하여 신호 복원 성능을 정량적으로 평가하고, 이를 실제 실험에서 획득된 데이터에 적용하여 검증한다. 본 논문의 Ⅱ장에서는 연구에서 사용된 다중 SAR 시스템 및 압축센싱 기법의 이론적 배경과 관련 기법을 설명한다. 이어서 Ⅲ장에서는 모의실험 및 차량 기반 실험 데이터를 통해 SMV-CS와 MMV-CS의 적용 결과를 제시하고 성능을 비교한다. 마지막으로 Ⅳ장에서는 본 연구의 결론과 향후 연구 방향을 논의한다.

Ⅱ. 이 론

2-1 바이/멀티스태틱 SAR 기하 구조

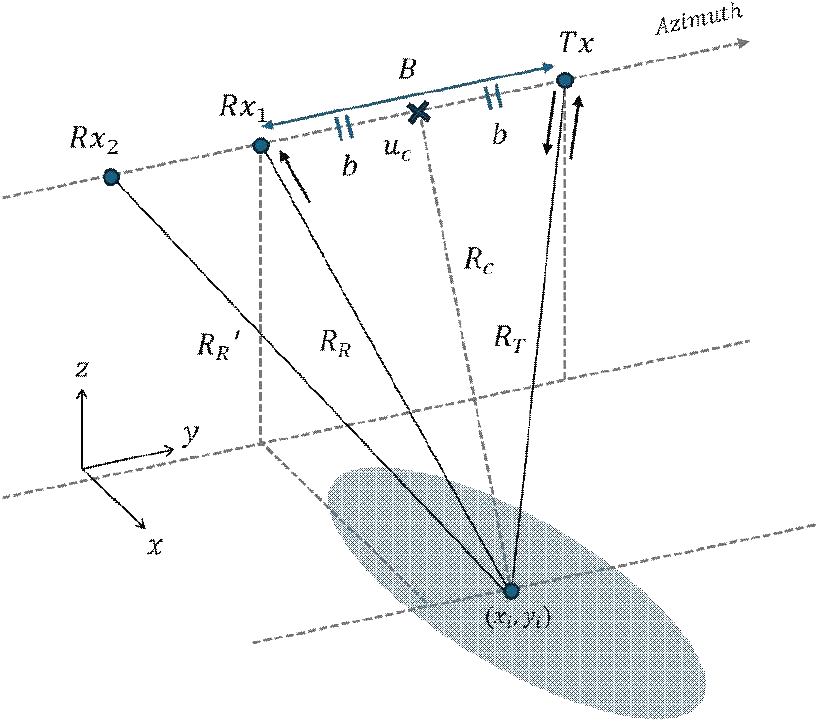
그림 1은 복수의 TanDEM 모드를 포함한 멀티스태틱 구조를 나타낸다. TanDEM 모드로 운용하는 바이/멀티스태틱 SAR는 송·수신기의 물리적인 분리로 송신기와 수신기 플랫폼 간의 기선 거리(baseline) B가 존재한다. 이때 송신기(Tx)와 첫 번째 수신기(Rx₁)의 사이의 주 축 중심점인 u_c를 기준으로 B를 동일한 크기의 두 b로 나뉜다. 바이스태틱 SAR 시스템은 모노스태틱 환경 대비 송신기와 수신기의 물리적 분리에 따라 거리 차이가 발생하며, 이를 통해 Tx와 Rx₁으로 이루어진 바이스태틱 거리를 모노스태틱 거리로 근사화하고자 한다. 모노스태틱에서의 플랫폼과 표적 사이의 거리를 R_mono=R_T, 바이스태틱 에서의 수신기와 표적 사이의 거리를 $R b i = 12 R T + R R$ 이라 할 때, R_mono는 BEM을 통해 R_mono≃R_c로 근사할 수 있다^[1]. 여기서 R_bi와 R_mono의 잔여 거리(residual range)는 식 (1)과 같이 계산할 수 있다.

R b i − R m o n o = 12 R T + R R − R c ≅ b b − y 1 R T − b b − 2 y 1 2 R T = b 2 2 R T

(1)

그림 1. | Fig. 1. 멀티스태틱 SAR 기하 구조 | The multistatic SAR geometry.

Download Original Figure

여기서 b는 B를 u_c를 기준으로 나눈 거리이고, y₁은 그림 1에 나타낸 방위 방향인 y축 좌표로, 송신기와 수신기 간의 상대적인 위치 관계를 정의하고자 사용되었다. 이를 통해 바이스태틱 거리 R_bi를 R_BEM으로 근사하여 표현하면 식 (2)와 같이 나타낼 수 있다^[1].

R b i ≈ R B E M = R c + b 2 2 R T

(2)

이러한 근사적 접근은 관측 거리가 기선 거리에 비해 충분히 큰 시나리오에서 바이스태틱 모드의 복잡한 기하 구조 해석을 용이하게 하며, 기존의 모노스태틱 기반 영상 형성 알고리즘을 활용할 수 있는 장점을 제공한다. 이를 통해 바이스태틱 SAR 시스템에서도 효율적이고 직관적인 영상 복원 과정이 가능해진다.

주파수 변조 연속파(FMCW, frequency modulated continuous wave) 레이다는 송신 신호의 주파수가 시간에 따라 선형적으로 변하는 특성을 가지며, 짧은 거리의 목표물 탐지에 적합하여 SAR 시스템에서도 자주 사용된다^[9]. 그러나 바이스태틱 SAR 시스템에서는 송·수신기가 물리적으로 분리되어있기 때문에 시간 동기화 문제가 발생할 가능성이 커 기존 연구들에서는 다양한 접근 방법이 제안되었다^[10],[11]. 이러한 문제를 해결하기 위해 본 논문에서는 송신기와 수신기의 국부 발진(LO, local oscillation) 신호를 무선으로 공유하여 동기화하는 방식을 채택한다. 일반적인 FMCW 신호는 식 (3)과 같이 운용 주파수 f_o와 주파수 변조율 k_r을 이용해 톱니파 형태로 시간 t에 대한 주파수 변조 신호로 나타낼 수 있다^[12]. 수신신호는 목표물로부터 반사되어 돌아오는 지연 시간 τ_R을 이용해 식 (4)와 같이 표현할 수 있다^[12].

s t (t) = exp j 2 π f o t + k r 2 t 2

(3)

s r (t − τ) = exp j 2 π f o t − τ R + k r 2 t − τ R 2

(4)

여기서 τ_R은 레이다 신호가 송신된 후 표적으로부터 반사되어 돌아올 때까지 걸리는 시간이다. 표적의 위치 (x_i,y_i)로부터 b를 고려하면 τ_R은 식 (5)와 같이 계산할 수 있다.

τ R = x i 2 + y i − u c + b 2 c + x i 2 + y i − u c − b 2 c

(5)

실제 데이터 획득을 위한 바이스태틱 FMCW 레이다의 송신기와 수신기는 레이다 신호 주파수의 1/2에 해당하는 주파수를 가지는 LO 신호를 무선으로 송수신하여 동기화된다. TanDEM 모드 바이/멀티스태틱 SAR의 플랫폼 간 거리 B로 인해 LO 신호가 τ_B만큼 지연되며, 이를 반영한 Rx₁에서의 LO 수신신호는 식 (6)과 같이 표현할 수 있다.

s L O, r (t − τ) = exp j 2 π f o 2 t − τ B + k r 4 t − τ B 2

(6)

주파수 체배기를 통해 수신된 LO 신호 s_LO,r(t)를 본래의 주파수로 변환시킨 신호를 s_LO(t)라고 할 때, s_LO(t)와 s_r(t)를 주파수 혼합기를 통해 주파수 하향 변환을 수행한다. 해당 변환을 거친 신호의 비트 주파수(beat frequency) 성분을 샘플링하여 바이스태틱 SAR 수신신호로 활용할 수 있으며 이때의 수신신호는 식 (7)과 같이 나타낼 수 있다.

S (t, τ) = σ x i, y i exp j 2 π f 0 τ R − τ B × exp j 2 π k r t τ R − τ B × exp − j π k r t τ R 2 − τ B 2

(7)

식 (7)의 σ(x_i,y_i)는 위치 (x_i,y_i)에서의 표적에 대한 반사도를 의미한다. 본 논문에서 사용한 멀티스태틱 FMCW SAR 시스템은 LO 신호를 무선으로 송·수신함으로써 τ_B의 영향을 받는다. 따라서 사용한 바이스태틱 시스템에서는 측정 거리를 R_bi와 비교하면 B(=cτ_B)만큼 짧아진다. 식 (7)의 마지막 항 $exp − j π k r τ R 2 − τ B 2$ 는 영상 형성 전에 보정되어야 하는 잔여 비디오 위상(RVP, residual video phase) 성분이다. 플랫폼 이동 및 관측 범위의 복잡도가 증가하는 바이스태틱 모드에서는 영상 품질 개선을 위해 RVP 성분을 제거하는 것이 필요하다^[9]. 또한, TanDEM 모드는 물리적으로 분리된 두 플랫폼이 동일한 간격을 유지하며 운용되므로 B는 일정하다. 즉, τ_B를 상수로 취급할 수 있어 측정 거리와 RVP 성분을 제거한 식을 바이/멀티스태틱 SAR 수신신호로 사용할 수 있다.

2-2 복수 측정 벡터 기반 압축센싱 기법

k개의 수신기를 운용하는 멀티스태틱 SAR 모드를 바이스태틱 SAR 모드의 집합으로 가정할 수 있다. 이 경우, 각 수신신호에 대한 압축센싱 모델은 식 (8)과 같이 설계할 수 있다.

y 1 = Φ 1 Ψ 1 α + z = Θ 1 α 1 + z = Φ 1 x 1 + z y 2 = Φ 2 Ψ 2 α + z = Θ 2 α 2 + z = Φ 2 x 2 + z ⋮ ⋮ ⋮ ⋮ y k = Φ k Ψ k α + z = Θ k α k + z = Φ k x k + z

(8)

식 (8)에서 y_k는 k개의 바이스태틱 수신기에서 수신된 관측 신호, Ψ는 주어진 신호의 산재성을 만족시키기 위한 변환 행렬이고 m ≪ n일 때, Φ는 각 신호에 맞는 m×n 크기의 측정 행렬을 의미한다. Θ는 Θ=ΦΨ로 표현되는 산재성을 만족시키는 측정 행렬이고 x는 x=Ψα로 산재성을 만족하여 복원하려는 원신호가 된다^[13]. z은 랜덤 잡음 신호를 의미하는 행렬이다. 본 연구에서는 다중 수신기가 동일한 영역을 관측한다는 조건을 전제로 함으로써 [y₁| ··· |y_k]에 대한 측정 행렬인 [Φ₁| ··· |Φ_k]을 Φ로 표현할 때, 복원하려는 원신호 [x₁| ··· |x_k]에 대한 Y는 식 (9)와 같이 표현할 수 있다.

Y = Φ X + z w h e r e Y = ⌈ y 1 | ⋯ | y k ⌉, X = ⌈ x 1 | ⋯ | x k ⌉

(9)

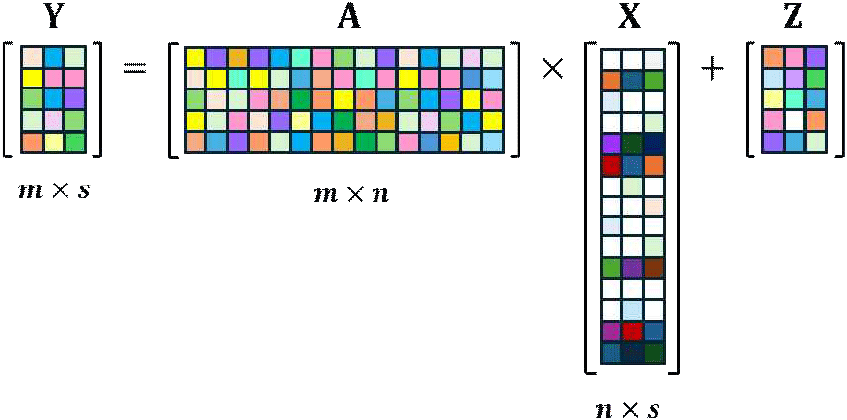
MMV 문제는 관측 신호를 가지는 원신호 집합의 복원을 다룬다. SMV 문제를 확장한 형태로, 복원하고자 하는 신호 X를 구성하는 벡터들이 공통 희소 패턴을 가지면 희소 신호 집합에 대한 복원이 가능한 것이다. 원신호와 측정 신호는 모두 벡터가 아닌 행렬로 구성되며 m, n, s는 양수이고 m < n이라고 할 때, m은 측정 행렬의 길이, n은 희소 행렬의 길이, s는 복수 측정 벡터의 개수이다. Y∈ℝ^m×s에 대해 측정 행렬이 A∈ℝ^m×n일 때, X∈ℝ^n×s이면, 가우시안 잡음 행렬 Z를 포함하는 Y는 식 (10)과 같은 선형 방정식으로 나타낼 수 있다^[7].

Y = A X + Z

(10)

그림 2는 이러한 MMV 문제에서 관측 행렬과 희소 행렬, 측정 행렬로 구성된 압축센싱 기법을 시각적으로 나타낸다. s개의 측정 벡터에 공통으로 포함된 희소 벡터를 동시에 추출함으로써 복원 과정에서 발생하는 오류를 억제하고 잡음에 대한 견고성을 높일 수 있을 것으로 기대할 수 있다.

그림 2. | Fig. 2. 복수 측정 벡터 기반 압축센싱 기법 도식화 | Visualization of compressed sensing based on multiple measurement vectors.

Download Original Figure

MMV 기반의 압축센싱 문제를 풀기 위해서는 다양한 방법을 적용할 수 있다. 본 논문에서는 식 (11)과 같이 표현되는 BPDN(basis pursuit denoise) 방법을 활용하여 최적해를 구한다^[14].

min X ‖ X ‖ 2, 0 s . t . ‖ Y − A X ‖ p 2 ≤ σ

(11)

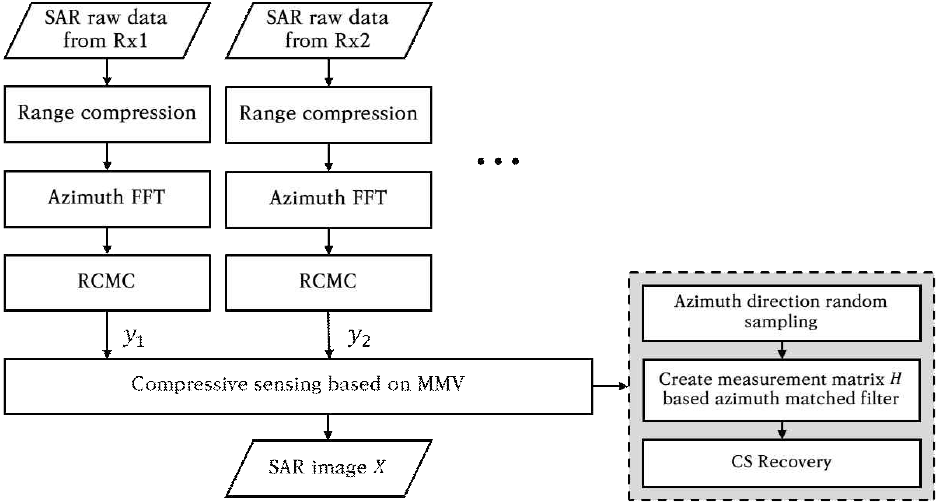
여기서 σ는 잡음 경계값이고 ∥·∥_2,0은 혼합 norm인l_2,0−norm으로, 서로 다른 norm을 결합하여 사용한다^[14]. l_2,0−norm은 먼저 행렬의 각 행에 대해 l₂−norm을 통해 행의 norm을 최소화하고, 각 열에 대해 l₀−norm을 수행하여 0이 아닌 열의 개수를 찾는다. 복수의 측정 벡터로 구성된 행렬에서 단일 벡터를 추정하기 위해 공통 희소성의 특성을 만족하는 성분을 반복적으로 찾는 과정이 필요하다. 이를 위해 본 논문에서는 독립적인 복수의 수신기에서 수신된 신호를 분석하고 융합하기 위해 MMV 신호를 입력 신호로 사용하여 신호를 복원하는 방법을 도입한다^[7]. 바이/멀티스태틱 SAR 신호에 MMV-CS를 적용하기 위해서는 복수의 수신기로 얻어진 각 신호가 공통 희소 패턴을 공유해야 한다. 하지만 실제로 복수의 수신신호는 서로 다른 희소 패턴을 가지는 것이 일반적이다. 따라서 공통 희소 패턴을 형성하기 위해서는 각 신호에 적합한 변환 행렬을 적용하여 공통 희소 패턴을 형성하는 과정이 요구된다. 이를 통해 공통 희소 패턴을 가지는 재구성된 신호를 획득할 수 있으며, 클러터 억제 성능을 개선할 수 있다. 이를 실현하고자 모의실험을 통해 독립적인 복수의 수신기로부터 수신된 신호를 형성하고, RDA(range-Doppler algorithm)를 기반으로 거리 방향 압축과 RCMC(range cell migration correction)를 수행한 후, SAR 영상 정합을 위해 MMV-CS를 활용하여 영상 복원을 진행한다. 식 (12)는 거리 방향 압축을 마친 신호 y_k에 대해 방위 방향 정합 필터를 기반으로 생성한 행렬을 통해 나타낸 선형 방정식이다.

y k = ϕ H k x k + z = Φ k x k + z

(12)

m ≪ n일 때, ϕ∈ℝ^m×n)은 랜덤 행렬, H∈ℂ^n×n)은 방위 방향 정합 필터를 기반으로 한 행렬일 때, Φ_k∈ℂ^m×n은 랜덤 행렬을 통해 행렬 크기를 감소시킨 방위 방향 정합 필터 기반 측정 행렬이다. x∈ℂ^n×1는 표적 응답 신호로, 압축센싱을 통해 복원되는 주요 산재 성분 벡터를 의미한다. 본 연구는 다중 수신기가 동일한 영역을 관측한다는 조건을 전제로 함으로써 동일한 표적에 대해 복수의 관측 데이터를 활용할 수 있어 MMV-CS를 적용하기에 적합하다. 하나의 수신기로부터 획득한 신호를 복원하기 위한 문제로 표현된 식 (12)를 확장하여, k개의 수신기를 운용하는 시나리오에 적용할 수 있다. 이때 복수의 관측 신호 Y=[y₁|···|y_k]에 대한 측정 행렬이 A일 때, 복원하려는 원신호 X=[x₁|···|x_k]에 대한 선형 방정식은 식 (13)으로 표현할 수 있다. 이를 RDA 과정에 적용한 영상 복원 흐름도는 그림 3과 같다.

Y = A X + z w h e r e Y = ⌈ y 1 | ⋯ | y k ⌉, X = ⌈ x 1 | ⋯ | x k ⌉

(13)

그림 3. | Fig. 3. RDA 기반 MMV-CS 적용 흐름도 | Flowchart of RDA-Based MMV-CS application.

Download Original Figure

2-3 1차원 신호에 대한 MMV-CS 적용

희소 패턴을 공유하는 두 개의 1차원 신호에 대해 MMV-CS을 적용하여 산재 정보를 복원하는 알고리즘을 구현하여 검증하는 모의실험을 수행하였다. 독립된 2개의 1차원 신호 벡터는 길이가 150이 되도록 설정하고, 최대 10개의 산재 신호를 공유하도록 설계하였다. 신호의 신호 대 잡음비(SNR, signal-to-noise ratio) 값을 20 dB로 설정하여 랜덤한 클러터 성분이 혼합된 상황을 고려하였으며, SMV 기반의 BPDN 기법과 MMV 기반의 BPDN 기법의 각각 적용하여 복원 성능을 비교하였다. 실험 결과는 그림 4에 나타나 있으며, 그림 4(a) 및 그림 4(b)는 각각 잡음 경계값 σ를 0.1과 1로 설정하여 확인한 결과이다.

그림 4. | Fig. 4. 1차원 신호에 대한 MMV-CS 복원 성능 | MMV-CS reconstruction performance for 1D signals.

Download Original Figure

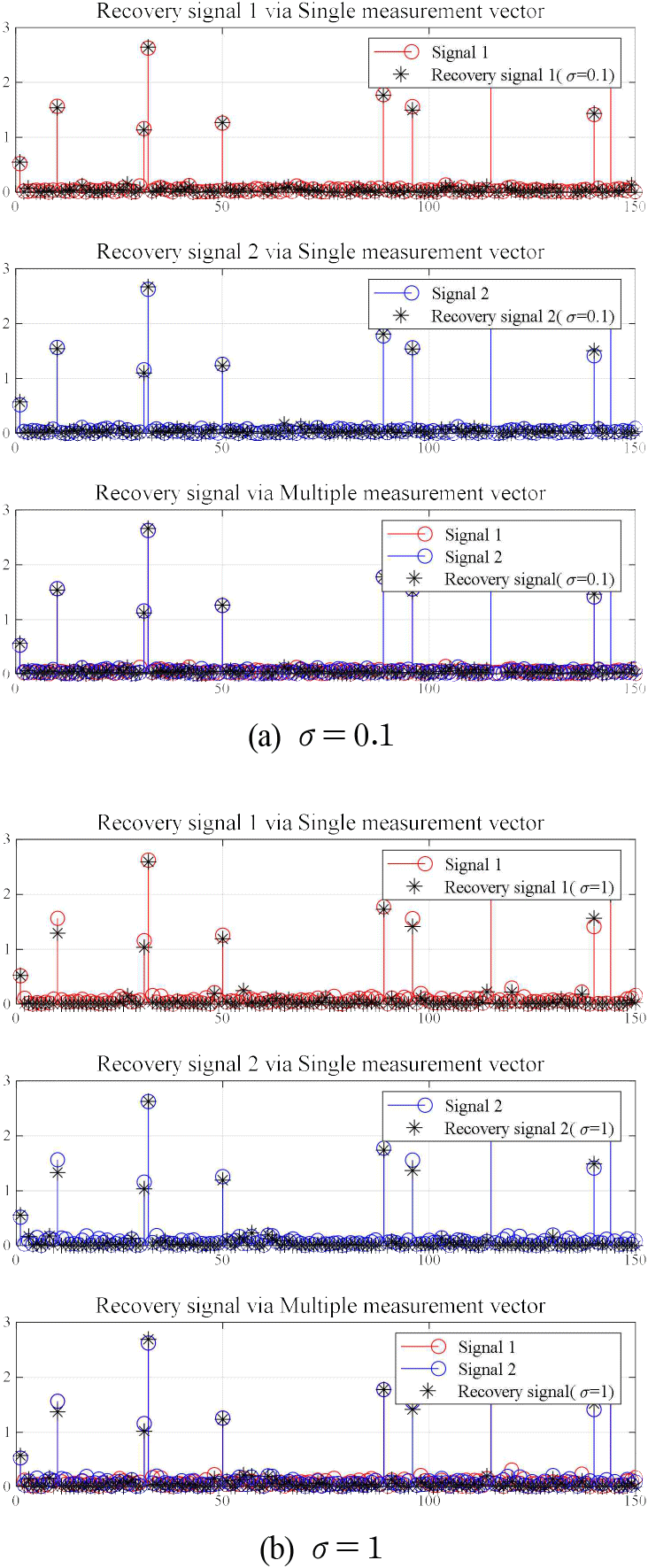
희소 패턴을 공유하는 신호는 MMV-CS를 적용할 경우, 서로의 복원을 돕게 되어 SMV-CS에 비해 원신호와 유사하게 복원이 가능한 것을 확인할 수 있다. 반면, 희소 패턴을 공유하지 않는 랜덤 신호 성분인 클러터는 온전한 신호 복원이 불가능하다. 이는 MMV-CS가 공유된 희소 패턴의 신호 복원에 유리하지만, 비공유 클러터 성분에 대해서는 복원 성능에 한계가 있음을 시사한다. 또한, 잡음 경계값이 낮은 경우(σ=0.1) 복원 성능이 더 우수하게 나타났다. 이는 낮은 잡음 경계값이 복원 과정에서 더 엄격한 제한 조건을 부여하여 신호 복원의 정확성을 향상시키는 결과로 해석할 수 있다.

Ⅲ. 모의실험 및 실데이터 적용

3-1 점 표적 기반 모의실험

실제 현장 실험에 앞서, 바이스태틱 SAR 모드의 실데이터 획득을 위한 시스템 환경 및 기하 구조를 모사한 모의실험을 수행하였다. 먼저 모노스태틱 모드를 위해 송신기(Tx)와 수신기(Rx1)가 동일한 위치에 있는 레이다 시스템을 가정하였다. 바이스태틱 1 모드는 Tx와 1 m 이격된 수신기(Rx2)를, 바이스태틱 2 모드는 Tx와 30 m 이격된 수신기(Rx3)를 각각 설정하여 모의실험을 진행하였다. 이러한 시스템은 복수의 바이스태틱 모드를 포함하고 있으므로 멀티스태틱 기하 구조의 모의 환경으로 볼 수 있다. 표준 스트립맵(stripmap) 운용 모드로 데이터를 획득하는 차량 플랫폼을 가정하였으며, 수신부에서는 RDA 기반의 신호처리를 통해 점 표적에 대한 영상을 생성하였다. 모의실험에 사용된 주요 시스템 변수는 표 1에 정리하였다.

표 1. | Table 1. 멀티스태틱 SAR 모의실험 파라미터 | Simulation parameters for multistatic SAR.

Parameter		Values
Center frequency [GHz]		9.9
Bandwidth [MHz]		400
Sampling frequency [MHz]		5
PRF [Hz]		999.5
Platform velocity [m/s]		18.9
Range to target distance [m]		300
Baseline [m]	Bistatic 1	1
Baseline [m]	Bistatic 2	30

Download Excel Table

단일 점 표적에 대한 영상 복원 성능을 분석하기 위해 먼저 각 모노/바이스태틱 수신신호에 대해 SMV-CS 기반 영상 복원을 수행하였다. 다음으로 복수의 수신신호를 통합한 MMV-CS 방식으로 영상을 복원하여 결과를 비교하였다. 복원 성능을 보다 현실적으로 평가하기 위해 점 표적 신호의 동적 범위(dynamic range)는 40 dB 이상이 되도록 설정하여 모의실험을 수행하였다. 또한, 산재도가 높음을 고려하여 원신호의 20 %에 해당하는 샘플만을 사용하여 복원을 수행하였으며, σ=0.1로 설정하였다. 생성된 단일 점 표적 영상과 압축센싱 적용 결과는 그림 5에 나타냈으며, 이를 통해 모노스태틱 및 바이스태틱 SAR 신호에서의 SMV-CS와 MMV-CS의 복원 성능을 시각적으로 비교할 수 있다.

그림 5. | Fig. 5. 점 표적 기반 멀티스태틱 SAR 시뮬레이션 및 압축센싱 적용 결과 | Point target-based multistatic SAR simulation and compressive sensing application results.

Download Original Figure

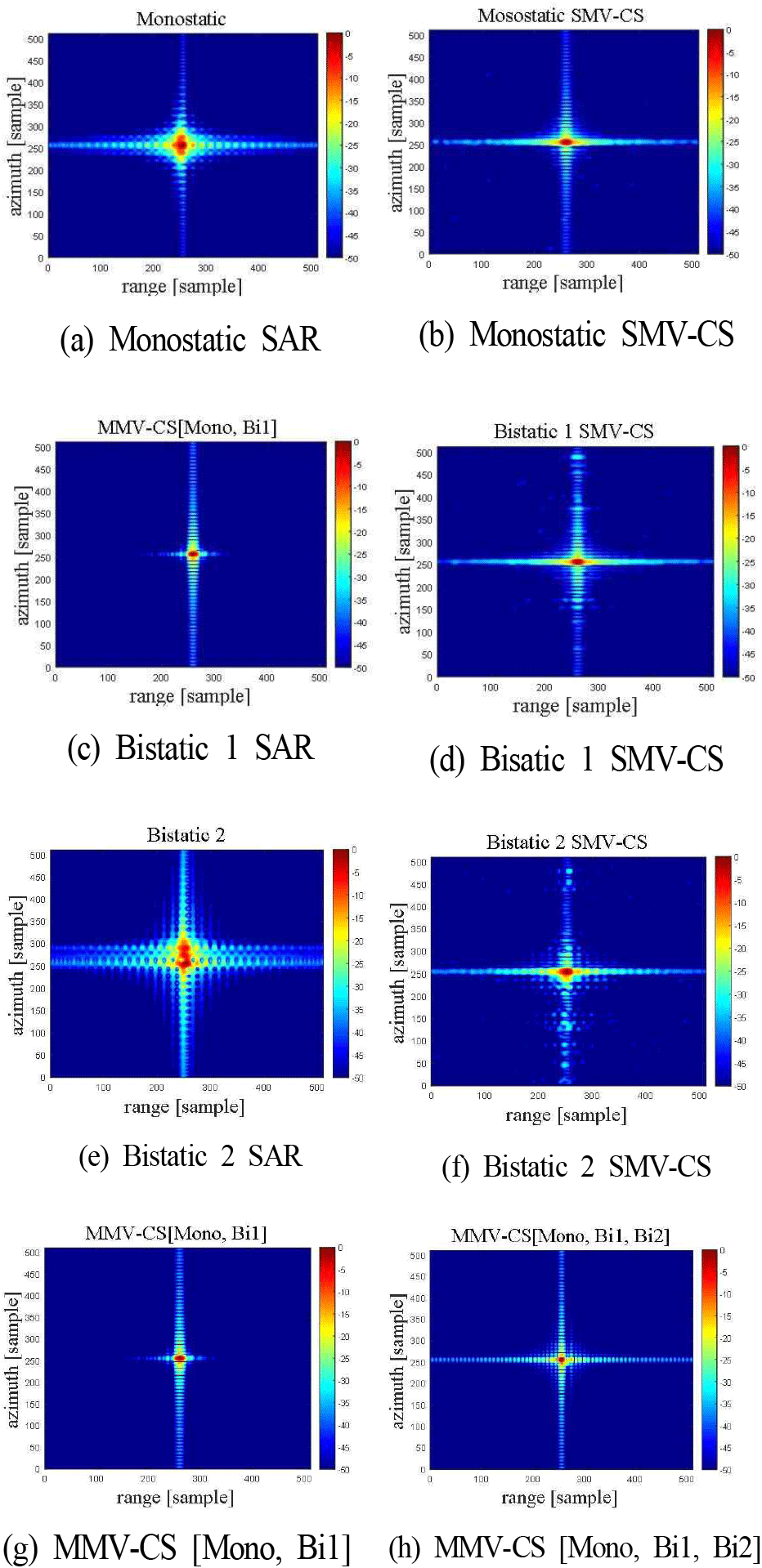
압축센싱 기법을 적용한 결과, 클러터가 효과적으로 제거되어 특정 영역에서는 신호 값이 0이 아닌 존재하지 않는 상태로 나타난다. 이 경우, 이론적으로 동적 범위가 무한대에 가까워질 수 있으며, 일부 영상에서는 명확한 동적 범위를 표현하는 것이 어렵다. 본 연구에서는 컬러바를 통해 시뮬레이션 영상의 동적 범위를 시각적으로 나타내었으며, 이를 통해 영상 내 신호 강도 차이를 직관적으로 분석할 수 있도록 하였다.

그림 5(g) 및 그림 5(h)는 복수의 수신신호를 통합한 MMV-CS 방식을 적용한 결과를 보인다. 단순 RDA가 적용된 그림 5(a), 그림 5(c) 및 그림 5(e)에 비해 높은 영상 품질을 보이는 것이 확인되며 SMV-CS가 적용된 그림 5(b), 그림 (d) 및 그림 5(f)에 비해서도 표적이 선명하고 신호 왜곡이 효과적으로 억제된 것을 확인할 수 있다. 이는 복수의 수신신호가 서로 상호 보완적으로 작용하여 신호 복원을 도운 것으로 설명된다. 특히, 기선 거리가 30 m로 증가한 바이스태틱 2 모드와 같이 신호의 왜곡이 커져 영상 정합 품질이 낮은 경우에서도 MMV-CS 기법은 안정적인 복원 성능을 제공하며, 점 표적의 에너지가 명확히 집중되는 모습을 확인할 수 있다. 결과적으로 SMV-CS는 단일 수신기의 데이터를 활용하여 신호를 복원했으나 제한된 복원력을 보이지만, MMV-CS는 복수의 수신신호를 통합적으로 활용하여 개선된 표적 복원 성능과 잡음 억제 효과를 나타냈다.

점 표적에 대한 정량적 분석을 위해 각 영상에 대한 TCR(target-to-clutter ratio)을 계산하였다. TCR은 표적 신호와 클러터 신호 간의 상대적인 에너지를 평가하여 SAR 영상에서 표적의 명확한 식별 가능성을 나타내는 지표로 사용된다^[15]. 본 연구에서는 클러터 대신 시스템 잡음 및 측정 오류를 포함하는 환경에서 표적 복원 성능을 평가하기 위한 지표로 활용하였다. 즉, TCR을 활용하여 표적 신호 대비 복원된 신호의 강도를 분석하고, 압축센싱 기법 적용에 따른 성능 향상을 정량적으로 평가하였다. 본 연구에서 정량적 평가를 위한 TCR은 식 (14)와 같이 정의된다.

T C R [d B] = 20 log 10 1 N T ∑ (i, j) ∈ T | S (i, j) | 1 N C ∑ (i, j) ∈ C | S (i, j) |

(14)

그림 5의 영상에서 2D 부엽 신호 레벨을 각각 −3 dB와 −15 dB 이상인 지점으로 표적 영역으로 설정한 후, 각각에 대한 TCR을 측정하였다. 이는 압축센싱 기법 적용 후 표적 신호가 복원되는 과정에서 신호 강도의 변화가 발생할 수 있기 때문에, 특정 신호처리 방식에 종속되지 않는 비교 기준을 설정하기 위한 것이다. 즉, 식 (15)에서 S(i,j)는 전체 영역, N_T는 표적 영역의 샘플 수, N_C는 클러터 영역의 샘플 수로 설정한다. 표 2는 SMV-CS와 MMV-CS 기법을 적용하여 각 기법의 TCR 성능을 비교한다.

표 2. | Table 2. 압축센싱 적용에 따른 점 표적 TCR 성능[dB] | Point target TCR performance with compressive sensing application [dB].

TCR threshold	Mode	No CS	SMV-CS	MMV-CS with Mono	MMV-CS with Mono, Bi1
−3 dB	Monostatic	53.12	56.29	-	-
	Bistatic 1	54.17	55.89	87.33	-
	Bistatic 2	51.66	55.57	81.71	92
−15 dB	Monostatic	46.48	49.92	-	-
	Bistatic 1	45.45	49.8	88.74	-
	Bistatic 2	43.9	48.82	85.74	90.67

Download Excel Table

모노스태틱, 바이스태틱 1, 바이스태틱 2 데이터를 각각 단독으로 압축센싱을 적용한 경우, TCR 값은 압축센싱 적용 전과 유사한 수준으로 나타났으나, 복수의 데이터를 상호 연동하여 활용하는 MMV-CS 기법을 적용하면 성능이 점진적으로 향상됨을 확인할 수 있다. 최종적으로 세 개의 데이터를 모두 결합한 MMV-CS 기법을 적용한 결과, 가장 높은 TCR 값을 기록하여 복원 성능이 극대화됨을 알 수 있다. 이는 복수의 수신신호 간 상호보완 효과를 통해 단일 수신기 데이터를 활용한 SMV-CS 대비 더 우수한 복원 성능과 잡음 억제 효과를 제공했음을 의미한다. 이러한 결과를 통해 압축센싱 기법이 SAR 데이터 복원 및 잡음 억제에 효과적으로 적용될 수 있을 것으로 예상할 수 있다. 일반적으로 바이스태틱 SAR는 모노스태틱 구조에 비해 관측 시간이 단축됨에 따라 도플러 대역폭이 감소하여 해상도 및 영상 품질이 저하되는 경향이 있다. MMV-CS 기법은 모노스태틱 SAR 영상 정보를 활용하여 저하된 바이/멀티스태틱 SAR 영상의 품질을 개선할 가능성을 제시한다. 본 연구에서 수행한 실험을 통해 복수의 데이터를 활용하는 MMV-CS 기법이 단일 데이터를 사용하는 SMV-CS 보다 안정적인 복원 성능을 제공할 수 있음을 입증하였다.

3-2 차량 기반 실험 데이터 획득 및 적용

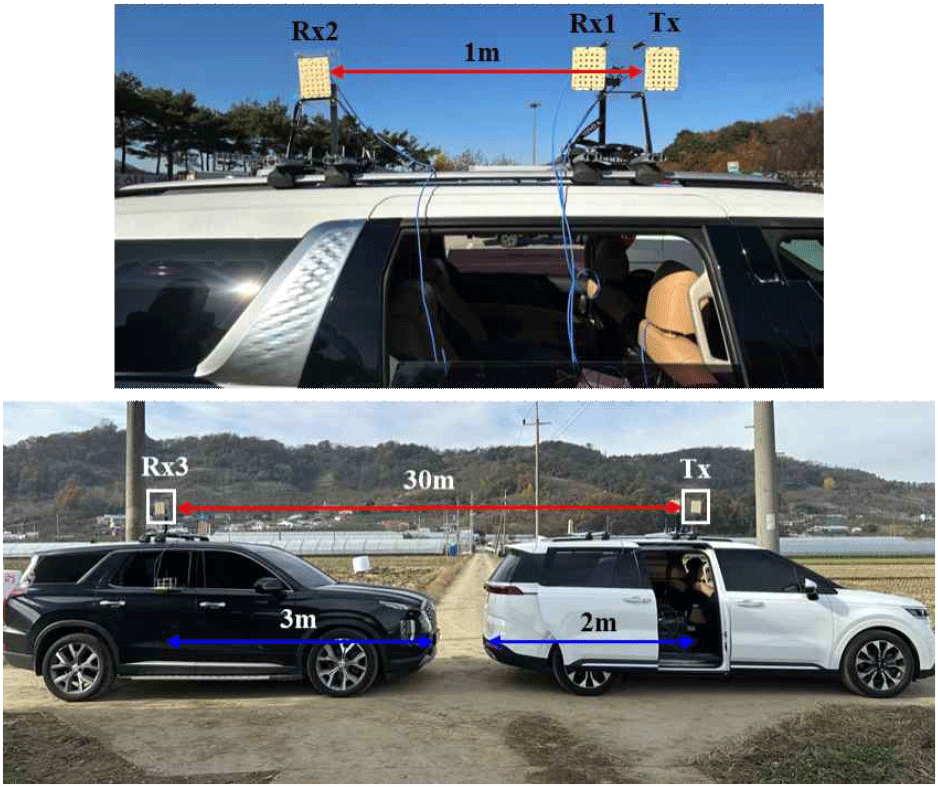
본 논문에서는 물리적으로 완벽히 분리된 구조의 멀티스태틱 SAR 시스템을 구현하여 차량 기반의 지상 실험을 수행하였다. 먼저 단일 송·수신기로 구성된 모노스태틱 모드를 구현하기 위해 Tx와 Rx1을 동일 플랫폼에 탑재하였다. 다음으로 바이스태틱 모드는 두 가지 형태로 구현하였다. 첫 번째는 바이스태틱 1 모드로, Tx와 Rx2가 동일 플랫폼에 탑재되어 있으나 물리적 위치가 1 m 간격으로 분리된 구조로 설정되었다. 두 번째는 바이스태틱 2 모드로, 선행 플랫폼의 Tx에서 송신된 신호를 후행 플랫폼에 탑재된 Rx3이 수신하도록 구성하였다. 두 플랫폼 간의 이격 거리는 약 30 m로 설정하였으며, 플랫폼 간의 물리적 분리를 통해 복잡한 바이스태틱 환경을 구현하였다. 본 논문에서는 바이스태틱 2 모드를 멀티스태틱 모드로 지칭한다.

멀티스태틱 시나리오의 실측 데이터를 확보하기 위해 교량 위 도로에서 하행 방향으로 두 대의 차량을 일정한 간격으로 운행하면서 실험을 수행하였다. 그림 6에 나타낸 바와 같이, 선행 차량 플랫폼에 Tx와 Rx1, Rx2를 탑재하고, 후행 차량 플랫폼에는 Rx3을 탑재하였다. Tx와 Rx3 시스템 간의 동기화는 무선 LO 신호 공유 방식으로 이루어졌으며, 이를 통해 바이스태틱 환경에서의 시간 동기화 문제를 해결하여 정확한 데이터 획득이 가능하도록 구성하였다. 두 차량 플랫폼의 이동 속도를 일정하게 유지하기 위해 25 m의 차간 거리를 유지하는 크루즈 모드를 사용하였으며 차량 길이를 반영한 두 플랫폼 간 최종 이격 거리는 약 30 m가 되도록 설정하였다. 정확한 이격 거리는 수신 데이터에서 거리 정보를 추출하여 보정하였다. 데이터 획득에 사용된 SAR 시스템 사양은 표 3에 나타내었다.

그림 6. | Fig. 6. 차량 기반 멀티스태틱 SAR 실험 운용 환경 | Operational environment for vehicle-based multistatic SAR experiment.

Download Original Figure

표 3. | Table 3. 차량 기반 SAR 시스템 실험 파라미터 | Experimental parameters for vehicle-based SAR system.

Parameter		Values
Center frequency [GHz]		9.9
Bandwidth [MHz]		400
Sampling frequency [MHz]		5
PRF [Hz]		999.5
Platform velocity [m/s]		18.9
Baseline B [m]	Bistatic	1
Baseline B [m]	Multistatic	30

Download Excel Table

그림 7의 1열은 모노스태틱, 바이스태틱, 멀티스태틱 SAR 데이터를 처리한 영상을 보인다. 각 영상에서 각면판 반사기(CR, corner reflector)로부터 반사된 점 표적이 명확히 확인된다. 모노스태틱과 바이스태틱 모드는 안정적으로 영상이 획득되었으나, 그림 7(c) 좌측 영상과 같이 30 m의 기선 거리를 가지는 멀티스태틱 SAR 영상은 데이터의 SNR이 낮아 CR의 반사 신호가 주변 잡음에 의해 일부 가려지는 현상이 확인되었다. 이는 긴 기선 거리를 가지는 멀티스태틱 환경에서 수신 신호 세기 감소로 인한 품질 저하로 해석된다. 또한 멀티스태틱 수신신호 수집 과정에서 기하 왜곡이 발생하므로 추가적인 품질 개선 과정이 요구됨을 시사한다. 본 실험에서는 그림 7의 2열에 나타낸 CR 표적 영역을 대상으로 압축센싱 기법을 적용하여 멀티스태틱 환경에서의 신호 품질과 복원 개선 가능성을 추가적으로 분석하였다.

그림 7. | Fig. 7. 모노/바이/멀티스태틱 SAR 실험 데이터 처리 결과(1열: 전체 영상, 2열: CR 영역) | Data processing results of mono/bi/multistatic SAR experiments (column 1: full image, column 2: CR region).

Download Original Figure

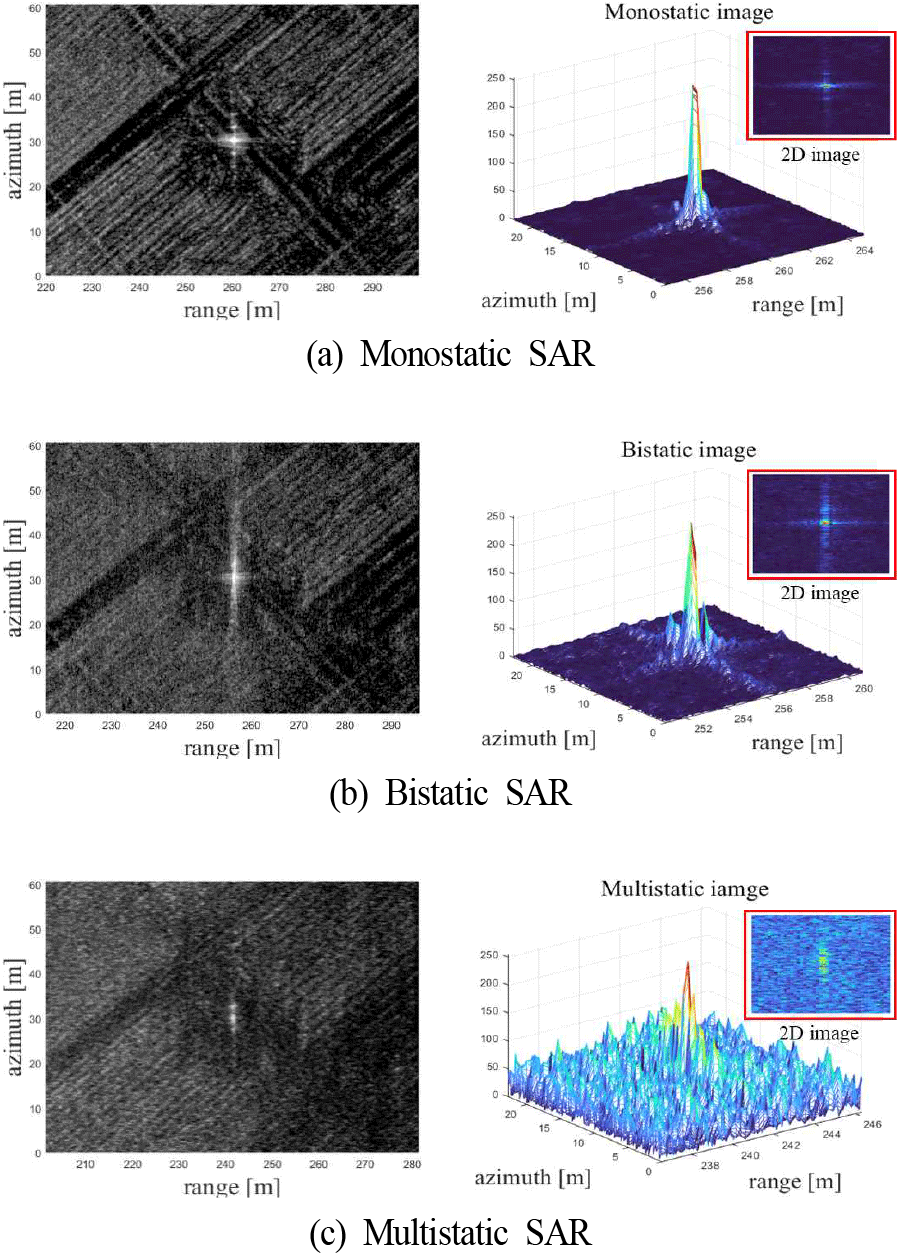
그림 8은 그림 7의 CR 영역 영상에 대해 50 % 압축률을 적용한 BPDN 기반 SMV-CS와 MMV-CS를 적용한 결과를 나타낸다. 그림 8(a), 그림 8(b) 및 그림 8(c)는 각각 모노스태틱, 바이스태틱, 멀티스태틱 데이터를 단독으로 처리한 SMV-CS 결과를 보여준다. 모노스태틱과 바이스태틱 데이터는 CR 반사 신호가 명확히 복원되었으나, 그림 8(c)의 멀티스태틱 데이터는 긴 기선 거리로 인한 SNR 감소로 인해 CR 반사 신호의 복원이 어려움을 확인할 수 있다. 다음으로 그림 8(d)는 모노스태틱과 바이스태틱 데이터를 통합하여 MMV-CS를 적용한 복원 결과를, 그림 8(e)는 모노스태틱과 바이스태틱, 멀티스태틱 데이터를 모두 통합하여 MMV-CS를 적용한 결과를 보인다. MMV-CS 기법은 멀티스태틱 데이터를 포함했음에도 불구하고 복수의 신호를 활용하여 복원 성능을 크게 개선한 모습을 나타낸다. 특히, SNR이 낮은 신호에 대해서도 MMV-CS는 복수의 데이터를 활용하여 더 뛰어난 신호 복원 성능을 제공할 수 있음을 입증한다. 이를 통해 MMV-CS에 포함되는 데이터의 구성에 따라 복원 성능이 달라질 수 있음을 확인할 수 있다.

그림 8. | Fig. 8. 모노/바이/멀티스태틱 SAR 영상의 표적 영역에대한 압축센싱 적용 결과 | Compressive sensing application results for target regions in mono/bi/multistatic SAR images.

Download Original Figure

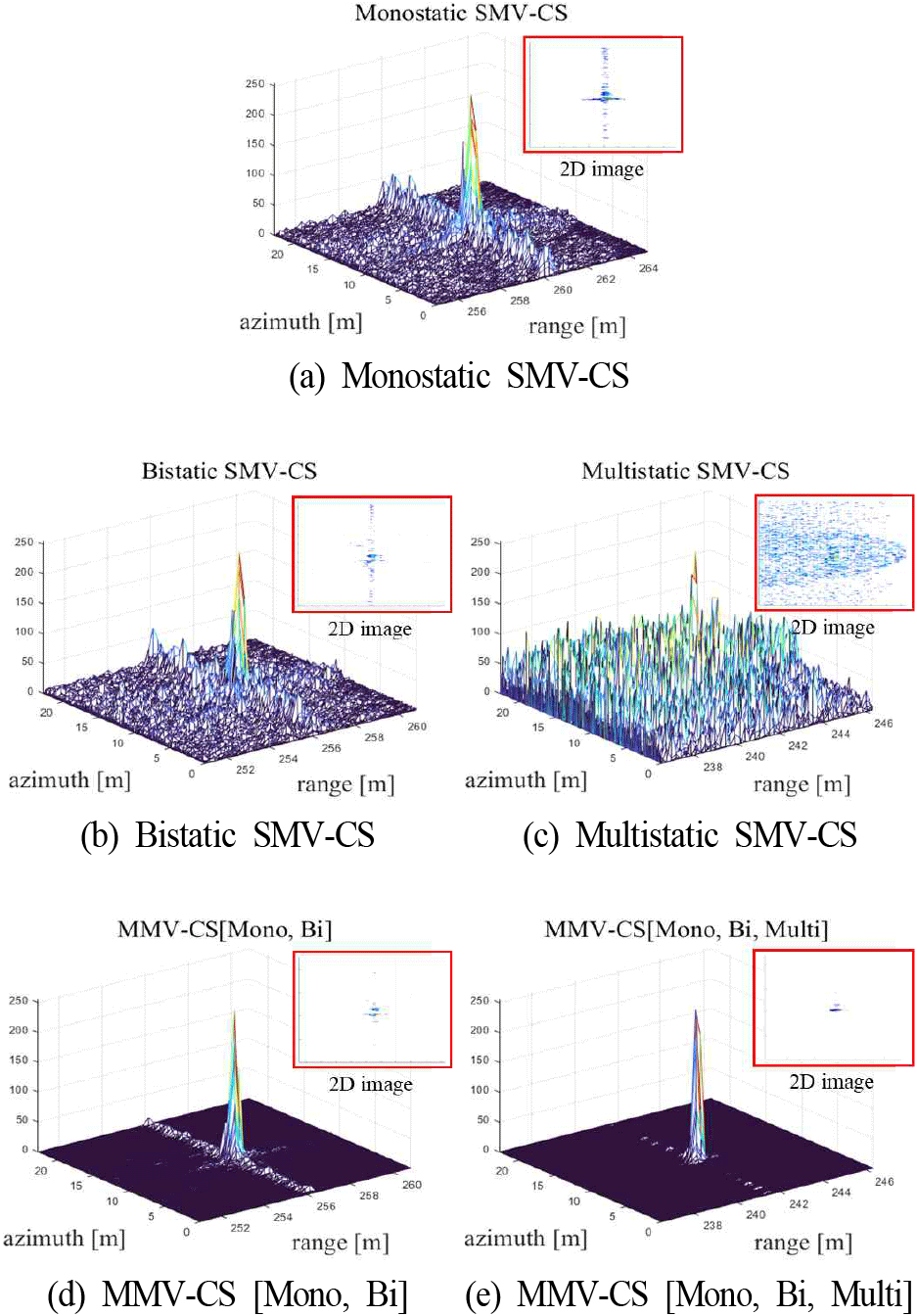
그림 8의 정량적인 복원 성능을 평가하기 위해 표적 영상에 대한 TCR 값을 계산하였으며 측정 결과는 표 4에 제시하였다. 압축센싱 기법을 적용하기 전 초기 영상 품질을 비교하면 모노스태틱 SAR 영상이 가장 우수한 품질을 나타냈으며, 바이스태틱, 멀티스태틱 영상 순으로 품질 저하가 증가하였다. 단일 플랫폼의 데이터를 활용하는 SMV-CS 기법을 적용했을 때, 모노스태틱 SAR에서는 소폭의 성능 향상이 확인된 반면, 바이스태틱과 멀티스태틱 SAR 영상에서는 각각 4 dB, 11 dB의 성능 개선이 이루어졌다. 다음으로 다중 데이터 결합을 위해 바이스태틱 데이터에 모노스태틱 데이터를 추가로 결합하여 MMV-CS 기법을 적용한 결과, TCR 값이 54 dB 이상으로, 멀티스태틱 데이터를 포함하면 64 dB까지 추가적인 성능 향상이 확인되었다. 이는 MMV-CS 기법이 복수의 데이터를 활용하여 신호 복원 성능을 극대화하며, 단일 수신기 기반의 SMV-CS보다 더욱 효과적으로 잡음을 억제할 수 있음을 시사한다. 특히, 초기 멀티스태틱 SAR 데이터는 저품질의 TCR 수준을 보였으나 MMV-CS를 통해 복수의 데이터를 결합하면서 성능이 점진적으로 개선되는 과정을 확인할 수 있다.

표 4. | Table 4. 모노/바이/멀티스태틱 SAR 영상 및 압축센싱 적용 결과에 대한 TCR 성능[dB] | The TCR performance for mono/bi/multistatic SAR images and compressive sensing application results [dB].

Mode	SAR image	SMV-CS	MMV-CS with Mono	MMV-CS with Mono, Bi
Monostatic	32.89	33.4	-	-
Bistatic	25.44	29.08	54.79	-
Multistatic	7.48	18.5	45.54	64.76

Download Excel Table

본 논문에서 수행된 멀티스태틱 SAR 실험에서는 무선 동기화로 인한 신호 손실과 수신신호의 기하 왜곡으로 인해 SAR 영상 정합 품질 개선에 제약이 있었다. 그러나 복수의 데이터를 통합하는 MMV-CS 기법 적용을 통해 보완적인 신호 복원과 품질 개선이 가능함을 확인할 수 있었다. 멀티스태틱 SAR 영상에 MMV-CS를 적용한 결과 TCR 값이 점진적으로 증가하다가 수렴하는 경향을 보였다. 이는 압축센싱 기법을 적용으로 해상도가 개선되면서 식 (14)의 표적 신호 에너지 레벨이 감소하여 나타나는 현상으로 해석된다.

Ⅳ. 결 론

본 연구는 멀티스태틱 SAR 환경에서 압축센싱 기법을 적용하여 신호 복원 성능을 분석하고, 복잡한 SAR 운용 환경에서 영상 품질을 개선하기 위한 방법을 제안하였다. 멀티스태틱 SAR 구조에서 획득된 데이터는 측정 과정의 기하 오차를 완전히 보정하기 어렵고 영상 품질이 충분히 향상되지 않는 한계가 있다. 이러한 한계를 극복하기 위해 복수의 수신신호를 통합적으로 활용하는 MMV-CS 기법을 적용한 결과, 복원 성능을 개선할 수 있었다. 본 연구에서 사용한 데이터는 멀티스태틱 SAR 환경에서 발생하는 요동에 대한 보상이 이루어지지 않은 상태로, 신호 품질이 최적화되지 않은 환경이었다. 이러한 조건에서도 MMV-CS는 복수 신호 간의 상호 정합 효과를 활용하여 바이/멀티스태틱 데이터의 신호 복원 성능을 개선할 가능성을 보여주었다. 본 논문에서는 편의상 BEM 근사 방식을 활용하여 멀티스태틱 SAR 영상을 생성하였는데, 이는 멀티스태틱 SAR 영상의 품질 저하와 모노스태틱 SAR 영상과의 정합 과정에서 오차를 유발할 수 있다. 따라서 본 논문의 MMV-CS 기법의 성능 개선에 한계가 존재하며 향후 연구에서는 BPA(back-projection algorithm) 정합을 수행하여 추가적인 성능 개선을 기대하고자 한다.

한편, MMV-CS 기법을 적용할 때 몇 가지 제한점이 존재할 수 있다. 본 연구에서는 SAR 영상 간의 완전한 기하 정합을 전제로 하였으나, 실제 환경에서는 기하 정합의 정확도가 낮을 경우 MMV-CS 기법을 적용하더라도 복원 성능 저하가 발생할 수 있다. 또한, MMV-CS 기법은 공통된 산재 표적을 추출하는 특성을 가지므로, 관측 각도의 차이로 인해 특정 플랫폼에서 표적이 명확하게 나타나지 않을 경우 일부 표적이 복원 과정에서 손실될 수 있다. 이러한 문제를 보완하기 위해 향후 연구에서는 공통되지 않은 강한 산재 표적을 선택적으로 포함할 수 있는 알고리즘을 개발하여 다양한 관측 각도의 정보를 효과적으로 융합하고, 표적 식별 성능을 보다 향상시킬 필요가 있다.

결론적으로, 멀티스태틱 SAR 데이터의 신호 품질 저하를 극복하기 위해서는 영상 정합 알고리즘 개선과 MMV-CS 기법의 최적화 연구가 지속될 필요가 있으며 이를 통해, 복잡한 운용 환경에서도 높은 품질의 영상을 안정적으로 획득할 수 있을 것으로 기대된다. 본 연구의 결과는 향후 군집 위성과 같은 다중 플랫폼 SAR 시스템에서 복수의 멀티스태틱 SAR 데이터를 효과적으로 통합하는 방향을 제시하며, 이를 통해 SAR 영상 복원의 신뢰성과 품질을 향상시키는 데 기여할 것으로 기대된다.

Acknowledgements

이 논문은 2024년 정부(방위산업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UI5111J5-911256202).

References

[1].

M. Soumekh, Synthetic Aperture Radar Signal Processing, New York, NY, John Wiley & Sons, 1999.

[2].

E. D. Jansing, Introduction to Synthetic Aperture Radar: Concepts and Practice, New York, NY, McGraw-Hill Education, 2021.

[3].

B. H. Ryu, B. S. Kang, M. J. Lee, and K. T. Kim, "Bistatic synthetic aperture radar imaging using a monostatic equivalent model," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 9, pp. 693-700, Sep. 2018.

[4].

D. L. Donoho, "Compressed sensing," IEEE Transactions on Information Theory, vol. 52, no. 4, pp. 1289-1306, Apr. 2006.

[5].

A. De Maio, Y. C. Eldar, and A. M. Haimovich, Compressed Sensing in Radar Signal Processing, Cambridge, Cambridge University Press, 2019.

[6].

S. Park, H. Choi, W. B. Lee, C. Kim, J. Kang, and H. N. Lee, "Recent analysis results on multiple measurement vectors model," in The Institute of Electronics and Information Engineers Conference, Busan, Jun. 2017, pp. 771-773.

[7].

J. Park, T. W. Ban, and B. C. Jung, "Sparse signal recovery with parallel orthogonal matching pursuit for multiple measurement vectors," Journal of the Korea Institute of Information and Communication Engineering, vol. 17, no. 10, pp. 2252-2258, Oct. 2013.

[8].

M. Martorella, D. Cataldo, and S. Brisken, "Bistatically equivalent monostatic approximation for bistatic ISAR," in 2013 IEEE Radar Conference(RadarCon13), Ottawa, Apr. 2013, p. 6586074.

[9].

K. M. Lee, I. S. Lee, H. S. Shin, J. W. Ok, J. H. Youn, and E. N. You, et al., "Signal modeling for bistatic FMCW radar asynchronization and its effect on ISAR images," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 3, pp. 218-231, Mar. 2023.

[10].

D. H. Shin, D. H. Jung, D. C. Kim, J. W. Ham, and S. O. Park, "A distributed FMCW radar system based on fiber-optic links for small drone detection," IEEE Transactions on Instrumentation and Measurement, vol. 66, no. 2, pp. 340-347, Feb. 2017.

[11].

M. Ash, M. Ritchie, K. Chetty, and P. V. Brennan, "A new multistatic FMCW radar architecture by over-the-air deramping," IEEE Sensors Journal, vol. 15, no. 12, pp. 7045-7053, Dec. 2015.

[12].

J. Hwang, J. Jung, D. Kim, J. W. Kim, H. S. Shin, and J. W. Ok, "Correction of continuous motion effects for airborne FMCW-SAR system," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 28, no. 5, pp. 410-418, May 2017.

[13].

H. N. Lee, S. J. Park, and S. C. Park, "Introduction to compressive sensing," The journal of Korea Institute of Electronics Engineers, vol. 38, no. 1, pp. 19-30, Jan. 2011.

[14].

A. Majumdar, Compressed Sensing for Engineers, Boca Raton, FL, CRC Press, 2018.

[15].

Y. Lim, S. Nam, "Target-to-clutter ratio enhancement of images in through-the-wall radar using a radiation pattern-based delayed-sum algorithm," Journal of Electromagnetic Engineering and Science, vol. 14, no. 4, pp. 405-410, Dec. 2014.