덕트 현상과 해수면을 고려한 DMFT 포물형 방정식 기반 전파 특성 분석

I. 서 론

해상에서의 전자파 전파 경로는 대기 굴절과 해수면 반사의 영향을 받아 복잡한 양상을 보인다. 특히 대기 굴절의 한 형태인 덕트 현상은 해상에서 빈번하게 발생하는데^[1], 전자파가 도파관에 갇힌 것처럼 진행하게 만들어 거친 해수면에 의한 영향을 심화시킨다. 따라서, 해상 환경에서의 레이다 운용을 위해서는 이러한 복합적인 전파 환경을 고려한 전파 분석이 필요하다.

기존의 해상 환경 전파 특성 분석 연구에서는 해수면의 유전율과 파고를 고려하지 않아, 해수면 반사 및 손실이 정밀하게 반영되지 않는 한계가 있었다. 또한, 대부분의 연구가 실제 기상 데이터 대신 삼선형 굴절률 모델이나 증발 덕트 모델을 이용하여 덕트 현상을 반영하였으나^[2],[3], 보다 정확한 경로 손실 예측을 위해서는 실제 기상 데이터를 활용할 필요가 있다. 이에 본 연구에서는 실제 기상 데이터와 함께 해수면의 유전율 및 파고를 반영하여 전파 특성을 분석하고자 한다.

본 연구에서는 해상 레이다 운용시 대기 굴절률과 파고가 경로 손실에 미치는 영향을 예측하기 위해 DMFT PE (discrete mixed Fourier transform parabolic equation)기법을 활용하였다. 또한, 보다 현실적인 분석을 위해 실제 대기환경과 해수면 조건을 반영하였다. 이를 통해 경로 손실을 분석하고, 실제 수신 전력 측정값과 비교하여 분석의 유효성을 검증하였다. 파고는 국내 해안의 파도 스펙트럼과 유사한 JONSWAP(joint north sea wave project) 스펙트럼을 적용하였다^[4]. 분석 결과, 파고로 인해 자유공간에서는 평균 1.6 dB, 덕트 현상이 발생한 경우 평균 2.5 dB의 추가적인 경로 손실이 발생하였다. 본 연구를 통해 해상 환경을 고려한 보다 정밀한 경로 손실 예측이 가능할 것으로 기대된다.

II. 본 론

DMFT PE의 구현을 위해 만족해야할 지표면에서의 경계조건은 식 (1)과 같이 정의된다.

수식에서 u는 전자기장의 세기, x는 고도, k₀은 자유공간에서의 파수, 그리고 εr은 해수면의 유전율을 의미한다. 식(1)의 경계조건을 만족하는 전자기장의 세기 u는 식 (2)와 같이 계산할 수 있다^[5].

와 dz는 각각 거리, 거리방향 격자 크기를, m은 수정 굴절률을 의미한다.

파고는 staircase approximation을 통해 고려하였다^[6]. 각 수평방향의 격자(dz) 위치에 따른 파도의 높이 h(z)를 고려하고, staircase approximation 기법을 적용하면 식 (3)과 같은 경계조건을 만족하게 된다.

따라서, 식 (2)를 통해 거리 방향으로의 다음 격자 위치의 전자기장 u(z + dz,ndx)을 구할 때 h(z)보다 낮은 높이에 대한 전자기장 세기를 0으로 변경한다.

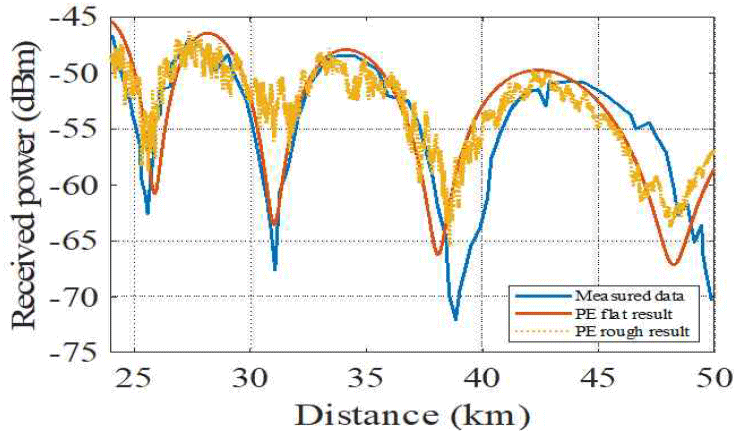
DMFT PE 기법의 검증을 위해 선행연구에서 수행된 해상 환경에서의 수신 전력 측정값과의 비교를 수행하였다^[7]. 참고논문의 측정환경을 고려하여 DMFT PE의 분석 결과와 측정값을 비교해 그림 1에 나타내었다.

그림 1. | Fig. 1. 수신 전력 비교 | Comparison of received power.

Download Original Figure

PE flat result, PE rough result는 각각 파도를 고려하지 않았을 때와 고려했을 때를 나타낸다. 파도를 고려했을 때의 결과가 더욱 경로 손실이 불규칙하게 변동하는 것을 확인할 수 있다. 측정값과 비교했을 때 거의 유사한 경향을 가지는 것으로 보이며, 일부 불일치는 측정 날짜와 위치에서의 정확한 굴절률을 반영하지 못하여 발생하는 것으로 판단된다.

대기와 파고를 고려한 해상 환경에서의 전파 특성 분석을 위해서 흑산도의 실제 기상 정보를 이용하여 대기 굴절률을 계산하였다. 먼저, 기압, 기온, 수증기압을 이용해 굴절도 N을 계산하고 지구 곡률이 반영된 수정 굴절률 m을 다음 수식들을 이용해 계산할 수 있다.

P: 기압(hPa), T: 절대온도(K), e: 수증기압(hPa)

x: 고도(km)

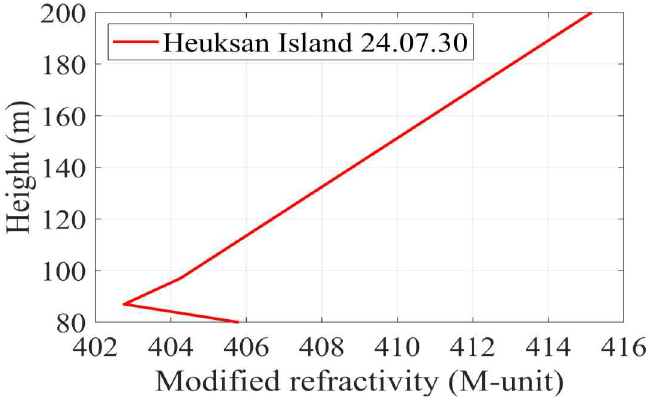
그림 2에서는 본 연구에서 사용한 2024년 7월 30일 흑산도의 수정 굴절도 분포를 나타내었다. 해당 일자는 일부 고도에서 기울기(∇M)가 음수로, 덕트가 발생한 환경을 나타낸다.

그림 2. | Fig. 2. 흑산도의 수정 굴절도 | Modified refractivity of Heuksan Island.

Download Original Figure

다음으로, 해수면의 유전율은 2 GHz에서 Debye 모델을 활용하여 계산한 결과인 71.2+j49.6을 적용하였다^[8]. 파고는 JONSWAP 스펙트럼을 역푸리에 변환을 적용하여 사용하였다^[9]. 전파 특성 분석은 DMFT PE를 이용하여 수행되었으며 분석에 사용된 설정은 표 1과 같다.

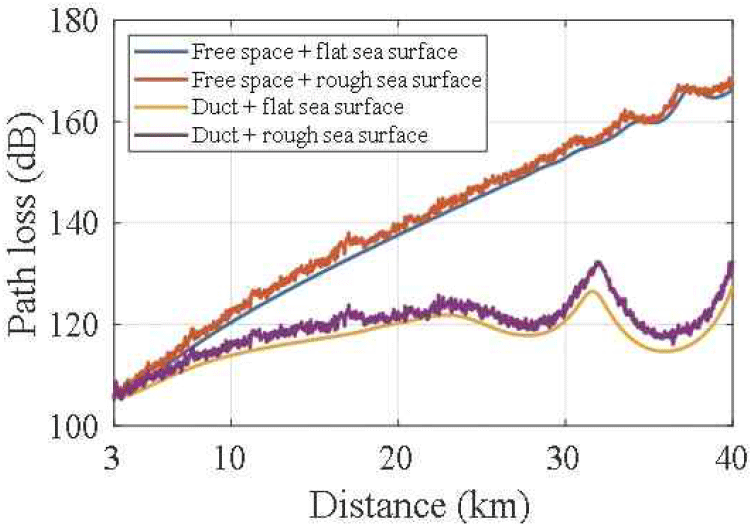
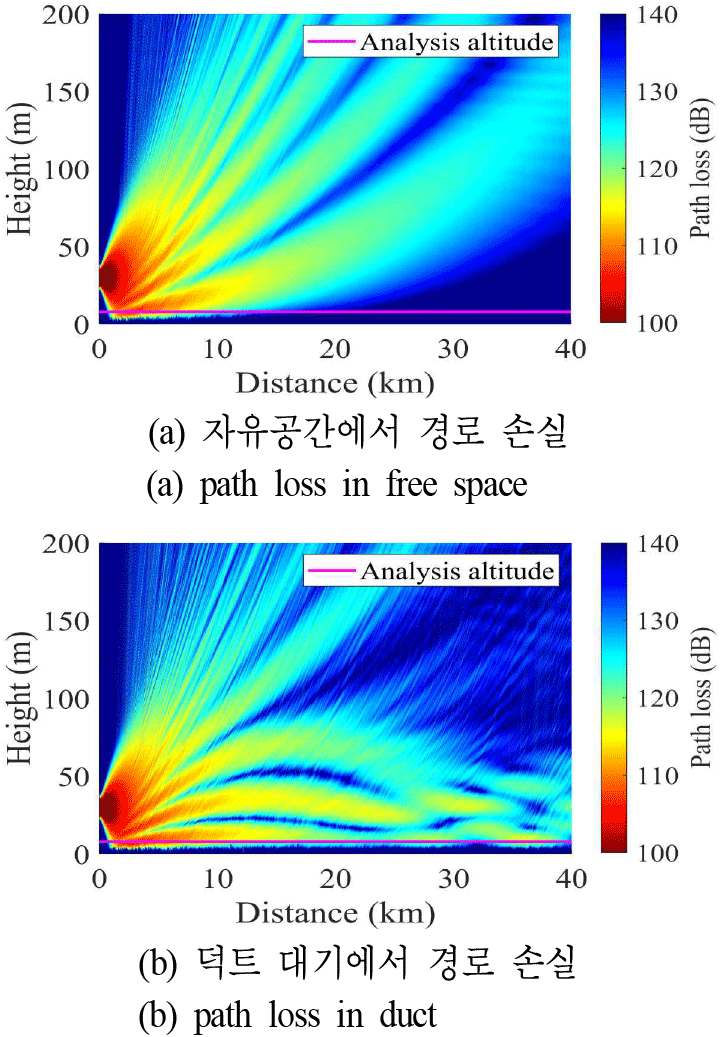
덕트 현상은 그림 2의 대기굴절률을 고려하였다. 그림 3에는 DMFT PE의 분석 결과인 경로 손실 분포를 나타내었다. 덕트 현상이 발생한 경우, 해수면과 인접한 고도에서 해수면에 의해 반사되는 성분이 증가하는 경향을 확인할 수 있다. 그림 4는 수신 안테나 또는 레이다가 장착되는 선박의 마스트 높이를 고려하여 그림 3의 고도 8 m에서 경로 손실 결과를 분석하였다^[10].

그림 3. | Fig. 3. 경로 손실 분석 결과 | Path loss analysis result.

Download Original Figure

그림 4. | Fig. 4. 환경별 거리에 따른 경로 손실 분석결과 | Path loss result in different environments.

Download Original Figure

표 1의 분석 조건에서는, 4 km 이내의 거리에서 자유공간과 덕트 대기에서의 경로 손실 차이는 3 dB 이하로 작고, 전파 거리가 증가함에 따라 경로 손실 차이는 점진적으로 증가하는 것을 확인할 수 있다. 자유공간과 덕트 대기에서의 최대 경로 손실 차이는 약 48 dB이다. 분석결과 덕트 현상이 발생했을 때 거친 해수면에 의한 손실은 자유공간일 때보다 크게 발생했다. 파고 고려 유무에 따른 경로 손실 차이의 평균과 최댓값은 자유공간에서 각각 1.6 dB, 5.2 dB이고, 덕트 대기에서는 각각 2.5 dB, 6.8 dB로 덕트 현상이 발생했을 때 거친 해수면에 의한 손실이 증가하게 되었다. 덕트 현상이 발생하면 전파는 도파관에 갇힌 것처럼 진행하며 굴절과 반사가 반복되어 전파 경로가 복잡해진다. 이러한 현상으로 그림 4에서 덕트 현상이 발생한 경우 약 28 km와 36 km에서 경로 손실이 급격히 감소한 구간이 나타난다.

III. 결 론

본 연구에서는 해양환경에서 덕트 현상과 파고가 전파 특성에 미치는 영향을 예측하기 위해 실제 기상 데이터를 기반으로 계산한 대기 굴절률와 파고를 고려하였고, DMFT PE(discrete mixed Fourier transform parabolic equation)를 활용하여 전파 특성을 분석했다. 분석한 환경에 대해서 파고를 고려했을 때 자유공간에서 평균 1.6 dB, 덕트 현상이 발생했을 때 평균 2.5 dB의 경로 손실이 증가하여 덕트 현상이 발생했을 때 파고에 의한 손실이 더 컸다. 본 연구에서 제시한 방법을 통해 레이다 운용 시 해상환경을 고려한 경로 손실을 예측할 수 있을 것으로 기대된다.