대기 굴절률 및 실제 지형을 고려한 포물형 방정식 기법 기반 레이다 탐지거리 분석

I. 서 론

레이다 탐지거리를 정확하게 예측하는 것은 레이다 시스템 설계 및 운용에 있어 핵심적인 요소이다. 레이다 시스템은 장비 자체의 물리적 요소뿐만 아니라 비균질한 대기 환경, 지구 곡률, 그리고 복잡한 지형 등 다양한 환경적 요인들의 영향을 받는다. 특히, 레이다의 운용 거리가 증가함에 따라 비균질한 대기 환경에 의한 전파 굴절의 영향이 증가하며, 이는 오탐지나 미탐지 등의 현상을 유발하여 레이다 탐지거리에 영향을 미친다^[1]. 또한, 한반도 서해안과 같이 복잡한 지형을 가진 환경에서는 대기 환경과 지형에 따른 레이다 성능 편차가 크게 발생할 수 있어, 이를 정확히 고려한 성능 예측이 필수적이다.

포물형 방정식 기법은 비균질한 매질에서의 전파 해석에 있어 계산 효율성과 정확성을 동시에 제공하여, 복잡한 대기 환경과 지형을 고려해야 하는 레이다 전파 해석에 적합하다^[2],[3]. 그러나, 기존의 포물형 방정식 기법 기반 연구들은 주로 거리-고도로 구성된 2차원 평면에서의 전파 특성 분석에 국한되어 있었다. 또한, 방위각 단위로 분석을 확장한 연구는 고도 오차 분석에 집중하여, 실제 레이다 운용 환경을 종합적으로 고려한 탐지거리 분석은 제한적이었다^[3].

본 논문에서는 한반도 서해안의 DEM(digital elevation model) 데이터를 활용하여 실제 지형을 반영하고, 지구 곡률을 고려한 수정 대기 굴절률이 적용된 포물형 방정식 기법 기반의 레이다 탐지거리 분석 방법을 제안한다. 제안된 방법은 경계조건을 PEC(perfect electric conductor)로 해석하는 split step fourier transform 기반의 포물형 방정식 기법(SSPE)을 방위각 단위로 순차적으로 수행하여 자유 공간과 덕트 현상 발생 시의 레이다 탐지거리를 분석한다.

II. 본 론

비균질한 대기 환경은 레이다 전파에 직접적인 영향을 미치는 요소이다. 대기의 비균질함은 대기 굴절률로 표현되며 전자파는 대기 굴절률의 변화에 따라 굴절된다. 대기 굴절률 n과 굴절 계수 N은 식 (1)과 기압, 기온, 수증기압으로 계산된다^[4].

P: 기압[hpa], T: 기온[°K], e: 수증기압[hpa]

실제 레이다 운용 환경에서는 지구 곡률의 영향도 고려해야 하므로, 이를 고려한 수정 굴절률 m과 수정 굴절 계수 M을 사용한다.

a_e: 지구반지름6378[km], x: 고도[km]

수정 굴절 계수 M의 고도에 따른 변화량 ∇M = dM/dx(M unit/km)의 값에 따라서 굴절 현상이 구분된다. 일반 굴절 (78 ≤ ∇M ≤ 157)현상이 발생하는 경우 지구 곡률과 같은 곡률로 전파가 굴절된다. 아굴절(∇M > 157)이 발생하는 경우 전파가 지구 곡률보다 작게 굴절되어 위를 향하여 레이다 탐지 거리가 감소할 수 있으며, 초굴절(0 > ∇M > 78) 및 덕트(∇M > 0) 현상이 발생하는 경우 지구 곡률보다 크게 굴절되어 전파가 지면을 향하여 탐지거리가 증가할 수 있다. 특히 덕트 층이 표면에 발생하는 표면 덕트 현상 발생 시 전파가 덕트 층에 갇혀 진행하여 레이다 탐지거리에 크게 영향을 미쳐 이에 대한 분석이 필요하다.

대기 굴절 현상과 함께 지형 조건 또한 레이다 성능에 영향을 미친다. 지형은 전파의 회절과 반사를 유발하며, 특히 대기 굴절 현상과 결합되어 동일한 운용 환경에서도 서로 다른 탐지 성능을 보일 수 있다. 따라서, 정확한 탐지거리 분석을 위해서는 정밀한 실제 지형을 반영하여야 한다. 이에 본 논문에서는 NASA에서 제공하는 30 m 해상도 DEM 데이터를 활용하여 그림 1과 같이 한반도 서해안 태안 지역의 실제 지형을 반영한 분석을 수행하였다.

포물형 방정식 기법은 식 (4)의 편미분 방정식인 Helmholtz’s equation의 해를 구하는 방식에 따라 구분된다. 그 중 경계면을 PEC로 해석하는 SSPE 기법은 식(5)와 같이 거리, 고도 별 step 단위로 전기장 세기를 계산한다. 수직 방향 변수는 로 고도를 의미하며 수평 방향 변수는 로 거리이다. F는 푸리에 변환을 나타내고, x와 k_x는 푸리에 변환 쌍이다. k_x = k₀sinθ이며 θ는 고도 각이다. 각 거리, 고도 step 별로 전기장의 세기를 계산하는 과정에서 수정 대기 굴절률을 반영하여 지구 곡률과 대기 굴절률을 고려하고, 불규칙한 지형 경계를 반영할 수 있다^[5]. 본 논문에서는 DEM 데이터의 해상도와 계산 정확도를 고려하여 거리 step Δz는 30 m, 고도 step Δx는 0.1 m로 설정하였다.

u : 전기장[V/m], m : 수정대기굴절률, k₀ : 자유공간파수[rad/m]

식 (5)를 통해 계산된 2차원 거리-고도 별 전기장의 세기와 다음의 식 (6)~식 (8)을 통해 경로 손실을 계산할 수 있다. PL(path loss)는 경로 손실, FSPL(free space path loss)는 자유 공간 경로 손실, PF(propagation factor)는 전파 계수이다.

레이다로부터 방사된 전자파가 특정 레이다 단면적을 가지는 표적에 반사되어 다시 돌아오는 레이다 수신 전력은 다음과 같이 구할 수 있다^[6].

P_t: 송신전력 [W]

G_r: 수신안테나이득

G_t: 송신안테나이득

σ: 표적레이다단면적[m²]

안테나 이득은 송수신 안테나가 동일하며 같은 경로를 통해 도달하였다고 가정하여, 식 (6)을 통해 계산한 경로 손실에 이를 반영하면 식 (10)과 같이 dB scale에서 레이다 수신 전력을 구할 수 있다.

그림 1의 서해안 태안 부근 분석 영역에서 레이다 탐지거리를 구하기 위해, 레이다 사이트를 기준으로 방위각을 0.1도씩 분할하여 각 방위각 별로 지형 데이터를 추출하였다. 이후 추출한 지형 데이터를 경계면으로 하는 SSPE기법을 통해 전기장을 구하고, 식 (6)~식 (10)을 통해 2차원 레이다 수신 전력을 계산하였다. 계산된 각 방위각 별 수신 전력값을 분석 고도에 따라 추출한 후 레이다가 표적을 탐지할 수 있는 최소 수신 전력인 sensitivity와 비교하여 레이다 탐지거리를 구하였다. 표 1과 같은 조건에서 정서 방향을 기준으로 방위각 −45도부터 45도까지 0.1도 간격으로 분석하여 일반 굴절과 표면 덕트 현상 발생 시 레이다 수신전력과 탐지거리를 비교하였다.

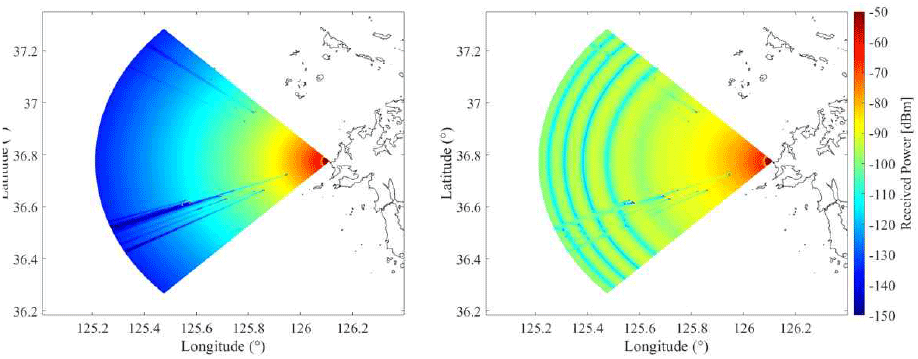
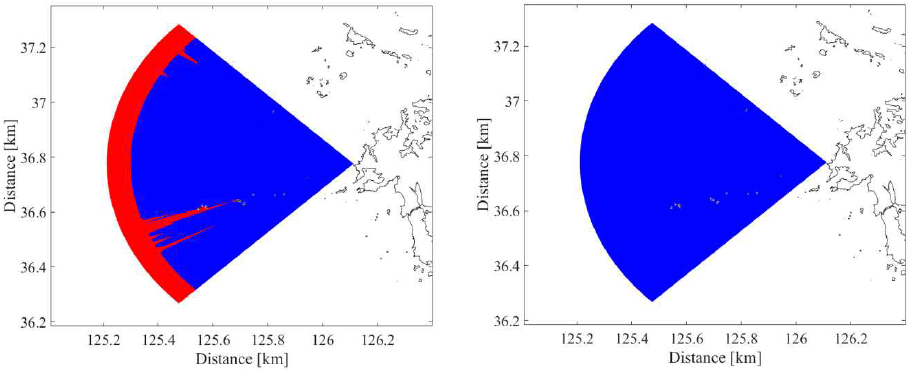
그림 2는 레이다 수신 전력을 나타낸 것이다. 그림 2의 좌측은 표 1의 조건에서 일반 굴절 발생 시 레이다 수신 전력이고, 우측은 표면 덕트 발생 시 레이다 수신 전력이다. 일반 굴절 발생 시, 정서방향 기준으로 남쪽의 위도 36.62°~36.73°, 경도 125.57°~125.95° 영역, 북쪽의 위도 36.73°~36.92°, 경도 125.75°~125.82° 부근에 존재하는 섬 지형에 의한 NLOS(none line of sight) 영역에서 주변 LOS(line of sight) 영역에 비해 크게 낮은 수신 전력 값을 가진다. 표면 덕트 발생 시, 전파가 지면으로 굴절되어 덕트 층에 갇혀 진행하므로 동일한 거리에서 일반 굴절 대비 높은 수신 전력값을 보였으며, 섬 지형에 의한 NLOS 영역에서도 주변부와 비슷한 수신 전력 값을 보였다. 레이다 수신 전력과 sensitivity (−130 dBm)를 비교하여 탐지거리를 구한 결과는 그림 3과 같다. 그림 3의 빨간색 영역은 레이다 수신 전력이 sensitivity보다 낮아 탐지가 불가능한 영역이고 파란색 영역은 sensitivity보다 높아 탐지가 가능한 영역이다. 일반 굴절 발생 시에는 80 km 운용 환경에서 약 70 km 부근과 섬 지형에 의한 NLOS 영역에서 탐지가 불가능한 것으로 분석되었다. 탐지 불가능 NLOS 영역은 정서방향 기준으로 남쪽으로는 약 위도 36.4°~36.9°, 경도 125.4°~125.7° 부근이며, 북쪽으로는 약 위도 37.1°~37.2°, 경도 125.4°~125.5°이다. 반면, 표면 덕트 발생 시에는 전파가 덕트층을 따라 전파되어 전 영역에서 탐지가 가능한 것으로 분석되었다. 이러한 결과는 레이다 탐지거리 분석에 있어 대기 굴절률과 지형이 모두 고려되어야 함을 보여준다.

III. 결 론

본 논문에서는 SSPE 기법을 활용하여 대기 굴절률과 실제 지형을 고려한 레이다 탐지거리 분석을 수행하였다. NASA에서 제공하는 30 m 해상도 DEM 데이터를 통해 한반도 서해안 태안 부근의 지형을 반영하였으며, 이를 방위각 단위로 분할하고 순차적으로 SSPE 기법에 적용하여 대기 굴절률과 지형을 고려한 레이다 탐지거리를 분석하였다. 분석 결과, 일반 굴절 조건에서는 탐지가 불가능한 영역이 표면 덕트 조건에서는 탐지가 가능한 것으로 나타났다. 이를 통해 동일한 레이다 운용 환경에서도 대기 굴절 현상에 따라 탐지거리가 크게 달라짐을 확인할 수 있다. 따라서 실제 레이다 시스템의 설계 및 운용을 위해서는 지형과 대기 굴절률을 모두 고려한 종합적인 성능 분석이 필수적이며, 본 논문에서 제안한 분석 방법이 유용하게 활용될 수 있을 것으로 기대된다.