I. 서 론
수신 신호에 대한 사전 정보 없이 신호의 변조방식을 자동으로 분류하는 기술을 자동 변조 분류(AMC, automatic modulation classification)라 하며, 단순한 변조방식 분류에 더해 신호의 대역폭, 심볼율, 채널 부호화 방식 등 변조 파라미터까지 추정하는 것을 보통 자동 변조 식별(AMR, automatic modulation recognition)이라 하여 구별한다. AMC 기술은 전자전, 전파 감시, 위협 신호 분석 등을 수행하는 군용 환경에서 처음으로 도입되었지만, 사용할 수 있는 스펙트럼이 점점 줄어들고 있는 통신 환경에서 스펙트럼 효율을 향상시키려는 인지 무선통신(cognitive ratio), 적응변조(adaptive modulation and coding) 시스템 등에서도 중요한 역할을 하고 있다[1]~[3].
사람이 스펙트럼 모양이나 스펙트럼의 시간적인 변화(즉 스펙트로그램)를 눈으로 보고 확인하던 수동 변조 분류에 이어 컴퓨터에 의해 자동으로 변조방식을 분류하는 방식은 크게 세 단계로 구분할 수 있다. 먼저 고전적인 방법으로 신호를 특징짓는 여러 특징변수(feature)를 추출하여 가능도를 기반(likelihood based)으로 하거나 특징변수를 기반(feature based)으로 하여 분류하는 방법이 있다[4],[5]. 이 방법들은 계산량이 많고 과표본화율, 특징변수들을 추출하는데 사용되는 신호의 길이 등의 영향을 크게 받는다.
다음 단계로 먼저 변조 신호에서 특징변수들을 추출한 다음 신경망(neural network)의 심층학습을 통해 분류하는 방법이 제안되었다[6],[7]. 마지막으로 기저대역 등가신호로 변환된 수신 신호를 직접 또는 FFT(fast Fourier transform) 같은 간단한 전처리 후 신경망에 직접 입력하는 방법이다. 이 방법은 특징변수들을 입력하는 방법에 비해 더 나은 분류 성능을 나타내는 것으로 확인되었으며[7],[8], CNN (convolutional neural network), LSTM(long short-term memory), GRU(gated recurrent unit) 구조를 기반으로 많은 학습 방법과 신경망이 제시되고 있다[9].
지금까지 수많은 자동 변조 분류 방법이 제시되었지만 대부분의 변조 방법이 디지털 변조이고 아날로그 변조는 고려하지 않거나 또는 일부의 변조 신호만 포함되어 있다[9]. 이 논문에서는 아날로그 변조 신호, 즉 진폭 변조(AM, amplitude modulation)와 주파수 변조(FM, frequency modulation) 신호의 분류에 중점을 두고자 한다. AM 신호로는 양측파대(DSB, double sideband)와 상측파대(USB, upper sideband), 하측파대(LSB, lower sideband) 각각에 대해 반송파 억압(SC, suppressed carrier)과 반송파 삽입(WC, with carrier)인 경우를 고려하여 모두 6가지 유형의 신호를 고려한다.
제시한 분류기는 CNN을 기반으로 완전연결망(fully connected network)을 출력부에 연결한 구조이다. CNN 구조를 선택한 이유는 변조 신호를 분류하는 데는 필터링과 유사한 역할을 하는 CNN이 비교적 복잡하지 않으면서도 시간적 변화의 상관성이 있는 데이터에 효과적인 LSTM이나 복잡한 VGG(visual geometry group), ResNet (residual network)에 비해 더 나은 성능을 나타내는 것으로 확인되었기 때문이다[7].
이 논문에서는 분류기의 입력 형태로 스펙트럼의 중심이 0 Hz 부근(주파수 옵셋이 발생하므로 정확이 0 Hz가 아닐 수 있음)에 위치하는 기저대역 복소 등가신호의 동위상 및 직교위상(IQ, inphase and quadrature phase) 성분, 크기 및 위상(MP, magnitude and phase), 주파수 영역 진폭 및 위상(AP, amplitude and phase) 성분, 스펙트로그램(SG, spectrogram) 등 4가지를 고려한다. 또한 스펙트럼의 중심주파수가 0 Hz로부터 편이가 발생하는 경우도 고려하여 분류기를 설계한다. 이 논문에서는 저자의 이전 논문[10]에서 생성한 변조 신호를 사용하여 분류 성능을 더 향상시키는 신경망 구조를 제시하고 입력 형태를 두 가지 더 추가하여 비교 분석하며 또 변조 신호의 스펙트럼 편이(shift)를 고려한다.
II. 신호 모델
이 논문에서 분류하고자 하는 신호는 신호에 대한 정보를 전혀 모르는 상태에서 신호의 스펙트럼만 측정한 후 수동으로 기저대역으로 옮겨진 신호라 가정한다. 이때 신호의 반송파 유무를 알 수 없으므로 스펙트럼의 중앙을 0 Hz에 위치시키게 된다. 한편 진폭변조 신호 중에서 단측파대(SSB, single sideband) 변조 신호의 경우 정보신호인 음성 신호가 대부분 저주파 대역에 집중되어 있기 때문에 기저대역 신호의 스펙트럼은 중심주파수에 대해 비대칭이고 또 신호대역의 구분이 명확하지 않다. 따라서 분류하고자 하는 신호는 대역 중심으로부터 표본화 주파수 대비 최대 ±20 %까지 편이되어 있다고 가정한다.
실제 상황에서 아날로그 변조 신호만 수신되는 것이 아니므로 이 논문에서는 아날로그 변조 신호 7가지 외에[11]에서 공개한 데이터 세트 RadioML2018.01A에 포함된 19가지의 디지털 변조 신호를 신경망 학습 시에 사용한다.
데이터 세트 RadioML2018.01A에는 고려하고자 하는 진폭변조 신호 중에서 일부가 포함되어 있지 않으므로 참고문헌 [11]과 유사한 환경을 고려하여 진폭변조 신호를 모두 생성하였다[10]. 변조하는 정보신호로는 Youtube에서 취득한 음성 및 음악 신호를 사용하였다. 먼저 통과대역 변조 신호를 생성한 후, 중심주파수를 0 Hz로 내리는 디지털 하향 변환(DDC, digital down conversion)과 저역 필터링을 하고 최종적으로 내림표본화(down-sampling)를 하여 표본율(sample rate)을 감축한다. 이 기저대역 신호열(sequence)은 식 (1)과 같이 나타낼 수 있다.
여기서 mI,mQ,는 각각 정보신호의 I,(inphase) 및 Q (quadrature phase) 성분을 나타내고, Ts,는 표본 간격, ΔF는 주파수 옵셋, ϕ는 시변 위상, ϕ0는 초기 위상을 나타낸다. 또 Ac는 반송파의 진폭을 나타내고(반송파 억압 변조인 경우는 Ac = 0), nI + jnQ 는 복소 가우스(Gauss) 잡음을 나타낸다.
스펙트럼의 중심주파수 편이는 생성 시에는 0으로 놓고 학습 시에 반영한다. 학습에 사용되는 신호열은 식 (2)와 같이 얻을 수 있다.
여기서 fdev는 표본율에 대해 정규화한 스펙트럼 편이를 나타내며 [−0.1 0.1] 사이에서 균일한 분포를 가진 불규칙 변수이다. 이것은 표본율의 ±20 % 범위까지 스펙트럼 편이를 고려함을 의미한다.
이 논문에서는 시간 영역 신호인 IQ와 MP, 주파수 영역 신호인 AP와 SG 등 4가지 형태의 신경망 입력을 고려한다. IQ 신호는 정규화시킨 신호열 (2)의 실수부와 허수부로서 식 (3) 및 식 (4)와 같이 표현된다.
여기서 |r|max는 rnew[n]의 최대 크기를 나타낸다.
시간 영역 신호의 크기와 위상을 입력하는 MP 신호는 식 (5) 및 식 (6)과 같이 나타낼 수 있다.
스펙트럼의 진폭과 위상을 입력하는 AP 신호는 기저대역 신호를 FFT 한 후 구하며 k번째 주파수에 대해 식 (7) 및 식 (8)과 같이 나타낼 수 있다.
여기서 X[k] = FET{xnew[n]}로 시간영역 신호열을 FFT 한 것이고, |X|max는 전체 주파수 성분 중에서 최대 진폭을 나타낸다.
스펙트로그램은 길이 N인 신호를 길이 M인 B개의 블록으로 나눈 다음, M각 블록을 점 FFT하여 구한다.
여기서 X[k,m]은 m번째 블록을 FFT한 것의 k번째 성분 값으로 SG 신호는 M × B 2차원 행렬이 된다. 스펙트로그램은 각 블록이 서로 겹치게 구하는 방법도 있지만 제안 방식에서는 M × B = N 을 만족하도록 겹치지 않게 블록을 나누었다[12].
분류기의 입력 형태는 신경망에 입력되기 전에 전처리 과정에서 변환하며, 그 결과 SG 신호열은 0과 1사이로, 나머지는 −1과 1 사이로 정규화된다.
III. 분류기 구조
분류기는 I, Q 복소신호열를 입력으로 받아 아날로그 변조방식 7가지와 그 외 방식(’Other’로 나타냄) 등 총 8개 그룹으로 분류한다. 분류기는 그림 1과 같이 전처리부를 포함하여 5개의 2차원 합성곱층(convolution layer)과 2개의 완전연결층(FCL, fully connected layer)으로 구성된다.
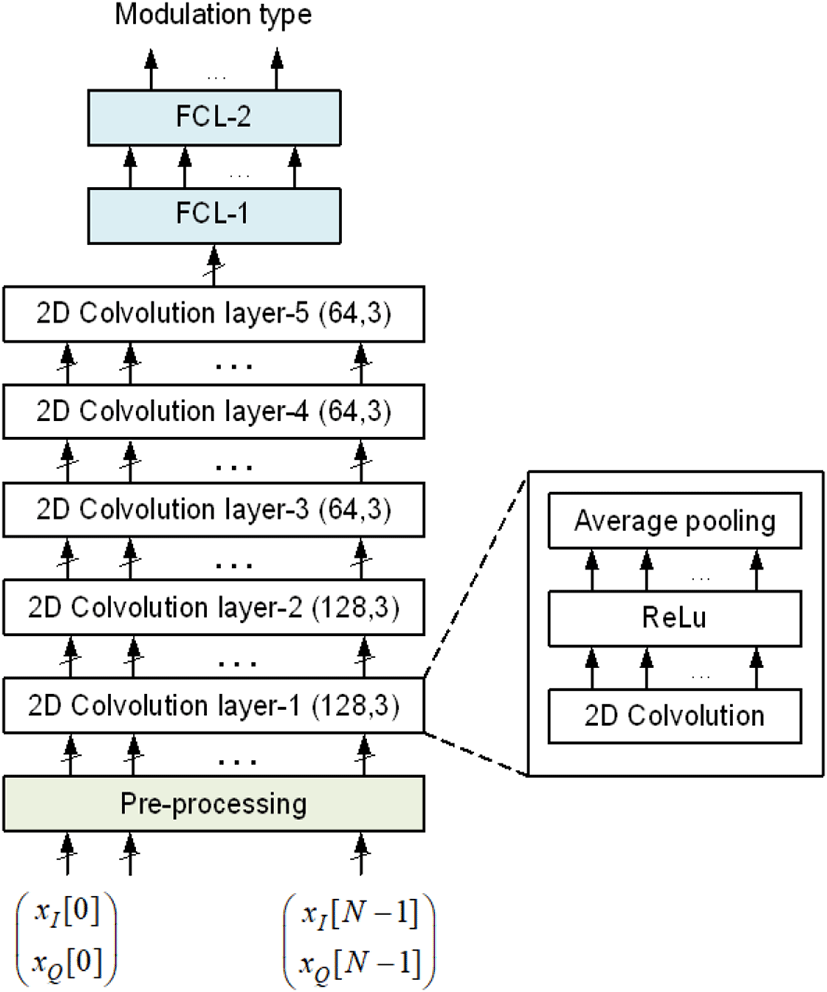
전처리부에서는 기저대역 복소신호열을 입력으로 받아 신경망의 4가지 입력 형태에 따라 식 (3)~식 (9)의 처리를 하고 다음에 연결되는 합성곱층의 입력 형식으로 변환하는 역할을 한다. 사용한 신경망(Matlab R2024b 함수를 사용함)은 복소신호를 처리할 수 없기 때문에 N × 1복소신호열 벡터를 N × 2 또는 M × B 실신호 행렬로 변환한다. 한편 2차원 합성곱층은 칼라 영상을 기반으로 설계되었기 때문에 H × W × C(H: 수직 화소 수, W: 수평 화소 수, C : RGB 채널 수) 3차원 행렬을 입력으로 받는다. 이 논문에서 사용한 신호열의 길이는 N=1,024이고 SG 신호의 경우 512×2이다. 따라서 전처리부 출력 신호는 IQ, MP, AP 입력인 경우 1×1,024×2 행렬이고, SG의 경우는 512×2×1 행렬이다.
신경망의 입력 길이는 클수록 분류 성능이 향상되지만 너무 크면 과적합(over-fitting) 현상이 발생하여 오히려 성능이 저하된다. 사용하고 있는 변조 신호는 대역폭 대비 약 6배 과표본화(over-sampling)된 신호로 이 경우 모의실험을 통해 1,024 길이가 적절한 값임을 확인할 수 있었다. SG 입력의 경우도 정해진 MB=1,024 조건에서 모의실험을 통해 512×2가 적절한 값임을 확인하였다.
한 개 합성곱층은 그림 1과 같이 합성곱을 수행하는 필터, 활성함수(activation function), 통합(pooling) 층으로 구성되어 있으며, 필터를 통해 입력 데이터의 고차 특징(higher-order feature)들을 추출하고 통합을 통해 압축하는 기능을 한다[9]. 5개 합성곱층의 필터 개수는 (128, 128, 64, 64, 64)이고, 필터 길이는 모두 3이다. 필터 길이는 입력 길이가 충분할 때 합성곱층이 3개 이상이면 크게 성능에 영향을 미치지 않았다. 이것은 전체 합성곱층을 통해 특징으로 추출되는 인접 데이터 개수가 유사하기 때문인 것으로 판단된다. 활성함수는 모두 ReLU(rectified linear unit) 함수를 사용한다. 마지막으로 통합은 필터링된 데이터 값을 모두 반영하고자 두 데이터의 평균을 취하는 AveragePooling을 적용한다. 따라서 첫 합성곱층 입력이 1×1,024×2행렬인 경우 필터링을 통해 128개의 1×1,024 벡터, 즉 1×1,024×128 행렬이 되고, 통합을 통해 128개의 1×512 벡터, 즉 1×512×128 행렬이 된다. 최종적으로 다섯 번째 합성곱층의 출력은 64개의 1×32 벡터, 즉 1×32×64 행렬이 된다. SG 입력의 경우는 다섯 번째 합성곱층의 출력이 64개의 4×1 벡터, 즉 4×1×64 행렬이 된다. CNN의 필터 개수, 필터 길이 등의 내부 파라미터는 모의실험을 통해 결정하였다.
완전연결망은 2개의 완전연결층으로 구성되며, CNN 출력을 입력으로 받아 분류기 최종 결과인 변조방식을 출력한다. 제1층은 3차원 CNN 출력을 1차원으로 펼친(flattening) L×1 벡터를 입력으로 받아 최종적으로 분류하고자 하는 그룹수 G에 대해 6G×1 벡터로 출력한다. 활성함수는 ReLU 함수를 사용한다.
분류기의 최종 출력인 제2층의 출력은 G = 8개 변조방식이고 그룹별 확률적인 결과를 얻기 위해 Softmax 활성함수를 사용한다.
신경망 전체에서 학습 가능 계수 수는 SG 입력의 경우 약 31만 개고, 나머지는 약 20만 개다.
IV. 모의실험 결과
네 가지 입력 형태에 대한 분류기의 성능을 평가하기 위해 입력 신호열의 길이가 모두 N=1,024로 동일한 조건에서 같은 구조의 신경망을 사용하고, 성능 지표로는 전체 신호열 개수에서 정확하게 분류한 비율을 나타내는 정확도(accuracy)를 사용한다[13].
먼저 신호대잡음비(SNR, signal to noise power ratio) −20 ~30 dB 사이에서 2 dB 간격으로 생성한 학습용 데이터를 생성하여 분류기를 학습시키고, 별도의 평가용 데이터를 통해 분류 정확도를 구한다. 학습용 데이터는 분류하고자 하는 각 그룹의 신호열 개수가 동일하게 분배한 후 전체 SNR에서 고르게 20만 개를 선택한다. 전체 20만 개의 학습용 신호열은 불규칙적으로 섞은 후 80 % : 10% : 10 %로 나누어 각각 훈련(train), 검증(validation), 시험(test)에 사용한다. 시험용 신호열은 학습을 통해 최종적으로 결정된 모델의 성능을 간단히 평가하기 위한 용도이며, 실제의 성능 평가는 별도의 평가용 데이터를 적용하여 수행한다.
그림 2는 전체 7개 변조방식 전체에 대한 분류 정확도를 4가지 입력 형태에 따라 나타낸 것이다. 여기서 스펙트럼 편이는 0이다. 그림을 보면 SNR 8 dB 이상에서는 거의 비슷한 분류 성능을 나타내지만, 그 이하에서는 주파수 영역 신호 AP나 SG를 입력하는 경우가 시간 영역 신호 IQ나 MP를 신호를 입력하는 경우에 비해 훨씬 더 나은 성능을 나타내는 것을 알 수 있다. 특히 SG는 신호의 스펙트럼 크기만 입력하는 것으로 정보가 더 줄었음에도 불구하고 시간영역 신호에 비해 더 나은 성능을 나타낸다. 이것은 아날로그 변조 신호의 경우 주파수 영역에서 신호의 특성이 더 잘 구별됨을 의미한다. SNR −16 ~8 dB 구간에서 보면 AP 입력인 경우 SG 입력에 비해 약간 분류 정확도가 높은데, 그 차이가 위상에 의한 것으로 판단된다. 그러나 그 우위도 SNR −16 dB 이하에서는 위상에 더 크게 영향을 주는 잡음 때문에 오히려 뒤바뀌고 있음을 볼 수 있다. 이로부터 위상보다는 스펙트럼 진폭에 더 많은 정보가 있음을 알 수 있다. 신경망의 학습 가능한 계수의 개수 차이가 크지 않은 상황에서, 이러한 결과는 시간 및 주파수 영역 입력에 대해 비교한 이전의 연구결과[10, 14–15]와 일치한다.
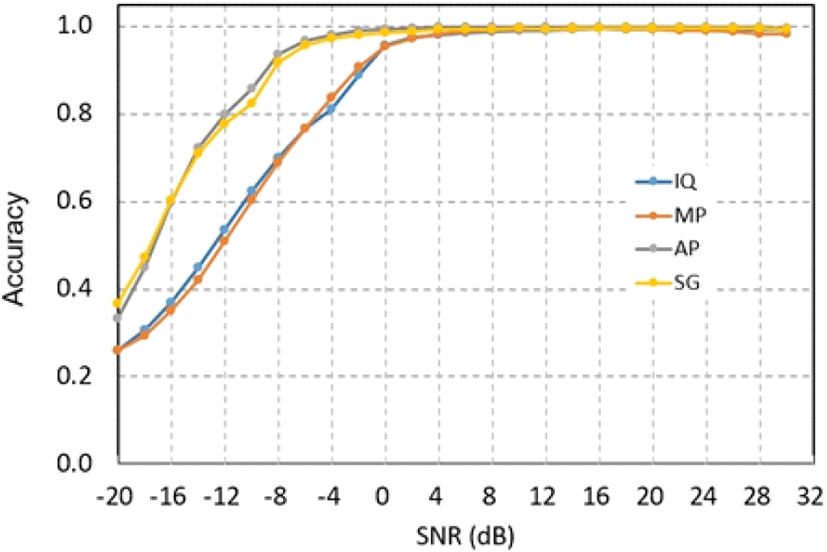
그림 3은 SNR이 −10, 0, 10 dB일 때 스펙트럼 편이에 따라 4가지 입력 형태의 분류 정확도를 나타낸 것이다. 범례의 괄호 안 숫자는 SNR을 나타낸다. 그림에서 보면 스펙트럼 편이가 가장 큰 값인 ±0.2를 제외하고는 입력 형태와 무관하게 거의 유사한 분류 정확도를 나타내는 것을 볼 수 있다. 다만 그림 2의 결과와 마찬가지로 SG 입력의 경우 SNR=−10 dB로 낮은 경우 스펙트럼 편이 정도에 따라 약간 진동하는 것을 볼 수 있다.
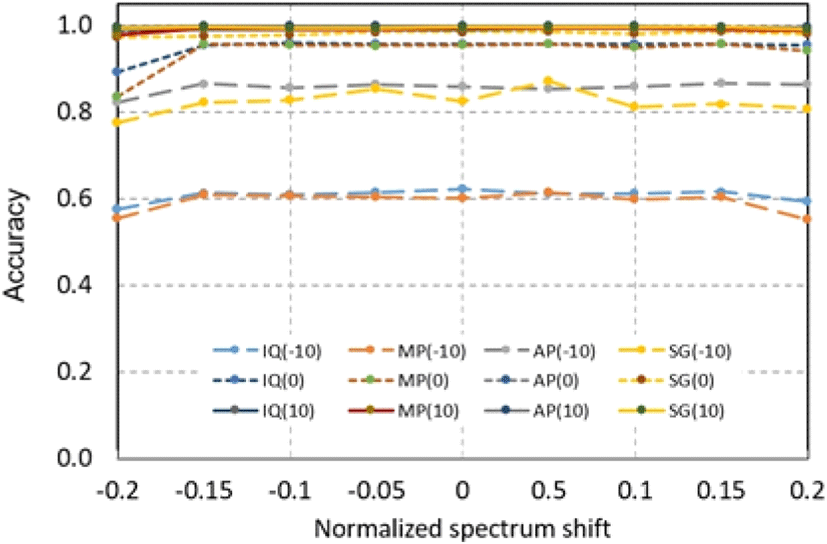
그림 4는 주파수 옵셋이 ±20 % 사이에서 균일하게 분포할 때 변조방식별로 분류 정확도를 나타낸 것이다. 그림을 보면 FM은 AM과 다르게 분류 정확도가 낮은 SNR에서는 SNR이 커짐에 따라 거의 일정하다가 어느 부분에 이르면 갑자기 커지는 형태를 나타낸다. 이것은 FM이 비선형 변조로 SNR에 대해 임계효과가 있기 때문으로 판단된다. AM의 경우 SNR≥−12 dB인 부분에서는 대체로 반송파가 삽입된 변조 신호의 정확도가 억압하는 방식에 비해 높다. 주파수 영역 신호인 AP나 SG 입력의 경우 7개 변조방식 모두 SNR≥−6 dB에서 정확도가 90 % 이상이지만, 시간 영역 신호인 IQ나 MP 입력의 경우 훨씬 더 높은 SNR≥0 dB에서 나타낸다. 가장 우수한 성능을 나타내는 AP 입력인 경우, −16 dB≤SNR≤−8 dB 범위에서 반송파가 삽입된 AM, 방송파가 억압된 AM, 그리고 FM의 3개 그룹으로 뚜렷하게 구별되고 SNR≥4 dB에서는 모든 변조 신호가 안정적으로 거의 유사한 분류 정확도를 나타내고 있다.
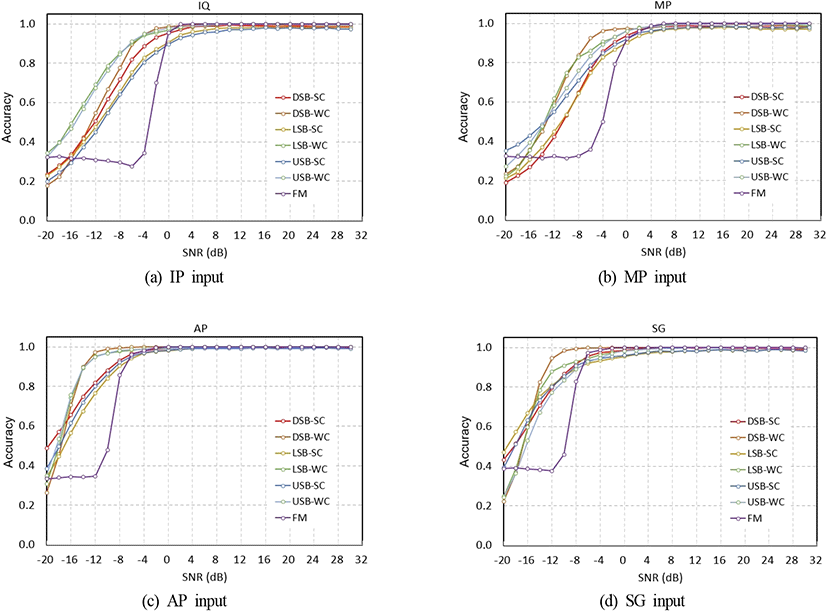
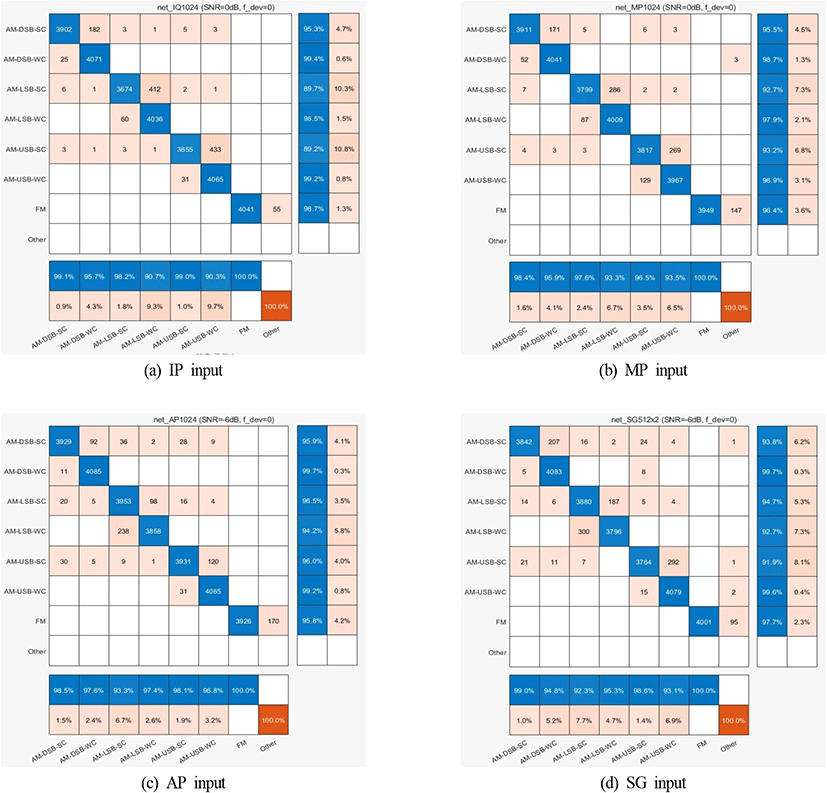
그림 5는 분류 상태를 나타내는 혼동행렬(confusion matrix)를 그림으로 나타낸 것이다. 신경망 입력 형태에 따른 오분류 상황을 보기 위해 분류을 90 % 부근을 선택하였다. 이 경우 IQ와 MP 입력은 SNR=0 dB이고, AP와 SG 입력은 SNR=−6 dB이다. 그림에서 가로축은 분류한 결과를 나타내고, 세로축은 실제 변조방식을 나타낸다. 또 그림에서 파란색 부분은 4,096개의 시험 신호열에 대해 정확하게 분류한 경우를 나타내는데, 그림 오른쪽 비율은 정확도를 나타내고 그림 아래쪽은 정밀도(precision)[13], 즉 특정 변조 신호라고 분류했을 때 정확하게 분류된 비율을 나타낸다. 살색 표시 부분은 잘못 분류한 경우를 나타낸다. 그림을 보면 FM에서 오분류가 발생하는 경우 모두 디지털 변조로 분류되고, AM의 경우는 DSB, LSB, USB 모두 SC와 WC 상호간으로 주로 오분류가 발생하는 것을 알 수 있다. 이것은 FM이 AM과는 변조 형태가 전혀 다르기 때문이며, AM 신호 생성 시 삽입하는 반송파의 진폭을 정보신호 최대 진폭의 1.2배로 비교적 작게 했기 때문인 것으로 판단된다.
V. 결 론
이 논문에서는 CNN을 기반으로 아날로그 변조 신호를 분류할 수 있는 분류기와 학습 방법을 제시하고 4가지 형태의 신경망 입력, 즉 시간 영역 신호인 IP, MP와 주파수 영역 신호인 AP, SG에 대해 그 분류 성능을 비교하였다. 또 실제 변조 신호 취득 시에 발생할 수 있는 스펙트럼 편이를 훈련 신호에 반영하는 방법을 제시하였다. 모의실험 결과 주파수 영역 신호를 입력하는 경우 분류 정확도 90 %를 기준으로 SNR이 6 dB 이상 낮았으며, 그 중에서도 위상 정보를 같이 사용하는 AP 입력의 경우가 SG 입력인 경우에 비해 약간 더 나은 정확도를 나타냈다. 스펙트럼 편이가 있는 경우에도 훈련 시에 반영한 ±20 % 범위 내에서 AP 입력의 경우에 거의 균일한 정확도를 나타내었다.
이 논문에서는 변조방식을 분류하기 위해 아날로그 변조 신호만을 다루었는데 향후 스펙트럼 특성이 다른 디지털 변조 신호를 포함하여 연구하고자 한다.



