The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(2):160-170

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.2.160

논문/REGULAR PAPERS

높은 전력 전송 효율 달성을 위한 다중 송수신 코일 배치 설계

전선재^†

Multiple-Transceiver Coil Arrangement Design for Achievement of High-Power Transfer Efficiency

Seon-Jae Jeon^†

국방과학연구소

Agency for Defense Development

^†Corresponding Author: Seon-Jae Jeon (e-mail: seonjae@add.re.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 19, 2024; Revised: Sep 17, 2024; Accepted: Oct 29, 2024

Published Online: Feb 28, 2025

요 약

본 논문에서는 다중 송수신 무선전력전송 시스템에서 전력 전송 효율을 크게 향상시키기 위한 코일 배치 설계 방안을 제안한다. 먼저 다중 송수신 코일을 사용하는 시스템의 전력 전송 효율의 특성을 파악하기 위해 시스템 등가회로로부터 전력 전송 효율을 간단히 정리한 다음 코일 간 상호 인덕턴스가 모두 매우 큰 값을 갖는 경우에 동일한 송신 전류를 적용함으로서 시스템의 전력 전송 효율이 최대로 근접함을 확인한다. 이러한 사실을 토대로 모든 송수신 코일 간 상호 인덕턴스 크기를 최대한 유지하기 위해 다수의 송신코일과 수신코일 각각을 완전하게 포개는 방식의 적층형 코일 배치 설계를 제안한다. 적층형 코일 배치의 우수한 전력 전송 효율 성능을 확인하기 위해 정규화된 전송 거리에 따른 시스템의 모든 코일 간 상호 인덕턴스 계산과 전력 전송 효율 시뮬레이션을 수행한다. 그리고 결과적으로 적층형 코일 배치의 전력 전송 효율이 기존의 평면형 코일 배치보다 최대 20 % 이상 더 우수함을 확인한다.

Abstract

In this study, a coil arrangement design method is proposed to significantly improve power transfer efficiency (PTE) in a multiple-transceiver wireless power transfer system. First, PTE equation is simplified through the system equivalent circuit. Then, it is verified that the system has identical Tx currents and large mutual inductances between each Tx coil and Rx coil are close to the maximum PTE. Based on the results, the design of the stacked coil structure Tx and Rx coils are perfectly overlapped such that the system can maintain large mutual inductances. To validate the remarkable PTE performance of the stacked structure, the calculation of mutual inductances among all coils and PTE simulation of the systems are conducted according to the normalized transmission distance. Consequently, the PTE of the stacked structure is up to 20 % higher than that of the conventional planar structure.

Keywords: Wireless Power Transfer; Power Transfer Efficiency; Mutual Inductance; Multiple Coils; Multiple-Transceiver

Ⅰ. 서 론

자기장을 이용하는 무선전력전송 기술은 코일을 통해 무선으로 효율적인 전력 전달이 가능한 장점이 있어 현재까지 대형 및 소형 전자기기 등에 활용되고 있으며 각광받고 있는 기술 중 하나이다^[1],[2]. 일반적인 무선전력전송 시스템은 한 쌍의 송신코일과 수신코일 사이의 상호 인덕턴스를 통해 전력을 전달하는 원리로 상호 인덕턴스와 직결되는 코일 간 결합계수가 크면 클수록 더 많은 전력을 전달할 수 있다. 그러나 결합계수는 코일 사이 거리가 일정 이상만 벌어져도 크게 감소하는 특성으로부터 일반적인 무선전력전송 시스템의 전력 전송 거리는 매우 제한적일 수밖에 없었다^[3]. 이러한 점을 개선하기 위해서 기존에는 송신코일의 너비를 조정하고 내부코일을 추가하여 시스템의 전력 전송 범위를 향상시키거나^[4] OP-AMP나 transistor와 같은 능동소자를 이용한 부성 임피던스 구현으로 코일의 품질계수를 높여 전력 전송 거리를 향상시키는 연구들도 진행되었다^[5],[6].

그럼에도 불구하고 여전히 존재하는 제한적인 전력 전송 거리를 더욱 증가시키기 위해 여러 개의 코일을 배치하는 구조의 무선전력전송 시스템도 연구되었다. 그 중 다중 송신코일 시스템은 사용되는 여러 개의 송신코일 배치에 따라 단 하나의 송신코일을 사용할 때보다 전력 전송 커버리지를 효과적으로 향상시킬 수 있었다^[7],[8]. 하지만 사용하는 송신코일의 개수가 많아질수록 송신코일 간 불필요한 결합으로 인해 전력 전송 효율 감소를 초래하는 문제가 발생하였으며, 이러한 문제를 해결하기 위해 무결합 코일 배치 방식^[9]이나 공진기의 커패시턴스를 조정하였다^[10]. 더 나아가 다른 연구에서는 기존의 평면형 배치에 대한 다중 송신코일 시스템의 전송거리 한계점을 밝혔으며^[11], 최근에는 여러 개의 송신코일을 완전하게 포개는 적층형 배치 구조를 통해 단 하나의 수신코일에 여러 개의 자기장을 효율적으로 집중시켜 전송 거리를 더욱 향상시킬 수 있는 연구까지 진행되었다^[12]. 그러나 이러한 연구에서 제안된 구조에 대해 해석된 수신코일은 단 하나이기 때문에 실생활 어플리케이션 별로 여러 수신코일을 효율적으로 배치 적용하는 방안을 연구하여 무선전력전송 시스템의 실생활 활용도를 높일 필요가 있다.

일반적으로 그림 1과 같이 시스템 내부의 여러 장치를 일정 시간 이상 작동시키기 위해 다수의 배터리 팩 혹은 셀을 적용하는 무인항공기(UAV, unmaned aerial vehicle)^[13]나 전기 자동차(EV, electric vehicle)^[14]는 내부 각각의 배터리를 동시에 충전하는 안정적인 밸런싱 무선 충전 구현과 동시에 전력 전송 효율을 증대시키기 위해 여러 개의 코일로부터 전력을 송수신할 필요가 있다.

그림 1. | Fig. 1. 여러 배터리 동시 충전을 위한 다중 송수신 무선전력전송 메커니즘 | Multiple-transceiver WPT mechanism for simultaneous charging of several batteries.

Download Original Figure

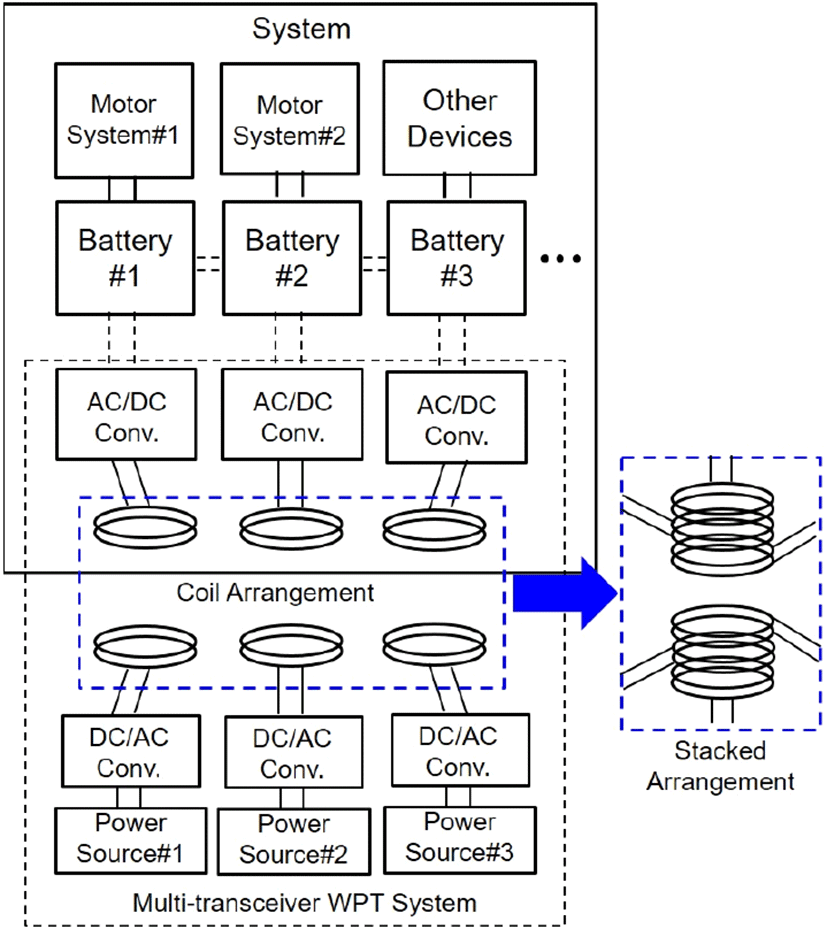
본 논문에서는 다중 송수신 무선전력전송 시스템의 최대 전력 전송 효율 조건에 대해 파악하고, 이러한 조건을 바탕으로 여러 배터리를 사용하는 UAV나 EV 시스템에 적용이 가능한 송수신 코일 배치 설계를 제안한다. 제안하는 적층형 배치 방법은 송수신 코일 사이 결합을 극대화하기 위해 각각의 송신코일과 수신코일을 완전히 포개는 구조이며, 이러한 배치 설계의 우수한 성능을 확인하기 위해 기존의 다중 송수신 코일 배치와 전송 거리에 따른 전력 전송 효율을 비교한다.

Ⅱ. 다중 송수신 무선전력전송 시스템의 최대 전력 전송 효율 조건

그림 2에서는 다중 송수신 코일을 사용하는 무선전력전송 시스템에 대한 등가회로를 나타냈다. 첫 번째 송신코일(L_T1)과 수신코일(L_R1) 그리고 n번째 송신코일(L_Tn)과 수신코일(L_Rn)은 각각의 상호 인덕턴스(M₁₁, M_n1, M_1n, M_nn)로 결합되며, 커패시턴스(C_T1, C_Tn, C_R1, C_Rn)를 통해 동작주파수에서 공진하게 된다. 먼저, 다중 송수신 무선전력전송 시스템에 대한 전력 전송 효율을 간단히 도출하기 위해 두 개의 송수신 코일을 사용하는 무선전력전송 시스템에 대한 행렬식은 키르히호프의 전압법칙을 통해 식 (1)과 같이 나타낼 수 있다.

V S 1 V S 2 00 = Z T 1 j w M T 12 − j w M 11 − j w M 12 j w M T 12 Z T 2 − j w M 21 − j w M 22 − j w M 11 − j w M 21 Z R 1 j w M R 12 − j w M 12 − j w M 22 j w M R 12 Z R 2 I T 1 I T 2 I R 1 I R 2

(1)

where Z_T1 = R_T1 + jwL_T1 + 1/jwC_T1,

Z_T2 = R_T2 + jwL_T2 + 1/jwC_T2,

Z_R1 = R_R1 + jwL_R1 + 1/jwC_R1,

Z_R2 = R_R2 + jwL_R2 + 1/jwC_R2

그림 2. | Fig. 2. 다중 송수신 무선전력전송 시스템 등가회로 | Equivalent circuit of multiple-transceiver WPT system.

Download Original Figure

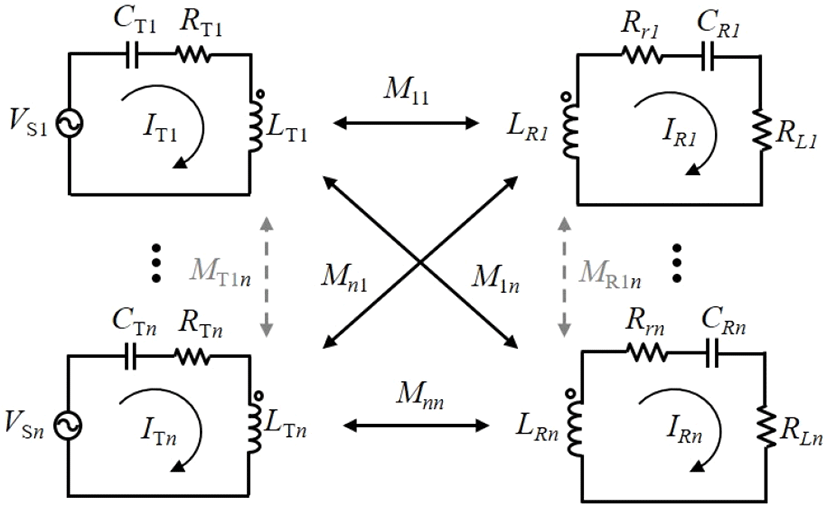
식 (1)에서 R_T1=R_S1+R_t1, R_T2=R_S2+R_t2, R_R1=R_r1+R_L1, R_R2= R_r2+R_L2이며, R_S는 전원 저항, R_t은 송신코일 저항, R_r은 수신코일 저항, R_L은 부하 저항이다. 여기서 불필요한 M_T12와 M_R12의 영향을 제거하기 위한 각 공진기의 커패시턴스는 식 (2)와 같으며 이를 식 (1)에 대입하면 공진주파수에서 식 (3)과 같이 간단히 표현될 수 있다.

C T 1 = 1 / w 2 L T 1 + w 2 M T 12 I T 2 I T 1 C T 2 = 1 / w 2 L T 2 + w 2 M T 12 I T 1 I T 2 C R 1 = 1 / w 2 L R 1 + w 2 M R 12 I R 2 I R 1 C R 2 = 1 / w 2 L R 2 + w 2 M R 12 I R 1 I R 2

(2)

V S 1 V S 2 00 = R T 1 0 − j w 0 M 11 − j w 0 M 12 0 R T 2 − j w 0 M 21 − j w 0 M 22 − j w 0 M 11 − j w 0 M 21 R R 1 0 − j w 0 M 12 − j w 0 M 22 0 R R 2 I T 1 I T 2 I R 1 I R 2

(3)

그리고 식 (3)을 통해 시스템의 출력전력과 입력전력은 식 (4) 및 식 (5)와 같이 정리된다.

P L = 12 I R 1 2 + I R 2 2 = w 02 M 11 I T 1 + M 21 I T 2 2 2 R R 1 2 R L 1 + w 02 M 12 I T 1 + M 22 I T 2 2 2 R R 2 2 R L 2

(4)

P I N = 12 V S 1 I T 1 + V S 2 I T 2 = R T 1 I T 1 2 + R T 2 I T 2 2 2 + w 02 M 11 I T 1 + M 21 I T 2 2 2 R R 1 + w 02 M 12 I T 1 + M 22 I T 2 2 2 R R 2

(5)

식 (4) 및 식 (5)를 통해 시스템 전력 전송 효율은 식 (6)과 같이 나타낼 수 있다.

η = P L P I N = w 02 A 2 R L 1 / R R 1 2 + w 02 B 2 R L 2 / R R 2 2 R T 1 I T 1 2 + R T 2 I T 2 2 + w 02 A 2 / R R 1 + w 02 B 2 / R R 2

(6)

where A = M₁₁I_T1 + M₂₁I_T2, B = M₁₂I_T1 + M₂₂I_T2

만약, 시스템에서 R_S=0이고 사용되는 모든 코일이 동일한 코일 저항(R_p)과 부하저항(R_L)을 갖는다고 할 때, 식 (6)은 식 (7)과 같이 간단히 정리된다.

η = w 02 R L R R 2 R P I T 1 2 + I T 2 2 / A 2 + B 2 + w 02 R R

(7)

where R_R = R_p + R_L,

그리고 만약, A와 B가 무한히 큰 값을 가질 때, 식 (8)과 같이 시스템의 이상적인 최대 전력 전송 효율이 구해질 수 있다.

lim A 2 + B 2 → ∞ η = R L R R

(8)

식 (8)에서 알 수 있듯이 시스템의 전력 전송 효율이 최대로 근접하기 위해서는 A와 B에 포함된 I_T1, I_T2, M12, M₁₂, M₂₁, M₂₂를 최적의 값으로 조합할 필요가 있게 된다.

만약, 송수신 코일 간 상호 인덕턴스가 모두 동일(M=M₁₁=M₂₁=M₁₂=M₂₂)하다면 식 (7)은 식 (9)와 같이 정리될 수 있다.

η = w 02 R L R R 2 R P I T 1 2 + I T 2 2 / 2 M 2 I T 1 + I T 2 2 + w 02 R R

(9)

그리고 ∂η/∂I_T1=0 만족하는 I_T2가 최적의 송신전류 조건이 되며, 식 (10)과 같이 도출될 수 있다.

I T 2, o p t = I T 1

(10)

식 (10)으로부터 모든 상호 인덕턴스가 동일한 상황에서 최대 효율을 위해서는 동일한 송신 전류를 가지도록 할 필요가 있음을 알 수 있다.

그리고 식 (9)에서 I₂=I₁를 적용하면 식 (11)과 같이 정리되며, 총 4개의 송수신 코일 간 상호 인덕턴스가 수신기 저항 대비 어느 정도 큰 값을 갖게 되면 식 (8)의 이상적인 최대 전력 전송 효율에 가까워질 수 있음을 예측해볼 수 알 수 있다.

η = w 02 R L R R 2 R P / 4 M 2 + w 02 R R

(11)

더 나아가 n개의 송수신 코일을 각각 사용하는 경우에 대한 시스템 행렬식은 식 (12) 및 식 (13)과 같이 정리될 수 있다.

V S 1 ⋮ V S n 0 ⋮ 0 = Z T 1 ⋯ j w M T 1 n − j w M 11 ⋯ − j w M 1 n ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ j w M T 1 n ⋯ Z T n − j w M n 1 ⋯ − j w M n n − j w M 11 ⋯ − j w M n 1 Z R 1 ⋯ j w M R 12 ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ − j w M 1 n ⋯ − j w M n n j w M R 12 ⋯ Z R n I T 1 ⋮ I T n I R 1 ⋮ I R n

(12)

where Z_Tn = R_Tn + jwL_Tn + 1/jwC_Tn,

Z_Rn = R_Rn + jwL_Rn + 1/jwC_Rn

C T i = 1 / w 2 L T i + w 2 ∑ j = 1, j ≠ i n M T i j I T j I T i C R i = 1 / w 2 L R i + w 2 ∑ j = 1, j ≠ i n M R i j I R j I R i

(13)

마찬가지로 매우 작은 시스템 전원 저항은 무시하고 동작주파수에서 불필요한 송신코일 간 상호 인덕턴스와 수신코일 간 상호 인덕턴스들의 영향을 제거한 다음 모든 송수신 코일 간 상호 인덕턴스와 송신전류가 각각 동일한 경우 행렬식은 식 (14)와 같다.

V S 1 ⋮ V S n 0 ⋮ 0 = R p ⋯ 0 − j w M ⋯ − j w M ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ 0 ⋯ R p − j w M ⋯ − j w M − j w M ⋯ − j w M R R ⋯ ​ ​ ​ ​ ​ 0 ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ − j w M ⋯ − j w M 0 ⋯ R R I T ⋮ I T I R 1 ⋮ I R n

(14)

그리고 식 (14)을 통해 전력 전송 효율은 식 (15)와 같이 간단히 정리될 수 있다.

η = w 02 R L R R 2 R P / n 2 M 2 + w 02 R R

(15)

마찬가지로 식 (15)에서 총 n²개의 송수신 코일 간 상호 인덕턴스가 수신기 저항 대비 어느 정도 큰 값을 가지거나 사용하는 송수신 코일의 개수가 증가하면 식 (8)의 이상적인 최대 전력 전송 효율에 가까워질 수 있음을 알 수 있다.

그러나 현실적으로 한정적인 공간에서 코일의 개수를 무한대로 증대시키거나 송수신 코일 간의 모든 상호 인덕턴스를 무한정 증가시키는 것은 불가능하다. 그러므로 실제 다중 송수신 무선전력전송 시스템이 이상적인 최대 전력 전송 효율에 최대한 근접하기 위해서는 사용할 어플리케이션에 허용 가능한 공간 내에서 송수신 코일의 적절한 개수를 정한 다음 효과적인 코일 배치를 통해 송수신 코일 간 모든 상호 인덕턴스를 일정 값 이상을 유지시키는 설계를 수행할 필요가 있다.

Ⅲ. 상호 인덕턴스에 따른 다중 송수신 무선전력전송 시스템 효율 분석

코일의 개수와 상호 인덕턴스의 크기 변화가 전력 전송 효율에 얼마나 영향을 미치는지 파악하기 위해 동일한 송신 전류를 갖는 다중 송수신 무선전력전송 시스템에서 전력 전송 효율을 계산하였다, 여기서 사용된 시스템 파라미터는 표 1과 같으며 코일은 상용 코일인 WT505090 모델 파라미터를 사용하였다.

표 1. | Table 1. 시뮬레이션을 위한 시스템 파라미터 | System parameters for simulation.

Notes	Symbol	Value
Tx/Rx coil inductance	L_T, L_R	14.6 μH
Tx/Rx coil resistance	R_t, R_r	0.07 Ω
Source resistance	R_S	0.01 Ω
Rx load resistance	R_L	1 Ω
Operating frequency	f ₀	100 kHz

Download Excel Table

그림 3에서는 2×2, 3×3, 4×4 송수신 코일 시스템의 송수신 코일 사이 특정 결합계수(k)가 약결합(k=0.01)부터 강결합(k=0.2)까지 변화할 때, 그 외 송수신 코일 간 상호 인덕턴스들이 k에 대한 상호 인덕턴스 $M = k L T L R$ 대비 0부터 1까지의 비율(M_Ratio)을 만족하는 경우에 대해 대한 전력 전송 효율을 계산하였다. 다시 말하면 M_Ratio=0.5 인 경우 2×2 시스템에서 송수신 코일 간 생성되는 상호 인덕턴스 4가지 중 M을 제외한 3가지 상호 인덕턴스가 모두 M의 절반의 값만 만족하는 시스템에 대한 전력 전송 효율을 계산한다는 의미가 된다. 표 2에서는 특정 전력 전송 효율을 달성하기 위한 k와 M_Ratio를 정리하였다. 2×2, 3×3, 4×4 시스템에 대한 최대 효율은 각각 0.928, 0.931, 0.933로 분포되면서 사용하는 송수신 코일의 개수가 증가됨에 따라 효율도 증가됨을 확인하였다. 더 나아가 표 2에서 확인할 수 있듯이 70, 80, 90 % 이상을 만족하는 특정 효율 영역이 코일 개수가 많을수록 더 넓어짐을 보였으며, 3×3 시스템의 경우 80 % 이상의 효율이 동일한 k 조건에서 2×2 시스템 대비 M_Ratio가 0.1 더 적은 0.3 이상까지도 만족되었다. 4×4 시스템도 3×3 대비 M_Ratio가 0.05 이상 더 적은 영역까지 확보되었으나 증가폭은 더 줄어드는 경향을 확인하였다.

그림 3. | Fig. 3. 상호 인덕턴스 비율에 따른 다중 송수신 무선전력전송 시스템의 전력 전송 효율 | Power transfer efficiency of multiple-transceiver WPT system accordi6ng to mutual inductance ratio.

Download Original Figure

표 2. | Table 2. 시스템 코일 개수에 따른 전력 전송 효율 달성 조건 | Achievement condition of power transfer efficiency according to the system coil arrangement.

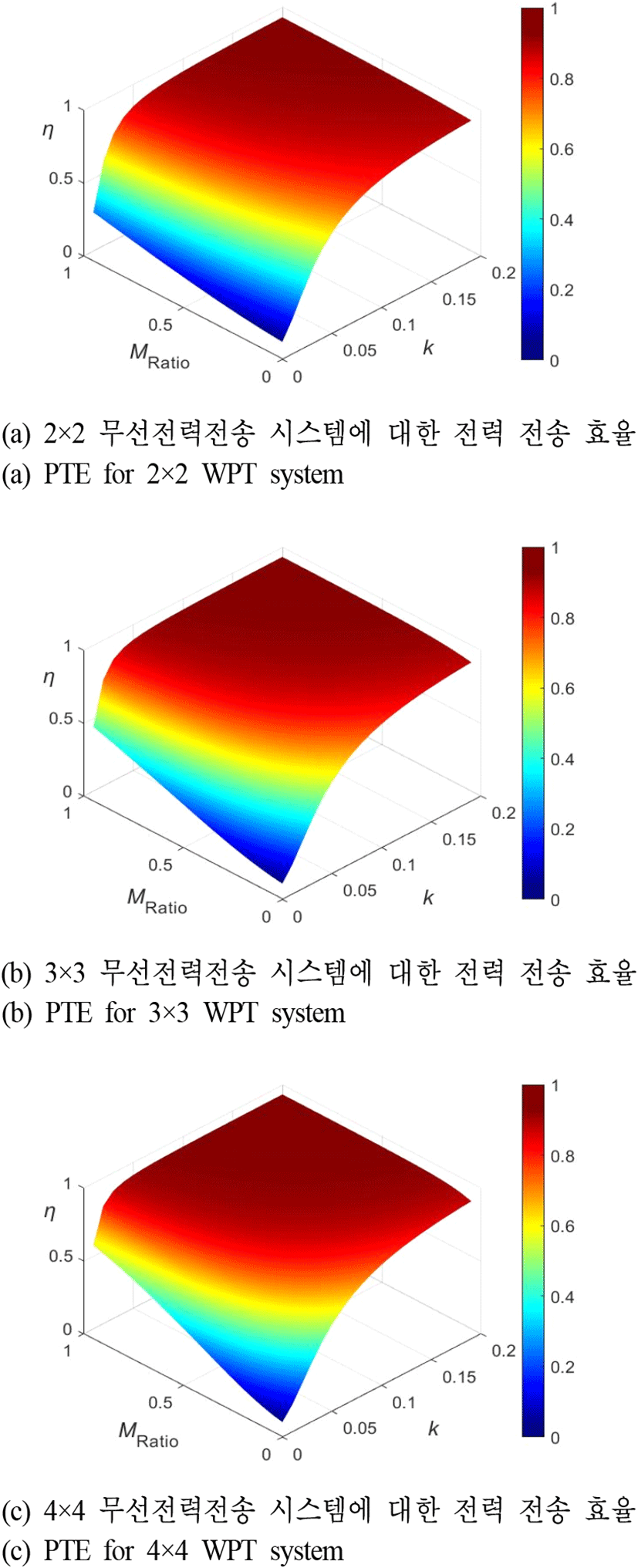
Power efficiency	k	M_Ratio for coil arrangement
Power efficiency	k	2×2	3×3	4×4
> 90 %	> 0.15	> 0.4	> 0.3	> 0.25
> 90 %	> 0.1	> 0.75	> 0.5	> 0.4
> 80 %	> 0.07	> 0.4	> 0.3	> 0.25
> 70 %	> 0.05	> 0.4	> 0.3	> 0.25

Download Excel Table

코일 개수 증가에 따른 효율 증가폭을 좀 더 직관적으로 확인하기 위해서 그림 4에서는 각각의 M_Ratio에 대한 다중 송수신 코일 시스템의 전력 전송 효율을 비교하였다. 마찬가지로 M_Ratio가 각각 0.2, 0.5, 0.9로 증가할수록 사용하는 코일의 개수가 증가함에 따라 효율도 전체적으로 증가하는 폭이 커지며 식 (8)의 최대 효율에 가까워지는 경향을 보였다. 그러나 M_Ratio가 0.9인 경우에도 불구하고 4×4 부터는 효율이 증가하는 폭은 꽤나 감소하였다. 이러한 결과로부터 시스템에서 최적의 코일 배치를 통해 M_Ratio가 1에 가깝게 높은 비율을 유지하더라도 코일 개수가 4×4보다 더 늘어나는 경우에는 더 이상의 유의미한 효율 증가는 어려울 것으로 예상할 수 있다.

그림 4. | Fig. 4. 상호 인덕턴스 비율과 코일 개수에 대한 전력 전송 효율 비교 | Power transfer efficiency comparison for mutual inductance ratio and the number of coils.

Download Original Figure

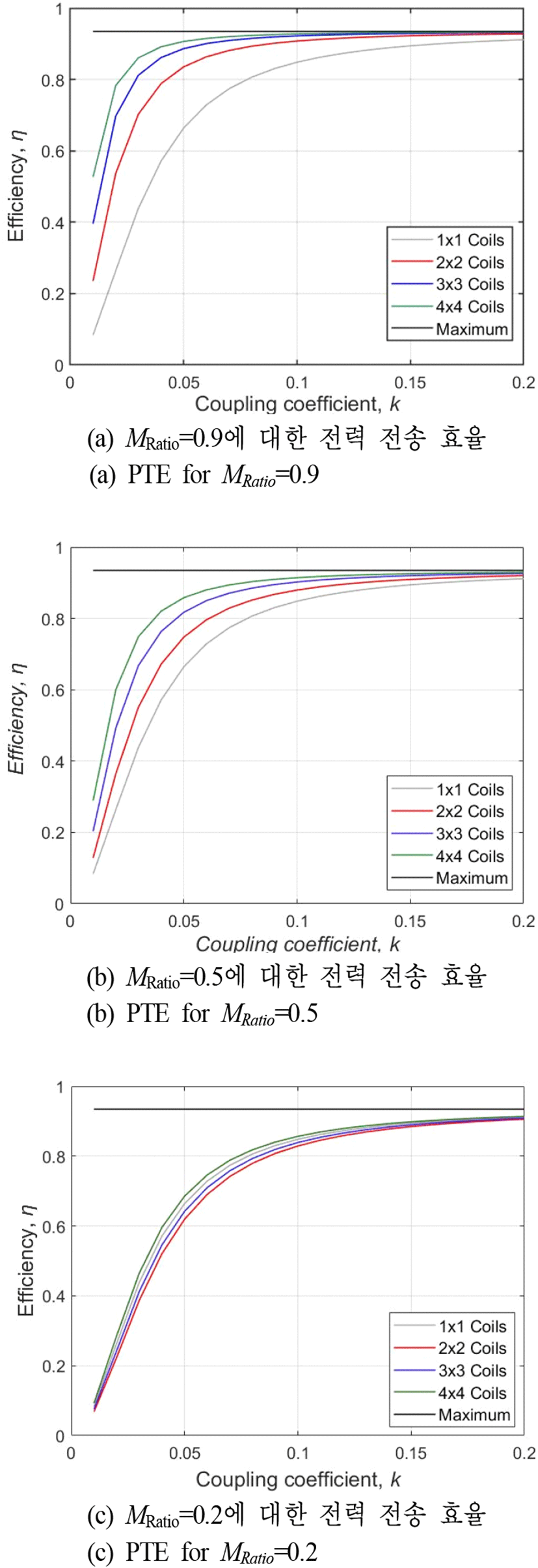
Ⅳ. 코일 배치에 따른 무선전력전송 시스템 전력 전송 효율 분석

위에서는 상호 인덕턴스 비율과 코일 개수에 대한 효율 비교를 통해 다중 송수신 코일 무선전력전송 시스템이 전력 전송 효율을 최대한 높이기 위해서는 송수신 코일 사이 상호 인덕턴스들이 가능한 모두 높게 유지 될 필요가 있음을 확인했다. 본 장에서는 시스템에서 다수의 송수신 코일 사이 상호 인덕턴스를 최대한 높이는 코일 배치를 제안하고 기존의 평면형 코일 배치^[15] 대비 효율이 얼마나 향상되는지 확인한다.

그림 5에서는 다중 송수신 무선전력전송 시스템의 적층형 코일 배치 구조와 기존의 평면형 배치 구조를 나타냈다. 사용되는 송수신 코일은 모두 동일하며 적층형 구조의 경우 송수신 코일 간 상호 인덕턴스를 최대로 높이기 위해서 송신코일들과 수신코일들이 각각 완전하게 겹쳐져 있다고 가정하였다. 추가적으로 여러 개의 코일로 적층형 배치를 구성할 때, 각 인접한 코일이 전기적으로 서로 연결되어 spiral 형태가 되지 않도록 litz wire가 절연재질로 감싸진 코일을 사용했다고 가정하였다. 그 이유는 실제로 sprial 코일이 다수의 턴을 갖을수록 인덕턴스도 증가하게 되지만 코일의 저항이 증가율이 더 커지면서 결국 코일의 품질계수 감소로 인해 전력 전송 성능이 기존보다 더 감소되기 때문이다^[12].

그림 5. | Fig. 5. 다중 송수신 코일 배치 비교 | Comparison of multiple-transceiver coil arrangements.

Download Original Figure

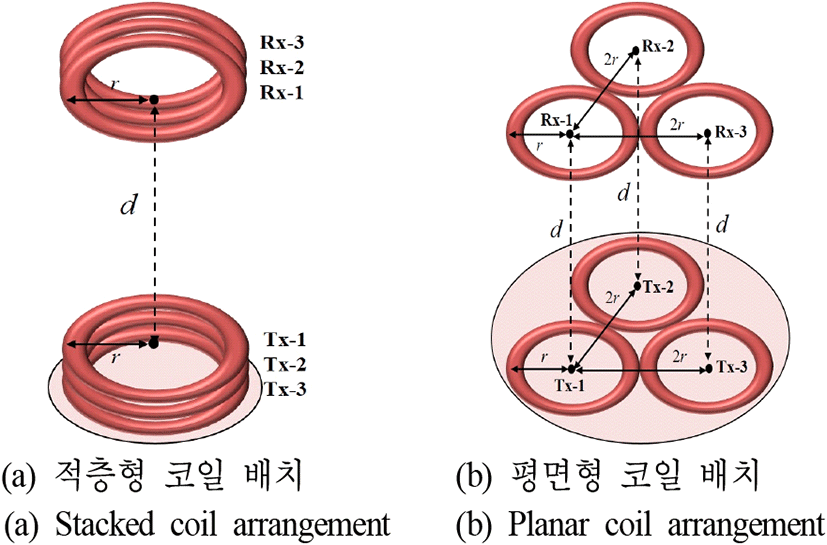
그림 5에서 전송 거리(d)에 따라 배치된 모든 코일 간 상호 인덕턴스를 계산하기 위해 참고문헌 [16]의 식 (5)를 이용하였으며, 계산 시 적용한 코일 WT505090 모델 외형 정보는 표 3에 정리하였다. 그리고 적층형 코일 배치 계산에서는 완전하게 적층되어 겹쳐진 코일들 간의 간격을 코일의 실제 물리적인 특성을 참고하여 1 mm로 적용하였다.

표 3. | Table 3. 상호 인덕턴스 계산을 위한 코일 파라미터 | Coil parameters for mutual inductance calculation.

Coil parameter	Value
Outer diameter	43 mm
Inner diameter	20.5 mm
Thickness	2 mm
Turns	10
Layer	2

Download Excel Table

그림 5의 구조에 대한 상호 인덕턴스 비율을 파악하기 위해 송수신 코일 사이 생성되는 상호 인덕턴스를 크기별로 파악할 필요가 있다. 3×3 송수신 코일에서 생성되는 상호 인덕턴스는 총 9가지이며, 적층형 코일 배치에서는 구조상 생성되는 송수신 코일간 상호 인덕턴스는 M₁₁ > M₁₂=M₂₁ > M₁₃=M₃₁=M₂₂ > M₂₃=M₃₂ > M₃₃를 만족한다. 그리고 평면형 배치의 경우는 구조상 M₁₁=M₂₂=M₃₃ > M₁₂=M₂₁=M₁₃=M₃₁=M₂₃=M₃₂를 만족하게 된다. 따라서 가장 큰 M₁₁을 제외한 다른 상호 인덕턴스에 M₁₁로 나눈 상호 인덕턴스 비율(M_Ratio)은 크기 별로 적층형은 4가지, 평면형은 1가지로 정리된다.

그림 6에서는 계산한 상호 인덕턴스 비율을 전송 거리를 코일의 반지름으로 나눈 정규화된 전송 거리(d/r)에 따라 나타냈다. 평면형 구조는 d/r=3(k₁₁=0.01) 이상부터 M_Ratio가 0.4 이상을 만족하였으며, d/r=2(k₁₁=0.028) 이하의 구간에서는 M_Ratio가 0.2 이하의 값을 가졌다. 반면에 적층형 구조에서는 d/r=0.04(k₁₁=0.66)~d/r=5.5(k₁₁=0.002) 구간의 모든 전송 거리에서 M_Ratio가 0.4 이상 만족하는 뚜렷한 차별점을 보였다.

그림 6. | Fig. 6. 정규화된 전송 거리에 따라 계산된 결합계수와 상호 인덕턴스 비율 | Calculated coupling coefficient and mutual inductance ratio according to transmission distance.

Download Original Figure

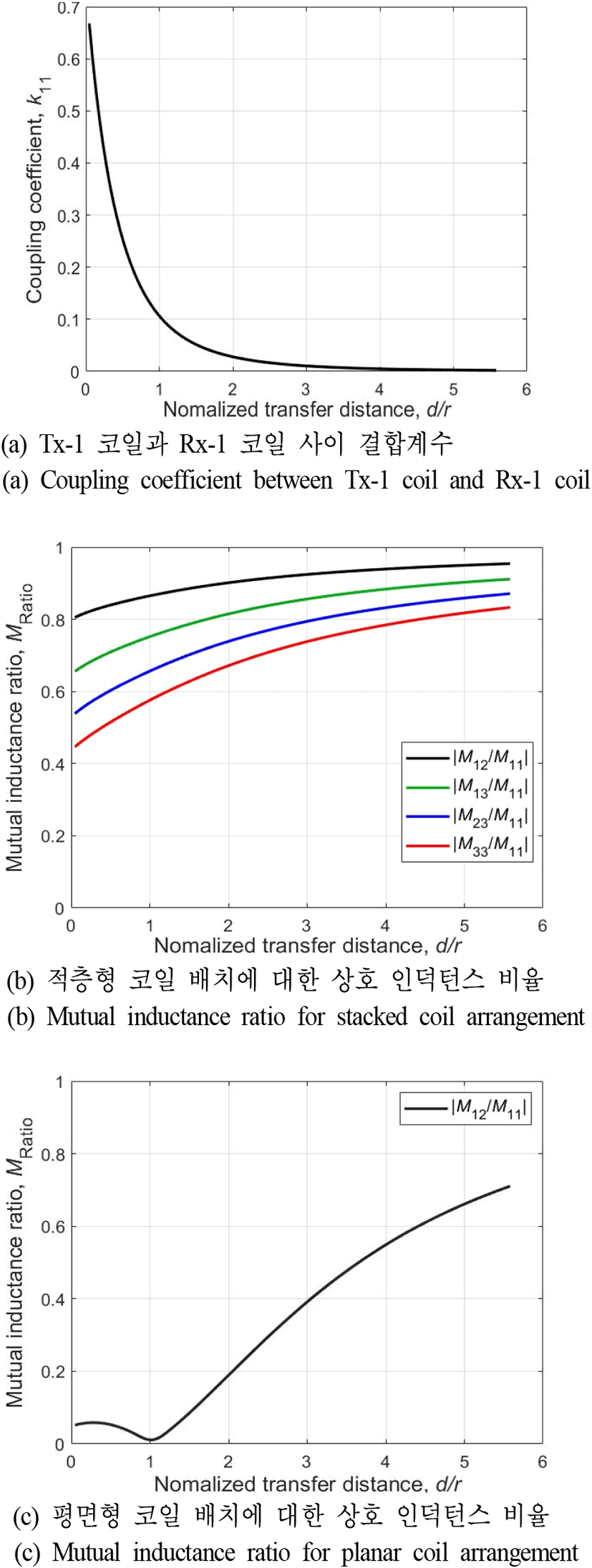
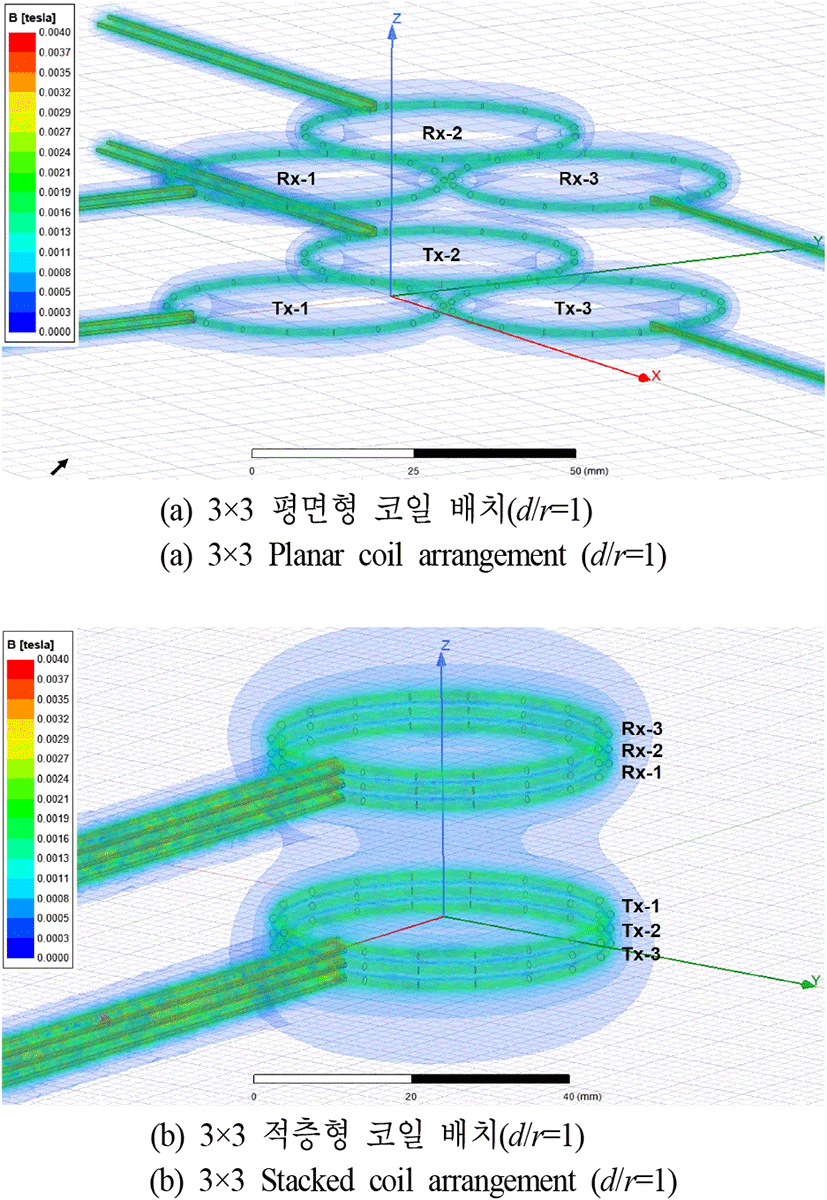
그림 7에서는 적층형과 평면형 코일 배치에 따라 계산된 상호 인덕턴스 비율에 대한 경향성이 유효한지 확인하기 위해 Ansys 사의 EM 시뮬레이션으로 3×3 코일을 구성하였다. 코일의 반지름은 표 3과 동일하며, 1-turn과 1-layer로 적용하였다. 그 결과, 앞에서 예상했던 것처럼 동일한 전송 거리(d/r=1)에서 적층형 배치가 평면형 배치보다 자속이 코일에 더 집중되는 경향을 확인할 수 있었다. 그리고 표 4에서는 d/r에 따른 상호 인덕턴스 비율에 대한 EM 시뮬레이션 결과와 계산결과를 비교하였으며 전반적으로 큰 차이 없이 유사함을 확인할 수 있었다.

그림 7. | Fig. 7. 다중 송수신 코일에 대한 EM 시뮬레이션 구성 | EM simulation for multiple-transceiver coils.

Download Original Figure

표 4. | Table 4. 3×3 코일 배치에 대한 상호 인덕턴스 비율 비교 | Comparison of mutual Inductance ratio for 3×3 coil arrangement.

d/r	Stacked								Planar
	\|M₁₂/M₁₁\|		\|M₁₃/M₁₁\|		\|M₂₃/M₁₁\|		\|M₃₃/M₁₁\|		\|M₁₂/M₁₁\|
	EM sim	Cal	EM sim	Cal	EM sim	Cal	EM sim	Cal	EM sim	Cal
1	0.86	0.86	0.75	0.75	0.66	0.65	0.58	0.57	0.002	0.01
2	0.89	0.9	0.8	0.81	0.72	0.73	0.64	0.67	0.18	0.18
3	0.91	0.92	0.83	0.85	0.75	0.79	0.68	0.73	0.36	0.39
4	0.92	0.93	0.85	0.88	0.78	0.83	0.72	0.78	0.49	0.54
5	0.93	0.95	0.86	0.90	0.8	0.85	0.74	0.81	0.59	0.66

Download Excel Table

전송 거리에 따른 다중 송수신 무선전력전송 시스템의 전력 전송 효율을 확인하기 위해 Keysight 사의 ADS 프로그램을 활용하였다. 그리고 표 5에서는 프로그램 시뮬레이션에 적용된 시스템 파라미터를 정리하였다.

표 5. | Table 5. 시뮬레이션을 위한 시스템 파라메터 | System parameters for simulation.

Notes	Symbol	Value
Operating frequency	f _o	100 kHz
Source voltage	V_S1, V_S2, V_S3	10 V
LCC inductance	L_S1, L_S2, L_S3	2.22 μH
LCC capacitance	C_P1, C_P2, C_P3	1.11 μF
Coil resonant capacitance	C_T1, C_T2, C_T3	0.17 μF
Tx resistance	R_T1, R_T2, R_T3	0.08 Ω
Rx coil resistance	R_r1, R_r2, R_r3	0.07 Ω
Tx/Rx coil inductance	L_T1, L_T2, L_T3 L_R1, L_R2, L_R3	14.6 μH
Tx current	I_T1, I_T2, I_T3	5 A
Rx load resistance	R_L1, R_L2, R_L3	1 Ω

Download Excel Table

시스템의 각 송신기 회로는 그림 8과 같이 송신코일 간의 상호 인덕턴스의 영향을 최소화하기 위해서 LCC 인버터를 적용하였으며 5 A의 동일한 송신전류를 갖도록 LCC 인버터의 L_S와 C_P를 조정하였다^[17]. 마찬가지로 시스템의 수신기에서는 수신코일 간의 불필요한 상호 인덕턴스의 영향을 최소화하기 위해 식 (13)의 커패시턴스 값을 적용해야하며, 여기서 필요한 i번째 수신전류(I_Ri)와 j번째 수신전류(I_Rj)의 비율은 식 (16)과 같이 정리된다. 하지만 이 식은 모든 수신전류를 파악하기 위한 매우 복잡한 계산 과정이 필요하기 때문에 전송 거리가 증가함에 따라 I_T > I_R인 특성을 고려하여 식을 근사해 적용하였다. 표 6에서는 수신기에 수신코일에 대한 공진 커패시턴스(C_fo)를 적용한 경우와 식 (13)로 도출한 커패시턴스(C_R)를 적용한 경우에 대한 ADS 시뮬레이션 결과를 비교하였으며, 모든 코일 간 상호 간섭이 있을 때 C_R을 적용한 경우 평면형 배치보다 적층형 배치가 더 높은 출력 전력과 전력 전송 효율을 달성함을 확인하였다.

그림 8. | Fig. 8. LCC 인버터가 적용된 송신기 등가회로 | Equivalent circuit of transmitter with LCC inverter.

Download Original Figure

표 6. | Table 6. 3×3 송수신 무선전력전송 시스템에 대한 ADS 효율 시뮬레이션 결과 | ADS simulation results for 3×3 multiple-transceiver WPT system.

d/r	Stacked arrangement				Planar arrangement
	with C_R		with C_fo		with C_R		with C_fo
	PTE	P_L (W)	PTE	P_L (W)	PTE	P_L (W)	PTE	P_L (W)
0.1	0.93	2722	0.88	50	0.93	1222	0.93	939
0.5	0.93	842	0.71	9	0.92	241	0.92	177
0.9	0.92	195	0.37	1	0.87	41	0.85	30
1.4	0.88	53	0.14	0.5	0.76	12	0.71	8
1.8	0.8	17	0.05	0.1	0.59	4	0.52	3
2.3	0.64	6	0.019	0.05	0.42	2	0.35	1
2.8	0.46	2	0.008	0.02	0.27	1	0.22	0.8
3.2	0.3	1	0.004	0.01	0.18	0.7	0.14	0.5

Download Excel Table

I R j I R i = ∑ k = 1 n M k j − ∑ k = 1, k ≠ j n M R j k I R k / I T ∑ k = 1 n M k i − ∑ k = 1, k ≠ i n M R i k I R k / I T ≈ ∑ k = 1 n M k j ∑ k = 1 n M k i

(16)

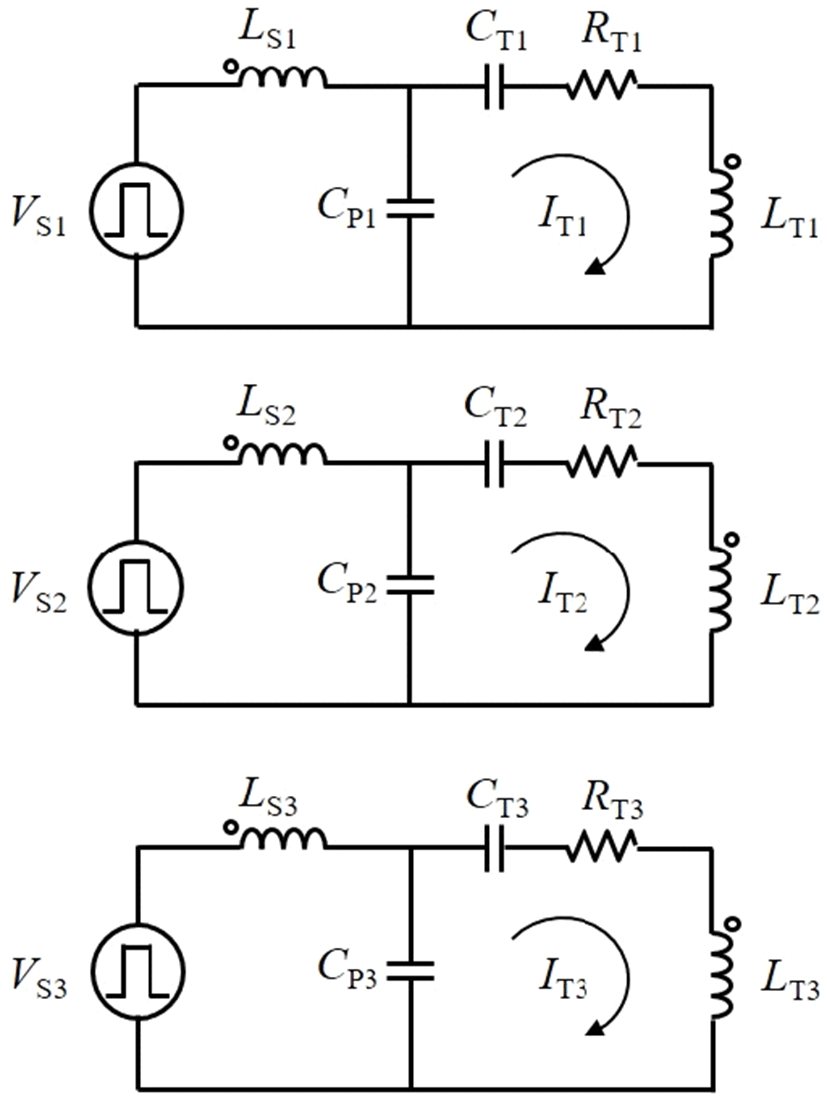
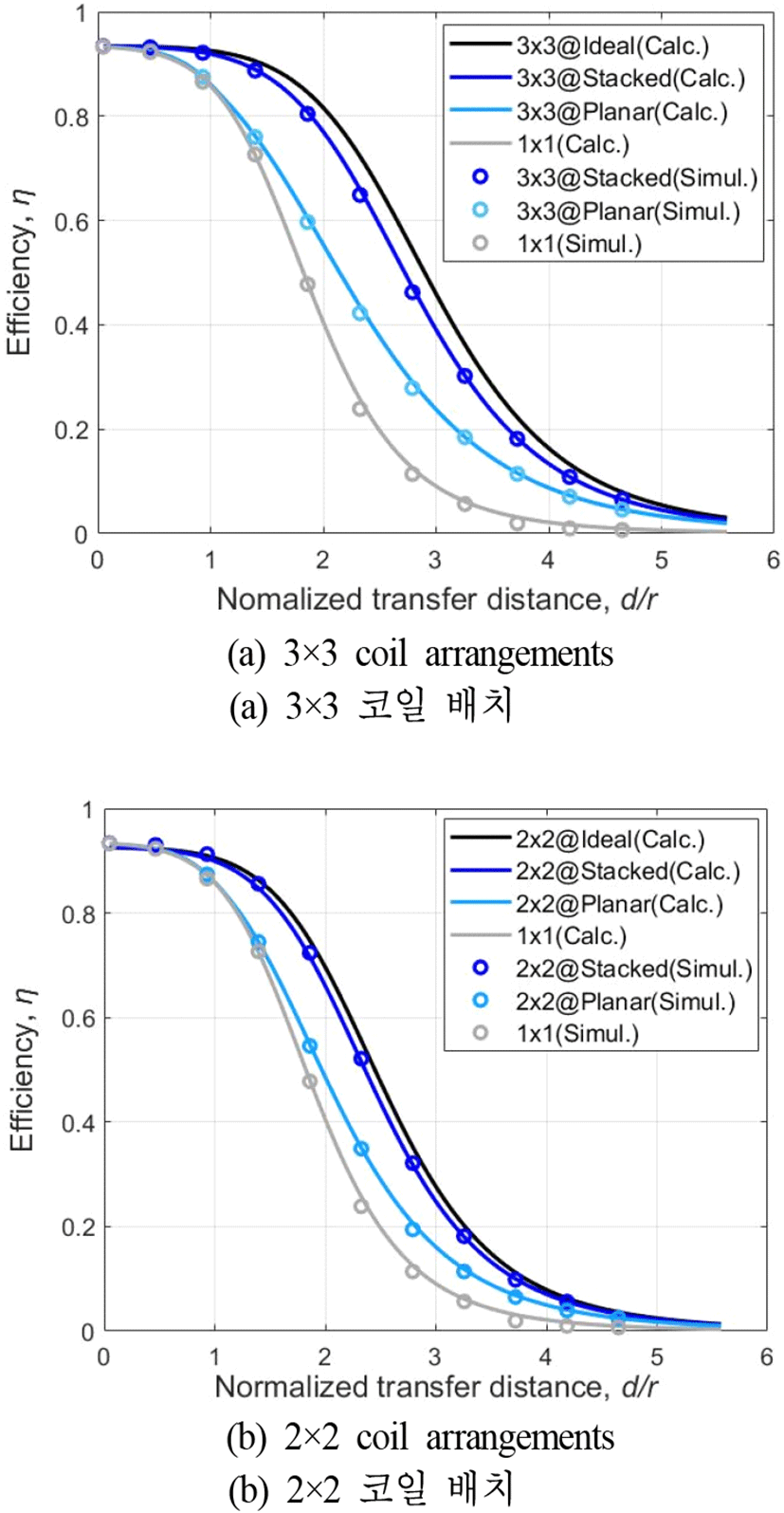
그림 9에서는 정규화된 전송 거리(d/r)에 따른 다중 송수신 무선전력전송 시스템의 전력 전송 효율을 나타냈다. 그림 6에서 예측했듯이 평면형 구조는 d/r=2 이하의 구간에서 0.2 이하의 작은 M_Ratio 특성으로부터 1×1 코일 시스템과 거의 유사한 결과를 보였다. d/r=2 이상부터는 M_Ratio의 증가로부터 1×1 코일 시스템보다 약간 더 향상된 효율 성능을 보였으나 상승폭은 미미하였다. 반면에 모든 전송거리 구간에서 M_Ratio가 0.4 이상을 만족하는 적측형 구조의 효율은 1×1 코일 시스템과 평면형 구조 시스템 보다 전반적으로 더 높은 효율 성능을 보였다. 특히, 3×3 배치에서는 d/r=1.86에서 적층형 구조는 평면형 구조보다 20 % 이상 더 높은 80 %의 효율을 달성할 수 있었으며, 송수신 코일 사이 모든 상호 인덕턴스가 M₁₁과 같은 이상적인 경우(M_Ratio=1)와 비교해도 큰 차이가 없을 만큼의 우수한 전력 전송 효율 성능을 확인할 수 있었다.

그림 9. | Fig. 9. 정규화된 전송 거리에 따른 전력 전송 효율 | Power transfer efficiency according to normalized transfer distance.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 다중 송수신 무선전력전송 시스템의 높은 전력 전송 효율 달성을 위한 효과적인 코일 배치 설계를 제안하였다. 먼저 다중 무선전력전송 시스템의 등가회로에 대한 해석을 통해 전력 전송 효율 수식을 간단히 정리하였다. 그리고 높은 전력 전송 효율 달성에 필요한 조건으로 사용하는 코일 개수를 증가에 따라 모든 송수신 코일 사이 가능한 큰 상호 인덕턴스가 요구된다는 사실을 확인하였다. 이러한 결과를 토대로 다중 송수신 코일 사이 모든 상호 인덕턴스를 최대로 유지시키기 위해 송수신 코일을 각각 완전히 겹치는 방식의 적층형 코일 배치 구조를 제안하였다.

제안하는 적층형 구조의 우수한 전력 전송 효율 성능을 확인하기 위해 시스템의 모든 송수신 코일 사이 상호 인덕턴스와 그 비율을 계산하고 전송 거리에 따른 전력 전송 효율 시뮬레이션 결과를 확인하였다. 그 결과, 제안하는 적층형 코일 배치는 기존의 평면형 코일 배치보다 최대 20 % 이상 더 높은 전력 전송 효율을 달성할 수 있었다.

본 논문의 분석 결과를 참고하였을 때, 제안하는 적층형 송수신 코일 배치는 높은 전력 전송 효율 성능을 보였지만 추후 수신기 측 컨버터까지 최적화된 실제 다중 송수신 무선전력전송 시스템 구현하여 여러 배터리 충전 성능에 대한 유효성 검증이 필요하다. 그리고 이러한 점이 검증된다면 UAV 및 EV 등의 어플리케이션에도 효율적으로 사용될 것으로 예상되며, 특히 지상의 발사대와 같은 제한적인 공간에서 운용되는 소형 무기체계에서의 충전 시스템에 적용한다면 보다 큰 효과를 볼 수 있을 것으로 기대된다.

References

[1].

S. Y. R. Hui, W. C. Ho, “A new generation of universal contactless battery charging platform for portable consumer electronic equipment,” IEEE Transactions on Power Electronics, vol. 20, no. 3, pp. 620-627, May 2005.

[2].

J. M. Miller, O. C. Onar, and M. Chinthavali, “Primary side power flow control of wireless power transfer for electric vehicle charging,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 3, no. 1, pp. 147-162, Mar. 2015.

[3].

T. C. Beh, M. Kato, T. Imura, S. Oh, and Y. Hori, “Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling,” IEEE Transactions on Industrial Electronics, vol. 60, no. 9, pp. 3689-3698, Sep. 2013.

[4].

T. H. Kim, G. H. Yun, W. Y. Lee, and J. G. Yook, “Asymmetric coil structures for highly efficient wireless power transfer systems,” IEEE Transactions on Microwave Theory and Techniques, vol. 66, no. 7, pp. 3443-3451, Jul. 2018.

[5].

S. H. Yoon, T. H. Kim, J. K. Park, S. T. Kim, G. H. Yun, and J. G. Yook, “Improvement of power transfer efficiency using negative impedance converter for wireless power transfer system with magnetic resonant coupling,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 28, no. 12, pp. 933-940, Dec. 2017.

[6].

T. H. Kim, G. H. Yun, W. Lee, and J. G. Yook, “Highly efficient WPT system with negative impedance converter for Q-factor improvement,” IEEE Access, vol. 7, pp. 108750-108760, Aug. 2019.

[7].

K. Hatanaka, F. Sato, H. Matsuki, S. Kikuchi, J. Murakami, and M. Kawase, et al., “Power transmission of a desk with a cord-free power supply,” IEEE Transactions on Magnetics, vol. 38, no. 5, pp. 3329-3331, Sep. 2002.

[8].

C. Sritongon, P. Wisestherrakul, N. Hansupho, S. Nutwong, A. Sangswang, and S. Naetiladdanon, et al., “Novel IPT multi-transmitter coils with increase misalignment tolerance and system efficiency,” in 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, May 2018, pp. 1-5.

[9].

H. J. Kim, K. Kim, S. Han, D. W. Seo, and J. W. Choi, “Nearly non-coupling coil array allowing many independent channels for magnetic communication,” IEEE Access, vol. 6, pp. 34190-34197, Jun. 2018.

[10].

S. J. Jeon, D. W. Seo, “Capacitance tuning method for maximum output power in multiple-transmitter wireless power transfer system,” IEEE Access, vol. 8, pp. 181674-181682, Oct. 2020.

[11].

S. J. Jeon, D. W. Seo, “Effect of additional transmitting coils on transfer distance in multipleple-transmitter wireless power transfer system,” IEEE Access, vol. 10, pp. 9174-9183, Jan. 2022.

[12].

H. Kim, S. J. Jeon, and D. W. Seo, “Experiment and analysis of a high-efficient stacked multiple-Tx WPT system with identical Tx currents,” International Journal of Electrical Power and Energy Systems, vol. 155, p. 109475, Sep. 2024.

[13].

H. Son, Y. Seon, and H. Ryu, “Multiple-copter(drone) and secondary battery,” Journal of the Korean Battery Society, vol. 1, no. 1, pp. 44-50, Jun. 2021.

[14].

A. Sharma, P. Zanotti, and L. P. Musunur, “Enabling the electric future of mobility: Robotic automation for electric vehicle battery assembly,” IEEE Access, vol. 7, pp. 170961-170991, Nov. 2019.

[15].

K. Kim, H. J. Kim, D. W. Seo, and J. W. Choi, “Magnetically decoupled modular coil array for dynamic wireless power transfer with magnetic beamforming,” IEEE Access, vol. 10, pp. 42121-42140, Apr. 2022.

[16].

S. Raju, R. Wu, M. Chan, and C. P. Yue, “Modeling of mutual coupling between planar inductors in wireless power applications,” IEEE Transactions on Power Electronics, vol. 29, no. 1, pp. 481-490, Jan. 2014.

[17].

S. Huh, D. Ahn, “Two-transmitter wireless power transfer with optimal activation and current selection of transmitters,” IEEE Transactions on Power Electronics, vol. 33, no. 6, pp. 4957-4967, Jun. 2018.

Author Information

전 선 재 [국방과학연구소/연구원]

jkiees-36-2-160-i1

https://orcid.org/0000-0002-8364-7752
2019년 2월: 한국해양대학교 전파공학과 (공학사)
2021년 2월: 한국해양대학교 전파공학과 (공학석사)
2021년 12월~현재: 국방과학연구소 연구원
[주 관심분야] 무선전력전송, 배터리, RF 등