The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(1):86-94

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.1.86

논문/REGULAR PAPERS

베이지안 최적화를 적용한 심층 학습 기반의 빔 형성 기술

유호근

, 임재혁^*

, 오선진^*

, 이의혁^*

, 정대교^*

, 김성권^*

, 오현수^**

, 이재훈^†

Deep Learning-Based Beamforming Design with Bayesian Optimization

Hogeun Yoo

, Jaehyuk Lim^*

, Sunjin Oh^*

, Euihyuk Lee^*

, Dae-kyo Jeong^*

, Sungkwon Kim^*

, Hyunsu Oh^**

, Jaehoon Lee^†

고려대학교 컴퓨터학과

^*국방과학연구소

^**(주)한화시스템

Department of Computer Science and Engineering, Korea University

^*Agency for Defense Development

^**Hanwha Systems Co., Ltd.

^†Corresponding Author: Jaehoon Lee (e-mail: ejhoon@korea.ac.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Oct 31, 2024; Revised: Nov 17, 2024; Accepted: Dec 31, 2024

Published Online: Jan 31, 2025

요 약

본 논문은 배열 안테나의 성능을 향상시키기 위해 심층 학습 기반의 빔 형성 기술을 탐구하며, 계산 비용을 최소화하면서 신호 대비 간섭 및 잡음 비율(SINR, signal to interference plus noise ratio)을 개선하는 것을 목표로 한다. 본 연구에서는 심층 학습을 활용해 수신 신호의 자기상관 행렬에서 최적의 빔 형성 가중치 벡터를 예측하는 방법을 제안한다. 심층 학습 중, 완전 연결 신경망(FNN, fully connected neural networks), 합성곱 신경망(CNN, convolutional neural networks), 순환 신경망(RNN, recurrent neural networks)을 사용해 수신 신호의 자기 상관 행렬로부터 가중치 벡터를 출력하도록 학습하고, 베이지안 최적화를 통해 각 모델의 하이퍼파라미터를 튜닝하였다. 실험 결과, FNN 모델이 원하는 SINR을 유지하면서 간섭을 최소화하는 빔을 형성하는 데 가장 우수한 성능을 보였다. 특히 FNN 모델은 다양한 신호 대비 잡음 비율(SNR, signal to noise ratio) 조건에서 최적 가중치 벡터 대비 SINR의 열화가 0.32 dB에 불과하여, 심층 학습 기반 빔 형성에 적합한 모델로 확인되었다. 이 연구는 배열 안테나에서 심층 학습을 활용한 빔 형성 기술이 효율성과 정확성을 높일 수 있는 것을 확인하였다.

Abstract

This study explores deep-learning-based beamforming techniques to enhance the performance of array antenna systems with the aim of reducing computational costs and improving the signal-to-interference-plus-noise ratio (SINR). In this study, a method is proposed to predict the optimal beamforming weight vector using deep learning. This approach involves training fully connected neural networks (FNN), convolutional neural networks (CNN), and recurrent neural networks (RNN) to learn the autocorrelation matrix of the received signals and output the weight vector. Bayesian optimization was employed to tune the hyperparameters of each model. The experimental results indicated that the FNN model exhibited the best performance in forming beams that maintained the desired signal while minimizing interference. Specifically, the FNN model demonstrated an SINR difference of only 0.32 dB from the theoretical optimal weight vector across various signal-to-noise ratio (SNR) conditions, confirming its suitability for deep learning-based beamforming. This study highlights the potential of deep-learning-based beamforming techniques to improve both the efficiency and accuracy of array antenna systems.

Keywords: Antenna Array; Bayesian Optimization; Beamforming; Deep Learning; Signal Processing

Ⅰ. 서 론

최근 배열 안테나 신호 처리 시스템에서는 다양한 간섭 신호와 잡음 환경에서 원하는 신호를 효율적으로 수신하기 위한 기술이 필수적이다. 특히, 다수의 안테나 배열을 이용한 빔 형성(beamforming) 기술은 신호 대비 잡음비(SNR, signal to noise ratio)를 극대화하고, 간섭 신호를 최소화함으로써 수신 신호의 품질을 향상하는 데 중요한 역할을 한다. 빔 형성 기술은 전통적으로 수학적 최적화 기법에 기반하여 설계되었으나, 최근 심층 학습(deep learning) 기술이 다양한 분야에서 성과를 이루면서 배열 안테나 신호 처리 분야에서도 적용되고 있다.

기존 연구에 따르면, 빔 형성 문제에서 기존 방법들이 가진 계산 복잡도와 환경 변화 적응 문제를 해결하는 데 심층 학습 모델이 효율적으로 사용되는 연구가 발표되고 있다. 다양한 신경망 구조를 활용하여 실시간 계산 능력과 높은 정확도를 제공함으로써 5G 및 차세대 통신, 초음파, 레이다 등에서 요구되는 성능을 충족시키고 있다^[1]~[3].

특히, 심층 학습 기반 빔 형성 가중치 추정 기술은 수신 신호를 학습하여 최적의 빔 형성 가중치 벡터(weight vectors)를 예측하는 방법으로 사용된다. 합성곱 신경망(CNN, convolutional neural network)을 적용하여 수신 신호의 공분산 행렬의 일부를 입력으로 사용하고, 신경망을 통해 최적의 가중치 벡터를 추정함으로써 간섭 신호를 최소화하고 신호 품질을 개선하는 연구가 발표되었다. 이러한 방법은 제한된 컴퓨팅 환경에서 빔 형성을 수행하는 데 효과적이다^[4],[5].

본 논문에서는 심층 학습을 활용한 빔 형성 가중치 추정 모델을 제안한다. 심층 학습 기반의 접근법은 대규모 데이터로부터 학습하여 비선형 문제를 효과적으로 해결할 수 있다. 특히, 본 연구는 완전 연결 신경망(FNN, fully connected neural network), 합성곱 신경망(CNN, convolutional neural network), 순환 신경망(RNN, recurrent neural network)과 같은 다양한 심층 학습 모델을 설계 및 비교하고, 베이지안 최적화(Bayesian optimization)를 이용하여 각 심층 신경망(DNN, deep neural network) 모델의 하이퍼파라미터를 최적화함으로써 모델 성능을 극대화하고자 한다. 이를 통해, 최적의 빔 형성 가중치를 추정하는 모델을 제안하고자 하며, 복잡한 간섭 및 잡음 환경에서도 원하는 신호를 정확하게 수신할 수 있는 심층 학습 기반의 빔 형성 기술을 구현하고, 해당 기술의 성능을 검증한다.

본 논문은 다음과 같이 구성된다. Ⅱ장에서는 신호 모델 설계 방법에 대해 살펴보고, Ⅲ장에서는 제안하는 심층 학습 모델 설계 방법을 설명한다. Ⅳ장에서는 실험 방법에 대해 설명하고, 각각의 모델별 성능을 비교/분석하며, Ⅴ장에서 결론을 맺는다.

Ⅱ. 신호 모델

2-1 신호 모델

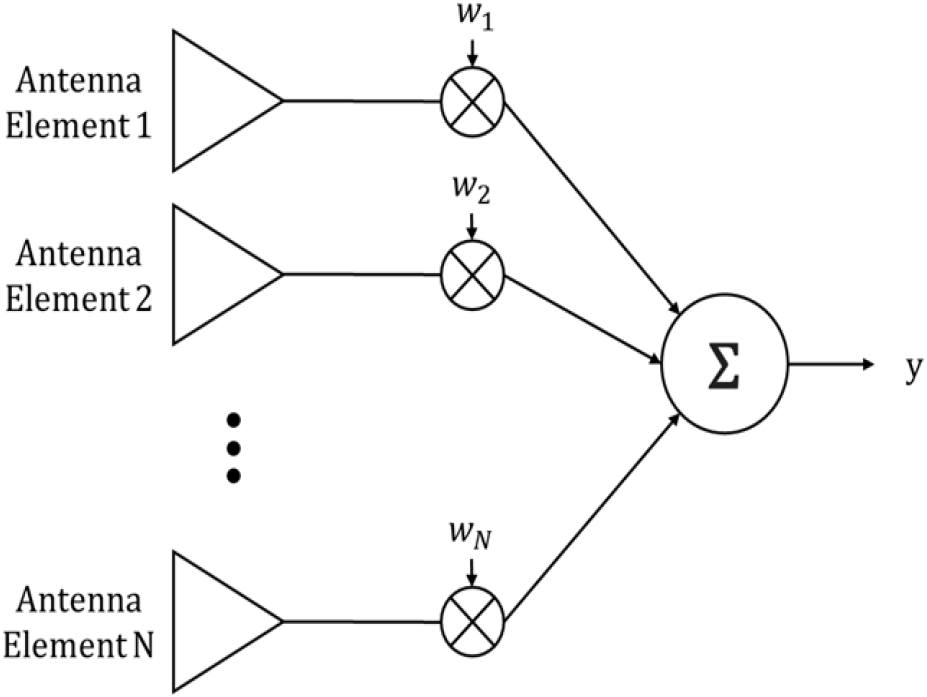
본 논문에서는 그림 1과 같이 N개의 안테나가 간격 d로 배치된 선형 배열 안테나(ULA, uniform linear array)에서의 수신 신호를 고려하였다. 1개의 원하는 신호 s(t)와 Q개의 간섭 신호 i_q(t)가 중심주파수 f_c에 존재할 때, k번째 안테나에서 시간 t에 수신된 신호를 식 (1)과 같이 표현할 수 있다.

x k (t) = s t − Δ t k, p e j 2 π f c t − Δ t k, p + ∑ q = 1 Q i q t − Δ t k, q e j 2 π f c t − Δ t k, q, k = 0, 1, 2, …, N − 1

(1)

그림 1. | Fig. 1. N개의 안테나가 있는 선형 배열 안테나 | Uniform linear array with N antennas.

Download Original Figure

Δt_k,p와 Δt_k,q는 각각 k번째 안테나에 각도 θ_p로 도착하는 원하는 신호와 각도 θ_q로 도착하는 간섭 신호의 시간지연이다.

수신기에서는 Downconversion 신호 x_p^′(t)를 샘플링 주기 T로 샘플링하여 수신 신호를 얻게 된다. 이때 수신 신호가 협대역이어서 샘플링 주기 T가 시간지연 Δt_k,p와 Δt_k,q보다 크다고 가정하면, 잡음을 고려한 k번째 안테나의 수신 신호는 식 (2)와 같다.

x k [n] = x k ′ (n T) = s [n] e − j 2 π f c Δ t k, p + ∑ q = 1 Q i q [n] e − j 2 π f c Δ t k, q + n k [n]

(2)

s[n]와 i_q[n]는 각각 샘플링된 s(nT)와 i_q(nT)이며, N개의 안테나에서 수신된 신호를 벡터 x[n]으로 표현하면 식 (3)과 같다.

x [n] = x 0 [n], x 1 [n], x 2 [n], …, x N − 1 [n] T = a θ p s [n] + ∑ q = 1 Q b θ q i q [n] + n [n]

(3)

여기서 n[n]는 잡음 신호 벡터, a(θ_p)와 b(θ_q)는 각각 원하는 신호, 간섭 신호들에 대한 조향 벡터(steering vector)이며 식 (4) 및 식 (5)와 같이 표현된다.

a θ p = 1, e − j 2 π d λ sin θ p, …, e − j 2 π (N − 1) d λ sin θ p T

(4)

b θ q = 1, e − j 2 π d λ sin θ q, …, e − j 2 π (N − 1) d λ sin θ q T

(5)

여기서, λ는 수신 신호의 파장이다. 시간 n에서 수신된 K개의 스냅샷(snapshot)을 식 (6)과 같이 가정할 때,

X [n] = [x [n], x [n − 1], …, x [n − K − 1]]

(6)

수신 신호에 대한 자기상관 행렬 R는 식 (7)과 같이 구할 수 있다.

R = 1 K X X H

(7)

여기서, X^H의 H는 에르미트 전치(Hermitian transpose)를 의미한다.

Ⅲ. 빔 형성 가중치 추정 심층 신경망 모델 설계

3-1 심층 신경망 모델의 입출력

본 논문에서는 수신 신호의 자기상관 행렬 R의 상부 삼각 행렬의 정규화 값을 입력으로 갖고, 최적의 가중치 벡터를 출력으로 갖는 심층 학습 네트워크 모델을 설계하였다.

제안하는 모델의 입력을 정의하기 위해, R의 상부 삼각 행렬의 정규화 값을 z를 식 (8)과 같이 정의하였다.

z = r ‖ r ‖

(8)

여기서, r=[R₁₂,…,R_1N,R₂₃,…,R_2N,R_(N-1)N]이며, R_ij는 R의 i행 j열을 의미한다.

일반적으로 심층 학습 네트워크 모델은 복소수에 대해 직접 학습을 수행할 수 없으며, 본 논문에서는 z를 실수부와 허수부로 분리하여 식 (9)와 같이 $z^$ 를 입력값으로 구성하였다.

z^= [Re (z), Im (z)]

(9)

제안하는 모델의 출력으로 신호 대비 간섭 및 잡음 비율(SINR, signal to interference noise ratio)을 최대화하는 안테나 배열의 가중치 벡터 w_o를 고려하였다. 원하는 신호의 자기상관 행렬 Γ, 간섭 신호와 잡음 신호의 자기상관 행렬 C에 대한 SINR은 식 (10)과 같다^[6].

S I N R = w H Γ w w H C w

(10)

식 (10)의 SINR을 최대로 하는 w를 이론적 최적의 가중치 벡터 w_o라 할 때, 식 (11)과 같이 계산할 수 있다^[6].

w o = C − 1 a a H C − 1 a

(11)

심층 신경망 모델의 출력값 $w 0^$ 에 대해서도 식 (12)와 같이 실수부와 허수부로 구성하였다.

w o^= Re w o, Im w o

(12)

따라서, 그림 2와 같이 $z^$ 를 제안하는 모델의 입력값으로 사용하며, N×(N-1)개의 입력 노드를 갖는다. $w 0^$ 를 제안하는 모델의 출력값으로 사용하며, 2×N개의 출력 노드를 갖는다.

그림 2. | Fig. 2. 심층 신경망 모델의 구조 | Structure of deep neural network models.

Download Original Figure

3-2 심층 신경망 모델 설계

본 논문에서는 최적의 빔 형성 가중치 추정 심층 학습 모델을 설계하기 위해 FNN, CNN, RNN 모델을 고려하였다. 각각의 모델에 대해 동일한 손실 함수(loss function)로 식 (13)과 같이 정의하였다.

L l o s s = 1 M ∑ i = 1 M y i − y i^2

(13)

여기서, y_i는 학습된 모델이 추정한 가중치 벡터이며, $y i^$ 는 검증 데이터의 가중치 벡터이다. 본 논문에서는 미니 배치 단위로 학습을 수행하였으며, M은 미니 배치의 크기이다. 이 손실 함수는 L2 손실 함수로, 제곱 오차(squared error)를 기반으로 예측된 가중치 벡터와 참 가중치 벡터 사이의 오차를 측정하여, 모델이 빔 형성 가중치를 정확하게 추정하는지를 평가한다. 모델이 학습 과정에서 최적의 가중치 벡터를 찾아낼 수 있도록 한다.

본 논문에서는 각 모델에 활성화 함수로 계산 효율성을 고려하여 ReLU(rectified linear unit)^[7]를 적용하고, 가중치 변수 갱신에는 Adam^[8]을 이용하였다. 학습 속도를 개선하면서, 과적합을 억제하기 위해 각 계층별로 배치 정규화 계층을 활성 함수 전에 포함하였다^[9].

활성화 함수로 사용되는 ReLU의 수식은 식 (14)와 같다.

y = x (x > 0) 0 (x ≤ 0)

(14)

3-2-1 FNN 모델

전방향 신경망이라고도 불리는 이 모델은 가장 기본적인 인공 신경망 구조로, 데이터가 입력층에서 출력층으로 방향성을 가지고 전달되는 특징이 있다. FNN은 여러 개의 은닉층을 가질 수 있으며, 각 층은 이전 층으로부터 입력을 받아 배치 정규화 계층을 통해 비선형 활성화 함수인 ReLU 적용한 후 다음 층으로 출력을 전달한다. FNN의 주요 목표는 주어진 입력과 출력 사이의 복잡한 함수 관계를 학습하는 것이다. FNN은 고정된 길이의 입력을 처리하는 데 적합하다.

FNN 모델의 네트워크 구조와 관련된 하이퍼파라미터로 완전 연결 계층, 배치 정규화 계층, ReLU 계층을 하나의 셋(set)으로 구성한 계층 셋의 깊이와 완전 연결 계층의 노드 수를 정의하는 너비가 있다. 본 논문에서는 FNN 모델의 입력으로 수신 신호의 자기상관 행렬 R에서, 상부 삼각 행렬의 정규화된 값을 N(N-1)×1 행렬로 사용하였다.

3-2-2 CNN 모델

CNN은 2차원 데이터 분석에서 주로 사용되는 신경망 모델이다. CNN은 입력 데이터의 공간적 구조를 유지하며, 패턴 인식과 같은 작업에 적합한 성능을 보인다. CNN은 컨볼루션 연산을 통해 입력 데이터로부터 특징을 추출하며, 이러한 특징들은 심층 신경망 구조를 통해 계층적으로 결합된다. CNN의 주요 장점은 입력 데이터의 위치나 크기에 불변성을 가지는 특징을 학습할 수 있다는 점이다.

CNN 모델의 네트워크 구조와 관련된 하이퍼파라미터로 합성곱 계층, 배치 정규화 계층, ReLU 계층을 하나의 셋으로 구성한 계층의 깊이와 합성곱 계층의 채널 수를 정의하는 너비가 있다. 본 논문에서는 CNN 모델의 입력으로 수신 신호의 자기상관 행렬 R에서, 상부 삼각 행렬의 정규화된 값을 N×(N-1) 행렬로 사용하였다.

3-2-3 RNN 모델

RNN은 순차적 데이터, 특히 시계열 데이터와 같이 시간적 종속성이 있는 데이터 처리에 특화된 신경망 모델이다. RNN은 이전 단계의 출력이 다음 단계의 입력으로 다시 피드백되는 순환 구조를 가지고 있어, 시퀀스의 맥락 정보를 유지하면서 학습할 수 있다. 이 특성은 RNN이 자연어 처리, 음성 인식, 시계열 예측 등의 응용 분야에서 매우 효과적으로 활용될 수 있게 한다. 그러나 RNN은 장기 의존성을 학습하는 데 어려움을 겪을 수 있으며, 이는 기울기 소실(vanishing gradient) 문제로 이어질 수 있다. 이를 해결하기 위해 LSTM(long short-term memory)이나 GRU(gated recurrent unit)와 같은 RNN의 변형 모델들이 제안되었으며, 본 논문에서는 LSTM 모델을 고려하였다.

RNN 모델의 네트워크 구조와 관련된 하이퍼파라미터로 LSTM 계층, 배치 정규화 계층, ReLU 계층을 하나의 셋으로 구성한 계층의 깊이와 LSTM 계층의 수를 정의하는 너비가 있다. 본 논문에서는 RNN 모델의 입력으로 수신 신호의 자기상관 행렬 R에서, 상부 삼각 행렬의 정규화된 값을 N(N-1)×1 행렬로 사용하였다.

3-3 베이지안 최적화

베이지안 최적화(Bayesian optimization)는 고비용 함수 또는 잡음이 있는 비선형 함수의 최적화를 위해 사용되는 방법으로, 하이퍼파라미터 조정과 같이 평가 비용이 높은 문제에서 효율적으로 최적의 값을 찾는 데 적합하다. 목표 함수(objective function)의 사전 정보를 활용하여 최적화를 수행하며, 일반적으로 가우시안 과정(GP, Gaussian process)과 같은 확률적 모델을 사용하여 목표 함수를 추정한다^[10].

본 논문에서는 각각 네트워크 구조에 대해 베이지안 최적화를 적용하여 검토하였다. 베이지안 최적화 대상 하이퍼파라미터로 신경망의 구조와 학습률을 고려하였으며, 모델별로 적용하였다. 베이지안 최적화 과정에서 각각의 모델별로 48회 반복 탐색을 수행하였으며, 모델 구조의 변화를 고려하여 학습률 또한 0.0001~0.01 범위에서 최적화하였다. 베이지안 최적화의 목적 함수는 모델의 손실값을 설정하여 이를 최소화하는 방향으로 최적화를 진행하였다.

각 모델별로 최적화 대상이 되는 하이퍼파라미터는 다음과 같다:

– FNN 모델: 완전 연결 계층, 배치 정규화 계층, ReLU 계층으로 구성된 계층 셋의 반복 횟수를 깊이로, 각 완전 연결 계층의 노드 수를 너비로 설정하였다.
– CNN 모델: 합성곱 계층, 배치 정규화 계층, ReLU 계층으로 구성된 계층 셋의 반복 횟수를 깊이로, 합성곱 계층의 채널 수를 너비로 설정하였다.
– RNN 모델: LSTM 계층, 배치 정규화 계층, ReLU 계층으로 구성된 계층 셋의 반복 횟수를 깊이로, LSTM 계층의 수를 너비로 설정하였다.

모든 모델에 대해 깊이에 대해서는 3~8개의 범위, 너비에 대해서는 4~64개의 범위를 설정하여 비교 분석하였다.

Ⅳ. 실험 방법

본 논문에서는 학습 데이터 생성 및 모델 학습, 베이지안 최적화 과정에 MATLAB R2024a(MathWorks, Natick, MA, USA)를 사용하였으며, MATLAB의 Deep learning Toolbox 24.1, Statistics and Machine Leaning Toolbox 24.1 을 사용하였다.

4-1 학습 데이터 구성

빔 형성을 위한 심층 학습 네트워크 모델을 구현하기 위해, 10개의 등방성(isotropic) 안테나로 구성된 선형 배열 안테나를 고려하였으며, 인접한 두 안테나 간의 간격 d는 λ/2로 설정하였다. 모델을 훈련하기 위한 데이터는 해당 선형 배열 안테나에 1개의 원하는 신호와 4개의 간섭 신호가 안테나에 수신될 때를 가정하여 생성하였으며, 신호 대비 잡음 비(SNR, signal to noise ratio)를 10 dB, 간섭 대비 신호 비(ISR, interference to signal)를 15 dB의 환경을 고려하였다.

원하는 신호는 30°에서 고정하고, 간섭 신호 2개는 −90°에서 0°까지, 1° 간격으로 각각 샘플링하여 생성하였다. 나머지 2개의 간섭 신호는 −40°, −70°에 위치에 생성하였다. 각 샘플링 각도 당 400개의 수신 신호를 생성하여 총 3,312,400개의 데이터를 생성하였다. 이를 학습 데이터와 검증 데이터 및 테스트 데이터로 8:1:1 비율로 나누어 활용하였으며, 서로 다른 모델에 대해 동일한 데이터로 학습 및 검증을 수행하였다.

4-2 모델 학습

학습 전에 학습 데이터를 랜덤한 순서로 섞어 모델이 일반화 성능을 갖도록 하고, 특정 패턴이나 순서에 의한 편향을 방지하였으며, 미니 배치 크기로 1801, 1 에폭(epoch)을 적용하여 학습하였다. 학습 과정에서 검증 데이터에 대해 가장 낮은 손실값을 기록한 시점의 모델을 학습에 대한 최종 출력으로 사용하였다.

4-2-1 모델에 대한 베이지안 최적화 적용 결과

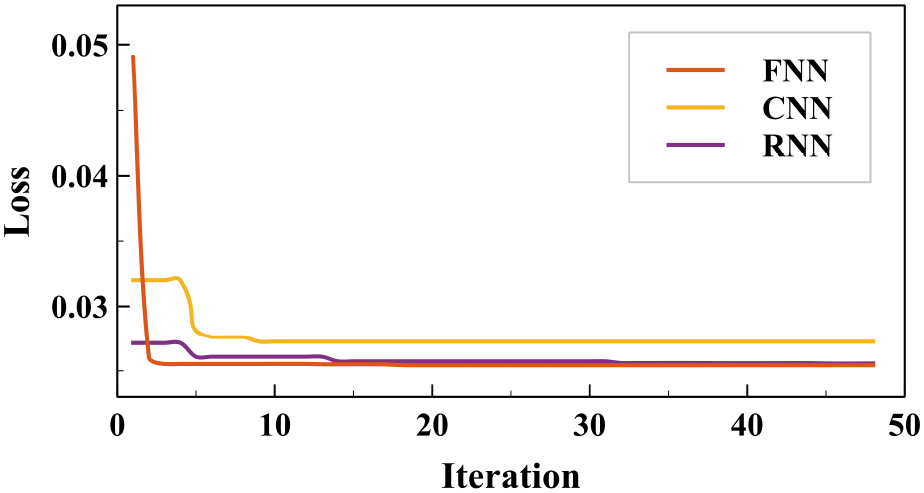
본 논문에서는 베이지안 최적화를 각각의 모델별로 48회 반복 탐색하여 최적의 네트워크 모델을 추정하였다. 그림 3과 같이 각 모델은 손실값을 기준으로 최적화하였으며, 근소한 차이로 FNN, RNN 구조가 CNN 구조에 비해 더 효과적으로 수렴하는 것을 볼 수 있다.

그림 3. | Fig. 3. FNN, CNN, RNN 모델 베이지안 최적화 | Bayesian optimization of FNN, CNN, and RNN models.

Download Original Figure

제안한 베이지안 최적화 방법에 따라 학습된 모델에 대한 목적 값 및 하이퍼파라미터 결과는 표 1과 같다. 이때, 목적 함수의 결과는 추정된 모델의 손실값이다. 일반적으로 낮을수록 최적화가 잘 되었음을 의미하며, 표 1의 결과에 따라, FNN 모델은 깊이 8, 너비 49, 학습률 0.00946에서 최저 손실값을 기록하며 최적의 성능을 보였다. CNN과 RNN 또한 각기 다른 최적화된 하이퍼파라미터 조합에서 성능이 도출되었으며, 모델별 최적화 결과는 실험적으로 검증되었다.

표 1. | Table 1. FNN, CNN, RNN 모델의 최적화 결과 | Optimization results of FNN, CNN, and RNN models

Model	Loss	Learning rate	Depth	Width	Number of parameters
FNN	0.02542	0.00946	8	49	23,393
CNN	0.02725	0.00995	8	5	10,760
RNN	0.02555	0.00854	8	59	234,132

Download Excel Table

4-3 학습 결과 및 평가

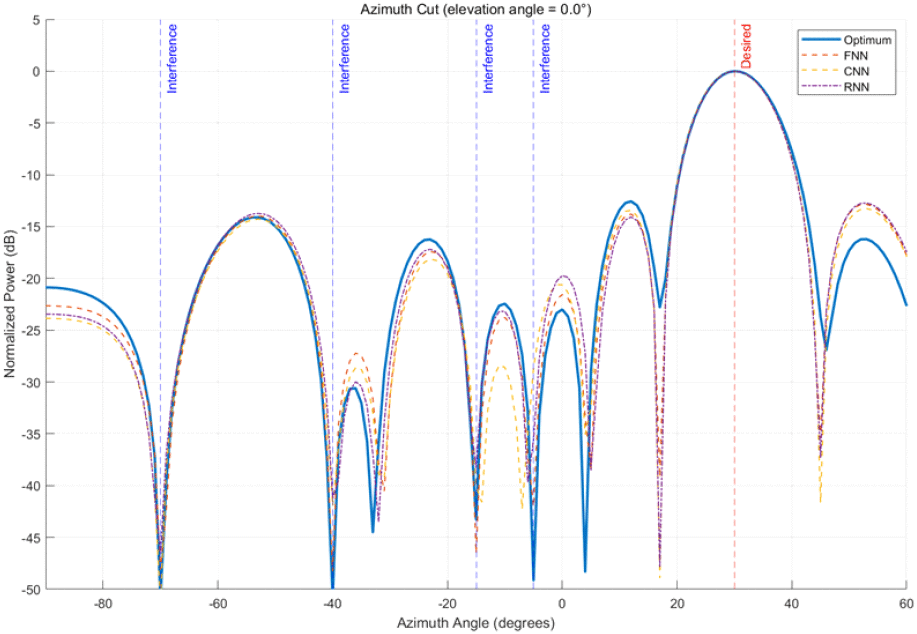
그림 4는 30°에서 원하는 신호를 수신하고, −70°, −40°, −15°, −5°에서 간섭 신호를 수신하는 환경에서 테스트 데이터를 사용하여 빔 패턴을 분석한 결과를 나타낸다. 신호 대비 잡음 비율 10 dB, 간섭 대비 신호 비율 15 dB 환경을 고려하였으며, 그림과 같이 원하는 신호의 방향으로는 보존하면서 간섭 신호 방향으로는 최소화하는 빔 패턴에서, FNN 모델이 다른 모델보다 간섭 신호의 위치를 정확하게 추정하면서 신호 감쇠 폭이 더 깊게 형성됨을 확인하였다. 그림 5는 30°에서 원하는 신호를 수신하고, 동시에 −80°, −70°, −40°, −20°에서 간섭 신호를 수신하는 환경에서 테스트 데이터를 사용하여 신호 대비 간섭 및 잡음 신호의 세기를 분석한 결과를 보여준다. 간섭 대비 신호 비율이 15 dB인 상황에서, 동일한 모델이 신호 대비 잡음 비율이 0 dB에서 15 dB까지 변하는 동안 학습된 모델의 강건성을 확인하였다. 각 모델 별로 최적의 가중치 벡터가 갖는 SINR과 비교하였을 때, FNN 모델은 최적 대비 전체 구간에 대한 평균 0.32 dB 차이가 확인되며, 다음으로 RNN 모델이 평균 0.41 dB, CNN 모델이 평균 1.02 dB로 확인되었다.

그림 4. | Fig. 4. FNN, CNN, RNN 모델의 빔 패턴 비교 | Comparison of beam patterns for FNN, CNN, and RNN models.

Download Original Figure

그림 5. | Fig. 5. 간섭 및 잡음 환경에서 FNN, CNN, RNN 모델 및 MPDR의 SINR 성능 비교 | SINR performance comparison of FNN, CNN, RNN models and the MPDR in interference and noise environments.

Download Original Figure

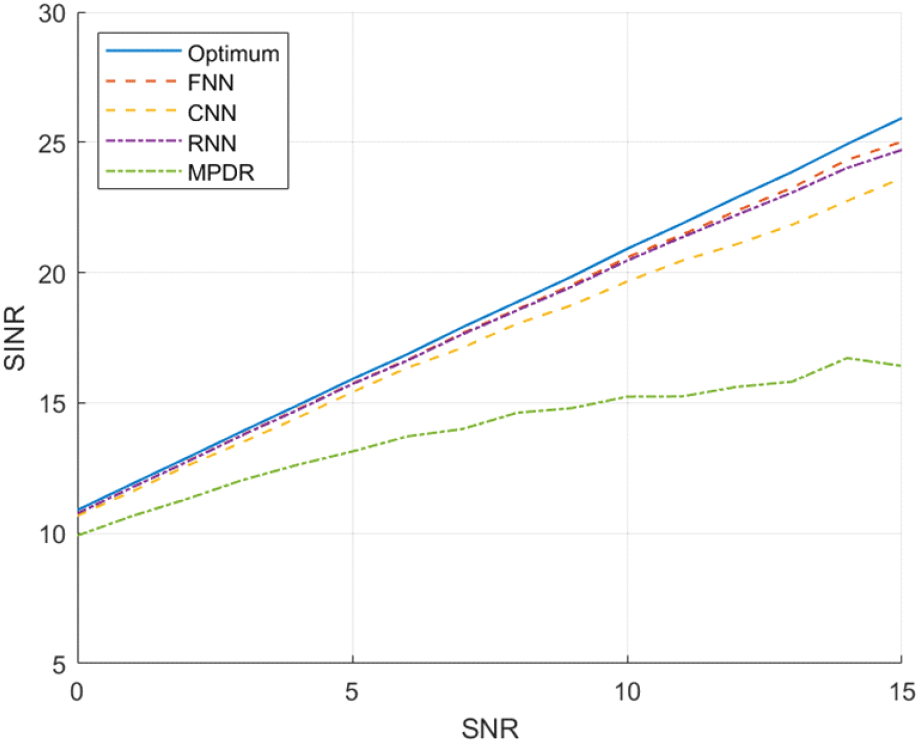
제안하는 딥러닝 기반의 빔 형성 모델은 원하는 신호에 대한 사전 정보가 없는 수신 신호의 자기상관 행렬 R을 입력으로 갖는다. 동등한 비교를 위해 수신 신호의 자기상관 행렬 R을 빔 형성 가중치 계산에 사용하는 빔 형성 알고리즘인 MPDR(minimum power distortionless response)를 비교하였으며 최적 대비 평균 4.44 dB 차이가 확인되었다. 모델별로 최적화된 표 1의 결과에서 예상할 수 있듯이, 모델의 효율성 측면과 신호 대비 간섭 및 잡음의 세기 측면에서도 모델 중 FNN이 빔 형성에 가장 적합한 모델임을 확인하였다.

Ⅴ. 결 론

본 논문에서는 간섭 신호 및 잡음 신호를 억제하기 위한 심층 학습 기반 빔 형성 기술을 연구하였다. 제안된 심층 학습 기반 모델은 동일하게 입력 데이터로 수신 신호의 자기 상관 행렬 R을 빔 형성 가중치 계산에 사용하는 빔 형성 알고리즘인 MPDR과 비교할 때, 신호 대 잡음비가 15 dB일 때, 신호 대 잡음 및 간섭비에서 MPDR에 비해 최소 7.04 dB에서 최대 8.92 dB까지 개선된 성능을 보였다.

모델별 최적 성능 비교를 위해 베이지안 최적화 알고리즘을 사용하여 하이퍼파라미터를 조정한 결과, FNN 모델이 가장 낮은 손실값을 기록하였다. 빔 형성 문제에서 주로 사용되는 수신 신호의 공분산 행렬 및 가중치 벡터는 단일 시점에서 독립적으로 처리되며, 시간적 또는 공간적 변화에 의존하지 않기 때문에, 시간적 종속성을 모델링하는 RNN이나 공간적 특징 추출에 특화된 CNN보다 입력과 출력 간의 관계를 단순히 학습하는 FNN이 더 적합한 것으로 보인다.

FNN 모델에서는 신호 대 잡음비가 0 dB에서 15 dB까지 변하는 환경에서, 최적의 가중치 벡터에 따른 신호 대비 간섭 및 잡음비와 비교해 0.32 dB의 차이만 나타났다. 이를 통해 심층 학습 기반 모델의 빔 형성 기술이 적용 가능함을 확인할 수 있었다.

Acknowledgements

이 논문은 2023년도 한화시스템(주)의 재원을 지원받아 수행된 연구임.

References

[1].

H. A. Kassir, Z. D. Zaharis, P. I. Lazaridis, N. V. Kantartzis, T. V. Yioultsis, and T. D. Xenos, "A review of the state of the art and future challenges of deep learning-based beamforming," IEEE Access, vol. 10, pp. 80869-80882, Aug. 2022.

[2].

B. Luijten, R. Cohen, F. J. de Bruijn, H. A. W. Schmeitz, M. Mischi, and Y. C. Eldar, et al, "Adaptive ultrasound beamforming using deep learning," IEEE Transactions on Medical Imaging, vol. 39, no. 12, pp. 3967-3978, Dec. 2020.

[3].

I. Mallioras, Z. D. Zaharis, P. I. Lazaridis, and S. Pantelopoulos, "A novel realistic approach of adaptive beamforming based on deep neural networks," IEEE Transactions on Antennas and Propagation, vol. 70, no. 10, pp. 8833-8848, Oct. 2022.

[4].

J. Yun, J. Lee, J. Joo, T. Jung, J. Park, and D. Lee, "Adaptive beamforming technology using convolutional neural networks based on unsupervised learning for jamming suppression," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 12, pp. 927-935, Dec. 2023.

[5].

P. Ramezanpour, M. J. Rezaei, and M. R. Mosavi, "Deep-learning-based beamforming for rejecting interferences," IET Signal Processing, vol. 14, no. 7, pp. 467-473, Sep. 2020.

[6].

I. S. Reed, J. D. Mallett, and L. E. Brennan, "Rapid convergence rate in adaptive arrays," IEEE Transactions on Aerospace and Electronic Systems, vol. AES-10, no. 6, pp. 853-863, Nov. 1974.

[7].

V. Nair, G. E. Hinton, "Rectified linear units improve restricted Boltzmann machines," in Proceedings of the 27th International Conference on Machine Learning(ICML-10), Haifa, Sep. 2010, pp. 807-814.

[8].

D. Kinga, J. Ba, "Adam: A method for stochastic optimization," in 3rd International Conference on Learning Representations(ICLR), San Diego, CA, May 2015, p. 6.

[9].

S. Ioffe, C. Szegedy, "Batch normalization: Accelerating deep network training by reducing internal covariate shift," 2020. Available: https://arxiv.org/abs/1502.03167

[10].

P. I. Frazier, "A tutorial on Bayesian optimization," Jul. 2018. Available: https://arxiv.org/abs/1807.02811