Ⅰ. 서 론
레이다는 목표 탐지 거리 또는 SNR을 확보하기 위해서는 충분한 EIRP를 만족해야 한다. 하지만 EIRP를 높이기 위해 안테나 방사소자의 개수를 늘리면 빔폭이 좁아져 모든 탐지 범위를 조향하는 시간이 늘어나게 된다. 충분한 개수의 소자를 사용함과 동시에 EIRP를 만족하기 위해서는 크기와 위상 조정을 통한 넓은 빔 형성이 필요하다.
크기와 위상을 조절하여 송신 넓은 빔 패턴을 만들기 위한 연구는 계속되어 왔다. 휴리스틱 알고리즘 혹은 랜덤 크기 조절 기법 등을 이용한 방법은 최적해를 찾기 때문에 많은 시간적 소요와 오류가 동반된다[1],[2]. 또한, 크기를 조절하기 힘든 포화상태의 Amp를 사용하는 송신기 같은 경우에는 위상 조절만을 통해서 넓은 빔을 만들 필요성이 대두되어 연구되어 왔다[3],[4]. 하지만 넓은 빔을 만들기 위한 수식화가 되어 있지 않아 경험적 또는 알고리즘을 통해 넓은 빔을 얻을 수 있었다.
본 연구에서는 정확한 수식을 통하여 넓은 빔 형성 원리와 정확한 넓은 빔폭 예측 및 계산을 수행할 수 있는 이진 위상 조절 송신 넓은 빔 기법을 제안한다. 제안된 방법은 단 두 개의 위상을 사용함으로서 소자별 발생할 수 있는 크기와 위상 오차에도 강인한 기법이다. 본 연구에서는 이진 위상 조절 기법을 수식적으로 전개하고 이를 바탕으로 빔폭, 이득 및 EIRP 등을 계산 할 수 있다. 최대 기존 좁은 빔폭 대비 2.1배 증가된 빔폭을 얻을 수 있으며 면적조절 넓은 빔 형성기법 대비 높은 EIRP를 갖는다.
Ⅱ. 이진 위상 조절 넓은 빔 설계
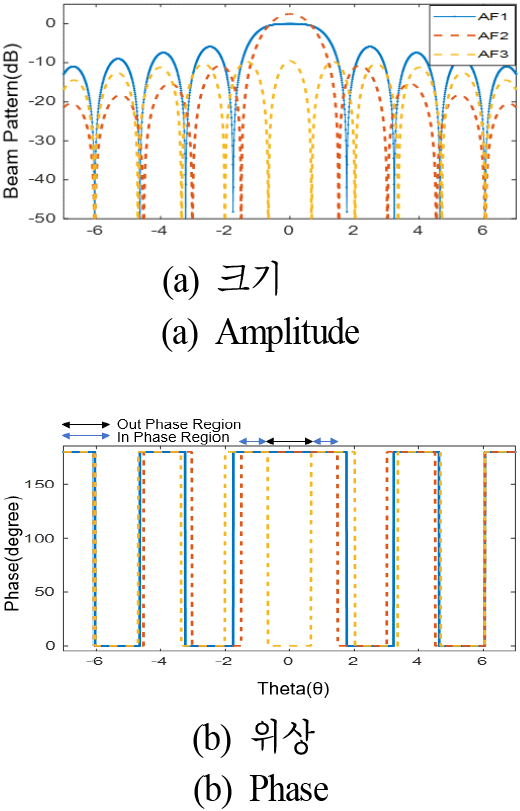
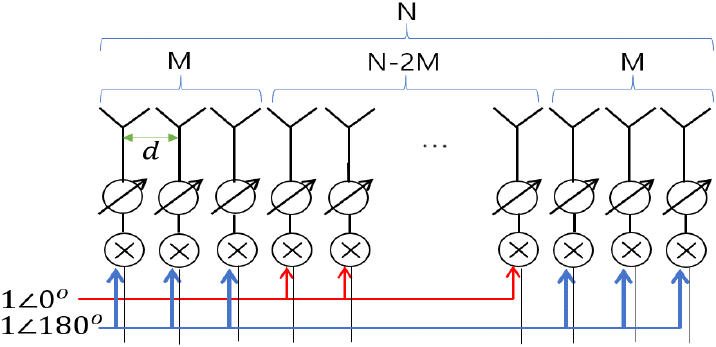
그림 1은 소자간격이 d인 N개의 선형 배열 구조에서 양끝 M개의 소자 위상이 180도 나머지(N−2M)는 0도의 outphase 배열 형상이다. 이를 그림 2와 같이 이진위상분포를 가진 전체 배열소자의 배열인자(AF, array factor)를 AF1로 정의하며 0도에 해당하는 소자를 AF2, 180도에 해당하는 소자를 AF3으로 정의한다. 본 기법은 다른 최적화 기법과 다르게 수식화 할 수 있다는 장점이 있다. 각 AF는 아래와 같이 수식화 함으로서 배열안테나의 이득, 빔폭 및 패턴 등을 계산하여 성능을 분석할 수 있다.
이때, d는 소자 간 거리, λ는 파장, N은 총 소자개수, 2 M은 outphase 소자 수를 의미한다. 본 연구에서는 총 100개(N)의 소자일 때 총 20개의 외각소자만 outphase를 갖는 (M=10) 구조일 때 각 AF 식 (1)~ 식 (3)에 해당하는 결과를 구하였다. AF 계산 결과는 그림 3과 같고, AF1 기준으로 normalization 하였다.
그림 3을 통해 넓은 빔이 형성되는 원리를 이해할 수 있다. 위상만을 보면 ±0.66도에서는 AF2와 AF3이 완벽하게 outphase 되어 peak빔을 눌러주며, 0.66~1.55도 사이에서는 inphase가 되어 크기가 증가하여 전체적으로 메인빔의 빔폭이 커지는 것을 확인할 수 있다. Outphase 소자 M의 개수가 늘어날수록 AF3의 peak-power는 커지고, 0.1N>M을 넘어가는 순간 메인빔의 리플(ripple)이 발생한다. 리플이 peak 대비 3 dB 이하로 내려가지 않으면 빔폭은 넓어질수 있으나 리플이 생긴 빔폭은 추후 모노펄스 빔형성에 사용하였을 시 정확도를 떨어뜨릴 수 있으므로 본 논문에서는 리플이 생기지 않는 범위에서만 분석을 진행하였다.
이진 위상 조절 넓은빔 형성 방법과 개구면을 통한 빔폭 조절 방법을 비교함으로서 제안된 방법의 성능 개선점을 확인할 수 있다.
우선 개구면을 통한 빔폭은 소자의 개수가 정해지면 최적화된 식 (4)와 같은 수식과 같이 정의할 수 있다.
이때 K는 인페이즈된 소자 개수이다. 본 논문에서는 소자에서 같은 크기의 파워가 방사되어 peak빔 포인트에서 소자의 크기와 위상에 의해 전자장이 더해진다고 할 때 전체 N−2M개의 0도 위상값을 갖는 소자와 2 M개의 180도 위상값을 갖는 소자에 의해 백터성분이 outphase되어 총 N−4M개 소자 파워가 합해져 이득이 형성된다.
표 1은 같은 이득을 갖을 때 식 (1)을 통한 제안하는 방법의 빔폭과 식 (4)를 이용한 소자(K=N−4M개)를 적용하여 빔폭을 계산하였다. 우선 제안된 이진 위상조절 방식(A)을 통한 빔폭은 기존 좁은 빔폭 대비 최대 107 % 증가하였다. 같은 이득일 때, 단순 개구면 조절(B)보다 최대 25 % 넓은 빔폭을 얻을 수 있음도 확인할 수 있다. 이는 같은 빔폭을 가질 때 이진 위상 조절 방식(A)이 개구면 조절(B)보다 더 큰 이득을 갖는 것과 같은 의미이다.
단일소자의 이득이 5 dBi이고 10 W라 가정하면, 앞서 분석했던 100개의 소자를 이용한 이진위상 조절 방식 EIRPp과 개구면 조절 방식 EIRPA 는 식 (5)~식 (7)로 정의할 수 있다.
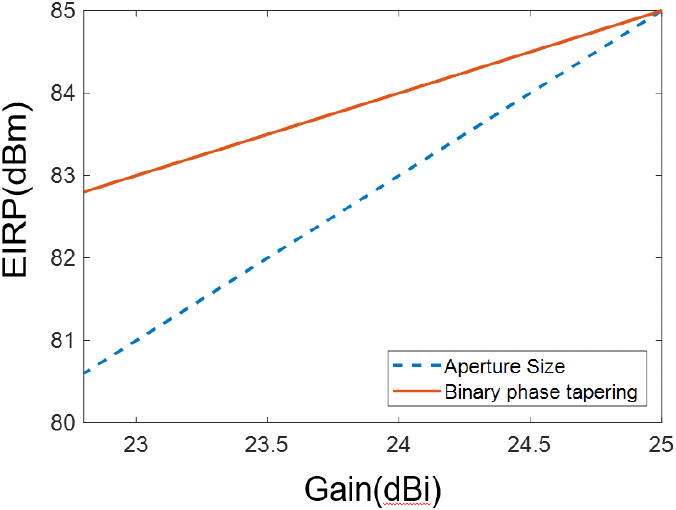
M의 개수 변화에 따른 EIRP 차이를 그림 4와 같이 확인할 수 있다. 이득이 25 dBi일때는 소자 100개가 모두 inphase 상태일 때이므로 개구면적 조절방식과 이진위상조절방식 모두 85 dBm의 EIRP를 갖는다. 하지만 outphase소자(M)가 증가할수록 위상 조절을 통한 넓은빔형성 방식이 더 높은 EIRP를 갖는 것을 확인할 수 있다. 사용 소자의 수가 많아지기 때문에 출력 파워의 크기가 더 커지기 때문이다.
Ⅲ. 2차원 넓은 빔 설계 및 결과
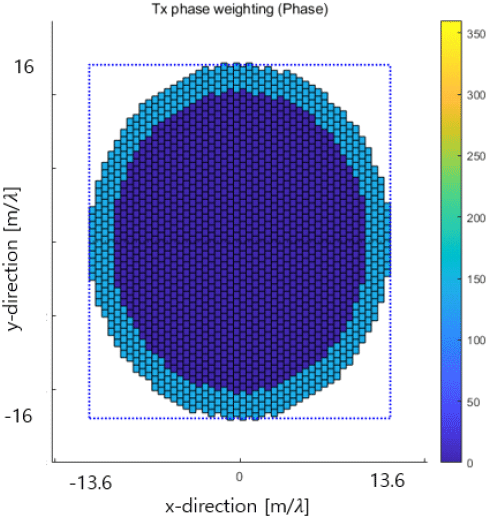
1D에 적용된 AF를 2D로 확장한 결과를 확인하기 위해 본 논문에서는 총 1,814개의 소자를 사용하며, 좁은 빔 대비 약 2배의 빔폭을 갖는 넓은 빔을 타겟으로 위상을 설계하였다. 위상 테이퍼링 적용 결과를 그림 5에서 볼 수 있다. 타원형 내부 파란영역에 대해서는 테이퍼링 값이 0으로 설정되어 있고 타원 이후부터 개구면 외각 끝까지 180도의 위상을 적용하였다.
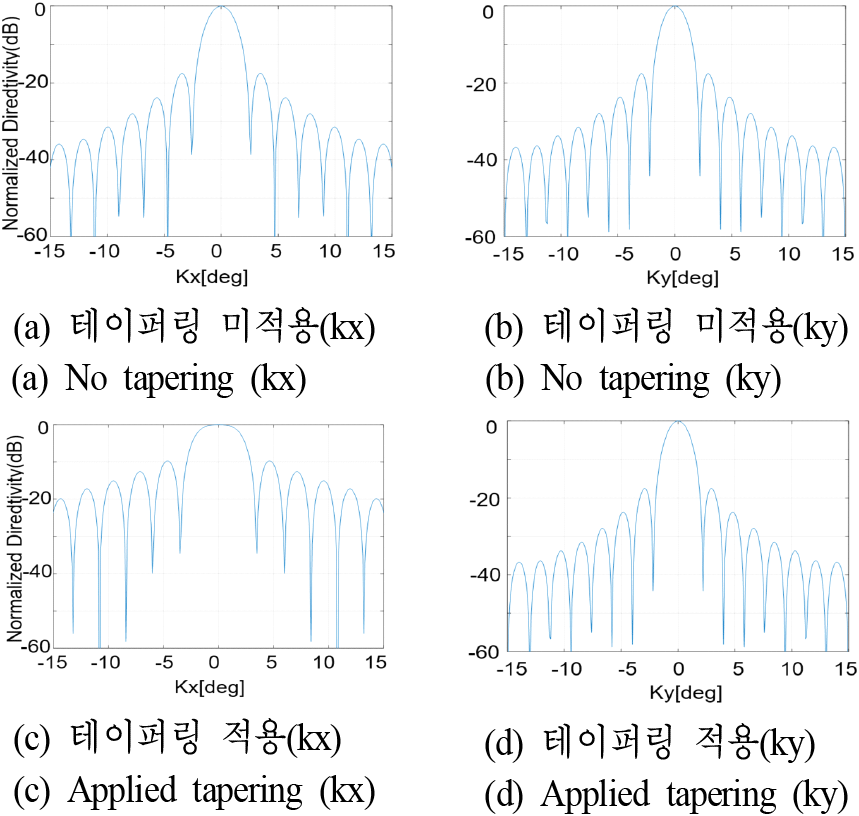
위상 테이퍼링 온·오프에 대한 방사패턴 결과가 그림 6과 같다. 안테나 개구면에 위상 가중치를 적용하지 않은 좁은빔의 빔폭은 2.1°×1.8°이다. 설계된 위상 테이퍼링 값을 적용후 얻은 안테나 빔폭은 4.2°×3.5°로 2배 증가된 빔폭을 확인할 수 있다. 1D의 계산 결과와 x축은(N=48, M=5, d/λ=0.57) 4.1도 y축은(N=48, M=5, d/λ=0.67) 3.5도로 동일한 빔폭 성능을 확보함을 확인하여 실제 계산 결과를 2D로 확장하여 적용할 수 있음을 증명하였다. 또한, 주빔에 리플이 생기지 않는 것을 확인할 수 있었다. 이는 레이다 시스템에 적용할 때 성능 확보 및 실 운용 적용에 적합하며 개구면 외각 소자의 위상값을 조절함으로써 능동반사손실 및 EIRP 등에서 안정적인 성능을 확보할 수 있다.