Ⅰ. 서 론
최근 유도탄 탐색기와 같은 소형 레이다에 적용할 수 있는 Ka 대역 능동위상배열안테나에 대한 연구가 활발히 진행 중이다[1]~[3]. 능동위상배열안테나 설계시 시스템의 최대 빔 조향각을 고려하여 그레이팅 로브가 생기지 않는 배열 간격을 결정하며, 이는 반 파장을 기준으로 조금 낮거나 높다. 때문에 S-파라미터 측정시 낮은 주파수에서는 커넥터 및 termination load의 크기에 비해 배열 간격이 넓어 문제가 없었지만, 높은 주파수에서는 물리적인 간섭이 발생할 수 있다. 때문에 본 논문에서 제시된 Ka대역 능동위상배열안테나의 능동반사계수 측정시 좁은 배열 간격으로 인한 인접 채널의 물리적인 간섭을 방지하기 위해 케이블이 포함된 측정 시스템 내에서 측정이 진행되어야 한다.
본 논문에서는 케이블이 포함된 Ka대역 능동위상배열 측정 시스템에서 케이블이 제외된 능동반사계수 측정을 위해 회로망 분석기의 시간 영역 변환 및 gating으로 케이블 입력단의 반사 특성을 제외하는 방법을 제시하였고, 능동위상배열안테나와 같이 신호가 동시에 입력되는 다중 입력 회로망에서의 유효성을 수학적으로 분석하였다. 또한 제안된 방식을 실제 측정에 적용하여 정확성을 검증하였다.
Ⅱ. 능동반사계수 측정 방안
측정을 위해 제작된 64채널 Ka대역 능동위상배열안테나의 배열 간격은 Dx(수평 방향)는 4.9 mm, Dy(수직 방향)는 5.1 mm이다. 따라서 인접 소자의 커넥터 간 물리적인 간섭을 방지하기 위해 직경이 작은 Mini-SMP 커넥터를 적용해야 한다. 또한 반사계수 측정시 측정 포트를 제외한 나머지 포트는 termination load로 연결해야 하는데, Mini-SMP termination load의 직경은 약 5.33 mm로 배열간격을 초과한다. 따라서 그림 1과 같이 2.92 mm to Mini-SMP 케이블이 포함된 측정 시스템이 요구된다.
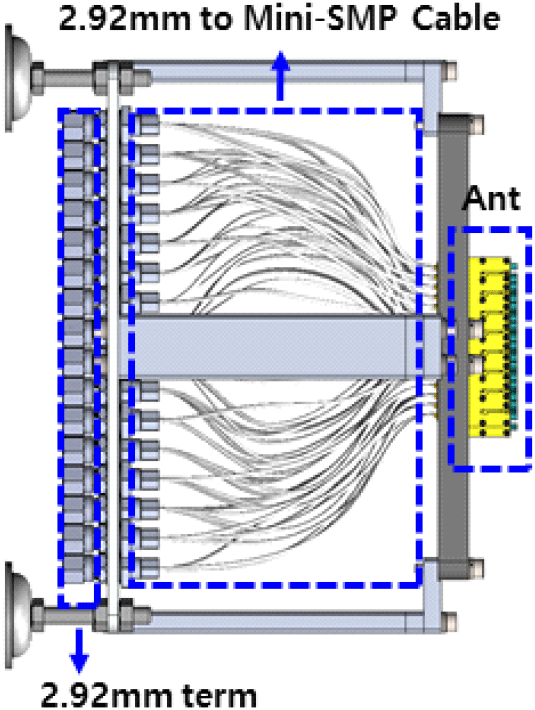
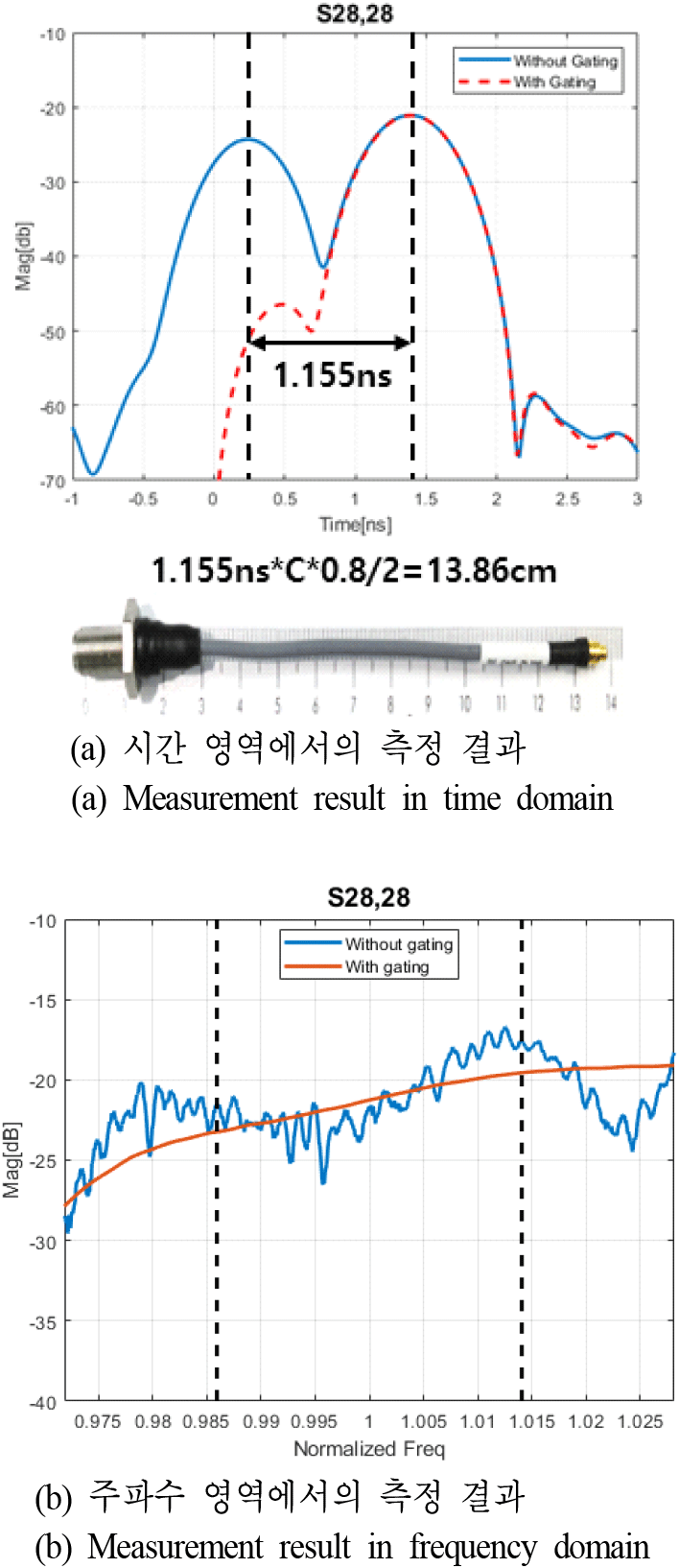
그림 2와 같은 측정 시스템 내에서 안테나만의 S-파라미터를 측정하기 위해 회로망 분석기의 시간 영역 변환 및 gating을 활용할 수 있다[4]. 그림 2(a)는 제작된 안테나의 중심 영역 포트인 포트 28의 시간 영역 반사계수 측정 결과를 나타낸 것으로 반사되어 돌아오는 경로를 포함하기 때문에 케이블 길이의 2배에 해당하는 만큼 케이블 입력단과 안테나 입력단의 반사신호가 떨어져 있음을 확인할 수 있다. 그림 2(a)의 빨간색 점선은 케이블 입력단의 반사 신호를 제외하기 위해 gating이 적용된 반사계수이며, 두 첨두치의 중간 지점을 gating의 시작 지점으로 지정하였다. 그림 2(b)는 주파수 영역에서 포트 28의 반사계수 측정데이터로 케이블 입력단의 반사 신호를 제외하는 것만으로 케이블에 의한 리플이 효과적으로 제거되는 것을 알 수 있다.
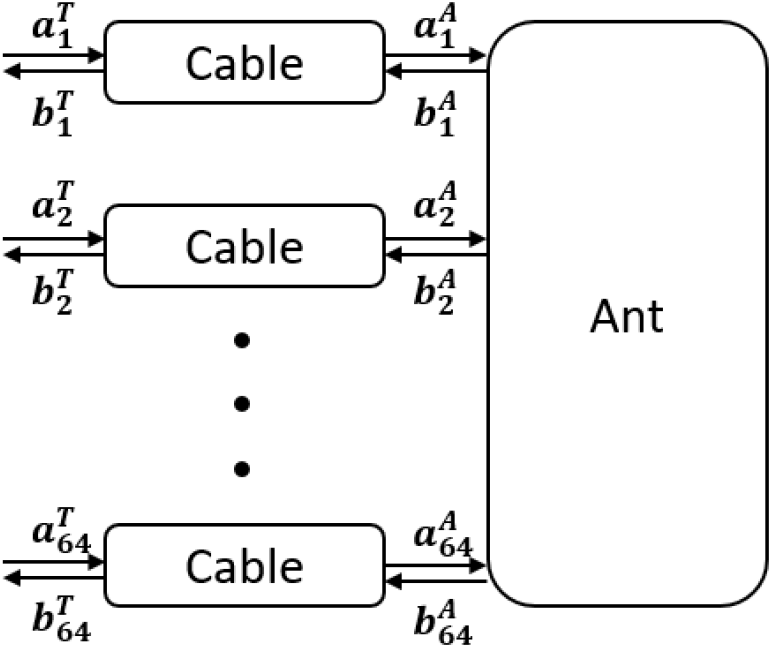
능동위상배열안테나는 다중 입력 회로망으로 신호가 동시에 입력되기 때문에 인접 채널에 의한 상호 결합량이 포함된 능동반사계수를 측정해야한다[5]. 따라서 시간 영역 gating 방식이 능동위상배열안테나에서도 유효한지 회로망 분석을 통해 검증할 필요가 있다. 이를 위해 그림 1의 측정 시스템을 그림 3과 같이 도식화하였다. 식 (1) 및 식 (2)의 ST, SA는 64by64 정사각 행렬로 ST는 케이블이 포함된 전체 측정 시스템, SA는 배열 안테나의 S-파라미터를 나타낸다. 마찬가지로 는 64by1 열벡터로 는 케이블이 포함된 전체 측정 시스템, 는 배열 안테나의 입사파와 반사파를 나타낸다. 식 (3)은 전체 시스템 입력단의 입사파, 반사파와 안테나 입력단의 입사파, 반사파의 케이블에 의한 관계식이다. 식 (1)~식 (3)을 정리하면 식 (4)와 같이 나타낼 수 있다. Gating을 적용하면 이므로 식 (4)는 식 (5)로 표현될 수 있다. 식 (5)의 (*ST)에서 I는 대각 행렬로 케이블 삽입 손실에 해당하는 약 −0.9 dB의 값을 가진다. ()ST에서 는 케이블의 안테나 입력단 반사계수에서 삽입 손실을 보상한 값으로 −16 dB이하이며, ST는 케이블이 포함된 각 채널의 반사계수 및 채널 간 상호 결합량으로 −15 dB이하이다. 따라서 ()ST의 모든 성분은 −31 dB 이하로 I에 비해 매우 작다. 따라서 식 (5)를 식 (6)으로 근사할 수 있으며, 다시 SA에 대하여 정리하면 식 (7)과 같이 나타낼 수 있다.
Ⅲ. 능동 반사 계수 측정 결과
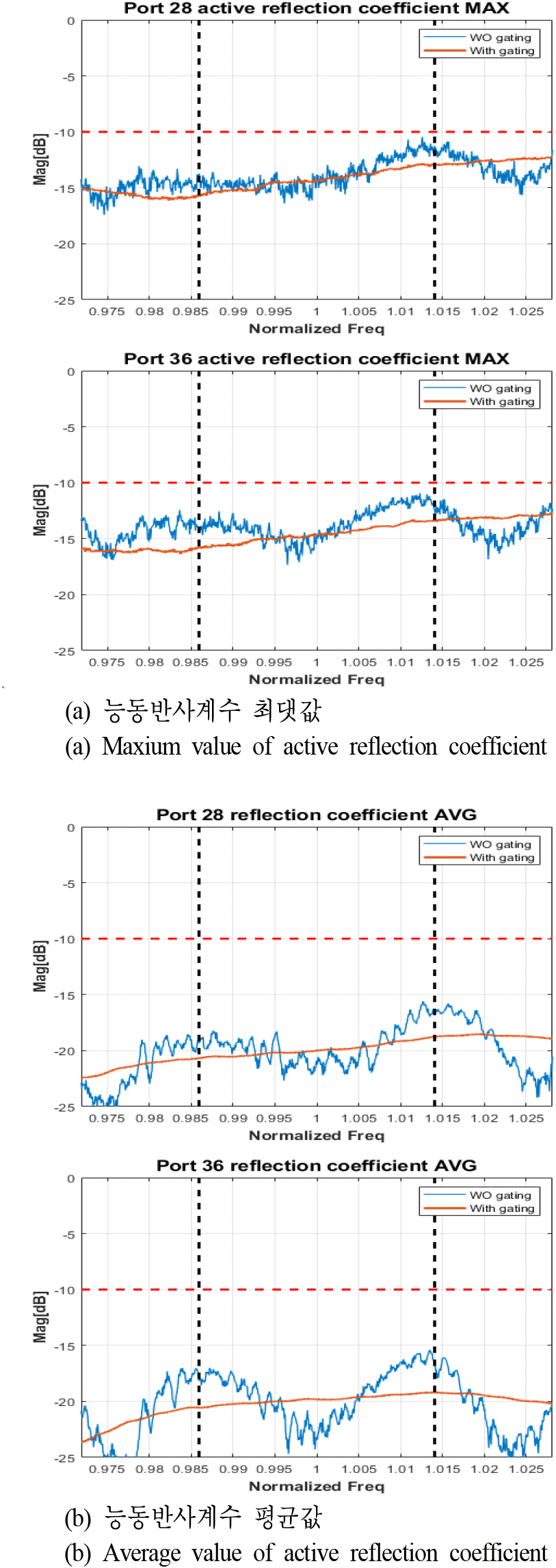
측정은 상호 결합에 의한 영향이 가장 큰 배열안테나의 중심 부분인 포트 28과 포트 36에 대하여 진행하였다. 각 포트별 총 64개의 S-파라미터를 측정하였고, 저장된 데이터를 Matlab을 이용하여 theta기준±40° 빔 조향각에 해당하는 위상 변이량을 각 채널에 장입 및 계산하였다. 계산 결과 포트 28, 36에 대하여 최댓값 −14.73 dB, −15.20 dB, 평균값은 −20.67 dB, −21.12 dB이다. 이를 식 (7)에 의해 케이블 2-way 삽입 손실 약 −1.79 dB를 보상하여 포트 28, 36에 대하여 최댓값은 −12.80 dB, −13.27 dB, 평균값은 −18.75 dB, −19.19 dB로 계산된다. 그림 4에 모든 측정 주파수에서의 결과를 나타냈고 케이블에 의한 리플이 gating에 의해 잘 제거됨을 확인할 수 있다.