The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(8):656-666

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.8.656

논문/REGULAR PAPER

전자전 장비를 사용한 해수면 저고도 고기동 표적의 효율적인 고각 추정

김현동

, 최남우^*

, 김상수^*

, 전성천^*

, 김경태

, 최인오^**^,^†

Efficient Estimation of Elevation Angle for Low-Altitude Maneuvering Target Using Electronic Warfare Equipment in Sea Surface Environment

Hyundong Kim

, Namwoo Choi^*

, Sangsu Kim^*

, Sungchun Jun^*

, Kyungtae Kim

, Inoh Choi^**^,^†

포항공과대학교 전기전자공학과

^*LIG 넥스원(주)

^**국립부경대학교 스마트모빌리티공학과

Department of Electrical Engineering, Pohang University of Science and Technology

^*LIG Nex1 Co. Ltd.

^**Department of Smart Mobility Engineering, Pukyong National University

^†Corresponding Author: Inoh Choi (e-mail: inoh@pknu.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 01, 2024; Revised: Aug 07, 2024; Accepted: Aug 13, 2024

Published Online: Aug 31, 2024

요 약

해상용 전자전 장비는 적 표적의 레이다 송신 신호를 모노 펄스 혹은 배열 안테나로 수신하여 적 표적의 방위각 및 고각을 추정한 후, 해당 각도 방향으로 재밍 신호를 송신하여 적 표적의 레이다 센싱을 방해하는 역할을 한다. 하지만, 최신 적 표적들은 전자전 장비 내에 해수면 다중 경로 전파 간섭을 유도하기 위해 저고도로 기동한다. 이때 다중 경로 전파 간섭은 전자전 장비가 적 표적의 고각을 정확하게 추정하지 못하게 하는 치명적인 문제를 야기한다. 본 논문에서는 상대적으로 적은 배열 안테나로 적 표적 고각을 추정하기 위한 알고리즘을 제안한다. 제안된 알고리즘은 1) 적 대공표적의 X-대역 레이다 송신 신호를 수신한 후, 기저대역으로 변환하여 샘플링된 복소 수신 신호를 획득하고, 2) 적 대공표적의 선형 주파수 변조 변수들을 입자 군집 최적화로 추정하여 보상한 후, 파장과 고각 간의 새로운 푸리에 관계를 활용하여 적 대공표적 고각을 추정한다. 시뮬레이션 결과, 기존 방식들과 달리 보다 간단한 전자전 장비 구조로 다중 경로 전파 간섭에도 불구하고, 적 표적 고각 추정이 가능함을 확인할 수 있었다.

Abstract

Electronic warfare equipment estimates the azimuth and elevation of an unknown target by processing radar echoes received from monopulse or array antennas and interrupts radar sensing by transmitting jamming signals to the target. However, state-of-the-art targets maneuver at low altitudes in a sea surface environment to deliberately produce interference through multi-path, which poses a significant challenge for accurately estimating the estimation of the elevation angle. In this study, we propose an algorithm to accurately estimate the elevation angle of a low-altitude target despite the presence of a few arrays. Assuming that the sampled complex echoes are obtained after down-converging from the X-band (i.e., 10 GHz) to the base band, the proposed method demodulates the unknown linear frequency modulation using particle swarm optimization (PSO) and estimates the elevation angle by exploiting the new Fourier relationship between the wavelength and elevation angle. The simulation results suggest that our proposed method can successfully estimate the elevation angle for low-altitude maneuvering targets in a sea-surface environment.

Keywords: Electronic Warfare Equipment; Low-Altitude Target; Multi-Path Interference; Estimation of Elevation Angle

Ⅰ. 서 론

전자전 상황에서 해상 표적의 각도를 추정하는 과정은 매우 중요하다. 이때, 전자전 장비는 적 표적으로부터 수신한 레이다 신호를 통해 방위각과 고각을 추정하며, 추정된 각도 방향으로 재밍 신호를 송신하여 적 표적의 레이다 센싱을 방해한다. 여기서 방위각과 고각을 추정하는 대표적인 방법으로는 모노 펄스 크기 비교 및 위상 비교 방법이 있다^[1]. 이 방법은 4개 안테나로부터 수신된 신호의 크기 혹은 위상의 합과 차의 비를 활용하여 각도 정보를 추출한다. 그러나 직접 경로로 수신된 신호에 고각 방향으로 다중 경로를 통해 들어온 해수면 반사 신호가 포함되는 경우, 각 신호들이 간섭을 일으켜 정확한 고각 추정이 어려워진다^[2],[3]. 최신 적 대공 표적은 저고도 고기동 비행을 통해 해수면으로부터 반사되는 다중 경로 신호를 유도함으로써, 전자전 장비가 적 대공 표적의 고각 추정하는 것을 어렵게 만든다.

최근 다중 경로로 해수면 반사 신호가 들어오는 상황에서 정확한 고각 추정을 어렵게 만드는 문제를 해결하기 위해 다양한 연구들이 수행되고 있다. 먼저, 적응형 빔포밍(adaptive beamforming) 기법^[4],[5]은 배열 안테나를 통해 안테나 빔 패턴을 형성한 후, 기존 모노 펄스 기법으로 얻은 각도를 바탕으로 해당 각도에 가중치를 더해 직접 경로를 통해 들어온 신호의 영향을 증대시킨다. 적응형 빔 패턴을 형성하는 방법으로는 LCMV(linear constraint minimum variance), MSLC(multiple side lobe canceler) 등이 존재한다. 최근에는 다양한 연구^[6]~[8]들이 빔 패턴 성능을 개선하기 위해 최적화 기법과 인공지능을 적용하고 있으며, 이를 통해 복잡한 전파 환경에서의 효율성을 높이고 있다. 특히, 진화 알고리즘, 다중 빔 패턴 형성 기술을 활용하여, 보다 정교한 빔 패턴 합성을 구현하고 있다. 하지만 정확한 각도 정보를 얻기 위한 빔을 형성하기 위하여 상당수의 배열을 사용하기 때문에 시스템적으로 구현하기 복잡한 어려움을 지니고 있다. 다음으로 EGM(elevation geo metric mean)^[9]~[11]은 두 개의 운용 주파수 수신 신호를 수신하여 직접 경로 및 다중 경로로 수신되는 신호들의 고각들을 각각 분리하여 추정하는 기법이다. 특히, 직접 경로를 통해 들어온 신호의 고각과 다중 경로를 통해 들어온 신호의 고각이라는 두 개의 미지수에 대하여 두 개의 운용 주파수 수신 신호들을 활용하여 미지수를 자명하게 추정하는 기법이다. 하지만, 적 대공 표적이 두 개 운용 주파수를 동기화시켜 사용해야 한다는 점에서 매우 제한적으로 활용 가능하다. 따라서, 적 대공 표적이 주로 송신하는 단일 운용 주파수 레이다 신호로부터 보다 간단한 배열 구조의 전자전 장비를 사용하여 해수면 다중 경로 환경에서 고각을 안정적으로 추정하기 위한 방안이 필요하다.

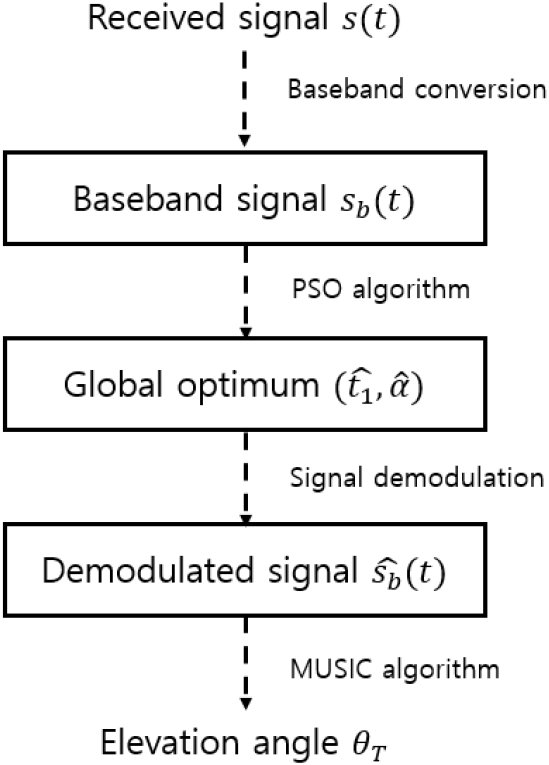
앞서 언급된 문제를 해결하기 위하여 본 연구에서는 적 대공 표적이 단일 X-대역 선형 주파수 변조 레이다 신호를 송신하고, 전자전 장비가 소수의 배열들로 이 신호들을 수신하는 상황을 가정한다. 이때, 수신된 신호를 기저대역으로 변환하여 샘플링된 이산 복소 신호를 획득한 후, PSO(particle swarm optimization)^[12]를 적용하여 적 대공 표적 레이다 신호의 선형 주파수 변조 변수들을 추정하여 복조한다. 이어 파장과 고각 사이의 새로운 푸리에 관계를 바탕으로 복조된 복소 이산 신호에 푸리에 변환(Fourier transform)을 수행하여 고각을 추정한다. 여기서, 높은 고각 해상도를 얻기 위해서는 적 대공 표적 송신 신호의 파장 범위가 넓어야 한다는 문제가 있기에, 고해상도 스펙트럼 추정 기법 중 하나인 다수 신호 식별 (MUSIC, multi ple signal classification) 알고리즘^[13]을 적용한다.

논문의 Ⅱ장에서는 전자전 장비와 표적 간 기하 변수를 정의하고, 해수면 환경에서 반사와 회절로 인한 신호의 크기와 위상 감쇄 정도를 분석한다. 또한, 다중 경로를 통한 신호가 간섭을 일으킬 때 발생하는 문제를 분석하고 시뮬레이션을 수행한다. Ⅲ장에서는 제안된 기법에 관하여 상세히 서술한다. Ⅳ장에서는 매트랩 기반 모의 시뮬레이션을 통해 제안된 기법이 높은 정확도로 각도 추정이 가능함을 검증한다.

Ⅱ. 전자전 장비와 표적 간 기하 변수 정의 및 해수면 다중 경로 간섭 영향 분석

2-1 전자전 장비와 표적 간 기하 변수 정의

적 표적과 전자전 장비 간의 기하 정보를 분석하기 위한 구조^[14]는 그림 1과 같다. 여기서 R_D는 적 표적으로부터 전자전 장비로 전파되는 레이다 신호의 직접 경로 거리이다. R₁과 R₂는 각각 전자전 장비로부터 반사 지점까지의 거리와 표적으로부터 지표면의 반사 지점까지의 다중 경로 거리를 나타내며, 식 (1)을 통해 아래와 같이 구해진다.

R D 2 = a E + h R 2 + a E + h T 2 − 2 a E + h T a E + h R cos r a E R 1 = a E 2 + a E + h R 2 − 2 a E a E + h R 2 cos r 1 a E R 2 = a E 2 + a E + h R 2 − 2 a E a E + h R 2 cos r 2 a E

(1)

그림 1. | Fig. 1. 지구 곡률을 고려한 전자전 장비와 표적 간 기하 구조 | Geometry between electric warfare equipment and target considering Earth's curvature.

Download Original Figure

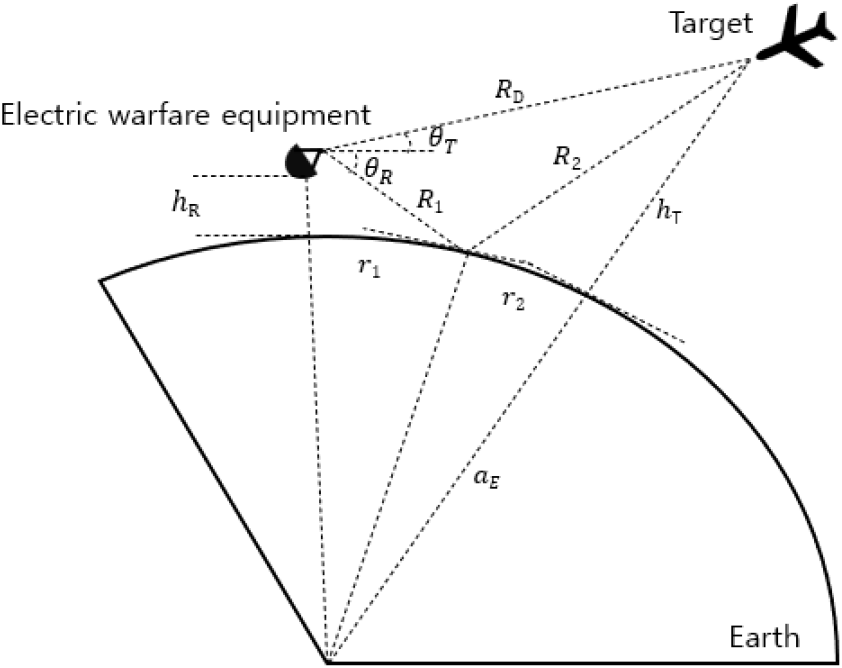
여기서 r₁과 r₂는 R₁과 R₂의 지표면 상으로 투영된 다중 경로 거리를 의미한다. r₁과 r₂의 합을 r로 표현할 때, 다중 경로 이차 방정식은 식 (2)처럼 정의된다.

2 r 13 − 3 r 12 r + r 2 − 2 a E h T + h R r 1 + 2 a E h R r

(2)

이때, a_E는 지구 반지름, h_R는 전자전 장비의 높이, h_T는 표적의 높이이다. r₁은 식 (3)과 같은 형태로 아래와 같이 유도되며, r₂는 r₂=r-r₁의 관계식을 통하여 구해진다.

r 1 = r 2 − p sin ξ 3

(3)

여기서 $p = 4 a E h R + h T + r 2 / 3$ , ξ=sin⁻¹(2a_E (h_T−h_R)r/p³)이다.

전자전 장비가 수신하는 적 표적 레이다 신호의 직접 경로 입사 고각 θ_T와 다중 경로 입사 고각 θ_R은 식 (4)와 같이 표현되며, 본 연구에서 최종적으로 추정해야 하는 미지수들이다.

θ T = sin − 1 h T + a E 2 − R D 2 − h R + a E 2 2 R D h R + a E θ R = sin − 1 R 12 + h R 2 + 2 a E h R 2 R 1 h R + a E

(4)

2-2 해수면 다중 경로 간섭 영향 분석

다중 경로를 통해 전자전 장비로 수신되는 해수면 반사 신호는 크게 1) 반사 성분과 2) 확산성분으로 구분된다. 직접 경로를 통해 수신된 신호를 s_direct라 정의할 때, 1) 반사 성분 s_spec은 식 (5)와 같이 표현되며, 프리넬 반사계수^[15] Γ에 관한 값들은 식 (6)으로 나타낼 수 있다.

S s p e c = Γ D ρ s S d i r e c t e − j α

(5)

Γ = sin ψ − ϵ − cos 2 ψ sin ψ + ϵ − cos 2 ψ D = 1 + 2 r 1 r 2 a E r s i n ψ − 12 ρ s = e − 8 π x 2 0 ≤ x ≤ 0.1 0.812537 1 + 8 π x 2 0.1 < x ≤ 0.3 α = 2 π R 1 + R 2 − R D λ

(6)

여기서 Γ는 다중 경로 신호의 해수면으로의 입사각 ψ와 해수면 복소 유전율 ϵ의 영향을 받는다. 이때, ϵ은 해상 염분과 온도에 대한 함수로 정의된다. D는 발산계수(divergence factor)로 지표면의 편평한 정도를 나타내며, 산란계수ρ_s는 해수면 거칠기 χ에 영향을 받는다.

다음으로 2) 확산 성분 s_diff은 s_direct에 확산 계수 ρ_d를 곱한 형태로 식 (7)처럼 표현되며, 식 (8)을 통해 ρ_d가 구성된다.

S d i f f = ρ d × S d i r e c t

(7)

ρ d = σ d x 12 + x 22 2 e j ϕ d σ d = 2 Γ 3.86 x 0 < x < 0.1 2 Γ 0.454 − 0.858 x 0.1 ≤ x < 0.5 2 Γ 0.025 0.1 ≤ x < 0.5

(8)

확산 계수를 구하기 위한 σ_d는 확산성분의 레일리 변수(Rayleigh parameter)이며, 해수면 거칠기 χ와 프레넬 반사 계수 Γ의 영향을 받는다. x₁, x₂는 가우시안(Gaussian) 랜덤변수, ϕ_d는 0과 2π사이의 값을 가짐으로써 레이다 신호가 해수면에서 무작위로 확산이 일어나는 크기와 방향 성분을 표현한다.

θ T = sin − 1 λ d π × tan − 1 Δ Σ

(9)

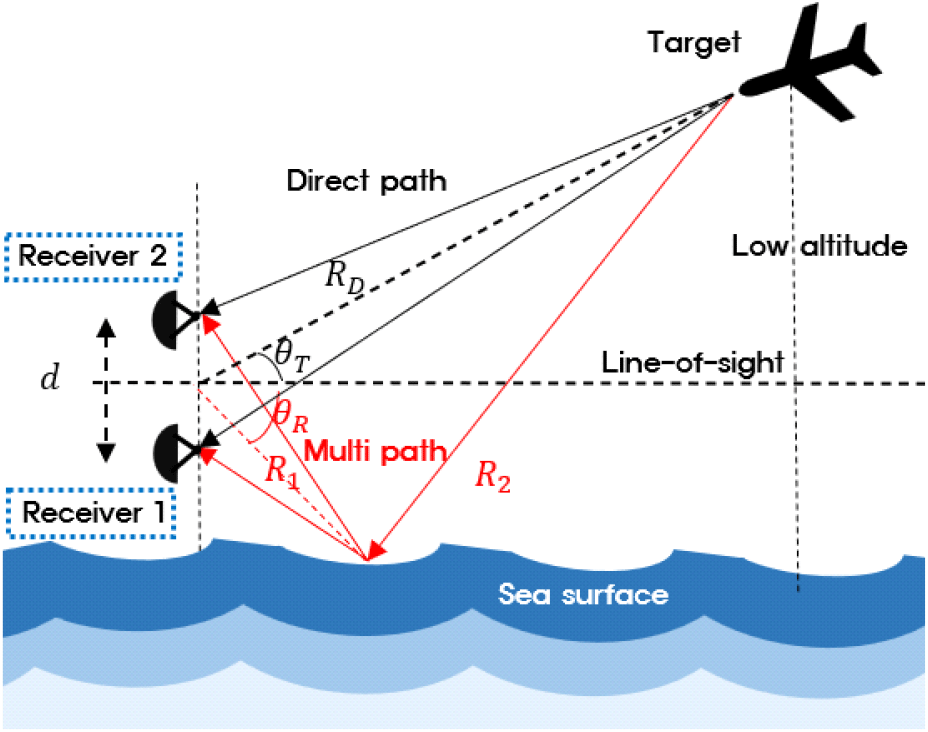
앞서 언급한 1) 반사 성분과 2) 확산 성분를 고려한 다중 경로 해수면 반사 신호의 간섭 정도를 분석하기 위해, 그림 2와 같이 2채널 안테나 기반 모노 펄스 위상 비교 방법을 사용하여 고각 추정 성능을 분석하였다. 다중 경로 간섭이 없는 경우, 두 안테나의 수신 신호 합(∑)과 차(Δ)의 비(Δ/∑)를 통해 식 (9)와 같이 직접 경로 고각 θ_T이 추정될 수 있다^[1].

그림 2. | Fig. 2. 저고도 해수면 환경에서 반사되는 다중 경로 반사 간섭 구조 | Configuration of interference caused by multi path reflection in low-altitude and sea-surface environment.

Download Original Figure

여기서 두 안테나 사이의 간격을 d, 신호의 파장을 λ, 그리고 $Δ Σ$ 는 식 (10)과 같이 정의하며, $P R$ 는 전자전 장비의 수신 전력이다. 이때, 식 (10)에 다중 경로 간섭 신호가 포함되어 있으므로, 기존 모노 펄스 위상 비교 방식을 통한 고각 추정은 불가능하다. 이를 확인하기 위해 100 km 떨어진 표적이 다가오며, 잡음이 없는 환경에서 레이다 신호를 송신하는 상황을 가정하였으며, 시뮬레이션 결과는 그림 3과 같다.

Δ Σ = 1 + ρ d i f f P R e j 2 π λ R T + d 2 sin θ T − e j 2 π λ R T − d 2 sin θ T + Γ D ρ s P R e j 2 π λ R 0 + R 1 + d 2 sin θ R − e j 2 π λ R 0 + R 1 − d 2 sin θ R 1 + ρ d i f f P R e j 2 π λ R T + d 2 sin θ T + e j 2 π λ R T − d 2 sin θ T + Γ D ρ s P R e j 2 π λ R 0 + R 1 + d 2 sin θ R + e j 2 π λ R 0 + R 1 − d 2 sin θ R

(10)

그림 3. | Fig. 3. 다중 경로 반사 간섭에 따른 직접 경로 고각 추정 결과 | Example of elevation angles estimated at direct path according to interference caused by multi path reflection.

Download Original Figure

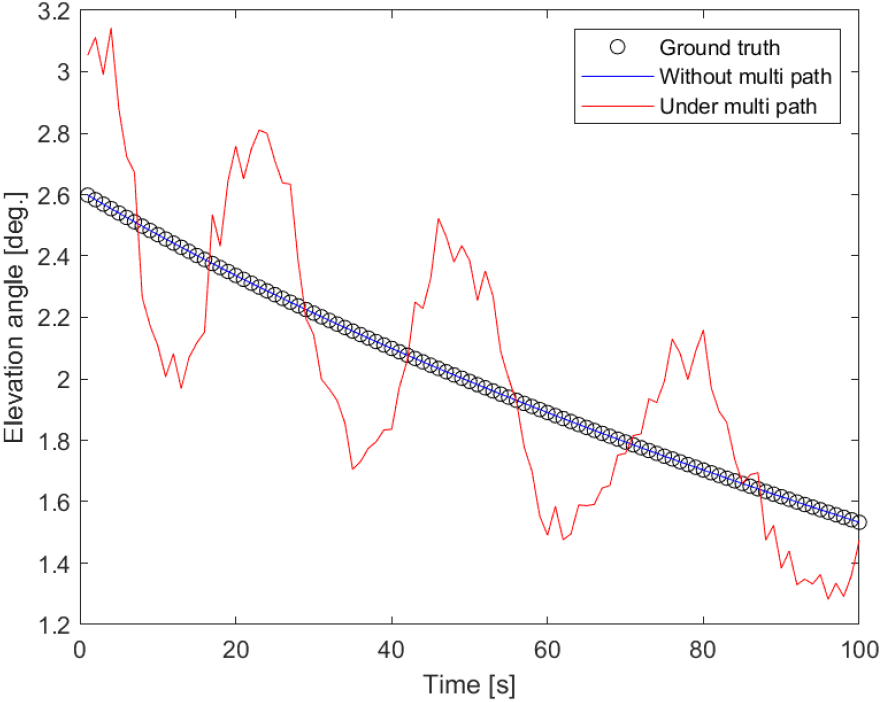
다중 경로 영향이 존재하지 않을 경우, 위상 비교 방법을 통하여 신호의 고각을 추정한 결과, 이론적 참값과 동일한 결과값이 도출되었다. 반면, 다중 경로 간섭이 존재하는 경우, 평균적으로 약 0.3°의 오차가 발생한다. 100 km의 장거리 표적의 경우, 0.3°의 오차는 약 520 m 정도의 거리 오차를 유발하기 때문에 전자전 상황에서 각도 오차를 줄이는 과정은 매우 중요하다. 그러나 기존 기법들^[4]~[11]은 안테나 배열의 수를 증가시키거나 2개 운용 주파수를 활용하여 각도 오차를 줄이는 방식을 사용하기 때문에 시스템 비용이 많이 들고, 적 표적의 비협조적인 송신 레이다 신호로부터 적 표적 고각을 추정해야 하는 전자전 상황에서는 효과적이지 않다. 따라서 본 연구에서는 간단한 전자전 장비 시스템 구조에서 다중 경로 해수면 반사 간섭 영향에도 불구하고 고각 추정 오차를 줄이는 방법을 제안한다.

Ⅲ. 제안된 기법

본 절에서는 해수면 다중 경로 반사 간섭 환경에서 고각 추정 오차를 줄이는 방법을 제안한다. 직접 경로 고각 추정을 위한 전자전 장비 구조는 그림 2와 같으며, 제안된 기법은 크게 1) 전자전 장비로 수신되는 적 표적의 선형 주파수 변조 신호 모델, 2) PSO 기법을 통한 선형 주파수 변조 변수 추정 및 복조, 3) MUSIC 기법을 통한 직접 경로 고각 추정의 세 단계로 서술된다. 특히, 기존 MUSIC을 사용하는 각도 추정(DOA, direction of arrival) 기법들은 공간상에 일정 간격으로 배치된 배열 요소(array factor) 특성을 활용하여 각도를 추정하지만, 본 연구에서는 DOA를 위하여 선형 주파수 변조로 인해 생기는 파장의 선형 변화와 고각 간의 새로운 푸리에 관계를 활용한다.

3-1 전자전 장비의 선형 주파수 변조 수신 신호 모델

제안된 기법을 위하여 적 표적이 X-대역 단일 운용 주파수에서 선형 주파수 변조 신호를 송신한다고 가정한다. 전자전 장비 구조는 고각 추정을 위해 그림 2와 같이 두 수신기가 수직 방향으로 d간격만큼 떨어져 배치되며, 단일 수신기에서 수신된 신호는 시간-주파수 영역에서 그림 4와 같이 표현된다.

그림 4. | Fig. 4. 시간-주파수 영역에서 적 표적의 선형 주파수 변조 수신 신호 예시 | Example of linear frequency modulated signal received from a target in a time-frequency domain.

Download Original Figure

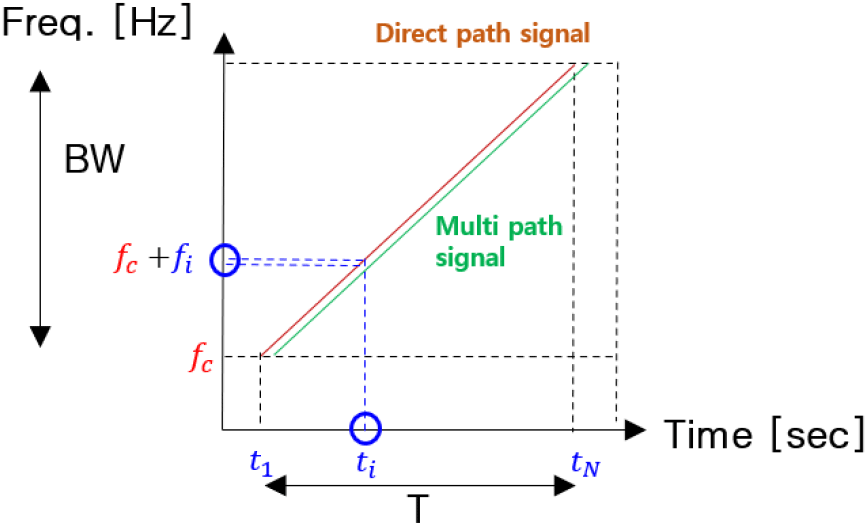
그림 4에서 BW는 신호의 대역폭, T는 펄스 송신 시간, f_c는 중심 운용 주파수로 정의된다. t_i는 i번째 샘플링된 순간 시간이며, 샘플개수는 N개이다. 이때, 두 경로로 수신되는 적 표적 신호는 빛의 속도로 전파되기 때문에 순간 시간 t_i에서 선형 변조 주파수는 f_c+f_i로 동일하다고 가정하며, 선형 변조된 i번째 주파수 f_i는 식 (11)과 같다.

f i = α t i − t 1 = B W T t i − t 1, i = 1, ..., N

(11)

여기서 t₁는 적 표적과 전자전 장비 간의 거리 차에 따른 지연시간이다. 그림 2에서의 두 수신기 사이 직접 경로 거리 차 dsin(θ_T)와 다중 경로 거리 차 dsin(θ_R)를 고려한, t_i시점에서 첫 번째 수신기 수신 신호를 정리하면 식 (12)와 같이 표현된다.

s t i = P R × e j 2 π f c + f i t i × e j 2 π f c + f i d s i n θ T c + P R 0 × e j 2 π f c + f i t i × e j 2 π f c + f i d s i n θ R c

(12)

여기서 반사와 회절로 인한 계수들을 고려한 다중 경로 수신 신호의 전력을 P_R0로 정의한다.

3-2 PSO 기반 선형 주파수 변조 변수 추정 및 복조

적 표적의 선형 주파수 변조 신호를 전자전 장비로 수신할 경우, 식 (12)를 기저대역 신호 s_b (t_i)로 식 (13)과 같이 변환한다.

s b t i = s t i × e − j 2 π f c t i = e j 2 π f i t i × P R × e j 2 π f c + f i d s i n θ T c + P R 0 × e j 2 π f c + f i d s i n θ R c

(13)

식 (13) 내 적 표적의 선형 주파수 변조 성분 $e j 2 π f i t i$ 을 복조하기 위하여, 식 (11)에서 2개 미지수인 지연시간 t₁과 선형 주파수 변조 기울기 α를 추정해야 한다. 이때, 제안된 기법에서는 경사 하강법(gradient descent)과 달리 지역 최소(local minimum)에 빠지지 않는 PSO 알고리즘을 활용하여 2개 미지수를 추정(i.e., 2차원 최적화 문제)하였다. 여기서, 2개 미지수를 성공적으로 복조할 경우, 식 (13)의 주파수 스펙트럼 엔트로피(entropy)가 낮아진다는 특성을 바탕으로 PSO 알고리즘을 적용하기 위하여 식(14)와 같이 임의의 2개 미지수로 복조한 신호의 주파수 스펙트럼을 추정한 후, 엔트로피 비용 함수(cost function)를 식 (15)와 같이 정의한다.

s^t i = s b t i × e − j 2 π α t i − t 1 t i S f i = F T s^t i, j = 1, ..., N

(14)

E n t r o p y = − ∑ j = 1 N S f j × log S f j

(15)

여기서 식 (14)의 FT{·}는 푸리에 변환 과정을 나타낸다. PSO 알고리즘은 광범위한 임의의 2개 미지수들로 계산한 엔트로피가 국부 최소(global minimum)에 수렴할 때까지 반복하여 동작한다^[12]. 최적화가 이상적으로 수행된 경우, 이상적으로 복조된 기저대역 수신 신호 $s b^t i$ 는 식 (16)과 같다.

s b^t i = P R × e j 2 π f c + f i d s i n θ T c + P R 0 × e j 2 π f c + f i d s i n θ R c

(16)

3-3 MUSIC 기법을 통한 직접 경로 고각 추정

앞서 정의된 식 (16)의 위상 부분 중 $f c + f i d c$ 를 x_i, sin(θ_T)를 $y θ T$ , sin(θ_R)를 $y θ R$ 로 치환하여 재정의하면 식 (17)과 같이 표현된다.

s b^t i = P R × e j 2 π x i y θ T + P R 0 × e j 2 π x i y θ R

(17)

여기서 f_i가 식 (11)과 같이 t_i에 관하여 선형적 관계를 맺으므로, 치환된 변수 x와 y 사이에 새로운 푸리에 관계가 성립함을 확인할 수 있다. 하지만, 치환된 변수 y의 해상도를 높이기 위해서는 치환된 변수 x를 광범위하게 획득해야 하지만, 이를 위해서는 선형 주파수 변조의 대역폭이 넓어야 하므로, 적 표적이 광대역폭을 반드시 사용해야 한다는 조건이 필요하다. 하지만, 적 표적이 항상 광대역폭을 사용한다는 보장이 없기 때문에, 본 논문에서는 한정된 대역폭 조건에도 높은 y의 해상도를 획득할 수 있는 고해상도 스펙트럼 추정 기법 MUSIC^[13]을 활용한다. MUSIC 알고리즘은 1) 방향 벡터(steering vector)를 형성하여 식 (17)에 곱한 후, 2) 이 신호에 대하여 고유치 분해(eigenvalue decomposition)를 수행하고 고윳값의 크기에 따라 신호 부 공간과 잡음 부 공간으로 나누고, 3) 잡음 공간과 방향 벡터의 직교성(orthogonality)을 활용하여 고해상도 주파수 스펙트럼을 추정한다^[13].

MUSIC 기법의 필요성을 검증하기 위하여 직접 경로 고각 35°, 다중 경로 고각 −10°, 중심주파수 10 GHz, 대역폭 500 MHz, 지연시간 0.5512 ms, 선형 주파수 변조 기울기 55.56 GHz/s에서 시뮬레이션 분석을 수행하였다. 이때 MUSIC 기법의 경우, 신호원을 2개로 설정하였으며 가장 큰 고윳값을 찾고자 하는 신호라고 정의하였다. 정규화된(normalized) 고해상도 주파수 스펙트럼은 그림 5와 같다.

그림 5. | Fig. 5. 푸리에 변환과 MUSIC 알고리즘 간의 고각 추정 비교 결과 | Comparison of DOA between Fourier transform and MUSIC algorithm.

Download Original Figure

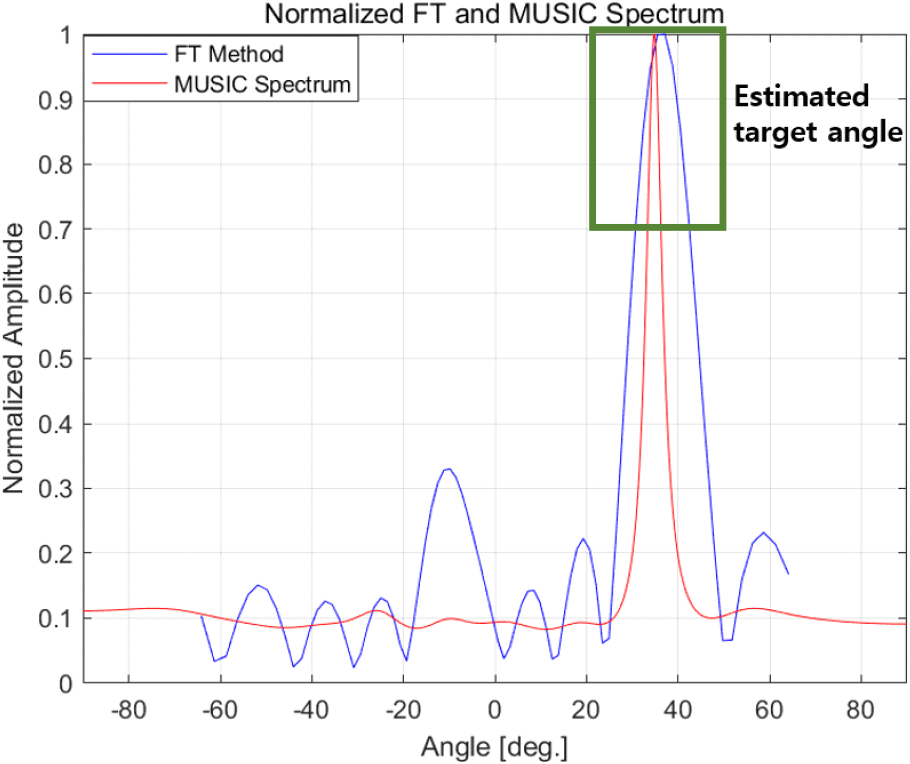
다중 경로 반사 신호의 수신 전력이 직접 경로 신호보다 감쇄 정도가 크기 때문에, 주파수 스펙트럼 중 크기가 가장 큰 부분을 직접 경로 고각 부분이라고 자명하게 추정할 수 있으며 이 부분은 그림 5에서 녹색 사각형으로 표시된다. 이때, PSO를 통하여 추정한 지연시간은 0.567 ms, 변조 기울기는 55.37 GHz/s로 계산되었으며, 시뮬레이션 수행 시간은 1.92초가 소요되었다. 추정 결과가 시뮬레이션 변수와 유사하며 수행 시간이 크게 걸리지 않는 점을 고려할 때, PSO를 통한 추정이 합리적이라고 판단된다. 푸리에 변환 및 MUSIC을 적용하여 추정된 직접 경로 고각은 표 1과 같다.

표 1. | Table 1. 기법에 따른 표적 각도 | Target angle depending on the methods.

Theoretical angle	Fourier transform	MUSIC algorithm
35 [deg.]	37.142 [deg.]	34.798 [deg.]

Download Excel Table

푸리에 변환을 사용하여 측정한 직접 경로 고각 오차는 2.142°이지만, MUSIC 알고리즘은 0.202°의 오차가 나타났다. 따라서 본 연구에서는 MUSIC 알고리즘을 통해 DOA를 수행하며, 제안된 기법의 직접 경로 고각 추정 순서도는 그림 6과 같다.

그림 6. | Fig. 6. 제안된 기법의 순서도 | Flowchart of the proposed method.

Download Original Figure

Ⅳ. 시뮬레이션 결과

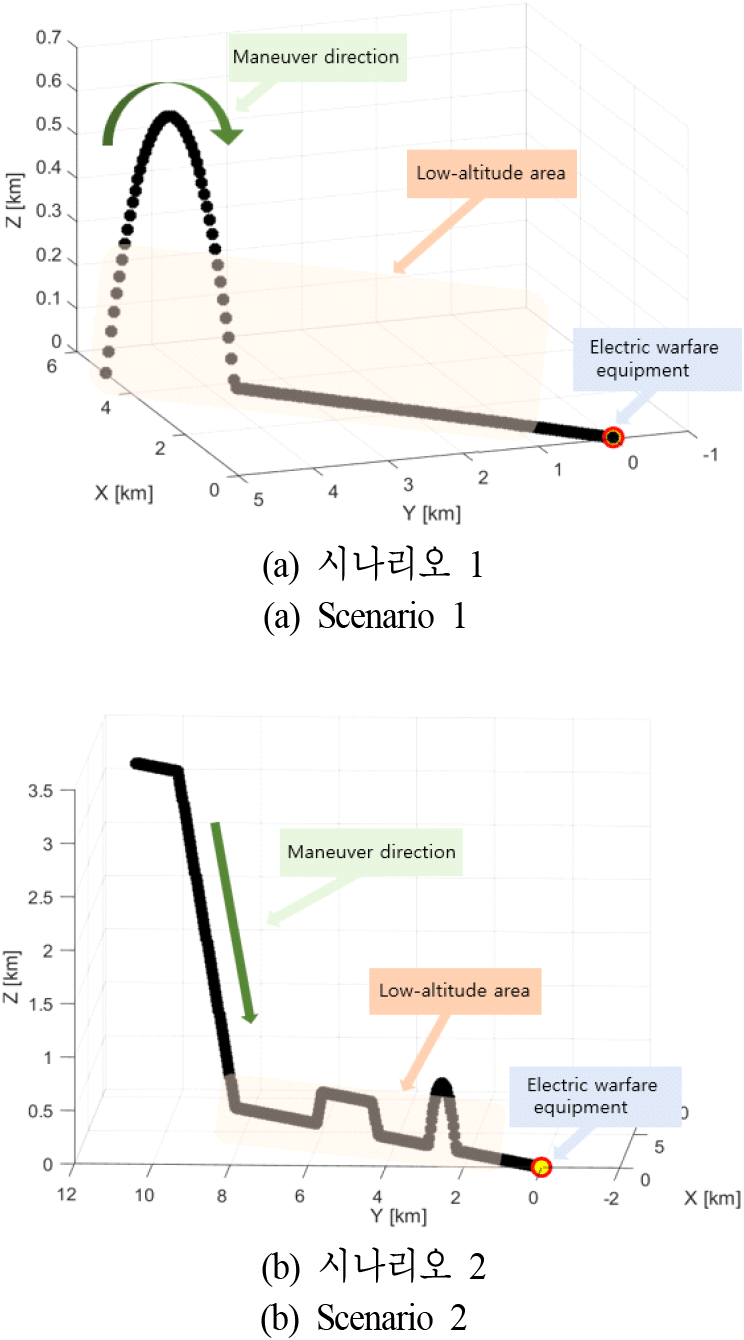
본 절에서는 비행 기동 특성에 따른 시나리오 상황들을 설정하여 제안된 기법의 직접 경로 고각 추정 정확도를 검증한다. 그림 7(a)의 시나리오 1은 지대지, 그림 7(b)의 시나리오 2는 공대지 상황에서의 미사일 궤적을 나타내며, 1초마다 표적 위치를 갱신한다. 또한 붉은 원은 전자전 장비 위치를 나타낸다. 시뮬레이션은 기존의 모노 펄스 위상 비교기법과 제안된 기법을 각 시나리오 상황에 적용하여 각도 오차를 비교한다. 전자전 장비 내 열잡음의 영향을 표현하는 SNR(signal to noise ratio)에 따라 성능 검증을 수행한다. 이를 통해, 제안된 기법이 해수면 다중 경로 간섭 및 열잡음이 존재하는 환경에서도 높은 정확도로 직접 경로 고각을 추정할 수 있음을 입증한다. 직접 경로 고각 추정 오차에 대한 정량적 평가는 RMSE (root mean square error)를 활용하며, 이는 식 (18)로 표현된다. 이때, M은 전체 비행시간, z는 이론값, $z^$ 은 측정값을 의미한다. 시뮬레이션 환경 변수는 표 2를 통해 제시된다.

RMSE = 1 M ∑ i = 1 M z i − z i^2

(18)

그림 7. | Fig. 7. 기동 시나리오에 따른 적 표적 기동 궤적 | Target trajectories according to flight scenarios.

Download Original Figure

표 2. | Table 2. 시뮬레이션 변수들 | Simulation parameters.

Parameters	Values
Carrier frequency	10 GHz
Frequency bandwidth	500 MHz
Signal duration time	0.01 s
Antenna height	3 m
Transmit power	1,000 W
Polarization	H-pol
Roughness factor	0.3
Dielectric constant	69.5633

Download Excel Table

4-1 첫 번째 시나리오 시뮬레이션 결과

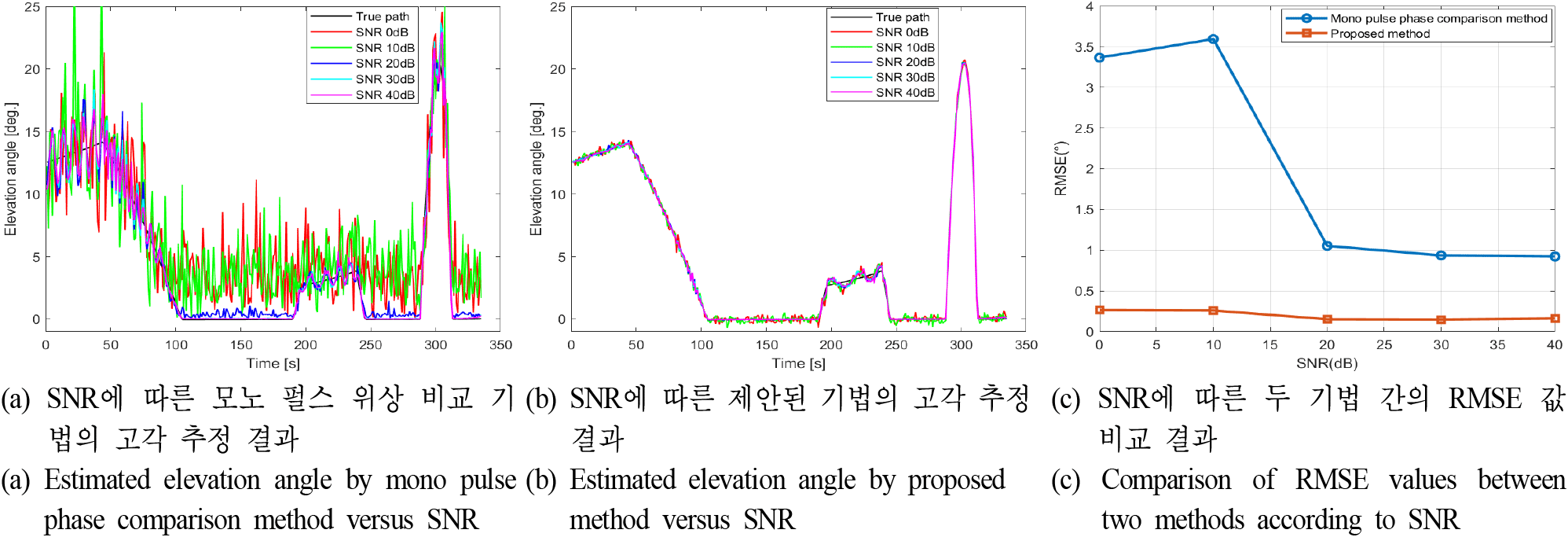
첫 번째 시뮬레이션 결과는 그림 8과 같이 나타났으며, 해수면 다중 경로 간섭 환경에서 기존 모노 펄스 위상 비교기법을 적용한 경우, 그림 8(a)와 같이 직접 경로 고각 추정 결과가 나타났다. SNR=40 dB에서 RMSE 값은 0.2907°, SNR=30 dB에서 0.2812°, SNR=20 dB에서 0.4415°, SNR=10 dB에서 3.4142°, SNR=0 dB에서 3.6348°이었다. SNR이 30 dB 이상일 경우, 직접 경로 고각 추정 오차가 크게 나타남을 확인할 수 있었다.

그림 8. | Fig. 8. 시나리오 1에서의 직접 경로 고각 추정 시뮬레이션 결과 | Simulation results of elevation angle estimation at the scenario 1.

Download Original Figure

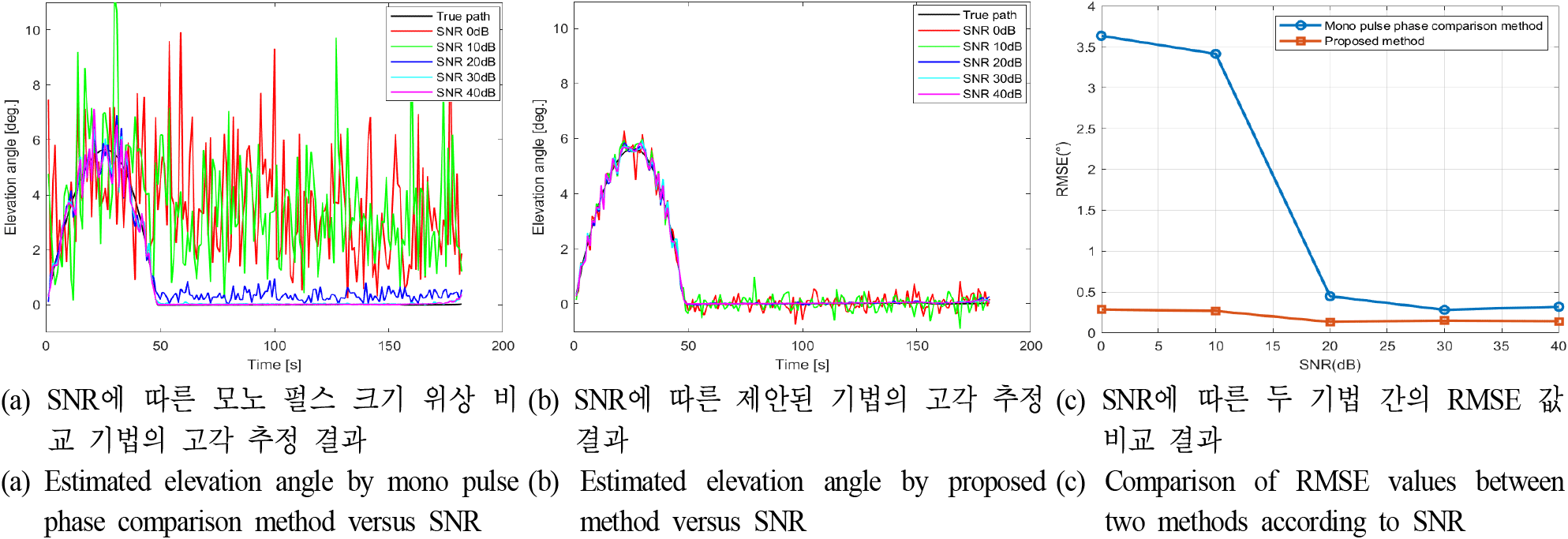
제안된 기법을 적용한 경우, 그림 8(b)와 같이 나타났으며, SNR=40 dB에서 RMSE 값은 0.1360°, SNR=30 dB에서는 0.1374°, SNR=20 dB에서는 0.1366°, SNR=10 dB에서는 0.2681°, SNR=0 dB에서는 0.2865°로 나타났다. 여기서 제안된 기법은 기존 기법과 달리 SNR의 변화에 따른 직접 경로 고각 추정 오차가 거의 변하지 않는다는 사실이 확인되었으며, 이를 통해 열잡음 환경에서도 직접 경로 고각을 강인하게 추정할 수 있음을 알 수 있었다. 또한, 시나리오 1의 전체 열잡음 환경에서 제안된 기법의 RMSE 값이 더 낮은 결과를 보임에 따라, 제안된 기법이 기존의 모노 펄스 위상 비교기법보다 직접 경로 고각 추정을 더 정확하게 수행할 수 있음을 확인하였다(그림 8(c)).

4-2 두 번째 시나리오 시뮬레이션 결과

두 번재 시나리오는 적 항공기에서 미사일을 발사하는 상황을 가정하며 시뮬레이션 결과는 그림 9와 같다. 기존 모노 펄스 위상 비교기법의 경우, SNR=40 dB에서 RM SE 값은 0.904, SNR=30 dB에서 0.9746, SNR=20 dB에서 1.0524, SNR=10 dB에서 3.5929°, SNR=0 dB에서 3.3651°로 계산된다(그림 9(a)). 반면, 제안된 기법의 경우, SNR= 40 dB에서 RMSE 값이 0.1515, SNR=30 dB에서 0.1532, SNR=20 dB에서 0.1539, SNR=10 dB에서 0.2596°, SNR=0 dB에서 0.2633°로 계산된다(그림 9(b)). 특히, 시나리오 2의 상황에서도 마찬가지로 제안된 기법의 해수면 다중 경로 간섭 영향 및 열잡음에 대한 강인성을 확인할 수 있었다. 또한 그림 9(c)를 통하여 제안된 기법이 기존 모노 펄스 위상 비교기법보다 더 정확하게 직접경로 고각 추정을 수행할 수 있음을 확인할 수 있었다.

그림 9. | Fig. 9. 시나리오 2의 시뮬레이션 결과 | Simulation results of the scenario 2.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 해수면 다중 경로 간섭 환경에서 표적의 직접 경로 고각 추정 기법을 제안하였다. 제안된 기법은 표적이 송신하는 선형 주파수 변조 신호의 주요 변수들을 PSO를 통해 추정하여 복조한 후, 새로운 푸리에 관계를 활용하여 MUSIC 알고리즘으로 직접 경로 고각을 추정한다. 특히, 기존 방식들과 달리 보다 간단한 전자전 장비 수신 시스템임에도 불구하고 해수면 다중 경로 간섭 영향 환경에서, 보다 안정적으로 직접 경로 고각 추정이 가능하였다.

Acknowledgements

이 연구는 LIG NEX1 산학협력과제 지원으로 연구되었음.

References

[1].

M. D. Skolnik, Radar Handbook, New York, NY, McGraw-Hill, 1990.

[2].

A. V. Mrstik, P. G. Smith "Multipath limitations on low-angle radar tracking," IEEE Transactions on Aerospace and Electronic Systems, vol. AES-14, no. 1, pp. 85-102, Jan. 1978.

[3].

D. Kwon, H. Ko, S. Hong, B. L. Cho, K. S. Kim, and C. H. Kim, "Research of selective exponential smoothing method for estimating low-altitude target elevation in marine multipath environment," The Journal of Korean Institute of Information Technology, vol. 20, no. 9, pp. 115-123, Sep. 2022.

[4].

D. Park, E. Yang, S. Ahn, and J. Chun, "Adaptive beamforming for low-angle target tracking under multipath interference," IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 4, pp. 2564-2577, Oct. 2014.

[5].

C. H. Lee, S. M. Chon, J. Park, H. K. Na, and S. H. Kim, "Improving the tracking accuracy of a low-altitude sea target in a multipath environment using adaptive beamforming techniques," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 32, no. 2, pp. 190-199, Feb. 2021.

[6].

S. H. Lee, I. O. Choi, M. S. Kang, and K. T. Kim, "Efficient sparse representation algorithm for accurate DOA estimation of multiple targets with single measurement vector," Microwave and Optical Technology Letters, vol. 60, no. 1, pp. 31-37, Jan. 2018.

[7].

M. Kang, J. Baek, "Efficient and accurate synthesis for array pattern shaping," Sensors, vol. 22, no. 15, p. 5537, Jul. 2022.

[8].

M. S. Kang, Y. J. Won, B. G. Lim, and K. T. Kim, "Efficient synthesis of antenna pattern using improved PSO for spaceborne SAR performance and imaging in presence of element failure," IEEE Sensors Journal, vol. 18, no. 16, pp. 6576-6587, Aug. 2018.

[9].

C. H. Lee, S. M. Chon, J. Park, H. K. Na, and S. H. Kim, "Multi-frequency monopulse direction detection method for suppression of multipath effects in low-altitude sea target tracking," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 32, no. 3, pp. 306-314, Mar. 2021.

[10].

M. A. Sebt, M. Goodarzi, and H. Darvishi, "Geometric arithmetic mean method for low altitude target elevation angle tracking," IEEE Transactions on Aerospace and Electronic Systems, vol. 59, no. 5, pp. 5111-5119, Feb. 2023.

[11].

W. Xiqin, P. Yingning, and M. Zhange, "An algorithm based on elevation geometric mean for monopulse radars to track a target at low altitude," in Proceedings of International Radar Conference, Beijing, Oct. 1996, pp. 739-742.

[12].

J. Kennedy, R. Eberhart, "Particle swarm optimization," in Proceedings of ICNN'95 - International Conference on Neural Networks, Perth, Nov.-Dec. 1995, pp. 1942-1948.

[13].

Y. Pedenko, N. Reznichenko, V. Zuykov, and S. Labazov, "The root-MUSIC method versus the amplitude sum-difference monopulse method in radar tracking of low-elevation targets over rough sea," in 2020 IEEE Ukrainian Microwave Week(UkrMW), Kharkiv, Sep. 2020, pp. 1-4.

[14].

A. Sinha, Y. Bar-Shalom, W. D. Blair, and T. Kirubarajan, "Radar measurement extraction in the presence of sea-surface multipath," IEEE Transactions on Aerospace and Electronic Systems, vol. 39, no. 2, pp. 550-567, Apr. 2003.

[15].

D. Kerr, Propagation of Short Radio Waves, New York, NY, McGraw-Hill, 1964.

Notes

김 현 동 [포항공과대학교/석사과정]

jkiees-35-8-656-i1

https://orcid.org/0009-0002-8398-3868
2023년 2월: 포항공과대학교 전자전기공학과 (공학사)
2023년 3월~현재: 포항공과대학교 전자전기공학과 석사과정
[주 관심분야] 레이다 신호 처리

최 남 우 [LIG넥스원/수석연구원]

jkiees-35-8-656-i2

https://orcid.org/0000-0001-8287-3312
2002년 2월: 명지대학교 전자공학과 (공학사)
2002년 10월~현재: LIG넥스원 수석연구원
[주 관심분야] 전자전 시스템, 신호처리, 방향탐지

김 상 수 [LIG넥스원/수석연구원]

jkiees-35-8-656-i3

https://orcid.org/0000-0002-2606-0947
2008년 2월: 성균관대학교 정보통신공학부 (공학사)
2007년 12월~현재: LIG넥스원 수석연구원
[주 관심분야] 전자전 시스템, 전자공격 기법 개발

전 성 천 [LIG넥스원/연구원]

jkiees-35-8-656-i4

https://orcid.org/0009-0000-9564-7568
2021년 8월: 충북대학교 전기공학부 (공학사)
2022년 10월~현재: LIG넥스원 연구원
[주 관심분야] 전자전 시스템, 신호처리, 방향탐지

김 경 태 [포항공과대학교/정교수]

jkiees-35-8-656-i5

https://orcid.org/0000-0003-1200-5282
1994년 2월: 포항공과대학교 전자전기공학과 (공학사)
1996년 2월: 포항공과대학교 전자전기공학과 (공학석사)
1999년 2월: 포항공과대학교 전자전기공학과 (공학박사)
2002년 3월~2011년 2월: 영남대학교 전자공학과 교수
2011년 3월~현재: 포항공과대학교 전자전기공학과 교수
2018년 1월~현재: 무인감시정찰기술연구센터장
[주 관심분야] 레이다 신호 처리 및 영상, 레이다 표적인식 및 패턴인식, 전자기수치해석 및 RCS 측정

최 인 오 [국립부경대학교/조교수]

jkiees-35-8-656-i6

http://orcid.org/0000-0002-0410-1066
2012년 8월: 부경대학교 전자정보통신공학과 (공학사)
2014년 8월: 부경대학교 전자공학과 (공학석사)
2020년 2월: 포항공과대학교 전자전기공학과 (공학박사)
2019년 12월~2021년 2월: 국방과학연구소 선임연구원
2021년 3월~2024년 2월: 국립한국해양대학교 전자전기정보공학부 전자통신공학전공 조교수
2024년 3월~현재: 국립부경대학교 정보융합대학 스마트모빌리티공학과 조교수
[주 관심분야] 이중대역 레이다자원관리, 휴먼 걸음걸이 센싱, 탄도미사일 방어시스템, 생체신호탐지, 미세도플러 분석/식별, 다중편파 SAR 영상 보정, 레이다표적식별, FMCW 차량 레이다 및 LiDAR 등