The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(6):517-520

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.6.517

단편논문/SHORT PAPERS

DPD 기반 전력증폭기 선형화 성능 평가를 위한 EVM-BER 변환

임동민^†

EVM-BER Conversion for Performance Evaluation of DPD-Based Power Amplifier Linearization

Dongmin Lim^†

경상국립대학교 전자공학과

Department of Electronic Engineering, Gyeongsang National University

^†Corresponding Author: Dongmin Lim (e-mail: dmlim@gnu.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: May 07, 2024; Revised: May 19, 2024; Accepted: May 24, 2024

Published Online: Jun 30, 2024

요 약

본 논문에서는 PAM/QAM 변조 방식에 적용 가능한 EVM-BER 변환 방안을 제시한다. 전송환경에 대한 지표로 SNR을 사용하여 변조 방식의 EVM과 BER을 분석한 후, EVM-BER 변환은 이분법을 이용하여 주어진 EVM 값에 해당하는 SNR 값을 결정하고 이 값에 대한 BER 값을 순차적으로 구하는 방식으로 수행된다. QAM 변조된 신호를 입력으로 DPD를 사용하는 전력증폭기의 출력을 측정하여 제안하는 변환 방식의 BER 예측 정확도를 기존 방식과 비교하여 검증한다.

Abstract

In this paper, we present an EVM-BER conversion method applicable to PAM/QAM modulations. Using SNR as an indicator of the transmission environment, we analyze the EVM and BER of the modulations. EVM-BER conversion is performed by determining the SNR value that corresponds to a given value of EVM using the bisection method, and then sequentially obtaining the BER value for this SNR. By measuring the output of power amplifiers equipped with a DPD using QAM-modulated signals as the input, the accuracy of the proposed conversion method in predicting the BER was verified by comparing it with the existing method.

Keywords: EVM-BER Conversion; PAM/QAM; Power Amplifiers; Digital Predistorter; Generalized Memory Polynomial

Ⅰ. 서 론

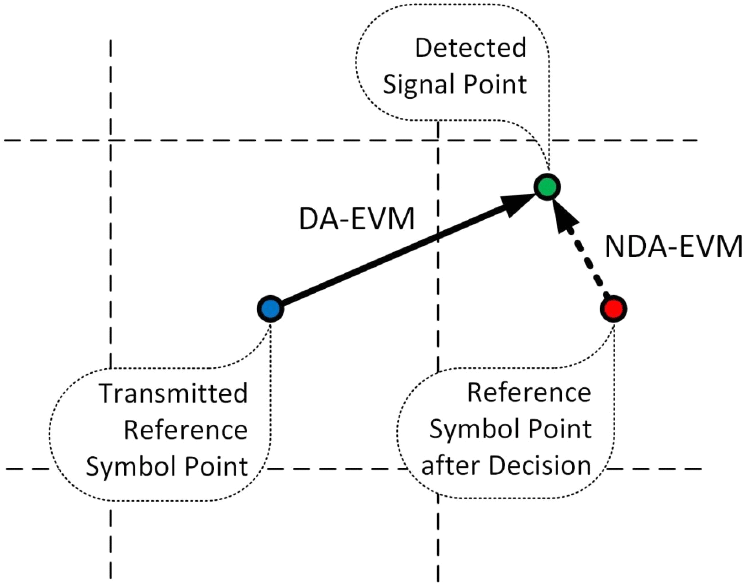
디지털 전송 시스템의 기초적인 성능 지표로 비트 에러율(BER, bit error rate), 에러 벡터 크기(EVM, error vector magnitude) 등이 널리 사용되고 있다^[1],[2]. BER은 디지털 전송의 궁극적인 성능 지표이나 실제 시스템에서의 측정은 프리앰블(preamble), 파이럿 심볼(pilot symbol) 등 전송되는 심볼값을 미리 알고 있는 경우로 한정된다. EVM은 동위상과 직교위상(IQ, in-phase and quadrature) 이득 및 위상 불일치, 국부 발진기 위상 잡음, 전력증폭기(PA, power amplifier) 비선형성, 심볼 타이밍 지터 등 시스템 불완전성으로 발생하는 전송 신호의 왜곡 현상을 종합적으로 반영한다. 전송되는 심볼값을 미리 알 수 있는 환경에서 EVM을 평가한 결과를 DA(data-aided) EVM, 일반 데이터 심볼을 대상으로 평가한 결과는 NDA(nondata-aided) EVM으로 구분하여 표시한다. DA-EVM 방식은 미리 알고 있는 전송 심볼값을 기준으로 검출된 신호값의 에러 벡터 크기를 측정하는 반면, NDA-EVM에서는 검출된 신호값에 가장 가까운 판정된 심볼값을 기준으로 에러 벡터 크기를 측정한다. 그림 1에 DA-EVM과 NDA-EVM을 비교하여 도시하였다. 본 논문에서는 일반 데이터 심볼을 이용하여 측정한 NDA-EVM 값을 BER 성능 지표로 변환하는 방안을 제시하고, 기존의 근사적인 변환 방식^[3]과 비교한다. 제안한 방안을 디지털 사전왜곡기(DPD, digital predistorter) 기반 전력증폭기 선형화의 성능 평가에 적용하여 대역내 신호 왜곡 개선 정도를 BER 기준으로 분석한다.

그림 1. | Fig. 1. DA-EVM과 NDA-EVM의 비교 | Comparison of DA-EVM and NDA-EVM.

Download Original Figure

Ⅱ. EVM-BER 변환

QAM(quadrature amplitude modulation) 변조 방식은 마이크로웨이브 근간망, Wi-Fi 등 고속 데이터 전송이 요구되는 디지털 전송 시스템에 널리 이용되고 있다. 부가 백색 정규 잡음(AWGN, additive white Gaussian noise) 채널에서 QAM 전송 환경에 대한 지표로 신호 대 잡음비(SNR, signal-to-noise ratio) γ= E_b/N₀를 사용한다. 여기서 E_b는 비트 에너지, N₀는 잡음의 전력밀도함수(PSD, power spectral density)이며, 동위상 또는 직교위상에 발생하는 잡음 전력 $σ n 2 = N 0 / 2$ 가 된다.

M-QAM 변조 방식은 서로 직교하는 반송파를 사용하는 두 개의 독립적인 $M − PAM$ 시스템으로 해석이 가능하며, 따라서 두 개의 반송파의 직교성이 유지되는 조건에서 M-QAM의 EVM과 BER 성능은 $M − PAM$ 과 동일하다^[4],[5]. 본 논문에서는 M-PAM 변조 방식에 대하여 NDA-EVM과 BER 성능을 SNR γ의 함수로 표시하고, EVM-BER 변환 방안을 제시한다. 이 결과는 M²-QAM의 EVM-BER 변환에 동일하게 사용할 수 있다.

M-PAM의 심볼 s_k (k ∈ 0, 1, … M-1)의 성상도(constellation)에서 위치를 x_k (2k − M + 1)d로 표시하고, 비트 패턴 λ_k는 BRGC(binary reflected Gray code)^[4]를 사용한다. 성상도에서 인접 심볼간의 거리는 2d이다. NDA-EVM은 검출 신호 X에 대한 에러 벡터 크기의 제곱에 대한 기댓값을 심볼 에너지로 정규화하여 다음과 같이 표시할 수 있다^[1].

EVM = 1 E s ∑ k = 0 M − 1 ∑ l = 0 M − 1 ∫ D l x − x l 2 f X | s k x d x P s k

(1)

식 (1)에서 E_s는 심볼 에너지, D_l은 심볼 s_l에 대한 ML (maximum likelihood) 기준에 의한 판정 영역(decision area)을 나타낸다. $f X | s k x$ 는 전송 심볼이 s_k인 조건에서 검출 신호 X의 조건 확률밀도함수를 나타낸다. AWGN 채널 환경에서 잡음이 정규 분포를 따르고, 분산이 $σ n 2$ 인 점을 고려하여 SNR γ에서 식 (1)을 정리하면 NDA-EVM은 식 (2)와 같이 구해진다^[4],[5].

EVM γ = 3 M 2 − 1 1 ρ γ − 4 2 π ρ γ ∑ k = 1 M − 1 1 − k M e − 2 k − 1 2 ρ γ 2 + 8 ∑ k = 1 M − 1 1 − k M 2 k − 1 Q 2 k − 1 ρ γ ρ γ = d σ n 2 = 6 log 2 M M 2 − 1 γ Q x = 1 2 π ∫ x ∞ e − x 2 / 2 d x

(2)

M-PAM의 BER은 하나의 심볼 전송에서 발생하는 비트 에러 개수에 대한 기댓값을 심볼당 비트수로 나누어 구할 수 있으며, SNR γ에서 정리하면 식 (3)과 같이 구해진다^[4],[5].

BER γ = 1 log 2 M ∑ k = 0 M − 1 ∑ l = 0 M − 1 d H λ k, λ l P s k, s l = 2 log 2 M ∑ k = 1 M − 1 δ ¯ k Q 2 k − 1 ρ γ δ ¯ k = ∑ i = 1 log 2 M 1 2 i − 1 2 log 2 M k − 1 / 2 2 i − 1 k − 1 / 2 2 i

(3)

식 (3)에서 d_H (λ_k, λ_l)는 두 비트 패턴 사이의 차이를 비트 수로 표시한 해밍 거리, P (s_k, s_l)는 전송 심볼은 s_k이고, 판정 심볼은 s_l인 확률, ⌊x⌉는 x의 반올림, ⌊x⌋는 x의 정수 부분을 표시한다.

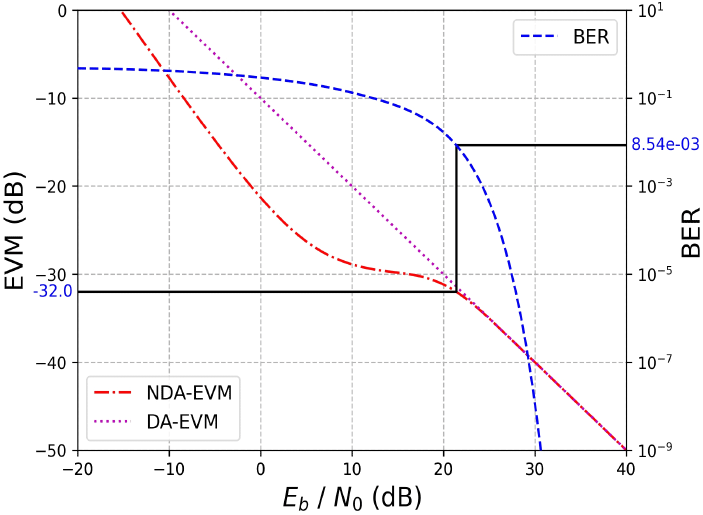
식 (2)의 EVM은 SNR γ에 대하여 연속적이며 단조 감소하는 함수이다. 따라서 중간값 정리(intermediate value theorem)에 의해 주어진 EVM 값에 대한 SNR γ 값이 하나 존재하며, 이분법(bisection method)^[6]등을 이용하여 해를 구할 수 있다. 이렇게 구한 SNR γ 값을 식 (3)에 대입하여 주어진 EVM 값에 해당하는 BER 값을 구할 수 있다. 기존의 변환 방식에서는 주어진 EVM 값을 DA-EVM으로 간주하여 SNR γ 값을 결정하고, 심볼 에러 발생 시 한 비트 에러만 발생한다고 가정하여 근사적으로 BER 값을 구하는 방식을 사용하였다^[3]. 따라서 기존 방식에서는 심볼 에러가 일정 수준 이상 발생하게 되면 BER 예측 정확도가 급격하게 떨어지는 문제점이 발생한다. 그림 2에 1024-QAM(32-PAM과 동일) 변조 방식에 대한 EVM-BER 변환 과정을 도시하였다. 예를 들어 측정된 EVM 값이 −32.0 dB인 경우, 식 (2)의 그래프에 의해 SNR γ는 21.41 dB가 되며 식 (3)의 그래프를 이용하여 BER 값 8.54×10⁻³을 구할 수 있다.

그림 2. | Fig. 2. EVM-BER 변환 절차 | EVM-BER conversion procedure.

Download Original Figure

Ⅲ. 전력증폭기 BER 성능 분석

변조된 전송 신호는 송신단의 전력증폭기 비선형성에 의해 신호 왜곡이 발생한다. 일반적으로 전송 신호의 대역폭 내에서의 신호 왜곡은 EVM으로, 대역외 스펙트럼 누설에 의한 인접 채널 간섭은 인접 채널 전력비(ACPR, adjacent channel power ratio)로 측정한다. 전력증폭기 선형화를 통한 전송 신호 품질 개선에는 다양한 방식이 사용되고 있다. 본 논문에서는 전력증폭기 입출력 신호를 측정하여 디지털 사전왜곡기(DPD)를 교차항을 포함하는 메모리 다항식(GMP, generalized memory polynomial)^[7] 모델로 학습시키는 방식을 이용한다.

실제 전력증폭기 데이터는 원격 전력증폭기 측정 시스템인 RF WebLab^[8]을 이용하여 측정한다. RF WebLab의 신호 증폭 체인은 선형 사전증폭기, 전력증폭기, 감쇠기로 구성되어 있으며, 전력증폭기의 최대 출력은 약 6 W이다. 측정 시스템은 입력 신호를 생성하고 전력증폭기 출력 신호를 측정하기 위한 벡터 신호 송수신기(VST, vector signal transceiver)와 제어용 PC로 구성되어 있다. 인터넷을 통하여 업로드된 사용자 데이터는 VST의 송신부에서 전력증폭기 입력 신호로 생성되며, 전력증폭기 출력은 VST 수신부에서 측정되어 사용자가 다운로드 받을 수 있다. RF WebLab에서는 이러한 데이터의 업로드와 다운로드를 실행하는 매트랩 파일을 제공하고 있다. VST에서 처리되는 신호의 중심주파수는 2.14 GHz, 대역폭은 160 Mz이며 (샘플링 속도 200 MHz), 입력 신호의 순간 전력은 −8 dBm, PAPR(peak-to-average power ratio)는 20 dB, 입력 신호의 샘플수는 1,000,000개로 제한된다.

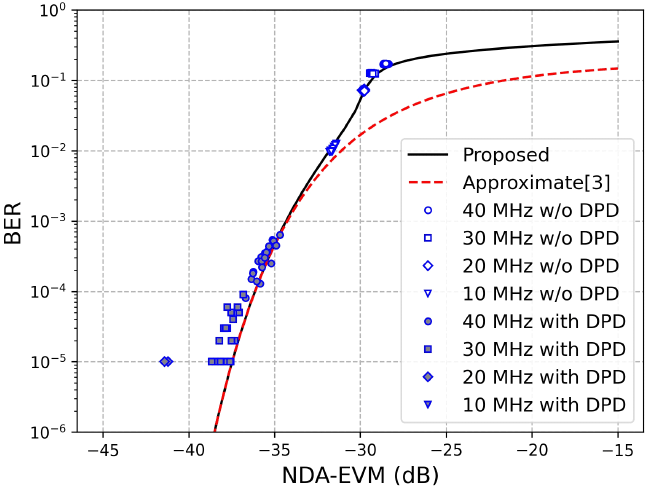
본 논문에서 전력증폭기 입력 신호는 1024-QAM 변조 방식으로 10,000개의 QAM 심볼과 rolloff factor 0.2의 square-root raised cosine 펄스를 이용하여 생성하였으며, 심볼당 샘플수를 조정하여 신호의 대역폭은 40, 30, 20, 10 MHz로 설정하였다. 측정에서 VST 입력을 −21 dBm으로 설정하였으며, 출력은 29.72 dBm으로 측정되었다. 전력증폭기 선형화에는 측정 데이터를 이용하여 DPD를 학습시킨 후, 학습된 DPD를 통과한 입력 신호에 대한 전력증폭기 출력을 다시 측정하는 방식으로 각 대역폭에 대하여 각각 20회 반복 측정하였다. 측정 데이터에서 EVM, BER 값을 구한 결과를 EVM-BER 변환 그래프와 함께 그림 3에 도시하였다. DPD를 사용하지 않은 전력증폭기에 대한 BER 측정 결과에서 제안한 EVM-BER 변환 방식의 예측 정확도가 기존의 근사적인 변환 방식^[3]과 비교하여 크게 개선됨을 확인할 수 있다. DPD를 사용하는 경우, 전력증폭기의 선형성이 개선되어 BER 값이 크게 감소하며, 낮은 BER 값으로 인하여 변동성이 증가하는 현상이 나타나고 있다. 또한 신호가 DPD와 전력증폭기를 거치면서 발생하는 왜곡 성분은 정규 분포에서 벗어날 가능성이 높아 변환 방식의 예측 정확도가 떨어질 수 있다. 각 대역폭에서 20회 측정한 BER, EVM의 평균값, EVM-BER 변환 그래프에서 BER 평균값에 해당하는 EVM 값을 구하여 EVM의 평균값과 비교한 EVM 오차를 표 1에 나타내었다. EVM 값에 대한 오차는 DPD를 사용하지 않은 경우, 최대 0.57 dB, DPD를 사용한 경우에는 최대 2.88 dB를 나타내고 있다.

그림 3. | Fig. 3. RF WebLab에서 측정한 전력증폭기의 BER 성능 | BER performance of PA measured at RF WebLab.

Download Original Figure

표 1. | Table 1. BER, EVM, EVM 오차 | BER, EVM, and EVM error.

Bandwidth/DPD	BER	EVM (dB)	EVM Error (dB)
40 MHz w/o DPD	1.71×10⁻¹	−28.55	−0.57
30 MHz w/o DPD	1.26×10⁻¹	−29.28	−0.25
20 MHz w/o DPD	7.15×10⁻²	−29.80	−0.03
10 MHz w/o DPD	1.06×10⁻²	−31.62	+0.11
40 MHz with DPD	3.08×10⁻⁴	−35.65	−0.31
30 MHz with DPD	3.00×10⁻⁵	−37.74	−0.85
20 MHz with DPD	1.00×10⁻⁶	−41.38	−2.88
10 MHz with DPD	0	−43.63	-

Download Excel Table

Ⅳ. 결 론

본 논문에서는 PAM/QAM 변조 방식에 적용 가능한 EVM-BER 변환 방안을 제시하였다. 1024-QAM 변조된 신호를 입력으로 DPD를 사용하는 전력증폭기의 출력을 측정하여 분석한 결과, 제안한 변환 방식은 심볼 에러의 발생이 빈번해지는 영역에서 기존 방식보다 우수한 BER 예측 정확도를 보여준다.

References

[1].

D. Brown, Y. Rahmat-Samii, “Error vector magnitude as a performance standard for antennas in the millimeter-wave era: Part 1: Metric comparisons and measurement concepts,” IEEE Antennas and Propagation Magazine, vol. 65, no. 5, pp. 25-34, Oct. 2023.

[2].

J. T. Son, J. T. Lim, J. E. Lee, J. H. Song, J. H. Kim, and M. S. Baek, et al., “Designing a 3.5 GHz Doherty power amplifier using GaAs HBT for 5G NR communications,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 12, pp. 873-878, Dec. 2023.

[3].

R. A. Shafik, M. Shahriar Rahman, and A. H. M. Razibul Islam, “On the extended relationships among EVM, BER and SNR as performance metrics,” in 2006 International Conference on Electrical and Computer Engineering, Dhaka, Dec. 2006, pp. 408-411.

[4].

E. Agrell, J. Lassing, E. G. Strom, and T. Ottosson, “Gray coding for multilevel constellations in Gaussian noise,” IEEE Transactions on Information Theory, vol. 53, no. 1, pp. 224-235, Jan. 2007.

[5].

H. A. Mahmoud, H. Arslan, “Error vector magnitude to SNR conversion for nondata-aided receivers,” IEEE Transactions on Wireless Communications, vol. 8, no. 5, pp. 2694-2704, May 2009.

[6].

Q. Kong, T. Siauw, and A. Bayen, Python Programming and Numerical Methods: A Guide for Engineers and Scientists, Elsevier Science, 2020.

[7].

D. R. Morgan, Z. Ma, J. Kim, M. G. Zierdt, and J. Pastalan, “A generalized memory polynomial model for digital predistortion of RF power amplifiers,” IEEE Transactions on Signal Processing, vol. 54, no. 10, pp. 3852-3860, Oct. 2006.

[8].

P. N. Landin, S. Gustafsson, C. Fager, and T. Eriksson, “WebLab: A web-based setup for PA digital predistortion and characterization [application notes],” IEEE Microwave Magazine, vol. 16, no. 1, pp. 138-140, Feb. 2015.